3. Поверхности второго порядка
Кривая при π2 ≤ ϕ ≤ 32π получится поворотом на угол π, равный периоду функции. Заданная кривая называется лемнискатой Бернулли, ее вид показан на рисунке 35.
Рис. 35
Задача 4
Построить кривую в полярной системе координат ρ =1+cos(ϕ− π4 ).
Решение
′ | π | ′ | . В новой системе | |
4 | ||||
Заменой ϕ = ϕ− | приведем уравнение к виду ρ = 1+ cos ϕ |
координат с полярной осью ϕ′ = 0 или ϕ = π4 , это уравнение кардиоиды, которая была построена в задаче 2. Вид кривой показан на рисунке 36.
Рис. 36
Определение
Поверхностью второго порядка называется множество точек, которое задается уравнением
Ax2 + By2 + Cz 2 + Dxy + Exz + Fyz + Gx + Hy + Pz + Q = 0 ,
где A, B,C, D, E, F,G, H , P,Q — заданные числа.
В некоторых случаях это уравнение определяет пару различных или совпадающих плоскостей, или одну единственную точку. Такие множества также называются поверхностью.
Если это уравнение определяет пустое множество, то есть, нет ни одной точки, координаты которой удовлетворяют этому уравнению, то говорят, что оно определяет мнимую поверхность.
42
Основными частными случаями уравнения поверхности второго порядка являются уравнения следующих поверхностей.
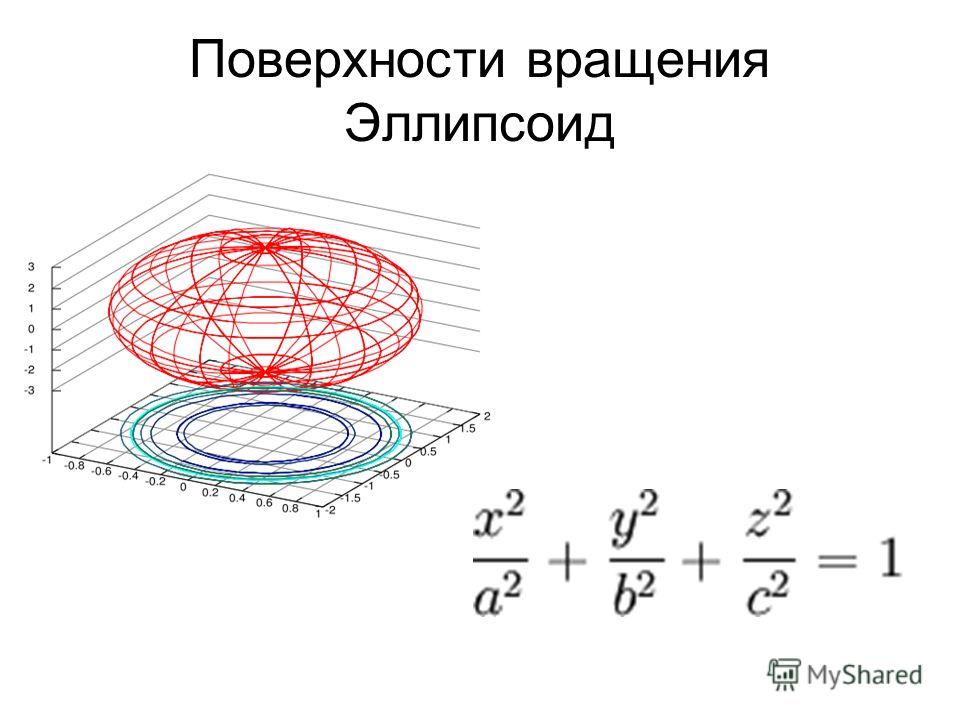
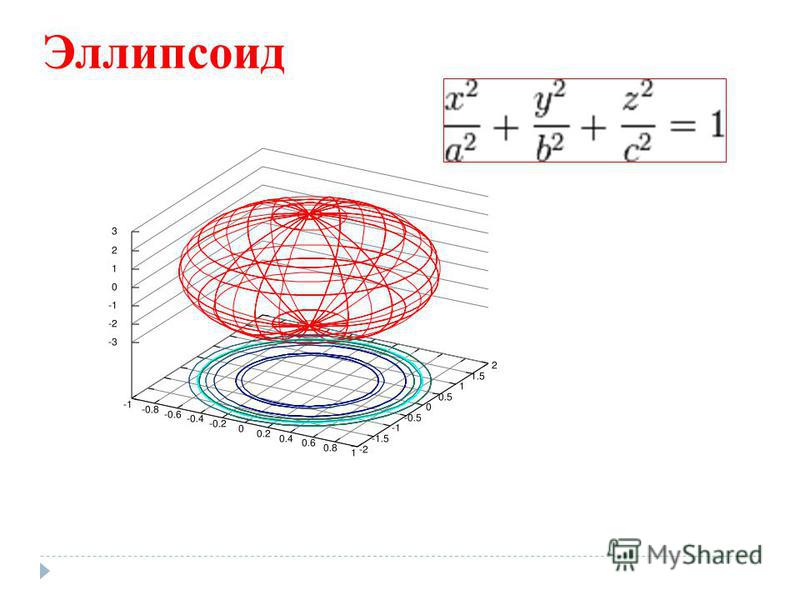
Эллипсоид
x2 | + | y2 | + | z 2 | =1 | , (a,b, c > 0) . | |
a2 | b2 | c2 | |||||
|
|
|
|
При a = b = c = 0 эллипсоид обращается в сферу радиуса a с центром в начале координат, т.
е. геометрическое место точек, отстоящих от начала координат на расстоянии a . Числа a,b,c называются полуосями эллипсоида. Если в уравнении эллипсоида заменить (одновременно или порознь) x на − x , y на − y , z на − z , то оно не изменится. Это означает, что поверхность симметрична относительно координатных плоскостей: x = 0, y = 0, z = 0 и начала координат. При x ≥ 0, y ≥ 0, z ≥ 0 часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением
z = c 1 − x2 − y2 , a2 b2
где x ≥ 0, y ≥ 0, | x2 | + | y2 | ≤1 . | |
a2 | b2 | ||||
|
|
|
|
Чтобы составить более точное представление об эллипсоиде, произведем сечения плоскостями, параллельными координатным плоскостям.
Например, пересекая
эллипсоид плоскостями z = h , (− c ≤ h ≤ c), получим в сечении эллипс
|
| x | 2 | + |
| y2 | = | 1 − | h3 | , или | x2 |
|
| + | y2 |
|
| =1 | ||||||
|
| a | 2 |
| b | 2 | c | 2 |
|
| h | 2 |
|
| h | 2 | ||||||||
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
|
|
|
|
|
|
|
| a2 1 | − |
|
|
| b2 1 | − |
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| c | 2 |
|
|
| c | 2 |
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
с полуосями a | 1 − | h3 | , | b 1 − | h3 | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
c | 2 | c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
Отсюда видно, что самый большой эллипс получается в сечении эллипсоида плоскостью | |
z = 0. | (− a ≤ h ≤ a ) и |
Аналогичная картина будет при сечении плоскостями x = hy = h , (−b ≤ h ≤ b ).
Точки (± a,0,0), (0, ± b,0) и (0,0, ± c ) лежат на эллипсоиде и называются его
вершинами.
Если какие-либо две полуоси равны между собой, то эллипсоид будет эллипсоидом вращения, т. е. получится от вращения эллипса относительно соответствующей оси координат.
Эллипсоид построен на рисунке 37.
z
c
b
x
Рис. 37.
43
Однополостный гиперболоид |
|
|
|
|
|
| |
| x2 | + | y2 | − | z2 | =1 | (a,b, c > 0) . |
| a2 | b2 | c2 | ||||
|
|
|
|
| |||
Из уравнения видно, что однополостный гиперболоид является поверхностью, симметричной относительно координатных плоскостей и начала координат.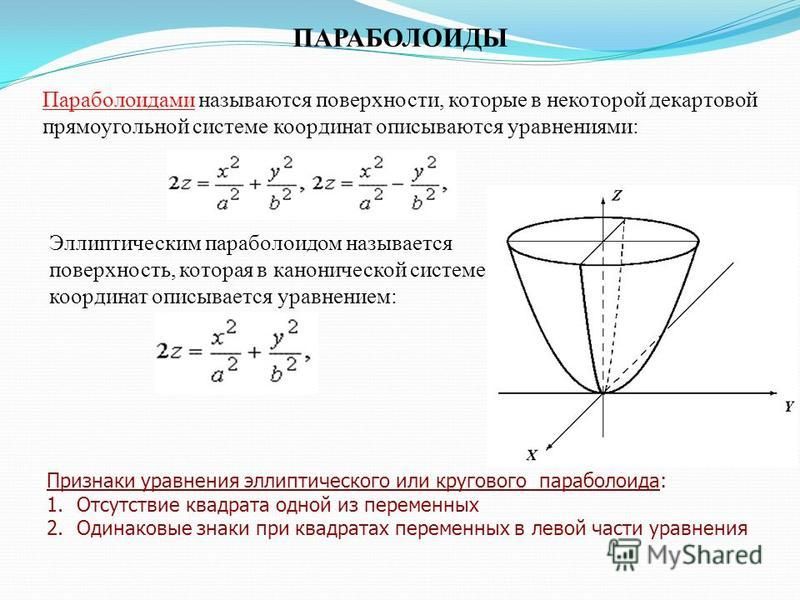
Числа a,b, c
называются полуосями однополостного гиперболоида. Точки (± a,0,0), (0, ±b,0) называются
еговершинами.
z
|
|
|
|
|
|
|
| a |
| b |
|
|
| y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
| x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Рис. |
|
|
|
|
|
| ||
В сечении поверхности плоскостью z = h получится эллипс |
|
| ||||||||||||||
|
| x2 | + | y2 | = | 1+ | h3 | , или | x2 |
| + | y2 |
| =1 | ||
|
| a2 | b2 | c2 |
| + h | 2 |
| + h | 2 | ||||||
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
| a2 1 |
|
| b2 1 |
|
| ||
|
|
|
|
|
|
|
|
|
| c | 2 |
|
| c | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
с полуосями a | 1+ | h3 | , b | 1+ | h3 | . |
|
|
|
|
|
|
|
| ||
c2 | c2 |
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
38.
В сечениях поверхности плоскостями x = ±h или y = ±h получатся гиперболы
y 2 | − | z 2 | =1− | h3 | или | x2 | − | z 2 | =1− | h3 | . | |
b2 | c 2 | a 2 | a2 | c2 | b2 | |||||||
|
|
|
|
|
|
Если h ≤ a , то действительной осью симметрии первой гиперболы является прямая,
параллельная оси Oy , а при |
| h |
| ≥ a — прямая, параллельная оси Oz . |
| |||||||||||||||
|
|
| ||||||||||||||||||
Аналогично для второй гиперболы. Если |
| h |
| ≤ b , | то действительной осью симметрии | |||||||||||||||
|
| |||||||||||||||||||
первой гиперболы является прямая, параллельная оси Ox , | а при |
| h |
| ≥ b — прямая, | |||||||||||||||
|
| |||||||||||||||||||
параллельная оси Oz . |
|
|
|
|
|
|
|
|
|
|
| |||||||||
Если a = b , то в сечении поверхности плоскостями z = ±h | будут окружности радиуса | |||||||||||||||||||
a 1+ (h3 / c2 ). | Исследуемая поверхность | в этом | случае образуется | от вращения | ||||||||||||||||
гиперболы | x2 | − |
| z2 | =1 около оси Oz . | Общий | вид однополостного | гиперболоида | ||||||||||||
a2 |
| c2 | ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
изображен на рисунке 38.
44
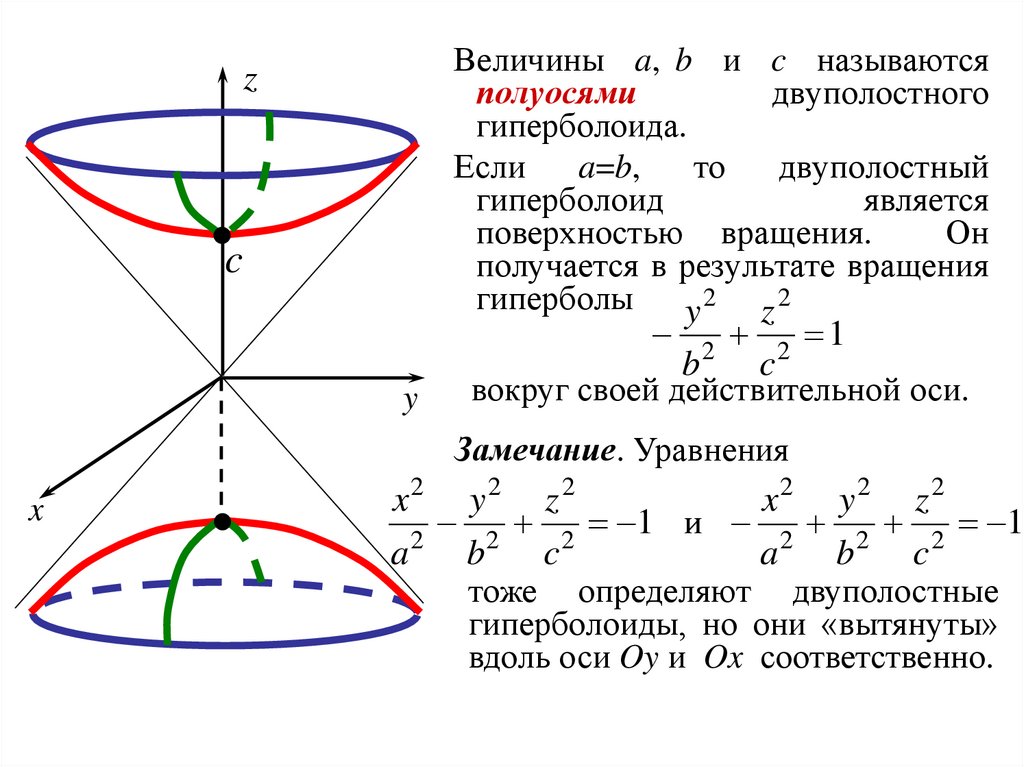
Двуполостный гиперболоид
x2 + y2 − z2 = −1, (a,b, c > 0) . a2 b2 c2
Так как уравнение содержит только квадраты переменных, то данная поверхность
симметрична | относительно координатных |
| плоскостей | x = 0, | y = 0, z = 0 и начала | ||||||||||||||||||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если записать уравнение поверхности в виде |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
|
|
| x2 | + |
| y2 | = −1+ |
| z 2 |
| , |
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
| a2 |
| b2 |
| c2 |
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
тоясно, что, пересекаяееплоскостью z = ±h , где |
|
| h |
| ≥ c , получимвсеченииэллипс | ||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
| x2 | + | y2 | = −1+ | h3 | , или |
|
|
| x2 |
|
|
| + |
|
|
| y2 |
|
| =1 | |||||||||||
|
| a2 | b2 | c2 |
|
|
|
|
|
|
| h | 2 |
|
|
|
| h | 2 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| a2 | −1 | + |
|
|
|
|
|
| b2 |
| −1 + |
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| c | 2 |
|
|
|
|
|
| c | 2 |
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
с полуосями a | (h3 / c2 )−1 и b |
| (h3 / c2 )−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
z
c O
y
−c
x
Рис. 39
При z = c в сечении получаются две точки (0,0,± c). При h < c число
(h3 / c2 )−1 < 0 , и поэтому нет точек пересечения поверхности и плоскости z = ±h . При сечении поверхности плоскостями x = ±h (y = ±h) получим гиперболы
− | y2 | + | z 2 |
| =1 + |
| h3 | и − | x2 | + | z2 | =1 + | h3 | . | ||||
b2 | c2 |
| a2 | a2 | c2 | b2 | ||||||||||||
|
|
|
|
|
|
|
|
|
| |||||||||
с вершинами на оси Oz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двуполостный гиперболоид построен на рисунке 39. |
|
|
| |||||||||||||||
Эллиптический параболоид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
| x2 |
| + | y | 2 | = 2z , ( p, q > 0) . |
|
| |||||||
|
|
|
| p2 |
| q | 2 |
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
| 45 |
|
|
|
|
|
|
Поверхности вращения, цилиндрические и канонические поверхности
Помощь в написании работы
О чем статья
Цилиндрическая поверхность
Цилиндрическая поверхность – это поверхность, которая образована прямыми, – образующими, параллельными заданной прямой и они пересекают данную кривую линию – направляющую (см.
рис. 1).
Рис. 1
В общем случае уравнение цилиндрической поверхности записывается .
В отдельных случаях, когда образующие цилиндрические поверхности параллельны одной из координатных осей, тогда у уравнения цилиндрической поверхности есть только две переменные. Причём, образующие цилиндрические поверхности параллельны той координатной оси, переменная которой в уравнении отсутствует:
– цилиндрическая поверхность с образующими ;
– цилиндрическая поверхность с образующими ;
– цилиндрическая поверхность с образующими .
Канонические поверхности
Канонические поверхности – это поверхности, которые образованы прямыми, образующими конуса, и которые проходят через данную точку – вершину конуса, – и пересекают данную кривую линию – направляющую конуса.
Допустим, – эллиптический конус (см. рис. 2), ось – ось симметрии, вершина в точке за направляющую можно взять линию – эллипс в плоскости .
Рис. 2
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов).
Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Поверхности вращения
Пусть в плоскости задана линия уравнением . Чтобы получить поверхность вращения линии вокруг, например, оси необходимо вместо переменной поставить в уравнение выражение . Уравнение описывает поверхность вращения линии вокруг оси (см. рис. 3).
Рис. 3
Поверхности второго порядка и их уравнения
Рассмотрим поверхности второго порядка и какие у них уравнения, которые считаются основными для решения задач:
1. Сфера – :
2. Эллипсоид – :
3. Однополостный гиперболоид – :
4. Двуполостный гиперболоид – :
5. Гиперболический параболоид – :
6. Конус – :
7. Эллиптический параболоид –
Примеры решения задач
Пример 1
Задача
Составить уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости и имеет уравнение , а образующие параллельны вектору .
Решение
Согласно условию задачи и тогда, по формуле у уравнения данной цилиндрической поверхности будет такой вид:
В итоге получается:
Ответ
Уравнение цилиндрической поверхности имеет такой вид:
Пример 2
Задача
Определить вид поверхности .
Решение
Необходимо данное уравнение привести к соответствующему виду:
Это уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости и образующими, параллельными оси .
Ответ
Уравнение определяет эллиптическую цилиндрическую поверхность.
Пример 3
Задача
Составить уравнение конической поверхности с вершиной в точке , и направляющей.
.
Решение
У данной конической поверхности такое уравнение:
После определённых преобразований у нас получается:
Ответ
Уравнение конической поверхности – .
Как видите, в любой задаче большую роль играют формулы, которые необходимо применять во время решения. Только тогда вы достигнете хороших результатов.
Средняя оценка 5 / 5. Количество оценок: 1
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
6366
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Помощь в написании работы
Как получить обслуживание для Surface
Чтобы получить обслуживание личного устройства Surface (не бизнес-устройства), вы можете отправить его, чтобы получить качественное обслуживание, выполняемое доверенными экспертами с использованием сертифицированных деталей.
Вы вернетесь и создадите свою лучшую работу на своем Surface.
Примечание. Если ваше устройство Surface является бизнес-устройством (принадлежит организации), обратитесь в службу поддержки Surface для бизнеса и образования.
Действия перед обращением в службу
Выберите любой заголовок ниже, и он откроется, чтобы показать дополнительную информацию:
Если вы еще не зарегистрировали свой продукт Surface, перейдите на страницу https://account.microsoft.com/devices, чтобы сделать это.
Для регистрации вам потребуется:
Учетная запись Microsoft (адрес электронной почты и пароль).
Ваша учетная запись Microsoft — это адрес электронной почты и пароль, которые вы используете для входа в Surface и службы Microsoft, такие как Outlook, OneDrive и Xbox Live.
Если у вас нет учетной записи Microsoft, вы можете получить ее бесплатно.Серийный номер обложки Surface или Surface Type Cover.
Дополнительные сведения см. в статье Поиск серийного номера на Surface.
Если у вас нет учетной записи Microsoft, вы можете получить ее бесплатно.Примечание. Неприменимо к наушникам Surface, наушникам Surface Earbuds или Surface Duo. Информацию об устранении неполадок с наушниками Surface см. в справке по наушникам Surface.
Перед отправкой Surface в сервисный центр попробуйте использовать набор средств диагностики Surface для устранения распространенных проблем с программным обеспечением. Дополнительную информацию см. в статье Устранение распространенных проблем с Surface с помощью набора средств диагностики Surface.
Если набор средств диагностики Surface не устраняет возникшую проблему, попробуйте выполнить сброс настроек Surface.
См. Восстановление или сброс настроек Surface.
Если ваш Surface не запускается или переходит в спящий режим и не просыпается, попробуйте разбудить его. См. Поверхность не включается или не выходит из спящего режима.
Если аккумулятор Surface не заряжается или у вас возникли другие проблемы с аккумулятором, см. раздел Аккумулятор Surface не заряжается или Surface не работает от аккумулятора.
Если Windows не запускается правильно при включении Surface, попробуйте устранить неполадки. См. Windows не запускается на Surface.
Если экран на Surface 4 Pro мерцает или зашифровывается, возможно, вам придется обновить его драйверы или предпринять другие шаги. См. Экран Surface Pro 4 мерцает или зашифрован.
Если эти вещи не работают, выполните поиск на этом сайте поддержки (тот, на котором вы находитесь прямо здесь) для получения информации о том, как решить конкретную проблему, или см. справку модели Surface и просмотрите темы, связанные с вашей моделью Surface.
Если вам по-прежнему не удается устранить проблему, см. раздел «Запрос на обслуживание» ниже.
Вы корпоративный клиент?
Для бизнес-клиентов предусмотрен отдельный процесс. См. справку по Surface для бизнеса.
Запрос услуги
Выберите любой заголовок ниже, и он откроется, чтобы показать дополнительную информацию:
Отправьте свой Surface
Если ни одно из предыдущих решений не решило вашу проблему, вы можете отправить свой Surface.
Если вы решите отправить его, перейдите в раздел Обслуживание и ремонт устройств и войдите в свою учетную запись Microsoft. Если ваше устройство уже зарегистрировано, выберите его и следуйте инструкциям. Если вашего устройства нет в списке, выберите Не видите свое устройство? , чтобы зарегистрировать его, затем следуйте инструкциям, чтобы получить услугу.
Благодаря этому процессу вы узнаете, находится ли ваша поверхность на гарантии или нет, и сколько она будет стоить, если применимо. В зависимости от продукта предлагаемая услуга может быть ремонтом или восстановленной заменой. После создания заказа вы получите адрес доставки, чтобы вы могли отправить его на своем устройстве. Перейдите к разделу «Часто задаваемые вопросы» для получения дополнительной информации.
Сервисные центры для личной поддержки
В некоторых странах и регионах Microsoft теперь предлагает центры обслуживания, которые предоставляют поддержку лично.
Сервисные центры предлагают расширенную поддержку, включая профессиональную проверку оборудования, устранение неполадок и восстановление системы. Если сотрудники сервисного центра не могут решить проблему, они могут помочь отправить ваше устройство в Microsoft для ремонта или замены.
Найдите участвующий в программе сервисный центр Best Buy для личной поддержки в США.
Найдите контактную информацию Surface Walk-in Center в Китае или Индии
Прежде чем отправить нам свой Surface, создайте резервную копию файлов и удалите все аксессуары. Дополнительные сведения см. в разделе Как подготовить Surface к обслуживанию. Чтобы узнать, как это сделать для Surface Duo, см. раздел Подготовка Surface Duo к обслуживанию.
Если вы отправляете свое устройство на обслуживание, вы можете проверить статус своего заказа на обслуживание по адресу https://account.microsoft.com/devices.
Когда вы получите устройство Surface из нашего сервисного центра, выполните действия, описанные в разделе Настройка устройства Surface после обслуживания. Для Surface Duo выполните действия, описанные в разделе Настройка Surface Duo после обслуживания.
Аксессуары (Типовые крышки, блок питания, адаптеры Surface) будут готовы к использованию, как только вы их подключите.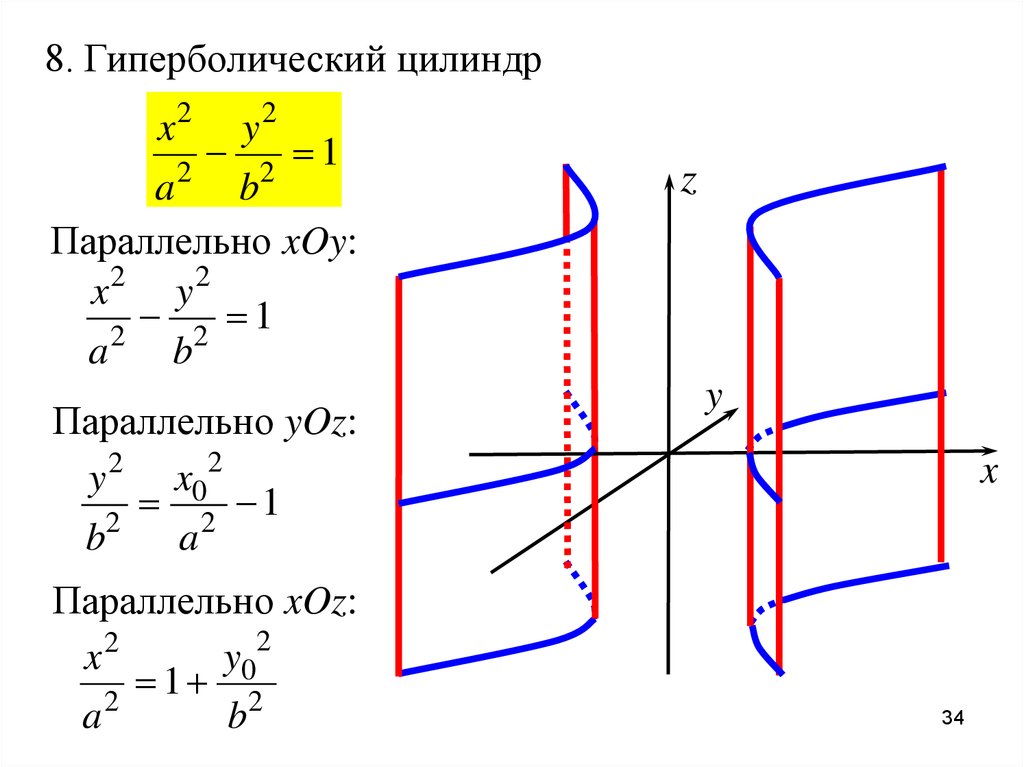
Часто задаваемые вопросы
Выберите любой заголовок ниже, и он откроется, чтобы показать дополнительную информацию.
В процессе онлайн-запроса на обслуживание мы сообщим вам, находится ли ваша поверхность на гарантии. Если гарантийный срок истек, вам может потребоваться оплатить сервисный сбор.
Если вы приобрели Microsoft Complete (не применимо к наушникам Surface), вы можете использовать одну из двух претензий о случайном повреждении для замены Surface. Единственная стоимость — это вычитаемая сумма по иску.
Устройства Surface, кроме Surface Duo
Страна | Валюта | Стоимость |
|---|---|---|
Австралия | австралийских долларов | 54 |
Австрия | евро | 49 |
Бельгия | евро | 49 |
Канада | канадских долларов | 49 |
Китай | юаня | 329 |
Дания | датских крон | 460 |
Франция | евро | 49 |
Германия | евро | 49 |
Ирландия | евро | 49 |
Италия | евро | 49 |
Япония | иен | 5400 |
Нидерланды | евро | 49 |
Новая Зеландия | новозеландских доллара | 59 |
Норвегия | норвежских крон | 399 |
Польша | злотых | 179 |
Португалия | евро | 49 |
Испания | евро | 49 |
Швейцария | евро | 49 |
США | долларов США | 49 |
Поверхностный дуэт
Страна | Валюта | Стоимость |
|---|---|---|
Канада | канадских долларов | 136 |
Франция | евро | 90 |
Германия | евро | 90 |
Япония | иен | 10800 |
Соединенное Королевство | фунта стерлингов | 81 |
США | долларов США | 99 |
Если у вас нет Microsoft Complete, стоимость зависит от того, какой у вас Surface.
См. Сколько стоит негарантийное обслуживание вашего устройства Surface?
Как правило, возврат устройства Surface после его отправки нам занимает от 3 до 12 рабочих дней, в зависимости от того, где вы живете, и при условии отсутствия каких-либо задержек с запасами или доставкой. Для Surface Studio агент поможет вам, и он может быть отправлен вам обратно быстрее.
Подлинные восстановленные продукты Microsoft были проверены, протестированы, очищены и восстановлены с использованием оригинальных деталей Microsoft. Каждый продукт проходит строгий процесс сертификации качества. Подлинные восстановленные продукты Microsoft помогают сократить количество отходов, что способствует достижению наших целей в области устойчивого развития. Узнайте больше о приверженности Майкрософт принципам устойчивого развития.
Восстановленный продукт, который вы получите, не будет включать такие аксессуары, как блок питания. Пожалуйста, не включайте какие-либо аксессуары при отправке неработающего продукта, если это не указано в инструкции, поскольку они могут быть вам не возвращены.
Если иное не предусмотрено обязательным положением вашего местного законодательства, на Восстановленный подлинный продукт Microsoft предоставляется гарантия в течение 90 дней или на оставшийся срок первоначальной гарантии (или плана защиты), в зависимости от того, какой из этих периодов дольше.
Microsoft предлагает негарантийное обслуживание в течение как минимум 3 лет после окончания производства.
Microsoft предлагает обслуживание в течение как минимум 3 лет с даты продажи. Сначала на него может распространяться ваша ограниченная гарантия или, если вы ее приобрели, дополнительный план защиты. После этого Microsoft предлагает послегарантийное обслуживание за отдельную плату.
Похожие темы
Вход в систему и выход из нее
Гарантия на поверхность: часто задаваемые вопросы
Информация о гарантии на поверхность
Настройте Surface после обслуживания
Информация о Центре самообслуживания (для Китая и Индии)
org/ListItem»>Как подготовить Surface к обслуживанию
org/ListItem»>Получите личную поддержку в США
Урок 11: Методы и схемы поверхности отклика
Давайте рассмотрим ситуацию первого порядка — метод наискорейшего подъема. Теперь помните, во-первых, мы не знаем, существует ли вообще «холм», поэтому мы начнем с того места, где, по нашему мнению, существует оптимум. Мы начинаем с натуральных единиц и используем закодированные единицы для проведения нашего эксперимента. Рассмотрим пример 11.1 в учебнике. Мы хотим начать в области, где \(x_{1} = \) время реакции (30-40 секунд) и \(x_{2} = \) температура (150-160 градусов), и мы хотим посмотреть на выход процесса в зависимости от этих факторов. В некотором смысле, с целью иллюстрации этой концепции, мы можем наложить эту область экспериментов на наш участок нашего неизвестного «холма». Очевидно, что мы проводим эксперимент в его натуральных единицах, но планы будут указаны в закодированных единицах, чтобы мы могли применить их к любой ситуации.
92\) дизайн и пять центральных точек. Теперь мы подгоняем эту модель первого порядка и исследуем ее.
Вводим фактические данные для A и B и измерения отклика Y.
Сначала подгоняем полную модель: См. Ex-11-1-output.doc
Подгоняем поверхность. Модель имеет два основных эффекта: один член перекрестного произведения, а затем один дополнительный параметр в виде среднего значения для центральной точки. Остатки в этом случае имеют четыре \(df\) , которые происходят от повторения центральных точек . Так как центральных точек пять, т. е. четыре \(df\) среди пяти центральных точек. Это мера чистой ошибки.
Начнем с проверки кривизны. Вопрос заключается в том, отличается ли среднее значение центральных точек от значений при \(x_{1},x_{2} = (0,0)\), предсказанных на основе модели отклика скрининга (основные эффекты плюс взаимодействие). Мы проверяем, находятся ли средние значения точек в центре на плоскости, соответствующей четырем угловым точкам.
Если бы p-значение было небольшим, это могло бы сказать вам, что среднее значение центральных точек находится выше или ниже плоскости, указывающей на кривизну поверхности отклика. Тот факт, что в данном случае он не имеет значения, указывает на отсутствие кривизны. Действительно, центральные точки ложатся точно на плоскость, соответствующую четвертным точкам.
В этом тесте есть только одна степень свободы, потому что в проекте есть только одно дополнительное место с точки зрения разрешения x .
Далее мы проверяем значительное влияние факторов. Из дисперсионного анализа мы видим, что взаимодействия нет. Итак, давайте переделаем эту модель без члена взаимодействия, оставив только члены A и B. У нас все еще есть среднее значение центральных точек, и наш AOV теперь показывает \(5\df\) для остаточной ошибки. Одним из них является несоответствие аддитивной модели, и, как и прежде, есть \(4\df\) чистой ошибки. У нас есть \(1\ df\) для кривизны, и несоответствие в этом случае — это просто взаимодействия из модели.
Что нам с этим делать? См. анализ Minitab и повторите эти результаты в EX11-1.mpx | Ex11-1.csv
Наша оценочная модель: \(\hat{y} = 40,34 + 0,775x_{1} + 0,325x_{2}\)
Таким образом, для любых \(x_{1}\) и \(x_{2}\) мы можем предсказать \(y\). Это соответствует плоской поверхности и говорит нам, что предсказанное \(y\) является функцией \(x_{1}\) и \(x_{2}\), а коэффициенты являются градиентом этой функции. В настоящее время мы работаем с закодированными переменными, поэтому эти коэффициенты безразмерны.
Если мы переместимся на 0,775 в направлении \(x_{1}\), а затем на 0,325 в направлении \(x_{2}\), это будет направление наискорейшего подъема. Все, что мы знаем, это то, что эта плоская поверхность является одной стороной «холма».
Метод наискорейшего подъема предлагает нам провести эксперимент первого порядка и найти направление, в котором «холм» идет вверх, и начать движение вверх по холму, выполняя дополнительные измерения в каждом \((x_{1}, x_{2}) \) до тех пор, пока отклик не начнет уменьшаться.
Если мы начнем с 0 в закодированных единицах, то сможем провести серию одиночных экспериментов на этом пути вверх по «холму» самого крутого спуска. Если мы сделаем это с размером шага \(x_{1} = 1\), то:
\(1\ /\ 0,775 = x_{2}\ /\ 0,325 \rightarrow x_{2} = 0,325\ /\ 0,775 = 0,42 \)
и, таким образом, размер нашего шага \(x_{1} = 1 \) определяет, что \(x_{2} = 0,42\), чтобы двигаться в направлении, определяемом как самый крутой подъем. Если мы сделаем шаги 1 в кодированных единицах, это будет пять минут с точки зрения единиц времени. И для каждого шага на этом пути мы поднимались бы на 0,42 закодированных единицы в \(x_{2}\) или примерно на 2 градуса по шкале температур.
| Этапы | Кодированные переменные | Естественные переменные | Общее лечение | ||
|---|---|---|---|---|---|
| \(x_1\) | \(x_1\) | \(\xi_1\) | \(\xi_1\) | г | |
| Происхождение | 0 | 0 | 35 | 155 | |
| \(\Дельта\) | 1,00 | 0,42 | 5 | 2 | |
| Начало + \(\Дельта\) | 1,00 | 0,42 | 40 | 157 | 41,0 |
| Начало + \(2 \Дельта\) | 2,00 | 0,84 | 45 | 159 | 42,9 |
| Начало + \(3 \Дельта\) | 3,00 | 1,26 | 50 | 161 | 47,1 |
| Начало + \(4 \Дельта\) | 4,00 | 1,68 | 55 | 163 | 49,7 |
| Начало + \(5 \Дельта\) | 5,00 | 2.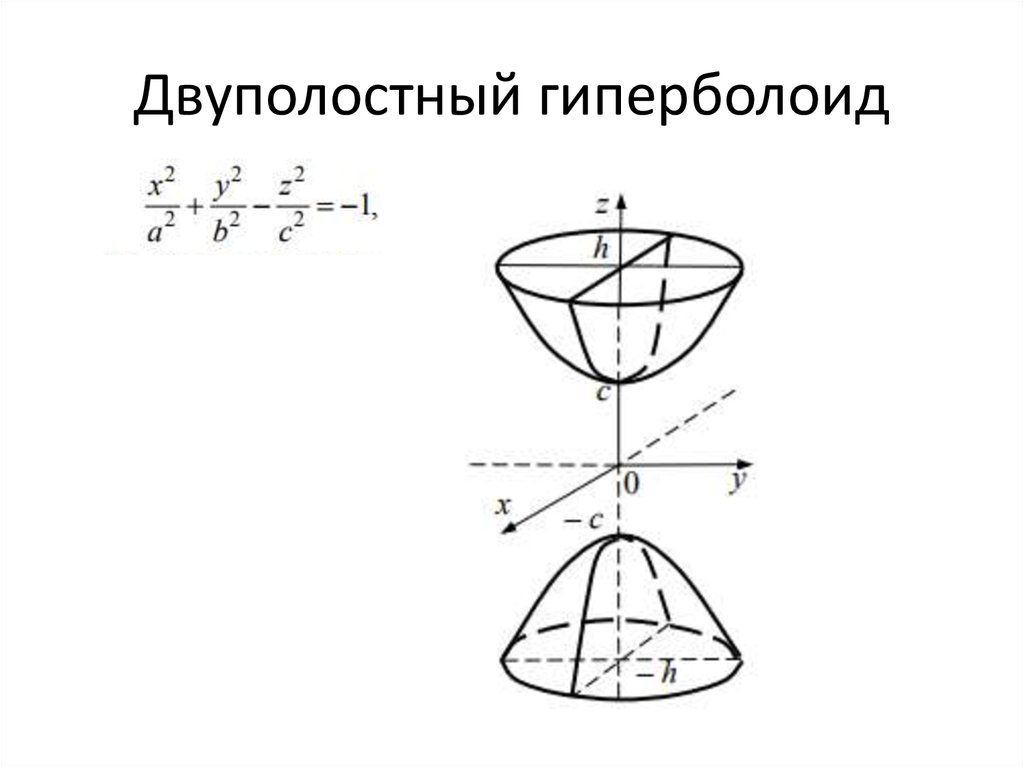 10 | 60 | 165 | 53,8 |
| Начало + \(6 \Дельта\) | 6,00 | 2,52 | 65 | 167 | 59,9 |
| Начало + \(7 \Дельта\) | 7,00 | 2,94 | 70 | 169 | 65,0 |
| Начало + \(8 \Дельта\) | 8,00 | 3,36 | 75 | 171 | 70,4 |
| Начало + \(9 \Дельта\) | 9,00 | 3,78 | 80 | 173 | 77,6 |
| Начало + \(10 \Дельта\) | 10.00 | 4,20 | 85 | 175 | 80,3 |
| Начало + \(11 \Дельта\) | 11.00 | 4,62 | 90 | 179 | 76,2 |
| Начало + \(12 \Дельта\) | 12.00 | 5,04 | 95 | 181 | 75,1 |
| Таблица 11-3 Эксперимент с самым крутым подъемом для примера 11-1 | |||||
Вот ряд шагов в дополнительных мерах пяти минут и 2º температуры.
Отклик нанесен на график и показывает увеличение, которое падает к концу.
Это довольно плавная кривая, и в действительности, вам, вероятно, следует пройти немного дальше пика, чтобы убедиться, что вы находитесь на пике. Но все, что вы пытаетесь сделать, это приблизительно выяснить, где находится вершина «холма». Если ваш первый эксперимент оказался не совсем правильным, возможно, вы пошли не в том направлении!
Возможно, вы захотите провести еще один эксперимент первого порядка, чтобы убедиться. Или вы можете провести эксперимент второго порядка, предполагая, что вы близки к вершине. Это то, что мы обсудим в следующем разделе. Эксперимент второго порядка поможет найти более точное положение пика.
Дело в том, что это довольно дешевый способ «обследовать гору», чтобы попытаться найти оптимальные условия.
Помните, что этот пример показан в двух измерениях, но вы можете работать в трех- или четырехмерном пространстве! Вы можете использовать тот же метод, подобрав модель первого порядка, а затем двигаясь вверх по поверхности отклика на k пространственных измерений, пока вы не подумаете, что находитесь близко к оптимальным условиям.
Если вы находитесь в более чем 2-х измерениях, вы не сможете получить хороший сюжет. Но это нормально. Метод наискорейшего подъема подскажет, где провести новые измерения, и вы узнаете отклик в этих точках. Вы можете продвинуться на несколько шагов и увидеть, что реакция продолжает расти или, возможно, нет, — тогда вы можете провести еще один эксперимент первого порядка и перенаправить свои усилия. Дело в том, что когда мы проводим эксперимент для модели второго порядка, мы надеемся, что оптимум будет в диапазоне эксперимента, а если нет, то мы экстраполируем, чтобы найти оптимум. В этом случае безопаснее всего провести еще один эксперимент вокруг этого предполагаемого оптимума.