Правила математика проценты: Как решать задачи с процентами? Примеры решений задач

правила нахождения процентов от числа и нахождение процентного выражения числа от другого

Деньги

Кредит онлайн

Кредитный рейтинг

Подбор кредитной карты

Потребительские кредиты

Автокредиты

Кредитные карты

Ипотека

Ипотека в новостройках

Вклады

Куда вложить деньги

Дебетовые карты

Брокерское обслуживание

Банкротство

Курсы обмена валют

Рейтинг банков

Список банков

Отзывы о банках

Займы

Займы онлайн

Займы на карту

Займы без отказа

Займы с плохой КИ

Займы без процентов

Лучшие займы

Займы под залог ПТС

Займы через Госуслуги

Займы до зарплаты

Долгосрочные займы

Рейтинг МФО

Список МФО

Отзывы об МФО

Страхование

ОСАГО

Каско

Страхование ипотеки

Страхование путешественников

Страхование квартиры

Страхование спортсменов

Добровольное медицинское страхование

От критических заболеваний

Страхование от укуса клеща

Страхование дома и дачи

Проверка КБМ

Рейтинг страховых компаний

Список страховых компаний

Отзывы о страховых компаниях

Статьи о страховании

Для бизнеса

Сервис регистрации самозанятых

Расчетно-кассовое обслуживание

Кредиты

Банковские гарантии

Эквайринг

Вклады

Регистрация бизнеса

Бухгалтерские услуги

Бизнес на маркетплейс

Лизинг

Внесение изменений в ИП и ООО

Ликвидация ИП

Рейтинг банков для бизнеса

Статьи о бизнесе

Отзывы о банках

Образование

Программирование

Дизайн

Управление

Аналитика

Маркетинг

Подготовка к ЕГЭ и ОГЭ

Разработка на Python

1С-программирование

QA-тестирование

Графический дизайн

Веб-дизайн

Английский язык

Рейтинг курсов

Отзывы о курсах

Статьи о курсах

Журнал

Главное

Спецпроекты

Тесты и игры

Вопросы и ответы

Блоги компаний

Рейтинг экспертов

Карты

Вклады

Кредиты

Инвестиции

Недвижимость

Страхование

Советы

Одним из базовых понятий математики является процент. Для того чтобы понять, что такое процент, достаточно разделить заданную целую величину на сто. Одна сотая часть будет одним процентом (обозначается 1%). Как в точных и экономических науках, так и в других сферах жизни проценты используются для обозначения долей по отношению к целому. При этом само целое обозначается как 100%. В некоторых случаях используется при сравнении двух величин: например, иногда стоимость товаров не сравнивается в денежных единицах, а оценивается, на сколько % цена одного товара больше или меньше цены другого. Термин также получил широкое распространение в банковском деле и в большинстве случаев используется в качестве синонима словосочетания «процентная ставка».

Третьим базовым типом математических задач на процентные вычисления являются такие задания, в которых необходимо использовать правило нахождения процентного выражения числа от другого (или соотношения двух величин). Оно гласит о том, что для решения необходимо второе число разделить на первое, после чего полученный результат умножить на сто. Подобное соотношение показывает, сколько % одно числовое значение составляет от другого (то есть, фактически речь идёт об отношении между двумя числовыми значениями, выраженном в %).

Лучшие предложения дня

Сравни.ру

Энциклопедия

Банки

Словарь

Что такое процент?

Текстовые задачи на проценты — что это, определение и ответ

Для быстрого и верного решения задач на проценты нужно понимание сути процента, умение считать проценты и внимательно читать условие.

С процентами нам постоянно приходится сталкиваться в повседневной жизни. «Скидка 30%», «Кредит без процентов за 5 минут», «Арендная плата выросла на 12%» — со всех сторон на нас сыплются рекламные слоганы и призывы. Но что же значит слово «проценты»? И как ими оперировать?

Проценты являются удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываются на них.

Что такое процент?

Процент – это всегда доля какого-то числа.

100% — все число

50% — половина

25% — четверть

Чтобы найти 1%, необходимо поделить всё число на 100.

Один процент – одна сотая доля.

Нахождение процента через деление на 100:

1. Делим изначальное число на 100 (таким образом получаем величину 1 процента от числа).

2. Умножаем на нужное нам количество процентов.

Например, чтобы найти 25% от 200, нужно:

1. Сначала найти, сколько составляет 1% от 200:

\(200:100 = 2\)

2.Умножить полученное значение на нужное нам количество процентов, то есть на 25:

\(2 \cdot 25 = 50\)

Нахождение процента через умножение на десятичную дробь:

Принцип действия тот же, однако 2 действия объединяем в одно – умножаем исходное число сразу на дробь.

1. Превращаем процент в дробь (отсчитываем 2 символа справа и ставим запятую), например:

\(115\% = 1,15\)

\(82\% = 0,82\)

\(7\% = 0,07\)

\(25\% = 0,25\)

2. Умножаем число на полученную дробь:

25% от \(200 = 200 \cdot 0,25 = 50\)

Нахождение процента упрощённым способом «по кубикам»

Пользуясь правилом перевода процента в десятичную дробь, а затем – правилом перевода десятичной дроби в обыкновенную, можем вывести стандартные соотношения:

\(1\% = \frac{1}{100}\)

\(\ 10\% = \frac{1}{10}\)

\(\ 20\% = \frac{1}{5}\)

\(\ 25\% = \frac{1}{4}\)

\(\ 50\% = \frac{1}{2}\)

\(\ 75\%\ = \frac{3}{4}\)

Тогда работу с дробями мы можем заменить простым умножением или делением.

Например, чтобы найти 25% от 200, можно 200 поделить на 4 и получить 50.

Итак, пользуясь методом кубиков всегда можно найти 50%, 25%, а также 1%,10% и 20%. Например:

Для вычисления 1% нужно поставить запятую после второго символа, а для нахождения 10% поставить запятую после первого символа.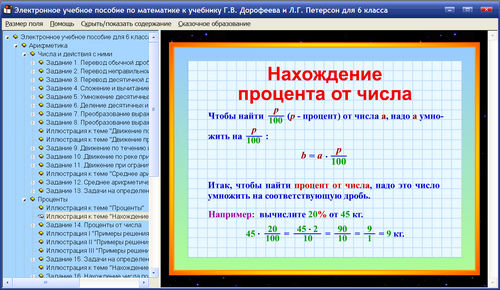

Далее, чтобы получить иной процент, нужно умножить полученное значение на нужное количество процентов. Например:

Как работать с процентами в текстовых задачах?

Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом – соответствующие проценты.

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно.

Например, если известно, что всего на прилавке имеется 200 груш, и нужно найти, сколько груш составляет 1%.

Составляем пропорцию:

200 груш – 100 %

x груш – 1 %

Пользуемся правилом произведения накрест лежащих значений:

\(200 \cdot 1 = x \cdot 100\)

Выражаем искомую величину:

\(x = \frac{200 \cdot 1}{100} = 2\)

Получаем готовое соотношение:

200 груш – 100 %

2 груши – 1 %

Итак, 1% от всего количества составляет 2 груши.

Или другая задача: известно, что 20% от всего количества составляет 40 груш. Сколько всего груш на прилавке?

Составляем пропорцию:

x груш – 100 %

40 груш – 20 %

Пользуемся правилом произведения накрест лежащих значений:

\(x \cdot 20 = 40 \cdot 100\)

Выражаем искомую величину:

\(x = \frac{40 \cdot 100}{20} = 200\)

Получаем готовое соотношение:

200 груш – 100 %

40 груш – 20 %

Итак, 100% — это 200 груш.

Видим, что пропорция отражает зависимость величин, по-другому это можно записать в виде двух дробей:

\(\frac{200}{2} = \frac{100}{1}\) или \(\frac{200}{40} = \frac{100}{20}\)

Процент — Формула | Как рассчитать процент?

Термин «процент» был адаптирован от латинского слова «percentum», что означает «на сто». Проценты — это дроби со 100 в знаменателе. Другими словами, это отношение между частью и целым, при котором значение «целого» всегда принимается равным 100.

Например, если оценки учащегося по математике равны 15 из 50, то можно рассчитать соответствующий процент путем выражения «полученных оценок» в виде доли от «общего количества оценок» и умножения результата на 100, т. Е. Процент оценок = 15 / 50 × 100 = 30%. Узнайте больше о процентах и ​​о том, как преобразовать их в дроби и десятичные числа.

1.	Что такое процент?
2.	Расчет процентов
3.	Формула процентов
4.	Преобразование между процентами и десятичными дробями
5.	Процентное изменение между двумя числами
6.	Часто задаваемые вопросы о процентах

Что такое процент?

Процент — это дробь или отношение, в котором значение целого (знаменатель) всегда равно 100. Например, если Сэм набрал 30% баллов за контрольную по математике, это означает, что он набрал 30 баллов из 100. , Это записывается как 30/100 в виде дроби и 30:100 в виде соотношения. Здесь «%» является символом процента и читается как «процент» или «процент». Этот символ процента всегда можно заменить на «делится на 100», чтобы преобразовать его в дробь или десятичный эквивалент.

Примеры процентов

• 10% = 10/100 (= 1/10 (или) 0,1)
• 25% = 25/100 (= 1/4 (или) 0,25)
• 12,5% = 12,5/100 (= 1/8 (или) 0,125)
• 50% = 50/100 (= 1/2 (или) 0,5)

Расчет процентов

Вычисление процентов означает нахождение доли от целого в пересчете на 100. Существует два способа вычисления процентов:

• Путем изменения знаменателя дроби на 100 : В этом методе мы просто находим эквивалентную дробь данной дроби так, чтобы результирующий знаменатель был равен 100. Тогда сам числитель является процентом. Например:
  4/25 = 4/25 × 4/4 = 16/100 = 16%
• Используя унитарный метод: В этом методе мы просто умножаем дробь на 100, чтобы получить процент. Например, процент, соответствующий дроби 4/25, равен:
  . 4/25 × 100 = 400/25 = 16%

Следует отметить, что первый метод расчета процента не предлагается в ситуациях, когда знаменатель не является множителем 100. В таких случаях мы используем унитарный метод. Давайте посмотрим, как найти процент, используя два подробно описанных выше метода.

Нахождение процента, когда общее значение равно 100

Когда у нас есть два или более значений, которые в сумме дают 100, процент этих отдельных значений от общего значения и есть само это число. Например, Салли купила для своего дома плитку трех разных цветов. Детали покупки приведены в следующей таблице.

Цвет	Количество плиток	Ставка за сотню	Фракция	Процент	Читать как
Желтый	39	39	39/100	39%	39 процентов
Зеленый	26	26	26/100	26%	26 процентов
Красный	35	35	35/100	35%	35 процентов

Нахождение процента, когда общее количество НЕ равно 100

Поскольку общее количество элементов равно 100, проценты можно легко вычислить, как показано выше. Что делать, если общее количество элементов не равно 100? Покажи нам.

Например, у Эммы есть браслет, состоящий из 8 красных и 12 синих бусин. Здесь общее количество бусин 8 + 12 = 20 (что не равно 100). В этом случае проценты можно рассчитать, как показано в таблице ниже (используя унитарный метод).

Но здесь проценты можно рассчитать, сделав знаменатель равным 100. Тогда получаем

• Процентное соотношение красных бусин = 8/20 × 5/5 = 40/100 = 40%
• Процент синих бусин = 12/20 × 5/5 = 60/100 = 60%

Посмотрите на следующий пример, который показывает преимущество унитарного метода над другим методом.

Пример: Как рассчитать процент отметок учащегося, набравшего 35 баллов из 40 по математике?

Решение: Здесь оценки студента 35/40. Но здесь знаменатель не является множителем 100. Таким образом, нахождение процента в унитарном методе здесь полезно.

Процент баллов = 35/40 × 100 = 87,5%.

Формула процентов

Процентная формула используется для нахождения доли целого в виде 100. Используя эту формулу, вы можете представить число как дробь от 100. Если вы внимательно наблюдаете, все три способа получения процентной доли, показанные выше, могут быть легко вычисляется по приведенной ниже формуле:

Процент = (Значение/Общее значение)×100

Пример: В классе из 40 детей 10 девочек. Тогда каков процент девушек?

Решение: Здесь количество девочек = 10.

Общее количество детей = 40.

По формуле процентов,

процент девочек = 10/40 × 100 = 25%.

Преобразование между процентами и десятичными дробями

Как мы уже видели, символ % всегда можно заменить на «/100». При преобразовании процентов в десятичные дроби и наоборот следует учитывать следующие моменты.

• чтобы преобразовать проценты в десятичные дроби, просто замените % на «делится на 100». Например, 40% = 40/100 = 0,4.
• , чтобы преобразовать десятичные дроби в проценты, просто умножьте на 100. Например, 0,4 = 0,4 × 100 = 40%.

Процентное изменение между двумя числами

Процентное изменение — это изменение значения количества за определенный период времени в процентах. Например, увеличение населения, уменьшение бедности и так далее. У нас есть формула, показывающая изменение количества в процентах. Есть два случая, которые могут возникнуть при расчете процентного изменения, а именно:

• Расчет процентного увеличения
• Рассчитать процентное уменьшение

Процентное увеличение

Процентное увеличение относится к процентному изменению значения при его увеличении за определенный период времени. Например, увеличение популяции, увеличение количества бактерий на поверхности и т. д. Увеличение в процентах можно рассчитать по следующей формуле:

Увеличение в процентах = (Увеличенное значение — Исходное значение)/Исходное значение × 100

Пример: Стоимость куртки увеличена со 100 до 150 долларов. Тогда на сколько процентов увеличивается цена?

Решение: Увеличение в процентах = (150 — 100) / 100 × 100 = 50%.

Процентное уменьшение

Процентное уменьшение относится к процентному изменению значения при его уменьшении за определенный период времени. Например, снижение уровня осадков, уменьшение числа больных Covid и т. д. Процентное снижение можно рассчитать по следующей формуле:

Уменьшение в процентах= (Исходное значение – Уменьшенное значение)/Исходное значение × 100

Пример: Количество осадков уменьшилось со 127 мм до 103 мм. Тогда каково соответствующее процентное снижение?

Решение: Процентное уменьшение = (127 — 103) / 127 × 100 = 18,9% (приблизительно).

Важные сведения о процентах:

• Чтобы вычислить процент числа от общего числа, просто используйте формулу число / общее число × 100.
• Увеличение или уменьшение любого количества можно выразить в процентах.
  Это называется процентным изменением.
• Дроби можно преобразовать в проценты и наоборот. Чтобы преобразовать дроби в проценты, умножьте на 100. Чтобы преобразовать проценты в дроби, разделите на 100.
• Проценты обратимы. Например, 50% от 60 равно 60% от 50.

☛ Похожие темы:

• Калькулятор процентов
• Калькулятор процентов к десятичной дроби
• Десятичный калькулятор процентов
• Калькулятор процентных долей

Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Решенные примеры в процентах

1. Пример 1: Роберту повысили зарплату на 5%. Его текущая зарплата составляет 70 000 долларов. Рассчитайте его пересмотренную зарплату после повышения.

   Решение:

   Текущая зарплата Роберта = 70 000 долларов

   Повышение = 5% от 70 000 = 5/100 × 70 000

   5 × 700 = 3500 долларов США

   Повышение зарплаты Роберта составляет 3500 долларов.

   Таким образом, его новая зарплата составит 70 000 долларов + 3500 долларов = 73 500 долларов.

   Ответ: Зарплата Роберта после повышения по службе составляет 73 500 долларов.

2. Пример 2: Нил купил новый сотовый телефон за 90 долларов. Стоимость телефона уменьшается на 3% от его первоначальной цены каждый год. Рассчитайте стоимость его мобильного через 1 год.

   Решение:

   3% от 90 = 3/100 × 90 = 2,7 доллара

   Таким образом, стоимость мобильного телефона через 1 год будет: 90 — 2,7 = 87,3 доллара

   Ответ: Стоимость мобильного через 3 года будет $87,3

3. Пример 3: Джон тратит 120 минут на учебу ежедневно. Он тратит 60 минут на математику, 30 минут на естественные науки и 30 минут на социальные науки. Затем найдите процент времени для каждого предмета.

   Решение:

   Процент времени на математику = 60/120 × 100 = 50%

   Процент времени на науку = 30/120 × 100 = 25% × 100 = 25%

   Ответ: Доля математики, естественных наук и социальных наук составляет 50%, 25% и 25% соответственно.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.0003

Часто задаваемые вопросы о процентах

Что такое процентное соотношение?

Процент определяется как заданная часть или сумма в каждой сотне. Это дробь со 100 в знаменателе, представленная символом «%».

Каковы реальные примеры процентов?

Некоторые реальные примеры процентов приведены ниже:

• Состав кислорода, двуокиси углерода, азота и т. д. в воздухе.
• Процент заряда батареи вашего телефона или ноутбука.
• Процент ваших оценок за тест.
• Процентное содержание питательных веществ в упаковке с пищевым продуктом.
• Сравнение количества пациентов, выздоровевших от Covid, между двумя или более городами производится в процентах и ​​т. д.

Как рассчитать средний процент?

Ниже приведены шаги для расчета среднего значения заданных процентов.

• Преобразование процентов в десятичные числа. Например, чтобы вычислить среднее значение 30% от 50 и 20% от 80, мы преобразуем их в десятичные формы, которые равны 0,3 и 0,2 соответственно.
• Запишите число, представленное каждым десятичным числом. В этом случае это будет 0,3×50=15 и 0,2×80=16 соответственно.
• Сложите полученные таким образом числа. (15+16=31).
• Найдите сумму размеров выборки. (50+80=130).
• Разделите общее число, полученное на шаге 3, на число, полученное на шаге 4. Таким образом, 31/130=0,24. Это десятичное число представляет 24%, что является требуемым средним процентом.

Как вычесть процент?

Чтобы вычесть процент из числа, просто умножьте это число на процент, который вы хотите сохранить. Например, чтобы вычесть 10% из 500, просто умножьте 90% на 500

Как найти процент?

Процент можно найти, разделив значение на общее значение, а затем умножив результат на 100. Для расчета процента используется следующая формула: (значение/общее значение)×100%.

Может ли процент быть больше 100?

Да, процент может быть больше 100, если у нас есть значение, превышающее общее значение.

Как найти процент от числа?

Процентное число — это значение числа из 100. Оно рассчитывается по формуле (часть/целое) × 100. Например, в классе 26 мальчиков и 24 девочки. Итак, процент мальчиков в классе равен 26/(26+24)×100=26/50×100=52%, значит, из 100 52 мальчика.

Что такое процентное изменение?

Изменение в процентах — это изменение в процентах от старого значения к новому значению. Он рассчитывается по следующей формуле: Процентное изменение = (разница между старыми и новыми значениями/старое значение) × 100%.

Как рассчитать процент оценок?

Чтобы рассчитать процент баллов, просто разделите полученные баллы на общее количество баллов и умножьте дробь на 100. Например, если количество полученных баллов равно 525, а общее количество баллов равно 600, то соответствующий процент равен 525/600 × 100 = 87,5

Какая формула преобразования процентов в десятичные дроби и наоборот?

Чтобы преобразовать проценты в десятичные, отбросьте символ процента (%), разделите его на 100 и запишите десятичную форму полученной таким образом дроби. Далее, чтобы перевести десятичные дроби в проценты, просто умножьте их на 100.

Знакомство с процентами

Когда мы говорим «Процент», мы на самом деле говорим «на 100»

Один процент ( 1% ) означает 1 на 100.

1% этой линии заштриховано зеленым: она очень маленькая, не так ли?

 

	50% означает 50 на 100 (50% этого поля зеленое)

25% означает 25 на 100 (25% этого поля зеленое)

Попробуйте сами:

числа/изображения/ani-pct. js

Примеры:

		100% означает все. Пример: 100% от 80 равно 100 100  × 80 = 80
		50% означает половину. Пример: 50% от 80 равно 50 100  × 80 = 40
		5% означает 5 / 100 . Пример: 5% от 80 равно 5 100  × 80 = 4

Использование процентов

числа/изображения/percentage.js

Используйте ползунок и попробуйте разные числа
(Что такое 40% от 80? Что такое 10% от 200? Что такое 90% от 10?)

Поскольку «Процент» означает «на 100», подумайте:

«это должно быть разделено на 100»

Итак, 75% действительно означает 75 100

И 100% это 100 100 , или точно 1
(100% любого числа это просто число, без изменений)

И 200% равно 200 100 , или точно 2
(200% любого числа в два раза больше числа)

 

A

Проценты также могут быть выражены как Десятичные числа или Дроби

Половину можно записать. ..       В процентах: 50% В виде десятичной дроби: 0,5 В виде дроби: 1 / 2

Подробнее об этом читайте в разделе «Десятичные числа, дроби и проценты».

Некоторые рабочие примеры

Пример: рассчитайте 25% из 80

25% = 25 100

и 25 100 × 80 = 20

SO 25% 80499

.

Пример: 15% из 200 яблок плохие. Сколько яблок плохих?

15% = 15 100

А 15 100 × 200		=  15 ×  200 100
		= 15 × 2
		=  30 яблок

30 яблоки плохие

Пример: если только 10 из 200 яблок плохие, сколько это процентов?

В виде дроби 10 200 = 0,05

В процентах это: 10 200 x 100 = 5%

 

5% из этих яблок плохие

Пример: Стоимость скейтборда снижена на 25%.

Старая цена была 120 долларов.
Найдите новую цену.

Сначала, найдите 25% от 120 долл. США:

25% = 25 100

и 25 100 × 120 = $ 300450 9003 9005 25% $ 120 = $ 300450

9002 25%. сокращение составляет 30 долларов США

 

Возьмите сокращение от оригинала цена

120 $ − 30 $ = 90 $

Цена скейтборда на распродаже $90

Расчетный трюк

Это небольшое правило может облегчить некоторые вычисления:

х% от у = у% от х

Пример: 8% от 50

8% от 50 равно 50% от 8

И 50% от 8 равно 4

Таким образом, 8% от 50 также равно 43

Слово

«Процент» происходит от латинской 9.0615 Процентов . Латинское слово Centum означает 100, например век — это 100 лет.

Проценты против Процентов

Мой словарь говорит, что «Процент» — это «результат, полученный путем умножения количества на процент».