Законы сложения и вычитания векторов
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
Составитель: Дзюба Л.М.Учитель ГОУ ЦО 173
Г. Санкт-Петербург
Сложить коллинеарные противоположно направленные вектора
а
в
О
.
а+в
Векторы а и в коллинеарные ,
найти сумму векторов.
а
С
в
в
а+в
а
О
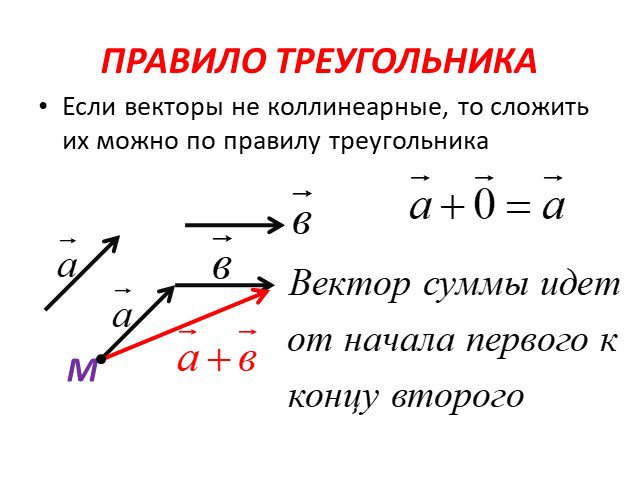
ПРАВИЛО
ТРЕУГОЛЬНИКА
в
в
а
а
а+в
1) От конца вектора а отложить вектор в, равный
2) Провести вектор из начала вектора а в конец
вектора в.

3) ВЫВОД: полученный вектор и будет суммой
векторов а и в.
ПРАВИЛО ПАРАЛЛЕЛОГРАММА
а
в
а
в
1) От начала вектора а отложить вектор в,
равный вектору в;
2) На векторах а и в как на сторонах
построить параллелограмм ;
3) Провести из общего начала векторов а
и в вектор –диагональ
параллелограмма.
4) ВЫВОД: полученный вектор будет
суммой векторов а и в.
ПРАВИЛО МНОГОУГОЛЬНИКА
а4
а1
а3
а2
а1
1 ) От конца вектора а1 отложить вектор а2 ,
равный вектору а2;
2) Повторить откладывание векторов
столько раз , сколько векторов нужно
отложить;
3) Провести вектор из конца вектора аn в
начало а.
ВЫВОД: полученный вектор в и будет
суммой векторов а 1 , а2 , а3 ,… и аn
а2
а3
а4
ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ
Для любых векторов а , в и с справедливы равенства:
1) а + в = в + а — переместительный закон
2) ( а + в ) + с = а + ( в + с ) — сочетательный закон
ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН.
1.Доказательство: Рассмотрим случай ,когда векторы а и в не
коллинеарны.
в
В
а
а
А
С
в
D
ОТ произвольной точки А отложим векторы
АВ = а и АD = в и на этих векторах
построим параллелограмм АВСD. По
правилу треугольника АС = АВ + АD = а + в.
Аналогично АС= АD + DС = в + а. Отсюда
Следует ,что а + в = в + а,
2.
СОЧЕТАТЕЛЬНЫЙ ЗАКОН.
Доказательство . От произвольной точки А отложим вектор
АВ = а , а от точки В вектор ВС = в , от точки С вектор СD=с.
Применяя правило треугольника , получаем:
(а + в ) + с = ( АВ + ВС )+ СD =АC+СD =АD
а + ( в + с) = АВ + (ВС + СD)=АВ + ВС = А D. Отсюда
следует , что ( а + в ) + с = а + ( в + с). Теорема доказана.
а
.
А
в
С
с
D
ВЫЧИТАНИЕ ВЕКТОРОВ
а
а
а- в
в
в
Разностью векторов а и в называется такой
вектор , сумма которого с вектором в равна
вектору а
Теорема: Для любых векторов а и в справедливо равенство
а – в = а +( — в ).

Доказательство. По определению разности векторов
( а – в ) + в =а. Прибавив к обеим частям этого равенства
вектор (-в), получим (а – в ) + в + (-в)= а+ (-в),или
(а – в ) +0=(-в), откуда а – в = а + (-в).
-в
В
а
в
а -в
.
О
А
а
Задача №754
А)
Дано:
х
х+y
В)
у
x +z
z
C)
z +y
Задача №755
Дано:
а
e
d
а
а +в +с + d +е
в
в
с
с
d
е
Задача № 756.
Дано:
-х
-y
x -z
-z
у
х
x
z
y
x
х-у
z
y
z-y
у
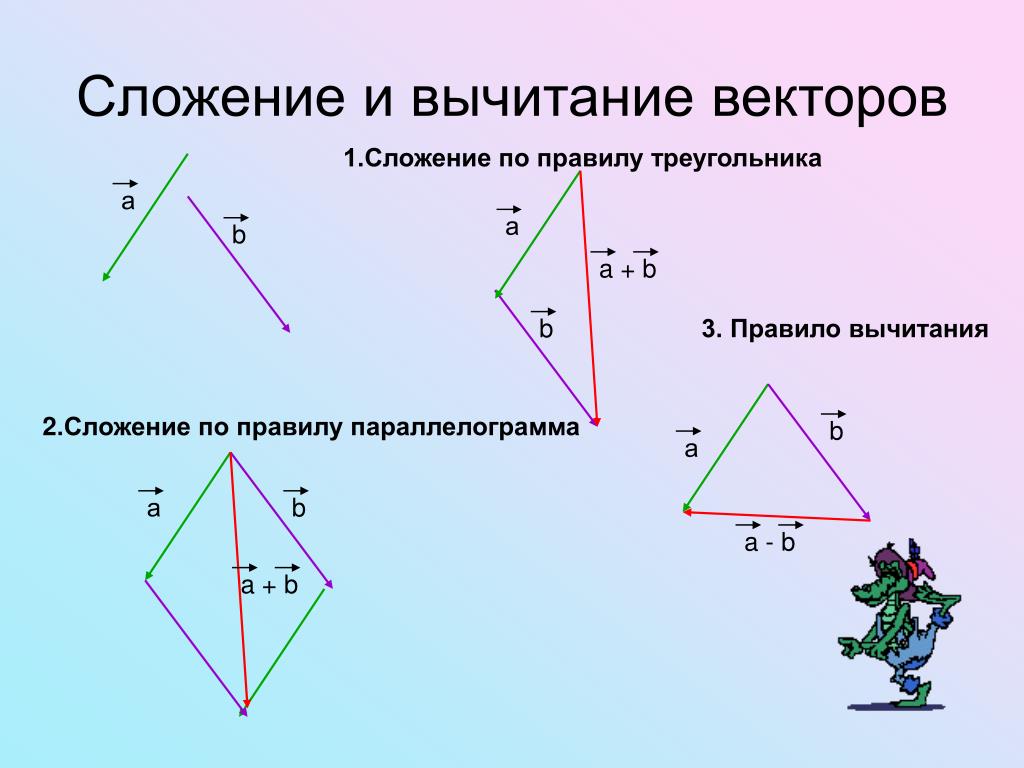
ЗАДАЧА : используя правило треугольника , постройте
векторы ОА = а +в
а
а
в
ОА
в
ЗАДАЧА: используя правило параллелограмма
постройте векторы ОР =х + у
х
P
Х+У= ОР
O
у
х.
у
Задача:
Используя правило треугольника,
найдите сумму векторов: а) РМ и МТ, б) СН и НС,
в) АВ + 0,г) 0 +СЕ.
Решение: а)РМ + МТ = РТ
б) СН +НС= СС= 0
в) АВ + 0 = АВ
г) 0 + СЕ= СЕ
Задача : Используя правило треугольника,
постройте векторы ОА = а + в и CВ = а +в.
Определите вид четырехугольника ОАВС.
А
а
в
В
С
М
К
а
в
в
а
о
Отложим от точки О вектор ОМ = а и от точки М вектор МА = в, тогда
ОА=ОМ + МА. Аналогично строим СК = а и КВ = в, тогда СВ = СК+КВ.
Т.к. ОА = а + в и CВ = а + в, то ОА=CВ , поэтому четырехугольникпараллелограмм.
СПАСИБО ЗА УРОК
English Русский Правила
Теория электричества
Теория электричества
ОглавлениеПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ.ВВЕДЕНИЕ. А. ВЕКТОРЫ И ВЕКТОРНЫЕ ПОЛЯ. § 1. Определение вектора. § 2. Сложение и вычитание векторов. § 3. Единичные и основные векторы, составляющие. § 4. Внутреннее или скалярное произведение. § 5. Внешнее или векторное произведение. § 6. Произведение трех векторов. § 7. Дифференцирование векторов по времени. II. ВЕКТОРНЫЕ ПОЛЯ. § 8. Гидродинамическое изображение. § 9. Безвихревое поле. Градиент и интеграл по кривой. § 10. Отдача поля источников, теорема Гаусса и расхождение вектора. § 11. Теоремы Грина. § 12. Точечные источники. § 13. Двойные источники. § 14. Вычисление безвихревого векторного поля из поля источников. 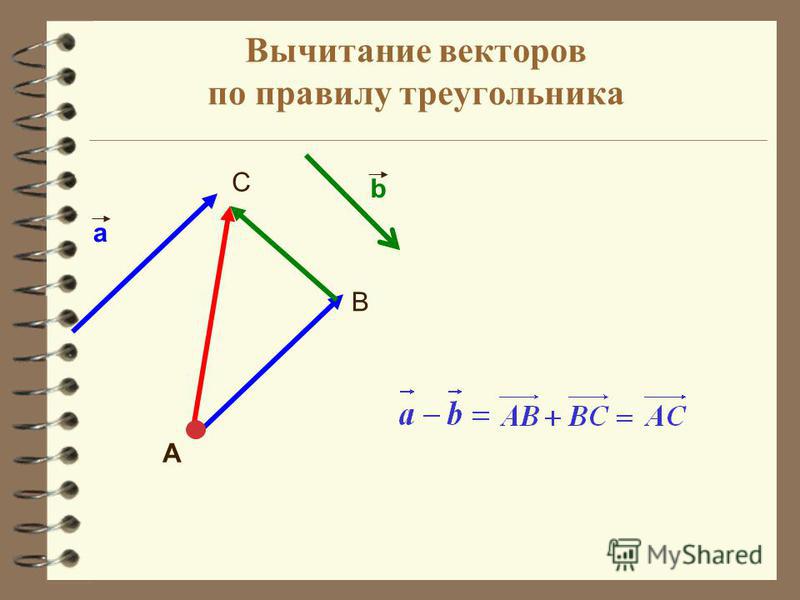 § 15. Источники и двойные слои, расположенные по поверхности. § 16. Однородный двойной слой. § 17. Вихрь и теорема Стокса. § 18. Вычисление векторного коля по его источникам и вихрям. § 20. Криволинейные ортогональные координаты. § 21. Тензоры. Полярные и аксиальные векторы. В. ЭЛЕКТРИЧЕСКОЕ ПОДЕ. § 22. Сила электрического поля. § 23. Поток электрических сил. § 24. Электростатический потенциал. § 25. Распределение электричества на проводниках. § 26. Емкость шарового и плоского конденсатора. § 27. Вытянутый эллипсоид вращения. § 28. Тачечный заряд вблизи проводящей плоскости. § 29. Точечный заряд и шаровой проводник. II. ДИЭЛЕКТРИКИ § 30. Плоский конденсатор с диэлектрическим промежуточным слоем. § 31. Диэлектрическая поляризация. § 32. Максвелловский вектор смещения D. § 33. Шаровой конденсатор. Диэлектрический слой бесконечной толщины.  § 34. Диэлектрический шар в однородном поле. III. ЭНЕРГИЯ И МЕХАНИЧЕСКИЕ СИЛЫ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ § 35. Заряды и металлические проводники в пустоте. § 36. Энергия поля при наличии изоляторов. § 37. Теорема Томсона. § 38. Диэлектрический шар в неоднородном поле. § 39. Механические силы в электростатическом поле. § 40. Электрострикция в химически однородных жидкостях и газах. § 41. Механическая сила на поверхности диэлектрика. § 42. Максвелловы натяжения. IV. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. § 43. Законы Ома и Джоуля. § 44. Ток проводимости. Ток смещения. Ток поляризации. § 45. Сторонние силы и электродвижущая сила. § 46. Гальваническая цепь. С. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 47. Сила магнитного поля в пустоте. § 48. Магнитное поле постоянных токов. § 49. Намагничение и магнитная восприимчивость § 50. Магнитная индукция. § 51. Закон индукции Фарадея. II. ЭЛЕКТРОДИНАМИКА ПОКОЯЩИХСЯ СРЕД § 52. Максвелловы уравнения для неподвижных тел. 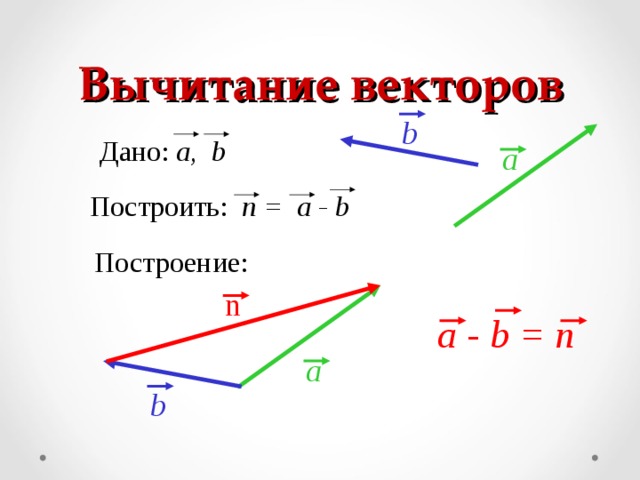 § 53. Магнитная энергия поля и Максвелловы натяжения магнитного поля. § 54. Единицы измерения электромагнитных величин. III. ЭЛЕКТРОДИНАМИКА. КВАЗИСТАЦИОНАРНЫХ ТОКОВ. § 55. Закон энергии для системы линейных токов. § 56. Самоиндукция и взаимная индукция. § 57. Вычисление коэффициентов индукции для некоторых частных случаев. § 58. Цепь тока с сопротивлением и самоиндукцией. § 59. Векторная диаграмма. § 60. Два контура (трансформатор). § 61. Цепь тока с самоиндукцией, емкостью и сопротивлением. IV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 62. Плоские волны в однородном изотропном диэлектрике. § 63. Плоские волны в однородных проводниках. § 64. Отражение от металлов. § 65. Вектор Пойнтинга в стационарном поле и в иоле периодическом во времени. § 66. Скин-эффект. § 67. Самоиндукция и емкость двойного провода. § 68. Волны вдоль идеальных проводников. § 69. Волны вдоль проводов при конечном сопротивления последних. § 70. Комплексный вектор Пойнтинга в телеграфном уравнении. 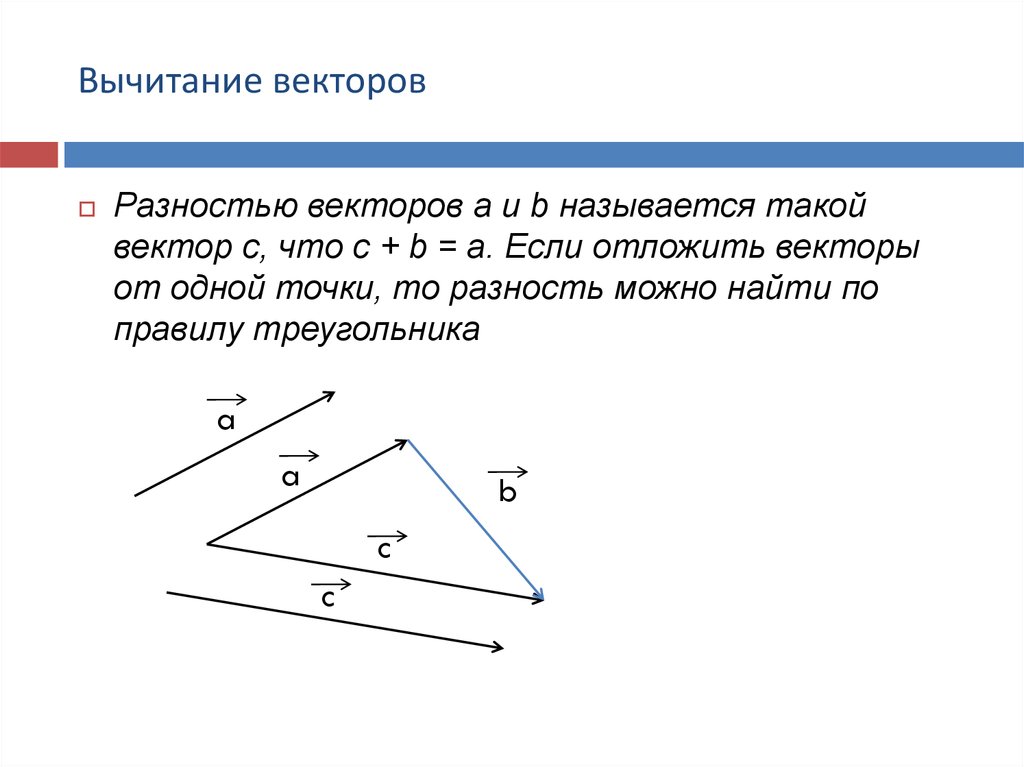 § 71. Общие электродинамические потенциалы. § 72. Решение Герца. § 73. Излучение линейного осциллятора. Д. ОБ ЭНЕРГИИ И СИЛАХ В МАКСВЕЛЛОВОЙ ТЕОРИИ § 74. Энергия поля как свободная энергия. § 75. Термические эффекты при постоянном объеме. § 76. Термодинамическая теория электрострикции. II. ДЕЙСТВИЯ СИЛ ПРИ ПОЛЯХ, ИЗМЕНЯЮЩИХСЯ ВО ВРЕМЕНИ. § 77. Максвелловы натяжения и принцип действия и противодействия. |
Сложение и вычитание векторов: графические методы
Векторы в двух измерениях
Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.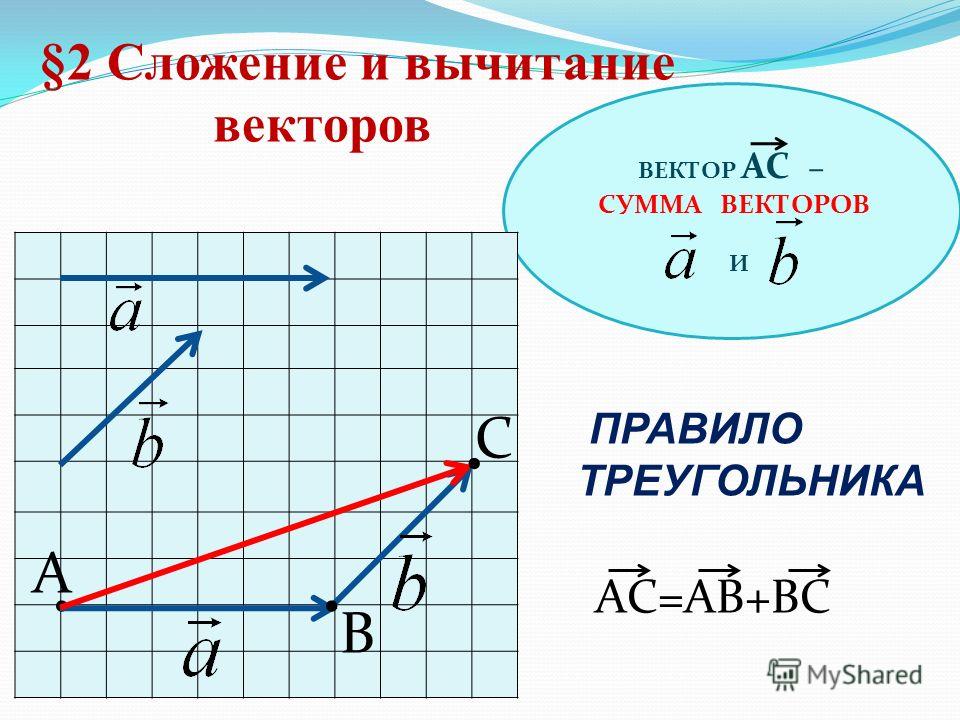
На рисунке 2 показано графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный символ, такой как D , обозначает вектор. Его величина представлена курсивным символом D , а его направление — θ .
Векторы в этом текстеВ этом тексте мы будем представлять вектор с переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором F , который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например, F , а направление переменной будет задано углом θ .
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Смещение 10,3 блока под углом 29,1º к северу от востока.
Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения Д .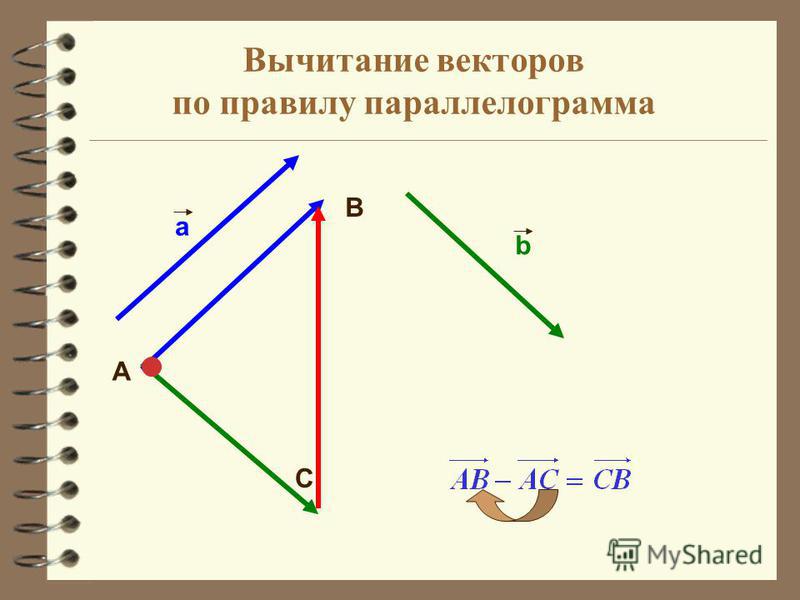 Используя транспортир, нарисуйте линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки. В этом примере величина D вектора составляет 10,3 единицы, а направление θ составляет 29,1º к северу от востока.
Используя транспортир, нарисуйте линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки. В этом примере величина D вектора составляет 10,3 единицы, а направление θ составляет 29,1º к северу от востока.
Сложение векторов: метод «голова к хвосту»
Метод «голова к хвосту» — это графический способ добавления векторов, описанный на Рисунке 4 ниже и в следующих шагах. хвост вектора является начальной точкой вектора, а начало (или кончик) вектора является конечным заостренным концом стрелки.
Рис. 4. Метод «голова к хвосту». Метод графического сложения векторов «голова к хвосту» проиллюстрирован для двух перемещений человека, идущего по городу, показанного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, равно 29,1º.
(c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, равно 29,1º.
Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 5
Шаг 2. Теперь нарисуйте стрелку, обозначающую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6
Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .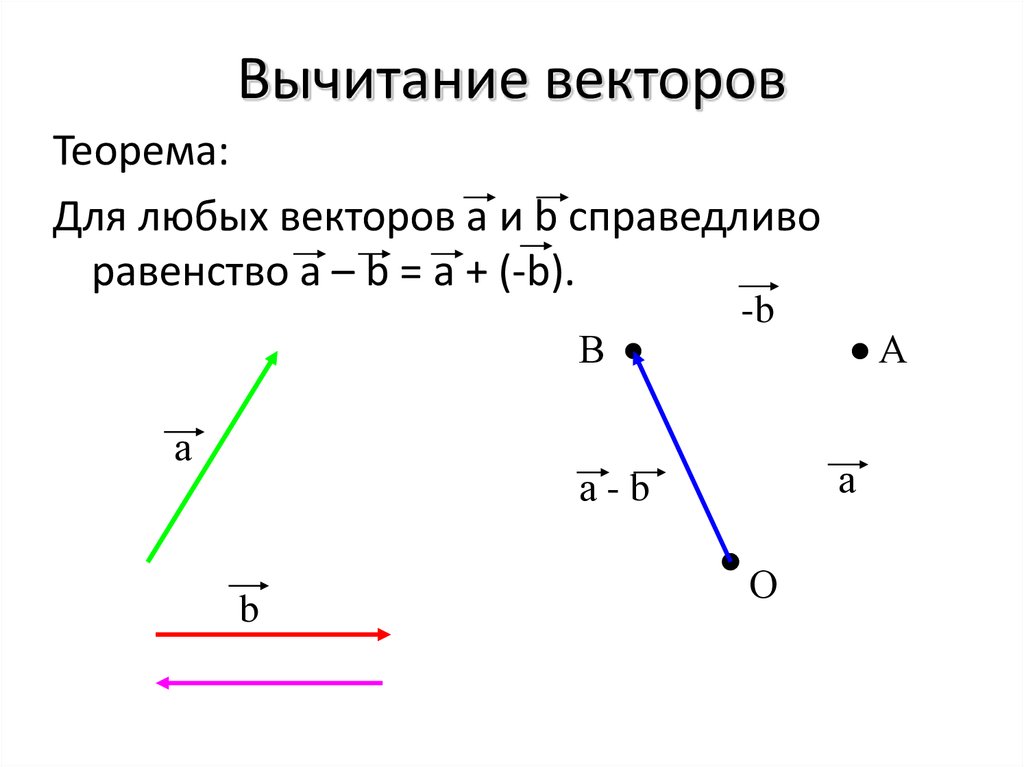
Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это равнодействующее или сумма других векторов.
Рисунок 7
Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета с помощью транспортира. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое сложение векторов с использованием метода «голова к хвосту»: прогулка женщины ровное поле. Сначала она проходит 25,0 м в направлении 49..0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
СтратегияПредставьте каждый вектор смещения графически стрелкой, обозначив первый A , второй B и третий C , делая длины пропорциональными расстоянию и направлениям, указанным относительно линия восток-запад. Описанный выше метод «голова к хвосту» позволит определить величину и направление результирующего смещения, обозначенного цифрой 9.0013 Р .
Решение(1) Нарисуйте три вектора смещения.
Рисунок 8.
(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рис. 9.
(3) Нарисуйте результирующий вектор R .
Рисунок 10.
(4) Используйте линейку для измерения величины R и транспортир для измерения направления R . Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.
Рисунок 11
В этом случае видно, что полное смещение R имеет величину 50,0 м и направлено в направлении 7,0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0º к югу от востока.
Обсуждение Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Таким образом, мы можем добавлять векторы в любом порядке, как показано на рисунке 12, и все равно получим то же решение.
Также важно отметить, что результирующая не зависит от порядка добавления векторов. Таким образом, мы можем добавлять векторы в любом порядке, как показано на рисунке 12, и все равно получим то же решение.
Рисунок 12.
Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.
A + B = B + A.
(Это верно и для сложения обычных чисел — вы получите тот же результат, сложите ли вы, например, 2 + 3 или 3 + 2 ) .
Это видео можно использовать для просмотра. Он включает в себя основы работы с векторами — рисование векторов/добавление векторов. Вы узнаете об основном понятии вектора, о том, как графически складывать векторы, а также о том, что графически означает умножение вектора на скаляр.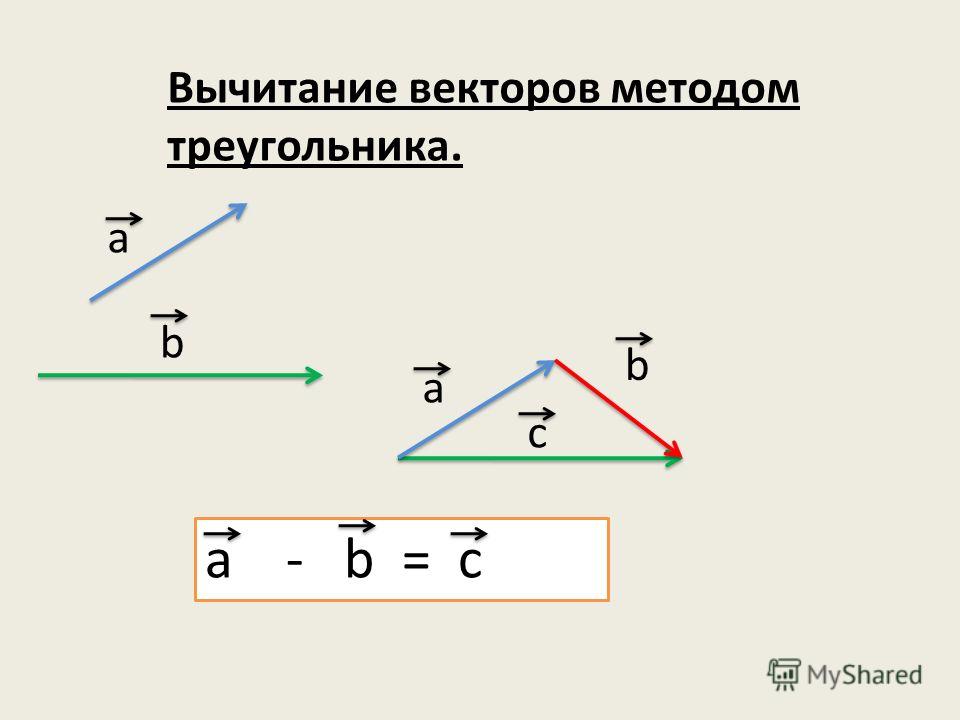
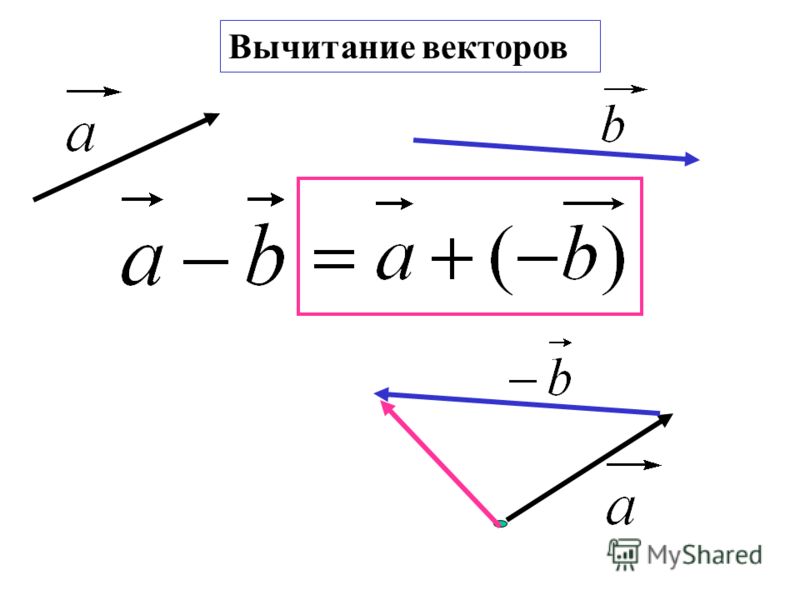
Вычитание векторов является прямым расширением сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть B из A, записанного A – B), мы должны сначала определить, что мы подразумеваем под вычитанием.0007 отрицательный вектора B определяется как –B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, B имеет ту же длину, что и -B, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Рис. 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, B является минусом 9.0013 –В ; он имеет ту же длину, но противоположное направление.
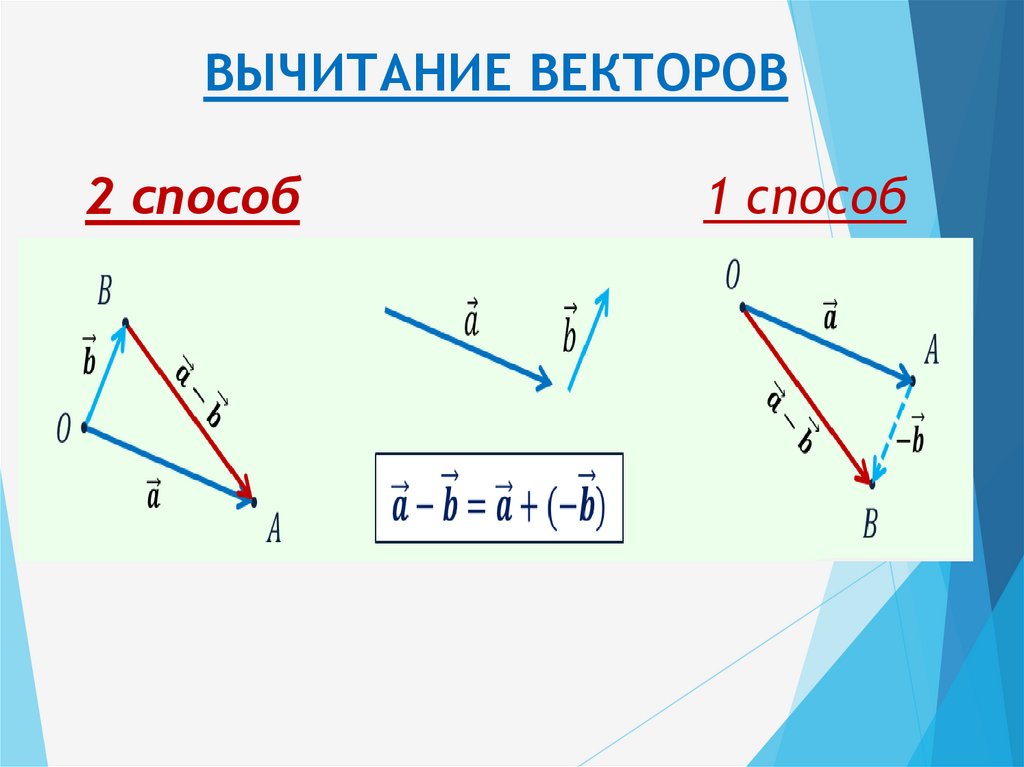
Затем вычитание вектора B из вектора A просто определяется как сложение –B с A . Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
A – B = A + (-B)
Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2)). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.
Пример 2. Графическое вычитание векторов: женщина, плывущая на лодке
Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0° к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112° к северу от востока (или 22,0° к западу от севера). Если женщина совершит ошибку и поедет в направлении против направления на второй этап поездки, где она окажется? Сравните это место с расположением дока.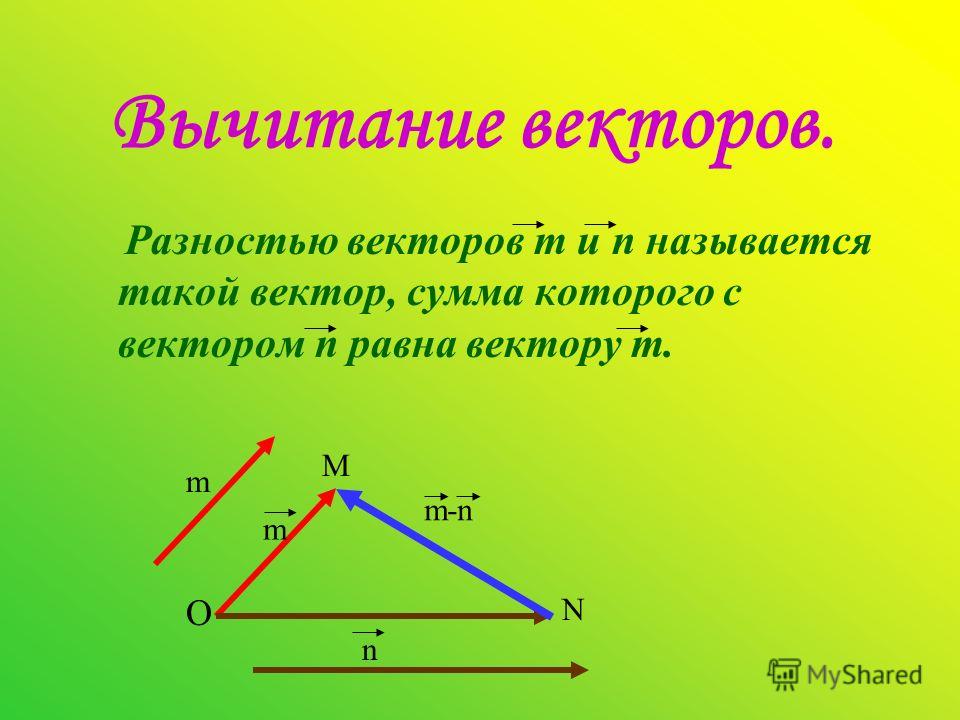
Рисунок 14.
СтратегияМы можем представить первый этап поездки вектором A , а второй этап поездки вектором B . Док находится по адресу A+B . Если женщина по ошибке едет в направлении , противоположном , для второго этапа пути, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от востока. Мы представляем это как –B , как показано ниже. Вектор –B имеет ту же величину, что и B, но в противоположном направлении. Таким образом, она окажется в локации A + (–B) , или A – B .
Рисунок 15
Выполним сложение векторов, чтобы сравнить местоположение причала, A + B , с местоположением, в которое по ошибке прибыла женщина, A + (-B) .
Решение (1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы А и –В .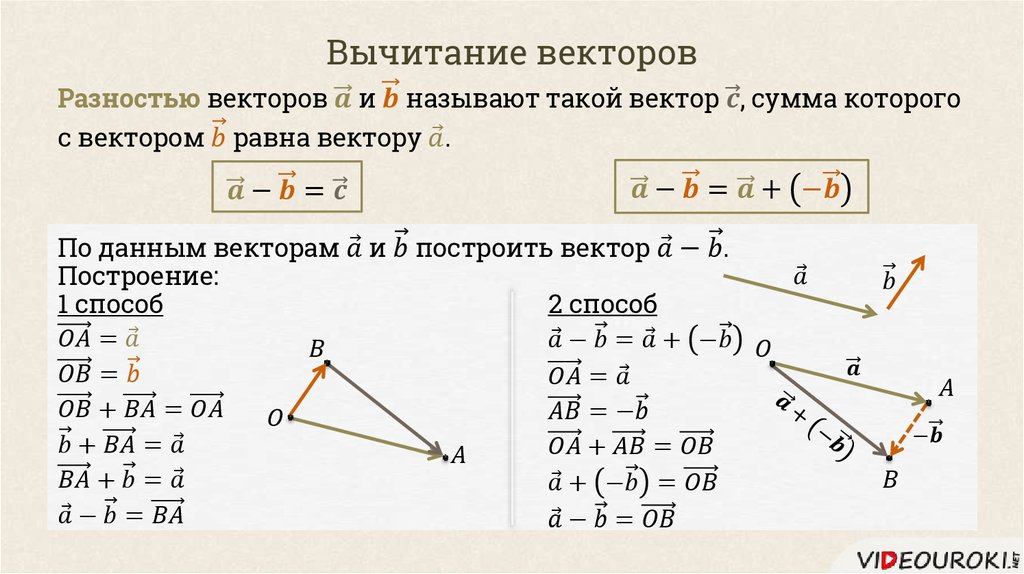
(2) Разместите векторы лицом к хвосту.
(3) Нарисуйте результирующий вектор R .
(4) С помощью линейки и транспортира измерьте величину и направление R .
Рисунок 16
В этом случае R = 23 . 0 м и θ = 7 . 5º к югу от востока.
(5) Чтобы определить местоположение дока, мы повторяем этот метод, чтобы добавить векторы A и B . Получаем результирующий вектор 9Рисунок 17
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
ОбсуждениеПоскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Умножение векторов и скаляров
Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м, или 82,5 м, в направлении 66,0 º к северу от востока.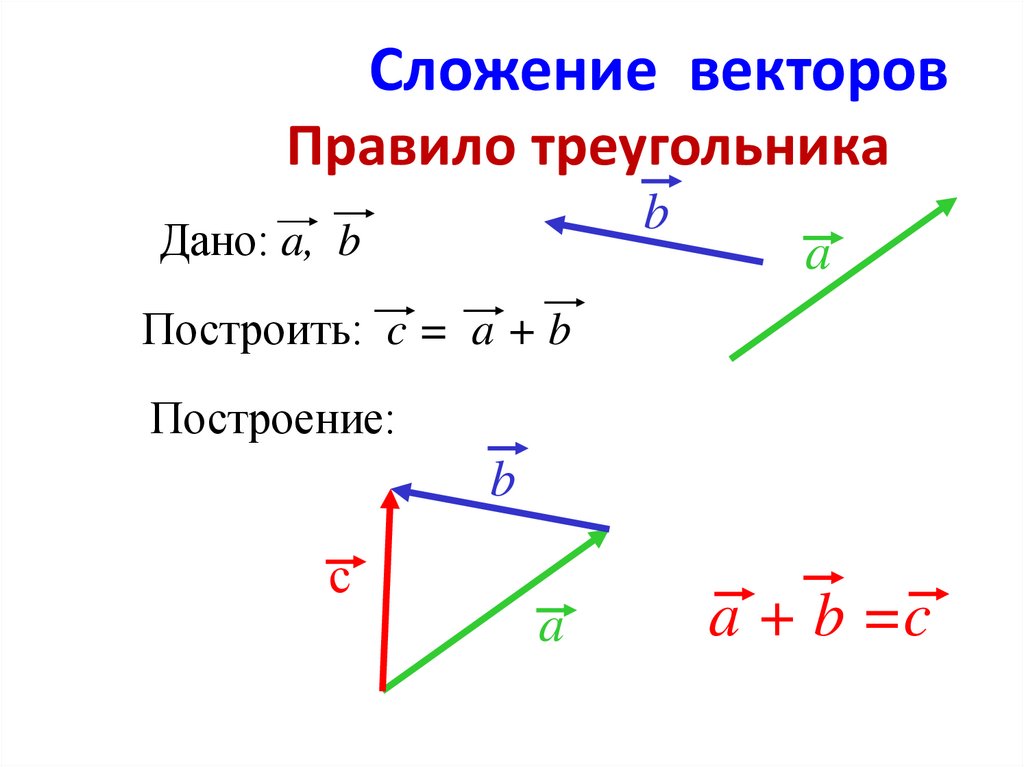
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор A умножается на скаляр c ,
- , величина вектора становится абсолютной величиной c A ,
- если c положительно, направление вектора не меняется,
- , если c отрицательно, направление меняется на противоположное.
В нашем случае c = 3 и A = 27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Разложение вектора на компоненты
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это связано с определением перпендикуляра компоненты одного вектора, например компоненты x – и y , или компоненты север-юг и восток-запад.
Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0º к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, применяемому для нахождения полного смещения.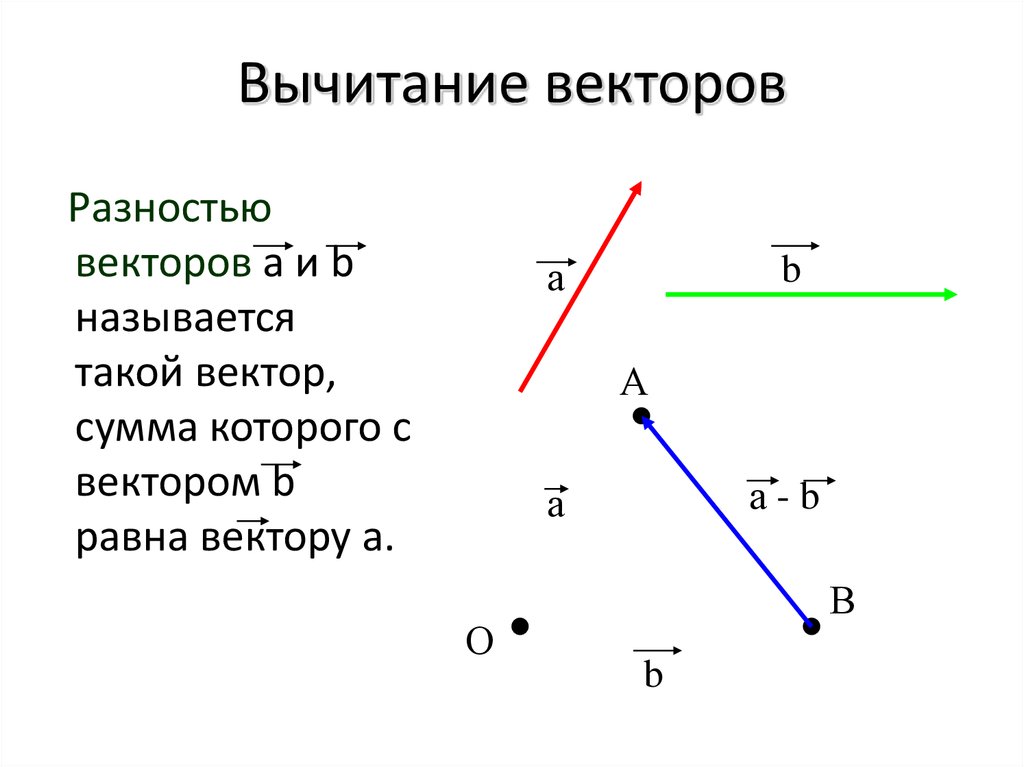 Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
PhET Explorations: Maze Game
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Нажмите, чтобы загрузить. Запуск с использованием Java.
Резюме
- Графический метод сложения векторов A и B включает в себя рисование векторов на графике и их сложение методом «голова к хвосту».
 Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно. - Графический метод вычитания вектора B из A включает добавление противоположного вектора B , который определяется как -B . В этом случае А – В = А + (-В) = R . Затем обычным образом применяется метод сложения «голова к хвосту» для получения результирующего вектора R .
- Сложение векторов коммутативно, так что A + B = B + A .
- Метод сложения векторов «голова к хвосту» заключается в том, что первый вектор рисуется на графике, а хвост каждого последующего вектора помещается в начало предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
- Если вектор A умножить на скалярную величину c , величина произведения будет равна cA .
 Если c положителен, направление произведения указывает на то же направление, что и A ; если c отрицательно, то направление произведения указывает на направление, противоположное A .
Если c положителен, направление произведения указывает на то же направление, что и A ; если c отрицательно, то направление произведения указывает на направление, противоположное A .
Концептуальные вопросы
1. Что из следующего является вектором: рост человека, высота над уровнем моря, возраст Земли, температура кипения воды, стоимость этой книги, население Земли, ускорение свободного падения?
2. Приведите конкретный пример вектора, указав его величину, единицы измерения и направление.
3. Что общего между векторами и скалярами? Чем они отличаются?
4. Два отдыхающих в национальном парке отправляются из своей хижины в одно и то же место на озере, каждый по своему пути, как показано ниже. Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста?
Рисунок 18.
5. Если пилоту самолета велят пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на рисунке 19.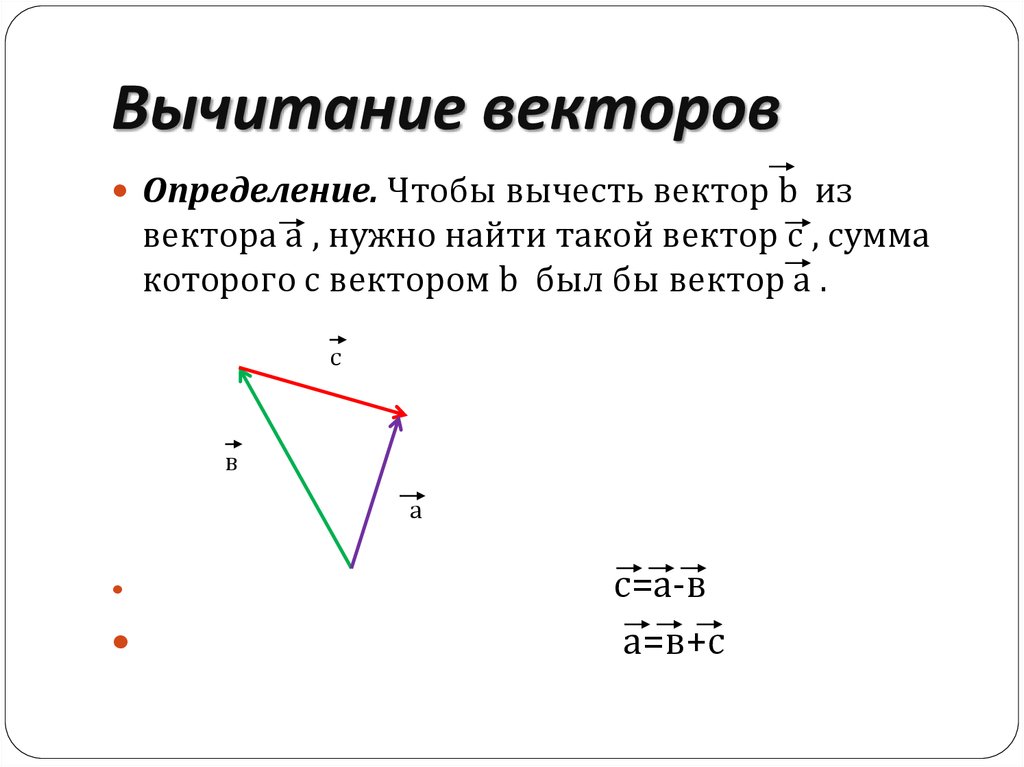 . Какая еще информация ему понадобится, чтобы добраться до Сакраменто?
. Какая еще информация ему понадобится, чтобы добраться до Сакраменто?
Рисунок 19.
6. Предположим, вы делаете два шага A и B (то есть два ненулевых перемещения). При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут сложиться, чтобы получить нуль? Максимальное расстояние, которое вы можете пройти от начальной точки A + B , равно сумме длин двух шагов?
7. Объясните, почему нельзя добавить скаляр к вектору.
8. Если вы сделаете два шага разной длины, сможете ли вы оказаться в исходной точке? В более общем смысле, могут ли два вектора с разными величинами дать в сумме ноль? Можно три или больше?
Задачи и упражнения
Используйте графические методы для решения этих задач. Вы можете предположить, что данные, взятые из графиков, имеют точность до трех цифр.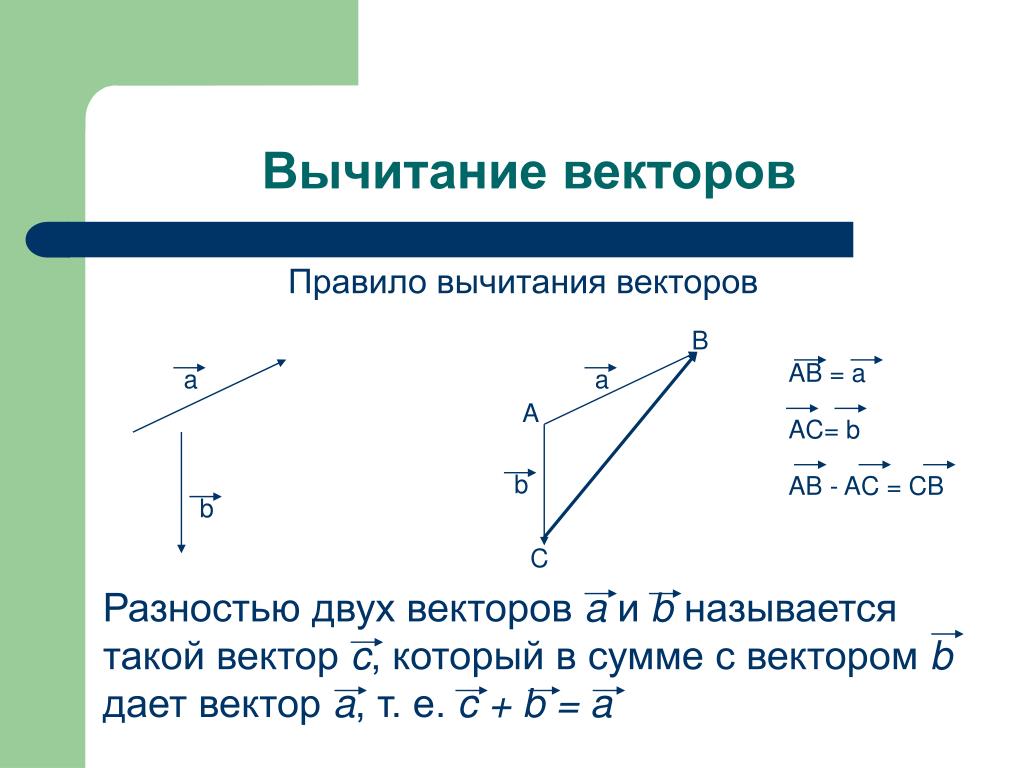
1. Найдите следующее для пути A на рис. 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
Рисунок 20. Различные линии обозначают пути, по которым идут разные люди, идущие по городу. Все блоки со стороной 120 м.
2. Найдите следующее для пути B на рисунке 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
3. Найдите северную и восточную составляющие смещения для туристов, показанных на Рисунке 20.
4. Предположим, вы прошли 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 21, то эта задача требует от вас найти их сумму R = A + B .
Рисунок 21. Два смещения A и B складываются, чтобы получить общее перемещение R , имеющее величину R и направление θ .
5. Предположим, вы сначала прошли 12,0 м в направлении 20° к западу от севера, а затем 20,0 м в направлении 40,0° к югу от запада. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 22, то эта задача находит их сумму R = A + B .)
Рисунок 22.
6. Повторите задачу выше, но поменяйте порядок двух шагов ходьбы; показать, что вы получаете тот же конечный результат. То есть вы сначала проходите отрезок B , который составляет 20,0 м в направлении точно на 40º к югу от запада, а затем проходите отрезок A , который составляет 12,0 м в направлении ровно 12,0 к западу от севера. (Эта задача показывает, что A + B = B + A .)
7. (a) Повторите задачу двумя предыдущими задачами, но на втором этапе вы пройдете 20,0 м в направлении 40° к северу от востока (что эквивалентно вычитанию B из A , т. е. к нахождению R’ = A – B ). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала пройдете 20,0 м в направлении на 40º к югу от запада, а затем 12,0 м в направлении на 20º к востоку от юга (что эквивалентно вычитанию A из B — это есть, чтобы найти R” = B – A = R’ Покажите, что это так.
е. к нахождению R’ = A – B ). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала пройдете 20,0 м в направлении на 40º к югу от запада, а затем 12,0 м в направлении на 20º к востоку от юга (что эквивалентно вычитанию A из B — это есть, чтобы найти R” = B – A = R’ Покажите, что это так.
8. Показать, что порядок сложения трех векторов не влияет на их сумму. Покажите это свойство, выбрав любые три вектора A , B и C , а также [latex]\mathbf{C}[/latex] , имеющие разную длину и направление. Найдите сумму A + B + C , затем найдите их сумму при сложении в другом порядке и покажите, что результат тот же. (Есть еще пять порядков, в которых A , B и C можно добавить; выберите только один.)
9. Покажите, что сумма векторов, рассмотренных в примере 2, дает результат, показанный на рисунке 17.
Покажите, что сумма векторов, рассмотренных в примере 2, дает результат, показанный на рисунке 17.
10. Найдите модули скоростей на рисунке 23.
Рисунок 23. Две скорости V A и V B складываются, чтобы получить общее значение V к .
11. Найдите компоненты V TOT вдоль x -и y на рисунке 23.
12. Найти компоненты V Tot вдоль набора из Perpendicle Axes rotto -r Ontocky Relitocky 300600. тем, что на рис. 23.
Глоссарий
- компонент (двумерного вектора):
- часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов
- коммутативный:
- относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму 90 647
- направление (вектора):
- ориентация вектора в пространстве
- голова (вектора):
- конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»
- метод «голова к хвосту»:
- метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора
- величина (вектора):
- длина или размер вектора; величина является скалярной величиной
- результат:
- сумма двух или более векторов
- Результирующий вектор:
- векторная сумма двух или более векторов
- скаляр:
- количество с величиной, но без направления
- хвост:
- начальная точка вектора; напротив наконечника или наконечника стрелки
Избранные решения задач и упражнений
1. (a) 480 м (b) 379 м, 18,4º к востоку от севера
(a) 480 м (b) 379 м, 18,4º к востоку от севера
3. северная составляющая 3,21 км, восточная составляющая 3,83 км
5,19,5 м, 4,6 к югу от запада
7. (а) 26,6 м, 65,1° к северу от востока (б) 26,6 м, 65,1° к югу от запада
9. 52,9 м, 90,1º относительно оси x .
11. x -компонент 4,41 м/с, y -компонент 5,07 м/с величину и направление. Примерами векторной величины являются перемещение, скорость, ускорение, сила и т. д. Вычитание и сложение векторов не подчиняются простым арифметическим правилам. Для вычитания и сложения векторов используется специальный набор правил.
Сложение векторов
Процесс сложения двух или более векторов называется сложением векторов. В зависимости от направления вектора векторное сложение подразделяется на два типа:
- Параллелограммный закон сложения векторов
- Треугольный закон сложения векторов
Метод сложения векторов выбирается в зависимости от расположения головы и хвоста векторов.
- Когда два вектора расположены «голова к хвосту», применяется треугольный закон сложения векторов
- Когда два вектора расположены голова к голове или хвост к хвосту, то сложение векторов выполняется по закону параллелограмма
Параллелограммный закон сложения векторов
Когда два вектора расположены голова к голове или хвост к хвосту, то сложение векторов выполняется по закону параллелограмма.
В соответствии с законом сложения векторов параллелограмма, когда предполагается, что два вектора являются смежными сторонами параллелограмма, тогда равнодействующей двух векторов является вектор, который проходит по диагонали через точку касания двух векторов.
Треугольный закон сложения векторов
Когда два вектора расположены голова к хвосту, применяется треугольный закон сложения векторов.
Согласно треугольному закону сложения векторов Если два вектора представлены двумя сторонами треугольника, взятыми в порядке величины и направления, то третья сторона этого треугольника определяет величину и направление результирующего вектора.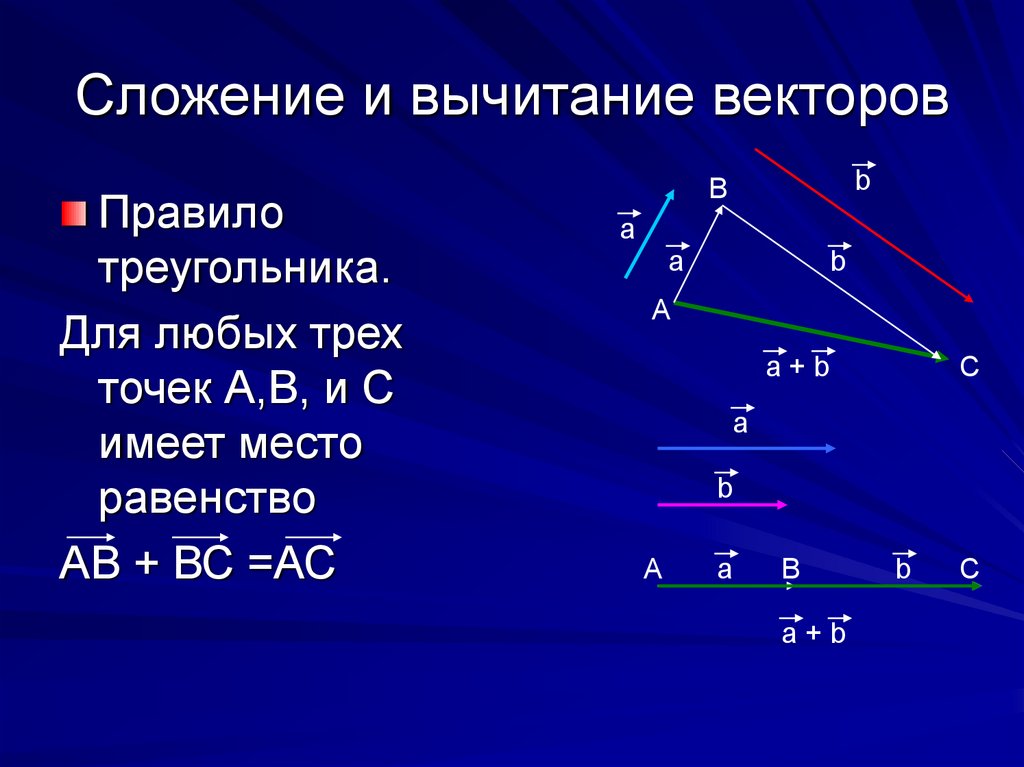
Почему добавление векторов важно?
В физике векторные величины, такие как сила, взаимодействуют друг с другом и оказывают результирующее воздействие на объекты, к которым они применяются. Поскольку воздействие/влияние всех этих сил учитывается при определении характера движения системы, для нахождения равнодействующей этих сил требуются такие операции, как сложение, вычитание и умножение этих сил.
Примеры сложения векторов
Если p = {4, -2, 2} и q = {1, -3, 2}. Определить p+q
Ответ.
p+q = {4,-2,2} – {1,-3,2}
p+q = {(4+1), -2+(-3), 2+2}
p+q = {5,-5,4}
Вычитание векторов
Вычитание векторов определяется как процесс вычитания координат одного вектора из координат другого вектора. При вычитании векторов направление вычитаемого вектора должно быть обратным. Это указывает на то, что длина одного вектора вычитается из другого вектора.
Вычитание векторов из 2 (двух) векторов a и b определяется как a – b .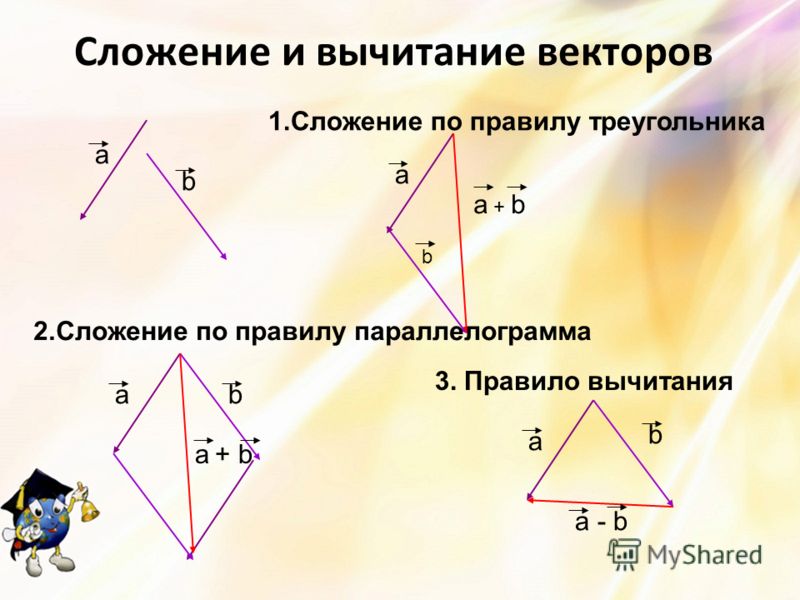 Это добавление отрицательного значения вектора b к вектору a, то есть a – b = a + (-b) . Следовательно, вычитание векторов включает в себя сложение векторов и отрицание вектора.
Это добавление отрицательного значения вектора b к вектору a, то есть a – b = a + (-b) . Следовательно, вычитание векторов включает в себя сложение векторов и отрицание вектора.
Правила вычитания векторов
Правила вычитания векторов:
- Вычитание векторов выполняется только между двумя векторами.
- Оба вектора при вычитании векторов будут иметь одинаковую физическую величину.
- Для векторного вычитания двух векторов a и b графически (для определения a–b) нам просто нужно сначала сделать их одинаковыми, а затем мы должны нарисовать вектор от вершины b до вершины a.
- Мы можем добавить -b (отрицательное значение вектора b, полученного путем умножения b на -1) к a, чтобы выполнить вычитание вектора, то есть a – b = a + (-b) .
- Когда векторы находятся в компонентной форме, нам просто нужно вычесть их соответствующие компоненты в порядке вычитания векторов.
Свойства векторного вычитания
- Когда вектор вычитается из самого себя, он называется нулевым вектором, то есть
p -q =0 (для вектора p)
- Вычитание вектора не коммутативно, то есть p – q может быть равно или не равно q – p
- Вычитание векторов также не является ассоциативным, то есть (p – q) – r может быть равно или не равно p – (q – r)
Заключение
Вектор определяется как величина, которая имеет как величину, так и направление.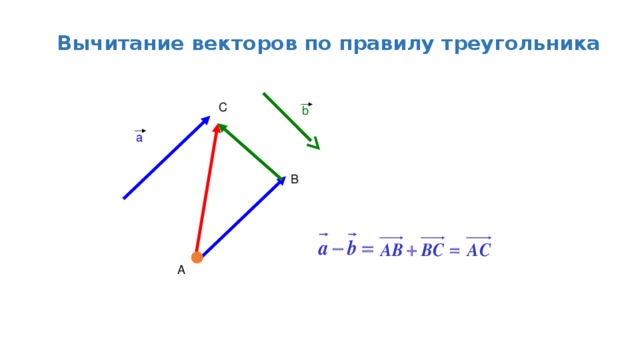

 Далее идет изложение теории электрического и магнитного полей. В конце книги изложены начала максвелловской теории электричества.
Далее идет изложение теории электрического и магнитного полей. В конце книги изложены начала максвелловской теории электричества.
 Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.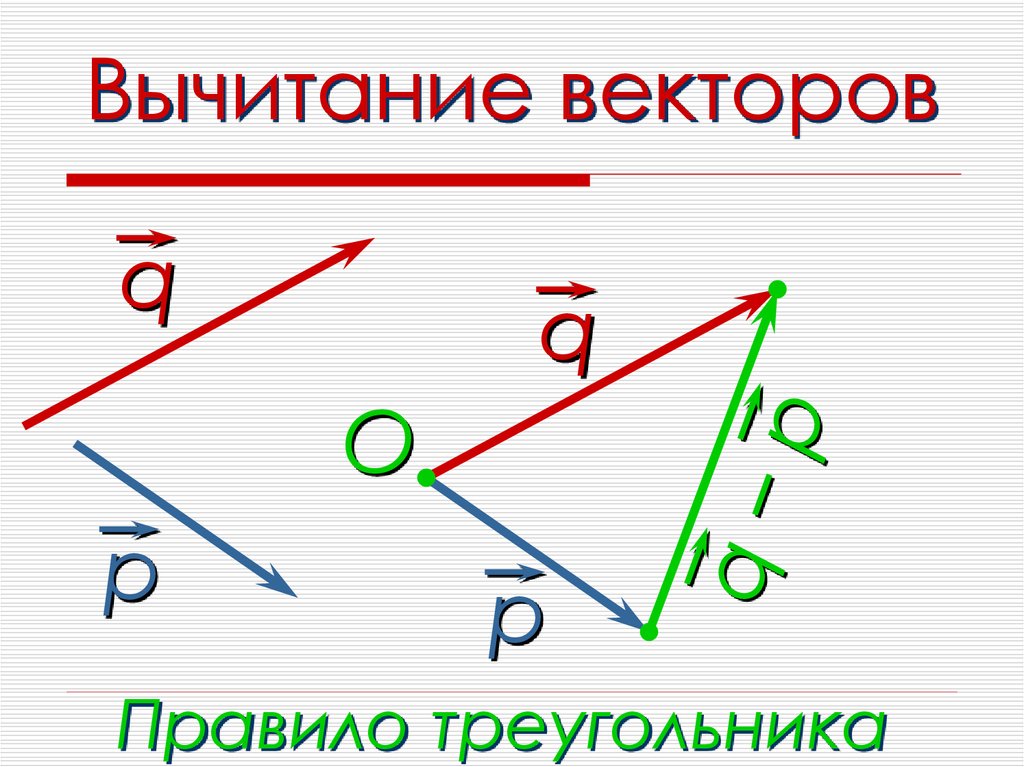 Если c положителен, направление произведения указывает на то же направление, что и A ; если c отрицательно, то направление произведения указывает на направление, противоположное A .
Если c положителен, направление произведения указывает на то же направление, что и A ; если c отрицательно, то направление произведения указывает на направление, противоположное A .