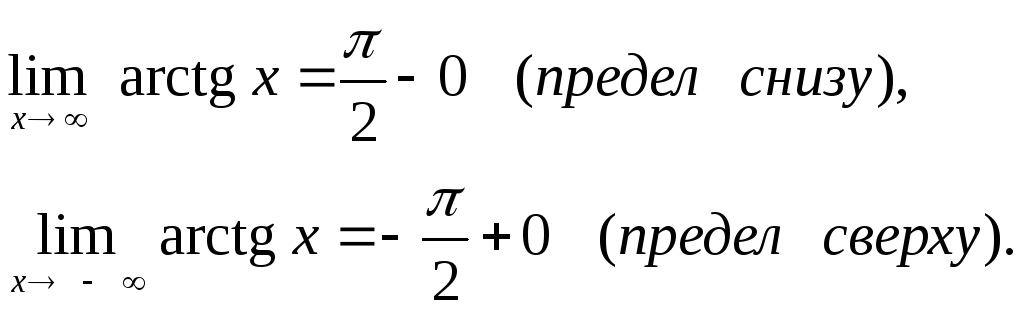Предел arctg x: Подскажите пожалуйста, как узнать значение arctg бесконечности? Ищу м

А при победе белогвардейцев в гражданской на сколько бы частей развалилась Россия и в каких пределах ее бы разрешили оставить заграничные хозяева этих предателей?

навеяно просмотром передачи 18 детей и это не предел. Вот вы бы потянули бы 18 детей при хорошем фин

Если толпе Внушить, что перельман вУмный и при этом на вопрос, чё он там открыл полпе сказать: «Ну вы же всё равно этого не понимаете», толпа будет Свято Веровать, что он вУмный?

Вам часто приходится выезжать за пределы МКАДа? Зачем? Вы испытываете при этом сильный стресс?

Смотрю я курс валют…Рубль идет за 3.85 к тенге…такого я в жизни не видел…4.50 предел всегда был…при любой власти..Заставляет задуматься..

— Почему $\lim\limits_{x \space \to \infty}\space{\arctan(x)} = \frac{\pi}{2}$?

Задавать вопрос

спросил 11 лет, 4 месяца назад

Изменено 11 лет, 4 месяца назад

Просмотрено 4к раз

$\begingroup$

В рамках этой задачи после подстановки мне нужно рассчитать новые лимиты.

Однако я не понимаю, почему так:

$$\lim_{x \to \infty}\space{\arctan(x)} = \frac{\pi}{2}$$

I попытался нарисовать единичный круг, чтобы посмотреть, что происходит с $\arctan$, когда $x \to \infty$, но я не знаю, как нарисовать $\arctan$. Это противоположность $\tan$, но вы вообще рисуете $\tan$?

Буду признателен за любую помощь.

• исчисление
• тригонометрия
• пределы

$\endgroup$

2

$\begingroup$

Наконец-то решил с помощью этой картинки.

• $\sin x = BC$
• $\cos x = OB$
• $\тангенс х =
долларов США
• $\кот x = EF$
• $\сек х = ОД$
• $\csc x = OF$

Обратите внимание, что наша номенклатура $\tan x$ на самом деле не является произвольной. $AD$ действительно является касательной к единичной окружности в точке A. Теперь ясно видно, что когда $\tan{(x)} = AD \to \infty$, то $\arctan{(AD)} = x = \frac {\pi}{2}$.

$\endgroup$

2

$\begingroup$

Если вы хотите сделать это геометрически, ваше доказательство будет самым простым. Если вы хотите сделать это аналитически, вы можете использовать тот факт, что $\mathrm{\tan} : (-\pi/2,\pi/2) \to \mathbb R$ является возрастающей непрерывной биекцией (даже гомеоморфизмом) , таким образом $$ \lim_{x \to \infty} \mathrm{arctan}(x) = \lim_{y \to \pi/2} \mathrm{arctan}(\mathrm{tan}(y)) = \lim_{y \ в \pi/2} y = \pi/2. $$ Другими словами, вы просто делаете замену переменных.

Надеюсь, это поможет,

$\endgroup$

$\begingroup$

Вот несколько иной способ увидеть, что $\lim\limits_{\theta\rightarrow {\infty}}\arctan\theta={\pi\over2}$.

Думая об единичной окружности, $\tan \theta ={y\over x}$, где $(x,y)$ — координаты точки на единичной окружности с исходным углом $\theta$, что происходит как $\тета\стрелка вправо\пи/2$? В частности, что происходит с $\tan\theta$ при $\theta\nearrow{\pi\over2}$?

Итак, координата $x$ направлена ​​к 0, а координата $y$ направлена ​​к 1.

Итак, в частном $$ у\над х, $$ числитель приближается к 1, а знаменатель становится сколь угодно малым; поэтому частное стремится к бесконечности.

Таким образом, $\lim\limits_{\theta\rightarrow {\pi\over2}}\tan\theta=\infty$ и, следовательно, $\lim\limits_{\theta\rightarrow {\infty}}\arctan\theta={\pi\over2}$.

$\endgroup$

$\begingroup$ 9+$.

Задавать вопрос

спросил

Изменено 4 года, 2 месяца назад

Просмотрено 2к раз

$\begingroup$

Мне трудно понять, что здесь написано в моем учебнике.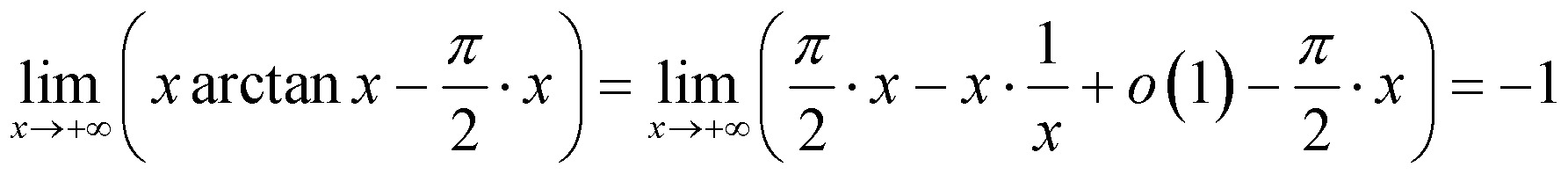 Кажется, переменная $t$ присваивается из ниоткуда, и я не уверен, почему они это делают. 9+} \arctan(\frac{1}{x-2})= \lim_{t \to \infty} \arctan(t)=\frac{\pi}{2}$$

Это находится на странице 132 «Исчисления: ранние трансцендентальные», 8-е издание, Джеймса Стюарта.

• исчисление
• пределы
• асимптотика

$\endgroup$

$\begingroup$

Забудьте о $t$ на секунду. Что произойдет с дробью $\frac{1}{x-2}$, если $x$ все больше приближается справа к числу $2$? Прежде всего, $x$ будет принимать все возможные значения, которые чуть больше, чем $2$: $2,1, 2,01, 2,001, 20001, 2,00001, 2,000001$ и т. д. Когда вы вычитаете $2$ из чего-то вроде $2,000001$ , что вы получаете? Вы получите число, которое будет очень, очень маленьким. А что произойдет, если вы разделите 1 на очень-очень маленькое число? Результат будет огромным! Это означает, что когда $x$ приближается к $2$ справа, дробь $\frac{1}{x-2}$ стремится к положительной бесконечности.