Пределы интегрирования: Определенный интеграл, Пределы интегрирования, функция Дирихле

Переменные пределы интегрирования

Хотя результат интегрирования — одно число, всегда можно использовать интеграл совместно с дискретным аргументом, чтобы получить результаты для многих значений параметра. Например, можно задать переменный предел интегрирования. На Рисунке 7 показано, как это сделать.

Рисунок 7: Переменные пределы интегрирования.

Отметим, что вычисления, подобные показанным на Рисунке 7, могут потребовать неоднократного вычисления интеграла. Это может привести к значительным затратам машинного времени, в зависимости от сложности интегралов, длины интервала интегрирования и значения встроенной переменной TOL.

Изменение точности вычисления интегралов

Численный алгоритм интегрирования Mathcad делает последовательные вычисления значения интеграла, увеличивая точность на каждом шаге, и возвращает значение, когда два последних значения отличаются меньше, чем на величину встроенной переменной TOL. На Рисунке 8 показано, как изменение значения TOL влияет на точность вычисления интеграла.

Чтобы вывести большее количество значащих цифр.

Рисунок 8: Влияние значения встроенной переменной TOL на вычисление интеграла.

При необходимости можно изменять точность вычислений, включив определения  для  значения TOL непосредственно в рабочий документ, как показано на Рисунке 8. Можно также сделать это с помощью команды Встроенные переменные из меню Математика. Чтобы увидеть эффект изменения точности вычислений, выберите команду Пересчитать все из меню Математика  для повторного вычисления всех выражений в рабочем документе. Если численный алгоритм Mathcad не достигает заданной точности, Mathcad отмечает интеграл сообщением об ошибке “не  сходится”. Эта ошибка может быть вызвана либо функцией, которая имеет особенности, либо наличием осцилляций в интервале интегрирования, либо слишком длинным интервалом интегрирования. При изменении точности необходимо помнить о соблюдении компромисса между точностью и временем вычисления, поскольку увеличение точности требует увеличения времени вычислений.

Криволинейные и двойные интегралы

Mathcad может быть использован для вычисления криволинейных интегралов в комплексной плоскости. Для этого сначала параметризуйте контур. Затем интегрируйте по параметру. Если параметр отличен от длины дуги, необходимо также включить производную параметризации как поправочный коэффициент. Пример приведен на Рисунке 9. Обратите внимание, что мнимая единица i, которая использована в определении пути, должна набираться как 1i.

В Mathcad можно также вычислять двойные или кратные интегралоы. Чтобы ввести знак двойного интеграла, наберите & дважды. Введите подинтегральное выражение, пределы и переменные интегрирования для каждого интеграла. На Рисунке 10 приведен пример.

Рисунок 9: Как в Mathcad вычислить криволинейный интеграл по пути в комплексной плоскости.

Имейте в виду, что двойные интегралы вычисляются дольше, чем простые интегралы. Везде, где возможно, используйте эквивалентный простой интеграл вместо двойного интеграла.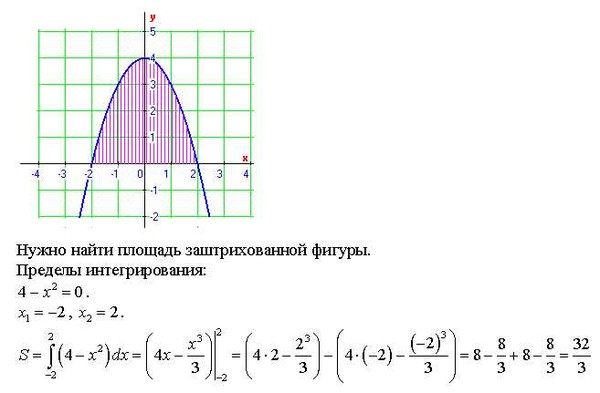

Рисунок 10: Двойные интегралы.

Булевы операторы могут возвращать значения только 0 или 1. Несмотря на это, они могут быть очень полезны. Пример на Рисунке 3 показывает использование булева оператора для установления переменного верхнего предела в операторе суммирования. На Рисунке 11 приведен пример, как булев оператор дает возможность определить значение индекса требуемого элемента массива. Сокровищница Методов и Формул, Электронная Книга, поставляемая MathSoft, содержит большое количество подобных полезных примеров.

Условие	Как ввести	Описание
w = z	[Ctrl] =	Булево равенство возвращает 1, если операнды равны; иначе 0
x > y	>	Больше чем.
x < y	<	Меньше чем.
x y	[Ctrl]0	Больше либо равно.
x y	[Ctrl]9	Меньше либо равно.
w z	[Ctrl]3	Не равно.

Четыре оператора >, <, и не могут применяться к комплексным числам, потому что понятия “больше” и “меньше” теряют значение в комплексной плоскости.

Рисунок 11: Использование булевых операторов.

Функции и операторы имеют много общего. Функция берет аргумент и возвращает результат. Оператор, аналогично, берет операнд и возвращает результат. Нетрудно заметить, что различия между функциями и операторами чисто внешние, а именно:

• Функции имеют имена, например tan или spline; операторы — обычно символы подобно + или x.

• Аргументы функции заключены в круглые скобки, они идут после имени  функции  и разделяются запятыми. Операнды же могут появляться в любом месте. Например, часто встречается запись f (x, y) , но редко x f y. Аналогично, часто используется запись x + y, но редко +(x, y).

Итак, операторы и функции — по сути, одно и то же. Аналогично тому, как определяются пользовательские функции, могут быть определены пользовательские операторы. Это возможно в Mathcad PLUS. Первый раздел описывает определение нового оператора, следующий — его использование, в последнем разделе показывается, как функции могут отображаться на манер операторов.

Определить в теории определенные интегралы: функции, пределы интегрирования и свойства с доказательством

С целью повышения точности решения практических задач, как в строительстве, так и экономике иногда нужен более «мощный» инструмент, который давал бы ответ на нестандартные условия. К примеру, вычисление площади покрытия не традиционной формы (половины параболы), изготовление конструкций, удаляемая или застраивая площадь и многое другое. Таким инструментом является именно интеграл, рамки исчисления которого, задает сам пользователь. Приведем примеры вычислений определенного интеграла с доказательством его свойств,

Содержание

Значение понятия

Рисунок 1. Общий вид криволинейной трапеции.

Невзирая на теоретическое обоснование, сразу дадим более четкое понятие этого термина. Определенным интегралом считается площадь криволинейной трапеции, которая за основания принимает снизу – ось абсцисс, а снизу саму функцию. Более наглядно это изображено на рисунке 1.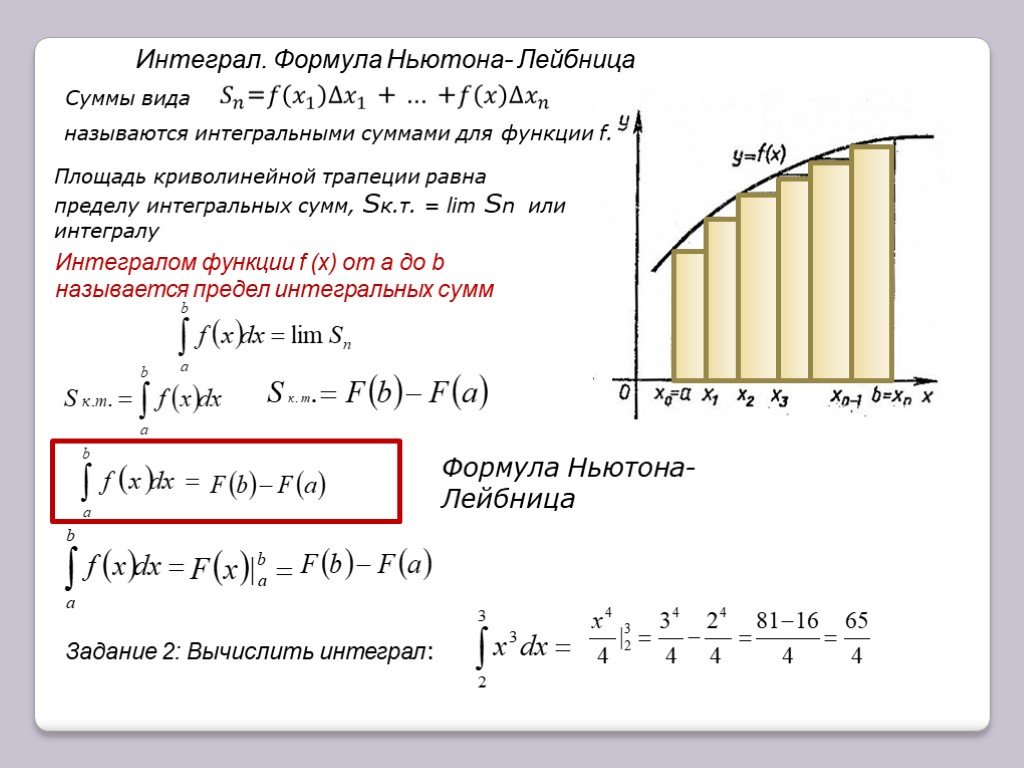 Такое трактование называется геометрическим, и более понятно, чем остальные.

В более классическом определении, численное выражение интеграла является величина какой – либо первообразной на выбранном и ограниченном промежутке (отрезке). На практике значение такого приращения может быть, как больше, так и меньше нуля. В отношении значения площади данный вопрос зависит от того, в какой полуплоскости находится кривая (верхней или нижней), такой и будет знак (на практике его значение отбрасывают). В численном выражение наше определение имеет такую формулу:

Опираясь на вышеуказанную формулу можем утверждать, что определенный интеграл представляет собой разность первообразной в крайних точках выбранного интервала (такой подход к определению называют формула Ньютона – Лейбница).

Это интересно! Первый признак равенства треугольников: доказательство

Свойства интеграла Римана на отрезке

Для того, чтобы безошибочно находить площади «кривых» трапеций, рассмотрим основные «приёмы», которые существенно облегчат этот процесс.

Основные свойства:

Площадь трапеции в отдельно взятой точке равна нулю. Формулой можно записать так:

Если функция определена между точками a и b, то справедливо следующее равенство:

Если под интегральные функции w(x) и t(x) определены на отрезке [k,c] и не имеют точек разрыва, нет таких точек в которых бы функции не имели значения, то справедливо равенство:

В случае если первообразная функция определена (вычислима в каждой точке) и пределы интегрирования лежат на отрезке [k,c], тогда под интегральную функцию можно записать в следующем виде:

Функция j(x) интегрируема на отрезке [a,d], только в том случае, когда сам отрезок [a,d] принадлежит большему отрезку [k,c].

Отметим, что данный список не включает в себя все свойства определенного интеграла и имеет продолжение. Указанные «хитрости» являются наиболее распространенными приемами, однако применять их нужно убедившись в их «работоспособности».

Для большей наглядности найдем значение интеграла, пределы интегрирования которого расположены на отрезке [3,5] для под интегральной

Решение. Согласно условию задачи, имеем следующую под интегральную функцию определенную на промежутке

Можем получить следующее:

Получается, что площадь криволинейной трапеции будет составлять ., вполне очевидно, что можно было и сразу взять определенный интеграл от заданной функции не прибегая к использованию свойства, однако такой подход более точно раскрывает возможности одного из свойств.

Допустим, что вместо функции с переменной x, находится 0 (такой вариант тоже считают функцией и совпадает с осью абсцисс). Тогда пытаясь найти определённый интеграл от постоянной получим:

Выходит, что если в под интегральной функции стоит нуль, то и первообразная, на каком бы отрезке не была определена, тоже будет равна нулю.

В случае, если требуется найти интеграл от константы, то следующее решение дает пример решения любого многочлена:

Откуда делаем вывод, что если требуется определить интеграл от нуля, то его значение (можно даже не расписывать) равен нулю, а если интеграл от числа, то разницу между концами отрезка нужно умножить на число под знаком интеграла.

Важно! Во время решения задач подобного плана, часто приходится комбинировать указанные приемы, для уменьшения сложности задания. Но используя такие переходы, не стоит забывать, что интегральная сумма всегда должна совпадать с первоначальной. Всегда проверяйте отрезок, на котором собираетесь интегрировать, иначе полученное значение будет отличаться от действительного.

«Умные» определения интегрирования непрерывной функции

Для удачного поиска первообразной необходимо знание и понимание таких понятий как: интегральная сумма, пределы интегрирования и общее понимание определения «интеграл функции».

Границы на определенном отрезке

Суть данного понятия заключается в том, что пределы интегрирования функции (это тот самый отрезок, который заранее определяется), это максимально граничные значения кривой, в которых она еще «действительна». К примеру, наша под интегральная определена на отрезке от 2 до 4. Это означает что мы можем найти первообразную для функции в точке со значением 2.000000001 (практически 2) и 3.9999999 (почти 4), но если пределы интегрирования больше (меньше), то все дальнейшие значения бессмысленны. Изобразим это на рисунке 2, где предложены возможные продолжения кривой.

Рисунок 2.Возможное поведение функции за пределами интегрирования.

Такое требование к пределам вытекает из того, что нам не известно определена ли функция за этими пределами или нет. А также то, как она поведет себя за своими пределами. По сути, функция верхнего основания говорит о том, как располагаются точки на указанном отрезке (вполне возможно, что за пределами это уже будет функция Дирихле, то есть будут точки разрыва). В своей сущности под понятием «интеграл функции» имеется в виду процесс поиска первообразной (первородной), из которой эта самая функция при поиске производной и получилась. Еще проще – действие обратное поиску производной.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Сумма

Представим, что дана произвольная трапеция, верхнее основание которой произвольная кривая. Если из образованной фигуры, образовать похожие внутри первоначальной. То получим бесконечное множество таких трапеций, у каждой из которых функция, определяющая верхнее основание, будет одинакова. Далее на каждом нижнем основании (малые отрезки) возьмём какую угодно точку, умножим значение функции в этой самой точке на разницу в основании, то получим площадь этой трапеции. Сумма площадей всех этих трапеций, будет равна площади изначально данной. Это будет интегральная сумма.

Рисунок 3. Сумма интегралов.

Математически это будет выглядеть так:

Для более понятного восприятия рекомендуем присмотреться к рисунку 3.

Полезное видео: что такое определенный интеграл?

Полезное видео: как решить определенный интеграл?

Вывод

При решении обычных задач или примеров данные определения редко имеют существенное значение. Но не лишним будет их правильное понимание и применение перед тем, как начнется само решение. Как правило, определенные интегралы, представляемые на ЕГЭ, все соответствуют данным критерием. Однако, теория проверяется тоже, и не стоит её отбрасывать ввиду сложности понимания.

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Пределы интегрирования — формулы, примеры

Пределы интегрирования используются в определенных интегралах. Применение пределов интегрирования к неопределенным интегралам превращает их в определенные интегралы. В выражении для интегрирования ∫ ^a _b f(x).dx для функции f(x) с пределами [a, b] a — верхний предел, b — нижний предел. Пределы интегрирования применяются в два этапа: сначала интегрирование функции дает ее первообразную, а затем к первообразной функции применяются пределы. 9a_b = F(a) — F(b) \)

Давайте узнаем больше о том, как решать пределы интегрирования, формулы пределов интегрирования, с помощью примеров, часто задаваемых вопросов.

1.	Каковы пределы интеграции?
2.	Как решить пределы интеграции?
3.	Формулы пределов интегрирования
4.	Примеры пределов интегрирования
5.	Практические вопросы
6.	Часто задаваемые вопросы об ограничениях интеграции

Каковы пределы интеграции?

Пределы интегрирования — это верхний и нижний пределы, которые применяются к интегралам. Интегрирование функции \(\int f(x)\) дает ее первообразную F(x), а пределы интегрирования [a, b] применяются к F(x), чтобы получить F(a) — F( б). Здесь в данном интервале [a, b] a называется верхним пределом, а b называется нижним пределом. 9a_b = F(a) — F(b) \)

Площадь, ограниченная функцией через граничные значения, находится путем интегрирования функции и применения пределов интегрирования.

a_b \) 9а_б = Ф(а) — Ф(б) \)

Таким образом, пределы интегрирования используются для нахождения простого числового значения данного интегрального выражения.

Формулы пределов интегрирования

Следующие важные формулы с пределами интегрирования используются для нахождения окончательного ответа определенных интегралов. Здесь формулы определенных интегралов помогают проинтегрировать заданную функцию и применить нижний и верхний предел для нахождения значения интеграла. 9a_{-a}f(x).dx = 0\), если f(x) — нечетная функция и f(-x) = -f(x).

☛ Похожие темы

• Антипроизводные
• Определенный интеграл
• Неопределенный интеграл
• Определенная интегральная формула
• Методы интеграции

 

Примеры пределов интегрирования

1. Пример 1: Найдите интеграл, применяя пределы интегрирования \(\int^3_{-3}x^5. dx\). 92x.dx=\frac{\pi}{4} — \frac{1}{2}\)​​

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по пределам интегрирования

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о пределах интеграции 9а_b = F(a) — F(b) \). Здесь интеграл от функции f(x) берется для получения первообразной функции F(x). Далее пределы [a, b] применяются как верхняя граница и нижняя граница, а разность значений функции берется для нахождения окончательного ответа.

Что вы называете интеграцией с ограничениями интеграции?

Процесс интегрирования, включающий пределы интегрирования, называется определенным интегралом. Интегрирование без каких-либо ограничений называется неопределенными интегралами.

Для чего используются пределы интегрирования?

Пределы интегрирования помогают найти площадь, ограниченную кривой, в пределах граничных значений. Пределы интегрирования помогают найти площадь, ограниченную функцией. Интегрирование функции f(x) дает первообразную функции, и, кроме того, верхняя и нижняя границы, заданные пределами интегрирования, применяются для нахождения площади, ограниченной кривой.

Интегральные границы / пределы интегрирования

Что такое границы интеграла?

Границы интеграла , также называемые пределами интегрирования , определяют область, которую вы будете интегрировать.
Пределы интегрирования для этого графика равны (0,2).

Верхние и нижние границы

Интеграл имеет две границы : нижнюю и верхнюю границы. Если вам дан интеграл, вы будете интегрировать между этими двумя границами.

Нижняя граница — это место, где вы запуск интегрирование. Вы найдете его под интегральным символом:

Верхняя граница — это линия, на которой вы прекращаете интегрирование. Он находится над символом интеграла:

В приведенном выше примере вы бы сказали, что границы интегрирования равны 0 и 2.

Как найти пределы интегрирования

найти ограниченную область (которую содержат функции), самый простой способ найти пределы интегрирования — построить график функций.

Например, вас попросили найти ограниченную площадь:

• y = 5 – x
• у = х
• у = 4 – 3х

На графике функции выглядят следующим образом:
Пределы интегрирования (черные точки) легко увидеть, если построить график функций.
Вы можете использовать свой графический калькулятор (я использовал графический онлайн-калькулятор в HRW), чтобы увеличить точку пересечения линий. Обратите внимание, что в этом примере область ограничена тремя функциями, поэтому вам потребуется выполнить более одного интегрирования, чтобы найти решение. Вы можете увидеть простой пример этой концепции здесь: Площадь между двумя кривыми.

Определенные интегралы и границы

Интегральные границы применимы только к определенным интегралам.

Если у вас есть непрерывная функция (т. е. такая, которая простирается до бесконечности), вы должны установить границы функции, чтобы интегрировать ее. Когда вы размещаете эти нижнюю и верхнюю границы, он становится определенным интегралом . Интеграл без границ называется неопределенным интегралом.

Как найти верхний предел интеграла

Находя верхний предел интеграла, вы находите определенный интеграл с верхней границей.

Интеграл с нижним пределом -1 и верхним пределом 1.

Шаги

Шаг 1: Определите рассматриваемую функцию . В интеграле это значение между символом интеграла и константой интегрирования (обычно обозначается как «dx» или, возможно, «dy»). В качестве примера мы назовем функцию чем-то простым, например, «f(x) = 4x».
Шаг 2: Определите пределы исчисления интеграла. Эти значения обычно обозначаются вверху и внизу знака интеграла. Верхняя граница — это значение вверху, а нижняя граница — это значение внизу символа. Допустим, что верхняя граница равна 2, а нижняя — 1,9.0165 Шаг 3: Выполните интегрирование функции с использованием неопределенных интегральных правил. Для f(x) = 4x увеличьте степень переменной на единицу и разделите всю функцию на новый показатель степени переменной. Например, интеграл f(x) = 4x становится 2x ² .
Шаг 4: Вставьте верхнюю границу интеграла во вновь интегрированную функцию . Мы заменяем нашу переменную ранее определенной верхней границей (которую мы оценили в 2). Тогда наша интегрированная функция принимает вид f(x) = 2(2) ² , где значение в скобках — это верхняя граница, заменившая переменную.
Шаг 5: Выполните математические вычисления. Не забывайте порядок действий — ваш ответ может привести к совершенно другому результату, если вы не выполните этот шаг!
f(x) = 2(2) ² = 2(4) = 8. Таким образом, для функции f(x) = 4x ее интегрирование с верхней границей 2 даст значение 8.

Вот и все!
Наверх

Issues

Даже если интеграл имеет границы, это не всегда означает, что у интеграла есть аналитическое решение. Например, между нижней границей и верхней границей может быть существенный разрыв. Всегда полезно изобразить функцию в виде графика, прежде чем пытаться ее интегрировать; в большинстве случаев этой проблемы можно избежать. Тем не менее, непрерывные функции с хорошим поведением обычно интегрируемы (King & Mody, 2010).

Ссылки

Кинг, М. и Моди, Н. (2010). Численные и статистические методы биоинженерии: приложения в MATLAB. Издательство Кембриджского университета.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Интегральные границы / пределы интеграции» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/integrals/integral-bounds/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.