Умножения и деление отрицательных чисел. Решение примеров.
- Альфашкола
- Статьи
- Умножения и деление отрицательных чисел
В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.
- \(«—«-\) при умножении минус на минус результат становится положительным;
- \(«-+»-\) при умножении минуса на плюс результат становится отрицательным;
- \(«+-«-\) при умножении плюса на минус результат становится отрицательным;
- \(«++»-\) при умножении плюса на плюс результат становится положительным.

Примеры умножения отрицательных чисел.
Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\)
Решение.
Отрицательное число при умножении на отрицательное станет положительным согласно правилу.
- \((-4)*(-4)=16\)
- \((-6)*(-5)=30\)
Ответ: \(16;30.\)
Задача 2. Вычислить: \((-10)*12\) и \((-7)*4.\)
Решение.
Отрицательное при умножении на положительное число станет отрицательным согласно правилу.
-10 * 12= -120
(-7)*4=-28
Ответ: \(-120; -28\)
Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)
Решение.
Положительное при умножении на отрицательное число станет отрицательным согласно правилу.
- \(11*(-11)=-121\)
- \(13*(-6)=-78\)
Ответ: \(-121;-78.\)
Деление отрицательных чисел
При делении действуют те же правила знаков, что и при умножении.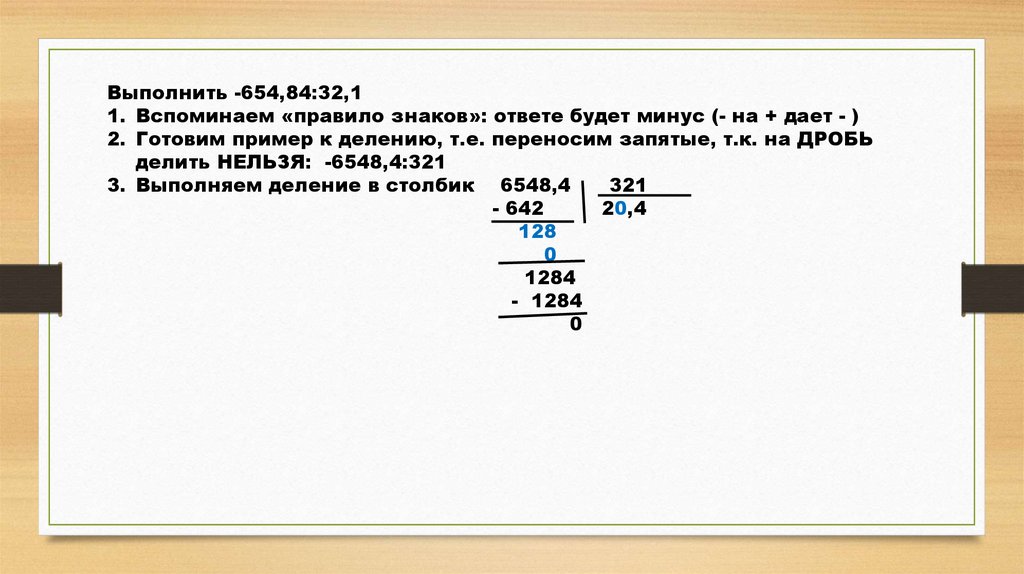
- \(«—«-\) при делении минус на минус результат становится положительным;
- \(«-+»-\)при делении минуса на плюс результат становится отрицательным;
- \(«+-«-\)при делении плюса на минус результат становится отрицательным;
- \(«++»-\) при делении плюса на плюс результат становится положительным.
Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\).
Решение.
- \(-16:(-4)=4\)
- \((-6):-2=3\)
Ответ: \(4;3.\)
Задача 5. Вычислить: \((-10):5\) и \((-12):6\).
Решение.
- \((-10):5=-2\)
- \((-12):6=-2\)
Ответ: \(-2;-2.\)
Задача 3. Вычислить: \(121:(-11)\) и \(169:(-13)\).
Решение.
- \(121:(-11)=-11\)
- \(169:(-13)=-13\)
Ответ: \(-11;-13.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Татьяна Николаевна Бычкова
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Преподаватель математики в 5-9 классах, подготовка к ОГЭ и ВПР. Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Алесандр Викторович Рудаков
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5 классов и по информатике для 7-9 классов, подготовка к ОГЭ. Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Андрей Алексеевич Тарасов
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-11 классов, ВПР/ОГЭ/ЕГЭ, и по физике 6-9 классы ВПР/ОГЭ.
Похожие статьи
- Как легко разделить на 0,5
- Признак делимости на 19
- Множество целых чисел
- Как поступить в МГИМО? Какие проходные баллы на бюджет (2018 / 2017)? Что нужно сдавать на ЕГЭ?
- Финансовый Университет при Правительстве РФ: Управление Персоналом
- Обучение во вторую смену: плюсы и минусы, как помочь ребенку адаптироваться
- Что такое педикулез и как с ним бороться
- Что такое конформизм или влияние чужого мнения на собственное поведение и мышление
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Почему минус на минус дает плюс?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.

Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов
Минус на плюс что дает?
Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.
Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.
| Минус на плюс, плюс на минус. |
Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился. Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.
Всегда.
Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.
| Минус на минус, плюс на плюс. |
Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.
Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?
Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.
Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.
Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.
Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.
Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.
Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. 2
2
В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?
(-2)+(-2)=-4
(-2)*(-2)=+4
Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.
Минус на минус даёт плюс. А почему?
Репетиторы ❯ Математика ❯ Минус на минус даёт плюс. А почему?
Автор: Владимир Л., онлайн репетитор по математике
●
21.09.2011
●
Раздел: Математика
Минус на минус даёт плюс – это правило, которые мы выучили в школе и применяем всю жизнь. А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием? С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10. Я никак не смогу отдать 13 яблок, потому что у меня их нет. Нужды в отрицательных числах не было долгое время.
Только с VII века н.э. отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе.
Рассмотрим пример, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7.
Что мы видим?
Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
§ Деление отрицательных чисел.
 Деление рациональных чисел
Деление рациональных чиселКоординатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если «a» и «b» положительные числа, то разделить число «a» на число «b», значит найти такое число «с», которое при умножении на «b» даёт число «a».
Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.
Поэтому, например, разделить число «−15» на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число «−15». Таким числом будет «−3», так как
(−3) · 5 = −15
значит
(−15) : 5 = −3
Примеры деления рациональных чисел.
- 10 : 5 = 2, так как 12 · 5 = 10
- (−4) : (−2) = 2, так как 2 · (−2) = −4
- (−18) : 3 = −6, так как (−6) · 3 = −18
- 12 : (−4) = −3, так как (−3) · (−4) = 12
Из примеров видно, что частное двух чисел с одинаковыми знаками — число
положительное (примеры 1, 2), а частное двух чисел с разными знаками—
число отрицательное (примеры 3, 4).
Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
- модуль делимого разделить на модуль делителя;
- перед результатом поставить знак «+».
Примеры деления чисел с одинаковыми знаками:
- (−9) : (−3) = +3
- 6 : 3 = 2
Чтобы разделить два числа с разными знаками, надо:
- модуль делимого разделить на модуль делителя;
- перед результатом поставить знак «−».
Примеры деления чисел с разными знаками:
- (−5) : 2 = −2,5
- 28 : (−2) = −14
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении
| + : (+) = + | + : (−) = − |
| − : (−) = + | − : (+) = − |
При вычислении «длинных» выражений, в которых фигурируют только умножение и деление,
пользоваться правилом знаков очень удобно. Например, для вычисления дроби
Например, для вычисления дроби
Можно обратить внимание, что в числителе два знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:
Запомните!
Частное от деления нуля на число, отличное от нуля, равно нулю.
0 : a = 0, a ≠ 0
Делить на ноль НЕЛЬЗЯ!
Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
- а : 1 = a
- а : (−1) = −a
- а : a = 1
, где «а» — любое рациональное число.
Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
- если a · b = с; a = с : b; b = с : a;
- если a : b = с; a = с · b; b = a : c
Данные зависимости используются для нахождения неизвестного
множителя, делимого и делителя (при решении уравнений), а также для
проверки результатов умножения и деления.
Пример нахождения неизвестного.
x · (−5) = 10
x = 10 : (−5)
x = −2
Знак «минус» в дробях
Разделим число «−5» на «6» и число «5» на «−6».
Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби.
Таким образом знак «минус» в дроби может находиться:
- перед дробью;
- в числителе;
- в знаменателе.
Запомните!
При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.
Это часто используется при выполнении действий с дробями, облегчая вычисления.
Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего
модуля вычитаем меньший по
правилам сложения чисел с разными знаками.
Пример.
Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое.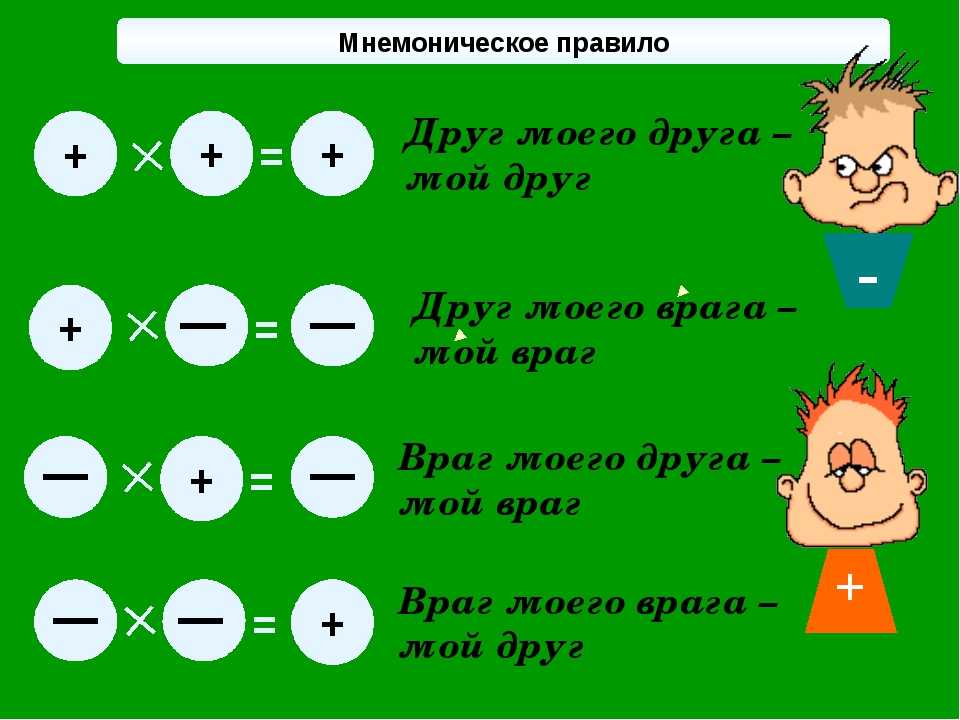 То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. В таких случаях применяется следующее правило:
В таких случаях применяется следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить множимое 2. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях применяется следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.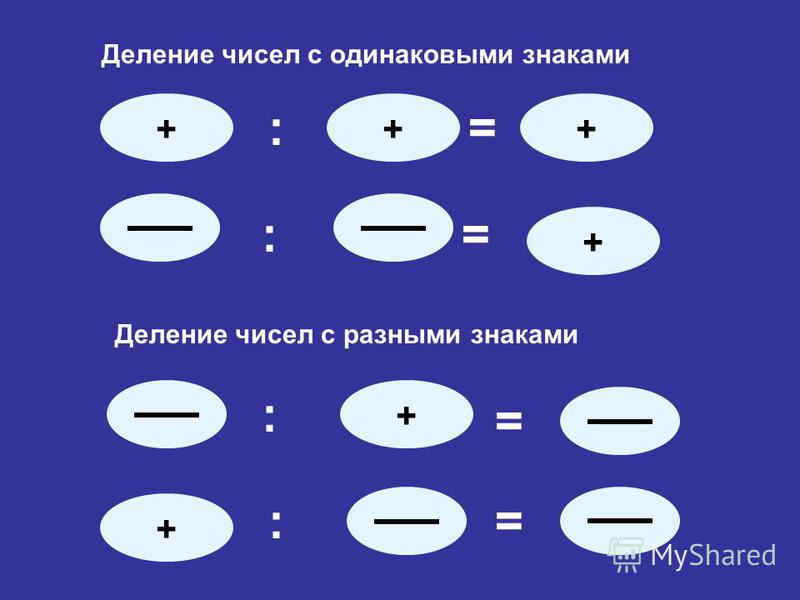
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4) = 3 : 1 = 3
Снова получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Умножение и деление отрицательных чисел
ВведениеСложение и вычитаниеЭкспоненты
Purplemath
Переходя от сложения и вычитания, как вы выполняете умножение и деление с отрицательными числами? На самом деле, мы уже рассмотрели самую сложную часть: вы уже знаете правила «знака»:
плюс умножить плюс равно плюс
(добавление большого количества горячих кубиков повышает температуру)
минус раз плюс минус
(удаление большого количества горячих кубиков снижает температуру)
плюс раз минус минус
(добавление большого количества холодных кубиков снижает температуру)
минус раз минус плюс
(удаление многих кубиков холода повышает температуру)
Содержание продолжается ниже
MathHelp.
 com
comУмножение и деление целых чисел
Правила знаков работают так же, как и при делении; просто замените «раз» на «делится на». Вот пример правил в делении:
(Помните, что дроби — это еще одна форма деления! «Дроби — это деление»!)
Некоторым людям нравится думать об отрицательных числах в терминах долгов. Так, например, если вы должны 10 долларов шести людям, ваш общий долг будет 6 × 10 долларов = 60 долларов. В этом контексте получение отрицательного ответа имеет смысл. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)?
Подумайте о перекусе в кафе. Когда вы идете платить, у ребенка возникают проблемы с вашей дебетовой картой. Он проводит ею шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет онлайн. Вы можете сказать по сумме, что да, он действительно взял с вас способ более одного раза. Некоторая часть этого общего дебета (отрицательная сумма на вашем счету) неверна.
Прежде чем звонить в свой банк, чтобы исправить ситуацию, вы хотите подтвердить количество перерасходов. Как вы можете понять это? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (например, 12,67 доллара США), которая является суммой одного платежа. Каждое списание — это минус на вашем счете, поэтому математика такова:
(- 76,02 доллара США) ÷ (- 12,67 доллара США) = 6
Таким образом, всего было действительно шесть списаний. Количество зарядов, 6, по подсчету количества событий, должен быть положительным . В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что поручить службе поддержки отменить ровно пять платежей.
Вы можете заметить, что люди «отменяют» знаки минус. Они пользуются тем фактом, что «минус умножить на минус — это плюс». Например, предположим, что у вас есть (−2)(−3)(−4). Любые два отрицательных числа, перемноженные вместе, становятся одним положительным. Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:
Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:
Я начну с того, что уберу одну пару знаков «минус». Потом умножу как обычно.
(-2)(-3)(-4)
= (-2)(-3) (-4)
= (+6) (-4)
= -24
Если вам дано длинное умножение с отрицательными числами, просто сократите знаки «минус» попарно:
Первое, что я сделаю, это посчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, и одна останется. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так.
(-1)(-2)(-1)(-3)(-4)(-2)(-1)
= (-1)(-2) (-1)(-3 )(−4)(−2)(−1)
= (+1)(+2) (−1)(−3)(−4)(−2)(−1)
= ( 1)(2) (-1)(-3) (-4)(-2)(-1)
= (1)(2) (+1)(+3) (-4) (−2)(−1)
= (1)(2)(1)(3) (−4)(−2) (−1)
= (1)(2)(1)( 3) (+4)(+2) (-1)
= (1)(2)(1)(3)(4)(2)(-1)
= (2)(3) (4)(2)(-1)
= 48(-1)
= -48
Я получил отрицательный ответ, поэтому я знаю, что мой знак правильный.
Вот еще один пример, показывающий тот же процесс отмены в контексте деления:
Отрицательные числа через круглые скобки
Основная трудность, с которой сталкиваются люди с отрицаниями, заключается в работе со скобками; особенно при взятии отрицания через круглые скобки. Обычная ситуация примерно такая:
−3( x + 4)
Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «по» скобкам:
3( x + 4) = 3( x ) + 3(4) = 3 x + 12
Те же правила применяются, когда вы имеете дело с отрицаниями. Если у вас возникли проблемы с отслеживанием, используйте маленькие стрелки:
← пролистните , чтобы просмотреть полное изображение →
Упростить 3 (
x − 5).
Мне нужно взять 3 через круглые скобки:
3( х — 5) = 3( х ) + 3(-5) = 3 х — 15
Упростить −2 (
x − 3).
Здесь я возьму «минус» через круглые скобки; Я буду распределять -2 на x и минус 3.
-2( х — 3) = -2( х ) — 2(-3) = -2 х + 2(+3) = -2 х + 6
Обратите внимание, как я тщательно следил за знаками в скобках. «Минус» был сохранен с 3 за счет использования другого набора скобок. Не стесняйтесь использовать группирующие символы, чтобы сделать ваше предполагаемое значение ясным как для оценщика, так и для вас самих.
Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразуя вычитание в умножение на минус:
Я начну с того, что напишу маленькую «1» перед скобками. Затем я нарисую стрелки от этой 1 к терминам в скобках, чтобы напомнить себе, что мне нужно сделать.
← пролистните для просмотра полного изображения →
Не бойтесь писать в этой маленькой «1» и рисовать эти маленькие стрелки. Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ.
Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ.
Я буду работать изнутри, упрощая сначала внутри внутренние символы группировки, в соответствии с Порядком операций. Итак, первое, что я сделаю, это пронесу −4 сквозь скобки. Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками, и, чтобы помочь мне отслеживать это -1, которое я буду распределять, я нарисую свои маленькие стрелки.
← пролистните для просмотра полного изображения →
Это сложно. Они заставляют меня вычесть дробь. Мне нужно сложить дроби, а значит сложить числители. Чтобы убедиться, что я не упустил из виду, что именно означает этот «минус» (а именно, что я минусую весь числитель второй дроби, а не только x ), я преобразую минус плюс -1:
← пролистните , чтобы просмотреть полное изображение →
Обратите внимание, что я перешел от вычитания дроби к добавлению отрицательной единицы, умноженной на дробь. Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями!
Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями!
Для дополнительной практики со скобками попробуйте здесь.
URL: https://www.purplemath.com/modules/negative3.htm
Страница 1Страница 2Страница 4
Положительные и отрицательные числа | SkillsYouNeed
Стандартные числа, большие нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.
Числа меньше нуля называются «отрицательными». Они имеют знак минус (-) перед ними, чтобы указать, что они меньше нуля (например, -10 или минус 10 ‘).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую прямую, инструмент, с которым вы, возможно, хорошо знакомы, особенно если ваши дети учатся в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними выполнять.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их, включив в них все числа, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или на клочке бумаги, а также очень сложно ошибиться в расчетах. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.
Вычитание отрицательных чисел
Если вы вычитаете отрицательное число, два отрицательных числа объединяются, чтобы получить положительное.
−10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Тогда сумма будет равна −10+10 = 0.
Тогда сумма будет равна −10+10 = 0.
Краткое примечание о скобках
Для ясности: вы никогда не будете писать два отрицательных знака рядом без скобок.
Таким образом, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли видеть, что использование двух отрицательных знаков было преднамеренным.
-10—10 неверно (и сбивает с толку)
-10-(-10) правильно (и более ясно)
Умножение и деление с положительными и отрицательными числами
При умножении или делении с комбинациями положительных и отрицательные числа, вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или разделяя числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа:
- Когда знаки двух чисел одинаковые , ответ будет положительным .
- Когда знаки двух чисел отличаются от , ответ будет отрицательным .

Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
(положительное число) × (отрицательное число) = отрицательное число
В качестве побочного вопроса это каким-то образом объясняет, почему вы не можете получить квадратный корень из отрицательного числа (подробнее об этом читайте на нашей странице Специальные числа и понятия ). Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает так же, когда у вас есть более двух чисел для умножения или деления. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Почему умножение двух отрицательных чисел дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто сбивает с толку и кажется нелогичным.
Чтобы объяснить, почему это так, вернитесь к числовым линиям, использованным ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и смотрите в положительном направлении, то есть в сторону 1, 2 и так далее. Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и повернитесь лицом в отрицательном направлении, то есть к −1, −2 и т. д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × -2 шага = -4 шага.
Отсюда отрицательный × положительный = отрицательный
В обоих этих примерах вы двигались вперед (т. е. в том направлении, в котором смотрели), положительное движение.
е. в том направлении, в котором смотрели), положительное движение.
- Снова вернитесь к нулю, но на этот раз вы пойдете назад (негативное движение). Снова повернитесь лицом в положительном направлении и сделайте два шага назад. Теперь вы стоите на −2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Следовательно, положительный × отрицательный = отрицательный - Наконец, снова вернитесь к нулю, повернитесь лицом в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата.
Отсюда отрицательный × отрицательный = положительный
- Два отрицания компенсируют друг друга. Вы можете увидеть это в речи:
- «Просто сделай это!» позитивное побуждение к действию.

- «Не делай этого!» просит кого-то не делать что-то. Это минус.
- «Не делай этого» означает «пожалуйста, сделай это». Два отрицания компенсируются и дают положительный результат как в математике, так и в речи.
- «Просто сделай это!» позитивное побуждение к действию.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный. Если у вас есть положительный и отрицательный, остается одна черточка, и ответ отрицательный. Это простая и наглядная памятка, несмотря на то, что она не обязательно удовлетворит тех, кто хочет понять правило.
Заключение
Отрицательные знаки могут показаться немного пугающими, но правила их использования просты и понятны. Помните об этом, и у вас не будет проблем.
Основные правила для положительных и отрицательных чисел
Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами.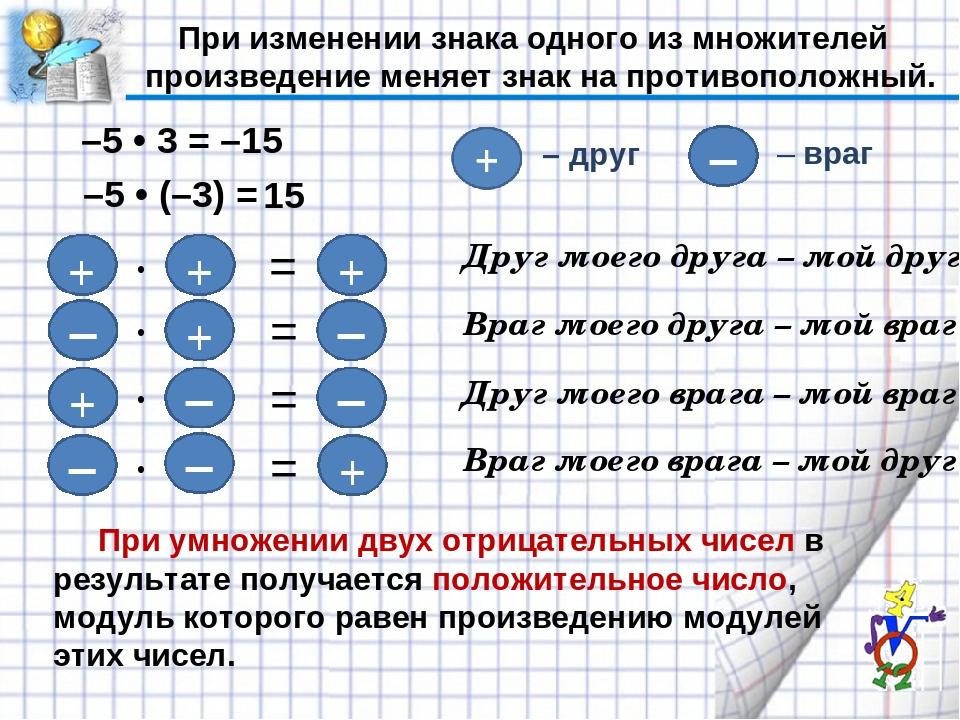 Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
правила сложения и вычитания двух положительных и отрицательных чисел
Реклама
Правила для чисел со знаком
При использовании положительных и отрицательных чисел вы используете правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.
Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.
Сложение: одинаковые знаки, сложите числа
Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:
Например:
- 1 + 1 = 2
- 51 + 32 = 83
- -14 + (-6) = -20
- -196 + (-71) = -267
Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.
Сложение: разные знаки, вычитание чисел
Если вы складываете положительные и отрицательные числа, вычтите меньшее число из большего и используйте знак из большего числа. Например:
- 6 + (-5) = 1
- -17 + 22 = 5
- -100 + 54 = -45
- 299 + (-1) = 298
Как видите, сложив числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.
Вычитание: Переключиться на сложение
Вычитание положительных и отрицательных чисел означает сложение противоположных чисел или аддитивное обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
- -3 — (+5) становится -3 + (-5) = -8
- 9 — (-7) становится 9 + (+7) = 16
- -14 — (+8) становится -14 + (-8) = -22
- 25 — (-90) становится 25 + (+90) = 115
Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно делайте их положительными. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.
Реклама
Умножение и деление: один и тот же знак, положительный результат
Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:
- 8 x 4 = 32
- (-8) x (-4) = 32
- 10 x 9 = 90
- (-10) x (-9) = 90
То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
- 12 ÷ 6 = 2
- -12 ÷ (-6) = 2
- 100 ÷ 5 = 20
- -100 ÷ (-5) = 20
числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.
Реклама
Умножение и деление: противоположный знак, отрицательный результат
При умножении положительного на отрицательное произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:
- 6 х (-7) = -42
- -7 х 6 = -42
- 12 х (-11) = -132
- — 11 x 12 = -132
Во всех этих случаях сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).
Знаки сходства и отличия в сложении и вычитании
Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки в ряду. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:
- 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
- 9 + (-8) = 1 (+- не похожи на знаки, поэтому уравнение представляет собой вычитание)
- 11 — (+13) = 2 (-+ разные знаки, поэтому уравнение представляет собой вычитание)
- 15 — (-10) = 25 (— подобны знакам, поэтому уравнение представляет собой сложение)
Этот метод следует тем же правилам, что и выше, но может помочь вам решить проблему быстрее, если вы предпочитаете работать с знаки заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас.
Понимание основ математики
Как только вы познакомитесь с основами математики и ее правилами, перед вами откроется весь математический мир. В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.
В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.
Штатный писатель
Умножение отрицательных значений дает положительное значение
GCfiIBPG7Aw
Когда мы умножаем:
| Пример | |||
| × | два плюса дают плюс: | 3 × 2 = 6 | |
| × | два отрицательных числа дают положительный: | (−3) × (−2) = 6 | |
| × | отрицательное и положительное делают отрицательное: | (-3) × 2 = -6 | |
| × | положительный и отрицательный делают отрицательный: | 3 × (−2) = −6 |
Да действительно два минуса дают плюс, и мы объясним почему , на примерах!
Знаки
Давайте поговорим о знаках .
«+» — положительный знак, «-» — отрицательный знак.
Когда число имеет без знака , это обычно означает, что оно положительное .
Пример: 5 на самом деле +5
И мы можем поставить () вокруг цифр, чтобы избежать путаницы.
Пример: 3 × −2 можно записать как (+3) × (−2)
Два Знака: Правила
«Два одинаковых знака дают положительный знак,
два разных знака дают отрицательный знак»
Пример: (−2) × (+5)
Знаки — и + (знак минус и знак плюс), поэтому они не похожи на знаки (они отличаются друг от друга)
Итак, результат должно быть отрицательное :
(−2) × (+5) = −10
Пример: (−4) × (−3)
Знаки — и — (оба знака отрицательные), поэтому они похожи друг на друга (подобны друг другу)
Таким образом, результат должен быть положительным :
(−4) × (−3) = +12
Почему при умножении двух отрицательных чисел получается положительное?
Ну, во-первых, объяснение «здравого смысла»:
Когда я говорю «Ешь!» Я призываю вас есть (положительно)
Но когда я говорю «Не ешьте!» Я говорю обратное (отрицательно).
Теперь, если я скажу: « НЕ НЕ ешьте!», я говорю, что не хочу, чтобы вы голодали, поэтому я снова говорю «Ешь!» (положительно).
Итак, два минуса дают плюс, и если вас это устраивает, то вам больше не нужно читать.
Направление
Все дело в направлении. Помните числовой ряд?
Итак, малыш Стивен делает свои первые шаги. Он делает 2 шага за раз и делает это три раза, поэтому он делает 2 шага x 3 = 6 шагов вперед:
.Малыш Стивен тоже может отступать назад (он умный малыш). Его папа возвращает его в исходное положение, а затем Стивен отступает на 2 шага назад и делает это три раза:
Отец Стивена снова возвращает его в исходное положение, но лицом в другую сторону. Стивен делает 2 шага вперед (для себя!), но движется в отрицательном направлении. Он делает это 3 раза:
Вернувшись в исходное положение снова (спасибо, папа!), по-прежнему глядя в отрицательном направлении, он пытается идти задом наперёд, снова делая два шага за раз, и делает это три раза:
Итак, идя назад, глядя в отрицательном направлении, он движется в положительном направлении.
Попробуйте сами! Попробуйте пройтись вперед и назад, затем еще раз, но лицом в другую сторону.
Играй с этим
Но, может быть, вы хотели бы увидеть его в действии? Используйте ползунки ниже:
числа/изображения/номер-линия-mult.js
Дополнительные примеры
Пример: Деньги
| Сэм дает вам три купюры по 10 долларов: | +3 × +10 = вы получаете 30 долларов | |
| Сэм дает вам три долга по 10 долларов: | +3 × −10 = вы теряете 30 долларов | |
| Сэм берет у вас три купюры по 10 долларов: | −3 × +10 = вы теряете 30 долларов | |
| Сэм берет у вас три долга по 10 долларов: | −3 × −10 = вы получаете 30 долларов |
Пример: видео с бегущими людьми
Люди бегут вперед, видео в обычном режиме:
Все нормально, люди бегут вперед: +1 × +1 = +1
Люди бегут вперед, но видео назад :
Похоже, люди бегут назад: +1 × −1 = −1
Люди бегут Назад , Видео Нормально:
Вы видите людей, бегущих назад: −1 × +1 = −1
Люди Бегут Назад , но Видео в Обратно :
Похоже, люди бегут вперед: − 1 × −1 = +1
Пример: уровень в резервуаре растет/падает
В баке 30 000 литров, каждый день вывозится 1000 литров. Сколько воды было в баке 3 дня назад ?
Сколько воды было в баке 3 дня назад ?
Мы знаем, что количество воды в резервуаре меняется на −1000 каждый день, и нам нужно вычесть это 3 раза (чтобы вернуться на на 3 дня назад ), поэтому изменение равно:
−3 × −1000 = + 3000
Полный расчет:
30000 + (−3 × −1000) = 30000 + 3000 = 33000
Итак, 3 дня назад в баке было 33000 литров воды.
Таблица умножения
Вот другой взгляд на это.
Сначала поиграйте с этим (пояснения ниже):
числа/изображения/mult-grid.js?min=-5&max=5
Начните с таблицы умножения (достаточно до 4×4):
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
Теперь посмотрим, что произойдет, когда мы войдем в негатива !
Пойдем назад через ноль:
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| -4 | -4 | -8 | -12 | -16 |
| -3 | -3 | -6 | -9 | -12 |
| -2 | -2 | -4 | -6 | -8 |
| -1 | -1 | -2 | -3 | -4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
Посмотрите на столбец «4»: там -16, -12, -8, -4, 0, 4, 8, 12, 16 . Получая 4 больше каждый раз.
Получая 4 больше каждый раз.
Просмотрите эту таблицу еще раз, убедитесь, что вам удобно, как она работает, потому что…
… теперь идем дальше налево , через ноль:
| × | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| -4 | 16 | 12 | 8 | 4 | 0 | -4 | -8 | -12 | -16 |
| -3 | 12 | 9 | 6 | 3 | 0 | -3 | -6 | -9 | -12 |
| -2 | 8 | 6 | 4 | 2 | 0 | -2 | -4 | -6 | -8 |
| -1 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| 2 | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 | 8 |
| 3 | -12 | -9 | -6 | -3 | 0 | 3 | 6 | 9 | 12 |
| 4 | -16 | -12 | -8 | -4 | 0 | 4 | 8 | 12 | 16 |
Мы можем следовать по строке (или столбцу), и значения постоянно меняются:
- Следуйте по «4» ряду: это идет -16, -12, -8, -4, 0, 4, 8, 12, 16 .
 Получая 4 больше каждый раз.
Получая 4 больше каждый раз. - Следуйте по строке «-4»: она идет 16, 12, 8, 4, 0, -4, -8, -12, -16 . С каждым разом становится на 4 меньше.
- и т.д…
Итак, все идет по единой схеме!
Также смотрите это в таблице реального умножения.
Как насчет умножения 3 или более чисел вместе?
Умножайте два за раз и следуйте правилам.
Пример. Что такое (−2) × (−3) × (−4) ?
Сначала умножьте (−2) × (−3). Два одинаковых знака дают положительный знак, поэтому:
(−2) × (−3) = +6
Далее умножьте +6 × (−4). Два разных знака дают отрицательный знак, поэтому:
+6 × (−4) = −24
Результат: (−2) × (−3) × (−4) = −24
330, 1615, 1616, 1617, 3447, 3448,331, 1618, 3170, 3171
Умножение отрицательных чисел — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы
Числа меньше нуля называются отрицательными числами. Числа выше нуля являются положительными числами. Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.
Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.
Учащиеся могут загрузить книгу «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» в формате PDF с веб-сайта Vedantu. Любой желающий может бесплатно загрузить PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» с веб-сайта. Умножение отрицаний — очень важная тема математики, по которой на экзаменах задают много вопросов. Правильное понимание темы необходимо для студентов, чтобы получить хорошие оценки на экзаменах. Эта тема важна для конкурсных экзаменов, таких как IIT и NEET. Таким образом, студенты должны приложить надлежащие усилия при изучении темы. Преподавательский состав Веданту, имеющий большой опыт обучения студентов, подготовил PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы».
Учащиеся могут использовать PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» для многих целей. Они могут использовать его для проверки перед экзаменами или для изучения темы.
Они могут использовать его для проверки перед экзаменами или для изучения темы.
Таким образом, учащиеся могут получить массу преимуществ, загрузив PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы».
Некоторые из тем, которые были объяснены в PDF-файле «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы», следующие:
Знаки
Правила умножения отрицательных чисел
Деление отрицательных чисел
Что происходит, когда мы умножаем отрицательные числа?
Знаки
Мы знаем, что «+» — положительный знак, «-» — отрицательный. Когда знак не обозначается перед числом, это обычно означает, что оно положительное.
Пример: 8 на самом деле +8
Примечание: Чтобы избежать путаницы со знаками, мы можем поставить () вокруг цифр. Например, 5 × −8 можно записать как 5 × (−8)
Правила умножения отрицательных чисел
Мы можем иметь положительные и отрицательные целые значения при работе с целыми числами при умножении. Существуют правила умножения и деления целых чисел, которые очень похожи на правила сложения и вычитания.
Если знаки разные, то ответ отрицательный.
Если знаки совпадают, ответ положительный.
См. описание ниже для лучшего понимания.
(Изображение будет загружено в ближайшее время)
Плюс Times Plus is Plus
Пример: 2 × 5 = 10
(Мы уже обсуждали, что если число не имеет знака, это обычно означает, что оно положительное. )
)
(Изображение будет загружено в ближайшее время)
Минус Умножить Минус равно Плюс
Пример: (-10) × (-5) = 50
Отрицательное, умноженное на Отрицательное, является положительным числом, что означает, что произведение двух отрицательных целых чисел всегда положительный.
(Изображение скоро будет загружено)
Плюс умножить на минус = минус
Пример: 5 x (-5) = — 25
Умножение отрицательных чисел на положительное число всегда дает отрицательное число.
(Изображение скоро будет загружено)
Минус Умножить на плюс минус
Примечание. Эти правила работают так же, как и правила деления целых чисел; вам просто нужно заменить «раз» на «делится на».
Деление отрицательных чисел
Деление отрицательных чисел работает так же, как и положительное, за исключением того, что результаты иногда бывают отрицательными. От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.
От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.
Expression | Quotient | Example |
Positive ÷ Positive | Positive | 25 ÷ 5 = + 5 |
Отрицательный ÷ Отрицательный | Положительный | — 25 ÷ — 5 = +5 |
Отрицательный ÷3 0504 | Negative | -25 ÷ 5 = -5 |
Positive ÷ Negative | Negative | 25 ÷ -5 = — 5 |
What happens when we Умножать негативы с помощью матриц?
Целочисленная матрица — это матрица, все элементы которой являются целыми элементами.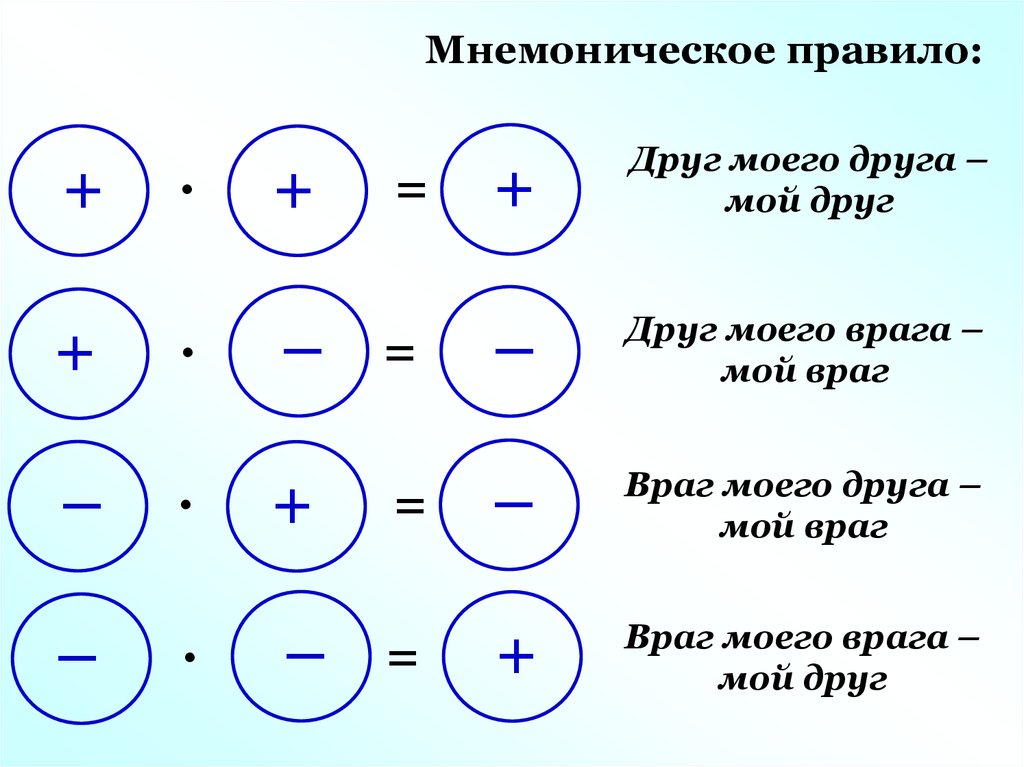 Отрицательное значение матрицы получается путем ее умножения на -1.
Отрицательное значение матрицы получается путем ее умножения на -1.
Итак, если A — заданная матрица
Тогда − A = − 1 A
Решенные примеры
1. Что такое −6 × 3?
Ответ: 6 х 3 равно 18. Но здесь у нас есть одно отрицательное и одно положительное число. Следовательно, знак ответа будет минус.
Следовательно, ответ равен −18.
2. Что такое −80 ÷ 8?
Ответ: 80 ÷ 8 равно 10. Опять же, у нас есть положительное и отрицательное число. Следовательно, в окончательном ответе знак будет отрицательным.
Следовательно, ответ равен −10.
3. Что такое −50 x −5?
Ответ: 50 x 5 равно 250. На этот раз у нас есть 2 отрицательных числа. Значит, в ответе будет положительный знак. Следовательно, ответ равен 250.
Заключение
Помните только 2 вещи, когда перемножаете отрицательные числа.
Почему студенты должны присоединиться к Веданту?
Учащиеся могут посещать онлайн-занятия для сдачи школьного экзамена или конкурсных экзаменов, таких как NEET или JEE. Они могут посещать занятия, не выходя из дома. Им просто нужно иметь работающее подключение к Интернету и устройство, такое как ноутбук, планшет или смартфон. У них также есть возможность скачать классы, чтобы просмотреть их позже для повторения. Студенты могут получить доступ к этим классам по очень доступным ценам, что делает их доступными для многих студентов.
На веб-сайте есть обширный банк вопросов с вопросами, основанными на шаблонах экзаменов, к которым они готовятся. Помимо этого, студенты могут получить доступ к другим ресурсам, таким как заметки о пересмотре, решения NCERT, решения для других книг, образцы документов, PYQ и онлайн-тесты.
Таким образом, присоединение к Веданту будет очень полезно для студентов.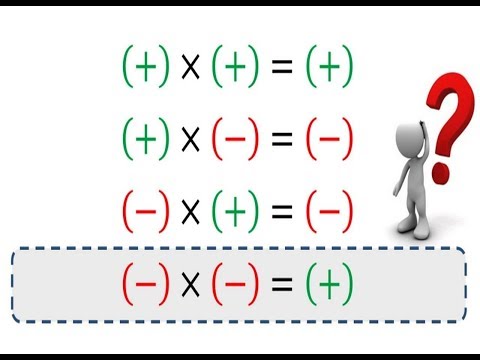
Видео-урок: Порядок действий: Отрицательные числа
Стенограмма видео
отрицательные числа, используя порядок операций.
Начнем с того, что вспомним некоторые ключевые факты об операциях с отрицательными числами. во-первых, правила сложения и вычитания. Прибавление отрицательного числа равносильно вычитанию положительного числа. Так, например, пять плюс минус семь — это то же самое, что пять минус семь. Это минус два. Мы говорим, что вычитание отрицательного числа равносильно добавлению положительного. Таким образом, пять минус минус семь — это то же самое, что пять плюс семь, то есть 12.
Затем мы переходим к правилам умножения и деления. Умножение или деление положительного числа на отрицательное число дает отрицательное
отвечать. Так, например, пять, умноженное на минус семь, дает минус 35, как и минус
пять умножить на семь. И, наконец, умножение или деление двух отрицательных чисел, то есть умножение отрицательного
отрицательным, дает положительный результат. Отрицательные пять, умноженные на отрицательные семь, дают положительное число 35,9.0003
Отрицательные пять, умноженные на отрицательные семь, дают положительное число 35,9.0003
А дальше вспомним, что мы подразумеваем под порядком операций. Это способ гарантировать, что все получат один и тот же ответ при выполнении задания. расчет. Аббревиатуры PEMDAS или BIDMAS сообщают нам порядок выполнения каждой части операции. расчет. Первая буква обозначает скобки или квадратные скобки. Что бы ни находилось внутри любого набора скобок, это первое вычисление, которое мы выполняем. Далее идут показатели или индексы. Мы оцениваем любые числа, возведенные в степень. Затем у нас есть умножение и деление. Так вот, они имеют тот же вес, то же самое значение. Так что, если есть два из них в одной сумме, мы идем слева направо.
Наконец, сложение и вычитание, опять же, имеют одинаковый приоритет. Поэтому, если их два в одной сумме, мы идем слева направо.
Давайте посмотрим, как мы можем объединить всю эту информацию, чтобы выполнить заказ
операции над отрицательными числами.
Заполните пропуск. Минус три минус два минус три равно чему.
Мы хотим оценить это числовое предложение. Всякий раз, когда мы выполняем вычисления, подобные этому, мы всегда должны учитывать Порядок операций. Иногда сокращенно PEMDAS или BIDMAS, это способ гарантировать, что каждый, кто выполняет этот расчет, получает тот же ответ. Первая буква обозначает круглые скобки или скобки BIDMAS. Сначала мы выполняем любые вычисления внутри пары круглых скобок. Обратите внимание, что при выполнении этих расчетов мы также используем порядок операций над любые проблемы в скобках. В этом случае у нас есть минус три минус два. И мы могли бы использовать числовую линию, чтобы оценить это. Начнем с отрицательной тройки на числовой прямой. Вычитание двух означает, что мы перемещаем два вниз по числовой прямой в отрицательном направлении. Так что это один, два, что оставляет нам минус пять. Итак, минус три минус два будет минус пять.
Следующая часть наших аббревиатур говорит нам оценивать любые показатели степени или индексы. И на самом деле, наш расчет не включает ничего из этого. Затем мы выполняем любое умножение или деление. Опять же, в расчете их нет. Однако необходимо выполнить некоторые дополнительные вычитания. Мы заменяем отрицательное число три минус два, бит, который мы вычислили ранее, на отрицательное значение.
пять. Помните, что в противном случае мы сохраняем вычисления в том же порядке. Итак, мы собираемся оценить минус пять минус три.
И на самом деле, наш расчет не включает ничего из этого. Затем мы выполняем любое умножение или деление. Опять же, в расчете их нет. Однако необходимо выполнить некоторые дополнительные вычитания. Мы заменяем отрицательное число три минус два, бит, который мы вычислили ранее, на отрицательное значение.
пять. Помните, что в противном случае мы сохраняем вычисления в том же порядке. Итак, мы собираемся оценить минус пять минус три.
Вернемся к нашей числовой строке. На этот раз мы начинаем с отрицательной пятерки. И мы перемещаемся на одну, две, три позиции вниз по числовой строке. Это приводит нас к отрицательной восьмерке. Таким образом, пробел, являющийся решением отрицательного числа три минус два минус три, равен минус восемь.
На самом деле в этом вопросе нам действительно не нужна была эта пара скобок. У нас были только вычитания в нашей сумме. А мы знаем, что при выполнении сложения и вычитания в одном вычислении мы
просто идите слева направо. Так или иначе, мы бы начали с вычисления минус три минус два, а затем
вычли из этого три.
Так или иначе, мы бы начали с вычисления минус три минус два, а затем
вычли из этого три.
В нашем следующем расчете мы рассмотрим выполнение некоторого умножения.
Вычислить минус 19 умножить на 19 умножить на минус пять умножить на минус два.
Чтобы оценить такой расчет, нам нужно рассмотреть порядок
операции. Помните, часто сокращенно PEMDAS или BIDMAS, это способ гарантировать, что
каждый, кто выполняет это вычисление, получает один и тот же ответ. Каждая буква обозначает определенную операцию. Мы начинаем с P, который обозначает круглые скобки или в BIDMAS означает скобки. Любые расчеты производим внутри нашей скобки. Теперь, в этом случае, у нас есть минус 19, отрицательная пятерка и отрицательная двойка внутри a
пара скобок. На этот раз это не говорит нам выполнить расчет. Нет расчета для выполнения. Это просто способ подчеркнуть, что мы на самом деле работаем с негативными
числа.
Далее у нас есть показатели степени или индексы. Далее следуют умножение и деление. Теперь умножение и деление имеют одинаковый приоритет. Итак, когда они выполняются в одном расчете, мы просто двигаемся слева направо. Правильно. Последние две буквы обозначают сложение и вычитание. И точно так же они имеют такое же значение. Поэтому, когда они у нас есть в одном и том же расчете, мы двигаемся слева направо.
Теперь, если мы посмотрим на наши вычисления, мы увидим, что умножение есть только для
выполнять. Таким образом, мы могли двигаться слева направо. Но есть дополнительный факт, который может быть полезен. И это умножение коммутативно. Это можно делать в любом порядке. Теперь, если бы в этой задаче были какие-либо другие операции, мы не смогли бы использовать эту
факт. Но здесь мы можем. Итак, что мы собираемся сделать, так это вычислить минус 19 умножить на 19 и
минус пять раз два. Причина, по которой это полезно, заключается в том, что мы знаем, что пять умножить на два равно 10. И довольно просто умножить на 10. Мы также знаем, что отрицательное число, умноженное на другое отрицательное число, дает
положительный. Итак, минус пять раз минус два тоже плюс 10.
И довольно просто умножить на 10. Мы также знаем, что отрицательное число, умноженное на другое отрицательное число, дает
положительный. Итак, минус пять раз минус два тоже плюс 10.
Далее мы посчитаем минус 19 умножить на 19. Что ж, начнем с вычисления 19 умножить на 19. И воспользуемся методом сетки. 10 умножить на 10 — это 100, а девять умножить на 10 — это 90. Наконец, девять умножить на девять — это 81. 19, умноженное на 19, — это сумма этих четырех значений; это 361. Это означает, что 19, умноженное на 19, равно 361. Мы знаем, что отрицательное число, умноженное на положительное, дает отрицательный результат. Итак, отрицательное число 19, умноженное на 19, равно отрицательному числу 361. Мы подсчитали, что отрицательное число 19, умноженное на 19, будет отрицательным 361 и пятью отрицательными значениями.
минус два будет 10. Итак, теперь мы собираемся вычислить минус 361, умноженный на 10. Мы знаем, что для умножения на 10 мы перемещаем цифры влево на один пробел. И когда мы это делаем, мы создаем пробел, который заполняем нулем. Таким образом, отрицательное число 361, умноженное на 10, равно отрицательному числу 3610. Таким образом, ответ на отрицательное число 19умножить на 19 умножить на минус пять раз на минус два
отрицательный 3610.
И когда мы это делаем, мы создаем пробел, который заполняем нулем. Таким образом, отрицательное число 361, умноженное на 10, равно отрицательному числу 3610. Таким образом, ответ на отрицательное число 19умножить на 19 умножить на минус пять раз на минус два
отрицательный 3610.
Оценить четыре минус 13 плюс отрицательный 19.
Всякий раз, когда мы пытаемся оценить числовое предложение, мы должны думать о порядок операций. Иногда сокращенно до PEMDAS или BIDMAS, это способ гарантировать, что каждый, кто выполняет этот расчет, получает тот же результат. Первая буква обозначает скобки или квадратные скобки. Мы оцениваем любую сумму внутри скобок. Здесь 13 плюс минус 19..
Теперь нас не должно сбивать с толку, что минус 19 сам находится внутри пары
скобки. В данном случае это не расчет; это просто показывает нам, что мы действительно работаем
с отрицательным числом. Итак, мы вычисляем 13 плюс минус 19. Прибавление минуса равносильно вычитанию плюса. Итак, 13 прибавить минус 19 — это то же самое, что 13 минус 19. И это минус шесть. Мы заменяем выражение в наших скобках на минус шесть, гарантируя, что мы
держите наш вопрос в том же порядке. И получается четыре минус минус шесть.
Прибавление минуса равносильно вычитанию плюса. Итак, 13 прибавить минус 19 — это то же самое, что 13 минус 19. И это минус шесть. Мы заменяем выражение в наших скобках на минус шесть, гарантируя, что мы
держите наш вопрос в том же порядке. И получается четыре минус минус шесть.
На самом деле осталось выполнить только одну операцию. Нет ни показателей, ни индексов, ни умножения, ни деления. У нас просто вычитание. Теперь вспомним, что вычесть минус — это то же самое, что добавить плюс. Итак, четыре минус минус шесть — это то же самое, что четыре плюс шесть, что равно 10. Таким образом, четыре минус 13 плюс минус 19 равно 10.
В нашем следующем примере мы постараемся включить еще несколько операций.
Вычислите 21 минус отрицательное число 19, деленное на пять, умноженное на три.
Всякий раз, когда нам представляют числовое предложение, которое мы хотим оценить
Ответ на, мы должны думать о порядке операций. Возможно, вы знаете, что это PEMDAS или BIDMAS, где каждая буква говорит нам об операции. что делаем и в каком порядке. Итак, давайте вспомним, что означают буквы. Первая буква обозначает скобки или квадратные скобки. Мы выполняем любые вычисления внутри пары круглых скобок. Теперь, если в этих скобках есть довольно сложная задача, мы еще раз
посмотрите, чтобы выполнить порядок операций над этим битом.
что делаем и в каком порядке. Итак, давайте вспомним, что означают буквы. Первая буква обозначает скобки или квадратные скобки. Мы выполняем любые вычисления внутри пары круглых скобок. Теперь, если в этих скобках есть довольно сложная задача, мы еще раз
посмотрите, чтобы выполнить порядок операций над этим битом.
В данном случае у нас просто 21 минус минус 19. И не забывайте, что минус 19 сам заключен в пару круглых скобок. Это просто способ подчеркнуть тот факт, что минус 19 — это минус. количество. Итак, вычислим 21 минус минус 19. Мы знаем, что вычитание отрицательного числа равносильно прибавлению положительного. Так что это то же самое, что 21 плюс 19, что равно 40. Теперь мы заменим это выражение, 21 минус минус 19, на 40 в наших вычислениях. Важно, чтобы мы сохранили порядок, поэтому мы не хотели бы добавлять 40 в конце. конец. Нужно 40 разделить на пять умножить на три.
Вернемся к PEMDAS и BIDMAS. E и I обозначают индексы или показатели степени, другими словами, нахождение степени
количество. Ну, у нас нет сил здесь. Следующие буквы обозначают умножение и деление. Теперь, если у нас есть более одного умножения или деления или умножения и
деления в одном и том же вычислении мы помним, что они имеют одинаковый старшинство или
такое же значение. И мы просто двигаемся слева направо. Мы начнем с вычисления 40, деленного на пять; это восемь. Итак, наш расчет теперь восемь раз три. Восемь раз три — это, конечно, 24. Итак, 21 минус минус 19.разделить на пять, умноженное на три, равно 24.
E и I обозначают индексы или показатели степени, другими словами, нахождение степени
количество. Ну, у нас нет сил здесь. Следующие буквы обозначают умножение и деление. Теперь, если у нас есть более одного умножения или деления или умножения и
деления в одном и том же вычислении мы помним, что они имеют одинаковый старшинство или
такое же значение. И мы просто двигаемся слева направо. Мы начнем с вычисления 40, деленного на пять; это восемь. Итак, наш расчет теперь восемь раз три. Восемь раз три — это, конечно, 24. Итак, 21 минус минус 19.разделить на пять, умноженное на три, равно 24.
В нашем самом последнем примере мы рассмотрим некоторые распространенные заблуждения относительно проблемы. с участием индексов.
Вычислить три раза минус четыре в квадрате минус семь плюс минус два.
Столкнувшись с такой проблемой, нам нужно подумать о порядке
операции. Здесь мы часто используем аббревиатуры PEMDAS или BIDMAS, где каждая буква в аббревиатуре
сообщает нам порядок, в котором мы выполняем вычисления. Первая буква P или B обозначает скобки или квадратные скобки соответственно. Начнем с выполнения любого вычисления внутри пары круглых скобок. Здесь семь плюс минус два. Теперь, конечно, добавить минус то же самое, что вычесть плюс. Таким образом, семь плюс минус два — это то же самое, что семь минус два. И это, конечно, равно пяти. Поэтому в нашем расчете мы заменяем семь плюс минус два на пять. И теперь это трижды минус четыре в квадрате минус пять.
Первая буква P или B обозначает скобки или квадратные скобки соответственно. Начнем с выполнения любого вычисления внутри пары круглых скобок. Здесь семь плюс минус два. Теперь, конечно, добавить минус то же самое, что вычесть плюс. Таким образом, семь плюс минус два — это то же самое, что семь минус два. И это, конечно, равно пяти. Поэтому в нашем расчете мы заменяем семь плюс минус два на пять. И теперь это трижды минус четыре в квадрате минус пять.
Следующая буква E или I обозначает показатели степени или индексы соответственно, другими словами,
любая мощность. Ну, у нас есть один из них. У нас есть минус четыре в квадрате. Итак, давайте оценим минус четыре в квадрате. Распространенным заблуждением является мнение, что минус четыре в квадрате — это минус 16. Но мы знаем, что возводить число в квадрат — это то же самое, что умножать его само на себя. Таким образом, минус четыре в квадрате — это минус четыре, умноженный на минус четыре. А так как умножая отрицательное число на другое отрицательное число, мы получаем положительное
16. Таким образом, мы заменяем минус четыре в квадрате на 16. Теперь наш расчет равен трижды 16 минус пять.
Таким образом, мы заменяем минус четыре в квадрате на 16. Теперь наш расчет равен трижды 16 минус пять.
Следующие две буквы обозначают умножение и деление. Теперь умножение и деление имеют равный приоритет. Поэтому, если в одном и том же расчете появляется более одного, мы двигаемся слева направо. На самом деле у нас здесь только одно умножение. Это три раза по 16. Три умножить на 16 — это 48. Таким образом, мы заменяем трижды 16 на 48. Теперь наш расчет равен 48 минус пять. Теперь еще одна распространенная ошибка здесь заключается в том, чтобы изменить порядок расчета и думаю, что нам нужно выполнить пять минус 48. На самом деле очень важно, чтобы мы сохраняли порядок вычисления.
Наши последние две буквы A и S обозначают сложение и вычитание. Но на самом деле, это все, что осталось сделать в любом случае. Нам нужно получить 48 минус пять. Это 43. Итак, три раза минус четыре в квадрате минус семь плюс минус два равно 43.
В этом видео мы узнали, что нам нужно применить порядок операций ко всем
расчеты, в том числе с отрицательными числами.




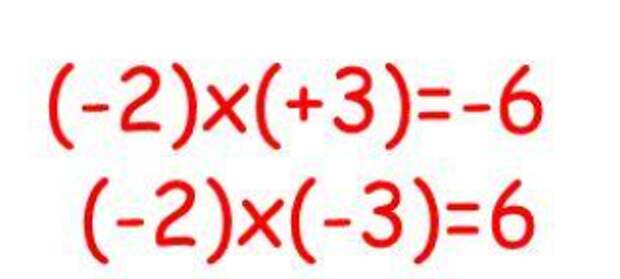 Получая 4 больше каждый раз.
Получая 4 больше каждый раз.