При сложении минус на минус дает плюс правило: Сложение Чисел с Разными Знаками

Что такое положительное минус отрицательное? – Обзоры Вики

):( Положительное число минус отрицательное число превращает двойное отрицательное число в положительное; сложите два числа, и получится положительное число.

Каковы правила для отрицательных и положительных чисел? Правила для положительных и отрицательных чисел

• Положительное число имеет значение больше нуля. …
• Отрицательное число имеет значение меньше нуля. …
• Сумма положительного числа и равного ему отрицательного числа равна нулю.
• Ноль не является ни положительным, ни отрицательным числом.

Дополнительно Как вы добавляете положительный и отрицательный? Добавление положительных и отрицательных чисел

1. Правило 1: Складывание положительных чисел с положительными числами — это обычное сложение.
2. Правило 2. Прибавляя положительные числа к отрицательным числам, считайте сумму, которую вы добавляете, вперед.
3. Правило 3. Прибавляя отрицательные числа к положительным числам, считайте в обратном порядке, как если бы вы вычитали.

Чему равно положительное плюс отрицательное? Когда у вас два отрицательных знака, один переворачивается, и они складываются, чтобы получить позитив. Если у вас есть положительный и отрицательный ответ, останется один штрих, и ответ будет отрицательным.

Как умножить отрицательное на положительное?

Когда вы умножаете отрицательное число на положительное число, ваш ответ отрицательное число. Неважно, в каком порядке находятся положительные и отрицательные числа, в которых вы умножаете, ответ всегда будет отрицательным числом. Ответ: -2 х 4 = -8.

Как умножать и делить отрицательные числа? Умножение и деление отрицательных чисел можно описать следующими правилами:

1. Умножение отрицательного и положительного дает отрицательное.
2. Умножение двух минусов дает плюс.
3. Разделение отрицательного и положительного приводит к отрицательному.
4. При делении двух отрицательных чисел получается положительное.

Что получится, если умножить минус на плюс? Когда вы умножаете отрицательное число на положительное число, то продукт всегда отрицательный.

Как вы выполняете отрицательное правило?

Как сложить положительное число?

Как складывать и вычитать положительные и отрицательные целые числа?

Сложение и вычитание

При сложении или вычитании отрицательных чисел может быть полезно использовать номерная линия . Чтобы складывать и вычитать числа, всегда начинайте отсчет с нуля. При сложении положительных чисел считайте вправо. При вычитании положительных чисел считайте влево.

Какая формула минус плюс?

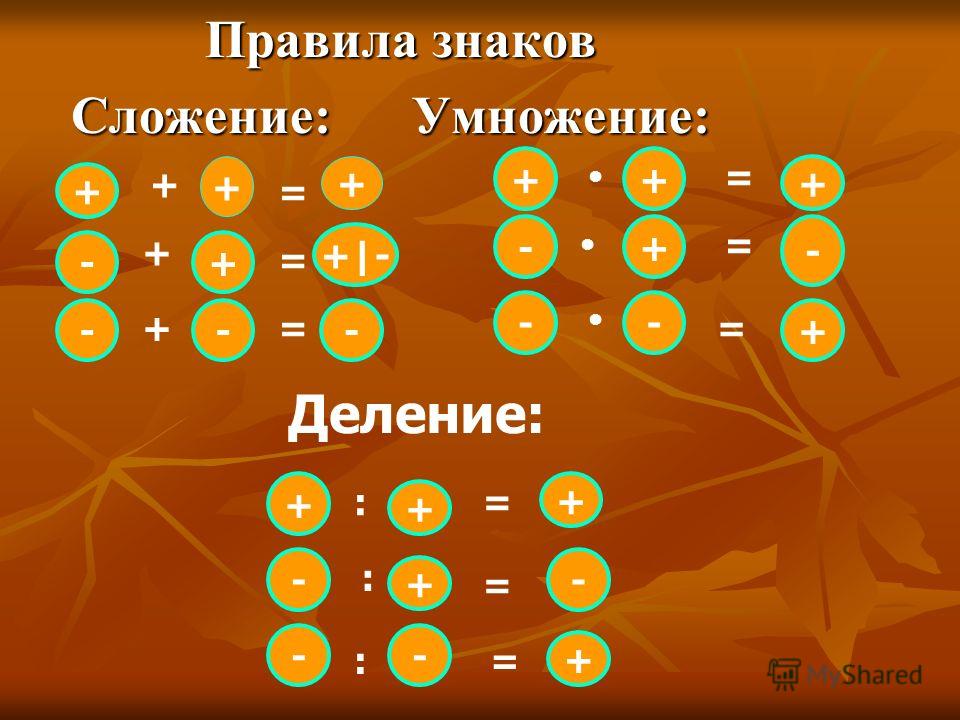
Формулы сложения/вычитания:

(-) + (-) = – (+) + (-) = + (абсолютное значение положительного числа больше) (+) + (-) = – (абсолютное значение отрицательного числа больше)

Что такое минус плюс минус? Хотя верно то, что отрицательное, умноженное на отрицательное, является положительным, отрицательный плюс отрицательный на самом деле отрицательный. При сложении чисел со знаком полезно думать о положительных числах как о выигрыше, а отрицательные числа как о потерях. Потеря плюс убыток — большая потеря.

2 минуса дают плюс при умножении? Тот факт, что продукт из два минуса это плюс это следовательно, это связано с тем фактом, что инверсия инверсии положительного числа снова является этим положительным числом. … Даже в таких общих, нечисловых контекстах свойство, что произведение двух отрицательных вещей положительно, все еще сохраняется.

Как умножить положительное число?

Что получится, если умножить минус на минус? Почему отрицательный раз отрицательный положительный.

Как складывать, вычитать, умножать и делить отрицательные числа?

Что дают два плюса? Когда мы умножаем:

		Пример
×	два положительных результата дают положительный результат:	3 2 × 6 = XNUMX XNUMX
×	два негатива дают положительный результат:	(−3) × (−2) = 6
×	отрицательный и положительный делают отрицательный:	(−3) × 2 = −6
×	положительное и отрицательное составляют отрицательное:	3 × (−2) = −6

2 минуса дают плюс при сложении?

Когда у вас два отрицательных знака, один переворачивается, а они складываются вместе, чтобы сделать положительный.

Почему умножение 2 отрицательных дает положительное? С каждым числом связано «аддитивное обратное» (своего рода «противоположное» число), которое при добавлении к исходному числу дает ноль. … Следовательно, тот факт, что произведение двух отрицаний является положительным, связано с тем, что обратное к положительному числу является обратным положительным числом.

правила и примеры (7 класс)

Основная функция скобок – менять порядок действий при вычислениях значений . Например , в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).

Пример. Раскройте скобку: \(-(4m+3)\).
Решение : \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение : \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Пример. Раскройте скобки \(5(3-x)\).
Решение : В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей

.

Пример. Раскройте скобки \(-2(-3x+5)\).
Решение : Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение : \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:

\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)

Пример. Раскройте скобки \((2-x)(3x-1)\).
Решение : У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.
Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:

Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…

Потом второе.

Шаг 3. Теперь перемножаем и приводим подобные слагаемые:

Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.

Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\) . Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\) . А если подставить минус единицу, получим правило \(-(a-b)=-a+b\) . Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Скобка в скобке

Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).

Чтобы успешно решать подобные задания, нужно:

— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение , просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.

Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:

Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение :

\(-(x+3(2x-1\)\(+(x-5)\) \())\)		Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается.
\(-(x+3(2x-1\)\(+x-5\) \())\)		Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке.
\(=-(x\)\(+3(3x-6)\) \()=\)		Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него.
\(=-(x\)\(+9x-18\) \()=\)
		И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные.

Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.

На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения.

Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.

Тема: Решение уравнений

Урок: Раскрытие скобок

Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.

Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.

Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.

Рассмотрим примеры.

Пример 1.

Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.

Пример 2.

Пример 3.

Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:

Замечание.

Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».

Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.

Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.

Иллюстрирующий пример и правило.

Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.

С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.

Сформулируем правило:

Пример 1.

Пример 2.

Правило не изменяется, если в скобках не два, а три или более слагаемых.

Пример 3.

Замечание. Знаки меняются на противоположные только перед слагаемыми.

Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.

Сначала умножим первую скобку на 2, а вторую — на 3.

Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.

1. Онлайн тесты по математике ().
2. Можно скачать указанные в п. 1.2. книги ().

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
2. Домашнее задание: № 1254, № 1255, № 1256 (б,г)
3. Другие задания: № 1258(в), № 1248

сформировать способность к раскрытию скобок с учетом знака, стоящего перед скобками;

развивающие:

развивать логическое мышление, внимание, математическую речь, умение анализировать, сравнивать, обобщать, делать выводы;

воспитывающие:

формирование ответственности, познавательного интереса к предмету

Ход урока

I. Организационный момент.

Проверь-ка дружок
Ты готов на урок?
Всё ли на месте? Всё в порядке?
Ручка, книжка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?

Начать урок я хочу с вопроса к вам:

Как вы думаете, что самое ценное на Земле? (Ответы детей. )

Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный ученый Аль-Бируни: “Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит”.

Пусть эти слова станут девизом нашего урока.

II. Актуализация прежних знаний, умений, навыков:

Устный счет:

1.1. Какое сегодня число?

2. Расскажите, что вы знаете о числе 20?

3. А где расположено это число на координатной прямой?

4. Назовите число ему обратное.

5. Назовите число ему противоположное.

6. Как называется число – 20?

7. Какие числа называются противоположными?

8. Какие числа называются отрицательными?

9. Чем равен модуль числа 20? – 20?

10. Чему равна сумма противоположных чисел?

2. Объясните следующие записи:

а) Гениальный математик древности Архимед родился в 0 287 г.

б) Гениальный русский математик Н.И.Лобаческий родился в 1792 г.

в) Первые олимпийские игры состоялись в Греции в – 776 г.

г) Первые Международные олимпийские игры состоялись в 1896 г.

д) XXII Олимпийские зимние игры состоялись в 2014 году.

3. Узнайте, какие числа крутятся на “математической карусели” (все действия выполняются устно).

II. Формирование новых знаний, умений, навыков.

Вы научились выполнять разные действия с целыми числами. Чем же будем заниматься дальше? Как будем решать примеры и уравнения?

Давайте найдем значение данных выражений

7 + (3 + 4) = -7 + 7 = 0
-7 + 3 + 4 = 0

Какой порядок действий в 1 примере? Сколько получилось в скобках? Порядок действий во втором примере? Результат первого действия? Что можно сказать об этих выражениях?

Конечно результаты первого и второго выражений одинаковы, значит между ними можно поставить знак равенства: -7 + (3 + 4) = -7 + 3 + 4

Что же мы сделали со скобками? (Опустили.)

Как вы думаете чем мы будем заниматься сегодня на уроке? (Дети формулируют тему урока.) В нашем примере, какой знак стоит перед скобками. (Плюс.)

И так мы подошли к следующему правилу:

Если перед скобками стоит знак +, то можно опустить скобки и этот знак +, сохраняя знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком +.

А как быть, если перед скобками стоит знак минус?

В этом случае нужно рассуждать так же как при вычитании: необходимо прибавить число противоположное вычитаемому:

7 – (3 + 4) = -7 + (-7) = -7 + (-3) + (-4) = -7 – 3 – 4 = -14

– Итак, мы раскрыли скобки, когда перед ними стоял знак минус.

Правило раскрытия скобок, когда перед скобками стоит знак “-“.

Чтобы раскрыть скобки, перед которыми стоит знак -, надо заменить этот знак на +, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.

Давайте послушаем правила раскрытия скобок в стихах:

Перед скобкой плюс стоит.
Он о том и говорит
Что ты скобки опускай
Да все знаки выпускай!
Перед скобкой минус строгий
Загородит нам дорогу
Чтобы скобки убирать
Надо знаки поменять!

Да ребята знак минус очень коварный, это “ сторож” у ворот(скобки), он выпускает числа и переменные только тогда, когда они поменяют “ паспорта”, то есть свои знаки.

Зачем вообще нужно раскрывать скобки? (Когда есть скобки, есть момент какой-то элемент незавершенности, какой-то тайны. Это – как закрытая дверь, за которой находится что-то интересное.) Вот сегодня мы изведали эту тайну.

Небольшой экскурс в историю:

Фигурные скобки появляются в сочинениях Виета (1593). Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и ещё больше Эйлеру.

Физкультминутка.

III. Закрепление новых знаний, умений, навыков.

Работа по учебнику:

№ 1234 (раскройте скобки) – устно.

№ 1236(раскройте скобки) – устно.

№ 1235 (найдите значение выражения) – письменно.

№ 1238 (упростите выражения) – работа в парах.

IV. Подведение итогов урока.

1. Объявляются оценки.

2. Дом. задание. п.39 №1254 (а, б, в),1255 (а, б, в),1259.

3. Чему мы сегодня научились?

Что нового узнали?

И завершить урок я хочу пожеланиями каждому из вас:

“К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай”.

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).

Правило раскрытия скобок при сложении

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.

Пример. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.

(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5

На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Раскрываем скобки при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.

Пример. (9 + 6) : 3=9: 3 + 6: 3

Как раскрыть вложенные скобки

Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.

При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть.

Пример. 12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b

«Раскрытие скобок» — Учебник по математике 6 класс (Виленкин)

Краткое описание:

В этом разделе Вы будете учиться раскрывать скобки в примерах. Для чего это нужно? Все для того же, что и раньше – чтобы Вам было легшее и проще считать, чтобы допускать меньше ошибок, а в идеале (мечта Вашего учителя математики) для того, чтобы вообще все решать без ошибок.
Вы уже знаете, что скобки в математической записи ставятся, если подряд идут два математических знака, если мы хотим показать объединение чисел, их перегруппировку. Раскрыть скобки означает избавиться от лишних знаков. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. А помните распределительное свойство умножения относительно сложения? Ведь в том примере мы также избавлялись от скобок для упрощения вычислений. Названное свойство умножения также можно применять для четырех, трех, пяти и более слагаемых. Для примера: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы заметили, что при раскрытии скобок числа, находящиеся в них не меняют знака, если стоящее перед скобками число положительное? Ведь пятнадцать – положительное число. А если решить такой пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+(-120)+(-135)+(-90)=-45-120-135-90=-390. У нас перед скобками стояло отрицательное число минус пятнадцать, когда мы раскрыли скобки все числа стали менять свой знак на другой — противоположный – с плюса на минус.
Исходя из вышеуказанных примеров, можно озвучить два основных правила раскрытия скобок:
1. Если у Вас перед скобками стоит положительное число, то после раскрытия скобок все знаки чисел, стоявших в скобках, не изменяются, а остаются точно такими же как и были.
2. Если у Вас перед скобками стоит отрицательное число, то после раскрытия скобок знак минуса больше не пишется, а знаки всех абсолютно чисел, стоявших в скобках, резко меняются на противоположные.
Для примера: (13+8)+(9-8)=13+8+9-8=22; (13+8)-(9-8)=13+8-9+8=20. Немного усложним наши примеры: (13+8)+2(9-8)=13+8+2*9-2*8=21+18-16=23. Вы заметили, что раскрывая вторые скобки, мы умножали на 2, но знаки оставались теми же как и были. А вот такой пример: (3+8)-2*(9-8)=3+8-2*9+2*8=11-18+16=9, в этом примере число два — отрицательное, оно перед скобками стоит со знаком минус, поэтому раскрывая их, мы меняли знаки чисел на противоположные (девять было с плюсом, стало с минусом, восемь было с минусом, стало с плюсом).

Что такое правило плюс-минус?

Если два положительных числа умножить или разделить, то ответ положительный. Если два отрицательных числа перемножить или разделить, то ответ положительный. Если положительное и отрицательное число умножить или разделить, ответ будет отрицательным.

Запрос на удаление

| Просмотреть полный ответ на ревизии maths.com

Какое правило для +-?

++ и −− работают как сложение положительного числа. +− и −+ работают как вычитание положительного числа.

Запрос на удаление

| Посмотреть полный ответ на mathcentre.ac.uk

Какова формула плюс-минус?

Формулы сложения/вычитания:

(-) + (-) = — (+) + (-) = + (абсолютное значение положительного числа больше) (+) + (-) = — (абсолютное значение отрицательного число больше)

Запрос на удаление

| Посмотреть полный ответ на cuemath. com

Каковы 4 правила числа?

«4 правила» (сложение, вычитание, умножение и деление) лежат в основе расчетов и решения задач. За прошедшие годы в школах был принят ряд методов обучения, и иногда бывает так, что опыт родителей не совпадает с опытом их детей.

Запрос на удаление

| Посмотреть полный ответ на blsschool.co.uk

Каковы правила для отрицательных и положительных целых чисел?

ПРАВИЛО 1: Произведение положительного целого числа на отрицательное число отрицательно. ПРАВИЛО 2: Произведение двух натуральных чисел положительно. ПРАВИЛО 3: Произведение двух отрицательных целых чисел положительно. ПРАВИЛО 1: Частное положительного целого числа и отрицательного целого числа отрицательно.

Запрос на удаление

| Посмотреть полный ответ на mgccc.edu

Выучите положительные и отрицательные числа — простой совет, чтобы запомнить правила!

Каковы 3 правила сложения целых чисел?

Каковы правила сложения целых чисел?

• Сумма целого числа и его обратной аддитивной величины равна 0. …
• Сложение двух положительных целых чисел всегда приводит к положительному значению, которое больше обоих целых чисел. …
• Сложение двух отрицательных целых чисел всегда приводит к отрицательному числу, которое меньше заданных чисел.

Запрос на удаление

| Посмотреть полный ответ на cuemath.com

Каковы 3 правила вычитания целых чисел?

Правила вычитания целых чисел

• Положительный — положительный = положительный, если первое целое число больше.
• Положительный — положительный = отрицательный, если второе целое число больше.
• Отрицательный — Отрицательный = отрицательный, если первое целое число больше.
• Отрицательный — Отрицательный = положительный, если второе целое число больше.

Запрос на удаление

| Посмотреть полный ответ на сайте Study.com

Что на первом месте плюс/минус или умножить?

Возвращаясь к приведенному выше примеру, правильным ответом будет первый ответ, поскольку он следует правилам BODMAS: деление может быть выполнено до умножения и должно быть выполнено до сложения, а умножение предшествует сложению.

Запрос на удаление

| Посмотреть полный ответ на ncl.ac.uk

Что такое правило 5 в математике?

Правило пяти — это эмпирическое правило в статистике, которое оценивает медиану совокупности путем выбора случайной выборки из пяти человек из этой совокупности. В нем говорится, что существует вероятность 93,75%, что медианное значение совокупности находится между наименьшим и наибольшим значениями в любой случайной выборке из пяти.

Запрос на удаление

| Посмотреть полный ответ на techtarget.com

Каковы законы математики?

Три наиболее широко обсуждаемых закона — это коммутативный, ассоциативный и распределительный законы. С годами люди обнаружили, что когда мы складываем или умножаем, порядок чисел не влияет на результат.

Запрос на удаление

| Посмотреть полный ответ на whatcom.edu

Как вы учите плюс-минус?

Практикуйте сложение и вычитание с предметами один раз в день. Возьмите за привычку в течение часа заниматься с ребенком сложением и вычитанием, используя предметы и карточки. Поработайте над сложением и вычитанием больших чисел с помощью объектов. Используйте новые карточки с дополнениями на них.

Запрос на удаление

| Посмотреть полный ответ на wikihow.com

Почему 2 минус плюс?

Таким образом, тот факт, что произведение двух отрицательных чисел является положительным, связан с тем фактом, что инверсия инверсии положительного числа снова является этим положительным числом.

Запрос на удаление

| Посмотреть полный ответ на math.toronto.edu

Каковы базовые математические знания для 7-го класса?

Некоторые темы, связанные с математикой 7 класса, следующие:

• Система счисления.
• Целые числа.
• Дроби.
• Десятичные числа.
• Измерение.
• Алгебра.
• Соотношение и пропорция.

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Как написать правило?

Написание правил и положений

1. Следуйте стандартной структуре схемы правил.
2. Добавьте любые маркированные или нумерованные списки в основную структуру документа.
3. Используйте в документе встроенную структуру заголовков вашего программного обеспечения для письма.
4. Используйте заголовки последовательно и везде, где это возможно.

Запрос на удаление

| Посмотреть полный ответ на eregs. github.io

Что такое шаблон правила?

Правило шаблона — это математическое отношение, используемое для нахождения значения каждого термина в последовательности. Для описания определенных последовательностей можно установить правило шаблона. Это алгебраическое уравнение, позволяющее быстро найти значение термина в последовательности, используя его ранг.

Запрос на удаление

| Посмотреть полный ответ на alloprof.qc.ca

Что такое пример правила?

Техника обучения понятиям, при которой учитель представляет правило или определение на примерах, а затем демонстрирует, как примеры соответствуют правилу.

Запрос на удаление

| Посмотреть полный ответ на theedadvocate.org

Что такое Bodmas?

БОДМАС — это аббревиатура, помогающая детям запомнить порядок математических операций — правильный порядок решения математических задач. Bodmas означает B-скобки, O-порядки (степени/индексы или корни), D-деление, M-умножение, A-сложение, S-вычитание.

Запрос на удаление

| Посмотреть полный ответ на сайте Thirdspacelearning.com

Вы сначала складываете или умножаете?

При необходимости напомните им, что по порядку операций умножение и деление предшествуют сложению и вычитанию.

Запрос на удаление

| Посмотреть полный ответ на hmhco.com

Почему мы используем Bodmas?

Когда вы завершаете математическое числовое предложение, включающее несколько различных операций, BODMAS помогает вам узнать, в каком порядке их выполнять. Все, что указано в скобках, должно быть завершено сначала, затем порядок, затем любое деление или умножение и, наконец, сложение или вычитание.

Запрос на удаление

| Посмотреть полный ответ на theschoolrun. com

Каков правильный порядок математики?

Мы можем запомнить порядок, используя PEMDAS: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо).

Запрос на удаление

| Посмотреть полный ответ на сайте khanacademy.org

Какая математическая операция идет первой?

Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, сложение и вычитание слева направо. Во-первых, начните со скобок.

Запрос на удаление

| Посмотреть полный ответ на сайте mometrix.com

Кто первым использует плюс и минус?

Символы «плюс» и «минус» стали широко использоваться в Англии только после того, как их использовал Роберт Рекорд в 1557 году в «Точилочном камне Витте». Рекорд писал: «Есть два других часто используемых знака, из которых первый сделан таким образом + и означает больше; другой сделан таким образом — и означает меньше».

Запрос на удаление

| Посмотреть полный ответ на mathshistory.st-andrews.ac.uk

Каковы 4 правила вычитания целых чисел?

Целочисленное вычитание

• Сначала сохраните первое число (известное как уменьшаемое).
• Во-вторых, измените операцию с вычитания на сложение.
• В-третьих, получить знак, противоположный второму числу (известному как вычитаемое)
• Наконец, продолжить обычное сложение целых чисел.

Запрос на удаление

| Посмотреть полный ответ на chilimath.com

Каковы два правила вычитания?

Правила. Сложение и вычитание однозначных чисел.
…
Правила

• Сложение двух положительных чисел всегда положительно.
• Сложение двух отрицательных чисел всегда отрицательно.
• Вычитание двух положительных чисел может быть как положительным, так и отрицательным.
• Вычитание двух отрицательных чисел может быть как положительным, так и отрицательным.

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Какое первое правило вычитания целых чисел?

Чтобы вычесть два целых числа, прибавьте противоположное второму целому числу к первому целому числу. Это можно записать символически как a — b = a + (-b).

Запрос на удаление

| Посмотреть полный ответ на alamo.edu

← Предыдущий вопрос
Как вы называете комнату в комнате?

Следующий вопрос →
Какие 3 растяжки выполнить сложнее всего?

Делают ли два минуса плюс? (1)

За последние несколько недель я посетил несколько классов 7, 8 и 9 классов, и одной из областей моего внимания были целые числа. Ни для кого не секрет, что целые числа могут быть проблематичными для многих студентов (и, я бы добавил, для взрослых). В беседе с некоторыми студентами я слышал такие фразы, как «Два минуса дают плюс»: так ли это на самом деле? Я видел, как студенты использовали это правило, чтобы потом сказать, что ¯3+¯3=6. Меня беспокоит то, что у студентов развились неправильные представления, потому что они перескакивали прямо к абстрактной части конкретно-диаграмма-абстрактной части этого континуума. Итак, вот некоторые упражнения, которые я использовал, чтобы помочь им пройти конкретную и диаграммную фазы, чтобы они могли понять смысл абстрактного:

1) Моя первая цель — научить учащихся складывать целые числа. Как и многие учителя, я использую плитки с целыми числами для конкретного представления целых чисел:

. Я говорю учащимся, что это самая важная концепция: если красная плитка представляет отрицательную 1, а желтая — положительную 1, то вместе они составляют одноименную «нулевую пару». Каждый раз, когда они видят нулевую пару, она представляет собой значение 0 (даже если вы видите две плитки).
Затем я прошу учащихся использовать плитки для обозначения таких величин, как ¯3 и 5:9.0003

Затем я прошу их использовать эти два набора для решения ¯3+5. Что полезно здесь, так это фактическое сложение (т.е. объединение двух групп) мы получаем что-то вроде этого:

Затем я даю ученикам другие примеры для работы:

Одна из вещей, которую я собираюсь сделать здесь, это заставить студентов визуализировать решение. Например, в четвертом вопросе выше учащиеся (которые использовали плитки для первых трех вопросов) смогли изобразить (мысленно или с помощью линейки) 19желтые плитки соединяются с 19 красными плитками (что дает 19 нулевых пар), оставляя 4 красные плитки, или отрицательные 4. 
После достаточного количества этих примеров я прошу учащихся закончить это утверждение:

Вскоре все пришли к единому мнению, что это то же самое, что вычитание положительного. Это намного лучше, чем говорить «минус и плюс дают минус».

2) После того, как мы установили, что добавление отрицательного значения равносильно вычитанию положительного, я хотел бы показать, как мы можем использовать числовую прямую, чтобы показать это:

Некоторым ученикам этот способ очень нравится, другим — меньше, но я позволяю им выбирать, какой метод им больше всего подходит.

3) Вычитание целых чисел также может быть смоделировано с помощью плиток целых чисел, но мне всегда нравилось представлять это таким образом. Сначала я вызываю трех студентов и даю каждому из них по четыре карточки. У двух из них есть карты с номерами от 1 до 4, а у третьего есть карты с номерами от ¯4 до ¯1. Затем я рассказываю очень, очень банальную шутку, например: «Как вы называете муху без крыльев? Прогулка!» и попросите студентов поставить мне оценку за мою шутку. Например, я мог бы получить это:

Я симулирую разочарование по поводу ученицы, которая поставила мне отрицательную оценку, и класс смеется над этим. Затем мы получаем мою сумму, в данном случае 4+2+¯3 дает 3. В этот момент я выражаю решительный протест против студента, который поставил мне отрицательную оценку до такой степени, что я требую, чтобы эта оценка была удалена и Я «провожаю» их в угол комнаты. Опять смех кругом. Затем я возвращаюсь к остальным ученикам:

Затем я спрашиваю студентов, какой у меня «новый» балл, и они говорят мне 6. Затем я говорю: «Мы начали с 3 и закончили с 6. Но что произошло между ними?» Ответ обычно такой: «Вы забрали минус 3». Затем я записываю, что они сказали:

Я повторяю это еще для пары плохих шуток, затем прошу их посмотреть на результаты и закончить это предложение:

Вычитание минуса равносильно…

консенсус заключается в том, что вычитание отрицательного равносильно добавлению положительного. Это сногсшибательно для некоторых студентов, и я говорю им, что могу понять, почему они могут найти это нелогичным, но это потому, что они всегда верили, что вычитание уменьшает.