Логарифмы: примеры и решения
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной.
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.
Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2.
 Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать. - Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм .
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения , но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
log 2 x = 4
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются —
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c одержали, обязательно нужно привести к уравнению вида:
log a f (x ) = log a g (x )
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел , одно из которых вообще не является логарифмом.

- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения , к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
log a f (x ) + log a g (x ) = log a f (x ) · g (x )
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
a = log b b a
Здесь нужно понимать: когда мы говорим «Любое основание b », то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения , а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
0
Давайте посмотрим, что происходит в нашем случае:
1 = log 2 2 1 = log 2 2
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания . Переходим к следующему шагу.
Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
log a b n = n · log a b
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k .
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n
), окажется в числителе. А то, что было степенью у основания, a
k
, отправится в знаменатель.
При этом то, что стояло в аргументе (в нашем случае это коэффициент n
), окажется в числителе. А то, что было степенью у основания, a
k
, отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log 2 2(9x 2 + 5) = log 2 (8x 4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9x 2 + 5) = 8x 4 + 14
Давайте раскроем скобки слева. Получим:
18x 2 + 10 = 8x 4 + 14
Перенесем все из левой части в правую:
8x 4 + 14 − 18x 2 − 10 = 0
Приведем подобные и получим:
8x 4 − 18x 2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4x 4 − 9x 2 + 2 = 0
Перед нами обычное биквадратное уравнение , и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x , а x 2 , потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная . И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x 2 + 5 (эта функция всегда положительна), либо 8x 4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9
Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.
Рациональные корни
Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1.
 Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.
Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ. - Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат , чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81
Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b , именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Примеры решения задач с логарифмами
Логарифмы (Логарифмирование)активно используются при решении задач, так как они значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение гораздо более простым сложением, деление на вычитание, а возведение в степень и извлечение корня заменяются умножением и делением на степень числа соответственно.
Прежде чем изучать примеры решения задач, мы советуем вам изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов. {2}-4=0 \Rightarrow(x-2)(x+2) \Rightarrow x_{1}=2, x_{2}=-2
\)
{2}-4=0 \Rightarrow(x-2)(x+2) \Rightarrow x_{1}=2, x_{2}=-2
\)
Оба значения принадлежат ОДЗ.
Логарифмические неравенства
ПРИМЕР
Перейдем к неравенствам от логарифмов к выражениям под знаком логарифма, в то время как основание логарифма меньше единицы (0,5 \(\ x-1На пересечении с ОДЗ мы находим, что \(\ x \in(1 ; 3) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Логарифмические уравнения Логарифмическая функция Десятичный логарифм Натуральный логарифм
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Как найти значение выражения с логарифмами — Dudom
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
*Переход к новому основанию
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Например:
Следствие из данного свойства:
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
При возведении в степень произведения в эту же степень возводится каждый множитель.
Так же необходимо знать следующее свойство:
*Данный контент (более 20 подробно решённых примеров) доступен только для зарегистрированных пользователей! Вкладка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После прохождения регистрации войдите на сайт и обновите данную страницу.
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
В этой статье вы познакомитесь со всеми типами логарифмических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.
16 видео помогут вам понять как использовать свойства логарифмов при упрощении логарифмических выражений.
Вы можете попытаться решить каждый пример самостоятельно, и затем свериться с ответом. А можете сначала посмотреть видео с решением аналогичного задания.
Пример 1. Найти значение выражения:
Видеорешение аналогичного задания:
Пример 2. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 3. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
youtube.com/embed/b09K5PDTxhY»>Пример 4. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 5. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 6. Найти значение выражения:
Видеорешение аналогичного задания:
Пример 7. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 8. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 9. Найти значение выражения:
Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 10. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 11. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 12. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 13. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 14. Найти значение выражения:
Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 15. Найти значение выражения:
Посмотреть ответ:
Видеорешение аналогичного задания:
Пример 16. Найти значение выражения:
Видеорешение аналогичного задания:
Логарифм по основанию (a) от (b) – это число (t) , которое показывает, в какую степень нужно возвести (a) , чтобы получить (b) .
Ограничения: числа (a) и (b) такие, что (a>0, a
e 1, b>0) .
Таким образом, верно основное логарифмическое тождество [Large<<color=t>>>]
Т.к. мы имеем право возводить в любую степень, то (tin mathbb) .
(lacktriangleright) Если (a,b,c) – числа, удовлетворяющие ограничениям: (a,b,c>0, a
e 1) , то справедливы следующие формулы:
[egin <|ccc|>hline extbf <(1)>log_a1=0&& extbf <(2)>log_aa=1\ &&\ extbf <(3)>log_=frac mnlog_ab&& extbf <(4)>a^<log_bc>=c^<log_ba>\ &&\ extbf <(5)>log_a=log_ab+log_ac&& extbf <(6)>log_a<dfrac bc>=log_ab-log_ac\ &&\ extbf <(7)>log_abcdot log_bc=log_ac & ext <или>& extbf<(7′>) log_bc=dfrac<log_ac><log_ab>\ &&\ hline end]
Заметим, что при выполнении ограничений данные формулы верны в обе стороны!
Некоторые частные случаи, которыми удобно пользоваться:
(lacktriangleright) Частные случаи формул (3) и (4): [m=log_a ext <и> b=a^<log_ab>]
С помощью первой формулы нагляднее видно, как заменить число на логарифм по нужному основанию:
(4=log_2<2^4>=log_2<16>) ;
а с помощью второй – как заменить число на степень с нужным основанием:
(4=3^<log_34>) .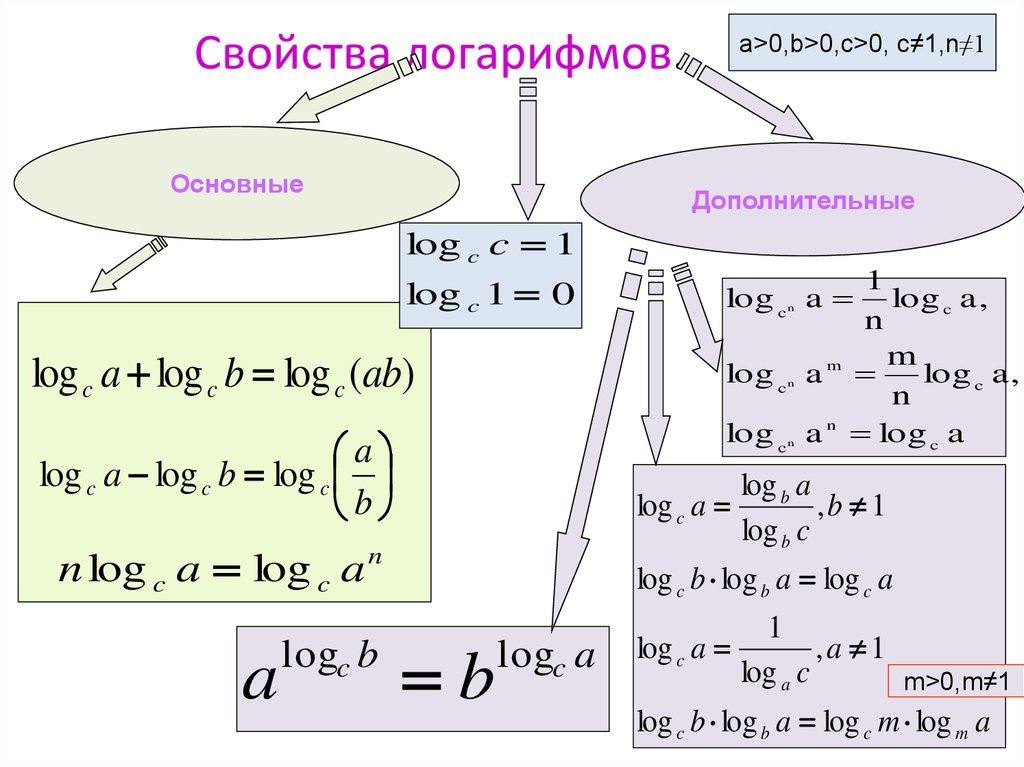
Что такое логарифмы? | Живая наука
Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.
Большинство научных калькуляторов вычисляют логарифмы только по основанию 10 и основанию e. (Изображение предоставлено: Bildagentur Zoonar GmbH | Shutterstock )Логарифм — это математическая операция, определяющая, сколько раз определенное число, называемое основанием, умножается само на себя, чтобы получить другое число. Поскольку логарифмы связывают геометрические прогрессии с арифметическими прогрессиями, примеры можно найти в природе и искусстве, например, расстояние между гитарными ладами, твердость минералов и интенсивность звуков, звезд, ураганов, землетрясений и кислот. Логарифмы даже описывают то, как люди инстинктивно думают о числах.
Логарифмы были изобретены в 17 веке шотландским математиком Джоном Нейпиром (1550–1617) в качестве инструмента для вычислений, который ввел этот термин из греческих слов, обозначающих соотношение ( logos ) и число ( arithmos ). До изобретения механических (а позже и электронных) калькуляторов логарифмы были чрезвычайно важны для упрощения вычислений, применяемых в астрономии, навигации, геодезии, а затем и в инженерии.
До изобретения механических (а позже и электронных) калькуляторов логарифмы были чрезвычайно важны для упрощения вычислений, применяемых в астрономии, навигации, геодезии, а затем и в инженерии.
Пример: складывание бумаги
Логарифмы характеризуют, сколько раз нужно сложить лист бумаги, чтобы получилось 64 слоя. Каждый раз, когда вы складываете бумагу пополам, количество слоев удваивается. С математической точки зрения, 2 (основание), умноженное на себя определенное количество раз, равно 64. Сколько умножений необходимо? Этот вопрос записывается как:
log 2 (64) = x
Логарифм можно рассматривать как обратную экспоненте, поэтому приведенное выше уравнение имеет тот же смысл, что и:
2 x = 64
х 2 х 2 х 2 х 2 = 64, 2 6 = 64. Это означает, что если мы согнем лист бумаги пополам шесть раз, он будет иметь 64 слоя. Следовательно, логарифм по основанию 2 числа 64 равен 6, поэтому log 2 (64) = 6.
Другой пример: измерение молекул
Когда вы берете 1 миллилитр жидкости, добавьте 99 мл воды, смешать раствор, а затем взять образец объемом 1 мл, 99 из каждых 100 молекул исходной жидкости заменяются молекулами воды, то есть остается только 1/100 молекул исходной жидкости. Иногда это называют «разбавлением C» от римской цифры «сотня». Учитывая, что 1 мл чистого спирта содержит примерно 10 22 (единица с 22 нулями) молекул, сколько потребуется разбавлений C, пока все, кроме одной молекулы , не будут заменены водой? Математически говоря, 1/100 (основание), умноженное на себя определенное количество раз, равно 1/10 22 , так сколько умножений необходимо? Этот вопрос записывается так:
log 1/100 (1/10 22 ) = 11
Таким образом, после разведения на 11 C останется только одна молекула исходного спирта. (Кроме того, это меньше половины 30-градусных разведений, распространенных в гомеопатии, что показывает, почему эта практика несовместима с современной химией. ) log(x) для десятичного логарифма и основания e , записанное как ln(x) для натурального логарифма (причина, по которой буквы l и n расположены наоборот, утеряна для истории). Число e , равное примерно 2,71828, является иррациональным числом (как пи) с неповторяющейся последовательностью десятичных знаков, простирающейся до бесконечности. Естественно возникающий в результате развития логарифмов и исчисления, он известен как постоянная Непера и число Эйлера в честь Леонарда Эйлера (1707–1783), швейцарского математика, который развил эту тему столетие спустя.
) log(x) для десятичного логарифма и основания e , записанное как ln(x) для натурального логарифма (причина, по которой буквы l и n расположены наоборот, утеряна для истории). Число e , равное примерно 2,71828, является иррациональным числом (как пи) с неповторяющейся последовательностью десятичных знаков, простирающейся до бесконечности. Естественно возникающий в результате развития логарифмов и исчисления, он известен как постоянная Непера и число Эйлера в честь Леонарда Эйлера (1707–1783), швейцарского математика, который развил эту тему столетие спустя.
Чтобы логарифмировать по основанию, отличному от 10 или e , мы используем свойство, присущее логарифмам. В нашем первом примере выше log 2 (64) можно ввести в калькулятор как «log(64)/log(2)» или «ln(64)/ln(2)»; любой из них даст желаемый ответ 6. Аналогично, log 1/100 (1/10 22 ) равно «log(1/10 22 )/log(1/100)» и «ln(1/ 10 22 )/ln(1/100)» для ответа 11.
Логарифмические шкалы в науке
Поскольку логарифмы связывают мультипликативные изменения с постепенными изменениями, логарифмические шкалы появляются в удивительном количестве научных и повседневных явлений. Возьмем, к примеру, интенсивность звука: чтобы увеличить громкость динамика на 10 децибел (дБ), необходимо подать на него в 10 раз большую мощность. Аналогично, для +20 дБ требуется в 100 раз больше мощности, а для +30 дБ — в 1000 раз. Говорят, что децибелы «растут арифметически» или «изменяются по логарифмической шкале», потому что они изменяются пропорционально логарифму какого-либо другого измерения; в данном случае мощность звуковой волны, которая «прогрессирует геометрически» или «изменяется в линейной шкале».
| Линейная шкала | Логарифмическая шкала | |||||
| Интенсивность звука | Power [× 10] | ↔ | Decibels (DB) | 808080808181818181818181818181818 гг. 2] | ↔ | ПРИМЕЧАНИЕ [+12 Половина шагов] |
| Яркость звезды | мощность на единицу площади [× 100] | ↔ | Magnity [-5] | |||
| [-5] | ||||||
8080. 0080 Energy [×1000] 0080 Energy [×1000] | ↔ | Richter Scale [+2] | ||||
| Wind intensity | Wind speed [×1.5] | ↔ | Beaufort Scale [+1] | |||
| Mineral hardness | Абсолютная жесткость [×3 (прибл.)] | ↔ | Шкала Мооса [+1] | |||
| Кислотность/основность | Концентрация ионов H+ [×10] | ↔ 90 pH | 1 |
Таблица показывает, что числа, относящиеся к различным линейным и логарифмическим системам, сильно различаются. Это связано с тем, что логарифмическая шкала часто сначала изобретается как метод характеристики без глубокого понимания измеримых явлений, стоящих за этой характеристикой. Хорошим примером является яркость звезд, которую ввел Гиппарх, живший во втором веке до нашей эры. Греческий астроном. Считалось, что самые яркие звезды на ночном небе имеют первую величину (m = 1), а самые слабые — шестую величину (m = 6). В 19В 20-м веке нашей эры английский астроном Норман Роберт Погсон обнаружил, что звездная величина представляет собой логарифм количества звездного света, попадающего на детектор.
Большинство других логарифмических шкал имеют аналогичную историю. То, что логарифмические шкалы часто идут первыми, предполагает, что они в некотором смысле интуитивно понятны. Это связано не только с нашим восприятием, но и с тем, как мы инстинктивно думаем о числах.
Линейный преподается; Логарифмическое — инстинктивное
Хотя логарифмические шкалы вызывают затруднения у многих (если не у большинства) студентов-математиков, они, как ни странно, во многом связаны с тем, как все мы инстинктивно думали о числах в младенчестве. Станислас Деан, профессор Коллеж де Франс и эксперт по распознаванию чисел, записал мозговую активность двух-трехмесячных младенцев, чтобы посмотреть, как они воспринимают изменения на экране компьютера. Переход от восьми уток к 16 уткам вызвал активность в теменной доле, показывая, что у новорожденных есть интуиция чисел. Реакция младенца тем меньше, чем ближе числа расположены друг к другу, но что интересно, так это то, как младенец воспринимает «близость». Например, восьмерка и девятка воспринимаются гораздо ближе друг к другу, чем единица и двойка. По словам Дехане, «похоже, их заботит логарифм числа». По сути, младенцы не думают о различиях, они думают о соотношениях.
Например, восьмерка и девятка воспринимаются гораздо ближе друг к другу, чем единица и двойка. По словам Дехане, «похоже, их заботит логарифм числа». По сути, младенцы не думают о различиях, они думают о соотношениях.
Исследование коренных жителей Амазонки, у которых «нет слов-числительных, кроме пяти, и они не произносят эти числа наизусть», показывает, что люди, если оставить их наедине со своими инстинктами, будут продолжать думать таким образом. Если кому-то показать один предмет слева и девять справа и спросить: «Что находится посередине?», мы с вами выберем пять предметов, но средний амазонец выберет три. Если думать в терминах отношений и логарифмических шкал (а не разностей и линейных шкал), один раз три равно трем, а трижды три равно девяти, поэтому три находится посередине между единицей и девятью.
Историческая мотивация развития логарифмов
Работа Джона Нэпьера 1614 года «Mirifici Logarithmorum Canonis Descriptio» («Описание чудесного канона логарифмов») содержала 90 страниц числовых таблиц, относящихся к логарифмам. Они были особенно полезны для упрощения вычислений. В следующем примере метод с использованием логарифмов использует тот факт, что проще складывать, чем умножать. Следующий пример на самом деле не стал проще, но он демонстрирует процесс использования логарифмических таблиц.
Они были особенно полезны для упрощения вычислений. В следующем примере метод с использованием логарифмов использует тот факт, что проще складывать, чем умножать. Следующий пример на самом деле не стал проще, но он демонстрирует процесс использования логарифмических таблиц.
37 × 59
Из версии таблиц Нейпира каждое из этих чисел может быть записано следующим образом: 10 1,5682 + 1,7709
, который оставляет:
10 3.3391
Из другой таблицы определяется окончательный ответ:
2183
Правила слайда
. методика расчета: Логарифмическая линейка . Для сложения чисел можно использовать две обычные (линейные) линейки, как показано на рисунке:
Линейные линейки можно использовать для сложения. Здесь показано, что 2 + 3 = 5. (Изображение предоставлено Робертом Дж. Кулманом) Подобно процедуре, показанной выше, две линейки можно использовать для умножения при печати в логарифмическом масштабе.
Эти отметки также соответствуют расстоянию между ладами на грифе гитары или укулеле. Музыкальные ноты различаются по логарифмической шкале, потому что все более высокие октавы (концы музыкальной гаммы) воспринимаются человеческим ухом как равномерно распределенные, даже если они создаются путем многократного разрезания струны пополам (умножения на ½). Между грифом и серединой гитарной струны будет 12 логарифмически расположенных ладов.
Дополнительные ресурсы
- Природа. Почему мы должны любить логарифмы (открывается в новой вкладке) Академия: Учебник по логарифму
Роберт Кулман, доктор философии, преподаватель и независимый научный писатель, живет в Мэдисоне, штат Висконсин. Он писал для Vice, Discover, Nautilus, Live Science и The Daily Beast. Роберт защитил докторскую диссертацию, превращая опилки в бензиновое топливо и химикаты для материалов, медицины, электроники и сельского хозяйства. Он сделан из химических веществ.
Он сделан из химических веществ.
Использование логарифмов в реальном мире – BetterExplained
Логарифмы повсюду. Вы когда-нибудь использовали следующие фразы?
- 6 фигурок
- Двойные цифры
- Порядок величины
- Процентная ставка
Вы описываете числа с точки зрения их степени 10, логарифма. А процентная ставка — это логарифм роста инвестиций.
Удивлены, что логарифмы так распространены? Я тоже. Большинство попыток в Математика в реальном мире (ТМ) указать на логарифмы в какой-то загадочной формуле или представить себя геологами, увлеченными шкалой Рихтера. «Ученым небезразличны бревна, и вам тоже следует. Кроме того, можете ли вы представить себе мир без цинка?»
Нет, нет, нет, нет, нет, нет! (Mama mia!)
Математика выражает понятия с помощью таких обозначений, как «ln» или «log». Найти «математику в реальном мире» означает столкнуться с идеями в жизни и увидеть, как они могут быть записаны с помощью нотации. Не ищите буквальные символы! Когда вы в последний раз писали знак деления? Когда вы в последний раз резали еду?
Не ищите буквальные символы! Когда вы в последний раз писали знак деления? Когда вы в последний раз резали еду?
Хорошо, хорошо, мы поняли: что такое логарифмы?
Логарифмы находят причину эффекта, т. е. ввод для некоторого результата
Обычный «эффект» заключается в том, что что-то растет, например, от 100 до 150 долларов за 5 лет. Как это случилось? Мы не уверены, но логарифм находит возможную причину: непрерывное возвращение ln(150/100) / 5 = 8,1% объясняет это изменение. Это может быть не фактическая причина (весь рост произошел в последний год?), но это плавное среднее значение, которое мы можем сравнить с другими изменениями.
Кстати, понятие «причина и следствие» имеет нюансы. Почему 1000 больше 100?
- 100 — это 10, которое выросло само по себе за 2 периода времени (10$ * 10$)
- 1000 — это 10, которые росли сами по себе за 3 периода времени (10$ * 10 * 10$)
Числа можно рассматривать как выходы (1000 — это «1000 выходов») и входы («Во сколько раз нужно увеличить 10, чтобы получить эти выходы?»). Итак,
Итак,
1000 выходов > 100 выходов
потому что
3 входа > 2 входа
Или другими словами:
лог(1000) > лог(100)
Почему это полезно?
Логарифмы помещают числа в удобную для человека шкалу.
Большие числа ломают нам мозг. Миллионы и триллионы «действительно велики», хотя миллион секунд — это 12 дней, а триллион секунд — это 30 000 лет. В этом разница между американским отпускным годом и всей человеческой цивилизацией.
Уловка для преодоления «слепоты к огромным числам» состоит в том, чтобы записывать числа в терминах «входных данных» (т. е. их степени по основанию 10). Эту меньшую шкалу (от 0 до 100) гораздо легче понять: 980$ = количество молекул во Вселенной
Шкала от 0 до 80 привела нас от одного предмета к количеству вещей во вселенной. Не так уж и плохо.
Логарифмы подсчитывают умножение как шаги
Логарифмы описывают изменения с точки зрения умножения: в приведенных выше примерах каждый шаг в 10 раз больше. 16$ ~ 65 536 раз больше памяти, к которой можно обратиться.
16$ ~ 65 536 раз больше памяти, к которой можно обратиться.
Процентные ставки
Как рассчитать темпы роста? Страна не собирается расти со скоростью 8,56% в год. Вы смотрите на ВВП в один год и на ВВП в следующий, и логарифмируете, чтобы найти неявных темпов роста.
Две мои любимые интерпретации натурального логарифма (ln(x)), т. е. натуральный логарифм 1,5:
- Предполагая 100% рост, сколько времени вам нужно, чтобы вырасти до 1,5? (0,405, менее половины периода времени)
- Предположим, что 1 единица времени, как быстро вам нужно расти, чтобы достичь 1,5? (40,5% в год, непрерывное начисление)
Логарифмы — это то, как мы определяем, насколько быстро мы растем.
Шкала измерения: Google PageRank
Google присваивает каждой странице в сети оценку (PageRank), которая является грубой мерой авторитета/важности. Это логарифмическая шкала, которая в моем понимании означает «PageRank подсчитывает количество цифр в вашем балле».
Таким образом, сайт с PageRank 2 («две цифры») в 10 раз более популярен, чем сайт с PageRank 1. Мой сайт имеет PageRank 5, а CNN имеет PageRank 9.4 доллара = 10 000).
Грубо говоря у меня получается около 7000 посещений/день. Используя мою математику конвертов, я могу предположить, что CNN получает около 7000 * 10 000 = 70 миллионов посещений в день. (Как я это сделал? В моей голове я думаю, что 7000 $ * 10000 = 70 * k * k = 70 * M$). У них может быть в несколько раз больше (100M, 200M), но, вероятно, не до 700M.
Google передает много информации с очень грубой шкалой (1-10).
Шкала измерения: Рихтер, децибел и т. д.
Вздох. Мы находимся в типичном примере «логарифмов в реальном мире»: шкала Рихтера и децибел. Идея состоит в том, чтобы поместить события, которые могут сильно различаться (землетрясения), в единую шкалу с небольшим диапазоном (обычно от 1 до 10). Как и в случае с PageRank, каждое увеличение на 1 балл означает 10-кратное увеличение мощности. Самое сильное землетрясение, зарегистрированное человеком, было 9 баллов..5; удар полуострова Юкатан, который, вероятно, привел к вымиранию динозавров, составил 13. Звуки могут варьироваться от очень тихих (пиндроп) до очень громких (самолет), и наш мозг может все это обрабатывать. В действительности звук двигателя самолета в миллионы (миллиарды, триллионы) раз мощнее пиндропа, и неудобно иметь шкалу от 1 до газиллиона. Логи держат все в разумных масштабах.
Самое сильное землетрясение, зарегистрированное человеком, было 9 баллов..5; удар полуострова Юкатан, который, вероятно, привел к вымиранию динозавров, составил 13. Звуки могут варьироваться от очень тихих (пиндроп) до очень громких (самолет), и наш мозг может все это обрабатывать. В действительности звук двигателя самолета в миллионы (миллиарды, триллионы) раз мощнее пиндропа, и неудобно иметь шкалу от 1 до газиллиона. Логи держат все в разумных масштабах.
Логарифмические графики
Вы часто будете видеть элементы, построенные в «логарифмической шкале». В моей голове это означает, что одна сторона подсчитывает «количество цифр» или «количество умножений», а не само значение. Опять же, это помогает отображать сильно различающиеся события по единой шкале (от 1 до 10, а не от 1 до миллиардов).
Закон Мура — отличный пример: мы удваиваем количество транзисторов каждые 18 месяцев (изображение любезно предоставлено Википедией).
Отличительной чертой логарифмических графиков является то, что экспоненциальные изменения (скорость процессора) отображаются в виде прямой линии. Рост в 10 раз в год означает, что вы неуклонно продвигаетесь вверх по шкале цифр.
Рост в 10 раз в год означает, что вы неуклонно продвигаетесь вверх по шкале цифр.
Вперёд и вверх
Если концепция известна, но не очень любима, значит, нам нужно развивать свою интуицию. Найдите аналогии, которые работают, и не соглашайтесь на помои, которые напичканы учебником. В моей голове:
- Логарифмы находят первопричину эффекта (см. рост, находят процентную ставку)
- Они помогают считать умножения или цифры с бонусом частичного подсчета (500k — это 6,7-значное число)
Счастливая математика.
Другие сообщения из этой серии 90 = 1?)
Значение журнала 10 — введение, примеры решений, таблица журнала и значения
Логарифмическая функция — это функция, обратная экспоненциальной функции.

Цель логарифма — рассказать нам о показателе степени.
Логарифмические функции используются для изучения свойств экспоненциальных функций и используются для решения различных экспоненциальных уравнений.
Существует два типа логарифмических функций.
Что вы подразумеваете под десятичной логарифмической функцией?
Логарифмическая функция или десятичный логарифм – это логарифм с основанием, равным 10.
Он также известен как десятичный логарифм из-за его основания.
Десятичный логарифм x обозначается как log x.
Что вы подразумеваете под натуральным логарифмом?
Натуральный логарифм – это логарифм с основанием, равным математической константе e.

Значение e, являющееся математической константой, приблизительно равно 2,7182818.
Натуральный логарифм x записывается как log e x.
Пример: log e 25 = ln 25.
Каково значение Log 10?
Значение log 10 может быть представлено либо с основанием 10, либо с основанием e.
Значение log 10 10 равно 1.
Значение log e 10, которое также можно записать в виде ln (10), равно 2,302585.
Примечание. В основном используется функция общего журнала.
Logarithms
We live in a log base of 10 worlds, we count and measure in powers of 10.
10 0 =1 | Log10(1) = 0 |
10 1 =10 | Log 1 0 (10) = 1 |
10 2 =100 | Log 10 (100) = 2 |
10 3 =1,000 | Log 10 (1,000) = 3 |
10 4 =10,000 | Log 10 (10,000) = 4 |
10 5 =1,00,000 | Log 10 (1,00,000) = 5 |
How to Calculate the Значение журнала 10?
Значение логарифмической базы 10 можно рассчитать либо с помощью обычной логарифмической функции, либо с помощью естественной логарифмической функции.
Рассчитаем значение log 10 с помощью десятичного логарифма.,
Значение log 10 10 равно логарифмической функции 10 по основанию 10.
Согласно определению логарифмической функции, если log a b = x, тогда a x = b.
Сравнивая лог 10 10 с определением, имеем базу, а=10 и 10 x =b,
Следовательно, значение log 10 будет следующим:
Мы знаем, что log a a=1.
Следовательно, значение log 10 по основанию 10 = 1, это из-за значения e 1 =1.
Как рассчитать значение логарифма 10 с помощью функции натурального логарифма?
Давайте посчитаем значение log 10, используя натуральный логарифм.
Значение log e 10 равно логарифмической функции 10 по основанию e.
Также обозначается как ln (10).
Таким образом, значение логарифма 10 с основанием e будет следующим:
log e 10 или ln (10) = 2,302585.
Here’s a Table Showing the Log 10 Value
Value of log 10 10 | log 10 10=1 |
Value of log e 10 | log e 10(ln 10) =2,302585 |
0.3010
Log 3
0.4771
Log 4
0.6020
Log 5
0.6989
Log 6
0.7781
Log 7
0.8450
Log 8
0. 9030
9030
Журнал 9
0,9542
Журнал 10
1
Вопрос 1: Найдите значение ln e.
Решение:
Натуральный логарифм числа x определяется как основание e логарифма x: логарифм e:
ln(e) = log e (e)
ln(e) — это число, которое мы должны увеличить, чтобы получить e.
е 1 = е.
Итак, натуральный логарифм числа e равен единице.
ln(e) = логарифм e (e) = 1.
Вопрос 2: Выразите log101 = 0 в экспоненциальной форме.
Решение: Учитывая log10 1 = 0.
Мы знаем, что logac=b ⇒ a b = c.
Следовательно, 10 0 = 1.
Важные свойства логарифмов, которые необходимо знать!
Правило | Значение | |
log A (A) = | ||
Log A (A) = | . |

 Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.


 Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.
Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.

