Примеры на десятичные дроби деление и умножение 5 класс: Умножение и деление десятичных дробей – правила (5 класс, математика)

Содержание

Умножение и деление десятичных дробей – правила (5 класс, математика)

4.4

Средняя оценка: 4.4

Всего получено оценок: 272.

4.4

Средняя оценка: 4.4

Всего получено оценок: 272.

Умножение и деление десятичных дробей – тема достаточно простая для 5 класса. Однако ученики в примерах часто ошибаются, путаясь в правильной постановке запятой. Чтобы не допускать досадных ошибок разберемся в теме подробнее.

Что такое десятичная дробь?

Десятичной дробью называют дробь, записанную с помощью разделительной запятой. Знаменателем такой дроби всегда является степень числа 10.

В обычной форме записи нельзя увидеть знаменатель. Он спрятан за количеством знаков после запятой. Количество знаков после запятой это степень, в которую нужно возвести число 10, чтобы получить знаменатель.

Десятичная дробь может быть положительной и отрицательной. Также существуют смешанные десятичные дроби, но неправильных десятичных дробей не бывает. Это невозможно из-за самой формы записи числа.

Умножение десятичных дробей

Для того, чтобы умножить десятичные дроби нужно следовать следующему алгоритму:

Посчитать количество знаков после запятой у обоих множителей. Причем нас интересует именно общее количество знаков после запятой. То есть нужно посчитать это значение для одного множителя, для другого, а потом сложить. Так мы получим число n – общее количество знаков после запятой у двух множителей.
После этого запятые убираются и числа перемножаются как целые.
С конца числа отсчитывается n количество знаков и ставится запятая.

Рассмотрим небольшой пример:

0,12*0,2 – общее количество знаков после запятой равняется 3. Уберем запятые и выполним умножение.

12*2=24 – теперь вернем запятую обратно.

0,12*0,2=0,024.

Обратите внимание, что нам не хватало знака перед числом для правильной постановки запятой, и мы просто поставили 0. Количество нулей, которые можно поставить перед или после числа неограниченно – они всегда там есть, просто их не пишут.

Деление дробей

Для того, чтобы разделить десятичные дроби, нужно следовать следующему алгоритму:

Из двух чисел выбрать то, у которого знаков после запятой большей. Это и будет число m – наибольшее количество знаков после запятой.
Нужно передвинуть в обоих числах: делимом и делителе – запятую вправо так, чтобы у чисел не оставалось дробных частей, то есть нужно у обоих чисел передвинуть запятую на m знаков.
Выполнить деление. Полученный результат уже является ответом, никаких дополнительных запятых добавлять не нужно.

Если не хватает дробей части у одного из чисел, чтобы передвинуть запятую, следует добавить нули. Так, если передвинуть запятую в числе 0,12 на 3 знака, то получится число 120

Рассмотрим пример деления:

0,12:0,2 – наибольшее число знаков: 2, значит, передвинем запятую и выполним деление.

12:2=6 – это и есть ответ, то есть:

0,12:0,2=0,6.

Что мы узнали?

Мы вспомнили, что такое десятичная дробь. Привели правила умножения и деления десятичных дробей, а также рассмотрели несколько примеров.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Веня Светлосанов
5/5
Лариса Казакова
5/5
Валентина Бурова
5/5
Эрнест Хабибуллин
5/5
Алексей Бражников
5/5
Илья Сафронов
5/5
Егор Якушин
4/5
Екатерина Графкина
5/5

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 272.

А какая ваша оценка?

Умножение и деление десятичных дробей

Умножение
Деление

Умножение

Умножение десятичных дробей сводится к умножению соответствующих натуральных чисел, и правильному определению места запятой в полученном результате.

Пример. Найти произведение чисел 2,13 и 1,2.

Решение: можно перемножить числа 2,13 и 1,2, заменив их обыкновенными дробями:

2,13 · 1,2	=	2	13	·	1	2	=	213	·	12	=
			100			10		100		10

=	213 · 12	=	2556	= 2,556.
	100 · 10		1000

Можно сказать, что мы перемножили натуральные числа, которые получатся если у данных десятичных дробей отбросить запятые. Так как знаменатели тоже перемножаются, то в знаменателе вышло число с тремя нулями, а в соответствующей десятичной дроби — три цифры после запятой. Значит в результате умножения двух десятичных дробей, ответ будет содержать столько знаков после запятой, сколько их было в обоих множителях вместе.

Данное произведение можно посчитать и столбиком, заменив дроби на натуральные числа:

Из рассмотренного примера можно сделать вывод, что:

Чтобы перемножить две десятичные дроби, достаточно перемножить их как натуральные числа, и в полученном произведении отделить справа запятой столько знаков, сколько их было в множимом и множителе вместе.

Данное правило работает и для умножения десятичной дроби на натуральное число. Только в случае, когда один из множителей — натуральное число, количество десятичных знаков в результате будет равно количеству знаков дробного множителя.

Пример. Найти произведение чисел 4,324 и 11:

Решение:

4,324 · 11 = 47,564.

Деление

Чтобы разделить десятичную дробь на целое число, нужно сначала разделить целую часть (если она есть), затем поставить запятую в неполном частном и приступить к делению дробной части:

В этом примере мы сначала разделили 13 на 4 и записали в частное 3, затем мы поставили в частном запятую, так как у нас в остатке осталась единица, которую на 4 мы уже поделить не могли, затем мы продолжили делить дробную часть.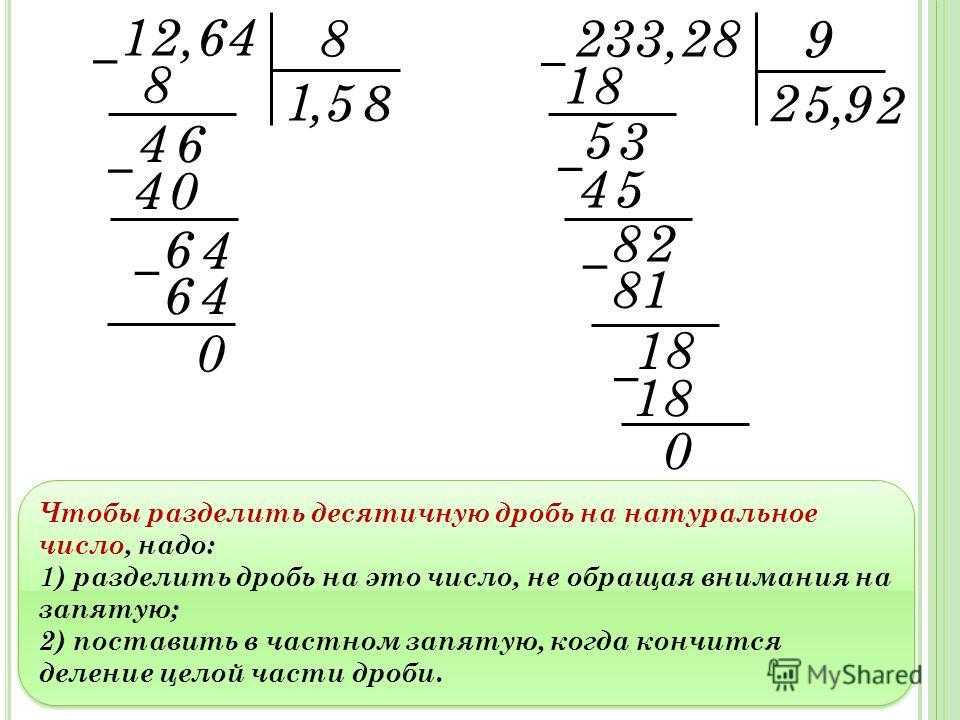 Особенность этого примера заключается в том, что когда мы получили в частном 9 сотых, то обнаружили остаток, равный 2 сотым, мы раздробили этот остаток на тысячные доли, получили 20 тысячных и довели деление до конца.

Чтобы разделить десятичную дробь (или целое число) на десятичную дробь, нужно в делимом и в делителе перенести запятую на столько цифр вправо, сколько их после запятой в делителе, после чего выполнить деление по правилу деления на целое число.

В качестве примера разделим 72,9 на 0,09:

Также можно осуществить деление десятичной дроби (или целого числа) на десятичную дробь, представив оба числа в виде обыкновенных дробей:

Таким образом, частное двух десятичных дробей всегда можно записать в виде обыкновенной дроби.

Математика 5 класс | Умножение и деление десятичных дробей

Учащиеся используют свои знания об умножении и делении целых чисел и дробей для умножения и деления десятичных дробей и применяют это понимание в контексте преобразования измерений.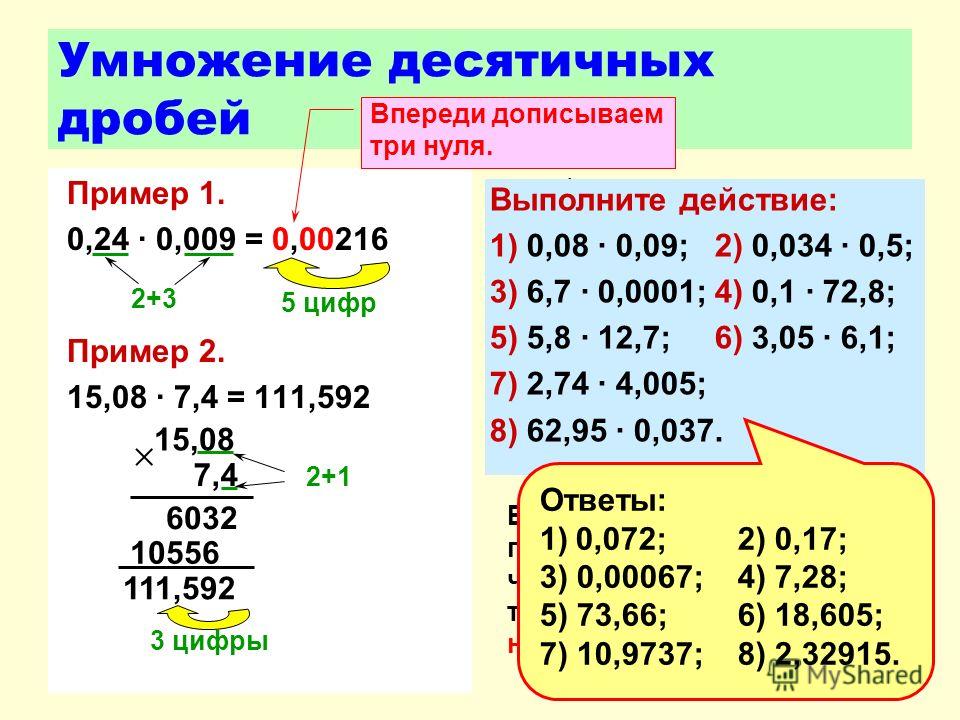

Раздел 6

5-й класс

Краткое содержание раздела

В Разделе 6 учащиеся используют свои процедурные знания об умножении и делении целых чисел в сочетании с недавно приобретенным пониманием дробей умножения и деления с помощью дробей, чтобы умножать и делить с помощью десятичных знаков, рассуждая о размещении десятичной точки. Затем они применяют это к контексту текстовых задач, в том числе связанных с преобразованием измерений.

В 4 классе учащиеся впервые познакомились с десятичной записью дробей и рассуждали об их размере (4.NF.5—7). Затем, в первом разделе 5-го класса, учащиеся развили более глубокое понимание десятичных дробей как расширения нашей системы стоимостных значений, понимание того, что отношения смежных единиц применимы и к десятичным числам (5.NBT.1), и использование это понимание сравнивать, округлять и представлять десятичные дроби в различных формах (5.NBT.2—4). Затем учащиеся научились умножать и делить на целые числа в Блоке 2 (5. NBT.5–6), навыки, от которых будут зависеть десятичные вычисления. В Разделе 3 учащиеся изучили два других действия с десятичными знаками, не рассмотренные в этом разделе: сложение и вычитание (5.NBT.7). В Разделе 5 учащиеся научились умножать и делить дроби, в том числе связывать дроби с операцией деления; умножение дроби на дробь, в том числе смешанных чисел; и деление единичной дроби на целое число и наоборот (5.NF.3—7), что поможет им разобраться в аналогичных случаях десятичного умножения и деления. Таким образом, этот раздел зависит от большого количества предшествующих знаний как в 4-м, так и в 5-м классе.

Этот блок начинается с умножения десятичной дроби на однозначное целое число, затем десятичной дроби на многозначное целое число и, наконец, десятичной дроби в другую десятичную дробь. Затем учащиеся переходят к делению десятичной дроби на однозначное целое число, затем к делению десятичной дроби на двузначное целое число и, наконец, к решению случаев, связанных с десятичными делителями. В этих темах учащиеся используют те же методы для вычисления десятичных произведений и частных, что и для целых чисел, но они должны рассуждать о расположении десятичной точки. Только на последнем занятии по каждой теме учащиеся обобщают схему расстановки запятой. Различные направления рассуждений, их преимущества и недостатки можно прочитать на стр. 19.и 20 из прогрессии NBT, связанные в разделе «Интеллектуальная подготовка для конкретного подразделения». Учащиеся также решают множество текстовых задач, а также пишут и решают выражения с десятичными знаками в качестве поддержки основной работы (5.OA.1, 5.OA.2). Наконец, модуль завершается тем, что учащиеся учатся преобразовывать стандартные единицы измерения разного размера в заданную систему измерения и решать текстовые задачи, в которых используются эти преобразования (5.MD.1), что расширяет работу 4-го класса по преобразованию из более крупного единицы измерения на меньшую (4.МД.1—2). Как отмечено в Progressions, «это прекрасная возможность укрепить представления о разрядности целых чисел и десятичных знаков, а также о связи между дробями и десятичными знаками (например, метры могут быть выражены как 2,5 метра или 250 сантиметров)» (GM Progression, стр. 26), а также вычисления с этими типами чисел (5.НБТ.7, 5.НФ), связывая таким образом работу по переводу единиц с основной работой разряда.

Рассуждения о расположении десятичной точки предоставляют учащимся много возможностей для математической практики, например, построения жизнеспособных аргументов и критики рассуждений других (MP.3), а также поиска и выражения регулярности в повторяющихся рассуждениях (MP.8) . Например, «учащиеся могут обобщить результаты своих рассуждений в виде конкретных числовых закономерностей, а затем в виде одной общей общей закономерности, такой как «количество знаков после запятой в произведении равно сумме числа знаков после запятой в каждом множителе»» (НБТ). Прогрессия, стр. 20).

В 6 классе учащиеся овладеют всеми десятичными вычислениями, которые они освоили в 5 классе (6.NS.3). В 7 классе учащиеся также узнают, что каждая дробь может быть представлена десятичной дробью, которая либо оканчивается, либо повторяется. Затем в 8-м классе учащиеся узнают, что конечные и повторяющиеся десятичные числа являются рациональными числами и что существуют иррациональные числа, десятичное представление которых не повторяется. Затем учащиеся используют работу, которую они начинают в этом разделе в 8 классе, в контексте научной нотации. Таким образом, у этого агрегата есть много интересных связей и приложений на долгие годы вперед.

Темп: 27 учебных дней (24 урока, 2 дня гибкого графика, 1 день оценки)

Fishtank Plus для математики

Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.

Узнать больше

Оценка

Следующие оценки сопровождают Раздел 6.

Предварительная часть

Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.

Промежуточный модуль

Предложите учащимся выполнить оценку промежуточного модуля после урока 16.

Последующий модуль

Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.

Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0
Самооценка студентов после окончания обучения

Расширенный пакет оценивания

Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в освоении содержания модуля.

Скачать образец

Подготовка блока

Интеллектуальная подготовка

Рекомендации по подготовке к преподаванию данного модуля

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Интеллектуальная подготовка для всех модулей

Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
Выполните все целевые задачи и снабдите их комментариями с учетом «Сводки модуля» и «Основных сведений».
Пройти итоговую оценку.

Интеллектуальная подготовка для конкретного модуля

Прочтите стр. 19–20 книги «Числа и операции с основанием 10», К-5 «Прогрессов для общих базовых государственных стандартов по математике».
Ознакомьтесь со справочным листом, который учащиеся получат при оценке в конце года в зависимости от штата, в котором вы живете, чтобы знать, какая информация предоставляется учащимся, а какую следует усвоить. Этот модуль был разработан на основе Справочного листа по математике для 5-го класса Массачусетской комплексной системы оценивания.
Прочтите следующую таблицу, в которой указаны модели, используемые в этом устройстве.

Модель зоны
Стандартный алгоритм умножения
Стандартный алгоритм деления

Основные понятия

Основные математические понятия, которые учащиеся поймут в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Общие методы, используемые для вычисления произведений и частных целых чисел, распространяются на произведения и частные десятичных дробей с дополнительным вопросом о размещении десятичной точки в решении. Есть несколько аргументов, которые учащиеся могут использовать для объяснения размещения десятичной точки в произведениях и частных десятичных дробях.
Учащиеся могут использовать оценку, чтобы оценить правильность своего решения. Как и при вычислении целых чисел, некоторые вычислительные оценки могут быть лучше других, в зависимости от того, какие числа выбраны для использования вместо фактических значений. Однако использование оценки для размещения десятичной точки не всегда является надежной стратегией, особенно в случаях, когда они увидят в более поздних оценках, таких как $${0,0043 \times 0,00078}$$.

При умножении более эффективно разлагать значение на меньшее количество цифр. В стандартном алгоритме это означает запись числа с меньшим количеством цифр внизу. Что касается десятичных дробей, число с меньшим количеством цифр не всегда означает число с наименьшим значением (например, $${17,15 \times 42}$$).

Материалы

Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого модуля

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Справочный лист MCAS для 5 класса (1 на учащегося)

Словарный запас

Термины и обозначения, которые учащиеся изучают или используют в модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

коэффициент преобразования

Чтобы увидеть весь словарный запас для Раздела 6, просмотрите наш глоссарий лексики для 5-го класса.

Модульная практика

Словесные задачи и упражнения на беглость речи

Получите доступ к ежедневной практике со словесными задачами и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.

Предварительный просмотр

Узнать больше

Схема урока

Тема A: Умножение десятичных дробей

Умножение однозначного целого числа на десятичное в случаях, связанных с основными фактами. Оцените произведение однозначного целого числа на десятичное, округлив числа до их наибольшего разряда.

5.НБТ.Б.7

Умножить однозначное целое число на десятичное.

5.НБТ.Б.7

Придумывайте обоснованные аргументы и критикуйте рассуждения других относительно размещения десятичной точки в вычислениях, включающих умножение однозначного целого числа на десятичное.

5.НБТ.Б.7

Умножить многозначное целое число на десятичное.

5.НБТ.Б.7

Умножение десятичной дроби на десятичную в случаях, связанных с основными фактами. Оцените произведение двух десятичных знаков, округлив числа до их наибольшего разряда.

5.НБТ.Б.7

Умножить десятичную дробь на десятичную.

5.НБТ.Б.7

Умножать с десятичными знаками во всех случаях, исходя из положения десятичной точки.

5.НБТ.Б.7

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема B: Деление десятичных дробей

Разделить десятичную дробь на однозначное целое число в случаях, связанных с основными фактами. Оцените частные с однозначными делителями путем округления чисел до совместимых чисел.

5.НБТ.Б.7

Разделить десятичную дробь на однозначное целое число.

5.НБТ.Б.7

Разделить десятичную дробь на однозначное целое число, требующее разложения по наименьшему разрядному значению.

5.НБТ.Б.7

Разделить десятичную дробь на двузначное целое число.

5.НБТ.Б.7

Разделить десятичную дробь на двузначное целое число, требующее разложения по наименьшему разрядному значению.

5.НБТ.Б.7

Разделить целое или десятичное число на 1 десятую или 1 сотую.

5.НБТ.Б.7

Разделите целое число или десятичную дробь на десятичную в случаях, связанных с основными фактами. Оцените частные с десятичными делителями путем округления чисел до совместимых чисел.

5.НБТ.Б.7

Разделить целое число или десятичную дробь на десятичную.

5.НБТ.Б.7

Деление с десятичной дробью во всех случаях, исходя из положения десятичной точки.

5.НБТ.Б.7

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема C: Десятичные выражения и реальные задачи

Решите реальные задачи, требующие интерпретации остатка во всех возможных случаях, включая дальнейшее разложение в десятичное число.

5.НБТ.Б.7

Решайте реальные задачи на умножение и деление с десятичными дробями.

5.НБТ.Б.7

Напишите и оцените числовые выражения, включающие умножение и деление с десятичными дробями.

5.НБТ.Б.7 5.ОА.А.1 5.ОА.А.2

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема D: Преобразование измерений и реальные проблемы

Выразите измерения в целом ряде более крупных единиц или смешанных единицах в единицах меньшего размера.

5.МД.А.1

Выражайте измерения дробным или десятичным числом больших единиц в единицах меньшего размера.

5.МД.А.1

Выражайте измерения целым числом меньших единиц в единицах большего размера.

5.МД.А.1

Выражайте измерения дробным или десятичным числом меньших единиц в единицах большего размера.

5.МД.А.1

Решите реальные проблемы, связанные с преобразованием измерений.

5.МД.А.1

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Общие базовые стандарты

Ключ

Основной кластер

Вспомогательный кластер

Дополнительный кластер

Основные стандарты

Стандарты содержания, рассматриваемые в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Измерения и данные

5.МД.А.1 — Преобразование между стандартными единицами измерения разного размера в заданной системе измерений (например, преобразование 5 см в 0,05 м) и использование этих преобразований при решении многоэтапных задач реального мира.

Числа и операции в десятичной системе счисления

5.НБТ.Б.7 — складывать, вычитать, умножать и делить десятичные дроби до сотых, используя конкретные модели или чертежи и стратегии, основанные на разрядном значении, свойствах операций и/или отношениях между сложением и вычитанием; свяжите стратегию с письменным методом и объясните используемую аргументацию.

Операции и алгебраическое мышление

5.ОА.А.1 — Используйте скобки, скобки или фигурные скобки в числовых выражениях и оценивайте выражения с этими символами.
5.ОА.А.2 — Пишите простые выражения, которые записывают вычисления с числами, и интерпретируйте числовые выражения без их вычисления. Например, выразите вычисление «сложите 8 и 7, затем умножьте на 2» как 2 × (8 + 7). Признайте, что 3 × (18932 + 921) в три раза больше, чем 18932 + 921, без необходимости вычислять указанную сумму или произведение.

Основополагающие стандарты

Стандарты, изучаемые в предыдущих разделах или классах, которые являются важной основой для текущего раздела

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Измерения и данные
4. МД.А.1
4.МД.А.2
Числа и операции в десятичной системе счисления
5.НБТ.А.1
5.НБТ.А.2
5.НБТ.Б.5
5.НБТ.Б.6
Числа и операции — дроби
5.NF.B.3
5.NF.B.4
5.NF.B.7
Будущие стандарты
Стандарты будущих классов или разделы, связанные с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Выражения и уравнения
6. EE.A.2
6.EE.A.3
6.EE.A.4
Система счисления
6.НС.Б.3
6.НС.Б.4
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE. MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
значок/стрелка/вправо/крупная копия
Модуль 5
Умножение и деление дробей
значок/стрелка/вправо/большой
Модуль 7
Шаблоны и координатная плоскость
Умножение и деление с десятичными дробями
Умножение десятичных дробей
Предположим, вы умножаете десятичную дробь на целое число, скажем 0,12 × 3 .
Это то же самое, что добавить десятичную дробь три раза: 0,12 + 0,12 + 0,12 . Вы можете думать об этом следующим образом: если у трех друзей есть 12 центов, вместе они имеют в общей сложности 36 центов
Немного сложнее, когда оба числа десятичные. Возьмите проблему 0,12 × 0,9 . Номер 0,9 меньше чем 1 , так что же означает сложение первого десятичного знака 0,9 раз?
Помните, что десятичные дроби просто другой способ записи дробей которые имеют силы 10 в знаменателе. Умножение числа на 0,9 это то же самое, что найти девять десятых этого числа. Таким образом, вы могли бы переписать проблему 0,12 × 0,9как
12 100 × 9 10 .
Затем вы должны перемножить числители и знаменатели, чтобы получить 108 1000 . Эта дробь такая же, как десятичная 0,108 .
Конечно, вам не нужно каждый раз преобразовывать в дробную запись.
Стандартный алгоритм умножения десятичных дробей
Сначала просто умножьте числа, как если бы они были целые числа . (Не выстраивайте десятичные точки!)
Затем подсчитайте общее количество знаков справа от десятичной точки в ОБОИХ числах, которые вы умножаете. Давайте позвоним на этот номер н . В своем ответе начните справа и двигайтесь н места слева и поставить десятичную точку.
Пример:
Умножить 3. 1 × 5.06 .
Шаг 1: Умножьте числа, игнорируя десятичную точку.
5 0 6 × 3 1 _ 5 0 6 + 1 5 1 8 0 _ 1 5 6 8 6
Шаг 2: В 3. 1 , есть 1 место справа от десятичной точки. В 5.06 , есть 2 . Итак, поскольку 1 + 2 «=» 3 , входить 3 десятичные знаки справа в вашем ответе.
1 5 . 6 ⌣ 8 ⌣ 6 ⌣
Вы можете проверить, что это разумно. 3.1 близко к 3 , и 5.06 близко к 5 , поэтому мы ожидаем ответ, близкий к 15 . И мы получили один!
Почему это работает? Опять же, на самом деле вы умножаете дроби. 3.1 означает 31 10 , и 5.06 означает 506 100 . Умножив эти дроби, мы получим 10 × 100 «=» 1000 в знаменателе, поэтому окончательный ответ выражается в тысячных. Когда вы добавляете общее количество знаков справа от десятичных знаков в факторах, то, что вы на самом деле это умножение десятичных степеней в знаменателях дробей.
Деление с десятичными дробями
Деление с десятичными дробями немного сложнее. В наши дни большинство учителей не возражают, если вы пользуетесь калькулятором. Но хорошо также знать, как сделать это самостоятельно, и вам всегда нужно хорошо оценивать ответ, чтобы вы могли убедиться, что ответ калькулятора разумен.
Напомним, что в задаче Икс ÷ у «=» г , также написано
у г Икс
Икс называется дивиденд , у это делитель , и г это частное .
Шаг 1: Оцените ответ по округление . Вы будете использовать эту оценку, чтобы проверить свой ответ позже.
Шаг 2: Если делитель не является целым числом, то переместить десятичный разряд н места справа, чтобы сделать его целым числом. Затем переместите запятую в делимом на такое же количество знаков вправо (при необходимости добавив несколько дополнительных нулей).
Шаг 3: Разделите как обычно. Если делитель не входит ровно, добавьте нули справа от делимого и продолжайте делить, пока не получите 0 остаток, или пока не появится повторяющийся шаблон.
Шаг 4: Поместите десятичную точку в частном прямо над тем местом, где десятичная точка теперь находится в делимом.
Шаг 5: Сравните свой ответ с вашей оценкой, чтобы убедиться, что она разумна.
Пример:
Разделять.
0,45 ÷ 3,6
Шаг 1: Так как делитель больше делимого, мы получим ответ меньше, чем 1 . С 0,45 составляет примерно одну десятую размера 3,6 , ожидаем ответ, близкий к 0,1 .
Шаг 2: Делитель не является целым числом, поэтому переместите десятичную точку на один разряд вправо, чтобы получить целое число. Также переместите запятую в делимом на одно место вправо.
36 4,5
Шаг 3: Делим нормально, добавляя лишние нули справа от 4,5 когда вы иссякнете.
36 125 4.500 3 6 _ 90 72 _ 180 180 _ 0
Шаг 4: Поставьте запятую в частном непосредственно перед запятой в делимом.
No related posts.