Мерзляк. Глава 2. Обыкновенные дроби
Админ
Онлайн учебник «Математика 6 класс / Мерзляк, Полонский, Якир — М.: Вентана-Граф». Глава 2. Обыкновенные дроби. Цитаты использованы в учебных целях. Ознакомительная версия перед покупкой учебника.
ОГЛАВЛЕНИЕ (2014 г.) ОГЛАВЛЕНИЕ (2021 г.)
Глава 2. Обыкновенные дроби
§ 7. Основное свойство дроби.
§ 8. Сокращение дробей.
§ 9. Приведение дробей к общему знаменателю. Сравнение дробей.
§ 10. Сложение и вычитание дробей с разными знаменателями.
§ 11. Умножение дробей.
§ 12. Нахождение дроби от числа.
§ 13.
§ 14. Деление дробей.
§ 15. Нахождение числа по заданному значению его дроби.
§ 16. Преобразование обыкновенной дроби в десятичную.
§ 17. Бесконечные периодические десятичные дроби.
§ 18. Десятичное приближение обыкновенной дроби.
Итоги главы 2
Глава 2. Обыкновенные дроби
§ 7. Основное свойство дроби.
Упражнения 187-209 (2021 год)
§ 8. Сокращение дробей.
§ 9. Приведение дробей к общему знаменателю. Сравнение дробей.
§ 10. Сложение и вычитание дробей с разными знаменателями.
§ 11. Умножение дробей.
§ 12. Нахождение дроби от числа.

§ 13. Взаимно обратные числа.
§ 14. Деление дробей.
§ 15. Нахождение числа по заданному значению его дроби.
§ 16. Преобразование обыкновенной дроби в десятичную.
§ 17. Бесконечные периодические десятичные дроби.
§ 18. Десятичное приближение обыкновенной дроби.
Итоги главы 2
Онлайн учебник «Математика 6 класс / Мерзляк, Полонский, Якир — М.: Вентана-Граф». Глава 2. Обыкновенные дроби. Цитаты использованы в учебных целях.
ОГЛАВЛЕНИЕ (2014 г.) ОГЛАВЛЕНИЕ (2021 г.)
Математика_УчебникиПохожие записи
Сравнение дробей с разными знаменателями – примеры (6 класс, математика)
4. 7
7Средняя оценка: 4.7
Всего получено оценок: 262.
4.7
Средняя оценка: 4.7
Всего получено оценок: 262.
Сравнение дробей с разными знаменателями – это не самая сложная тема математики 6 класса. Тем не менее, стоит раз и навсегда разобраться в вопросе, чтобы не допускать досадных ошибок.
Что такое дробь?
Дробь это неоконченная операция деления. Очень часто в вычислениях на практике существуют ситуации, когда разделить число невозможно даже с использованием десятичных дробей. Зато такую операцию можно записать в виде обыкновенной дроби и продолжить расчет, не теряя при этом точности.
Если разделить одно число на другое нацело не получается, можно округлить получаемый результат. Но тогда теряется точность расчета, поэтому стоит округлять только конечный результат вычислений.
Что такое знаменатель дроби?
Обыкновенная дробь записывается с помощью горизонтальной черты.
Число, расположенное сверху, называется числителем. Числитель это делимое неоконченной операции деления.
Числитель это делимое неоконченной операции деления.
Число, расположенное снизу – знаменатель. В качестве знаменателя записывают делитель неоконченной операции деления.
Частные случаи сравнения дробей
Разберем несколько частных случаев сравнения дробей:
- Если у дробей знаменатели равны, то больше та дробь, числитель которой больше.
- Если у дробей равны числители, то больше та дробь, знаменатель которой меньше.
- Если числители и знаменатели дробей равны, то и такие дроби равны.
Обратите внимание на то, что в результате вычислений может получится дробь с числителем, равным нулю. В таком случае вся дробь равна нулю и следует немедленно преобразовать дробь в ноль. Но при этом в знаменателе нуля быть не может.
Сравнение дробей с разными знаменателями
Распишем алгоритм сравнения дробей с разными знаменателями и числителями:
- Обращаем внимание на знаменатель. Нужно найти наименьшее общее кратное двух чисел.
 Это наименьшее число, которое делится на оба знаменателя. Для этого нужно выполнить разложение на множители. В случае, когда оба знаменателя – простые числа, стоит просто перемножить их, чтобы найти искомое число.
Это наименьшее число, которое делится на оба знаменателя. Для этого нужно выполнить разложение на множители. В случае, когда оба знаменателя – простые числа, стоит просто перемножить их, чтобы найти искомое число. - Найденное число является общим знаменателем, к которому и нужно привести две дроби. Нужно воспользоваться основным правилом дроби и помножить числитель и знаменатель каждой из дробей так, чтобы в итоге получились дроби с одинаковыми знаменателями.
- У нас получилось два числа с одинаковыми знаменателями, значит, больше та дробь, числитель которой больше.
Пример
Сравним две дроби:
${7\over{8}}$ и ${5\over{10}}$
- Разложим число 8 на простые множители:
2*2*2=8
- Разложим число 10 на множители:
5*2=10
- Найдем наибольшее общее кратное:
5*2*2*2=40
- Приведем оби дроби к одному знаменателю:
$${7\over{8}} ={{7*5}\over{8*5}}={35\over{40}}$$
$${5\over{10}}={{5*4}\over{10*4}}={20\over{40}}$$
- Сравним полученные дроби:
${35\over{40}} >{20\over{40}}$, значит
$${7\over{8}}>{5\over{10}}$$
Что мы узнали?
Мы поговорили о сравнении дробей.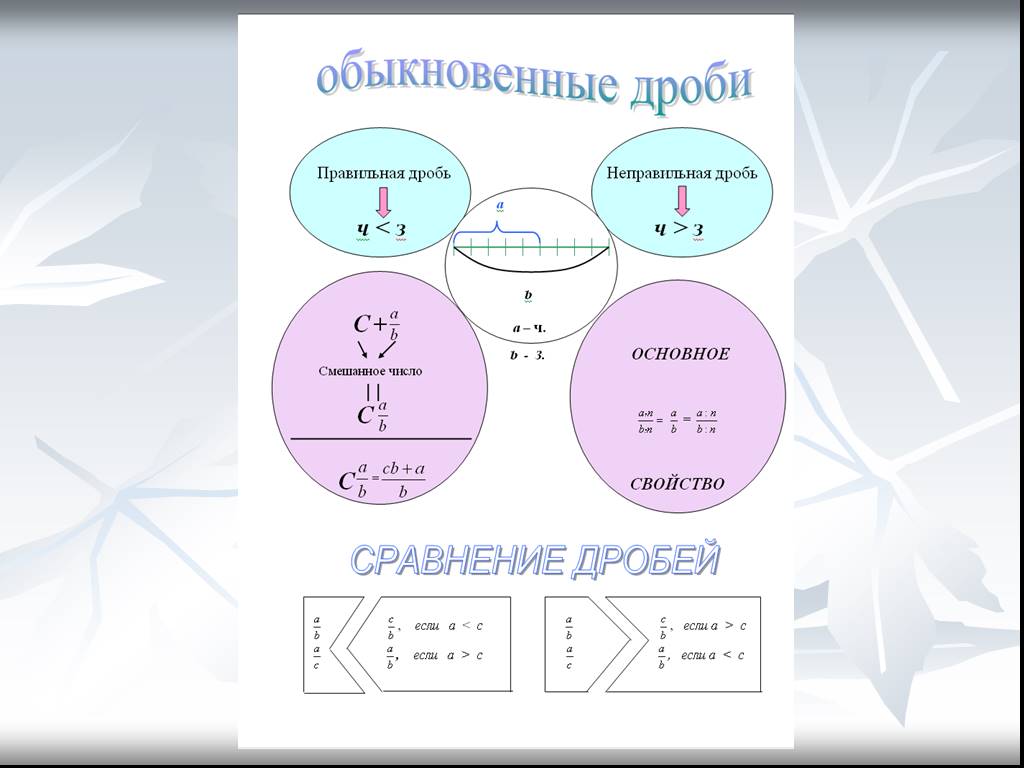 Рассмотрели алгоритм и привели пример сравнения дробей с разными знаменателями.
Рассмотрели алгоритм и привели пример сравнения дробей с разными знаменателями.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Анна Ножеева
4/5
Влада Волосожар
5/5
Саша Романов
5/5
Артём Розин
5/5
Оценка статьи
4.7Средняя оценка: 4.7
Всего получено оценок: 262.
А какая ваша оценка?
Common Core Math: класс 4: дроби
Wolfram|Alpha Примеры: Common Core Math: класс 4: дробиО, о! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
Примеры для
В четвертом классе учащиеся складывают и вычитают дроби с одинаковыми знаменателями и сравнивают дроби с разными знаменателями.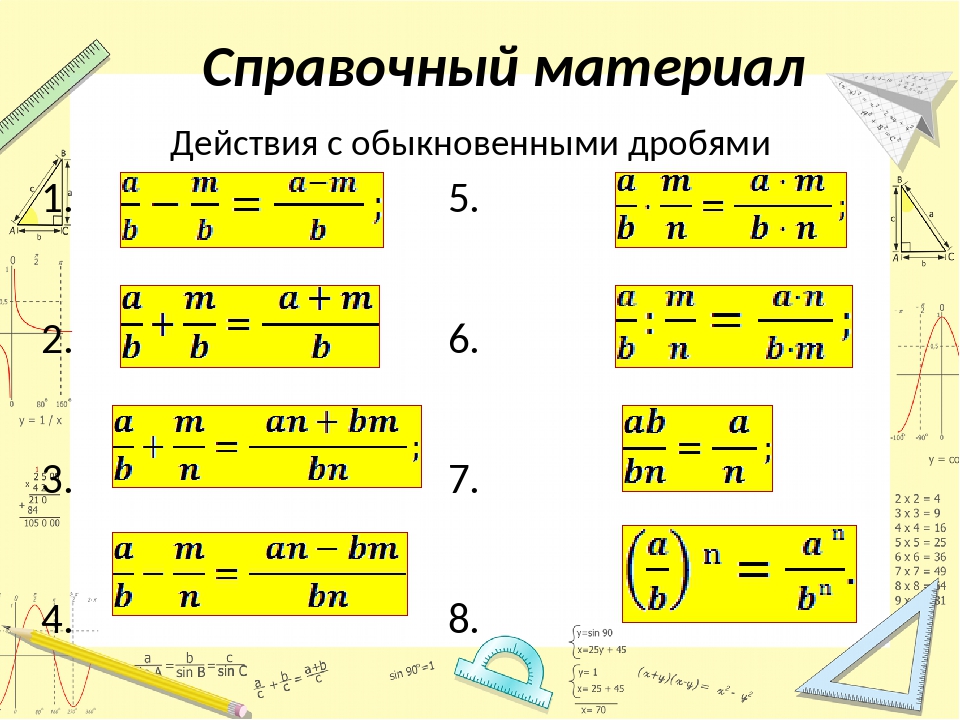 Используя визуальные модели, учащиеся умножают дроби на целые числа и получают эквивалентные дроби. Вводится десятичная запись, поскольку учащиеся используют десятичные числа для выражения и сравнения дробей со знаменателем 10 или 100. Как для дробей, так и для десятичных дробей учащиеся используют символы неравенства для записи результатов своих сравнений.
Используя визуальные модели, учащиеся умножают дроби на целые числа и получают эквивалентные дроби. Вводится десятичная запись, поскольку учащиеся используют десятичные числа для выражения и сравнения дробей со знаменателем 10 или 100. Как для дробей, так и для десятичных дробей учащиеся используют символы неравенства для записи результатов своих сравнений.
Стандарты Common Core
Получить информацию об Стандартах Common Core.
Поиск конкретного стандарта:
CCSS.Math.Content.4.NF.A.1Общий базовый стандарт четвертого класса NF.B.3c классАрифметика дробей
Выполнение сложения, вычитания и умножения дробей.
Дроби сложения и вычитания (CCSS.Math.Content.4.NF.B.3a):
1/5 + 2/51/8 + 1/8 + 1/85/10 + 20/100три шестых плюс две шестых7 /8 — 4/88/12 — 3/12пять третей минус одна третьСложение и вычитание смешанных чисел (CCSS.Math.Content.4.NF.B.3c):
3 1/8 + 2 5/82 3/4 — 1 1/41 + 3/3 + 1/3один и а половина плюс четыре трети7/4 + 3/4Умножение дроби на целое число (CCSS.
 Math.Content.4.NF.B.4): 1/5 * 1012 * 2/3одна шестая из 18
Math.Content.4.NF.B.4): 1/5 * 1012 * 2/3одна шестая из 18Эквивалентные дроби
Определите эквивалентные дроби.
Определить эквивалентность дробей (CCSS.Math.Content.4.NF.A.1):
2/4 = 5/10равно ли 1/4 2/6?Десятичное представление
Запись дробей в десятичном представлении.
Выражение дроби в виде десятичной дроби (CCSS.Math.Content.4.NF.C.6):
Десятичная форма 5/1024/100 в виде десятичной дроби3 десятичные долиИнтерпретация десятичной дроби (CCSS.Math.Content.4.NF .C.6):
0.7 как дробное число 0,5263 сотыхИДТИ ДАЛЬШЕ
Пошаговые решения для арифметики
Веб-приложение Pre-Algebra
Бесплатные неограниченные задачи по арифметике
Основные EXAMPSRELATE Математика: дроби
Сравнение дробей
Рассуждение о размерах дробей.
Сравните величины дробей (CCSS.Math.Content.4.NF.A.2):
что больше, 7/8 или 3/4? На 5/8 меньше 5/6? Сравните половину и две пятыеСравните величины десятичных дробей (CCSS.
 Math.Content.4.NF.C.7): что меньше, 0,2 или 0,02? на 0,4 больше, чем 0,1? что больше, десятая или сотая?
Math.Content.4.NF.C.7): что меньше, 0,2 или 0,02? на 0,4 больше, чем 0,1? что больше, десятая или сотая?- Pro
- Веб-приложения
- Мобильные приложения
- Products
- Business
- API & Developer Solutions
- Resources & Tools
- About
- Contact
- Connect
- ©2022 Wolfram Alpha LLC
- Terms
- Конфиденциальность
- wolfram.com
- Язык Wolfram
- Mathematica
- Демонстрации Wolfram
- Wolfram for Education
- MathWorld
CMP3 Grade 6 — Connected Mathematics Project
6-1 Prime Time
Понятия и пояснения | Примеры домашних заданий | Math Background
В Prime Time учащиеся изучат важные свойства целых чисел. Многие из этих свойств связаны с умножением и делением. Исследования помогут учащимся понять отношения между множителями, кратными, делителями и произведениями. Учащиеся также узнают, как распределительное свойство связывает умножение и сложение. Исследования в этом разделе помогут учащимся понять следующие идеи.
Учащиеся также узнают, как распределительное свойство связывает умножение и сложение. Исследования в этом разделе помогут учащимся понять следующие идеи.
- Классифицировать числа как простые или составные
- Определите, в каких ситуациях требуются общие делители, общие кратные, наименьшее общее кратное или наибольший общий делитель
- Разработка стратегий поиска множителей и кратных, наименьших общих кратных и наибольших общих множителей
- Признать и использовать тот факт, что каждое целое число можно записать ровно одним способом в виде произведения простых чисел
- Использовать экспоненциальное представление для записи повторяющихся множителей
- Свяжите разложение двух чисел на простые множители с наименьшим общим кратным и наибольшим общим делителем двух чисел
- Признать, что Распределительное свойство связывает мультипликативную и аддитивную структуры целых чисел
- Используйте свойства операций с числами, включая Распределительное свойство и соглашение о порядке операций, для записи эквивалентных числовых выражений
- Использование множителей и множителей для решения задач, объяснение некоторых числовых фактов из повседневной жизни
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задать ему эти вопросы. В этом модуле вы можете задать такие вопросы, как:
В этом модуле вы можете задать такие вопросы, как:
- Поможет ли мне решить задачу разбиение числа на множители?
- Какие общие делители и общие кратные имеют числа?
- Что множители и кратные числа говорят мне о ситуации?
- Когда может быть полезно записать число в виде факторизованной формы или в виде суммы?
6-2 Сравнение деталей
Понятия и пояснения | Примеры выполненных домашних заданий | Справочная информация по математике
В задании Сравнение битов и кусочков ваш ребенок разовьет навыки использования дробей, десятичных знаков, отношений и процентов для измерения и сравнения величин.
Исследования в этой главе помогут вам понять, как:
- Использовать язык соотношений и обозначения для сравнения величин
- Различать дроби как числа и отношения как сравнения
- Используйте различные стратегии масштабирования и разделения, чтобы рассуждать пропорционально
- Думайте о дробях и десятичных дробях как о положениях и расстояниях на числовой прямой
- Гибкое перемещение между дробными, десятичными и процентными представлениями
- Найдите абсолютные значения и противоположности и используйте их для описания величин реального мира
- Используйте дроби, десятичные числа и проценты для оценки чисел
- Используйте контекст, модели, рисунки или оценки, чтобы рассуждать о ситуациях
- Использовать эквивалентность дробей и отношений для решения задач
- Используйте таблицы тарифов и тарифы для решения задач
Пока ваш ребенок работает над задачами в этом модуле, задавайте себе вопросы о ситуациях, связанных с дробями, десятичными числами, отношениями и процентами.
- Какие модели или диаграммы могут быть полезны для понимания ситуации и отношений между величинами?
- Это сравнительная ситуация? Если да, то использую ли я отношения или вычитание?
- Какие стратегии можно использовать для поиска эквивалентных форм этих дробей, десятичных знаков, отношений или процентов?
- Какие стратегии можно использовать для сравнения или упорядочения набора дробей, десятичных знаков и процентов?
- Какие стратегии я могу использовать, чтобы рассуждать о числах больше или меньше 0?
- Как я могу использовать расценки за единицу или таблицу расценок для сравнения?
6-3 Давайте будем рациональными
Понятия и пояснения | Примеры домашних заданий | Математический фон
На занятии Let’s Be Rational ваш ученик разовьет понимание четырех основных арифметических операций с дробями, включая смешанные числа. Они также описывают стратегии использования этих операций при решении задач с дробями.
Ваш ребенок научится:
- Использовать ориентиры и другие стратегии для обоснованной оценки результатов операций с дробями, включая смешанные числа
- Разработка способов моделирования сумм, разностей, произведений и частных, включая использование площадей, полос дробей и числовых рядов
- Поиск правил для обобщения шаблонов в операциях с дробями
- Используйте свои знания о дробях, эквивалентности дробей и свойствах чисел для разработки алгоритмов сложения, вычитания, умножения и деления дробей
- Распознать, когда сложение, вычитание, умножение или деление являются подходящими операциями для решения задачи
- Напишите семейства фактов, чтобы показать обратную связь между сложением и вычитанием, а также между умножением и делением
- Решайте задачи, используя действия над дробями, в том числе со смешанными числами
- Поиск значений переменных с помощью операций над дробями, включая смешанные числа
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задавать ему такие вопросы, как:
- Какие модели или диаграммы могут быть полезны для понимания проблемной ситуации и отношений между величинами?
- Какие модели или диаграммы могут помочь вам решить, какая операция полезна при решении проблемы?
- Какова разумная оценка ответа?
6-4 Покрытие и окружение
Понятия и пояснения | Примеры домашних заданий | Предпосылки к математике
В задании Покрытие и окружение ваш ученик будет исследовать площади и периметры фигур. Особое внимание уделяется четырехугольникам и треугольникам. Ваш ребенок также изучит площадь поверхности и объем прямоугольных призм. Расследования в этом подразделении помогут им
Особое внимание уделяется четырехугольникам и треугольникам. Ваш ребенок также изучит площадь поверхности и объем прямоугольных призм. Расследования в этом подразделении помогут им
- Проанализируйте, что означает измерение площади и периметра
- Связать периметр с окружением фигуры и площадь с покрытием фигуры
- Разработка стратегий, процедур и формул, выраженных словами или символами, для нахождения площадей и периметров прямоугольников, параллелограммов и треугольников
- Исследовать отношения между периметром и площадью, в том числе то, что одно может меняться, а другое остается неизменным
- Проанализируйте, как площадь треугольника и площадь параллелограмма связаны с площадью прямоугольника
- Используйте сети, сделанные из прямоугольников и треугольников, для определения площади поверхности призм
- Найдите объем прямоугольных призм с дробными длинами сторон
- Используйте периметр, площадь, площадь поверхности и объем для решения задач.

Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задавать такие вопросы, как:
- Какие атрибуты формы важно измерять?
- Требуется точный ответ?
- Как узнать, задействована ли площадь или периметр фигуры?
- Что я ищу, когда нахожу площадь? Когда я найду периметр?
- Какие соотношения площади, периметра или того и другого помогут решить проблему?
- Как определить площадь поверхности призмы по сетке или трехмерному изображению призмы?
- Чем отличается площадь двумерной фигуры от площади поверхности призмы?
6-5 Decimal Ops
Понятия и пояснения | Примеры домашних заданий | Математический фон
В Decimal Ops ваш ученик научится понимать и использовать четыре операции (+, -, x, ÷,) над десятичными числами. Ваш ребенок также улучшит ваше понимание и навыки работы с процентами.
Ваш ученик научится:
- Складывать, вычитать, умножать и делить десятичные дроби
- Оценка результатов десятичных операций
- Знайте, когда использовать каждую операцию в ситуации с десятичными дробями
- Связывание операций с десятичными дробями с задачами, связанными со ставками единиц
- Используйте проценты для решения задач
Когда ваш ребенок сталкивается с новой задачей, полезно задать такие вопросы, как:
- Какие операции над десятичными числами или процентами помогут в решении этой задачи?
- Какие алгоритмы помогут с расчетами?
- Примерно сколько будет сумма, разность, произведение или частное?
- Что десятичные дроби и/или проценты в задаче говорят мне о ситуации?
6-6 Переменные и шаблоны
Понятия и пояснения | Примеры домашних заданий | Math Background
В разделе Variables and Patterns ваш ребенок изучит некоторые основные идеи алгебры и узнает, как использовать эти идеи для решения задач и принятия решений.
Исследования в этом разделе помогут вашему учащемуся научиться:
- Распознавать ситуации, в которых переменные связаны предсказуемым образом
- Описать закономерности изменения слов, таблиц данных, графиков и уравнений
- Используйте таблицы данных, графики, уравнения и неравенства для решения задач
Пока ваш ребенок работает над задачами в этом разделе, задавайте ему вопросы о проблемных ситуациях, которые включают связанные количественные переменные:
- Какие переменные в задаче?
- Какие переменные зависят или изменяются по отношению к другим?
- Как можно использовать таблицу, график, уравнение или неравенство для представления и анализа связи между переменными?
6-7 Данные о нас
Понятия и пояснения | Примеры домашних заданий | Math Background
В Data About Us вы узнаете о различных способах сбора, организации, отображения и анализа данных. В этом модуле ваш учащийся научится:
- Использовать процесс исследования данных, задавая вопросы, собирая и анализируя данные и интерпретируя данные, чтобы отвечать на вопросы
- Организовывать и представлять данные с помощью таблиц, точечных диаграмм, линейных диаграмм, гистограмм, гистограмм и диаграмм «ящики с усами»
- Опишите общую форму распределения и определите, симметрично ли оно относительно центрального значения
- Вычислите среднее значение, медиану и режим распределения данных и используйте эти меры, чтобы указать, что является типичным для распределения
- Описать изменчивость распределения путем выявления кластеров и пробелов, а также путем расчета размаха, межквартильного размаха (IQR) и среднего абсолютного отклонения (MAD)
- Определите, какие статистические меры центра и разброса следует использовать для описания конкретного распределения данных
- Различать категориальные данные и числовые данные и определять, какие графики и статистические данные можно использовать для представления каждого типа данных
- Сравнение двух или более распределений данных, включая использование мер центра и разброса для сравнения
Когда вы сталкиваетесь с новой проблемой, полезно задать себе вопросы.

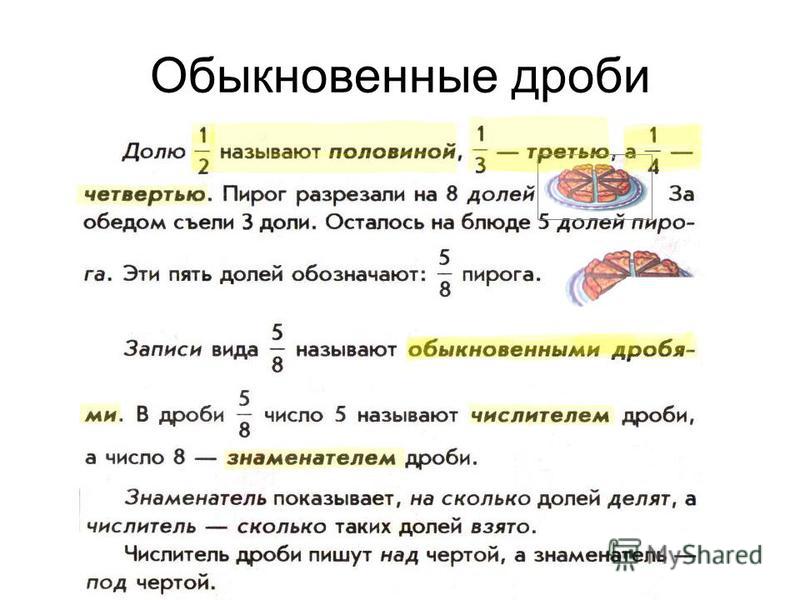 Это наименьшее число, которое делится на оба знаменателя. Для этого нужно выполнить разложение на множители. В случае, когда оба знаменателя – простые числа, стоит просто перемножить их, чтобы найти искомое число.
Это наименьшее число, которое делится на оба знаменателя. Для этого нужно выполнить разложение на множители. В случае, когда оба знаменателя – простые числа, стоит просто перемножить их, чтобы найти искомое число.