50.Матричная игра – это частный случай антагонистической игры, при
котором обязательно выполняется одно из требований:
а) один из игроков выигрывает.
б) функция выигрыша игрока может быть задана матрицей.
в) стратегии игроков задаются матрицей.
51.Пусть матричная игра задана матрицей, в которой все элементы
неотрицательны. Цена игры положительна:
а) да,
б) нет.
в) нет однозначного ответа.
52. Верхняя цена игры всегда меньше нижней цены игры.
а) да.
б) нет.
б) вопрос некорректен.
53. Оптимальная стратегия для матричной игры не единственна:
а) да.
б) нет.
в) вопрос некорректен.
г) нет однозначного ответа.
54. Цена игры существует для матричных игр в чистых стратегиях всегда.
А) да.
б) нет.
в) вопрос некорректен.
55.
Какие стратегии бывают в матричной
игре: а) чистые.
б) смешанные.
в) и те, и те.
56. Если в игровой матрице все строки одинаковы и имеют вид ( 4 5 0 1), то
какая стратегия оптимальна для 1-го игрока?
а) первая чистая.
б) вторая чистая.
в)любая.
57. Какое максимальное число седловых точек может быть в игре
размерности 5*6 ( матрица может содержать любые числа) :
а) 5.
б)11.
в)30.
58. Максимум по X минимума по y и минимум по y максимума по X функции
выигрыша первого игрока:
а) всегда одинаковые числа.
б) всегда разные числа.
в) ни то, ни другое.
59. Могут ли в какой-то антагонистической игре значения функции
выигрыша обоих игроков для некоторых значений переменных равняться 1?
а) всегда.
б) иногда.
в) никогда.
60. Пусть в антагонистической игре X=(1,2)- множество стратегий 1-го
игрока, Y=(5,8)- множество стратегий 2-го игрока( по две стратегии у
каждого).
Является ли пара ( 1;2) седловой точкой
в этой игре :
а) всегда.
б) иногда.
в) никогда.
61.Бывает ли в матричной игре размерности 2*2 1 седловая точка?
а) Всегда.
б) иногда.
в) никогда.
62.Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет
вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.4,
0.1,0.1,0.4). Какова размерность этой матрицы?
а)2*4.
б)6*1.
в) иная размерность.
63. Если известно, что функция выигрыша 1-го игрока равна числу 2 в
седловой точке, то значения этой функции могут принимать значения:
а) любые.
б) только положительные.
в) только не более числа 2.
64. Принцип доминирования позволяет удалять из матрицы за один шаг:
а) целиком столбцы,
б) отдельные числа.
в) подматрицы меньших размеров.
65. В графическом методе решения игр 3*3 для нахождения оптимальных
стратегий игроков:
а)
строится два треугольника.
б) строится один треугольник.
в) треугольники не строятся вовсе.
66. График нижней огибающей для графического метода решения игр 2*m
представляет в общем случае функцию:
а) монотонно убывающую.
б) монотонно возрастающую.
в) немотонную.
67. Если в антагонистической игре на отрезке [0;1] функция выигрыша 1-го
игрока F(x,y) равна 2*x+C, то в зависимости от C:
а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) иной вариант
68.Чем можно задать задачу принятия решения в условиях неопределенности
на конечных множествах:
а) двумя матрицами.
б) выигрышами.
в) чем-то еще.
69. В антагонистической игре произвольной размерности выигрыш первого
игрока – это:
а) число.
б) множество.
в) вектор, или упорядоченное множество.
г) функция.
70. В матричной игре 3*3 две компоненты смешанной стратегии игрока:
а)
определяют третью.
б) не определяют.
71. Биматричная игра может быть определена:
а) двумя матрицами одинаковой размерности с произвольными элементами,
б) двумя матрицами не обязательно одинаковой размерности,
в) одной матрицей.
72. В матричной игре элемент aij представляет собой:
а) проигрыш 2-го игрока при использовании им j-й стратегии, а 2-м – i-й
стратегии.
б) оптимальную стратегию 2-го игрока при использовании противником i-й
или j-й стратегии,
в) выигрыш 1-го игрока при использовании им j-й стратегии, а 2-м – i-й
стратегии,
73. Элемент матрицы aij соответствует седловой точке. Возможны
следующие ситуации:
а) этот элемент строго больше всех в столбце.
б) этот элемент строго больше всех по порядку в строке.
в) в строке есть элементы и больше, и меньше, чем этот элемент.
74.В биматричной игре размерности 4*4 может быть ситуаций равновесия:
а)
не более 4.
б) не более 8.
в) не более 16.
75.В методе Брауна-Робинсон каждый игрок при выборе стратегии на
следующем шаге руководствуется:
а) стратегиями противника на предыдущих шагах.
б) стратегиями противника в будущем.
в) своими стратегиями.
76. По критерию Вальда каждый игрок исходит из того, что:
а)случится наиболее плохая для него ситуация.
б) все ситуации равновозможны.
в) все ситуации возможны с некоторыми заданными вероятностями.
Teoria igr s_otvetami по тест
Тесты по курсу «Теория игр»
1.При каких значениях α критерий Гурвица обращается в критерий Вальда?
а)>0.
@б)=1.
в)<0.
2.В чем отличие критерия Сэвиджа от остальных изученных критериев принятия решения:
@а) Он минимизируется.
б) Он максимизируется.
в) Он не всегда дает однозначный ответ.
3.Антагонистическая игра может быть задана:
а) множеством стратегий
обоих игроков и седловой точкой.
@б) множеством стратегий обоих игроков и функцией выигрыша первого игрока.
4.Матричная игра – это частный случай антагонистической игры, при котором обязательно выполняется одно из требований:
а) один из игроков имеет бесконечное число стратегий.
б) оба игрока имеют бесконечно много стратегий.
в) оба игрока имеют одно и то же число стратегий.
@г) оба игрока имеют конечное число стратегий.
5.Пусть матричная игра задана матрицей, в которой все элементы положительны. Цена игры положительна:
@а) да.
б) нет.
в) нет однозначного ответа.
6.Цена игры всегда меньше верхней цены игры, если обе цены существуют:
а) да.
@б) нет.
в) вопрос некорректен.
7.Оптимальная смешанная стратегия для матричной игры меньше любой другой стратегии.
а) да.
б) нет.
@в) вопрос некорректен.
г) нет однозначного ответа.
8.Цена игры существует
для матричных игр в смешанных стратегиях всегда.
@а) да.
б) нет.
9.Каких стратегий в матричной игре размерности, отличной от 1*,
больше:
а) чистых.
@б) смешанных.
в) поровну и тех, и тех.
10.Если в матрице все столбцы одинаковы и имеют вид ( 4 5 0 1), то какая стратегия оптимальна для 2-го игрока?
а) первая.
@б)вторая.
в)любая из четырех.11.Какое максимальное число седловых точек может быть в игре размерности 2*3 (матрица может содержать любые числа)
а) 2.
б)3.
@в)6.
12. Максимум по x минимума по y и минимум по y максимума по x функции выигрыша первого игрока:
а) всегда разные числа, первое больше второго.
@б) не всегда разные числа; первое не больше второго.
в) связаны каким-то иным образом.
13. Могут ли в какой-то антагонистической игре значения функции выигрыша обоих игроков для некоторых значений переменных быть равны одному числу?
а)да, при нескольких
значениях этого числа.
б) нет.
@в) да, всего при одном значении этого числа.
14.Пусть в антагонистической игре X=(1;2)- множество стратегий 1-го игрока, Y=(5;8)- множество стратегий 2-го игрока. Является ли пара (1;5) седловой точкой в этой игре:
а) всегда.
@б) иногда.
в) никогда.
15.В матричной игре размерности 2*2 есть 4 седловых точки?
а) Всегда.
@б) иногда.
в) никогда.
16.Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.4, 0, 0.6). Какова размерность этой матрицы?
@а) 2*3.
б) 3*2.
в) другая размерность.
17.Если известно, что функция выигрыша 1-го игрока равна числу 1 в седловой точке, то значения этой функции могут принимать значения:
@а) любые.
б) только положительные.
в) только не более числа 1.
18. Принцип доминирования позволяет удалять из матрицы за один шаг:
@а) целиком строки.
2, то в зависимости от C:
@а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) третий вариант.
22.Чем можно задать матричную игру:
@а) одной матрицей.
б) двумя матрицами.
в) ценой игры.
23. В матричной игре произвольной размерности смешанная стратегия любого игрока – это:
а) число.
б) множество.
@в) вектор, или упорядоченное множество.
г) функция.
24. В матричной игре 2*2 две компоненты смешанной стратегии игрока:
@а) определяют значения друг друга.
б) независимы.
25. Биматричная игра может быть определена:
а) двумя матрицами только с положительными элементами.
@б) двумя произвольными матрицами.
в) одной матрицей.
26. В матричной игре элемент aij представляет собой:
@а) выигрыш 1-го игрока при использовании им i-й стратегии, а 2-м – j-й стратегии.
б) оптимальную
стратегию 1-го игрока при использовании противником i-й или j-й стратегии.
в) проигрыш 1-го игрока при использовании им j-й стратегии, а 2-м – i-й стратегии.
27.Элемент матрицы aij соответствует седловой точке. Возможны следующие ситуации:
@а) этот элемент строго меньше всех в строке.
б) этот элемент второй по порядку в строке.
в) в строке есть элементы и больше, и меньше, чем этот элемент.
28. В биматричной игре размерности 3*3 ситуаций равновесия бывает:
а) не более 3.
б) не менее 6.
@в) не более 9.
29. В методе Брауна-Робинсон каждый игрок при выборе стратегии на следующем шаге руководствуется:
@а) стратегиями противника на предыдущих шагах.
б) своими стратегиями на предыдущих шагах.
в) чем-то еще.
30. По критерию математического ожидания каждый игрок исходит из того, что:
а) случится наихудшая для него ситуация.
б) все ситуации равновозможны.
@в) все или некоторые ситуации возможны с некоторыми заданными вероятностями.
31. Антагонистическая игра может быть задана:
а) множеством стратегий
игроков и ценой игры.
@б) множеством стратегий обоих игроков и функцией выигрыша второго игрока.
в) чем-то еще.
32. Матричная игра – это частный случай антагонистической игры, при котором обязательно выполняется одно из требований:
а) один из игроков выигрывает.
б) игроки имеют разное число стратегий.
@в) можно перечислить стратегии каждого игрока.
33. Пусть матричная игра задана матрицей, в которой все элементы отрицательны. Цена игры положительна:
а) да.
б) нет.
@в) нет однозначного ответа.
34. Цена игры меньше верхней цены игры, если оба показателя существуют.
а) да.
б) не всегда.
@в) никогда.
35. Оптимальная смешанная стратегия для матричной игры не содержит нулей:
а) да.
б) нет.
в) вопрос некорректен.
@г) не всегда.
36. Цена игры — это:
@а) число.
б) вектор.
в) матрица.
37. Каких стратегий в матричной игре больше:
а) оптимальных.
б) не являющихся оптимальными.
@в) нет однозначного ответа.
38.Если в матрице все столбцы одинаковы и имеют вид ( 4 5 0 1), то какая стратегия оптимальна для 1-го игрока:
а) первая чистая.
@б) вторая чистая.
в) какая-либо смешанная.
39.Какое максимальное число седловых точек может быть в игре размерности 5*5 ( матрица может содержать любые числа) :
а) 5.
б)10.
@в)25.
40.Пусть в антагонистической игре X=(1;2)- множество стратегий 1-го игрока, Y=(2;8)- множество стратегий 2-го игрока. Является ли пара (2;2) седловой точкой в этой игре :
а) всегда.
б) иногда.
@в) никогда.
41.Бывает ли в биматричной игре (размерности 3*3) 4 ситуации равновесия?
а) Всегда.
@б) иногда.
в) никогда.
42. Пусть в матричной игре размерности 2*3 одна из смешанных стратегий 1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.3, x, 0.5). Чему равно число x?
@а)0.4.
б)0.2.
в) другому числу.
43.Матричная игра – это частный случай биматричной, при котором: а) матрицы А и В совпадают.
б) из матрицы A можно получить матрицу В путем транспонирования.
@в) выполняется что-то третье.
44. В биматричной игре элемент bij представляет собой:
а) выигрыш 1-го игрока при использовании им i-й стратегии, а 2-м – j-й стратегии.
б) оптимальную стратегию 1-го игрока при использовании противником i-й или j-й стратегии.
@в) выигрыш 2-го игрока при использовании им j-й стратегии, а 1-м – i-й стратегии.
45. В биматричной игре элемент aij соответствует ситуации равновесия. Возможны следующие ситуации:
а) этот элемент строго меньше всех в столбце.
@б) этот элемент больше всех в строке.
в) в столбце есть элементы и больше, и меньше, чем этот элемент.
46. В матричной игре, зная стратегии каждого игрока, можно найти цену игры:
а) да.
@б) нет.
в) вопрос некорректен.
47.
Для какой
размерности игровой матрицы критерий Вальда обращается в критерий Лапласа?
а)1*5
@б)5*1
в)только в других случаях.
48. В чем отличие критерия Вальда от остальных изученных критериев принятия решения:
а) Он минимизируется
б) Он максимизируется
@в) При расчете не используются арифметические операции сложения и вычитания.
49.Антагонистическая игра может быть задана:
а) седловыми точками.
@б) множеством стратегий обоих игроков и функцией выигрыша второго игрока.
в)седловой точкой и ценой игры.
50.Матричная игра – это частный случай антагонистической игры, при котором обязательно выполняется одно из требований:
а) один из игроков выигрывает.
@б) функция выигрыша игрока может быть задана матрицей.
в) стратегии игроков задаются матрицей.
51.Пусть матричная игра задана матрицей, в которой все элементы неотрицательны. Цена игры положительна:
а) да,
б) нет.
@в) нет однозначного
ответа.
52. Верхняя цена игры всегда меньше нижней цены игры.
а) да.
б) нет.
@б) вопрос некорректен.
53. Оптимальная стратегия для матричной игры не единственна:
а) да.
б) нет.
в) вопрос некорректен.
@г) нет однозначного ответа.
54. Цена игры существует для матричных игр в чистых стратегиях всегда.
@А) да.
б) нет.
в) вопрос некорректен.
55. Какие стратегии бывают в матричной игре:
а) чистые.
б) смешанные.
@в) и те, и те.
56. Если в игровой матрице все строки одинаковы и имеют вид ( 4 5 0 1), то какая стратегия оптимальна для 1-го игрока?
а) первая чистая.
б) вторая чистая.
@в)любая.
57. Какое максимальное число седловых точек может быть в игре размерности 5*6 ( матрица может содержать любые числа) :
а) 5.
б)11.
@в)30.
58. Максимум по x минимума по y и минимум по y максимума по x функции выигрыша первого игрока:
а) всегда одинаковые
числа.
б) всегда разные числа.
@в) ни то, ни другое.
59. Могут ли в какой-то антагонистической игре значения функции выигрыша обоих игроков для некоторых значений переменных равняться 1?
а) всегда.
б) иногда.
@в) никогда.
60. Пусть в антагонистической игре X=(1,2)- множество стратегий 1-го игрока, Y=(5,8)- множество стратегий 2-го игрока( по две стратегии у каждого). Является ли пара ( 1;2) седловой точкой в этой игре :
а) всегда.
б) иногда.
@в) никогда.
61.Бывает ли в матричной игре размерности 2*2 1 седловая точка?
а) Всегда.
@б) иногда.
в) никогда.
62.Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.4, 0.1,0.1,0.4). Какова размерность этой матрицы?
а)2*4.
б)6*1.
@в) иная размерность.
63. Если известно, что функция выигрыша 1-го игрока равна числу 2 в седловой точке, то значения этой функции могут принимать значения:
@а) любые.
б) только положительные.
в) только не более числа 2.
64. Принцип доминирования позволяет удалять из матрицы за один шаг:
@а) целиком столбцы,
б) отдельные числа.
в) подматрицы меньших размеров.
65. В графическом методе решения игр 3*3 для нахождения оптимальных стратегий игроков:
@а) строится два треугольника.
б) строится один треугольник.
в) треугольники не строятся вовсе.
66. График нижней огибающей для графического метода решения игр 2*m представляет в общем случае функцию:
а) монотонно убывающую.
б) монотонно возрастающую.
@в) немотонную.
67. Если в антагонистической игре на отрезке [0;1] функция выигрыша 1-го игрока F(x,y) равна 2*x+C, то в зависимости от C:
а) седловых точек нет никогда.
@б) седловые точки есть всегда.
в) иной вариант
68.Чем можно задать задачу принятия решения в условиях неопределенности на конечных множествах:
а) двумя матрицами.
б) выигрышами.
@в) чем-то еще.
69. В антагонистической игре произвольной размерности выигрыш первого игрока – это:
а) число.
б) множество.
в) вектор, или упорядоченное множество.
@г) функция.
70. В матричной игре 3*3 две компоненты смешанной стратегии игрока:
@а) определяют третью.
б) не определяют.
71. Биматричная игра может быть определена:
@а) двумя матрицами одинаковой размерности с произвольными элементами,
б) двумя матрицами не обязательно одинаковой размерности,
в) одной матрицей.
72. В матричной игре элемент aij представляет собой:
@а) проигрыш 2-го игрока при использовании им j-й стратегии, а 2-м – i-й стратегии.
б) оптимальную стратегию 2-го игрока при использовании противником i-й или j-й стратегии,
в) выигрыш 1-го игрока при использовании им j-й стратегии, а 2-м – i-й стратегии,
73. Элемент матрицы aij соответствует седловой точке. Возможны следующие ситуации:
@а) этот элемент строго больше всех в столбце.
б) этот элемент строго больше всех по порядку в строке.
в) в строке есть элементы и больше, и меньше, чем этот элемент.
74.В биматричной игре размерности 4*4 может быть ситуаций равновесия:
а) не более 4.
б) не более 8.
@в) не более 16.
75.В методе Брауна-Робинсон каждый игрок при выборе стратегии на следующем шаге руководствуется:
@а) стратегиями противника на предыдущих шагах.
б) стратегиями противника в будущем.
в) своими стратегиями.
76. По критерию Вальда каждый игрок исходит из того, что:
@а)случится наиболее плохая для него ситуация.
б) все ситуации равновозможны.
в) все ситуации возможны с некоторыми заданными вероятностями.
77. Антагонистическая игра может быть задана:
а) множеством стратегий игроков и ценой игры.
б) множеством стратегий первого игрока и функцией выигрыша второго игрока.
@в) чем-то еще.
78. Матричная игра – это частный случай антагонистической игры, при котором иногда выполняется только одно из требований:
а) выигрыш первого
игрока не равен проигрышу второго.
@б) игроки имеют равное число стратегий.
в) множество стратегий каждого — более чем счетное множество.
79. Пусть матричная игра задана матрицей, в которой все элементы отрицательны. Цена игры может быть равной нулю:
@а) да.
б) нет.
в) нет однозначного ответа.
80. Нижняя цена меньше верхней цены игры:
а) да.
@б) не всегда.
б) никогда.
81. Сумма компонент смешанной стратегия для матричной игры всегда:
@а) равна 1.
б) неотрицательна.
в) положительна.
г) не всегда.
82. Смешанная стратегия — это:
а) число.
@б) вектор.
в) матрица.
83. Каких стратегий в матричной игре больше:
а) оптимальных.
б) чистых.
@в) нет однозначного ответа.
84. Если в матрице все столбцы одинаковы и имеют вид ( 4 3 0 2), то какая стратегия оптимальна для 2-го игрока?
a)первая.
б)третья.
@в)любая.
85. Какое максимальное число седловых точек может быть в игре размерности 3*3 ( матрица может содержать любые числа):
а) 3.
@б)9.
в)27.
86.Пусть в антагонистической игре X=(1;5)- множество стратегий 1-го игрока, Y=(2;8)- множество стратегий 2-го игрока. Является ли пара (1,2) быть седловой точкой в этой игре :
а) всегда.
@б) иногда.
в) никогда.
87. Бывает ли в биматричной игре размерности 3*3 ровно 2 ситуации равновесия?
а) Всегда.
@б) иногда.
в) никогда.
88. Пусть в матричной игре размерности 2*3 одна из смешанных стратегий 1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.3, x, x). Чему равно число x?
а)0.7
б)0.4
@в)чему-то еще.
89. Матричная игра – это частный случай биматричной, при котором всегда справедливо:
а) матрица А равна матрице В, взятой с обратным знаком.
@б) матрица A равна матрице В.
в) Произведение матриц А и В -единичная матрица..
90. В биматричной игре элемент bij представляет собой:
а) выигрыш 2-го игрока при использовании им i-й стратегии, а 1-м – j-й стратегии,
б) оптимальную стратегию 2-го игрока при использовании противником i-й или j-й стратегии/
@в) что-то иное.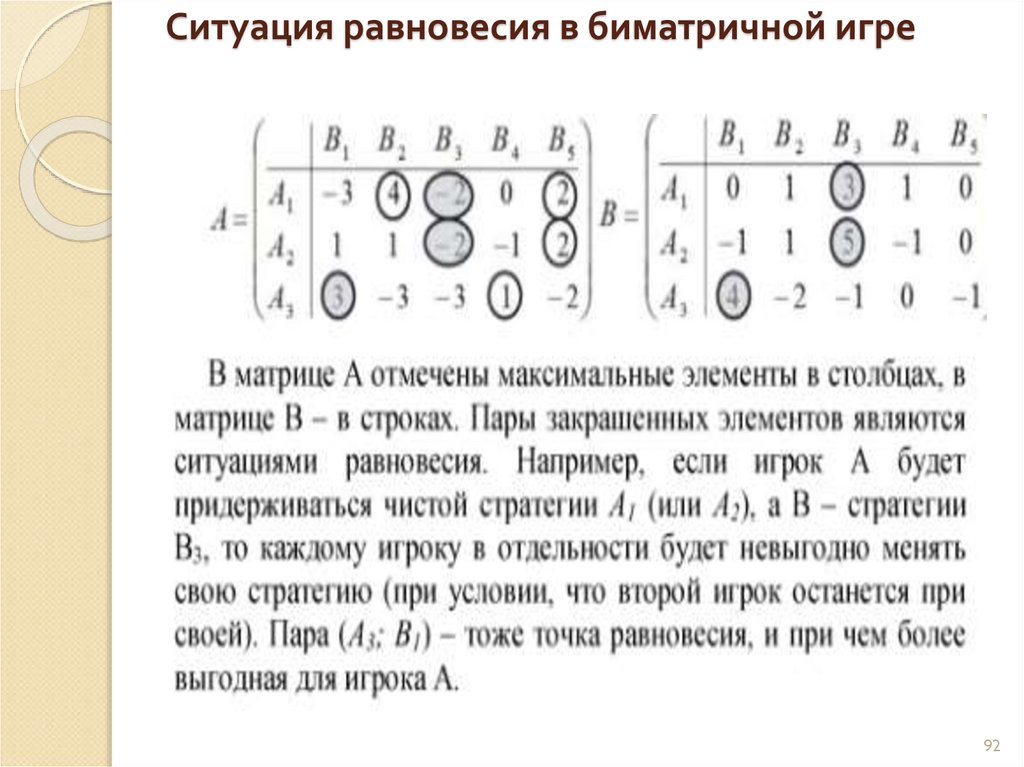
91.В биматричной игре элемент aij соответствует ситуации равновесия. Возможны следующие ситуации:
@а) в столбце есть элементы, равные этому элементу.
б) этот элемент меньше некоторых в столбце.
в) этот элемент меньше всех в столбце.
92. В матричной игре, зная стратегии каждого игрока и функцию выигрыша, цену игры в чистых стратегиях, можно найти:
а) всегда.
@б) иногда.
в) вопрос некорректен.
93.
Позиционная игра может быть сведена к …
a). Биматричной игре
@б). Матричной игре
в). Дифференциальной игре
г). Бесконечной игре
94. Шахматы – это …
a). Матричная игра
б). Биматричная игра
@в). Позиционная игра с полной информацией
г). Позиционная игра с неполной информацией
95. Крестики и нолики это …
a). Матричная игра
б). Биматричная игра
@в). Позиционная игра с полной информацией
г). Позиционная игра с неполной информацией
96..
Конечная бескоалиционная игра двух игроков с ненулевой суммой – это.
@a). Биматричная игра
б). Матричная игра
в). Антагонистическая игра
г). Дифференциальная игра
97. Каждая биматричная игра …
@a). Имеет по крайней мере одну ситуацию равновесия
б) Всегда имеет точно одну ситуацию равновесия
в) Всегда имеет бесконечно много ситуаций равновесия
г). Не имеет ситуаций равновесия
98. Антагонистическая игра это …
a). Игра с не нулевой суммой
б). Биматричная игра
@в).Игра с нулевой суммой
г). Статистическая игра
д). Игра с природой
99. Конечная игра двух игроков с нулевой суммой называется …
a). Биматричной игрой
б). Кооперативной игрой
в). Дифференциальной игрой
@г). Матричной игрой
Д). Конечномерной игр
100. Матричная игра имеет решение в чистых стратегиях, если …
(отметить все верные условия)
a). Нижняя чистая цена игры больше верхней чистой цены игры
@б). Игра имеет седловую точку
в). Нижняя чистая цена игры меньше верхней чистой цены игры
г).
Игра не имеет седловой точки
@д). Нижняя чистая цена игры и верхняя чистая цена игры равны
101. Упрощение платежной матрицы некоторой матричной игры возможно за счет …
a). Исключения отрицательных стратегий
б). Построения графической интерпретации игры
в). Исключения оптимальных чистых стратегий
г). Сведения матричной игры к задаче линейного программирования
@д). Исключения доминируемых стратегий
102. Решение матричной игры в смешанных стратегиях целесообразно, если
a). Игра повторяется один раз
б). Игра имеет седловую точку
@в). Игра повторяется большое число раз
г). Нижняя и верхняя цены игры равны
103. Выберите верное утверждение
a). Любая матричная игра имеет решение в чистых стратегиях
@б). Любая матричная игра имеет решение, по крайней мере, в смешанных стратегиях
в). В любой матричной игре есть доминируемые стратегии
г). В любой матричной игре есть седловая точка
104.
.
Если a – нижняя чистая цена игры, b – верхняя чистая цена игры, то для любой
матричной игры верно неравенство:
a). a < b
@б). a £ b
в). a > b
г). a ³ b
105. Выберите смешанную стратегию, которая может быть решением некоторой игры для игрока А:
A)
Б)
В)
@Г)
106. Если все элементы платежной матрицы преобразовать по формуле , , то …
@a). Оптимальные стратегии игроков не изменятся
б). Все компоненты оптимальных стратегий надо умножить на b
В). Ко всем компонентам оптимальных стратегий надо прибавить g
Г). Все компоненты оптимальных стратегий надо умножить на b и прибавить к ним g
107. Если у матричной игры с платежной матрицей цена игры равна 1,65, тогда цена игры, заданной матрицей равна
@101,65…
108. Цена игры с платежной матрицей равна 550. Цена игры с платежной матрицей равна …
a). 450
б). 550
@в). 5,5
г). 6,5
109. Для решения матричной игры как задачи линейного программирования необходимо, чтобы …
@a).
Цена игры была положительной
б). Игра имела размерность 2х2
в). Сумма компонентов смешанных стратегий игроков равнялась 1
г). Игра не имела решения в чистых стратегиях
110). Задача принятия решений в условиях неопределенности, когда игрок взаимодействует с окружающей средой называется …
a). Антагонистической игрой
б). Игрой в нормальной форме
@в). Игрой с природой
г). Позиционной игрой
111). Двое заключенных знают, что если оба сознаются в преступлении, то каждый получит по 7 лет наказания. Если оба не сознаются – по 3 года. Если один сознается, а другой нет, то сознавшийся получит 1 год, а не сознавшийся 10 лет. Стратегии игрока А: сознаваться (А1), не сознаваться (А2). Стратегии игрока В: сознаваться (В1), не сознаваться (В2). Выберите платежную матрицу игрока А. Элементы в матрицах – срок наказания заключенного, строки матрицы соответствуют стратегиям игрока А, столбцы – стратегиям игрока В.
a).
б)
@в)
г)
112.
Двое заключенных знают, что если оба сознаются в преступлении, то каждый
получит по 7 лет наказания. Если оба не сознаются – по 3 года. Если один
сознается, а другой нет, то сознавшийся получит 1 год, а не сознавшийся 10 лет.
Стратегии игрока А: сознаваться (А1), не сознаваться (А2). Стратегии игрока В:
сознаваться (В1), не сознаваться (В2). Выберите платежную матрицу игрока В.
Элементы в матрицах – срок наказания заключенного, строки матрицы соответствуют
стратегиям игрока А, столбцы – стратегиям игрока В.
А)
@Б)
В)
Г)
.
113. Позиционная игра может быть сведена к …
А). Биматричной игре
@Б). Матричной игре
В). Дифференциальной игре
Г). Бесконечной игре
114. В позиционной игре с полной информацией …
@А). Всегда существуют оптимальные чистые стратегии
Б). Иногда существуют оптимальные чистые стратегии
В). Не существует..
Доминируемая стратегия в теории игр Объяснение
Доминируемая стратегия в теории игр возникает, когда один игрок имеет более доминирующую стратегию по сравнению с другим игроком.
Как мы видели, концепция решения с доминированием равновесия может быть полезным инструментом. В дилемме заключенного, как только Игрок 1 осознает, что у него есть доминирующая стратегия, ему не нужно думать о том, что сделает Игрок 2. Игрок 1 знает, что он может просто использовать свою доминирующую стратегию и получить больше выгоды, чем играя что-то еще. Игры, в которых все игроки имеют доминирующие стратегии, по-прежнему являются стратегическими в том смысле, что выигрыш зависит от того, что делают другие игроки, а наилучший ответ — нет.
Что такое доминирующая стратегия в теории игр?
Доминирующая стратегия в теории игр возникает, когда один игрок имеет более сильную и эффективную стратегию по сравнению с другим игроком. Это означает, что когда один игрок применяет эту стратегию, он всегда будет лучше, чем любая стратегия, которую использует его противник.
Но что, если не у всех игроков есть доминирующие стратегии? Что, если никто из игроков этого не сделает?
Как идентифицировать доминируемую стратегию в теории игр
Повторное удаление доминируемых стратегий является одним из распространенных, но утомительных способов решения игр, в которых нет строго доминирующей стратегии.
Он включает в себя итеративное удаление доминируемых стратегий. Существует два типа доминируемых стратегий.
Типы доминируемых стратегий в теории игр
- Строго доминируемая стратегия : Это стратегия, которая всегда дает худший результат, чем альтернативная стратегия, независимо от того, какую стратегию выбирает противник.
- Стратегия со слабым доминированием : Это стратегия, которая дает такой же или худший результат, чем альтернативная стратегия.
На первом шаге итеративного процесса удаления из пространства стратегий каждого из игроков удаляется не более одной доминирующей стратегии, поскольку ни один рациональный игрок никогда не стал бы использовать эти стратегии. Это приводит к новой, меньшей игре.
Некоторые стратегии, которые раньше не доминировали, могут доминировать в маленькой игре. Первый шаг повторяется, создавая новую, еще меньшую игру, и так далее. Процесс останавливается, когда ни для одного игрока не найдена доминируемая стратегия.
Этот процесс действителен, поскольку предполагается, что рациональность среди игроков общеизвестна. То есть каждый игрок знает, что остальные игроки рациональны, и каждый игрок знает, что остальные игроки знают, что он знает, что остальные игроки рациональны, и так до бесконечности.
Существует две версии этого процесса. Первая (и предпочтительная) версия предполагает только устранение строго доминируемых стратегий. Если после завершения этого процесса у каждого игрока остается только одна стратегия, этот набор стратегий представляет собой уникальное равновесие Нэша.
Второй вариант предполагает исключение как строго, так и слабо доминируемых стратегий. Если в конце процесса у каждого игрока есть единственная стратегия, этот набор стратегий также является равновесием по Нэшу. В отличие от первого процесса устранение слабо доминируемых стратегий может устранить некоторые равновесия по Нэшу. В результате равновесие Нэша, найденное путем исключения слабо доминируемых стратегий, может быть не единственным равновесием Нэша.
В некоторых играх, если мы удаляем слабо доминируемые стратегии в другом порядке, мы можем получить другое равновесие Нэша.
Я использовал много терминов, поэтому давайте рассмотрим пример, чтобы прояснить эти понятия.
Подробнее о науке о данныхОсновы теории вероятностей и статистики Термины, которые необходимо знать
Пример доминируемых стратегий
Рассмотрим следующую стратегическую ситуацию, которую мы хотим представить в виде игры.
Два бара, бар A и бар B, расположены рядом друг с другом в центре города. Каждый бар стремится максимизировать доход и выбирает, какую цену установить за пиво: 2 доллара, 4 доллара или 5 долларов. В каждом баре 60 потенциальных клиентов, из них 20 местных жителей и 40 туристов. Местные жители будут покупать в баре с самой низкой ценой (и будут выбирать случайным образом, если в двух барах установлена одинаковая цена). Туристы в любом случае будут выбирать бар случайным образом.
Создание матрицы выплат
После того, как мы определили игроков и стратегии, мы можем начать создавать нашу матрицу выплат:
Пустая матрица выплат.
| Изображение: Майкл КингстонТеперь мы можем заполнить выплаты. Нам говорят, что каждый бар заботится только о максимизации дохода (количество проданных сортов пива, умноженное на цену). Давайте посмотрим на профиль стратегии (2 доллара, 5 долларов). То есть, когда бар A взимает 2 доллара, а бар B — 5 долларов. В этом случае в бар А пойдут все местные жители, как и половина туристов. Это дает бару А всего 40 бутылок пива, проданных по цене 2 доллара за штуку, или 80 долларов дохода. Бар B привлекает только половину туристов из-за более высокой цены. Это дает бару B всего 20 сортов пива, проданных по цене 5 долларов за штуку, или 100 долларов дохода.
Начало заполнения матрицы. | Изображение: Michael KingstonЗатем мы можем заполнить остальную часть таблицы, рассчитав доходы таким же образом.
Заполненная платежная матрица. | Изображение: Майкл Кингстон Первое, что следует отметить, это то, что ни у одного из игроков нет доминирующей стратегии. Для слитка А не существует цены, которая дала бы ему более высокий доход, чем любая другая цена, которую он мог бы установить, независимо от того, какую цену устанавливает слиток Б.
Например, цена в 4 доллара дает слитку А более высокую прибыль, чем любая другая цена, если слиток Б стоит 5 долларов. Но что, если в баре B не 5 долларов, а пиво стоит 2 доллара? В этом случае цена в 4 доллара больше не является лучшим ответом для бара А. Цена в 5 долларов будет.
Стратегии со строгим доминированием Пример
Концепция решения, которую мы разработали до сих пор, — стратегии с доминированием равновесия — здесь бесполезна.
Логика равновесия в доминирующих стратегиях заключается в том, что если у игрока есть стратегия, которая всегда является лучшей, мы ожидаем, что он будет ее использовать. Но что, если у игрока есть стратегия, которая всегда хуже какой-то другой стратегии? Разумно ожидать, что он никогда не будет использовать стратегию, которая всегда хуже другой.
Стратегия S игрока i строго доминируется другой стратегией S’, если для каждой возможной комбинации стратегий всех других игроков S’ дает игроку i более высокие выигрыши, чем S.
игра выше? Да. Стратегия «2 доллара» всегда дает меньшие выплаты в баре А, чем «4 доллара» или «5 долларов». Давайте посмотрим, почему в стратегии строго доминирует стратегия $4 для бара A:
- Если ожидается, что бар B сыграет 2 доллара, бар A может получить 60 долларов, играя также по 2 доллара, и может получить 80 долларов.
- Если ожидается, что бар B сыграет 4 доллара, бар A может получить 80 долларов, также сыграв 2 доллара, и может получить 120 долларов, сыграв 4 доллара. $160, играя $4.
Следовательно, бар А никогда не будет использовать стратегию $2. Для любой возможной стратегии противника бара А существует стратегия, которая дает более высокую выплату, чем стратегия в 2 доллара. Мы можем обобщить это и сказать, что рациональные игроки никогда не используют строго доминируемые стратегии.
Подробнее о науке о данных4 Основные навыки, необходимые каждому специалисту по данным
Повторное удаление строго доминируемых стратегий Пример
Первый раунд удаления
это игра полной информации.
Бар Б знает выплаты Бара А. Таким образом, если мы можем определить, что 2 доллара никогда не будут разыграны, потому что это строго доминируемая стратегия, Бар Б тоже может это заметить. Таким образом, бар B может обоснованно ожидать, что бар A никогда не будет играть по $2.
Это симметричная игра, поэтому то же самое справедливо и для бара B. Два доллара — это строго доминируемая стратегия для бара B, и бар A тоже об этом знает. Мы можем удалить доминируемые стратегии из матрицы выплат следующим образом:
Первый раунд удаления. | Изображение: Michael Kingston. Сделав это, мы потеряли все ячейки, соответствующие профилю стратегии, в котором используется доминирующая стратегия. Это как раз и есть наша цель, которая состоит в том, чтобы удалить исходы, в которых разыгрываются доминирующие стратегии, из множества исходов, которые мы считаем возможными.
Второй раунд удаления
Теперь у нас осталось четыре профиля стратегии (и четыре соответствующих результата).
Теперь давайте снова поставим себя на место бара А. Бар A знает, что он не будет играть по $2, как и его оппонент. Бар А также знает, что Бар Б знает об этом. Теперь бар А сравнивает стратегии $4 и $5 и замечает, что, как только стратегия $2 убирается со стола для обоих игроков, стратегия $5 доминирует над стратегией $4. То есть:
- Если B оценивает свое пиво в 4 доллара, то в результате получается 120 долларов, а при цене 5 долларов получается 100 долларов.
- Если B оценивается как 5 долларов, цена 4 доллара дает 160 долларов, а сопоставление по 5 долларов дает 150 долларов. к любой стратегии, которую мог бы использовать рациональный игрок. Итак, мы можем удалить его из матрицы. Игра симметрична, поэтому те же рассуждения справедливы и для бара B. Второй раунд удаления. | Изображение: Майкл Кингстон
Теперь у нас ровно один профиль стратегии — пиво в обоих барах стоит 4 доллара. Мы использовали повторяющееся удаление доминируемых стратегий, чтобы получить этот профиль стратегии.
- Повторное удаление доминируемых стратегий: Это метод, который включает сначала удаление всех строго доминируемых стратегий из исходной матрицы выплат. Как только этот первый шаг удаления завершен, затем изучается сокращенная матрица, и любые стратегии, которые доминируют в этой новой, уменьшенной матрице, удаляются. Этот процесс продолжается до тех пор, пока стратегии нельзя будет удалить.
- Рационализируемые стратегии : Когда многократное удаление доминируемых стратегий приводит только к одному стратегическому профилю, говорят, что игра разрешима на основе доминирования. В более общем смысле стратегии, которые остаются после процесса повторного удаления строго доминируемых стратегий, известны как рационализируемые стратегии.
- Равновесие в строго доминирующих стратегиях : В то время как поиск равновесия в строго доминирующих стратегиях включает в себя поиск стратегии, которая всегда является наилучшей реакцией для каждого игрока, поиск равновесия посредством повторного удаления включает в себя итеративное исключение из рассмотрения стратегий, которые никогда не бывают лучшими ответы. Обратите внимание, что доминирующая стратегия (когда она существует) по определению строго доминирует над всеми остальными.
Игры и технологии Чему мы можем научиться у 4 сверхчеловеческих игровых ИИ
Недостаток метода доминируемых стратегий
Оба метода имеют один общий существенный недостаток: они не всегда сужают круг того, что может произойти в игре к приемлемо небольшому количеству возможностей. Например, в игре существует равновесие в доминирующих стратегиях, только если у всех игроков есть доминирующая стратегия. Если это не так, эта концепция решения не очень полезна.
Точно так же в некоторых играх могут отсутствовать стратегии, которые можно удалить с помощью повторного удаления.
Даже среди игр, в которых есть некоторые доминирующие стратегии, оставшийся набор рациональных стратегий может быть очень большим. Предсказательная сила может быть недостаточно точной, чтобы быть полезной.У игрока есть доминирующая стратегия, если эта стратегия дает ему более высокий выигрыш, чем что-либо другое, что он мог бы сделать, независимо от того, что делают другие игроки. Если у игрока есть доминирующая стратегия, ожидайте, что он ее использует.
У игрока есть строго доминируемая стратегия, если эта стратегия дает ему меньший выигрыш, чем любая другая стратегия, которую он мог бы использовать, независимо от того, что делают другие игроки. Если у вас строго доминируемая стратегия, ожидайте, что другие игроки будут предвидеть, что вы никогда не будете ее использовать, и соответственно будут выбирать свои действия.
Мы рассмотрели два метода определения «вероятного» исхода игры.
- Поиск равновесия доминирующей стратегии . Это замечательно, если доминирующая стратегия существует, однако часто доминирующей стратегии не существует. Это ограничивает полезность этой концепции решения.
- Итеративно удалить строго доминируемые стратегии . Итеративное удаление — полезный, хотя и громоздкий инструмент для исключения из рассмотрения доминируемых стратегий.
Однако ни один из этих методов не гарантирует возврата приемлемо небольшого набора ожидаемых результатов. К счастью, существует концепция решения, которая гарантирует возврат приемлемо небольшого набора ожидаемых результатов, известного как равновесие Нэша.
Теория игр II: доминирующие стратегии
Сводка
В этом LP мы узнаем все, что есть об одновременных играх. Эти игры, используемые при рассмотрении игры, в которой игроки перемещаются или разыгрывают свои стратегии одновременно, обычно используются во многих областях. От военных стратегий до соглашений о сговоре анализ этих ситуаций как одновременных игр может помочь нам найти лучший способ действовать.Доминирующие стратегии считаются лучшими, чем другие стратегии, независимо от того, что могут делать другие игроки. В теория игр , существует два вида стратегического доминирования:
строго доминирующая стратегия – это та стратегия, которая всегда обеспечивает большую полезность игроку, независимо от стратегии другого игрока;
— Слабо доминирующая стратегия – это та стратегия, которая обеспечивает как минимум одинаковую полезность для всех стратегий другого игрока и строго большую для какой-то стратегии.
Равновесие с доминирующей стратегией достигается, когда каждый игрок выбирает свою собственную доминирующую стратегию. В дилемма заключенного , доминирующей стратегией для обоих игроков является признание, а это означает, что равновесие «признание-признание» является доминирующей стратегией равновесия (подчеркнуто красным), даже если это равновесие не является оптимальным по Парето равновесием (подчеркнуто зеленым).
Следует отметить, что любое равновесие доминирующей стратегии всегда является равновесием по Нэшу . Однако не все равновесия Нэша являются равновесиями доминирующей стратегии.
Исключение доминируемых стратегий обычно используется для упрощения анализа любой игры. Дальнейший путь состоит в том, чтобы исключить для каждого игрока все стратегии, которые кажутся «неразумными», что значительно сократит количество равновесий. Этот метод довольно прост в использовании, когда имеются только строго доминируемые стратегии, но устранение слабо доминируемых стратегий может оказаться проблематичным, в результате чего игра не будет похожа на исходную со стратегической точки зрения.
Хорошим примером устранения стратегии доминирования является анализ битвы в море Бисмарка. В этой игре, как показано в соседней игровой матрице, у Кенни нет доминирующей стратегии (сумма выигрышей первой стратегии равна сумме второй стратегии), но у японцев есть слабо доминирующая стратегия, заключающаяся в том, чтобы пойти Север (выигрыши равны для одной стратегии, но строго лучше для другой).
Обратите внимание, что доминирующая стратегия (когда она существует) по определению строго доминирует над всеми остальными.
Даже среди игр, в которых есть некоторые доминирующие стратегии, оставшийся набор рациональных стратегий может быть очень большим. Предсказательная сила может быть недостаточно точной, чтобы быть полезной.
Это замечательно, если доминирующая стратегия существует, однако часто доминирующей стратегии не существует. Это ограничивает полезность этой концепции решения.
