Приведение определителя к треугольному виду
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Пример
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычтем строку №3, умноженную на 9/21.
Умножим элементы матрицы находящиеся на диагонали.
Метод приведения определителя к треугольному виду — Студопедия
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
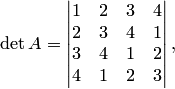
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент 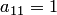 первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на 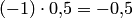 , т.е. умножить на (-2):
, т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы 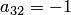
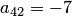 второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента
второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента 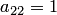 и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:Осталось сделать равным нулю элемент 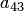 . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
. К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
приведение к треугольному виду — ПриМат
Дальнейшие преобразования будут проще, если элемент $a_{11}$ равен 1 или -1. Для этого из первой строки вынесем 3 за знак определителя:
$\Delta =\left|\begin{array}{rrrr}-3 & 9 & 3& 6\\ -5 & 8 & 2 & 7\\ 4 & -5 & -3 & -2\\ 7 & -8 & -4 & -5 \end{array}\right|=3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1& 2\\ -5 & 8 & 2 & 7\\ 4 & -5 & -3 & -2\\ 7 & -8 & -4 & -5 \end{array}\right|$
Далее нам нужно получить нули в первом столбце. Домножим первую строку на -5 и прибавим ко второй, на 4 и прибавим к третей, на 7 и прибавим к четвертой:
$\Delta =3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1 & 2\\ 0 & -7 & -3 & -3\\ 0 & 7 & 1 & 6\\ 0 & 13 & 3 & 9 \end{array}\right|$
Аналогично, дальнейшие вычисления будут проще, если элемент $a_{22}$ равен 1 или -1. Для этого вторую строку умножим на 2 и прибавим к четвертой строке. Далее поменяем вторую и последнюю строку местами. Перед определителем появится знак «-«.
$\Delta =3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1 & 2\\ 0 & -7 & -3 & -3\\ 0 & 7 & 1 & 6\\ 0 & -1 & -3 & 3 \end{array}\right|=-3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1 & 2\\ 0 & -1 & -3 & 3\\ 0 & 7 & 1 & 6\\ 0 & -7 & -3 & -3 \end{array}\right|$
Далее нам нужно получить нули во втором столбце под элементом $a_{22}$. Для этого умножим вторую строку на 7 и прибавим к третей, на -7 и прибавим к четвертой.
$\Delta =-3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1 & 2\\ 0 & -1 & -3 & 3\\ 0 & 0 & -20 & 27\\ 0 & 0 & 18 & -24 \end{array}\right|$
Прибавим последнюю строку к третьей, потом умножим третью строку на 9 и прибавим к четвертой:
$\Delta =-3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1 & 2\\ 0 & -1 & -3 & 3\\ 0 & 0 & -2 & 3\\ 0 & 0 & 18 & -24 \end{array}\right|=-3\cdot\left|\begin{array}{rrrr}-1 & 3 & 1 & 2\\ 0 & -1 & -3 & 3\\ 0 & 0 & -2 & 3\\ 0 & 0 & 0 & 3 \end{array}\right|$
Привели определитель к треугольному виду. Его значение равно произведению элементов, стоящих на главной диагонали:
$\Delta=-3\cdot\left(\left(-1\right)\cdot\left(-1\right)\cdot\left(-2\right)\cdot\left(3\right)\right)=18$
[свернуть]
1. Методы вычисления определителей n – го порядка.
Основываясь на понятиях определителей второго и третьего порядков, можно аналогично ввести понятие определителя порядка n. Определители порядка выше третьего вычисляются, как правило, с использованием свойств определителей, сформулированных в п. 1.3., которые справедливы для определителей любого порядка.
Используя свойство определителей номер 90 введем определение определителя 4-го порядка:
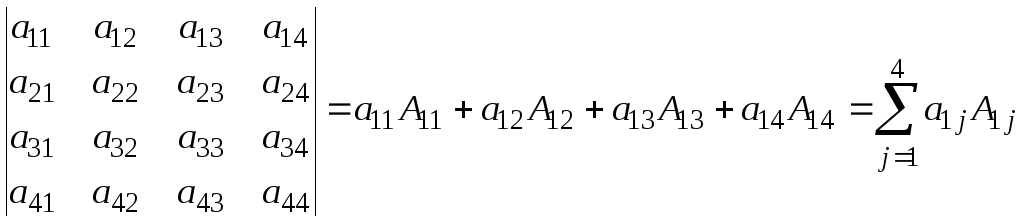 .
.
Пример 2. Вычислить, используя подходящее разложение.
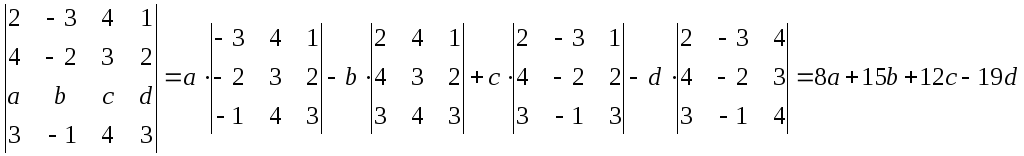 .
.
Аналогично вводится понятие определителя 5-го, 6-го и т.д. порядка. Значит определитель порядка n :
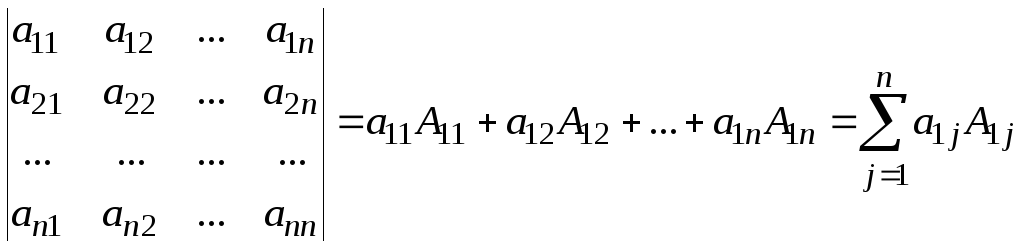 .
.
Все свойства определителей 2-го и 3-го порядков, рассмотренные раннее, справедливы и для определителей n-го порядка.
Рассмотрим основные методы вычисления определителей n-го порядка.
Метод понижения порядка определителя основан на следующем соотношении (i фиксированное число):

 (разложение определителя поi-ой
строке). Либо
(разложение определителя поi-ой
строке). Либо  (разложение поj-тому
столбцу).
(разложение поj-тому
столбцу).
Замечание: прежде чем применять этот метод, полезно, используя основные свойства определителей, обратить в нуль все, кроме одного, элементы его некоторой строки или столбца. (Метод эффективного понижения порядка)
Метод приведения к треугольному виду заключается в таком преобразовании определителя, когда все его элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. В этом случае определитель равен произведению элементов его главной диагонали.
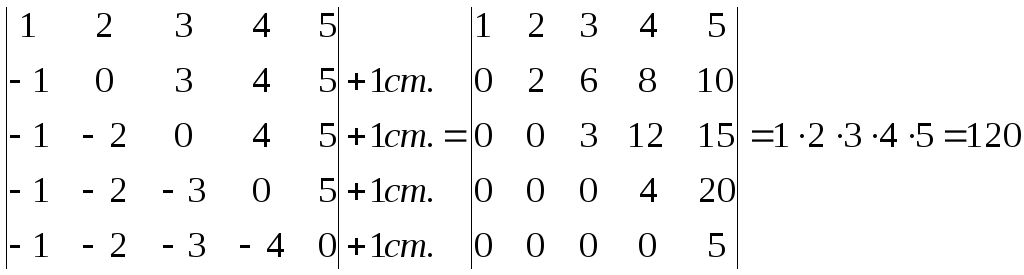
Пример 3. Вычислить, приведением к треугольному виду.

Пример 4. Вычислить, используя метод эффективного понижения порядка
.
Решение: по свойству 40 определителей из первой строки вынесем множитель 10, а затем будем последовательно умножать вторую строку на 2, на 2, на 1 и складывать соответственно с первой, с третьей и четвертой строками (свойство 80).
 .
.
Полученный определитель можно разложить по элементам первого столбца. Он будет сведен к определителю третьего порядка, который вычисляется по правилу Саррюса (треугольника).
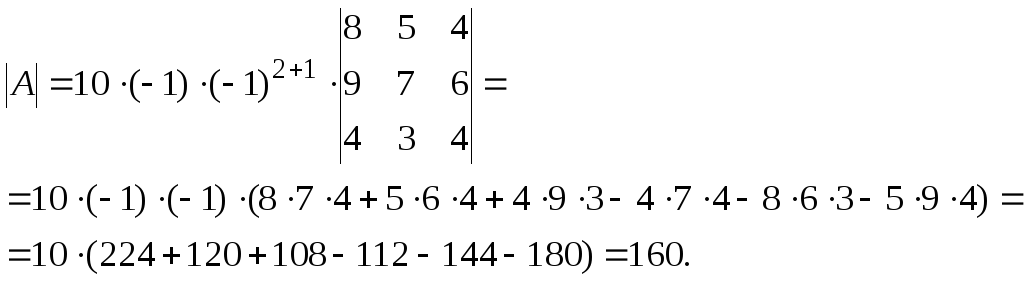
Пример 5. Вычислить определитель, приведением к треугольному виду.
 .
.
Пример 3. Вычислить, используя рекуррентные соотношения.
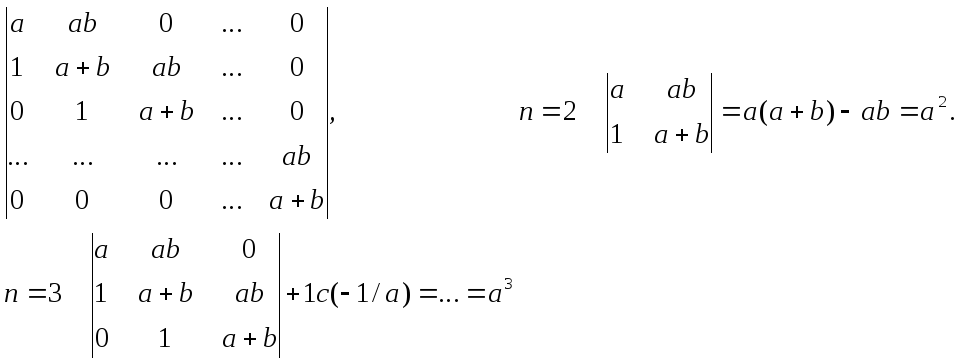
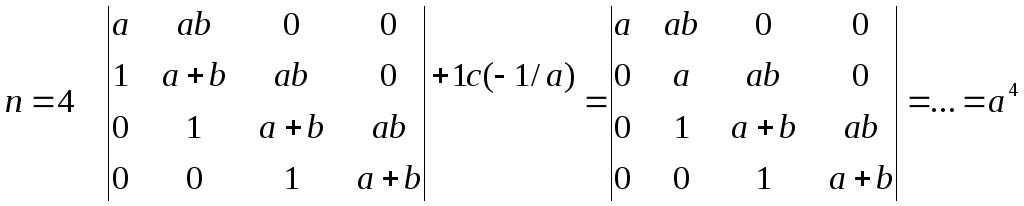 .
.
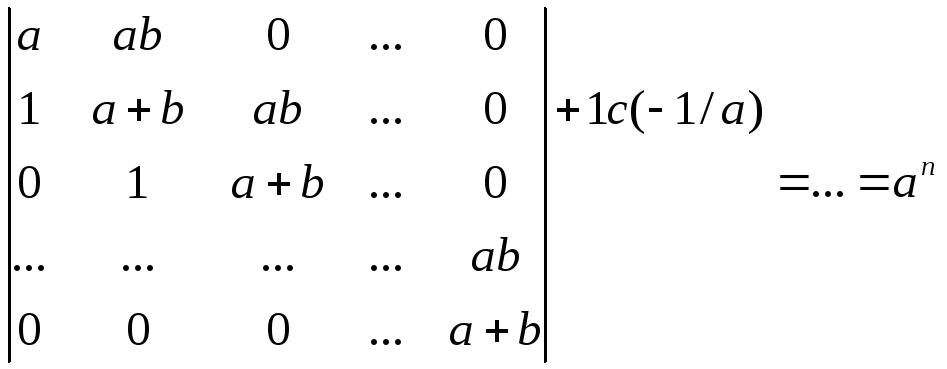 .
.
Лекция 4. Обратная матрица. Ранг матрицы.
1. Понятие обратной матрицы
Определение 1. Квадратная матрица А порядка n называется невырожденной, если ее определитель |A| ≠ 0. В случае, когда |A| = 0, матрица А называется вырожденной.
Только для квадратных невырожденных матриц А вводится понятие обратной матрицы А-1.
Определение 2. Матрица А-1 называется обратной для квадратной невырожденной матрицы А, если А-1А = АА-1 = Е, где Е – единичная матрица порядка n.
Определение 3. Матрица  называетсяприсоединенной, ее элементами являются алгебраические
дополнения
называетсяприсоединенной, ее элементами являются алгебраические
дополнения  транспонированной матрицы
транспонированной матрицы .
.
Алгоритм вычисления обратной матрицы методом присоединенной матрицы.
Находим определитель исходной матрицы. Если определитель равен нулю, то обратной матрицы не существует. Если определитель отличен от нуля, то матрица А невырожденная и обратная матрица существует.
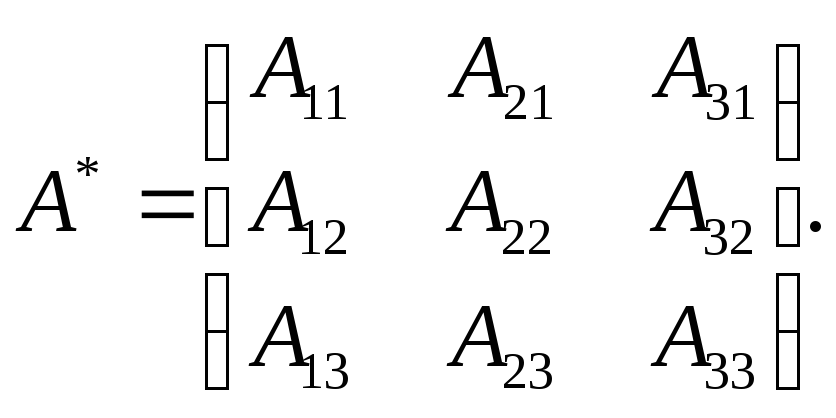
Находим присоединенную матрицу А*, элементы которой являются алгебраическими дополнениями элементов транспонированной матрицы А.

Вычислим обратную матрицу по формуле
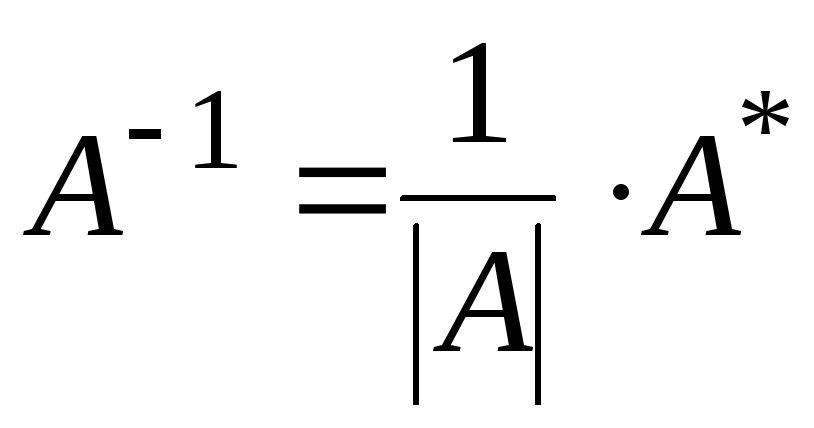 ,
где
,
где  .
.
Проверяем правильность вычисления А-1А = АА-1 = Е. (Е – единичная матрица)
Матрицы А и А-1 взаимообратные. Если |A| = 0, то обратная матрица не существует.
Пример
1. Дана
матрица А. Убедиться, что она невырожденная,
и найти обратную матрицу 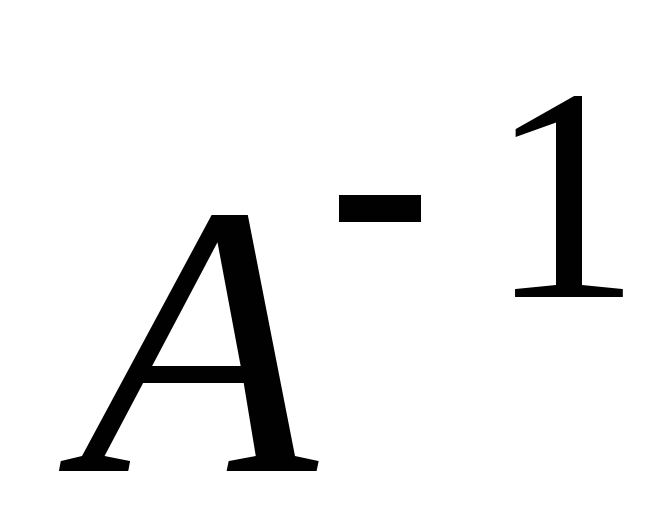 .
.
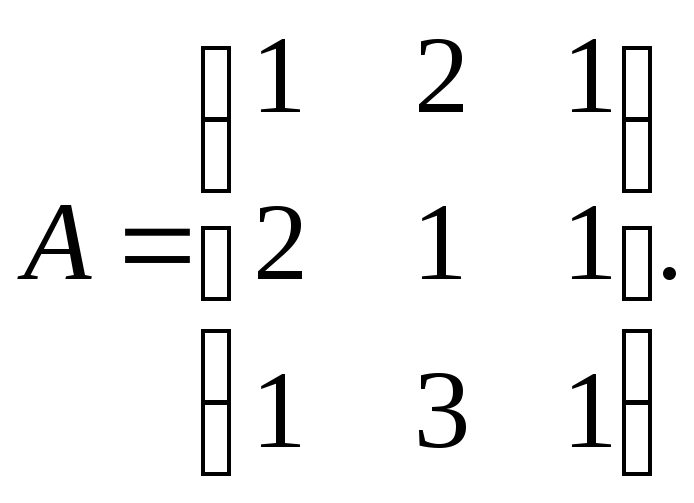
Решение: 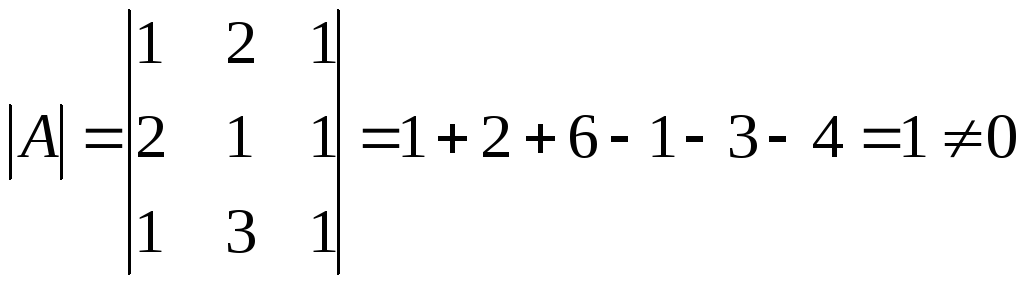 .
Следовательно матрица невырожденная.
.
Следовательно матрица невырожденная.
Найдем обратную матрицу. Составим алгебраические дополнения элементов матрицы А.
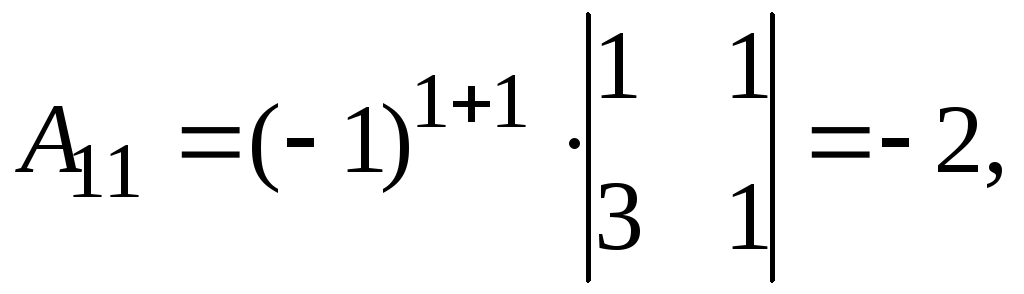
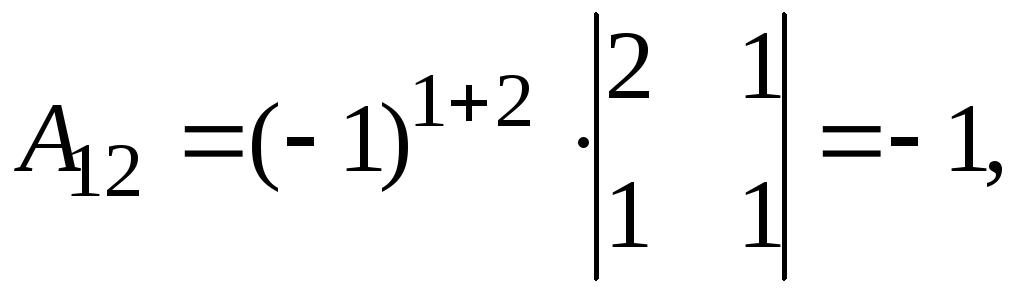
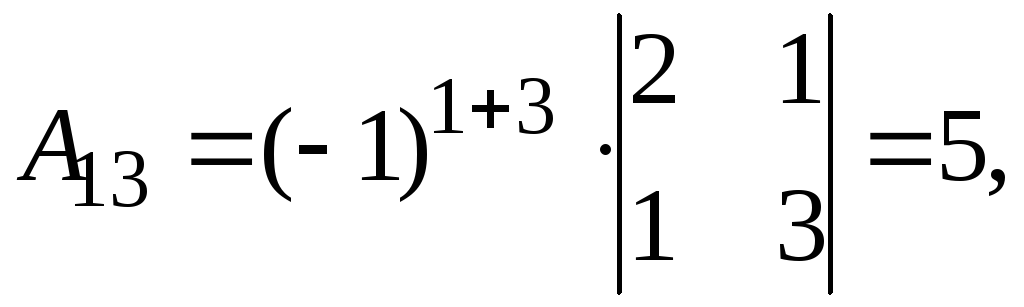
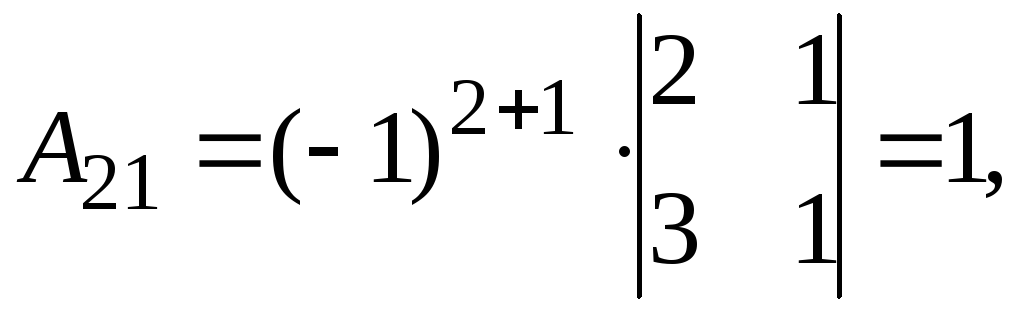
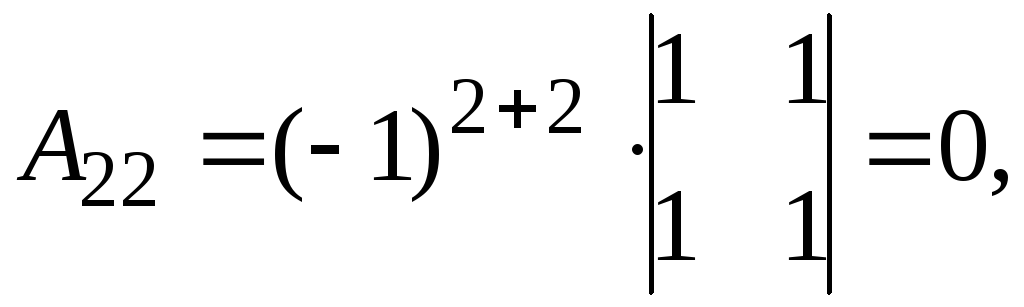
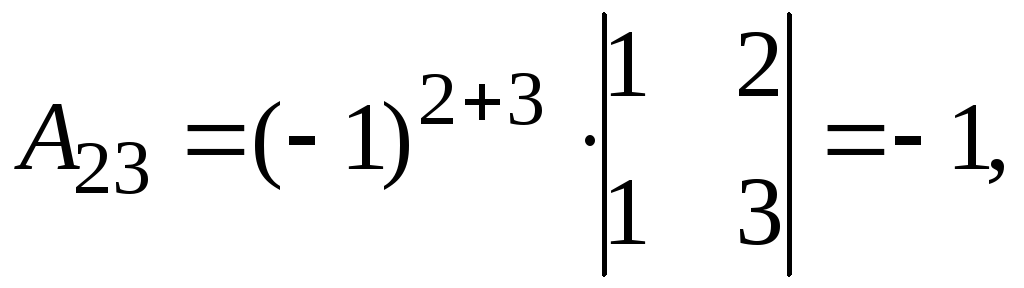
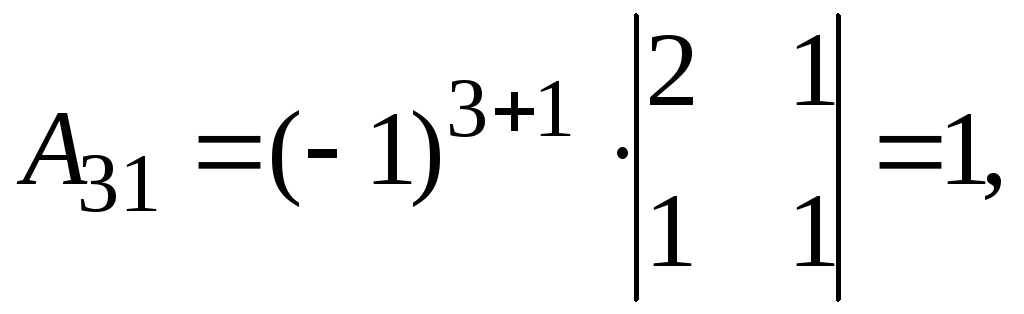
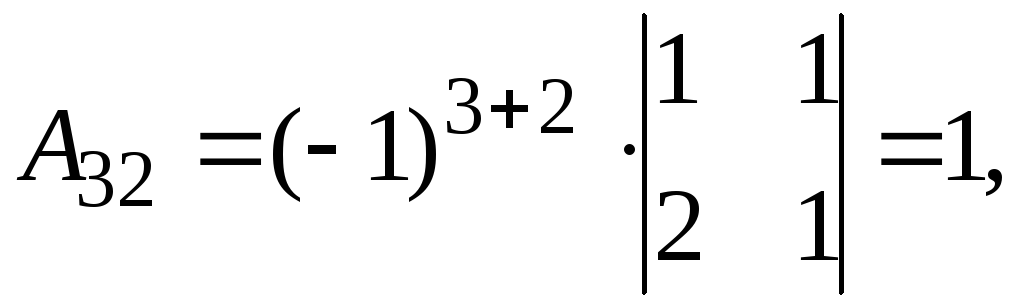
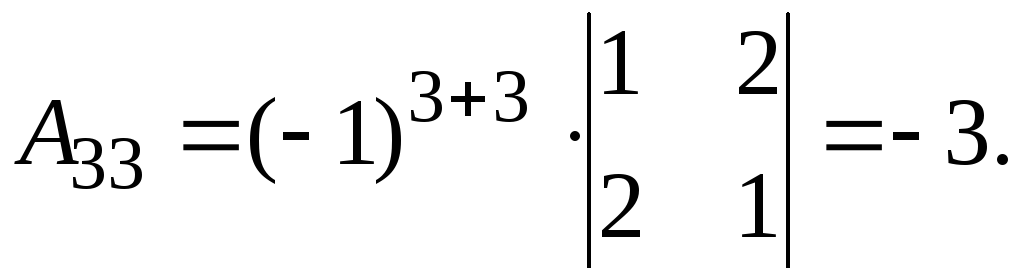
Получаем 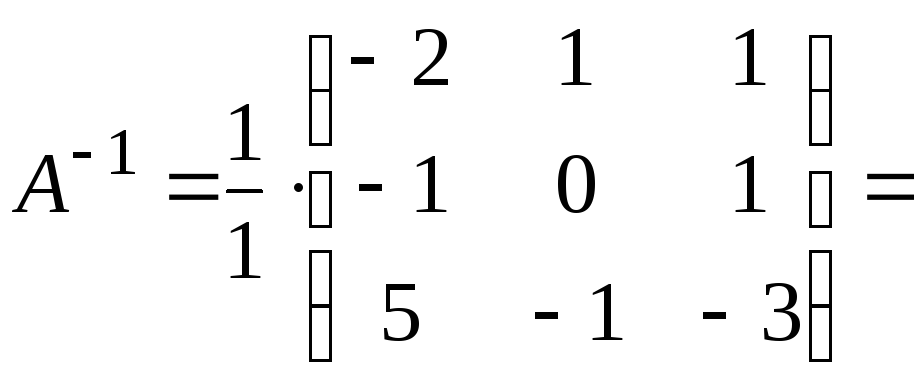
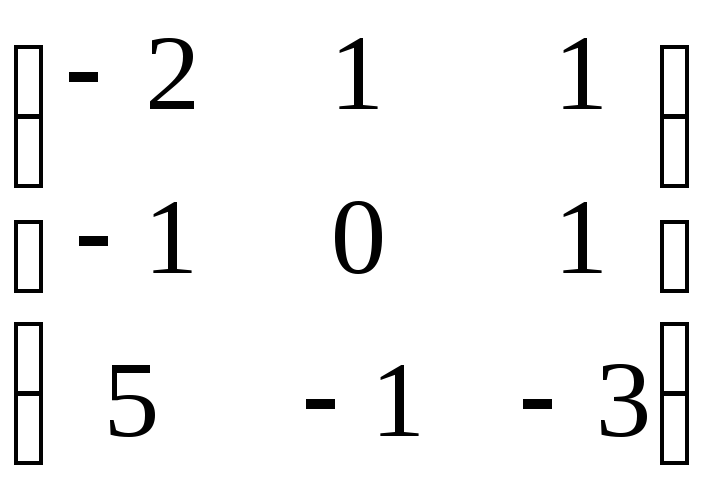 .
.
Как вычислить определитель невырожденной матрицы (n * n) с помощью элементарного преобразования в C?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
,Как мне найти определитель матрицы, используя форму эшелона строк?
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
- Исчисление
- Геометрия
- Prealgebra
- тригонометрия и алгебра
- Статистика
Новый метод вычисления детерминантов матрицы n n (n 3) путем приведения детерминантов ко 2-му порядку
Примечания к определителю
 ENGG2012B Заметки по высшей инженерной математике по определению Лектор: Кеннет Шум Лекция 9-18 февраля 2013 г. Определитель системы линейных уравнений определяет, является ли решение уникальным без
ENGG2012B Заметки по высшей инженерной математике по определению Лектор: Кеннет Шум Лекция 9-18 февраля 2013 г. Определитель системы линейных уравнений определяет, является ли решение уникальным без
Характеристический многочлен
 Физика 116A Зима 2011 Характеристический многочлен 1 Коэффициенты характеристического многочлена Рассмотрим проблему собственных значений для матрицы A n n, A v = λ v, v 0 (1) Решение этой задачи
Физика 116A Зима 2011 Характеристический многочлен 1 Коэффициенты характеристического многочлена Рассмотрим проблему собственных значений для матрицы A n n, A v = λ v, v 0 (1) Решение этой задачи
Блок 18 Детерминанты
 Блок 18 Детерминанты С каждой квадратной матрицей связано число, называемое определителем.В этом разделе мы определим, как вычислить это число, а также рассмотрим некоторые свойства
Блок 18 Детерминанты С каждой квадратной матрицей связано число, называемое определителем.В этом разделе мы определим, как вычислить это число, а также рассмотрим некоторые свойства
РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ
 РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ Линейные системы Ax = b широко используются в прикладной математике. Они возникают как прямые постановки задач реального мира; но чаще они возникают в рамках численного анализа
РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ Линейные системы Ax = b широко используются в прикладной математике. Они возникают как прямые постановки задач реального мира; но чаще они возникают в рамках численного анализа
Сук-Гын Хван и Джин-Ву Пак
 Bull.Корейская математика. Soc. 43 (2006), No. 3, pp. 471 478 ПРИМЕЧАНИЕ О ЧАСТИЧНОЙ РАЗРЕШИМОСТИ ЗНАКОВ Сук-Гын Хван и Джин-Ву Пак Аннотация. В этой статье мы доказываем, что если Ax = b является частично знакоразрешаемой линейной
Bull.Корейская математика. Soc. 43 (2006), No. 3, pp. 471 478 ПРИМЕЧАНИЕ О ЧАСТИЧНОЙ РАЗРЕШИМОСТИ ЗНАКОВ Сук-Гын Хван и Джин-Ву Пак Аннотация. В этой статье мы доказываем, что если Ax = b является частично знакоразрешаемой линейной
26. Детерминанты I. 1. Предыстория.
 26. Детерминанты I 26.1 Предыстория 26.2 Определения 26.3 Уникальность и другие свойства 26.4 Существование И как тщательный анализ более пешеходной точки зрения, и как переход к не зависящей от координат точке
26. Детерминанты I 26.1 Предыстория 26.2 Определения 26.3 Уникальность и другие свойства 26.4 Существование И как тщательный анализ более пешеходной точки зрения, и как переход к не зависящей от координат точке
Примечание о сопутствующих матрицах
 Линейная алгебра и ее приложения 372 (2003) 325 33 www.elsevier.com/locate/laa Примечание о сопутствующих матрицах Мирослав Фидлер Академия наук Чешской Республики Институт компьютерных наук Pod
Линейная алгебра и ее приложения 372 (2003) 325 33 www.elsevier.com/locate/laa Примечание о сопутствующих матрицах Мирослав Фидлер Академия наук Чешской Республики Институт компьютерных наук Pod
АНАЛИЗ ДАННЫХ II. Матричные алгоритмы
 АНАЛИЗ ДАННЫХ II Матрица Алгоритмов Матрица подобия Для набора данных D = {x i}, i = 1, .., n, состоящего из n точек в R d, пусть A обозначает симметричную матрицу подобия n n между точками, заданную как где
АНАЛИЗ ДАННЫХ II Матрица Алгоритмов Матрица подобия Для набора данных D = {x i}, i = 1, .., n, состоящего из n точек в R d, пусть A обозначает симметричную матрицу подобия n n между точками, заданную как где
Четыре [10,5,4] двоичных кода
![The four [10,5,4] binary codes The four [10,5,4] binary codes](/800/600/https/docplayer.net/thumbs/40/20775341.jpg) 1 Предварительные сведения Четыре [10 ,,] двоичных кода Есть четыре различных [10; ; ] двоичные коды.Мы докажем это умеренно элементарным способом, используя тождества Мак-Вильямса в качестве основного инструмента. (Для модели
1 Предварительные сведения Четыре [10 ,,] двоичных кода Есть четыре различных [10; ; ] двоичные коды.Мы докажем это умеренно элементарным способом, используя тождества Мак-Вильямса в качестве основного инструмента. (Для модели
Решение домашнего задания 2
 Решение домашнего задания 2 Елена Бормашенко 23 сентября 2011 г. Раздел 1.4: 1 (a) (b) (i) (k), 4, 5, 14; Раздел 1.5: 1 (a) (b) (c) (d) (e) (n), 2 (a) (c), 13, 16, 17, 18, 27 Раздел 1.4 1. Вычислите следующее, если
Решение домашнего задания 2 Елена Бормашенко 23 сентября 2011 г. Раздел 1.4: 1 (a) (b) (i) (k), 4, 5, 14; Раздел 1.5: 1 (a) (b) (c) (d) (e) (n), 2 (a) (c), 13, 16, 17, 18, 27 Раздел 1.4 1. Вычислите следующее, если
Математика 312 Домашнее задание 1 Решения
 Математика 31 Домашнее задание 1 Решения Последнее изменение: 15 июля 01 июля Это домашнее задание нужно сдать в четверг, 1 июля, в 13:10. Пожалуйста, сдайте его во время урока или в мой почтовый ящик в главном математическом кабинете (рядом с 4W1) Пожалуйста,
Математика 31 Домашнее задание 1 Решения Последнее изменение: 15 июля 01 июля Это домашнее задание нужно сдать в четверг, 1 июля, в 13:10. Пожалуйста, сдайте его во время урока или в мой почтовый ящик в главном математическом кабинете (рядом с 4W1) Пожалуйста,
9.2 Обозначение суммирования
 9. Обозначение суммирования 66 9. Обозначение суммирования В предыдущем разделе мы ввели последовательности, а теперь мы представим обозначения и теоремы, касающиеся суммы членов последовательности. Начнем с
9. Обозначение суммирования 66 9. Обозначение суммирования В предыдущем разделе мы ввели последовательности, а теперь мы представим обозначения и теоремы, касающиеся суммы членов последовательности. Начнем с
Собственные значения и собственные векторы
 Глава 6 Собственные значения и собственные векторы 6. Введение в собственные значения Линейные уравнения Ax D b происходят из задач установившегося состояния.Собственные значения имеют наибольшее значение в динамических задачах. Решение
Глава 6 Собственные значения и собственные векторы 6. Введение в собственные значения Линейные уравнения Ax D b происходят из задач установившегося состояния.Собственные значения имеют наибольшее значение в динамических задачах. Решение
ГЕНЕРАЦИОННЫЕ УСТАНОВКИ КИТ КОНРАД
 ГЕНЕРИРУЮЩИЕ НАБОРЫ КИТ КОНРАД 1 Введение В R n каждый вектор может быть записан как уникальная линейная комбинация стандартного базиса e 1 ,, e n Понятие более слабое, чем базис, — это остовное множество: набор векторов
ГЕНЕРИРУЮЩИЕ НАБОРЫ КИТ КОНРАД 1 Введение В R n каждый вектор может быть записан как уникальная линейная комбинация стандартного базиса e 1 ,, e n Понятие более слабое, чем базис, — это остовное множество: набор векторов
Решение линейных систем
 Глава 3 Решение линейных систем В этой главе мы изучаем алгоритмы для, возможно, наиболее часто встречающейся проблемы в научных вычислениях, решения линейных систем уравнений.Запускаем
Глава 3 Решение линейных систем В этой главе мы изучаем алгоритмы для, возможно, наиболее часто встречающейся проблемы в научных вычислениях, решения линейных систем уравнений.Запускаем
ЗНАК РАЗРЕШЕНИЯ
 Знак перестановки Кейт Конрад 1. Введение На протяжении всего обсуждения n 2. Любой цикл в S n является продуктом транспозиций: тождество (1) есть (12) (12), а k-цикл с k 2 может быть написано
Знак перестановки Кейт Конрад 1. Введение На протяжении всего обсуждения n 2. Любой цикл в S n является продуктом транспозиций: тождество (1) есть (12) (12), а k-цикл с k 2 может быть написано
6. Факторизация Холецкого.
 6.Факторизация Холецкого EE103 (осень 2011-12) треугольные матрицы: прямая и обратная подстановка факторизации Холецкого, решающая Ax = b с положительно определенной инверсией положительно определенной матрицы
6.Факторизация Холецкого EE103 (осень 2011-12) треугольные матрицы: прямая и обратная подстановка факторизации Холецкого, решающая Ax = b с положительно определенной инверсией положительно определенной матрицы
ЛИНЕЙНАЯ АЛГЕБРА. 23 сентября 2010 г.
 ЛИНЕЙНАЯ АЛГЕБРА 3 сентября 00 г. Содержание 0. LU-разложение ……………………………… 0. Инверсия и транспонирование …………………………… 0.3 Пробелы в столбцах и пустые пробелы …………………….. …
ЛИНЕЙНАЯ АЛГЕБРА 3 сентября 00 г. Содержание 0. LU-разложение ……………………………… 0. Инверсия и транспонирование …………………………… 0.3 Пробелы в столбцах и пустые пробелы …………………….. …
Непрерывность корня Перрона
 Линейная и полилинейная алгебра http://dx.doi.org/10.1080/03081087.2014.934233 ArXiv: 1407.7564 (http://arxiv.org/abs/1407.7564) Непрерывность корня Перрона Карл Д. Мейер Департамент математики, Север
Линейная и полилинейная алгебра http://dx.doi.org/10.1080/03081087.2014.934233 ArXiv: 1407.7564 (http://arxiv.org/abs/1407.7564) Непрерывность корня Перрона Карл Д. Мейер Департамент математики, Север
МАТ188х2С Lec0101 Бурбулла
 Линейное преобразование T: R m R n — это функция, которая переводит векторы из R m в векторы из R n, такие что и T (u + v) T (u) + T (v) T (kv) k T (v) для всех векторов u
Линейное преобразование T: R m R n — это функция, которая переводит векторы из R m в векторы из R n, такие что и T (u + v) T (u) + T (v) T (kv) k T (v) для всех векторов u
160 ГЛАВА 4.ВЕКТОРНЫЕ ПРОСТРАНСТВА
 160 ГЛАВА 4. ВЕКТОРНЫЕ ПРОСТРАНСТВА 4. Ранг и нулевое значение В этом разделе мы рассмотрим отношения между пространством строк, пространством столбцов, пустым пространством матрицы и ее транспонированием. Получим фундаментальные результаты
160 ГЛАВА 4. ВЕКТОРНЫЕ ПРОСТРАНСТВА 4. Ранг и нулевое значение В этом разделе мы рассмотрим отношения между пространством строк, пространством столбцов, пустым пространством матрицы и ее транспонированием. Получим фундаментальные результаты
1.2. Последовательные различия
 1. Применение индуктивного мышления: шаблоны чисел В предыдущем разделе мы представили индуктивное рассуждение и показали, как его можно применить для прогнозирования того, что будет дальше в списке чисел
1. Применение индуктивного мышления: шаблоны чисел В предыдущем разделе мы представили индуктивное рассуждение и показали, как его можно применить для прогнозирования того, что будет дальше в списке чисел
Классификация матриц Картана
 Глава 7 Классификация матриц Картана В этой главе мы описываем классификацию обобщенных матриц Картана Эту классификацию можно сравнить с грубой классификацией разновидностей в терминах
Глава 7 Классификация матриц Картана В этой главе мы описываем классификацию обобщенных матриц Картана Эту классификацию можно сравнить с грубой классификацией разновидностей в терминах
Арифметика и алгебра матриц
 Арифметика и алгебра матриц Math 572: Алгебра для учителей средней школы Университет Монтаны 1 Действительные числа 2 Связь в классе: системы линейных уравнений 3 Рациональные числа 4 Иррациональные
Арифметика и алгебра матриц Math 572: Алгебра для учителей средней школы Университет Монтаны 1 Действительные числа 2 Связь в классе: системы линейных уравнений 3 Рациональные числа 4 Иррациональные
Примечания к линейной алгебре
 Примечания к линейной алгебре Глава 19 ЯДРО И ИЗОБРАЖЕНИЕ МАТРИЦЫ Возьмем матрицу нм a 11 a 12 a 1m a 21 a 22 a 2m a n1 a n2 a nm и представим ее как функцию A: R m R n Ядро матрицы A определяется как Примечание
Примечания к линейной алгебре Глава 19 ЯДРО И ИЗОБРАЖЕНИЕ МАТРИЦЫ Возьмем матрицу нм a 11 a 12 a 1m a 21 a 22 a 2m a n1 a n2 a nm и представим ее как функцию A: R m R n Ядро матрицы A определяется как Примечание
Глава 7.Группы перестановок
 Глава 7 Группы перестановок () Мы начали изучение групп с рассмотрения плоских изометрий В предыдущей главе мы узнали, что конечные группы плоских изометрий могут быть только циклическими или диэдральными
Глава 7 Группы перестановок () Мы начали изучение групп с рассмотрения плоских изометрий В предыдущей главе мы узнали, что конечные группы плоских изометрий могут быть только циклическими или диэдральными
0 0 такой, что f x L всякий раз, когда x a
 Эпсилон-Дельта Определение предела Некоторые утверждения элементарной математики кажутся такими же загадочными, как одно, определяющее предел функции f () в точке = a, 0 0, такой что f L всякий раз, когда перевод:
Эпсилон-Дельта Определение предела Некоторые утверждения элементарной математики кажутся такими же загадочными, как одно, определяющее предел функции f () в точке = a, 0 0, такой что f L всякий раз, когда перевод:
Глава 6.Ортогональность
 6.3 Ортогональные матрицы 1 Глава 6. Ортогональность 6.3 Определение ортогональных матриц 6.4. Матрица A размера n n ортогональна, если A T A = I. Примечание. Мы увидим, что столбцов ортогональной матрицы должно быть
6.3 Ортогональные матрицы 1 Глава 6. Ортогональность 6.3 Определение ортогональных матриц 6.4. Матрица A размера n n ортогональна, если A T A = I. Примечание. Мы увидим, что столбцов ортогональной матрицы должно быть
1 Наборы и обозначения наборов.
 ЛИНЕЙНАЯ АЛГЕБРА МАТЕМАТИКА 27.6. ПРУЖИНА 23 (КОЭН) ЛЕКЦИЯ ЗАМЕЧАНИЯ Множества и обозначения множеств. Определение (наивное определение множества).Набор — это любая коллекция объектов, называемых элементами этого набора. Мы будем больше всего
ЛИНЕЙНАЯ АЛГЕБРА МАТЕМАТИКА 27.6. ПРУЖИНА 23 (КОЭН) ЛЕКЦИЯ ЗАМЕЧАНИЯ Множества и обозначения множеств. Определение (наивное определение множества).Набор — это любая коллекция объектов, называемых элементами этого набора. Мы будем больше всего
Примеры индукционных доказательств
 Рабочий лист по математике 3: индукционные доказательства III, образцы доказательств А.Дж. Примеры индукционных доказательств Хильдебранда Ниже приведены модельные решения некоторых практических задач на рабочих листах индукции. Решения предоставлены
Рабочий лист по математике 3: индукционные доказательства III, образцы доказательств А.Дж. Примеры индукционных доказательств Хильдебранда Ниже приведены модельные решения некоторых практических задач на рабочих листах индукции. Решения предоставлены
Подобные матрицы и жорданова форма
 Подобные матрицы и жорданова форма Мы почти охватили всю основу линейной алгебры, как только мы закончили разложение по сингулярным значениям, мы увидим все самые важные темы.A T A положительный
Подобные матрицы и жорданова форма Мы почти охватили всю основу линейной алгебры, как только мы закончили разложение по сингулярным значениям, мы увидим все самые важные темы.A T A положительный
Матричная дифференциация
 1 Введение Матричная дифференциация (и некоторые другие вещи) Рэндал Дж. Барнс, Департамент гражданского строительства, Университет Миннесоты, Миннеаполис, Миннесота, США На протяжении всей презентации у меня есть
1 Введение Матричная дифференциация (и некоторые другие вещи) Рэндал Дж. Барнс, Департамент гражданского строительства, Университет Миннесоты, Миннеаполис, Миннесота, США На протяжении всей презентации у меня есть
Минорные и сомножители: операции со строками
Несовершеннолетние и кофакторы: Операции со строками (стр. 3 из 3)
- Найдите следующее определитель, развернув строку или столбец по вашему выбору:
Нет конкретной строки или столбец выглядит лучше (легче), чем другие.я думаю, я сначала сделаю несколько операций со строками (и столбцами), чтобы получить некоторые больше нулей в определителе.
А! Это намного лучше. Теперь я могу развернуться по первой строке или по первому или второму столбцу, и мои вычисления будут намного проще, чем если бы я придерживался оригинального определитель.
Я думаю, что пойду вниз первый столбец.Единственный кофактор, который мне действительно нужно вычислить, — это A 2,1 :
Затем значение определителя 15 .
Я уже упоминал что есть другие способы манипулировать детерминантами. Вы можете сделать другое строковые операции, к которым вы привыкли, но они меняют значение определителя.Правила такие:
Если поменять местами
(переключатель) две строки (или столбцы) матрицы A чтобы получить B ,
, затем det ( A )
= det ( B ) .
Если умножить строку
(или столбец) из A на некоторое значение « k »
чтобы получить B ,
, затем det ( A )
= (1/ k ) det ( B ) .
Другими словами, если умножить строку (или столбец), не добавляя ее в другую строку (или столбец), тогда вы нужно следить за этим множителем и делить его в конце. И при переключении двух строк (или столбцов) необходимо изменить знак на ответ в конце.
Проблема с этими правилами в том, что легко потерять из виду, на что вы умножали и как много раз вы меняли строки, поэтому я стараюсь держаться подальше от те операции.Но если вы будете осторожны, эти другие операции могут быть удобно. Возвращаясь к последнему определителю (см. Выше), посмотрите на эти переключатели строк: Авторские права Элизабет Stapel 2006-2011 Все права защищены
Я сделал переключение на две строки, поэтому У меня два изменения знака, которые возвращают меня к исходному знаку. И теперь, развернув первый столбец, я получаю:
Вы это видели? Манипулируя определитель в треугольную форму, значение определителя превратилось быть произведением значений на диагонали (умноженное на два знака изменения, которые практически ничего не меняли).
Умножение по диагонали намного проще , чем делать все миноры и сомножители. Дано возможность, почти всегда лучше выполнять строковые операции и только затем сделайте «расширение». Если только у вас нет инструктора, который абсолютно настаивает на том, что раскрывает детерминанты в их исходной форме, попробуйте сначала выполнить некоторые операции со строками (и столбцами). Если вам нужно определить детерминанты ручное выполнение операций сделает вашу жизнь немного менее беспорядочной.
Мы уже видели определяющие правила. Еще два:
Для матриц A и B , дет ( AB ) = det ( A ) det ( B ) .
Если A n -by- n , затем det ( кА ) = k n det ( A ) .
Мы также видели, что определитель треугольной матрицы C это просто произведение элементов по диагонали.Это говорит нам, что определитель единичной матрицы I является det ( I ) = 1. И это приводит к Иногда полезный результат:
Любая обратимая матрица А имеет обратный матрица A 1 так что ( A ) ( A 1 ) = ( A 1 ) ( A ) = I . Поскольку det ( AA 1 ) = det ( I ) = 1, тогда, независимо от значения det ( A ) is, значение det ( A 1 ) должно быть обратной величиной det ( A ).Например, если det ( A ) = 2/3, тогда det ( A 1 ) = 3/2, так дет ( AA 1 ) = det ( A ) det ( A 1 ) = (2/3) (3/2) = 1 = det ( I ).
А что, если А не обратимый? Подумайте: какое число не имеет обратного? Номер нуль. Единственное значение для det ( A ) что не позволяет A быть обратимым равно нулю.Отсюда получаем следующее правило:
Если матрица A не имеет обратного, тогда det ( A ) = 0 , и наоборот наоборот.
Вас могут спросить на некоторых укажите «определить, является ли следующая матрица обратимой, используя детерминанты «. Вопрос будет просить вас запомнить вышеизложенное правило, и чтобы увидеть, равен ли определитель нулю или нет.Вы будете , а не можно ожидать, что на самом деле будет найдено обратное.
Если вы не собираетесь много дальше по математике вы можете обойтись без калькулятора выполнить большую часть или все ваши детерминантные вычисления за вас. Но если ты дальнейшее планирование (например, к дифференциальным уравнениям или линейным алгебра), а затем убедитесь, что вы научились делать определители вручную. Вы почти наверняка понадобится навык.
<< Предыдущая Вверх | 1 | 2 | 3 | Возвращение в индекс
Цитируйте эту статью как: | Стапель, Елизавета.
«Минорные и сомножители: строковые операции». Purplemath .
Доступно по номеру |

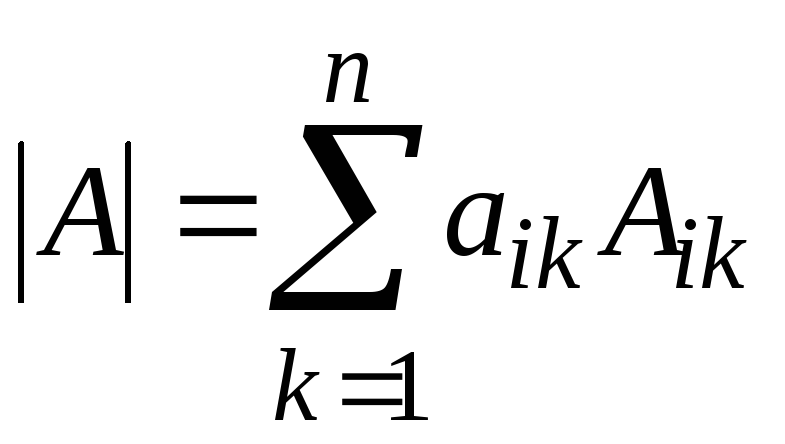
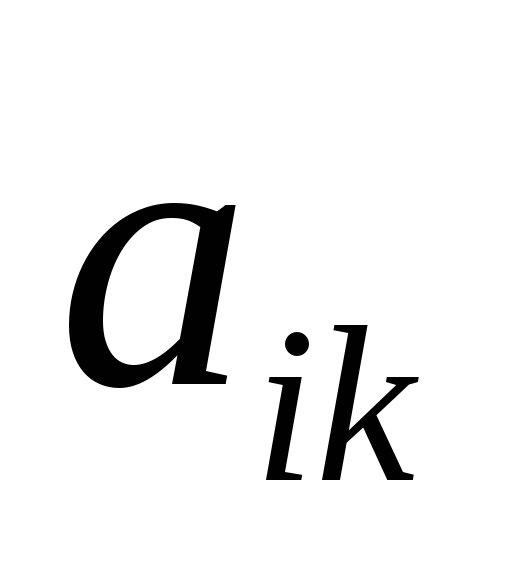 (разложение определителя поi-ой
строке). Либо
(разложение определителя поi-ой
строке). Либо 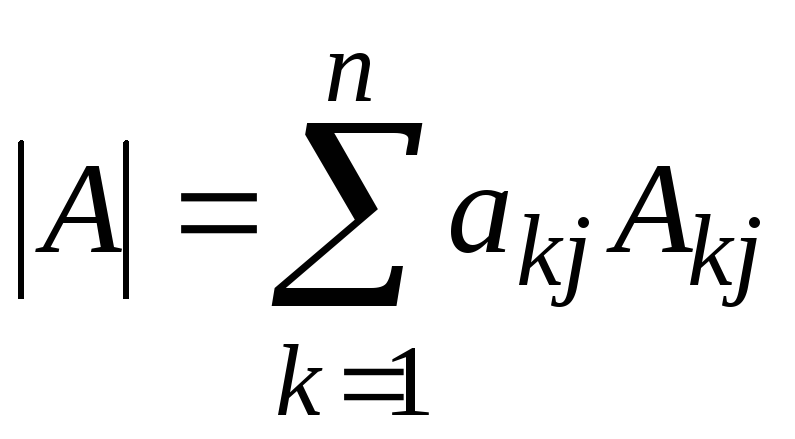 (разложение поj-тому
столбцу).
(разложение поj-тому
столбцу).