Процентное соотношение двух чисел онлайн: Процентное отношение двух чисел | Онлайн калькулятор

Как посчитать процент от числа и долю в Эксель

Расчеты с процентами – относятся к одним из самых популярных действий, выполняемых в программе Эксель. Это может быть умножение числа на определенный процент, определение доли (в %) от конкретного числа и т.д. Однако, даже если пользователь знает, как выполнить расчеты на листке бумаги, он не всегда может повторить их в программе. Потому сейчас, мы детально разберем, как именно считаются проценты в Эксель.

Содержание

• Считаем долю от общего числа
• Находим процент от числа
• Заключение

Считаем долю от общего числа

Смотрите также: “Как включить/отключить макросы в Excel”

Для начала разберем довольно распространенную ситуацию, когда нам нужно определить долю одного числа (в процентах) в другом. Ниже приведена математическая формула для выполнения данной задачи:

Доля (%) = Число 1/Число 2*100%, где:

• Число 1 – собственно говоря, наше исходное числовое значение
• Число 2 – итоговое число, долю в котором мы хотим выяснить

К примеру, давайте попробуем вычислить, какова доля числа 15 в числе 37. Результат нам нужен в процентах. В данном значение “Числа 1” равно 15, а “Числа 2” – 37.

1. Выбираем ячейку, где нам нужно произвести расчеты. Пишем знак “равно” (“=”) и далее формулу расчета с нашими числами: =15/37*100%.
2. После того, как мы набрали формулу, нажимаем клавишу Enter на клавиатуре, и результат сразу же отобразится в выбранной ячейке.

У некоторых пользователей в результирующей ячейке вместо процентного значения может отобразится простое число, причем, иногда с большим количеством цифр после запятой.

Все дело в том, что не настроен формат ячейки для вывода результата. Давайте это исправим:

1. Кликаем правой кнопкой мыши по ячейке с результатом (неважно, до того, как мы написали в ней формулу и получили результат или после), в появившемся перечне команд щелкаем по пункту “Формат ячеек…”.
2. В окне форматирования мы окажемся во вкладке “Число”. Здесь в числовых форматах кликаем по строке “Процентный” и в правой части окна указываем желаемое количество знаков после запятой. Наиболее распространенный вариант – “2”, его мы и ставим в нашем примере. После этого жмем кнопку OK.
3. Готово, теперь мы получим в ячейке именно процентное значение, что и требовалось изначально.

Кстати, когда формат отображения в ячейке настроен в виде процентов, вовсе не обязательно в формуле писать “*100%“. Достаточно будет выполнить простое деление чисел: =15/37.

Давайте попробуем применить полученные знания на практике. Допустим, у нас есть таблица с продажами по различным наименованиям, и нам нужно вычислить долю каждого товара в суммарной выручке. Для удобства лучше вывести данные в отдельный столбец. Также, у нас должна быть заранее посчитана итоговая выручка по всем наименованиям, на которую мы будем делить продажи по каждому товару.

Итак, приступим к выполнению поставленной задачи:

1. Выбираем первую ячейку столбца (не считая шапку таблицы). Как обычно, написание любой формулы начинается со знака “=“. Далее пишем формулу расчета процента, аналогично рассмотренному примеру выше, только заменив конкретные числовые значения адресами ячеек, которые можно прописать вручную, либо добавляем их в формулу кликами мыши. В нашем случае, в ячейку E2 нужно написать следующее выражение: =D2/D16. Примечание: не забываем заранее настроить формат ячеек результирующего столбца, выбрав отображение в виде процентов.
2. Нажимаем Enter, чтобы получить результат в заданной ячейке.
3. Теперь нам нужно произвести аналогичные расчеты для остальных строк столбца. К счастью, возможности Эксель позволяют избежать ручного ввода формулы для каждой ячейки, и этот процесс можно автоматизировать путем копирования (растягивания) формулы в другие ячейки. Однако тут есть небольшой нюанс. В программе по умолчанию при копировании формул происходит корректировка адресов ячеек согласно смещению. Когда речь идет о продажах каждого отдельного наименования, так и должно быть, но координаты ячейки с итоговой выручкой должны оставаться неизменными. Чтобы ее зафиксировать (сделать абсолютной), нужно перед обозначениями строки и столбца добавить символ “$“. Либо, чтобы не печатать этот знак вручную, выделив адрес ячейки в формуле, можно просто нажать клавишу F4. По завершении нажимаем Enter.
4. Теперь осталось растянуть формулу на другие ячейки. Чтобы это сделать, наводим курсор на правый нижний угол ячейки с результатом, указатель должен поменять форму на крестик, после чего, растягиваем формулу вниз, зажав левую кнопку мыши.
5. Вот и все. Как мы и хотели, ячейки последнего столбца заполнились долями продаж каждого конкретного наименования продукции в совокупной выручке.

Разумеется, в расчетах вовсе не обязательно заранее считать итоговую выручку и выводить результат в отдельную ячейку. Все можно сразу посчитать с помощью одной формулы, которая для ячейки E2 выглядеть так: =D2/СУММ(D2:D15).

В данном случае, мы сразу посчитали общую выручку в формуле расчета доли, используя функцию СУММ. О том, как ее применять, читайте в нашей статье – “Как в Экселе посчитать сумму ячеек“.

Как и в первой варианте, нам нужно зафиксировать цифру по итоговым продажам, однако, так как в расчетах не принимает участие отдельная ячейка с нужным значением, нам нужно проставить знаки “

$” перед обозначениями строк и столбцов в адресах ячеек диапазона суммы: =D2/СУММ($D$2:$D$15).

Находим процент от числа

Смотрите также: “Как посчитать количество строк в таблице Excel”

А сейчас давайте попробуем вычислить процент от числу в виде абсолютного значения, т.е. в виде другого числа.

Математическая формула для расчета выглядит следующим образом:

Число 2 = Процент (%) * Число 1, где:

• Число 1 – исходное число, процент по которому нужно вычислить
• Процент – соответсвенно, величина самого процента
• Число 2 – финальное числовое значение, которое требуется получить.

Например, давайте узнаем, какое число составляет 15% от 90.

1. Выбираем ячейку, в которой будем выводить результат и пишем формулу выше, подставляя в нее наши значения: =15%*90.Примечание: Так как результат должен быть в абсолютном выражении (т.е. в виде числа), формат ячейки – “общий” или “числовой” (но не “процентный”).
2. Нажимаем клавишу Enter, чтобы получить результат в выбранной ячейке.

Подобные знания помогают решать множество математических, экономических задач, физических и других задач. Допустим, у нас есть таблица с продажами обуви (в парах) за 1 квартал, и мы планируем в следующем продать на 10% больше. Нужно определить, какому количеству пар для каждого наименования соответствуют эти 10%.

Чтобы выполнить задачу, выполняем следующие шаги:

1. Для удобства создаем новый столбец, в ячейки которого будем выводить результаты расчетов. Выбираем первую ячейку столбца (на считая шапки) и пишем в ней формулу выше, заменив конкретное значение сходного числа на адрес ячейки:
   =10%*B2.
2. После этого жмем клавишу Enter, и результат сразу же отобразится в ячейке с формулой.
3. Если мы хотим избавиться от цифр после запятой, так как в нашем случае количество пар обуви может исчисляться только целыми числами, переходим в формат ячейки (как это сделать, мы разобрали выше), где выбираем числовой формат с отсутствием десятичных знаков.
4. Теперь можно растянуть формулу на оставшиеся ячейки столбца.

В случаях, когда нам нужно получить разные проценты от разных чисел, соответственно, нужно создать отдельный столбец не только для вывода результатов, но и для значений процентов.

1. Допустим, наша таблица содержит такой столбец “E” (Значение %).
2. Пишем в первой ячейке результирующего столбца все ту же формулу, только теперь и конкретное значение процента меняем на адрес ячейки с содержащейся в ней процентной величиной: =E2*B2.
3. Щелкнув Enter получаем результат в заданной ячейке. Осталось только растянут его на нижние строки.

Заключение

Во время работы с таблицами нередко возникает потребность производить расчеты с процентами. К счастью, функционал программы Эксель позволяет выполнять их с легкостью, причем, если речь идет об однотипных вычислениях в больших таблицах, процесс можно автоматизировать, что позволит сэкономить немало времени.

Смотрите также: “Как закрепить заголовок таблицы в Эксель”

Калькулятор процентов: проценты от числа

Этот бесплатный сервис позволяет вычислять проценты

Преобразование процентов в число

Что такое % из ?

Преобразование числа в проценты

это сколько процентов
?

Увеличение/уменьшение в процентах

плюс-минус %
= какое значение?

Процентное изменение между двумя значениями

Разница между  
и = какой процент?

Как пользоваться нашим калькулятором

Здесь вы найдете несколько простых процентных калькуляторов с примерами.

Вы можете использовать наши простые калькуляторы процентов для расчета процентов. В качестве десятичного разделителя можно использовать запятую или точку. Вам не нужно использовать разделители тысяч, потому что этот калькулятор рассматривает и запятую, и точку как десятичный разделитель. Для того, чтобы рассчитать проценты онлайн, нажмите на кнопку. Результат появится на следующей странице. Если есть ошибки, поле результата будет пустым. Попробуйте этот удобный онлайн-инструмент, чтобы проверить свои проблемы с процентами. Найдите процентное изменение между двумя числами или вычислите процент значения до и после. Наша цель — предложить лучший онлайн-калькулятор процентов с быстрыми и полезными ответами. Всякий раз, когда вам нужно рассчитать проценты или узнать, как рассчитать проценты, этот бесплатный веб-сайт поможет вам. Мы надеемся, что вам понравится время, проведенное на сайте. Пожалуйста, не стесняйтесь, присылайте нам свои комментарии или предложения.

Расчет процентов (теория и примеры)

Мы объясним, как рассчитываются проценты, и приведем несколько примеров.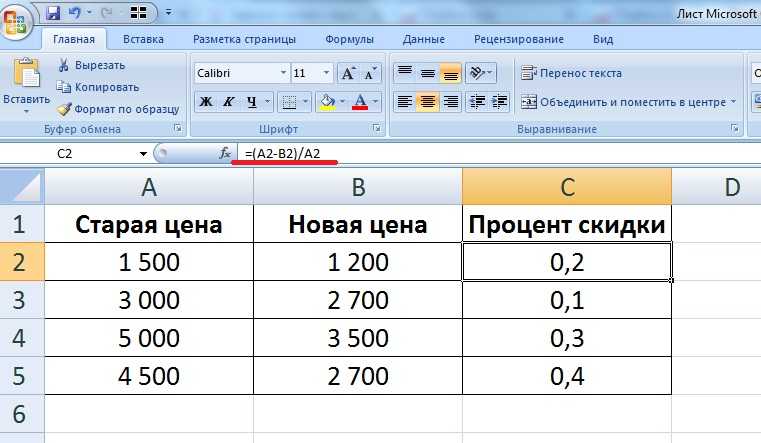

1. Вводный пример
Давайте рассмотрим пример с различными способами описания отношения:

20 из 80 британцев верят, что солнце вращается вокруг земли.
5 из 20 британских дипломатов — женщины.
25 из 100 британских домохозяйств состоят из одного человека.
Сравнивать эти отношения может быть немного сложно, но если мы запишем их в процентах, они эквивалентны: 25%, что составляет 25 из 100.

Этот пример показывает практичность широкого использования процентов, поэтому мы должны уметь понимать и вычислять проценты.

2. Определение и расчет процентов
Процент — это способ обозначения соотношения посредством ссылки на число 100. Чтобы рассчитать процент, мы идентифицируем общее число как 100%.

Процент n % означает n лиц из 100.

Например:
50% — это половина от общего количества (50 из 100).
25% — это четверть от общего числа (25 из 100).
20% — это пятая часть от общего числа (20 из 100).

Пример
Рассчитаем долю блондинов в классе из 80 учеников, из которых 12 блондинов.
Поскольку из 80 студентов 12 блондинок, соотношение блондинок составляет: R = 12 / 80
Обратите внимание, что в знаменателе мы пишем общее количество студентов, а в числителе — количество блондинок.

Так как мы хотим записать соотношение относительно 100, мы пишем 100 в числителе:
R = x /100

Поскольку отношение должно быть равным, мы устанавливаем оба выражения равными для вычисления
12/80 = x/100

Решаем уравнение первой степени (100 в знаменателе мультипликативно переходит в другую часть): 12/80 = x/100 → x = 12 * 100/80 → x = 15
Итак, мы находим, что 15 из 100 студентов блондинки, то есть 15% студентов блондинки.

3. Правило трех
Чем выше коэффициент, тем выше процент. Это означает, что процент прямо пропорционален коэффициенту. Следовательно, мы можем рассчитать процент, применив простое правило трех.

Пример:
Вспомните приведенный выше пример: в классе из 80 учеников 12 блондинок. Рассчитаем процент студентов-блондинок, применив правило трех (используя таблицу):

Students	Percentage
80	100
1	100/80
12	12 * 100 / 80 = 15%

A few more examples

Пример 1 60% от 900 = ??? (900/100) х 60 = 540 Сначала проверяем, сколько составляет один процент: делим 900 на 100. Получаем 9. Затем умножаем один процент на 60 (60% = 60 на сотню = 60 процентов), так что 9х 60 = 540.

Пример второй 90 = ??? % от 125 90 х (100/125) = 72 % Сначала посчитаем, сколько стоит одна единица: делим 125 на 100. Затем мы умножаем одну единицу на 90, потому что хотим знать, сколько будет 90 единиц. Таким образом мы вычисляем процент.

Пример третий На сколько процентов изменится от 150 до 190? (190-150) х (100/150) = 26,66 % 150 соответствует 100%. Таким образом, процент одной единицы представлен 100/150. 190-150 равно 40. Таким образом, 40 единиц составляют 40 x (100/150) = 26,66 % . Таким образом, мы вычисляем процентное увеличение или уменьшение.

Что такое проценты?

Один процент — это одна сотая. Мы используем %, чтобы указать это. Итак, 5 процентов — это то же самое, что 5%, 0,05, 5/100 или пять сотых. Это так просто! Это хорошо, но обычно мы используем не только проценты. Иногда мы хотим показать соотношение между двумя числами. Например: что такое 40% от 20? Это 40 сотых от 20, поэтому, если мы разделим 20 печенек на 100 равных частей (удачи в этом!), 40 из этих частей составляют наши 40% от 20 печенек. Давайте посчитаем: 40/100 * 20 = 8. Здесь действует небольшая хитрость: если вы хотите разделить на сто, просто переместите запятую на два знака влево. В нашем расчете 40/100*20 мы могли бы сделать и так: (40*20)/100 (то же самое). 40 * 20 равно 800. Переместите запятую в числе 800 на 2 знака влево, и вы получите 8,00. Введите эти значения в верхней части страницы, 40 и 20. Тогда вы получите «40% от 20 равно 8». В другом случае вы хотите указать, например, на сколько процентов уменьшилось или увеличилось число. Например, если у вас есть 10 яблок и вы едите 2 из них… То вы потеряли 20% яблок. Почему? Потому что 8 — это 80% от 10. Все яблоки были 100%, теперь у нас осталось 80%, поэтому количество яблок уменьшилось на 20% (потому что 100 — 80 = 20). Используйте для этого наш инструмент увеличения процента.

Происхождение

Термин процент происходит от латинского per center (на сотню) и обозначается знаком «%», или просто «процент» или «процент». В математике процент — это число в дробях от 100. Американцы говорят проценты, британцы предпочитают использовать проценты.

Проценты для растворов

Процент не всегда должен обозначать несколько сотых от целого. Таким образом, решения также отображаются в процентах. Физиологический солевой раствор называют, например, раствором 0,9% поваренной соли. Эти 0,9% означают, что раствор содержит 0,9 г соли на 100 мл (= 100 г). Таким образом, процент здесь относится к массе. Объемный процент часто указывает дополнение: «vol», тогда мы получаем, например: 14% vol или 14% vol.

Процентные пункты

Процентный пункт, также обозначаемый как %-пункт, используется для обозначения абсолютной разницы между значениями, выраженными в процентах. Таким образом, процент — это сотая часть, а процентный пункт — это расчетная единица, выражающая изменение процента.

Пример

Если проценты по вашему сберегательному счету вырастут с 2% до 3%, вы можете выразить это как «увеличение на 50% от старой процентной ставки» или как «увеличение на 1 процентный пункт» (что составляет 1% от первоначальной процентной ставки). весь). «Увеличение на 1%» неясно, потому что это может означать увеличение на 1% от 2 (0,02), в результате чего общее количество составляет 2,02% вместо 3%.

Промилле

1 промилле – это 1 тысячная часть, слово промилле также означает «промилле». Промилле обозначается как ‰, например процент (%), но с 3 «нулями» вместо 2. Здесь 1 промилле = 0,1%.

Для получения дополнительной информации о процентах нажмите здесь: Википедия

Калькулятор процентов | ОтметитьРассчитать

Процент — это число или пропорция, представляющая долю от 100. Он часто обозначается символом «%» или как «процент» или «процент» . Например, 35% равны десятичной дроби 0,35 или дроби

История процента

В Древнем Риме, задолго до появления десятичной системы счисления, расчеты часто производились порциями, которые были произведениями 1/100. Расчет с этими частями был равен вычислению процентов. По мере того, как в Средние века развивались номиналы наличных денег, расчеты со знаменателем 100 становились все более стандартными, и с конца пятнадцатого до середины шестнадцатого века такие расчеты стали регулярно включаться в математические сочинения. К семнадцатому веку стало стандартом указывать стоимость кредита в сотых долях.

Процентные вычисления, связанные с обнаружением процентов, не являются чрезвычайно хлопотными, и любой человек, не имеющий достаточной информации об этом, может использовать эту технику для получения результатов. Людям часто нужно узнавать ставки, в конце концов, в повседневной жизни. Студентам, учителям, бухгалтерам и представителям многих профессий необходимо отображать числа в процентах.

Формула процентов

Несмотря на то, что процентная формула может быть записана в разных формах, в основном это алгебраическое сравнение, включающее три значения.

P × V ₁ = V ₂
Где:
P = Процентное значение
V ₁ = Значение, которое будет изменено процентным значением
V ₂ = Результат

При вычислении процента, который необходимо ввести, будет фактический процент, а не его десятичное представление.

ПРИМЕР: P × 30 = 1,5

P =

= 0,05 × 100 = 5%

Эта формула требует, чтобы процент был в десятичной форме, так что решение для P можно просто умножить на 100, чтобы преобразовать в проценты.

Формула процентного изменения

Увеличение и уменьшение в процентах можно рассчитать, вычислив разницу между двумя значениями и сравнив ее с начальным значением. Математически это означало бы, что мы должны найти абсолютное значение разницы между двумя значениями, а затем разделить результат на начальное значение, фактически вычислив, насколько изменилось начальное значение.

Это можно сделать, сначала преобразовав процент в его десятичную форму, а затем либо вычитая (уменьшая), либо добавляя (увеличивая), в соответствии с требованиями вопроса, десятичный эквивалент от и до 1. Умножение исходного числа на это значение будет дать вам либо увеличение, либо уменьшение числа на заданный процент. Для пояснения обратитесь к приведенному ниже примеру.

ПРИМЕР: 500 увеличилось на 10% (0,1)
500 × (1 + 0,1) = 550

500 уменьшилось на 10%
500 × (1 – 0,1) = 450

Формула процентной разницы

Процентную разницу между двумя единицами можно рассчитать, просто разделив разницу между единицами V1 и V2 на среднее значение этих двух чисел. Результат умножается на 100, что должно дать нам процент.

Разница в процентах =

|V 1 — V 2 | (В 1 + В 2 )/2

× 100

Пример:

|10 — 6| (10 + 6)/2

=

= 0,5 = 50%

1. Как рассчитать процент

Процентное значение можно рассчитать, умножив числовое значение коэффициента на 100. Например, чтобы найти 30 апельсинов в процентах от 300 апельсинов, сначала рассчитаем соотношение 30/300 = 0,1, а затем умножим 0,1 на 100. чтобы получить 10% в качестве результирующего ответа.
Чтобы вычислить проценты из других процентов, преобразовать определенный процент в доли 100 или десятичные дроби и увеличить их.
Например: 400% от 300%: (400/100) × (300/100) = 40 × 30 = 1200 = 1200/100 = 12%.

Существуют различные формулы для процентных задач. Самая основная формула — X / Y = P x 100. Приведенные ниже уравнения представляют собой разные версии этой формулы.

Давайте рассмотрим три основные проблемы с процентами, где X и Y представляют числа, а P представляет процент:

1. Найти P процентов от X
2. Найдите, сколько процентов X составляет Y
3. Найти X, когда P процентов от него равно Y

2. Как рассчитать процент от числа

Используйте эту процентную формулу: P% * X = Y
Пример: Что такое 10% от 150?

• Преобразуйте это в уравнение, используя процентную формулу: P% * X = Y
• P равно 10%, X = 150, поэтому уравнение принимает вид 10% * 150 = Y
• Преобразуйте эти 10% в десятичную дробь, удалив знак процента и разделив на 100: 10/100 = 0,10
• Подставив 0,10 вместо 10 % в это уравнение: 10 % * 150 = Y становится 0,10 * 150 = Y
  0,10 * 150 = 15
  Y = 15
  Таким образом, 10 % от 150 равно 15
• Дважды проверьте полученное значение с исходным вопросом: чему равно 10% от 150?
  Умножить 0,10 * 150 = 15

3.

Как определить, какой процент X составляет Y

Используйте формулу процентов: Y/X = P%
Пример: Сколько процентов от 60 составляет 12?

• Преобразуйте это в уравнение, используя процентную формулу: Y/X = P%
  X равно 60,
  Y = 12, отсюда следует, что 12/60 = P%
  Отсюда следует, что 12/60 = 0,20
• Важно! Результат, который вы получите, всегда будет в десятичной, а не в процентной форме. умножьте результат на 100, чтобы преобразовать его в проценты.
  Преобразование 0,20 в проценты: 0,20 * 100 = 20% Таким образом, 20% от 60 равно 12.
• Дважды проверьте результат с исходным вопросом: какой процент от 60 составляет 12?
  Получаем, 12/60 = 0,20, и умножаем на 100, чтобы получить процент, 0,20 * 100 = 20%

4. Как найти X, если P в процентах от него составляет Y

Используйте процентную формулу Y/P% = X
Пример: 25 составляет 20% от какого числа?

• Преобразуйте это в уравнение, используя процентную формулу: Y/P% = X
  Y равно 25
  P% = 20, таким образом, получится уравнение как 25/20% = X
• Преобразуйте этот процент в десятичную дробь, разделив его на 100.
• Преобразование: 20/100 = 0,20
• Подставив 0,20 вместо 20% в уравнение: 25/0,20 = X
  Отсюда следует, что 25/0,20 = X
  X = 125, поэтому 25 составляет 20% от 125.
• Дважды проверьте результат с исходным вопросом: 25 составляет 20% от какого числа?
  25/0,20 = 125

5. Как преобразовать проценты в десятичные числа

Сначала убираем знак процента, а затем делим число на 100
ПРИМЕР: 15,0% = 15./100 = 0,150

6. Как преобразовать десятичную дробь в проценты

Умножьте на 100 и добавьте знак процента к числу
ПРИМЕР: 0,86 = 0,86 * 100 = 86,0%

Неправильно делить число на 100 и одновременно использовать знак процента.