Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| Joe Black |
| ||
26/03/13 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Joe Black |
| ||
26/03/13 |
| ||
| |||
| Aritaborian |
| ||
11/06/12 |
| ||
| |||
| grizzly |
| ||
09/09/14 | |||
| |||
| Joe Black |
| |
26/03/13 | ||
| ||
| Aritaborian |
| |
11/06/12 | ||
| ||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Химия
| Похожие вопросы |
CaC2->C2h3->C6H6->C6H6-NO2->C6H6-Nh3
Приведите структурные формулы двух изомерных углеводородов C7h26 каждый из которых при хлорировании на cвету может образовать два первичных хлорпроизводных , но не образует третичных.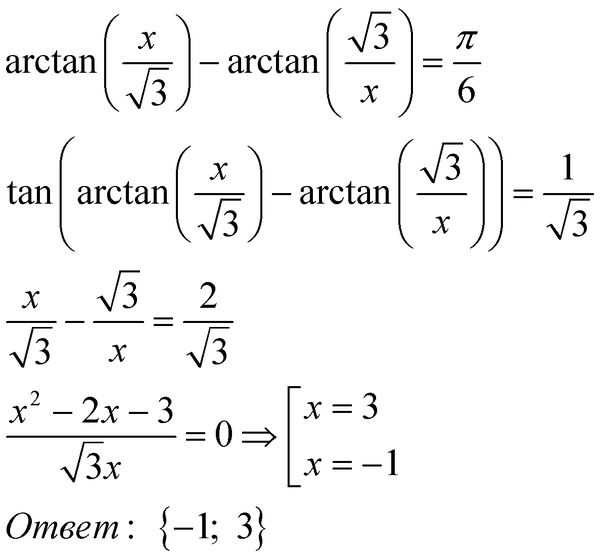 Назовите эти угл
Назовите эти угл
В каком году была сформулирована теория — предшественница кислородной теории горения.
составьте уравнения реакций, укажите условия, с помощью которых можно осуществить следующие превращения веществ:
http://pixs.ru/showimage/10638jpg_8717069_14466280.jpg http://pixs.ru/showimage/11638jpg_4139996_14466295.jpg…
Пользуйтесь нашим приложением
Производная арктан(х) (арктангенс)
Похожие материалы
сообщите об этом объявлении
сообщите об этом объявлении
Содержание урока
Как отличить арктангенс?
Арктангенс, известный как арктангенс или сокращенно арктангенс, обычно обозначается как тангенс -1 (некоторая функция). Чтобы быстро дифференцировать его, у нас есть два варианта:
1.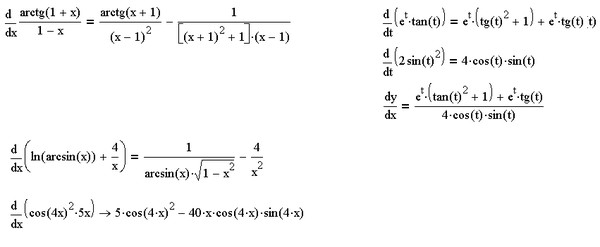 ) Используйте правило простой производной.
) Используйте правило простой производной.
2.) Выведите производное правило, а затем примените правило.
В этом уроке мы покажем производное правило для tan -1 (u) и tan -1 (x). Есть четыре примера задач, которые помогут вашему пониманию.
В конце урока мы увидим, как выводится производное правило.
Производная от Arctan(u)
Правило производной для arctan(u) задается следующим образом:
Где u — функция одной переменной, а штрих ‘ обозначает производную относительно этой переменной. Вот несколько примеров функции одной переменной 9 3 – 3y + 4 u) правило, но с заменой каждого экземпляра u на x . Поскольку производная x равна просто 1, числитель упрощается до 1. Правило производной для arctan(x) задается как:
Где ‘ обозначает производную по x.
Примеры задач
Производная арктангенса (2x)
Найдите производную по x тангенса −1 (2x).
Решение:
Производная Arctan(1/x)
Найдите производную по x от tan −1 (1/x).
Решение:
Производная Arctan(4x)
Найдите производную по x от tan −1 (4x).
Решение:
Производная Arctan(x
2 + 1)Найдите производную по x от tan −1 (x 2 + 1).
Решение:
Дополнительный урок: Что делает Arctan дифференцируемым?
Arctan является дифференцируемой функцией, потому что ее производная существует в каждой точке ее области определения . На изображении ниже показан один период arctan(x). Кривая непрерывна и не имеет острых углов.
Если на графике есть острый угол, производная в этой точке не определена. Итак, если вы встретите функцию, график которой имеет острые углы, она не будет дифференцируема в каждой точке своей области определения.
График функции f(x) = arctan(x) для одного периода.

 Рассмотрим окружность радиуса 1 с центром в точке (0;0). Проведём радиус OM так, что OM образует угол с осью Ох. Проведём перпендикуляр МА к оси Ох. Получили прямоугольный треугольник ОМА. Пусть . Тогда:
Рассмотрим окружность радиуса 1 с центром в точке (0;0). Проведём радиус OM так, что OM образует угол с осью Ох. Проведём перпендикуляр МА к оси Ох. Получили прямоугольный треугольник ОМА. Пусть . Тогда: Да и второе равенство непонятное.
Да и второе равенство непонятное. 12.2016, 14:00
12.2016, 14:00 
 вздох.мюсли
вздох.мюсли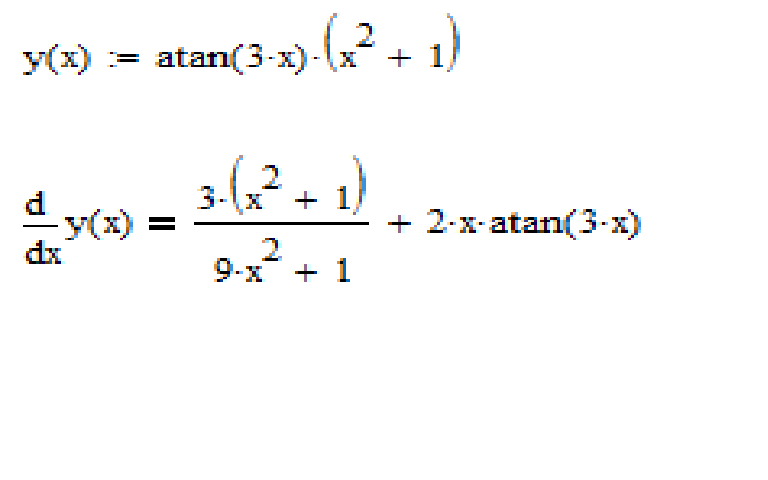 .. — Учеба и наука
.. — Учеба и наука 11.17
11.17