Арккосинус — frwiki.wiki
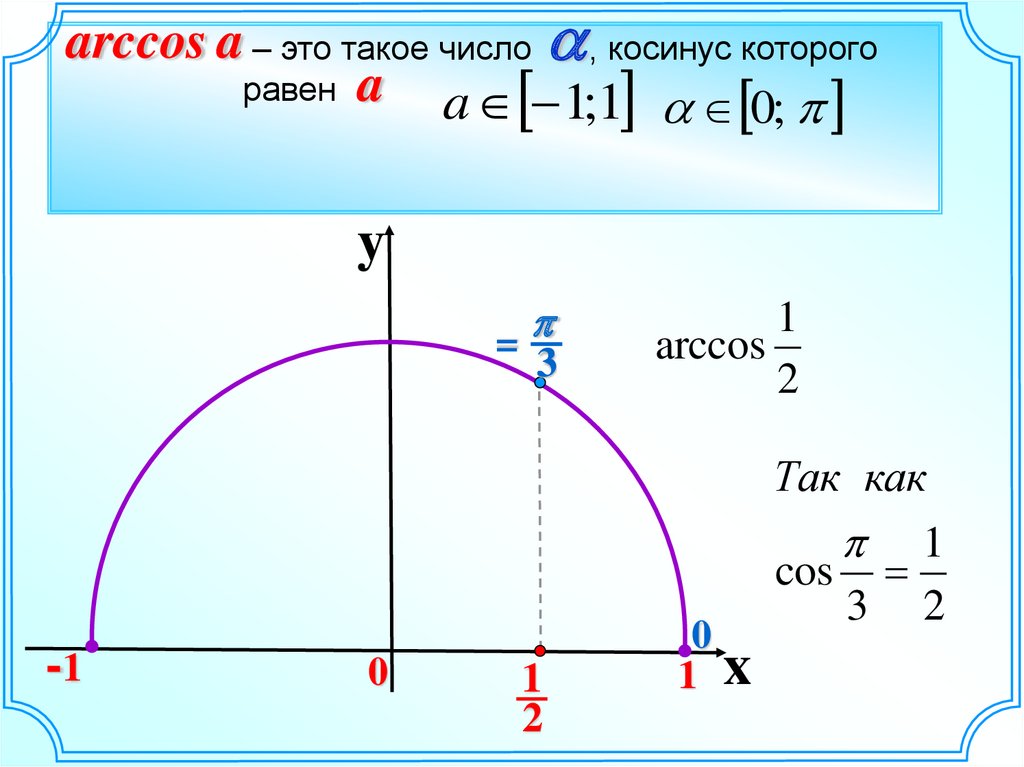
В математике, то Арккосинус из действительного числа включенных в широком смысле между -1 и 1 является единственной мерой угла чей косинус равен этому номеру, между нулевым углом и плоским углом .
Функция, которая ассоциируется с любым вещественным числом включенной в широком смысле между -1 и 1 значением его дугой косинуса в радианах отмечаются ARccOS (ArcCos или ACOS во французской нотации, и соз -1, иногда экос или ОКС, на английском языке обозначений Саксонский).
Это то обратная часть тригонометрического косинус функции по интервалу [0, π ] Таким образом, в декартовой системе координат ортонормальное к плоскости, то кривая представитель дуги косинуса получается из кривой ограничения. Косинуса по оси симметрия линии уравнения y = x .
Резюме
- 1 Определение
- 2 свойства
- 2.1 Тригонометрические отношения
- 2.
- 2.1.2 Связь с синусом
- 2.1.3 «Обращение» тригонометрических формул
- 2.
- 2.2 Производная
- 2.3 Неопределенная интегральная форма
- 2.4 Примитивы
- 2.5 Связь между арккосинусом и арксинусом
- 2.6 Комплексная логарифмическая форма
- 2.1 Тригонометрические отношения
- 3 Ссылка
- 4 См. Также
- 4.1 Связанные статьи
Определение
Функция определяется как функция, обратная on, т.е. это уникальная функция, такая что: arccos:[-1,1]→[0,π]{\ displaystyle \ arccos: [- 1,1] \ rightarrow [0, \ pi]}потому что{\ displaystyle \ cos}[0,π]{\ displaystyle [0, \ pi]}
Характеристики
Тригонометрические отношения
Нет паритета
В отличие от функций арк синуса и арктангенса, функция не допускает четности. Однако он обладает следующим свойством:arccos{\ displaystyle \ arccos}
Связь с пазухой
Достаточно использовать отношение с, чтобы получить следующее соотношение:потому что(Икс)2+грех(Икс)2знак равно1{\ Displaystyle \ соз (X) ^ {2} + \ sin (X) ^ {2} = 1}Иксзнак равноarccos(Икс){\ Displaystyle X = \ arccos (х)}
«Обращение» тригонометрических формул
Исходя из любой тригонометрической формулы, мы можем «инвертировать» ее, получив соотношение между значениями обратных функций, но которое чаще всего будет справедливо только в ограниченных интервалах.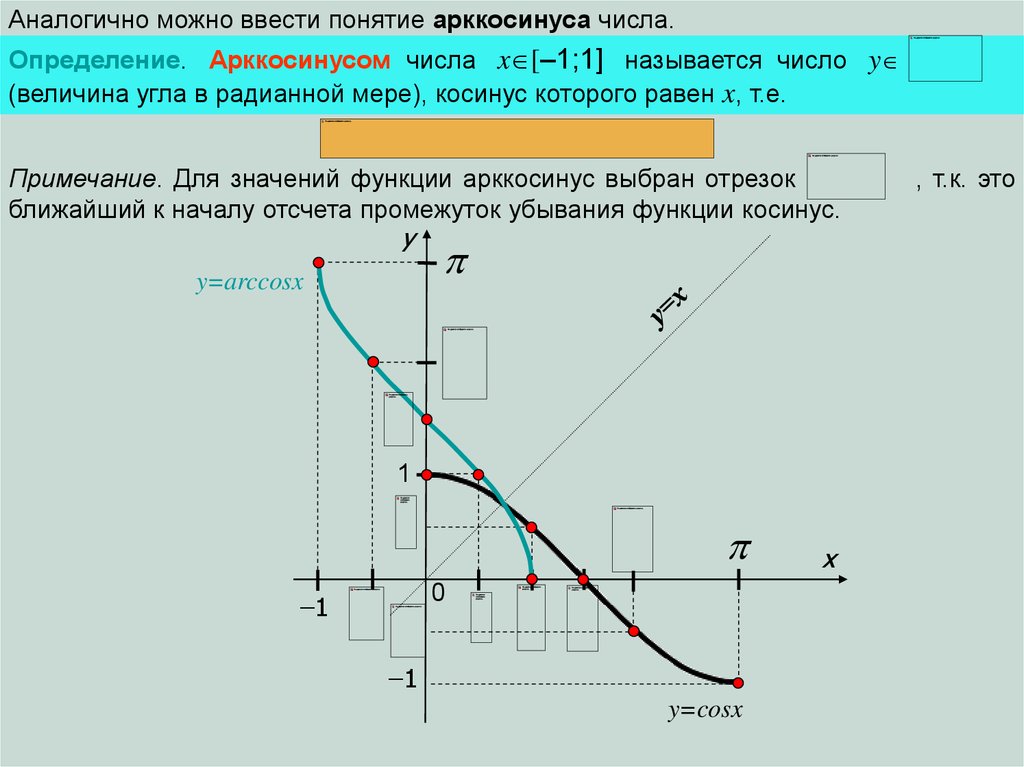
{2}}} \ right) = {\ frac {\ pi} {2}} — \ arcsin (x).}
Справка
- ↑ Нотация из математической программы в CPGE, с. 10 .
Смотрите также
Статьи по Теме
- Касательная дуга
- Взаимная круговая функция
Тригонометрия | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Круговая тригонометрия |
| ||||||||
| Гиперболическая тригонометрия |
| ||||||||
| |||||||||
<img src=»https://fr.
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
$(2) \,\,\,$ $\dfrac{d}{dx}{\, \Big(\arccos{(x)}\ Big)}$
По первому принципу дифференцирования производная функции арккосинуса может быть доказана математически. На самом деле, он используется как формула в дифференциальном исчислении. Поэтому давайте изучим вывод формулы дифференцирования обратной функции cos.
Производная функции косинуса в предельной форме
Дифференцирование функции арккосинуса по $x$ записывается в предельной форме из математического определения производной. 9{-1}{x}}}{0}$
$=\,\,\,$ $\dfrac{0}{0}$
Значение функции является неопределенной формой, выражающей, что предел функции нельзя вычислить математически прямой подстановкой. Поэтому приходится думать о другом способе вычисления функции.
Упрощение обратной тригонометрической функции
Теперь вернемся к определению производной функции арккосинуса в предельной форме для ее вычисления в другом подходе.
9{-1}{x}}{h}}$
В математическом анализе нет предельных правил для функции арккосинуса, но есть предельные правила для арксинуса и тангенса. Следовательно, мы должны подумать о преобразовании функций арккосинуса либо в функции арксинуса, либо в функции арктангенса. На самом деле не существует фундаментального подхода для преобразования функции обратного косинуса в функцию обратного тангенса, но можно преобразовать функцию обратного косинуса в функцию обратного синуса с помощью постоянного свойства функций обратного синуса и косинуса. 92}}\Big)}{h}}$
Предел обратной тригонометрической функции дает нам неопределенный вид, когда мы пытаемся вычислить функцию прямой подстановкой, когда $h$ приближается к нулю.
Обратное тригонометрическое выражение почти такое же, как предельное правило функции обратного синуса, но нам нужно сделать некоторые приемлемые корректировки, чтобы получить его в требуемом виде. Итак, попробуем получить требуемую форму для применения формулы.
2}\Big)}}{h}}$ $\times$ $1\Bigg)$ 92}}$
Калькулятор — arccos(ln(x)) — Solumaths
Arccos, расчет онлайн
Резюме:
Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
arccos online
Описание:
Функция арккосинуса является обратной функцией функция косинуса, это вычисляет арккосинус числа онлайн .
Число, к которому вы хотите применить функцию арккосинуса, должно принадлежать диапазону [-1,1].
- Расчет арккосинуса
- Таблица замечательных значений
- Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
Чтобы вычислить арккосинус числа , просто введите число и примените функция arccos .
Таким образом, для , вычисляющего , арккосинус числа, следующего за 0,4,
вы должны ввести
arccos(`0.
| arccos(`-1`) | `pi` |
| arccos(`-sqrt(3)/2`) | `5*pi/6` |
| `3*pi/4` | |
| arccos(`-1/2`) | `2*pi/3` |
| arccos(`0`) | `` pi/2` |
| arccos(`1/2`) | `pi/3` |
| arccos(`sqrt(2)/2`) | `pi/4` |
| Arccos (` sqrt (3)/2`) | `pi/6` |
| ARCCOS (` 1`) | |
| ARCCOS (`1`) | |
| ARCCOS (` 1`) | |
| (`1`) | |
| (` 1`) | |
| 4 (`1`) 9025 | |
| 4 (` 1`) 9025 | |
| 4 : arccos(x), где x — число. Иногда используются другие обозначения: acos Примеры:arccos(`1`) возвращает 0 Производная арккосинуса :Чтобы дифференцировать функцию арккосинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арккосинуса 92)` Предел арккосинуса : Калькулятор предела позволяет вычислить пределы функции арккосинуса. предел arccos(x) is limit(`»arccos»(x)`) Обратная функция арккосинуса :обратная функция арккосинуса — это функция косинуса, отмеченная как cos. Графический арккосинус :Графический калькулятор может отображать функцию арккосинуса в заданном интервале. Онлайн-расчет с арккосинусом См. также Список связанных калькуляторов: |
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.