Производная f x f y: Кафедра математики Физического факультета МГУ им. М.В.Ломоносова

26. Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных.

Теорема 1(для функции двух переменных)

Пусть функция f(x,y) определенна со своими частными производными fx,fy,fxy,fyx в некоторой окрестности точки (x0,y0), и при этом fxy и  fyx непрерывны в этой точке. Тогда  эти производные равны ( результат не зависит от порядка дифференцирования).

fxy(x0,y0)=fyx(x0,y0)

Теорема 2(обобщение)

Если у функции n переменных смешанные частные производные m-го порядка непрерывны в некоторой точке, а производные низших порядков непрерывны в окрестности этой точки, то частные производные порядка m  не зависят от порядка дифференцирования.

<Вернуться назад>

27. Дифференцируемость функции нескольких переменных. Дифференциал.

Обозначения:  или  – частная производная по «икс»  или  – частная производная по «игрек»

Полный дифференциал первого порядка функции двух переменных имеет вид:

И по неоднократным просьбам читателей, полный дифференциал второго порядка:

Пусть функция  дифференцируема в точке , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно  и нелинейного членов:

где  при .

Определение

Дифференциалом функции называется линейная относительно  часть приращения функции. Она обозначается как  или . Таким образом:

Замечание

Дифференциал функции составляет основную часть ее приращения.

Замечание

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Замечание

Формулу для дифференциала функции можно записать в виде:

Отсюда получаем, что

Итак, это означает, что производная может быть представлена как обыкновенная дробь — отношение дифференциалов функции и аргумента.

Геометрический смысл дифференциала

Дифференциал функции в точке  равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .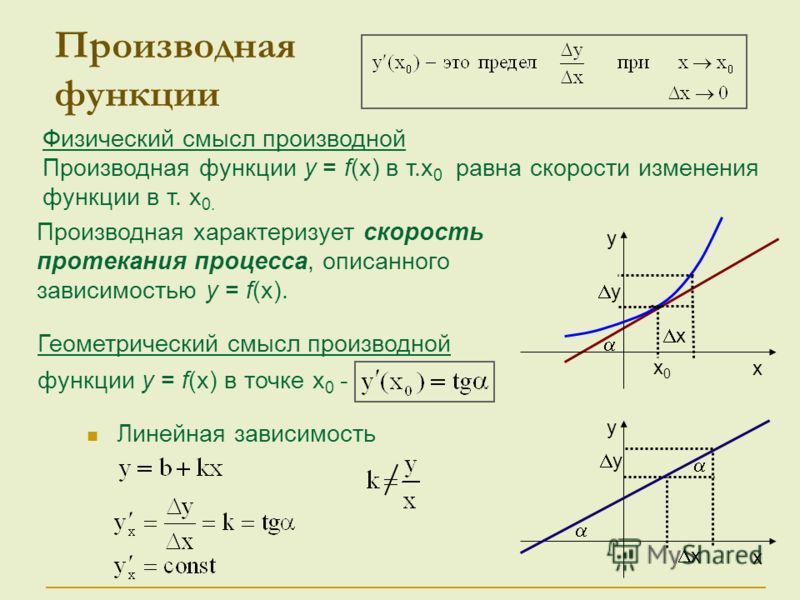

<Вернуться назад>

28. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума.

Локальный экстремум функции двух переменных       Необходимое условие локального экстремума дифференцируемой функции 

     Если  — точка экстремума функции f, то

 и  или 

     Достаточные условия локального экстремума дважды дифференцируемой функции 

     Обозначим  

(Также принято обозначать: D-M_1,2,3 ; A,B,C – Uxx_, Uxy, …)

     Если D > 0, A > 0, то  — точка минимума.

     Если D > 0, A < 0, то  — точка максимума.

     Если D < 0, экстремума в точке  нет.

     Если D = 0, необходимы дополнительные исследования.

Пример от 3х переменных:

Решение  Найдем стационарные точки заданной функции, то есть точки, в которых выполняется необходимое условие существования экстремума. Для функции трех переменных  стационарные точки (координаты точек) находятся из системы  Для заданной функции , ,  

и система примет вид  Решениями системы являются  и  Получили две стационарные точки  и . Для проверки достаточных условий экстремума в стационарной точке необходимо определить знаки определителей ,   и  в этой точке. Найдем , , , , , . Для точки  ,

,  .

Так как , , , то в точке  функция имеет максимум, при этом  . Для точки  ,

,

.

Так как , , , то в точке  функция не имеет экстремума.

<Вернуться назад>

Справка

1. Q: Как перейти по ссылке на определенный вопрос?

A: Нажать на ссылку, потом — на появившуюся ссылку под ней:

Или “ctrl + ЛКМ”.

2. Q: Как добавить закладку?

A: Выделить фрагмент текста, на который будет сделана закладка, нажать в верхнем меню “Вставка” -> “Закладка”

3.

Q: Как добавить ссылку на закладку?

A: Выделить текст будущей ссылки, нажать сочетание “ctrl + K”, кликнуть в появившеся меню “Закладки >” и выбрать нужную закладку.

4. Q: Как вставить разделитель после вопроса, чтобы следующий всегда был на новой странице?

A: Нажать ctrl + Enter

Спасибо!

Всем, кто писал ответы на вопросы:

1. Линар Саитов

2. Арсений Автомонов

3. Хитров Николай

<Вернуться назад>

By IKBO-08-16 & IKBO-13-17

2016-2018

©mirea

Производная по направлению. Градиент — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас.

Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Пусть функция z=f(x,y) определена в некоторой
окрестности точки М(х,у).
l – некоторое направление, задаваемое единичным
вектором
l (cos , cos )
где
l cos 2 cos 2 1
т.к.
3
2
;
2
…
cosα, cosβ – косинусы углов, образованных данным
вектором с осями координат. Они называются
направляющими косинусами.
При перемещении в направлении l точки М(х,у) в
точку
M1 ( x x, y y)
Функция z получит приращение

l z f ( x x, y y) f ( x, y)
которое называется приращением функции
данном направлении l.
z в
Если
то
MM 1 l
x l cos
y l cos
l z f ( x l cos , y l cos ) f ( x, y)
z f ( x, y )
y
x
x
M
y
z
M1
l
Производной по направлению z l
функции двух переменных z=f(x,y)
называется предел отношения
приращения функции в этом
направлении к величине перемещения
Δl при
l 0
l z
zl lim
l 0 l
Производная
по
направлению
характеризует
скорость изменения функции в направлении l.
Рассмотренные ранее производные
z x
и
z y
есть производные по направлениям, параллельным
осям абсцисс и ординат, соответственно.
Покажем, что
zl z x cos z y cos
z
z
z
z
l z x y l cos l cos
x
y
x
y
Делим обе части на Δl и переходим к пределу:
l z
z
z
lim
lim
cos lim
cos
l 0 l
l 0 x
l 0 y
z x cos z y cos
Градиентом функции двух переменных
z=f(x,y) называется вектор с
координатами
( z x ; z y )
z z
z
;
x y
Рассмотрим скалярное произведение ( , l )
z
Скалярное произведение в координатах имеет
вид:
(a , b ) a1b1 a2b2 a3b3
Поскольку
z z
z
;
x y
l (cos , cos )
Тогда
z
z
( z , l )
cos
cos
x
y
z x cos z y cos zl
( z , l ) zl
Производная по направлению есть скалярное
произведение градиента и единичного
вектора, задающего данное направление.
Поскольку скалярное произведение максимально,
если вектора одинаково направлены, то
Градиент функции в данной точке
характеризует направление максимальной
скорости изменения функции в данной
точке.
Если задана функция трех переменных f(x,y,z), то
градиент будет являться трехмерным вектором с
компонентами:
Или
f f f
;
;
x y z
( f x ; f y ; f z )
Пусть задана дифференцируемая
функция z=f(x,y) и пусть в точке
М(х0,у0) величина градиента
отлична от нуля. Тогда градиент
перпендикулярен линии уровня,
проходящей через данную точку.

English     Русский Правила

Страница не найдена | CUHK Математика

×

Предупреждающее сообщение

В вашем поиске использовано слишком много выражений И/ИЛИ. В этот поиск были включены только первые 7 терминов.

×

Сообщение об ошибке

Запрашиваемая вами страница не существует. Для вашего удобства был выполнен поиск по запросу курс ИЛИ конструктор ИЛИ 1617 ИЛИ math3010f ИЛИ решение ИЛИ 20to ИЛИ 20упражнение ИЛИ 205 ИЛИ 202017 ИЛИ 2 ИЛИ pdf .

1. MATh3010F — Усовершенствованное исчисление I — 2016/17

   https://www.math.cuhk.edu.hk/course/1617/math3010f
   
   Курс Имя: Advanced Calculus I Преподаватель: Доктор Юн ВАН Курс Год: 2016/17 Срок: S …

2. MATh3010E — Расширенное исчисление I — 2021/22

   https://www.math.cuhk.edu.hk/course/2122/math3010e
   Курс Название: Продвинутый математический анализ I Преподаватель: Доктор Пхёнвон SUH Курс Год: 2021/22 Срок: С …

3. MATh3221T2 — Лаборатория математики II — 2018/19

   https://www.math.cuhk.edu.hk/course/1819/math3221t2
   Курс Название: Лаборатория математики II Преподаватель: Доктор Чарльз Чун Че LI Курс Год: 2018/19 Срок: 2 …

4. MATh2010H — Университетская математика — 2019/20

   https://www.math.cuhk.edu.hk/course/1920/math2010h
   Курс Имя: Университет Преподаватель математики: Доктор Чанхао ЧЕН Курс Год: 2019/20 Срок: 2 . ..

5. MATh3221 — Лаборатория математики II — 2020/21

   https://www.math.cuhk.edu.hk/course/2021/math3221
   Курс Название: Лаборатория математики II Преподаватель: Доктор Чарльз Чун Че LI Курс Год: 2020/21 Срок: 2 …

6. MATh2010F — Университетская математика — 2017/18

   https://www.math.cuhk.edu.hk/course/1718/math2010f
   Курс Имя: Университет Преподаватель математики: Доктор Пинг Шун ЧАН Курс Год: 2017/18 Срок: 1 Если вы не видите материалов курса ниже этой строки, нажмите здесь . …

7. MATh4270A — Обыкновенные дифференциальные уравнения — 2019/20

   https://www.math.cuhk.edu.hk/course/1920/math4270a
   Курс Название: Обыкновенные дифференциальные уравнения Преподаватель: уточняется Курс Год: 2019/20 Срок: 1 …

8. MATh4290 — Математическое моделирование — 2019/20

   https://www. math.cuhk.edu.hk/course/1920/math4290
   Курс Имя: Преподаватель математического моделирования: Д-р Лина ЧЖАО Курс Год: 2019/20 Срок: 2 …

9. MATh2030H — Линейная алгебра I — 2018/19

   https://www.math.cuhk.edu.hk/course/1819/math2030h
   Курс Название: Линейная алгебра I Преподаватель: Профессор Лэй ЧЖАН Курс Год: 2018/19 Срок: S …

10. MATh2010H — Университетская математика — 2014/15

    https://www.math.cuhk.edu.hk/course/1415/math2010h
    Курс Имя: Университет Преподаватель математики: Доктор … Курс Год: 2014/15 Срок: 2 Объявление (4/1) Вот примерный план… Тесты и экзамены Тест Предлагаемое решение 1 Решения раствор 1 раствор 2 …

Производная вектор-функции: определение, формула, примеры

Узнайте о производной вектор-функции, ее формуле, а также различных примерах и способах ее вычисления.

от Алана Уокера — Опубликовано на 06 марта 2023 г.

Введение в производную векторнозначной функции

Исчисление — это исследование непрерывной скорости изменения, которое позволяет нам найти скорость мгновенных функций, таких как векторнозначная функция. Но вопрос в том, как мы можем найти производную векторной функции, поскольку она имеет разное количество компонентов, таких как i, j и k. Давайте разберемся, как найти производную векторной функции.

Понимание производной векторнозначных функций

Векторнозначная функция — это функция одной или нескольких переменных, диапазон которых представляет собой набор многомерных векторов. Она также известна как векторная функция. Такого рода функция имеет как величину, так и направление. В исчислении вектор-функция используется для определения кривой в пространстве как набора конечных точек. Если кривая гладкая, то возможно, что она имеет производную.

Определение производной вектор-функции аналогично определению вещественной функции одной переменной. Но поскольку область значений вектор-функции состоит из набора векторов, то это будет верно и для области значений производных вектор-функции.

Производная вектор-функции

Первый принцип производной используется для определения производной вектор-функции. Этот метод также известен как дельта-метод. Для функции f(x) принцип производной задается следующим образом:

$$f'(x)=\lim_{\Delta t\to 0}\frac{f(x+\Delta x)-f(x )}{\Delta x}$$

Где f'(x) — производная от f(x). Теперь мы определим такое же определение для производной вектор-функции. Для этого предположим, что r (t) — дифференцируемая вектор-функция, определенная на открытом интервале (a, b), производная от r (t) будет выражаться как:

$$\vec{r}(t)=\lim_{\Delta t\to 0}\frac{\vec{r}(t+\Delta t)-\ vec{r}(t)}{t}$$

Если r (t) определено на отрезке [a, b], то также должны существовать следующие пределы:

$$\vec{ r} ‘(a) = \ lim _ {\ Delta t \ to 0+} \ frac {\ vec {r} (a + \ Delta t) — \ vec {r} (a)} {\ Delta t} $ $

А,

$$\vec{r}'(b)=\lim_{\Delta t\to 0-}\frac{\vec{r}(b+\Delta t)-\vec{r}(b )}{\Delta t}$$

Поскольку тот же принцип используется для определения производной вектор-функции, мы также можем считать ее мгновенной скоростью изменения. Следовательно, все правила производных также могут быть определены для вычисления производной вектор-функции. Давайте разберемся с правилами вычисления производной векторной функции.

Правила производных вектор-функций

Существует шесть правил производных вектор-функций. Для двух вектор-функций r и u мы можем определить все правила производных, такие как:

1. Если c является скаляром, умноженным на r(t), то правило скалярного умножения равно

   .

   $$\frac{d}{dt}[c\vec{r}(t)]=c\vec{r}'(t)$$

2. Если r(t) и u(t) сложить или вычесть вместе, правило суммы и разности производной равно

   $$\frac{d}{dt}[\vec{r}(t)\pm\vec{u}(t)]=\vec{r}'(t)\pm\vec{u}'( т) $$

3. Если существует произведение r(t) и u(t), правило произведения производной

   $$\frac{d}{dt}[\vec{r}(t)\vec{u}(t)]=\vec{r}'(t)\vec{u}(t)+\vec {r}(t)\vec{u}'(t)$$

4. Если есть скалярная функция, умноженная на векторную функцию, правило скалярного произведения: 

   $$\frac{d}{dt}[f(t). \vec{r}(t)]=f'( t)\vec{r}(t)+f(t)\vec{r}'(t)$$

5. Если векторная функция комбинируется с другой функцией, цепное правило производной

   $$\frac{d}{dt}[\vec{r}(f(t))]=\vec{r}'(f(t)).f'(t)$$

6. Если векторную функцию умножить на саму себя, получится постоянная функция. Тогда производная векторной функции будет

   $\vec{r}(t).\vec{r}(t)=c\quad тогда \quad \vec{r}(t).\vec{r}(t)=0$

Как вычислить производную вектор-функции?

Чтобы вычислить производную вектор-функции, нам необходимо выполнить указанные шаги.

1. Определите векторнозначную функцию.
2. Применить первый принцип производной и использовать производные правила в соответствии с используемой функцией.
3. Производная будет применяться ко всем компонентам векторной функции, таким как i, j и k.
4. При необходимости упростите.

Давайте разберемся, как вычислить производную векторной функции на следующих примерах. 92-4t+3)j$$

Существует два метода вычисления производной этой функции. Во-первых, использовать метод первого принципа, а во-вторых, использовать обычные производные правила. Итак, мы будем использовать первый принцип:

Следовательно, производная данной векторной функции равна 3i + (2t — 4)j.

Связанные темы

Подобно производной векторной функции, в исчислении существует множество других понятий производных, таких как неявное дифференцирование и частная производная. Мы можем определить их один за другим, например:

• Неявное дифференцирование

  Процесс нахождения производной неявной функции известен как неявное дифференцирование. Но конкретной формулы для неявного дифференцирования не существует. Мы можем использовать теорему о неявной функции, чтобы легко найти производную. Математически это выражается как:

  $f'(x)=-\frac{F_x}{F_y}$

• Частная производная

  Частная производная используется для вычисления производной функции многих переменных.

  No related posts.