Производная функции — расчет онлайн
Расчет f'(x)
Основная переменная
ввод одной буквы
f =
Разделить расчет: использовать a*b 8 не ab6 и страница
Этот инструмент вычисляет производную функции.
Допускаются обычные функции: синус, косинус, тангенс, логарифм (log), экспонента, корень и т. д. (см. таблицу ниже).
Как пользоваться этим калькулятором?
| Переменные | Функция может иметь одну или несколько переменных, но только одну основную переменную. Переменная представляет собой одну строчную или прописную букву. Примеры: Функция f с одной главной переменной: f(x) = 4*x Функция g с одной главной переменной x и дополнительным параметром m, g(x) = 4*x*m + x + 1 , В этом случае введите x в поле «основная переменная» | |
|---|---|---|
| Номера | Использовать точку в качестве десятичного разделителя 9 (мощность), Для оператора умножения введите a*b, а не a.  b или ab. Пример: 2*х. b или ab. Пример: 2*х. | |
| Константы | Вы можете использовать следующие константы: e (прибл. 2,72) Примеры: f(x) = pi * x или f(x) = e * (x+ 1+2*д) 2 | |
| Общие функции | Вы можете использовать эти функции в выражении f(x) sqrt(x) (квадратный корень), exp(x) (экспоненциальная функция), log(x) или ln (натуральный логарифм), | |
| Тригонометрические функции | Вы можете использовать эти функции в выражении f(x) sin (синус), cos (косинус), tan (тангенс), cot (котангенс), сек. секанс), csc (косеканс), | |
| Обратные тригонометрические функции | Вы можете использовать эти функции в выражении f(x) arcsin (арксинус), arccos (арккосинус), arctg (арктангенс), arccot (аркотангенс), | 20 сек. арксеканс), арксеканс), arccsc (арккосеканс), |
| Гиперболические функции | Вы можете использовать эти функции в выражении f(x) sh (гиперболический синус), cosh (гиперболический косинус), tanh (гиперболический тангенс), coth (гиперболический котангенс), sech (гиперболический секанс), 70 9090 csch (гиперболический секанс) | |
| Обратные гиперболические функции | Вы можете использовать эти функции в выражении f(x) asinh (обратный гиперболический синус), acosh (обратный гиперболический косинус), atanh (обратный гиперболический тангенс), 92` | |
| `u @ v` | `v’*u’ @ v` |
См. также
Примитивная функция
Калькулятор ряда Тейлора
Калькулятор предельной функции
Значение функции
Определенный интеграл
Исчисление I — интерпретация производной
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Производные
/ Толкование производной
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3.2: Интерпретация производной
Прежде чем перейти к разделу, в котором мы узнаем, как вычислять производные, избегая ограничений, которые мы оценивали в предыдущем разделе, нам нужно бросить беглый взгляд на некоторые интерпретации производной. . Все эти интерпретации возникают в результате напоминания о том, как возникло наше определение производной. Определение появилось благодаря тому, что мы заметили, что все задачи, над которыми мы работали в первом разделе главы «Ограничения», требовали от нас оценки одного и того же предела.
Скорость изменения
Первая интерпретация производной – это скорость изменения. 2} — 16t + 35\). Определите каждое из следующих.
2} — 16t + 35\). Определите каждое из следующих.
- Объем воды в баке увеличивается или уменьшается в \(t = 1\) минуту?
- Увеличивается или уменьшается объем воды в баке через \(t = 5\) минут?
- Как быстрее изменяется объем воды в баке: \(t = 1\) или \(t = 5\) минут?
- Объем воды в баке никогда не меняется? Если да, то когда?
Показать все решения Скрыть все решения
Показать обсуждение
В решении этого примера мы будем использовать оба обозначения для производной просто для того, чтобы вы познакомились с различными обозначениями.
Нам понадобится скорость изменения объема, чтобы ответить на эти вопросы. Это означает, что нам понадобится производная этой функции, так как это даст нам формулу для скорости изменения в любой момент времени \(t\). Теперь обратите внимание, что функция, определяющая объем воды в резервуаре, — это та же самая функция, которую мы видели в примере 1 в последнем разделе, за исключением того, что буквы изменились. Изменение букв между функцией в этом примере и функцией в примере из последнего раздела не повлияет на работу, поэтому мы можем просто использовать ответ из
этот пример с соответствующей заменой букв.
Изменение букв между функцией в этом примере и функцией в примере из последнего раздела не повлияет на работу, поэтому мы можем просто использовать ответ из
этот пример с соответствующей заменой букв.
Производная.
\[V’\left( t \right) = 4t — 16\hspace{0,5 дюйма}{\rm{OR}}\hspace{0,5 дюйма}\frac{{dV}}{{dt}} = 4t — 16 \]
Вспомним из нашей работы в первом разделе пределов, что мы определили, что если скорость изменения была положительной, то количество увеличивалось, а если скорость изменения была отрицательной, то количество уменьшалось.
Теперь мы можем решить задачу.
а Увеличивается или уменьшается объем воды в баке через \(t = 1\) мин? Показать решение
В этом случае все, что нам нужно, это скорость изменения объема при \(t = 1\)или,
\[V’\влево( 1 \вправо) = — 12\hпробел{0,5 дюйма}{\rm{ИЛИ}}\hпробел{0,5 дюйма}{\влево.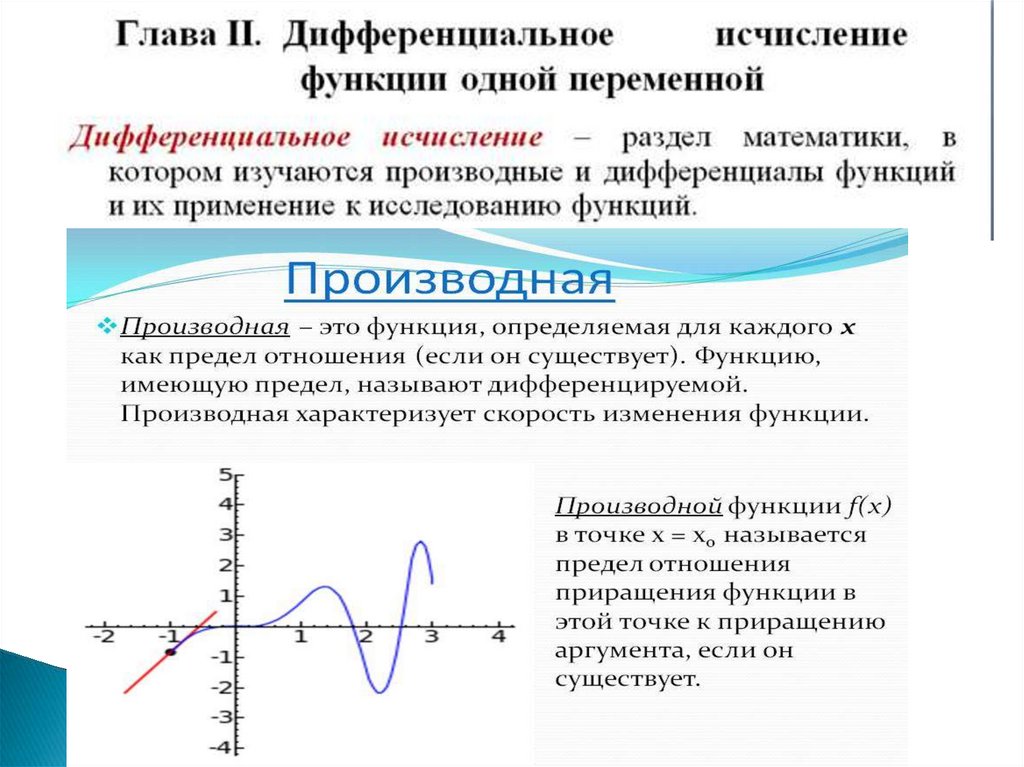
Итак, при \(t = 1\) скорость изменения отрицательна, поэтому объем в это время должен уменьшаться.
b Увеличивается или уменьшается объем воды в баке через \(t = 5\) минут? Показать решение
Опять же, нам понадобится скорость изменения при \(t = 5\).
\[V’\влево( 5 \вправо) = 4\hпробел{0,5 дюйма}{\rm{ИЛИ}}\hпробел{0,5дюйма}{\влево. {\ frac {{dV}}{{dt}}} \right|_{\,t = 5}} = 4\]
В этом случае скорость изменения положительна, поэтому объем должен увеличиваться при \(t = 5\) .
в Изменяется ли быстрее объем воды в баке через \(t = 1\) или \(t = 5\) минут? Показать решение
Чтобы ответить на этот вопрос, мы обращаем внимание только на величину скорости изменения, и нас не волнует знак скорости изменения.
d Всегда ли объем воды в баке не меняется? Если да, то когда? Показать решение
Объем не будет изменяться, если его скорость изменения равна нулю. Чтобы иметь скорость изменения, равную нулю, это означает, что производная должна быть равна нулю. Итак, чтобы ответить на этот вопрос, нам нужно будет решить
\[V’\left( t \right) = 0\hspace{0.5in}{\rm{OR}}\hspace{0.5in}\frac{{dV}}{{dt}} = 0\]
Это достаточно просто сделать.
\[4t — 16 = 0\hspace{0,5 дюйма} \Стрелка вправо \hspace{0,5 дюйма}t = 4\]
Итак, при \(t = 4\) громкость не меняется. Обратите внимание, что все это говорит о том, что в течение короткого мгновения громкость не меняется. Это не говорит о том, что в этот момент громкость перестанет меняться постоянно.
Это не говорит о том, что в этот момент громкость перестанет меняться постоянно.
Если мы вернемся к нашим ответам из частей (а) и (б), мы сможем получить представление о том, что происходит. При \(t = 1\) объем уменьшается, а при \(t = 5\) объем увеличивается. Итак, в какой-то момент времени громкость должна переключиться с уменьшения на увеличение. Это время равно \(t = 4\).
Это время, в течение которого громкость переходит от уменьшения к увеличению, поэтому в течение самого короткого момента времени громкость перестанет изменяться, поскольку она переходит от уменьшения к увеличению.
Обратите внимание, что одна из наиболее распространенных ошибок, которую учащиеся допускают в подобных задачах, заключается в том, что они пытаются определить возрастание/убывание по значениям функции, а не по производным. В этом случае, если мы возьмем значения функции при \(t = 0\), \(t = 1\) и \(t = 5\), мы получим,
\[V\влево( 0 \вправо) = 35\hspace{0,5 дюйма}V\влево( 1 \вправо) = 21\hspace{0,5 дюйма}V\влево( 5 \вправо) = 5\]
Очевидно, что по мере перехода от \(t = 0\) к \(t = 1\) объем уменьшается. Это может привести нас к выводу, что при \(t = 1\) объем уменьшается. Однако мы просто не можем этого сказать. Все, что мы можем сказать, это то, что между \(t = 0\) и \(t = 1\) объем в какой-то момент времени уменьшился. Единственный способ узнать, что происходит прямо в точке \(t = 1\), состоит в том, чтобы вычислить \(V’\left( 1 \right)\) и посмотреть на его знак, чтобы определить увеличение/уменьшение.
В этом случае \(V’\left( 1 \right)\) отрицательно, и поэтому объем действительно уменьшается при \(t = 1\).
Это может привести нас к выводу, что при \(t = 1\) объем уменьшается. Однако мы просто не можем этого сказать. Все, что мы можем сказать, это то, что между \(t = 0\) и \(t = 1\) объем в какой-то момент времени уменьшился. Единственный способ узнать, что происходит прямо в точке \(t = 1\), состоит в том, чтобы вычислить \(V’\left( 1 \right)\) и посмотреть на его знак, чтобы определить увеличение/уменьшение.
В этом случае \(V’\left( 1 \right)\) отрицательно, и поэтому объем действительно уменьшается при \(t = 1\).
Теперь, если бы мы подставили функцию, а не производную, мы бы получили правильный ответ для \(t = 1\), хотя наши рассуждения были бы неверны. Важно не допустить, чтобы это дало вам представление о том, что так будет всегда. Это просто сработало в случае \(t = 1\).
Чтобы увидеть, что это не всегда работает, давайте теперь посмотрим на \(t = 5\). Если мы подставим \(t = 1\) и \(t = 5\) в объем, мы снова увидим, что по мере перехода от \(t = 1\) к \(t = 5\) объем уменьшился. Опять же, однако все это говорит о том, что объем уменьшился где-то между \(t = 1\) и \(t = 5\). Это НЕ говорит, что объем уменьшается при \(t = 5\). Единственный способ узнать, что происходит прямо в
\(t = 5\) заключается в вычислении \(V’\left( 5 \right)\), и в этом случае \(V’\left( 5 \right)\) положительно, и поэтому объем фактически увеличивается при \(t = 5\).
Опять же, однако все это говорит о том, что объем уменьшился где-то между \(t = 1\) и \(t = 5\). Это НЕ говорит, что объем уменьшается при \(t = 5\). Единственный способ узнать, что происходит прямо в
\(t = 5\) заключается в вычислении \(V’\left( 5 \right)\), и в этом случае \(V’\left( 5 \right)\) положительно, и поэтому объем фактически увеличивается при \(t = 5\).
Будьте осторожны. Когда вас попросят определить, возрастает или убывает функция в какой-либо точке, обязательно посмотрите на производную. Это единственный верный способ получить правильный ответ. Мы не пытаемся определить, увеличилась/уменьшилась ли функция к тому времени, когда мы достигли определенной точки. Мы ищем, чтобы определить, увеличивается ли функция в данный момент.
Наклон касательной
Это следующая основная интерпретация производной. Наклон касательной к \(f\left( x \right)\) в точке \(x = a\) равен \(f’\left( a \right)\). Тогда касательная задается как
\[y = f\left( a \right) + f’\left( a \right)\left( {x — a} \right)\]
Пример 2. Найдите касательную к следующей функции в точке \(z = 3\).
\[R\влево( z \вправо) = \sqrt {5z — 8} \]
Найдите касательную к следующей функции в точке \(z = 3\).
\[R\влево( z \вправо) = \sqrt {5z — 8} \]
Показать решение
Сначала нам нужна производная функции, и мы нашли ее в примере 3 в последнем разделе. Производная,
\[R’\left( z \right) = \frac{5}{{2\sqrt {5z — 8} }}\]
Теперь все, что нам нужно, это значение функции и производная (для наклона) в точке \(z = 3\).
\[R\left( 3 \right) = \sqrt 7 \hspace{0.5in}m = R’\left( 3 \right) = \frac{5}{{2\sqrt 7 }}\]
Тогда касательная
\[y = \sqrt 7 + \frac{5}{{2\sqrt 7 }}\left( {z — 3} \right)\]
Скорость
Напомним, что это можно рассматривать как частный случай интерпретации скорости изменения. Если положение объекта определяется как \(f\left( t \right)\) через \(t\) единиц времени, то скорость объекта в \(t = a\) определяется как \(f’ \влево( а \вправо)\).
Если положение объекта определяется как \(f\left( t \right)\) через \(t\) единиц времени, то скорость объекта в \(t = a\) определяется как \(f’ \влево( а \вправо)\).
Пример 3. Предположим, что положение объекта через \(t\) часов определяется выражением \[g\left( t \right) = \frac{t}{{t + 1}}\]
Ответьте на два вопроса об этом объекте.
- Объект движется вправо или влево через \(t = 10\) часов?
- Объект когда-нибудь перестает двигаться?
Показать все решения Скрыть все решения
92}}}\]а Движется ли объект вправо или влево через \(t = 10\) часов? Показать решение
Чтобы определить, движется ли объект вправо (скорость положительна) или влево (скорость отрицательна), нам нужна производная при \(t = 10\).
\[g’\влево( {10} \вправо) = \frac{1}{{121}}\]
Итак, скорость в точке \(t = 10\) положительна, поэтому объект движется вправо в точке \(t = 10\).
b Перестает ли когда-нибудь двигаться объект? Показать решение
Объект перестанет двигаться, если его скорость никогда не будет равна нулю. Однако обратите внимание, что рациональное выражение может быть равно нулю только в том случае, если числитель равен нулю. Поскольку числитель производной (и, следовательно, скорости) является константой, он не может быть равен нулю.
Следовательно, объект никогда не перестанет двигаться.
На самом деле здесь можно сказать немного больше. Объект всегда будет двигаться вправо, так как скорость всегда положительна.
Здесь мы рассмотрели три основные интерпретации производной. Вам нужно будет запомнить их, особенно скорость изменений, так как они будут постоянно появляться на протяжении всего курса.
Прежде чем мы покинем этот раздел, давайте поработаем еще с одним примером, который включает в себя некоторые идеи, обсуждаемые здесь, и является просто хорошим примером для работы.
Пример 4 Ниже приведен эскиз функции \(f\left( x \right)\). Нарисуйте график производной этой функции \(f’\left( x \right)\).
Показать решение
На первый взгляд это кажется почти невыполнимой задачей. Однако, если у вас есть базовые знания об интерпретации производной, вы можете получить набросок производной. По большей части это не будет идеальным эскизом, но вы сможете получить большинство основных функций производной в эскизе.
Начнем со следующего наброска функции с парой дополнений.
Обратите внимание, что в точках \(x = — 3\), \(x = — 1\), \(x = 2\) и \(x = 4\) касательная к функции горизонтальна. Это означает, что наклон касательной должен быть равен нулю. Теперь мы знаем, что наклон касательной в определенной точке также является значением производной функции в этой точке. Таким образом, мы теперь знаем, что
\[f’\влево( { — 3} \вправо) = 0\hspace{0.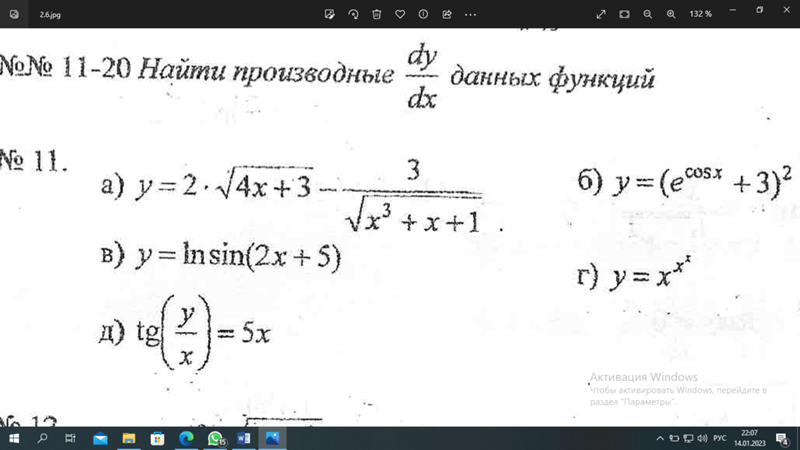 5in}f’\влево( {- 1} \right) = 0\hspace{0.5in}f’\влево( 2 \right) = 0\hspace{0.5in}f’\left( 4 \right) = 0\]
5in}f’\влево( {- 1} \right) = 0\hspace{0.5in}f’\влево( 2 \right) = 0\hspace{0.5in}f’\left( 4 \right) = 0\]
Это хорошая отправная точка для нас. Это дает нам несколько точек на графике производной. Он также разбивает область определения функции на области, в которых функция возрастает и убывает. Из наших обсуждений выше мы знаем, что если функция возрастает в точке, то производная должна быть положительной в этой точке. Точно так же мы знаем, что если функция убывает в какой-то точке, то производная в этой точке должна быть отрицательной.
Теперь мы можем дать следующую информацию о производной.
\[\begin{align*} x & < - 3 & \hspace{0.5in}f'\left( x \right) & < 0\\ - 3 < x & < - 1 & \hspace{0.5in }f'\left( x \right) & > 0\\ — 1 < x & < 2 & \hspace{0.5in}f'\left( x \right) & < 0\\ 2 < x & < 4 & \hspace{0.5in}f'\left( x \right) & < 0\\ x & > 4 & \hspace{0.5in}f’\left(x \right) & > 0\end{align*}\ ]
Помните, что здесь мы приводим знаки производных, и они являются исключительно функцией возрастания или убывания функции. Знак самой функции здесь совершенно безразличен и никак не повлияет на знак производной.
Знак самой функции здесь совершенно безразличен и никак не повлияет на знак производной.
Может показаться, что у нас недостаточно информации для получения эскиза, но мы можем получить немного больше информации о производной из графика функции. Мы знаем, что в диапазоне \(x < - 3\) производная должна быть отрицательной, однако мы также видим, что в этом диапазоне производная должна возрастать. Здесь она отрицательна, пока мы не достигнем \(x = - 3\), и в этой точке производная должна быть равна нулю. Единственный способ, чтобы производная была отрицательной слева от \(x = - 3\) и равна нулю в точке \(x = - 3\) означает, что производная будет возрастать по мере увеличения \(x\) до \(x = -3\).
Теперь в диапазоне \( — 3 < x < - 1\) мы знаем, что производная должна быть равна нулю на концах и положительна между двумя концами. Непосредственно справа от \(x = - 3\) производная также должна возрастать (поскольку она начинается с нуля, а затем становится положительной, следовательно, она должна возрастать). Таким образом, производная в этом диапазоне должна начинаться с возрастания и в конечном итоге должна вернуться к нулю при \(x = — 1\). Таким образом, в какой-то момент этого интервала производная должна начать уменьшаться, прежде чем она достигнет \(x =
— 1\). Теперь мы должны быть осторожны здесь, потому что это просто общее поведение здесь, на двух конечных точках. Мы не будем знать, где производная переходит от увеличения к убыванию, и она вполне может меняться между увеличением и уменьшением несколько раз, прежде чем мы достигнем \(x = — 1\). Все, что мы можем на самом деле сказать, это то, что непосредственно справа от \(x = — 3\) производная будет возрастать, а непосредственно слева от \(x = — 1\) производная будет уменьшаться.
Таким образом, производная в этом диапазоне должна начинаться с возрастания и в конечном итоге должна вернуться к нулю при \(x = — 1\). Таким образом, в какой-то момент этого интервала производная должна начать уменьшаться, прежде чем она достигнет \(x =
— 1\). Теперь мы должны быть осторожны здесь, потому что это просто общее поведение здесь, на двух конечных точках. Мы не будем знать, где производная переходит от увеличения к убыванию, и она вполне может меняться между увеличением и уменьшением несколько раз, прежде чем мы достигнем \(x = — 1\). Все, что мы можем на самом деле сказать, это то, что непосредственно справа от \(x = — 3\) производная будет возрастать, а непосредственно слева от \(x = — 1\) производная будет уменьшаться.
Далее, для диапазонов \(-1 < x < 2\) и \(2 < x < 4\) мы знаем, что производная будет равна нулю в конечных точках и отрицательной между ними. Кроме того, следуя приведенному выше типу рассуждений, мы можем видеть в каждом из этих диапазонов, что производная будет уменьшаться справа от левой конечной точки и увеличиваться слева от правой конечной точки.
Наконец, в последней области \(x > 4\) мы знаем, что производная равна нулю в точке \(x = 4\) и положительна справа от \(x = 4\). Опять же, следуя приведенным выше рассуждениям, производная также должна возрастать в этом диапазоне.
Соединяя весь этот материал вместе (и всегда используя самые простые варианты увеличения и/или уменьшения информации), мы получаем следующий набросок для производной.
Обратите внимание, что это было сделано с фактической производной и поэтому на самом деле является точным. Любой набросок, который вы сделаете, вероятно, не будет выглядеть точно так же. «Горбы» в каждой из областей могут быть, например, в разных местах и/или на разных высотах. Также обратите внимание, что мы отказались от вертикальной шкалы, потому что, учитывая информацию, которую мы получили на данный момент, не было реального способа узнать эту информацию.
Однако это не означает, что мы не можем получить некоторое представление о конкретных точках производной, кроме тех, где мы знаем, что производная равна нулю. Чтобы убедиться в этом, давайте посмотрим на следующий график функции (не производной, а функции).
Чтобы убедиться в этом, давайте посмотрим на следующий график функции (не производной, а функции).
В точках \(x = — 2\) и \(x = 3\) мы нарисовали пару касательных линий. Мы можем использовать базовую концепцию подъема/наклона для оценки значения производной в этих точках.
Начнем с \(x = 3\). У нас есть две точки на линии здесь. Мы можем видеть, что каждый из них находится примерно на четверть пути от линии сетки. Таким образом, принимая во внимание это и тот факт, что мы проходим через одну полную сетку, мы можем видеть, что наклон касательной и, следовательно, производной приблизительно равен -1,5.
При \(x = — 2\) похоже (с некоторой грубой оценкой), что вторая точка находится примерно на 6,5 сетки выше первой точки, и поэтому наклон касательной здесь и, следовательно, производная, составляет приблизительно 6,5 .
Вот набросок производной с включенным вертикальным масштабом, из которого видно, что на самом деле наши оценки довольно близки к реальности.
