X 2 2x производная. Найти производную: алгоритм и примеры решений
Дата: 10.05.2015
Правила дифференцирования.
Чтобы найти производную от любой функции, надо освоить всего три понятия:
2. Правила дифференцирования.
3. Производная сложной функции.
Именно в таком порядке. Это намёк.)
Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.
Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции» и «продифференцировать функцию» — это одно и то же.
Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.
Сосредоточимся и вспомним все-все-все арифметические операции.
Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:
В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.
Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).
Рассмотрим несколько примеров. Сначала — самые простые.
Найти производную функции y=sinx — x 2
Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U , а x 2 — функция V. Имеем полное право написать:
y» = (sinx — x 2)» = (sinx)»- (x 2)»
Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных.
y» = (sinx)» — (x 2)» = cosx — 2x
Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.
А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:
Найти производную функции y=sinx — x 2 +cosx — x +3
Смело пишем:
y» = (sinx)» — (x 2)» + (cosx)» — (x)» + (3 )»
В конце урока дам советы по облегчению жизни при дифференцировании.)
Практические советы:
1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.
2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.
3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \).
Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
\(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение
\(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то
указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) .
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.
2} $$
Приложение
Решение производной на сайт для закрепления пройденного материала студентами и школьниками. Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия.
Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент. Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости.
Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси. В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы.
Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат. Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела.
Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины. Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему.
Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения. Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве.
С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия.
Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно. Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт.
Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк. Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров. Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6.
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу.
Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9.
Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Производная
Производная – отношение приращения функции к приращению ее аргумента при приращении аргумента стремящемся…
ЭЙ-ЭЙ, СТОЙТЕ!!! Куда вы побежали-то? Сейчас легко и просто всё объясню! Приготовьтесь, текста будет много. Зато понятно и наглядно. Так же в конце будут разобраны примеры из ЕГЭ.
Понятие производной на интервале
Пусть у нас есть некоторая линейная функция, определенная на промежутке \([a;b]\). Что значит слово «определенная»? Это значит, что для любого \(x\) из этого промежутка значений мы можем найти соответствующий \(y\) (смотрите, например, следующий график).
Возьмем на этом промежутке \([a;b]\) некоторое значение аргумента — \(x_A\). Ему соответствует точка \(A\) на графике и значение функции \(y_A\).
Теперь дадим выбранному значению \(x_A\) некоторое приращение \(∆x\). Эта запись — \(∆x\) — читается как «дельта икс» и означает величину изменения икса.
То есть мы увеличиваем значение \(x_A\) на \(∆x\). Тогда мы сдвинемся по оси \(x\) и попадем в некое \(x_B\) равное \(x_A+∆x\).
Очевидно, что «расстояние» между \(x_B\) и \(x_A\) равно как раз \(∆x\) (см. график), то есть приращению аргумента. И это приращение аргумента есть «длина» интервала, который мы рассматриваем.
Значению аргумента \(x_B\) соответствует точка \(B\) на графике и значение функции \(y_B\).
Давайте обозначим «расстояние» между \(y_B\) и \(y_A\) как некоторое \(∆y\) (аналогично тому, как это было сделано на оси \(x\)).
Что такое \(∆y\)? Подумайте – был аргумент равный \(x_A\), ему соответствовало значение функции \(y_A\).
Потом мы аргумент увеличили на \(∆x\) (до \(x_B\)), при этом значение функции тоже выросло до \(y_B\). Что такое тогда \(∆y\) равное разности между \(y_B\) и \(y_A\)? Верно, это приращение значения функции при соответствующем приращении аргумента!
Так вот — если мы теперь разделим \(∆y\) на \(∆x\), то получим производную функции на интервале \(∆x\) (от \(x_A\) до \(x_B\)). В этом суть понятия «производная» на интервале – это просто число, которое получится, если поделить длину отрезка ∆y на длину соответствующего ему отрезка \(∆x\).
Производная на интервале — это отношение приращения функции на интервале к ширине этого интервала (то есть приращению аргумента).
Внимание! Это определение не математически строгое, а «по смыслу», для понимания.
То есть, производная на интервале показывает насколько сильно изменилась функция по отношению к некоторому изменению аргумента этой функции.
Или по-другому: производная на интервале характеризует скорость роста функции на этом интервале.
Действительно, посмотрите два графика ниже.
На первом графике при росте аргумента с \(3\) до \(4\), функция выросла с \(1\) до \(4\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac{∆y}{∆x}=\frac{3}{1}=3\)
На втором графике при росте аргумента с \(3\) до \(4\), функция выросла с \(2\) до \(3\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac{∆y}{∆x}=\frac{1}{1}=1.\)
Легко заметить, что график слева «круче», а график справа – более «пологий», т.е. \(f(x)\) растет быстрее, чем \(g(x)\). И производная слева – больше, чем справа. Это логично, ведь фактически производная – это дробь \(\frac{∆y}{∆x}\), а если числитель дроби увеличить, то и значение всей дроби тоже растет.
Производная на интервале характеризует скорость роста функции. Чем больше производная – тем быстрее растет функция на интервале.
Хорошо, теперь вопрос на засыпку тем, кто читал внимательно. А что будет с производной, если график линейной функции падает?
Давайте рассмотрим эту ситуацию.
Функция \(f(x)\) падает, то есть при росте аргумента, значение функции становиться все меньше.
Действительно, при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит, \(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\).
Тогда значение производной на интервале \((3;4)\) равно \(\frac{∆y}{∆x}=\frac{-3}{1}=-3\).
То есть, если функция на интервале падает – производная станет отрицательна.
Причем, чем круче падает функция, тем больше по модулю будет значение производной. Посмотрите на графики ниже, и вы в этом сами убедитесь.
На первом графике при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac{∆y}{∆x}=\frac{-3}{1}=-3\).
На втором графике при росте аргумента с \(2\) до \(3\), функция упала с \(2\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-2=-1\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac{∆y}{∆x}=\frac{-1}{1}=-1\).
Если функция падает – производная на интервале отрицательна.
Осталось рассмотреть последнюю ситуацию — а если функция в точке не возрастает и не убывает? Что будет с производной в этом случае? Смотрите график ниже.
Вот, например, функция, имеющая прямолинейный участок, параллельный оси \(x\) на интервале \((2;4)\).
Понятно, что если мы рассмотрим этот интервал, то изменение функции \(∆y\) на нем равно нулю, ведь на нем функция не растет и не падает и для любой точки равна \(2\).
И тогда производная равна \(\frac{∆y}{∆x}=\frac{0}{∆x}=0\).
Если функция не растет и не падает – производная на интервале равна \(0\).
Понятие производной в точке
Хорошо, мы разобрали производную на интервале для линейной функции. А если функция отличается от прямой?
Первый порыв ответить: «да какая разница, делаем также!» — неверен. Дело в том, что на прямой была не важна длина рассматриваемого интервала, ведь для неё значение производной – постоянная величина на любом интервале. Смотрите на график ниже:
Если мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(3\). То есть, \(∆x=4-2=2\), \(∆y=3-1=2\), т.е. значение производной на интервале \((2;4)\) равно \(\frac{∆y}{∆x}=\frac{2}{2}=1\).
Если мы рассмотрим интервал по иксу с \(2\) до \(3\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=3-2=1\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;3)\) равно \(\frac{∆y}{∆x}=\frac{1}{1}=1\).
И на любом другом интервале будет тоже самое — и на \((2;5)\), и на \((3;4)\), и на \((3;5)\) – производная везде равна \(1\). Это и логично, ведь скорость роста функции везде одинакова.
Теперь давайте посмотрим график некоторой нелинейной функции.
Если мы рассмотрим интервал по иксу с \(2\) до \(5\), то на нем прирост значения функции – с \(1\) до \(4\). То есть, \(∆x=5-2=3\), \(∆y=4-1=3\), т.е. значение производной на интервале \((2;5)\) равно \(\frac{∆y}{∆x}=\frac{3}{3}=1\).
Если же мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=4-2=2\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;4)\) равно \(\frac{∆y}{∆x}=\frac{1}{2}=0,5\).
2\), построенный на компьютере с высокой точностью, на интервале от \(-5\) до \(5\). Видно, что график ну очень далек от прямой.
А если рассмотреть тот же график, но на более узком интервале?
Вот тот же график, но уже на интервале от \(0\) до \(2\). Видно, что он изрядно «распрямился».
А вот он же на интервале от \(1\) до \(1,1\). Визуально он уже мало отличается от прямой, хотя на самом деле очень небольшое искривление все же есть. Понятно, что если сжимать интервал еще сильнее, то вскоре график будет практически неотличим от прямой.
Таким образом, вся вышеописанная логика вполне применима и для нелинейных графиков, но только на очень маленьких интервалах. А что мы получим, если будем БЕСКОНЕЧНО уменьшать ширину интервал? Мы будем сжимать его до точки. А что такое «ширина интервала»? Это ни что иное как \(∆x\)! Значит, чтобы найти производную в точке, мы должны посмотреть приращение функции на бесконечно малом (или, говоря более научно, стремящемся к нулю) приращении аргумента.
Именно так в математике и вводится понятие производной в точке:
Производная в точке – есть отношение приращения функции к соответствующему приращению ее аргумента при приращении аргумента, стремящемся к нулю.
Таким образом, вся описанная выше логика дифференцирования линейных функций, применима для бесконечно малых участков функций нелинейных. Значит, и все сделанные ранее выводы будут верны. Например, если нелинейная функция в точке (точнее, на бесконечно малом интервале в окрестности этой точки) возрастает, то производная в точке будет положительна. А если функция в точке убывает — производная будет отрицательна.
Остается вопрос – а есть ли на нелинейных функциях точки, где производная равна нулю? Ответ – да, в точках экстремумов. Помните, что это за точки такие?
Экстремумы – это точки максимумов и минимумов функции.
Напомню, что максимумом функции называется самая «высокая» точка на некотором интервале, а минимумом, соответственно, самая «низкая».
2 (x+1)-15\).Она имеет максимум при \(x=1\) и минимум при \(x=5\).
И в этих точках функция действительно не растет и не падает.
Давайте посмотрим на большем масштабе, чтобы в этом убедится.
Вот окрестность точки максимума \(x=1\) с очень маленьким шагом.
А это окрестность точки минимума \(x=5\) с очень маленьким шагом.
Думаю, комментарии излишни. Вообще говоря, чтобы понять, что в максимумах и минимумах функция «останавливается» достаточно просто внимательно об этом подумать.
Вдумайтесь, как образуется, допустим, максимум? Функция растет, растет, но после какой-то точки начинает падать. Значит, функция меняет «направление движения» на противоположное. Но это невозможно сделать без остановки! Попробуйте бежать в одну сторону, а потом взять и резко побежать в обратную (не просто повернуть, а именно в противоположную сторону). Вы в любом случае остановитесь при смене направления хоть на долю секунды.
Также и функции. С минимумом — аналогично.
Таким образом, получается, что в окрестности точек минимума и максимума функция идет параллельно оси \(x\). И в них производная равна нулю. Слово «в окрестности», употребленное выше, означает «очень-очень близко возле точки». Например, промежуток \((1,99999; 2,00001)\) можно назвать окрестностью точки со значением \(2\).
Подведем итоги:
— Чем больше значение производной функции в точке – тем быстрее в этой точке растет функция.
— Если производная в точке положительна, функция в этой точке растет, если производная в точке отрицательна, функция в ней падает.
— В точках максимумов и минимумов функции – производная равно \(0\).
Эти принципы стоит запомнить (а еще лучше просто понять), потому что с их помощью можно решать огромное количество задач на производные, в том числе и из ЕГЭ.
Пример (ЕГЭ).
На рисунке изображен график функции, определенной на интервале \((-3;7)\). Определите количество целых точек, в которых производная данной функции отрицательна.
Решение: Начинаем анализировать. Где производная будет отрицательна? Там, где функция падает, то есть от точки А до точки В и от точки С до точки D.
При этом в задаче просят найти количество ЦЕЛЫХ точек. А что такое «целая точка»? Это такая точка графика, у которой икс целое число (например, \(-5\), \(0\) или \(17\), но не \(3,25\) или \(0,7\)).
То есть нам нужны именно такие точки на участках АВ и CD графика. Всего их четыре (обозначены на графике красным ромбом). Обратите внимание, что точка С в ответ не входит, так как это точка максимума и в ней производная равно \(0\), а ноль неотрицателен.
Ответ: 4.
Пример (ЕГЭ). На рисунке изображен график функции \(y=f(x)\) и отмечены точки \(−2\), \(1\), \(3\) и \(9\).
В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Решение: Давайте думать.
В точке с координатой \(-2\) функция убывает (падает), значит производная будет отрицательна (ведь она показывает, как раз изменение функции).
В точке с координатой \(1\) – функция медленно растет, значит производная будет, во-первых, положительна, а во-вторых, мала по значению (ведь рост медленный).
В точке с координатой \(3\) – максимум, значит функция не растет и не падает, следовательно, производная будет равна нулю.
И наконец, в точке \(9\) – функция растет и быстро (по крайней мере, быстрее, чем в точке \(1\)). Значит здесь производная положительна и велика.
Таким образом, с учетом всех предыдущих рассуждений, делаем вывод: наибольшее значение производной будет в точке \(9\).
Ответ: \(9\).
Довольно часто в практике попадаются обратные задачи – когда дан график производной, а анализировать надо график функции.
Вот, например, такая задача из ЕГЭ:
Пример (ЕГЭ). На рисунке изображен график \(y'(x)\) -производной для функции \(y(x)\). Найдите количество точек экстремумов функции \(y(x)\) на изображенном интервале.
Решение: Экстремумы – это точки минимумов и максимумов функции. Но у нас дан график производной, а не функции. А что происходит с производной в тех точках, где на функции минимум или максимум?
Верно, в этих точках производная равна нулю. Значит, нам нужны все точки, где значение производной ноль! Это точки А, B, C, D и Е. Всего их \(5\), это и есть ответ задачи.
Ответ: \(5\).
Пример (ЕГЭ). На рисунке изображен график \(y'(x)\) — производной для функции \(y(x)\) определенной на интервале \((−7; 7)\). Найдите промежутки возрастания функции \(y(x)\). В ответе укажите длину наибольшего из них.
Решение: Мы знаем, что если функция возрастает – производная положительна, а если падает – то отрицательна.
Однако верно и обратное:
— если производная положительна – функция растет,
— если производная отрицательна – функция падает.
Исходя из этого становиться очевидно, что исходная функция \(y(x)\) возрастает на участках \((-5;-2)\) и \((1;6)\) – они выделены зеленым. И длина наибольшего из них равна \(5\).
Ответ: \(5\).
Премаркет. Второе дно — в подарок?
Американские индексы обновили трехмесячные низы и вышли в область годовых минимумов. Технически игроки на повышение могут уцепиться за идею второго дна, но окажется ли область 3600 п. в S&P 500 разворотной — большой вопрос. Нефть марки Brent не удержала статистические пределы риска и пролилась до январских минимумов, но сегодня контракты могут вернуть планку $85.
Тенденции биржевого вторника и на что обратить внимание инвесторам сегодня — в обзоре.
Безостановочное падение последних дней привело индексы Штатов на минимумы года. А если смотреть по закрытию широкого рынка S&P 500, то это минимумы аж с ноября ковидного 2020 г. Оценки скоротечного июльско-августовского отскока на фоне ожиданий послаблений ФРС себя полностью оправдали. Сохраняется глобальный нисходящий тренд рынка акций.
Федрезерв даже не думает останавливаться в сжатии ликвидности на волне бушующей инфляции в стране, а значит, ожидать масштабных покупок бумаг было бы странно. К концу года ключевая ставка наверняка перевалит за 4% — по нашим расчетам, это будет соответствовать уровню 3200 п. по S&P 500.
Это значит, что технический отскок, наблюдаемый сегодня утром во фьючерсах — не более чем снятие перепроданности инструментов. Формация двойного дна, скорее всего, не раскроется в полной мере, и индексы потекут дальше на юг.
Утренняя производная на S&P 500 прибавляет 0,6%, поднимаясь к 3690 п. На волне локального движения вверх пределами может выступать область 3750–3800 п.
, а далее риски для игры на повышение видятся высокими. Сегодня фактор американского поводыря сыграет за покупателей акций в Азии и Европе — можно допустить отскок после сильной волны распродаж.
Маркеры риска продолжают обновлять максимумы. Доходности 10-летних гособлигаций США показали 3,9%, чего не было с 2010 г. А индекс доллара США DXY подскочил на очередные пики начала 2000-х, выше 114,5 п. Непримиримость ФРС и нерешительность других центробанков приводят к резкой девальвации евро, иены, фунта, юаня, но в ближайшие пару сессий вероятно затишье на валютном рынке.
О нервозности игроков говорит индекс волатильности VIX. «Индикатор страха» ожидаемо перевалил вверх за планку 30 п. Тем не менее в ближайшие дни изменчивость рынка акций может снизиться, что обеспечит некоторое послабление для фондовых быков. На среднесрочной перспективе ожидать возвращения VIX к средним значениям в 20 п. не приходится, спокойствие с рынка ушло.
Рынок Азии
Некоторым утешением для европейских быков, что ориентируются при принятии инвестиционного решения на фактор Азиатско-Тихоокеанского региона, может служить замедление темпа падения индексов акций.
После вчерашних распродаж австралийский ASX незначительно отскакивает. Потеряв накануне 2,5%, японский Nikkei показывает +0,5%.
На треть процента поднимается Shanghai Composite, а вот гонконгский Hang Seng вновь падает на процент, к минимумам 11-летней давности, на фоне высокой уязвимости ИТ-сектора к росту процентных ставок. Не добавляет оптимизма рынкам Поднебесной кризис энергоносителей, проблемы в строительном секторе, обострившаяся в последние месяцы геополитика вокруг Тайваня. Региональные фондовые тренды, однозначно, вниз.
Что ждать сегодня
В США выйдут данные по заказам товаров длительного пользования. Ожидается значительная просадка показателя на фоне экономии на дорогостоящих товарах в эпоху высокой инфляции и резко возросшей стоимости кредита. Это приведет к дальнейшему сжатию ВВП, после двух кварталов подряд экономической рецессии может наступить третий, а по году темп роста экономики Штатов может вообще обнулиться.
Американский институт нефти представит свои сводки по изменению недельных запасов сырья. Неделей ранее наращение резервов замедлилось, но все равно наблюдался прирост. Если сегодня произойдет выбытие сырой нефти, это несколько поддержит фьючерсы на Brent. Однако более важные данные рынок получит лишь завтра на отчете Минэнерго страны.
СырьеСнижение Brent продолжилось, и по итогам понедельника контракты потеряли еще 2,5%. В моменте истекающий фьючерс уходил под $84. Цены опустились к 8-месячным минимумам, к уровням, которые были еще до геополитической вспышки в Европе. Актуальный фьючерс на декабрь сегодня утром поднимается на полпроцента к $83,5 при дневном минимуме у $82,5.
Поддержки, рассматриваемые в качестве технической опоры, на основе прежней волатильности инструментов, устояли в августе, но в сентябре дали слабину. Теперь $85 и $90 выступают сопротивлениями. На фоне перепроданности фьючерсов вероятность возврата Brent на $85 видится значительной.
На стороне продавцов сырья — жесткий монетарный тренд и ралли в глобальном долларе. А за покупателей может выступить ОПЕК+, видя рост волатильности рынка и риски падающих цен для добычи. Не забываем и о геополитической риск-премии, которая полностью ушла из котировок нефти и газа, но новые санкции против энергетических потоков России могут быстро ее расширить.
КотировкиПо состоянию на закрытие рынков:
Индекс S&P 500 3655 п. (-1%)
Nasdaq 10 802 п. (-0,6%)
Shanghai Composite 3059 п. (+0,3%)
Нефть Brent $84,1 (-2,4%)
ConocoPhillips — $1,4. Дивидендная доходность 1,39%.
Узнайте больше• По кому ударят новые налоги: Berkshire, Amazon и другие компании
• Цены на газ падают. Почти 10% всего за день
• Расписание неторговых дней на российских площадках в октябре
БКС Мир инвестиций
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная от 2 до x — Формула, доказательство, примеры
Производная от 2 до x равна 2 x ln 2.
Мы можем вычислить эту производную, используя различные методы дифференцирования, такие как первый принцип производных и формулу для производной экспоненциальной функции, а также использование натурального логарифма с последующим неявным дифференцированием. Математически мы можем записать формулу для производной от 2 к x как d(2 x )/dx = 2 x ln 2. Формула для производной функции f(x) = a x определяется выражением a x ln a. Используя эту формулу, производная 2 по x определяется как (2 x )’ = 2 x ln 2.
Далее в этой статье мы исследуем производную 2 по x и ее формулы с использованием различных методов оценки производных. Мы также решим различные примеры, связанные с производной от 2 к x и другими функциями для лучшего понимания концепции.
| 1. | Какова производная от 2 до х? |
| 2. | Производная от 2 до х с использованием первого принципа |
3. | Производная от 2 до х с использованием логарифмического дифференцирования |
| 4. | Производная от 2 до х с использованием цепного правила |
| 5. | Часто задаваемые вопросы о производной от 2 до x |
Чему равна производная от 2 к х?
Производная от 2 к x равна 2 x ln 2. Мы можем записать это как d/dx (2 x ) = 2 x ln 2 (или) (2 x )’. = 2 x ln 2. Поскольку «ln» — не что иное, как натуральный логарифм (log с основанием «e»), мы можем записать эту формулу как d/dx (2 x ) = 2 x logₑ 2 . т. е.
2 до x математически записывается как 2 x , и это экспоненциальная функция (но НЕ степенная функция). Потому что его база (2) является константой, а его показатель (x) является переменной. Таким образом, мы используем формулу d/dx(a x ) = a x ln a, чтобы найти производную от 2 к x, но мы не должны использовать правило степени d/dx (x n ) = n x n-1 здесь, поскольку 2 x НЕ является степенной функцией.
Чтобы доказать производную от 2 к x, прямым методом является использование производной экспоненциальной функции a 9Формула 0909 x , которая гласит:
d/dx(a x ) = a x ln a
. x ln 2
Следовательно, формула доказана.
Производная от 2 до x Формула
Как отмечалось выше, формула для производной от 2 до x задается как d(2 x )/dx = 2 x ln 2 (или) (2 x )’ = 2 x ln 2. Существуют различные другие способы доказать формулу производной от 2 к x. Вот несколько из них.
- Использование первого принципа
- Использование логарифмического дифференцирования
- Использование цепного правила
Докажем формулу в каждом из этих случаев.
Производная от 2 до х с использованием первого принципа
Предельное определение производной, также известное как первый принцип, гласит, что производная функции y = f(x) находится с использованием предела:
f'(x) = lim h→ 0 [f(x + h) — f(x)] / h — (1)
Так как f(x) = 2 x , то f(x + h) = 2 x + h .
Подставив в (1) эти значения: m + n = a m · a n . Используя это, мы имеем
f'(x) = lim h→0 [2 x · 2 h — 2 x ] / h
= lim ч→ 0 2 x [ 2 ч — 1] / ч
= lim ч → 0 2 x · limₕ→ ₀ 9 /
[ 2 — ч]= 2 x · lim h→0 [ 2 h — 1] / h
Используя одну из предельных формул, lim h→0 [a h — 1] / h = ln а.
f'(x) = 2 x ln 2
Следовательно, производная от 2 к формуле x доказана.
Производная от 2 до х с использованием логарифмического дифференцирования
Мы используем логарифмическое дифференцирование, чтобы найти производную функции, которая имеет переменную в показателе степени. В этом процессе мы применяем «log» (или) «ln» с обеих сторон, а затем дифференцируем с обеих сторон. Предположим, что дифференцируемая функция равна y = 2 x .
Взяв «ln» с обеих сторон,
ln y = ln 2 x
Используя свойства логарифмов, ln a m = m ln a. Используя это,
ln y = x ln 2
Дифференцируя обе части по x,
d/dx (ln y) = d/dx (x ln 2)
Используя постоянное правило умножения производных,
d/dx (ln y) = ln 2 d/dx (x)
Используя правило производная правила ln x, d/dx (ln x) = 1/x, а также цепное правило в левой части,
(1/y) dy/dx = ln 2 (1)
Умножение обеих частей на y ,
dy/dx = y ln 2
Подставляя здесь y = 2 x , получаем
d/dx (2 x ) = 2 x ln 2
Отсюда мы доказали производную от 2
х будет 2 x ln 2. Вы можете попробовать вывести ту же формулу, применив «логарифм» с обеих сторон.
Производная от 2 до х с использованием цепного правила
Используя одно из свойств натуральных логарифмов, e ln a = a для любого ‘a’.
Таким образом, мы имеем
e ln 2 = 2 (или) 2 = e ln 2
Увеличив показатель степени с обеих сторон на x,
2 x = (e x ln 2)
У нас есть ( м ) н = a мн . Используя это на предыдущем шаге,
2 x = e x ln 2
Дифференцируя обе части по x,
d/dx (2 x ) = d/dx (e x ln 2 )
Мы знаем, что производная от e x равна e x , а также применяя цепное правило справа,
d/dx (2 x ) = e x ln 2 · d/dx (x ln 2)
= e x ln 2 · (ln 2)
= e ln 2 x · (ln 2)
Используя то же свойство e ln a = снова a,
d/dx (2 x 90) x ln 2
Отсюда получается производная от 2 к формуле x.
Важные моменты по производной 2 в степени х:
- Производная 2 в степени х: логₑ 2.
- Обратите внимание, что 2 x — это экспоненциальная функция, но НЕ степенная функция.
- Используйте производную формулы x , но НЕ производную формулы x n , чтобы найти производную от 2 до x.
☛Связанные темы:
- Производные правила
- Производные обратного триггера
- Неявное дифференцирование
Часто задаваемые вопросы о производной от 2 до x
Чему равна производная числа 2 в степени x?
Производная 2 в степени x имеет две формулы:
- d/dx (2 x ) = 2 x ln 2
- d/dx (2 x ) = 2 x logₑ 2
Как найти производную от 2 до x?
Чтобы найти производную от 2 к x , просто примените формулу d/dx (a x ) = a x ln a и подставьте a = 2 в эту формулу. Тогда мы получаем d/dx (2 x ) = 2 x ln 2.
Мы также можем найти производную от 2 к x, используя первый принцип производных, цепное правило и неявное дифференцирование. 9x ln 2. Это следует из формулы d/dx (a x ) = a x ln a.
Что такое n
th Производная от 2 до x?Мы знаем, что d/dx (2 x ) = 2 x ln 2. Давайте продифференцируем его несколько раз, чтобы определить закономерность.
- Производная 1 st от 2 x равна 2 x ln 2.
- Производная 2 и от 2 x равна 2 x (ln 2) 2 .
- Производная 3 rd от 2 x равна 2 x (ln 2) 3 .
- …
- Производная n th от 2 x равна 2 x (ln 2) n .
Что такое производная от 2 до х в терминах Ln?
Производная экспоненциальной функции равна (a x ) ‘ = a x ln a.
Подставляя a = 2 i это, (2 x )’ = 2 x ln 2.
Что такое производная от 2 до x в логарифмическом выражении?
Производная 2 x обычно выражается через «ln» как d/dx (2 x ) = 2 x ln 2. Но мы знаем, что ln = logₑ, и, следовательно, та же самая формула может можно записать как d/dx (2 x ) = 2 x logₑ 2.
Чему равна вторая производная от 2 до x?
Вторая производная от 2 в степени x равна 2 x 92) Есть два метода, которые можно использовать для вычисления производной ln(2x 2 ). Первый метод заключается в использовании цепного правила для производных. Второй метод заключается в использовании свойств журналов для записи ln(2x 2 ) в дифференцируемую форму без необходимости использования цепного правила. Нахождение производной от ln(2x
2 ) с использованием цепного правила выражение, которое также можно было бы дифференцировать, если бы оно стояло само по себе.
В этом случае:
- Мы знаем, как дифференцировать 2x 2 (ответ 4x)
- Мы знаем, как дифференцировать ln(x) (ответ 1/x)
Это означает цепочку Правило позволит нам выполнить дифференцирование функции ln(2x 2 ).
Чтобы выполнить дифференцирование, цепное правило говорит, что мы должны дифференцировать выражение, как если бы оно было выражено только через x, если мы затем умножаем этот результат на производную от того, чем на самом деле выражено выражение (в данном случае производная от 2х92)
ln(2x 2 ) представляет собой стандартную логарифмическую функцию ln(x), за исключением того, что она не имеет x в качестве аргумента, вместо этого она имеет другую функцию от x (2x 2 ).
Назовем функцию в аргументе g(x), что означает:
g(x) = 2x 2
Отсюда следует, что:
ln(2x 2 ) = ln(g( x))
Итак, если функция f(x) = ln(x) и функция g(x) = 2x 2 , то функция ln(2x 2 ) можно записать как составную функцию.
f(x) = ln(x)
f(g(x)) = ln(g(x)) (но g(x) = 2x 2 )
f(g(x)) = ln(2x 2 )
Определим эту составную функцию как F(x):
F(x) = f(g(x)) = ln(2x 2 )
Мы можем найти производную из ln(2x 2 ) (F'(x)) с использованием цепного правила.
Цепное правило:
Для двух дифференцируемых функций f(x) и g(x)
Если F(x) = f(g(x))
Тогда производная F(x) равна F'(x) = f'(g(x)).g'(x)
Теперь мы можем просто подставить f(x) и g(x) в цепное правило. Но прежде чем мы это сделаем, просто вспомним производную натурального логарифма.
Производная ln(x) по x равна (1/x)
Производная ln(s) по s равна (1/s)
Аналогичным образом производная ln(2x 2 ) по отношению к 2x 2 (1/2x 2 ).
Мы будем использовать этот факт как часть цепного правила, чтобы найти производную ln(2x 2 ) относительно x .
Как найти производную от ln(2x 2 ) с помощью цепного правила: Используя цепное правило, мы находим, что производная от ln(2x 2 ) равна 2/x . производная согласно приведенным выше расчетам). Просто имейте в виду, что не все приведенные ниже формы математически правильны. 92 = 2/x Поскольку ln — натуральный логарифм, применяются обычные свойства логарифмов. Свойство произведения бревен утверждает, что ln(xy) = ln(x) + ln(y). Другими словами, получение журнала продукта равно суммированию журналов каждого члена продукта. Поскольку 2x 2 является произведением 2 и x 2 , мы можем использовать свойства журналов, чтобы переписать ln(2x 2 ): f(x) = ln(2x 2 ) = ln(2) + ln(x 2 ) Свойство мощности журналов утверждает, что ln(x y ) = y.ln(x). Другими словами, возведение логарифма х в степень равносильно умножению логарифма х на эту степень. Таким образом, мы можем комбинировать правила произведения и мощности журналов, чтобы перезаписать ln(2x 2 ) как: f(x) = ln(2x 2 ) = ln(2) + ln(x 2 ) = ln(2) + 2.ln(x) Как найти производную от ln(2x 2 ), используя свойство произведения бревен Чтобы вычислить вторую производную функции, нужно просто продифференцировать первую производную. Исходя из вышеприведенного, мы нашли, что первая производная от ln(2x 2 ) = 2/x. Итак, чтобы найти вторую производную от ln(2x 2 ), нам просто нужно продифференцировать 2/x . Если мы продифференцируем 2/x, то получим (-2/x 2 ). ► Вторая производная от ln(2x 2 ) = -2/x 2 Содержание | Главная Производная. Урок 5, Раздел 2: Задачи 90 923 Назад к Разделу 1 Производная f ( x ) = 2 x — 5 Уравнение касательной к кривой Производная от f ( x ) = x 3 Задача 1. Пусть f ( x ) = 2 x − 5, а) Запишите частное разности и упростите его. Чтобы увидеть ответ, наведите указатель мыши на цветную область. б) Оценить f ‘ ( x ) в x = 9 и х = -9. по теореме 4 урока 2. Скорость изменения f ( x ) равна 2 для всех значений х . f ‘ ( x ) является константой. Но это должно быть очевидно. 91 769 y 91 770 = 2 91 769 x 91 770 – 5 – это уравнение прямой линии, у которой 91 769 наклона 91 770 равно 2. (Тема 9 предварительного исчисления.) А значение наклона прямой линии – это скорость изменения 91 769 · 91 770. по отношению к x — столько единиц y на каждую единицу x . Касательной к прямой линии нет, потому что касательная по определению касается кривой только в одной точке. Пример. Уравнение касательной к кривой. а) Рассчитайте наклон линии, касательной к y = x 2 в точке б) Каково уравнение этой прямой? Раствор. а) Наклон касательной к кривой в точке x = 4 представляет собой значение б) Уравнение прямой имеет следующий вид: у = ах + б , , где a — наклон линии. Следовательно, поскольку a = 8, уравнение у = 8 х + б . Чтобы найти значение b , мы можем действовать так же, как в решении 1 задачи 1 из урока 34 алгебры. Поскольку x = 4 в функции y = x 2 , то y = 16.
пара координат (4, 16) решит это уравнение: Уравнение касательной у = 8 х — 16, См. проблему 2f) ниже. Проблема 2 . а) Вычислите производную от f ( x ) = x 3 . Следуйте последовательности a) [Hint: ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + б 3 . Тема 25 предварительного исчисления.] b) Оценить наклон касательной к y = x 3 при x = 4, Наклон при x составляет 3 x 2 . Следовательно, при x = 4 наклон равен 3 · 16 = 48, c) Оцените наклон касательной к y = x 3 при x = −2. 3 · (−2) 2 = 3 · 4 = 12. d) Какова скорость изменения f ( x ) = x 3 при x = −1. 3 · (−1) 2 = 3 · 1 = 3. При x = −1 функция увеличивается со скоростью 3 единицы y на единицу x . e) Какова скорость изменения этой функции при x = 5, 3 · 5 2 = 3 · 25 = 75. При x = 5 функция увеличивается со скоростью 75 единиц по и на единицу x . f) Уравнение касательной к y = x 3 при x = 5, При x = 5 наклон касательной равен 75. Следовательно, уравнение касательной будет у = 75 х + б . Чтобы найти b , действуйте, как в примере выше. Когда x = 5, тогда y = x 3 = 125, так что пара (5, 125) решает это уравнение. 125 = 75 · 5 + b . Следовательно, 91 769 b 91 770 = −250. Уравнение касательной у = 75 х — 250. Задача 3. Докажите: Прямая, касающаяся y = x 2 в точке ( a , a 2 ), делит пополам расстояние a от начала координат. Пусть x будет x точкой пересечения касательной. Затем мы должны доказать, что х = а /2. Вертикальный катет этого прямоугольного треугольника равен a 2 . Горизонтальный отрезок равен a − x . Следовательно, наклон этой линии равен Но наклон этой линии равен 2 a , потому что производная от x 2 равна 2 x . Следовательно, Задача 4. Чтобы увидеть, как было упрощено разностное частное, см. Урок 3 Предварительного исчисления, Задача 11c. б) Какова скорость изменения функции при x = 4? c) Какова скорость изменения функции при x = ¼? скорость 16 единиц и на единицу х . Посмотрите на график. Чем ближе к 0, тем больше скорость изменения. Чем дальше от 0, тем меньше скорость изменения. В каждой точке этого графика касательная имеет отрицательный наклон — производная всегда отрицательна. При движении слева направо значения этой функции всегда уменьшаются. Получаем следующий результат: То есть Форма В дальнейшем мы будем использовать эту форму. Назад к Разделу 1 Следующий урок: правила для производных Содержание | Главная Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн. Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] Нахождение производных функций с помощью определения производной может быть длительным и, для некоторых функций, довольно сложным процессом. Например, ранее мы обнаружили, что ddx(x)=12xddx(x)=12x, используя процесс, который включал умножение выражения на сопряженное перед вычислением предела. Процесс, который мы могли бы использовать для оценки ddx(x3)ddx(x3) с помощью определения, хотя и похож, но более сложен. В этом разделе мы разрабатываем правила нахождения производных, позволяющие обойти этот процесс. Начнем с основ. Функции f(x)=cf(x)=c и g(x)=xng(x)=xn, где nn — натуральное число, являются строительными блоками, из которых строятся все многочлены и рациональные функции. Сначала мы применяем предельное определение производной, чтобы найти производную постоянной функции, f(x)=c.f(x)=c. Для этой функции как f(x)=cf(x)=c, так и f(x+h)=c,f(x+h)=c, поэтому мы получаем следующий результат: f′(x)=limh→0f(x+h)−f(x)h=limh→0c−ch=limh→00h=limh→00=0.f′(x)=limh→0f(x+ h)−f(x)h=limh→0c−ch=limh→00h=limh→00=0. Правило дифференцирования постоянных функций называется постоянным правилом. В нем говорится, что производная постоянной функции равна нулю; то есть, поскольку постоянная функция представляет собой горизонтальную линию, наклон или скорость изменения постоянной функции равен 0,0. Мы повторяем это правило в следующей теореме. Пусть cc — константа. Если f(x)=c,f(x)=c, то f′(x)=0.f′(x)=0. В качестве альтернативы мы можем выразить это правило как ddx(c)=0.ddx(c)=0. Найдите производную f(x)=8.f(x)=8. Это всего лишь одношаговое применение правила: f′(x)=0.f′(x)=0. Найдите производную g(x)=−3.g(x)=−3. Мы показали, что ddx(x2)=2xandddx(x1/2)=12x−1/2.ddx(x2)=2xandddx(x1/2)=12x−1/2. В этот момент вы можете увидеть начало развития шаблона для производных формы ddx(xn).ddx(xn). Мы продолжаем изучение формул производных путем дифференцирования степенных функций вида f(x)=xnf(x)=xn, где nn — натуральное число. Мы разрабатываем формулы для производных этого типа функций поэтапно, начиная с натуральных степеней. Найти ddx(x3).ddx(x3). ddx(x3)=limh→0(x+h)3−x3h=limh→0x3+3x2h+3xh3+h4−x3hОбратите внимание, что первый член в разложении (x+h)3 равен x3, а второй член равен 3x2h. Все остальные члены содержат степени h, которые в два раза больше.=limh→03x2h+3xh3+h4hНа этом шаге x3члены были отменены, остались только члены, содержащие h.=limh→0h(3×2+3xh+h3)hВынесите из общего множителя h.=limh→0( 3×2+3xh+h3) После сокращения общего множителя h единственный член, не содержащий его3×2.=3×2, переходит к 0.ddx(x3)=limh→0(x+h)3−x3h=limh→0x3+3x2h+3xh3+h4− x3hОбратите внимание, что первый член в разложении (x+h)3 равен x3, а второй член равен 3x2h. Найти ddx(x4).ddx(x4). Как мы увидим, процедура нахождения производной общего вида f(x)=xnf(x)=xn очень похожа. Хотя часто неразумно делать общие выводы из конкретных примеров, заметим, что при дифференцировании f(x)=x3,f(x)=x3 степень при xx становится коэффициентом при x2x2 в производной, а степень при xx в производной уменьшается на 1. Следующая теорема утверждает, что правило степени выполняется для всех положительных целых степеней x.x. Со временем мы распространим этот результат на отрицательные целые степени. Позже мы увидим, что это правило также может быть распространено сначала на рациональные степени xx, а затем на произвольные степени x.x. Имейте в виду, однако, что это правило не применяется к функциям, в которых константа возводится в переменную степень, например, f(x)=3x. Пусть nn — целое положительное число. Если f(x)=xn,f(x)=xn, то f′(x)=nxn−1.f′(x)=nxn−1. В качестве альтернативы мы можем выразить это правило как ddxxn=nxn−1.ddxxn=nxn−1. Для f(x)=xnf(x)=xn, где nn — натуральное число, мы имеем f′(x)=limh→0(x+h)n−xnh.f′(x)=limh→0(x+h)n−xnh. Поскольку (x+h)n=xn+nxn−1h+(n2)xn−2h3+(n3)xn−3h4+…+nxhn−1+hn, Поскольку (x+h)n=xn+nxn−1h+(n2) xn−2h3+(n3)xn−3h4+…+nxhn−1+hn, мы видим, что (x+h)n−xn=nxn−1h+(n2)xn−2h3+(n3)xn−3h4+…+nxhn−1+hn.(x+h)n−xn=nxn−1h+(n2)xn− 2h3+(n3)xn−3h4+…+nxhn−1+hn. Затем разделите обе части на ч : (x+h)n−xnh=nxn−1h+(n2)xn−2h3+(n3)xn−3h4+…+nxhn−1+hnh.(x+h)n−xnh=nxn−1h+(n2)xn− 2h3+(n3)xn−3h4+…+nxhn−1+hnh. Таким образом, (x+h)n−xnh=nxn−1+(n2)xn−2h+(n3)xn−3h3+…+nxhn−2+hn−1. Наконец, f′(x)=limh→0(nxn−1+(n2)xn−2h+(n3)xn−3h3+…+nxhn−1+hn)=nxn−1.f′(x)=limh→0( nxn−1+(n2)xn−2h+(n3)xn−3h3+…+nxhn−1+hn)=nxn−1. □ Найдите производную функции f(x)=x10f(x)=x10, применяя степенное правило. Используя правило степени с n=10,n=10, получаем f′(x)=10×10−1=10×9.f′(x)=10×10−1=10×9. Найдите производную f(x)=x7.f(x)=x7. Мы находим наши следующие правила дифференцирования, рассматривая производные сумм, разностей и постоянных кратных функций. Так же, как и при работе с функциями, существуют правила, облегчающие нахождение производных функций, которые мы складываем, вычитаем или умножаем на константу. Пусть f(x)f(x) и g(x)g(x) — дифференцируемые функции, kk — константа. Тогда выполняется каждое из следующих уравнений. Правило суммы. Производная суммы функции ff и функции gg равна сумме производной функции ff и производной g.g. ddx(f(x)+g(x))=ddx(f(x))+ddx(g(x));ddx(f(x)+g(x))=ddx(f(x) )+ddx(g(x)); то есть для j(x)=f(x)+g(x),j′(x)=f′(x)+g′(x).forj(x)=f(x)+g(x),j ′(х)=f′(х)+g′(х). Правило разности. Производная разности функции f и функции g такая же, как разность производной f и производной g:g: ddx(f(x)−g(x ))=ddx(f(x))−ddx(g(x));ddx(f(x)−g(x))=ddx(f(x))−ddx(g(x)); , то есть для j(x)=f(x)−g(x),j′(x)=f′(x)−g′(x).forj(x)=f(x)− g(x),j′(x)=f′(x)−g′(x). Постоянное множественное правило. ddx(kf(x))=kddx(f(x));ddx(kf(x))=kddx(f (Икс)); , то есть forj(x)=kf(x),j′(x)=kf′(x).forj(x)=kf(x),j′(x)=kf′(x) . Здесь мы приводим только доказательство правила сумм. Остальные следуют аналогичным образом. Для дифференцируемых функций f(x)f(x) и g(x),g(x) положим j(x)=f(x)+g(x).j(x)=f(x)+ г(х). Используя предельное определение производной, имеем j′(x)=limh→0j(x+h)−j(x)h.j′(x)=limh→0j(x+h)−j(x)h. Путем замены j(x+h)=f(x+h)+g(x+h)j(x+h)=f(x+h)+g(x+h) и j(x)=f (x)+g(x),j(x)=f(x)+g(x), получаем j′(x)=limh→0(f(x+h)+g(x+h))−(f(x)+g(x))h.j′(x)=limh→0(f(x +h)+g(x+h))−(f(x)+g(x))h. Переставляя и перегруппировывая термины, мы имеем j′(x)=limh→0(f(x+h)−f(x)h+g(x+h)−g(x)h).j′(x)=limh→0(f( х+h)−f(x)h+g(x+h)−g(x)h). Теперь мы применяем закон сумм для пределов и определение производной, чтобы получить j′(x)=limh→0(f(x+h)−f(x)h)+limh→0(g(x+h)−g(x)h)=f′(x)+g ′(x).j′(x)=limh→0(f(x+h)−f(x)h)+limh→0(g(x+h)−g(x)h)=f′( х)+g'(х). □ Найдите производную g(x)=3x2g(x)=3×2 и сравните ее с производной f(x)=x2.f(x)=x2. Мы используем правило степени напрямую: (2x)=6x. Так как f(x)=x2f(x)=x2 имеет производную f′(x)=2x,f′(x)=2x, мы видим, что производная g(x)g(x) в 3 раза больше производная f(x).f(x). Эта взаимосвязь показана на рис. 3.18. Рисунок
3.18
Производная g(x)g(x) в 3 раза больше производной f(x).f(x). Найдите производную f(x)=2×5+7.f(x)=2×5+7. Начнем с применения правила дифференцирования суммы двух функций, за которым следуют правила дифференцирования постоянных кратных функций и правило дифференцирования степеней. f′(x)=ddx(2×5+7)=ddx(2×5)+ddx(7)Применить правило сумм.=2ddx(x5)+ddx(7)Применить постоянное кратное правило.=2(5×4) +0Применить правило степени и правило констант.=10×4.Simplify.f′(x)=ddx(2×5+7)=ddx(2×5)+ddx(7)Применить правило суммы.=2ddx(x5)+ddx( 7) Применить постоянное кратное правило. = 2 (5×4) + 0 Применить правило степени и постоянное правило. = 10×4. Упростить. Найдите производную f(x)=2×3−6×2+3.f(x)=2×3−6×2+3. Найдите уравнение касательной прямой к графику f(x)=x2−4x+6f(x)=x2−4x+6 при x=1.x=1. Чтобы найти уравнение касательной, нам нужны точка и наклон. Чтобы найти точку, вычислите f(1)=12−4(1)+6=3. Это дает нам точку (1,3).(1,3). Поскольку наклон касательной в точке 1 равен f′(1),f′(1), мы должны сначала найти f′(x).f′(x). Используя определение производной, имеем f′(x)=2x−4f′(x)=2x−4 , поэтому наклон касательной равен f′(1)=−2.f′(1)=−2. Используя формулу точки-наклона, мы видим, что уравнение касательной линии имеет вид y−3=−2(x−1).y−3=−2(x−1). Преобразуя уравнение прямой в виде точки пересечения, получаем y=−2x+5.y=−2x+5. Найдите уравнение касательной к графику f(x)=3×2−11f(x)=3×2−11 при x=2.x=2. Используйте форму точка-наклон. Теперь, когда мы изучили основные правила, мы можем приступить к изучению некоторых более сложных правил. Первый исследует производную произведения двух функций. Хотя может показаться заманчивым предположить, что производная произведения является произведением производных, аналогично правилам суммы и разности, правило произведения не следует этому образцу. Пусть f(x)f(x) и g(x)g(x) — дифференцируемые функции. Тогда ddx(f(x)g(x))=ddx(f(x))·g(x)+ddx(g(x))·f(x).ddx(f(x)g(x ))=ddx(f(x))·g(x)+ddx(g(x))·f(x). То есть, , если j(x)=f(x)g(x), то j′(x)=f′(x)g(x)+g′(x)f(x).ifj(x )=f(x)g(x), тогда j′(x)=f′(x)g(x)+g′(x)f(x). Это означает, что производная произведения двух функций равна произведению первой функции на вторую плюс производная второй функции на первую функцию. Начнем с предположения, что f(x)f(x) и g(x)g(x) — дифференцируемые функции. В ключевом моменте этого доказательства нам нужно использовать тот факт, что, поскольку g(x)g(x) дифференцируема, она также непрерывна. В частности, мы используем тот факт, что, поскольку g(x)g(x) непрерывна, limh→0g(x+h)=g(x). Применяя предельное определение производной к j(x)=f(x)g(x),j(x)=f(x)g(x), мы получаем j′(x)=limh→0f(x+h)g(x+h)−f(x)g(x)h.j′(x)=limh→0f(x+h)g(x+h) −f(x)g(x)h. Добавляя и вычитая f(x)g(x+h)f(x)g(x+h) в числителе, мы получаем j′(x)=limh→0f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g( x)h.j′(x)=limh→0f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g (х)ч. После разделения этого частного и применения закона сумм для пределов производная становится равной j′(x)=limh→0(f(x+h)g(x+h)−f(x)g(x+h)h)+limh→0(f(x)g(x+h) )−f(x)g(x)h).j′(x)=limh→0(f(x+h)g(x+h)−f(x)g(x+h)h)+limh →0(f(x)g(x+h)−f(x)g(x)h). Переставляя, получаем j′(x)=limh→0(f(x+h)−f(x)h·g(x+h))+limh→0(g(x+h)−g(x)h·f (x)).j′(x)=limh→0(f(x+h)−f(x)h·g(x+h))+limh→0(g(x+h)−g(x )h·f(x)). Используя непрерывность g(x),g(x), определение производных от f(x)f(x) и g(x),g(x) и применяя предельные законы, мы приходим к правило продукта, j′(x)=f′(x)g(x)+g′(x)f(x). □ Для j(x)=f(x)g(x),j(x)=f(x)g(x) используйте правило произведения, чтобы найти j′(2)j′(2), если f(2 )=3,f′(2)=−4,g(2)=1,f(2)=3,f′(2)=−4,g(2)=1 и g′(2)= 6.g'(2)=6. Поскольку j(x)=f(x)g(x),j′(x)=f′(x)g(x)+g′(x)f(x),j(x)=f(x )g(x),j′(x)=f′(x)g(x)+g′(x)f(x), и, следовательно, j′(2)=f′(2)g(2 )+g′(2)f(2)=(−4)(1)+(6)(3)=14.j′(2)=f′(2)g(2)+g′(2) f(2)=(−4)(1)+(6)(3)=14. Для j(x)=(x2+2)(3×3−5x),j(x)=(x2+2)(3×3−5x) найти j′(x)j ′(x), применяя правило произведения. Проверьте результат, сначала найдя произведение, а затем дифференцируя его. Если мы установим f(x)=x2+2f(x)=x2+2 и g(x)=3×3−5x,g(x)=3×3−5x, то f′(x)=2xf′(x) =2x и g′(x)=9×2−5. j′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3×3−5x)+(9×2−5)(x2+2). j′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3×3−5x)+(9×2−5)(x2+2). Упрощая, имеем j′(x)=15×4+3×2−10.j′(x)=15×4+3×2−10. Для проверки видим, что j(x)=3×5+x3−10xj(x)=3×5+x3−10x и, следовательно, j′(x)=15×4+3×2−10.j′(x)=15×4 +3×2−10. Используйте правило произведения для получения производной от j(x)=2×5(4×2+x).j(x)=2×5(4×2+x). Разработав и применив правило произведения, мы теперь рассмотрим дифференцирование частных функций. Как мы видим из следующей теоремы, производная частного не есть частное производных; скорее, это производная функции в числителе, умноженная на функцию в знаменателе, минус производная функции в знаменателе, умноженная на функцию в числителе, и все это делится на квадрат функции в знаменателе. Чтобы лучше понять, почему мы не можем просто взять частное производных, имейте в виду, что ddx(x2)=2x,notddx(x3)ddx(x)=3×21=3×2. Пусть f(x)f(x) и g(x)g(x) — дифференцируемые функции. Тогда ddx(f(x)g(x))=ddx(f(x))·g(x)−ddx(g(x))·f(x)(g(x))2.ddx( f(x)g(x))=ddx(f(x))·g(x)−ddx(g(x))·f(x)(g(x))2. То есть, , если j(x)=f(x)g(x), то j′(x)=f′(x)g(x)−g′(x)f(x)(g(x ))2.если j(x)=f(x)g(x), то j′(x)=f′(x)g(x)−g′(x)f(x)(g(x))2 . Доказательство правила отношения очень похоже на доказательство правила произведения, поэтому здесь оно опущено. Вместо этого мы применяем это новое правило для нахождения производных в следующем примере. Используйте правило отношения, чтобы найти производную k(x)=5x24x+3.k(x)=5x24x+3. Пусть f(x)=5x2f(x)=5×2 и g(x)=4x+3.g(x)=4x+3. Таким образом, f′(x)=10xf′(x)=10x и g′(x)=4.g′(x)=4. k′(x)=f′(x)g(x)−g′(x)f(x)(g(x))2=10x(4x+3)−4(5×2)(4x+3 )2.k′(x)=f′(x)g(x)−g′(x)f(x)(g(x))2=10x(4x+3)−4(5×2)(4x+ 3)2. Упрощая, получаем k′(x)=20×2+30x(4x+3)2.k′(x)=20×2+30x(4x+3)2. Найдите производную h(x)=3x+14x−3.h(x)=3x+14x−3. Теперь можно использовать правило отношения для расширения правила степени для нахождения производных функций вида xkxk, где kk — отрицательное целое число. Если kk — отрицательное целое число, то ddx(xk)=kxk−1.ddx(xk)=kxk−1. Если kk — отрицательное целое число, мы можем установить n=−k,n=−k, так что n будет положительным целым числом с k=−n.k=−n. Поскольку для каждого положительного целого числа n,x−n=1xn,n,x−n=1xn, теперь мы можем применить правило отношения, установив f(x)=1f(x)=1 и g(x)=xn. ddx(x−n)=0(xn)−1(nxn−1)(xn)2.ddx(x−n)=0(xn)−1(nxn−1)(xn)2. Упрощая, мы видим, что ddx(x−n)=−nxn−1x2n=−nx(n−1)−2n=−nx−n−1.ddx(x−n)=−nxn−1x2n=−nx(n−1)− 2n=-nx-n-1. Наконец, обратите внимание, что, поскольку k=−n,k=−n, подстановкой мы имеем ddx(xk)=kxk−1.ddx(xk)=kxk−1. □ Найдите ddx(x−4).ddx(x−4). Применяя правило расширенной степени с k=−4,k=−4, мы получаем ddx(x−4)=−4x−4−1=−4x−5.ddx(x−4)=−4x−4−1=−4x−5. Используйте расширенное степенное правило и постоянное кратное правило, чтобы найти производную от f(x)=6×2.f(x)=6×2. Может показаться заманчивым использовать правило отношения для нахождения этой производной, и это, конечно, не будет неправильным. f′(x)=ddx(6×2)=ddx(6x−2)Переписать6x2as6x−2.=6ddx(x−2)Применить постоянное кратное правило.=6(−2x−3)Использовать расширенное правило мощности для дифференцироватьx-2.=-12x-3Упростить.f'(x)=ddx(6×2)=ddx(6x-2)Переписать6×2как6x-2.=6ddx(x-2)Применить постоянное кратное правило.=6(-2x- 3) Используйте расширенное правило мощности, чтобы дифференцировать x-2.=-12x-3Упростить. Найдите производную g(x)=1x7g(x)=1×7, используя правило расширенной степени. Как мы видели из примеров в этом разделе, редко случается, что нам приходится применять только одно правило дифференцирования, чтобы найти производную данной функции. На этом этапе, комбинируя правила дифференцирования, мы можем найти производные любой полиномиальной или рациональной функции. Позже мы встретимся с более сложными комбинациями правил дифференцирования. Для k(x)=3h(x)+x2g(x),k(x)=3h(x)+x2g(x) найти k′(x).k′(x) . Для нахождения этой производной требуется правило сумм, правило постоянного кратного и правило произведения. k′(x)=ddx(3h(x)+x2g(x))=ddx(3h(x))+ddx(x2g(x)) Применить правило сумм.=3ddx(h(x))+ (ddx(x2)g(x)+ddx(g(x))x2) Применить правило множителя констант к дифференцированию3h(x) и правило произведения к дифференцированиюx2g(x).=3h′(x)+2xg(x)+g ′(x)x2k′(x)=ddx(3h(x)+x2g(x))=ddx(3h(x))+ddx(x2g(x)) Применить правило сумм.=3ddx(h(x) )+(ddx(x2)g(x)+ddx(g(x))x2) Применить правило множителя констант для дифференцирования3h(x) и правило произведения для дифференцированияx2g(x). Для k(x)=f(x)g(x)h(x),k(x)=f(x)g(x)h(x) выразить k′(x )k′(x) через f(x),g(x),h(x),f(x),g(x),h(x) и их производные. Мы можем думать о функции k(x)k(x) как о произведении функции f(x)g(x)f(x)g(x) и функции h(x).h(x). То есть k(x)=(f(x)g(x))·h(x).k(x)=(f(x)g(x))·h(x). Таким образом, k′(x)=ddx(f(x)g(x))·h(x)+ddx(h(x))·(f(x)g(x)) Примените правило произведения к произведение off(x)g(x)andh(x).=(f′(x)g(x)+g′(x)f(x))h(x)+h′(x)f(x) g(x)Применить правило произведения tof(x)g(x).=f′(x)g(x)h(x)+f(x)g′(x)h(x)+f(x) g(x)h′(x).Simplify.k′(x)=ddx(f(x)g(x))·h(x)+ddx(h(x))·(f(x)g( x)) Примените правило произведения к произведению off(x)g(x)andh(x).=(f′(x)g(x)+g′(x)f(x))h(x)+h ′(x)f(x)g(x)Применить правило произведения tof(x)g(x).=f′(x)g(x)h(x)+f(x)g′(x)h (x)+f(x)g(x)h′(x). Упростить. Для h(x)=2x3k(x)3x+2,h(x)=2x3k(x)3x+2 найти ). Эта процедура типична для нахождения производной рациональной функции. h′(x)=ddx(2x3k(x))·(3x+2)−ddx(3x+2)·(2x3k(x))(3x+2)2Применить правило частных.=(6x2k(x )+k′(x)·2×3)(3x+2)−3(2x3k(x))(3x+2)2Применить правило произведения, чтобы найтиddx(2x3k(x)).Useddx(3x+2)=3. =−6x3k(x)+18x3k(x)+12x2k(x)+6x4k′(x)+4x3k′(x)(3x+2)2Simplify.h′(x)=ddx(2x3k(x))·( 3x+2)−ddx(3x+2)·(2x3k(x))(3x+2)2Применить правило частных.=(6x2k(x)+k′(x)·2×3)(3x+2)−3 (2x3k(x))(3x+2)2Применить правило произведения к findddx(2x3k(x)).Useddx(3x+2)=3.=−6x3k(x)+18x3k(x)+12x2k(x)+ 6x4k′(x)+4x3k′(x)(3x+2)2Упростить. Найти ddx(3f(x)−2g(x)).ddx(3f(x)−2g(x)). Определите значения xx, для которых f(x)=x3−7×2+8x+1f(x)=x3−7×2+8x+1 имеет горизонтальную касательную. Чтобы найти значения xx, для которых f(x)f(x) имеет горизонтальную касательную, мы должны решить f′(x)=0.f′(x)=0. Поскольку f′(x)=3×2−14x+8=(3x−2)(x−4),f′(x)=3×2−14x+8=(3x−2)(x−4), мы должны решить (3x−2)(x−4)=0.(3x−2)(x−4)=0. Таким образом, мы видим, что функция имеет горизонтальные касательные в точках x=23x=23 и x=4x=4, как показано на следующем графике. Рисунок
3.19
Эта функция имеет горизонтальные касательные на x = 2/3 и x = 4. Положение объекта на оси координат в момент времени tt определяется как s(t)=tt2+1.s(t)=tt2+1. Какова начальная скорость тела? Поскольку начальная скорость v(0)=s′(0),v(0)=s′(0), начнем с нахождения s′(t)s′(t), применяя правило частных: с ′(t)=1(t2+1)−2t(t)(t2+1)2=1−t2(t2+1)2. После вычисления мы видим, что v(0)=1.v(0)=1. Найдите значения xx, для которых график f(x)=4×2−3x+2f(x)=4×2−3x+2 имеет касательную, параллельную прямой y=2x+3.y=2x+3 . Автомобильные гонки Формулы-1 могут быть очень увлекательными и привлекать множество зрителей. Дизайнеры трасс Формулы-1 должны обеспечить достаточное пространство на трибунах вокруг трассы для размещения этих зрителей. Однако автомобильные гонки могут быть опасными, и соображения безопасности имеют первостепенное значение. Трибуны должны располагаться так, чтобы зрители не подвергались опасности в случае потери водителем управления автомобилем (рис. 3.20). Рисунок
3.20
Трибуна рядом с прямой трассой Circuit de Barcelona-Catalunya, расположенная там, где зрителям ничего не угрожает. ********** Безопасность особенно важна на поворотах. Если водитель недостаточно замедлится перед входом в поворот, автомобиль может соскользнуть с гоночной трассы. Обычно это просто приводит к более широкому повороту, который замедляет водителя. Но если водитель полностью потеряет управление, машина может полностью вылететь с трассы по касательной к кривой гоночной трассы. Предположим, вы проектируете новую трассу Формулы-1. Один участок пути можно смоделировать функцией f(x)=x3+3×2+xf(x)=x3+3×2+x (рис. 3.21). Текущий план предусматривает строительство трибун вдоль первой прямой и вокруг части первого поворота. Планируется, что передний угол трибуны будет располагаться в точке (−1,9,2.8).(−1.9,2.8). Мы хотим определить, представляет ли эта локация опасность для зрителей, если водитель потеряет контроль над автомобилем. Рисунок
3.21
(a) Один участок беговой дорожки можно смоделировать функцией f(x)=x3+3×2+x. Для следующих упражнений найдите f′(x)f′(x) для каждой функции. 106. f(x)=x7+10f(x)=x7+10 107. f(x)=5×3−x+1f(x)=5×3−x+1 108. f(x)=4×2−7xf(x)=4×2−7x 109. f(x)=8×4+9×2−1f(x)=8×4+9×2−1 110. f(x)=x4+2xf(x)=x4+2x 111. f(x)=3x(18×4+13x+1)f(x)=3x(18×4+13x+1) 112. f(x)=(x+2)(2×2−3)f(x)=(x+2)(2×2−3) 113. f(x)=x2(2×2+5×3)f(x)=x2(2×2+5×3) 114. f(x)=x3+2×2−43f(x)=x3+2×2−43 115. f(x)=4×3−2x+1x2f(x)=4×3−2x+1×2 116. f(x)=x2+4×2−4f(x)=x2+4×2−4 117. f(x)=x+9×2−7x+1f(x)=x+9×2−7x+1 Для следующих упражнений найдите уравнение касательной T(x)T(x) к графику заданной функции в указанной точке. Используйте графический калькулятор, чтобы построить график функции и касательной. 118. [T] y=3×2+4x+1y=3×2+4x+1 в (0,1)(0,1) 119. [T] y=2×2+1y=2×2+1 в (1,3)(1,3) 120. [T] y=2xx−1y=2xx−1 в точке (−1,1)(−1,1) 121. [T] y=2x−3x2y=2x−3×2 в точке (1,−1)(1,−1) Для следующих упражнений предположим, что функции f(x)f(x) и g(x)g(x) являются дифференцируемыми функциями для всех x.x. Найдите производную каждой из функций h(x).h(x). 122. h(x)=4f(x)+g(x)7h(x)=4f(x)+g(x)7 123. ч(х)=x3f(х)ч(х)=x3f(х) 124. h(x)=f(x)g(x)2h(x)=f(x)g(x)2 125. h(x)=3f(x)g(x)+2h(x)=3f(x)g(x)+2 Для следующих упражнений предположим, что f(x)f(x) и g(x)g(x) являются дифференцируемыми функциями со значениями, указанными в следующей таблице. Используйте следующую таблицу для расчета следующих производных. Определение цепного правила = f'(g(x)).(4x) g(x) = 2x 2 ⇒ g'(x) = 4x = (1/2x 2 ).4x f(g(x)) = ln(2x 2 ) ⇒ 9) = (f’ 9) /2x 2
(The derivative of ln(2x 2 ) with respect to 2x 2 is (1/2x 2 )) = 2/x LN 2x 2 ► Производное LN 2x 2 = 2/x LN 2 X квадрат ► Производное LN 2 X квадрат = 2/x Нахождение производной от ln(2x
2 ) с использованием свойств логарифма
f(x) = ln(2) + 2ln(x) f’9000 = 0 + ln(x) ln2 — константа, производная от константы равна 01569 = 2/x Вторая производная ln(2x
2 )
Производная от y = x³. Производная y = 1/x
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам! f ( x + ч ) − f ( x )
9 000 ч = 2( x + h ) − 5 − (2 x − 5)
h = 2 х + 2 ч − 5 − 2 x + 5
ч = 2 ч
ч = 2. f ( x ) = 2 = 2, 
а) на кривой, где x = 4,
а) производная от x = 4.
Производная от y = x 2 равна 2 x . Следовательно, при 91 505 а) 91 769 x 91 770 = 4 наклон касательной равен 8. 16 = 8 · 4 + б = 32 + б . Поэтому б = −16. 
а) Задача 1. f ( x + ч ) − f ( x )
9 000 ч = ( x + ч ) 3 − x 3
ч = x 3 + 3 x 2 h + 3 x h 2 + h 3 − x 3
h = 3 x 2 ч + 3 x ч 2 + ч 3
ч = 3 x 2 + 3 x ч + ч 2 . 
f ‘ ( x ) = (3 х 2 + 3 x ч + ч 2 ) = 3 x 2 . 
a 2
a − x . a 2
a − x = 2 и a 2 = 2 и ( и − x ) и = 2( а — х ) = 2 а — 2 х 2 x = 2 а − а = а x = а
2
а) Показать: д
дх 1
х = − 1
x 2 . д
дх 1
х = = В x = 4, — 1
x 2 = − 1
16 . Функция убывает со скоростью из 1
16 единицы размера и единицы размера x . 
В x = ¼, — 1
x 2 = -16. Функция убывает на д
дх 1
х = − 1
x 2 . д
дх x −1 = − x −2 . 
д
дх x n = n x n −1
=Даже 1 доллар поможет. 3.3 Правила дифференциации. Исчисление, том 1
Цели обучения
Основные правила
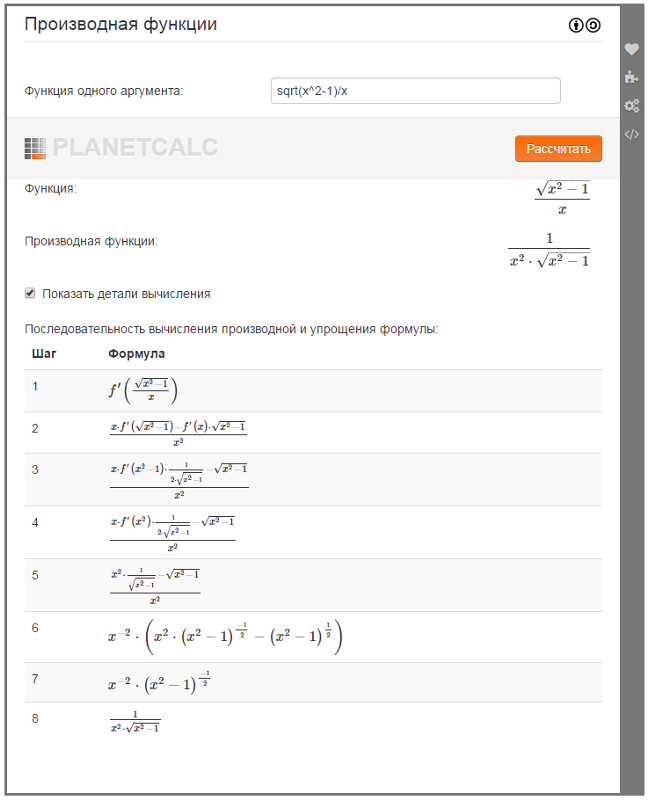Чтобы эффективно находить производные полиномов и рациональных функций, не прибегая к предельному определению производной, мы должны сначала разработать формулы для дифференцирования этих основных функций. Постоянное правило
Теорема
3.2
Постоянное правило
Пример
3.17
Применение постоянного правила
Решение
Контрольно-пропускной пункт
3.11
Правило силы
Прежде чем сформулировать и доказать общее правило для производных функций этого вида, рассмотрим частный случай ddx(x3).ddx(x3). Когда мы пройдем этот вывод, обратите внимание, что техника, используемая в этом случае, по существу такая же, как и техника, используемая для доказательства общего случая. Пример
3.18
Дифференцирование x3x3
Решение
Все остальные члены содержат степени h, которые в два раза больше.=limh→03x2h+3xh3+h4h limh→0h(3×2+3xh+h3)hВынесите за скобки общий множитель h.=limh→0(3×2+3xh+h3)0923 Контрольно-пропускной пункт
3.12
f(x)=3x. Теорема
3.3
Правило силы
Доказательство
(x+h)n−xnh=nxn−1+( n2)xn−2h+(n3)xn−3h3+…+nxhn−2+hn−1. Пример
3.19
Применение степенного правила
Решение
Контрольно-пропускной пункт
3.13
Сумма, разность и постоянные множественные правила
Эти правила резюмируются в следующей теореме. Теорема
3.4
Сумма, разность и постоянные множественные правила
Производная константы k , умноженное на функцию f , равно константе, умноженной на производную: Доказательство
Пример
3.20
Применение правила постоянного множителя
Решение
Пример
3.21
Применение основных правил производных
Решение
Чтобы лучше понять последовательность, в которой применяются правила дифференцирования, мы используем обозначения Лейбница во всем решении: Контрольно-пропускной пункт
3.14
Пример
3,22
Нахождение уравнения касательной прямой
Решение
f(1)=12−4(1)+6=3. Контрольно-пропускной пункт
3.15
Правило продукта
Чтобы понять, почему мы не можем использовать этот шаблон, рассмотрим функцию f(x)=x2,f(x)=x2, производная которой равна f′(x)=2xf′(x)=2x, а не ddx(x) · ddx (х)=1·1=1.ddx(x)·ddx(x)=1·1=1. Теорема
3,5
Правило продукта
Доказательство
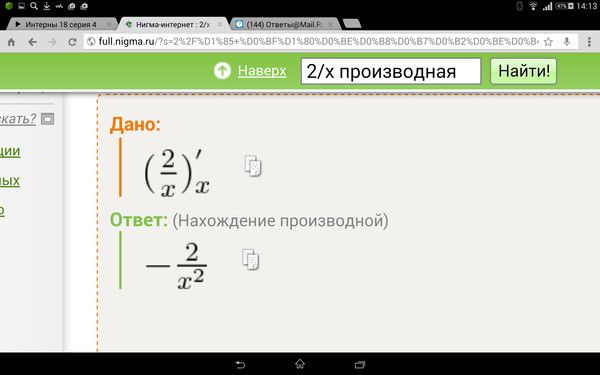limh→0g(x+h)=g(x).
j′(x)=f′(x)g(x)+g′(x)f( Икс). Пример
3,23
Применение правила произведения к функциям в точке
Решение
Пример
3,24
Применение правила произведения к биномам
Решение
g′(x)=9×2−5. Таким образом, Контрольно-пропускной пункт
3.16
Частное правило
ddx(x2)=2x,notddx(x3)ddx(x)=3×21=3×2. Теорема
3,6
Частное правило
Пример
3,25
Применение правила отношения
Решение
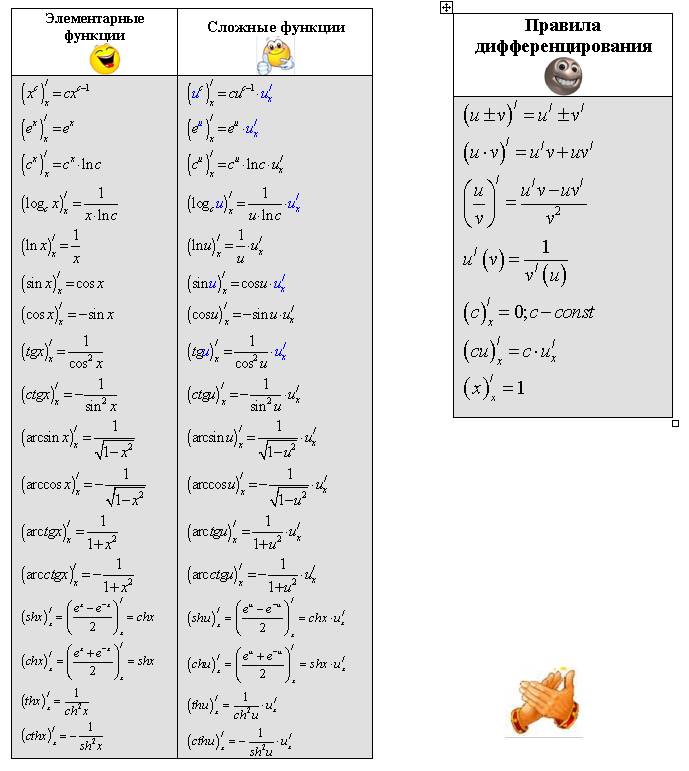Подставляя в частное правило, мы имеем Контрольно-пропускной пункт
3.17
Теорема
3,7
Расширенное правило мощности
Доказательство
g (х)=хп. В этом случае f′(x)=0f′(x)=0 и g′(x)=nxn−1.g′(x)=nxn−1. Таким образом, Пример
3,26
Использование расширенного правила мощности
Решение
Пример
3,27
Использование расширенного степенного правила и постоянного кратного правила
Решение
Однако гораздо проще дифференцировать эту функцию, сначала переписав ее как f(x)=6x−2.f(x)=6x−2. Контрольно-пропускной пункт
3.18
Объединение правил дифференциации
Хорошее эмпирическое правило, которое можно использовать при применении нескольких правил, состоит в том, чтобы применять правила в порядке, обратном порядку, в котором мы оцениваем функцию. Пример
3,28
Объединение правил дифференцирования
Решение
=3h′(x)+2xg(x) +g′(x)x2 Пример
3,29
Расширение правила произведения
Решение
Пример
3.
30 Комбинация правила частного и правила произведения
Решение
Контрольно-пропускной пункт
3.19
Пример
3.31
Определение, где функция имеет горизонтальную касательную
Решение
Пример
3,32
Определение скорости
Решение
s′(t)=1(t2+1)−2t(t) (t2+1)2=1−t2(t2+1)2. Контрольно-пропускной пункт
3.20
Студенческий проект
Трибуны Формулы-1
f(x)=x3+3×2+x. (b) Передний угол трибуны расположен в точках (−1.9, 2.8).(−1.9, 2.8). Раздел 3.
3 Упражнения хх 11 22 33 44 ф(х)ф(х) 33 55 −2−2 00 г(х)г(х) 22 33 −4−4 66 f'(x)f'(x) −1−1 77 88 −3−3 г'(х)г'(х) 44 11 22 99
126.
Найдите h′(1)h′(1), если h(x)=xf(x)+4g(x).h(x)=xf(x)+4g(x).
127.
Найдите h′(2)h′(2), если h(x)=f(x)g(x).h(x)=f(x)g(x).
128.
Найдите h′(3)h′(3), если h(x)=2x+f(x)g(x).h(x)=2x+f(x)g(x).
129.
Найдите h′(4)h′(4), если h(x)=1x+g(x)f(x).h(x)=1x+g(x)f(x).
В следующих упражнениях используйте следующий рисунок, чтобы найти указанные производные, если они существуют.
130.
Пусть h(x)=f(x)+g(x).h(x)=f(x)+g(x). Найти
- ч'(1),ч'(1),
- ч'(3),ч'(3) и
- ч'(4).ч'(4).
131.
Пусть h(x)=f(x)g(x).h(x)=f(x)g(x). Найти
- ч'(1),ч'(1),
- ч'(3),ч'(3) и
- ч'(4).ч'(4).
132.
Пусть h(x)=f(x)g(x). h(x)=f(x)g(x). Найти
- ч'(1),ч'(1),
- ч'(3),ч'(3) и
- ч'(4).ч'(4).
Для следующих упражнений
- оценивают f'(a),f'(a) и
- начертите график функции f(x)f(x) и касательной в точке x=a.x=a.
133.
[Т] f(x)=2×3+3x−x2,a=2f(x)=2×3+3x−x2,a=2
134.
[Т] f(x)=1x−x2,a=1f(x)=1x−x2,a=1
135.
[Т] f(x)=x2−x12+3x+2,a=0f(x)=x2−x12+3x+2,a=0
136.
[Т] f(x)=1x−x2,a=−1f(x)=1x−x2,a=−1
137.
Найдите уравнение касательной к графику f(x)=2×3+4×2−5x−3f(x)=2×3+4×2−5x−3 в точке x=−1.x=−1.
138.
Найдите уравнение касательной к графику f(x)=x2+4x−10f(x)=x2+4x−10 при x=8. x=8.
139.
Найдите уравнение касательной к графику f(x)=(3x−x2)(3−x−x2)f(x)=(3x−x2)(3−x−x2) при x= 1.х=1.
140.
Найдите точку на графике f(x)=x3f(x)=x3 такую, что касательная в этой точке имеет точку пересечения xx, равную 6.
141.
Найдите уравнение прямой, проходящей через точку P(3,3)P(3,3) и касательной к графику f(x)=6x−1.f(x)=6x−1.
142.
Определите все точки на графике f(x)=x3+x2−x−1f(x)=x3+x2−x−1, для которых
- касательная горизонтальна
- касательная имеет наклон −1,−1.
143.
Найдите квадратичный многочлен такой, что f(1)=5,f′(1)=3f(1)=5,f′(1)=3 и f″(1)=−6.f″(1) =-6.
144.
Автомобиль, движущийся по автостраде с движением, проехал s(t)=t3−6t2+9ts(t)=t3−6t2+9t метров за tt секунд.
- Определить время в секундах, когда скорость автомобиля равна 0.
- Определите ускорение автомобиля, когда скорость равна 0.
145.
[T] Сельдь, плывущая по прямой, прошла s(t)=t2t2+2s(t)=t2t2+2 фута за tt секунд.
Определите скорость селедки, когда она пролетела 3 секунды.
146.
Популяция в миллионах полярных камбал в Атлантическом океане моделируется функцией P(t)=8t+30,2t2+1, P(t)=8t+30,2t2+1, где tt измеряется в годах.
- Определите начальную популяцию камбал.
- Определите P'(10)P'(10) и кратко интерпретируйте результат.
147.
[T] Концентрация антибиотика в кровотоке tt часов после введения определяется функцией C(t)=2t2+tt3+50,C(t)=2t2+tt3+50, где измеряется КК в миллиграммах на литр крови.
- Найдите скорость изменения C(t). C(t).
- Определите скорость изменения для t=8,12,24,t=8,12,24 и 36,36.
- Кратко опишите, что происходит по мере увеличения количества часов.
148.
Книгоиздатель имеет функцию затрат, заданную формулой C(x)=x3+2x+3×2, C(x)=x3+2x+3×2, где x — количество экземпляров книги в тысячах, а C — стоимость книги в долларах. Оцените C′(2)C′(2) и объясните его значение.
149.
[T] Согласно закону всемирного тяготения Ньютона сила FF между двумя телами постоянной массы m1m1 и m2m2 определяется формулой F=Gm1m2d2,F=Gm1m2d2, где GG — гравитационная постоянная, а dd — расстояние между телами.
- Предположим, что G, m1 и m2 G, m1 и m2 являются константами. Найти скорость изменения силы FF на расстоянии d.d.
- Найдите скорость изменения силы FF с гравитационной постоянной G=6,67×10−11G=6,67×10−11 Нм2/кг2, Нм2/кг2 на двух телах, находящихся на расстоянии 10 м друг от друга и массе 1000 кг каждое.
Как написать и использовать производный символ в LaTeX
латекс11 часов назад
от Prateek Jangid
Существует фундаментальный подход к исчислению, известный как производные. Вычисление производной функции вещественной переменной включает измерение того, насколько чувствительно изменение входного значения (аргумента) к изменению выходного значения (значения функции).
При вычислении любого математического числа или вопроса о производных необходимо писать символ производной. Вот почему обработчики документов, такие как LaTeX, предоставляют простые исходные коды для написания производных символов. Итак, в этом уроке мы дадим вам краткую информацию о том, как написать и использовать производный символ в LateX.
Как написать и использовать производный символ в LaTeX?
Вы можете отображать производные по-разному в LaTeX, поэтому давайте начнем с простого исходного кода для написания производного символа: 92} $$
\end{document}
Вывод
Вы можете легко использовать производный символ с физикой
\usepackage{физика}
\begin{document}
$$ \dv{z}f(z) , \dv[2]{t} $$
\end{document}
Вывод
Точно так же вы можете использовать производные исходные коды \usepackage и \odv для записи производного символа в LaTeX: 92 $ + 4x
\ END {Document}
Выход
Вы можете использовать следующую исходную код, чтобы представить Derivative Symblative Symbore in Symblaity Symbore in Symb }
\usepackage{physics}
\begin{document}
\[First \; заказ \; производная = \dv{x}{y}\]
\[Секунда \; заказ \; производная = \dv[2]{x}{y}\]
\[Третий \; заказ \; производная = \dv[3]{x}{y}\]
\[\вдоц\]
\[Кт\; заказ \; производная = \dv[k]{x}{y}\]
\end{document}
Вывод
Давайте возьмем другой пример, чтобы показать производную уравнение , включая раздел пределов и дробей:
\documentclass{article}
\usepackage{mathtools}
\usepackage{xfrac}
\begin{document}
\[
f'(x) = \lim \limits_{h \rightarrow 0} \frac{(x^2 + 2xh + h^2) — x^2}{h}
\]
\ END {Document}
Выход
.
Их определяют реальные многомерные функции. Это также происходит в различных порядках производных. Чтобы использовать символ частной производной в LaTeX, вы можете вручную использовать код \partial.Предположим, у вас есть функция f(y1, y2…yn), и вы хотите вывести ее относительно yi. Вы можете получить его, когда другие переменные постоянны. Поэтому этот вывод обозначается как ∂f / ∂yi. Символ частной производной — это общая производная с «фигурными буквами d». 9k} $
\end{document}
Вывод
Вместо того, чтобы вручную писать указанный выше производный символ, вы также можете использовать пакет физики. Чтобы использовать символ частной производной пакета Physics, используйте код \pdv таким же образом, как и в общей производной:
\documentclass{article}
\usepackage{physics}
\usepackage{xfrac}
\ начало {документ}
$$ \pdv{f}{y}{x} = \pdv{f}{x}{y} = 3 $$
\end{document}
Вывод
Многие функции недоступны в пакете Physics, поэтому вместо него можно использовать производный пакет:
\documentclass{article}
\usepackage{derivative}
\begin{document}
$$ u_{xy } = \pdv{u}{y,x} $$
\end{document}
Выход
Оценочная полоса используется, когда известно значение переменной вместе с производной. Код \eval используется для записи строки оценки производным символом, который завершает все выражение:
\documentclass{article}
\usepackage{physics}
\begin{document}
$$ \eval{ 5 + \dv{x}{t}_{t=0} } $$
$$ \eval{\pdv[2]{f}{x}}_{x=0} $$
\end {документ}
Вывод
Точечная производная в LaTeX
В LaTeX вы можете создавать временные и точечные производные вручную. Для точечных производных требуется только следующий исходный код:
\documentclass{article}
\usepackage{physics}
\begin{document}
$$\dv{x}{t} = \dot{x}$$
$$\dv[2]{x}{t} = \ddot{x} $$
$$\dv[3]{x}{t} = \ddot{x} $$
\end {документ}
Вывод
Обратите внимание, что для кодов \dot и \ddot не требуется никакого пакета, а для кодов \dddot требуется физика \usepackage.