Гиперболические функции — sh, ch, th, cth, sech, csch
ОПРЕДЕЛЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
Гиперболический синус
sh x = (ex — e-x)/2
Гиперболический косинус
ch x = (ex + e-x)/2
Гиперболический тангенс
th x = (ex — e-x)/(ex + e-x)
Гиперболический котангенс
cth x = (ex + e-x)/(ex — e-x)
Гиперболический секанс
sech x = 2/(ex + e-x)
Гиперболический косеканс
csch x = 2/(ex — e-x)
ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
th x = sh x/ch x
cth x = 1/th x = ch x/sh x
sech x = 1/ch x
csch x = 1/sh x
ch2x — sh2x = 1
sech2x + th2x = 1
cth2x — csch2x = 1
ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ
sh(-x) = -sh x
ch(-x) = ch x
th(-x) = -th x
sech(-x) = sech x
cth(-x) = -cth x
ФОРМУЛЫ СЛОЖЕНИЯ
sh (x ± y) = sh x ch y ± ch x sh y
ch (x ± y) = ch x ch y ± sh x sh y
th(x ± y) = (th x ± th y)/(1 ± th x.th y)
cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)
ФОРМУЛЫ ДВОЙНЫХ УГЛОВ
sh 2x = 2 sh x ch x
ch 2x = ch2x + sh2x = 2 ch2x — 1 = 1 + 2 sh2x
th 2x = (2th x)/(1 + th2x)
ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ
$\text{sh} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{2}}$ [+ если x > 0, — если x
$\text{ch} \frac{x}{2} = \sqrt{\frac{\text{ch} x + 1}{2}}$
$\text{th} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{\text{ch} x + 1}}$ [+ если x > 0, — если x
$= \frac{\text{sh} x}{\text{ch} x — 1} = \frac{\text{ch} x + 1}{\text{sh} x}$
ФОРМУЛЫ КРАТНОСТИ УГЛОВ
sh 3x = 3 sh x + 4 sh3 x
ch 3x = 4 ch 3 x — 3 ch x
th 3x = (3 th x + th3 x)/(1 + 3 th2x)
sh 4x = 8 sh3 x ch x + 4 sh x ch x
ch 4x = 8 ch4 x — 8 ch2 x + 1
th 4x = (4 th x + 4 th3 x)/(1 + 6 th2 x + th4 x)
СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh2 x = ½ch 2x — ½
ch2 x = ½ch 2x + ½
sh3 x = ¼sh 3x — ¾sh x
ch3 x = ¼ch 3x + ¾ch x
sh4 x = 3/8 — ½ch 2x + 1/8ch 4x
ch4 x = 3/8 + ½ch 2x + 1/8ch 4x
СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh x + sh y = 2 sh ½(x + y) ch ½(x — y)
sh x — sh y = 2 ch ½(x + y) sh ½(x — y)
ch x + ch y = 2 ch ½(x + y) ch ½(x — y)
ch x — ch y = 2 sh ½(x + y) sh ½(x — y)
sh x sh y = ½(ch (x + y) — ch (x — y))
ch x ch y = ½(ch (x + y) + ch (x — y))
sh x ch y = ½(sh (x + y) +
ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
В следующем мы принимаем, что x > 0. Если x < 0 используем соответствующий знак, как указано формулами в разделе «Функции отрицательных аргументов»
| ~ | $sh x = u$ | $ch x = u$ | $th x = u$ | $cth x = u$ | $sech x = u$ | $esch x = u$ |
| $sh x$ | $u$ | $\sqrt{u^2 — 1}$ | $\frac{u}{\sqrt{1 — u^2}}$ | $\frac{1}{\sqrt{u^2 — 1}}$ | $\frac{\sqrt{1 — u^2}}{u}$ | $\frac{1}{u}$ |
| $ch x$ | $\sqrt{1 + u^2}$ | $u$ | $\frac{1}{\sqrt{1 — u^2}}$ | $\frac{u}{\sqrt{u^2 — 1}}$ | $\frac{1}{u}$ | $\frac{\sqrt{1 + u^2}}{u}$ |
| $th x$ | $\frac{u}{\sqrt{1 + u^2}}$ | $\frac{\sqrt{u^2 — 1}}{u}$ | $u$ | $\frac{1}{u}$ | $\sqrt{1 — u^2}$ | $\frac{1}{\sqrt{1 + u^2}}$ |
| $cth x$ | $\frac{\sqrt{1 + u^2}}{u}$ | $\frac{u}{\sqrt{u^2 — 1}}$ | $\frac{1}{u}$ | $u$ | $\frac{1}{\sqrt{1 — u^2}}$ | $\sqrt{1 + u^2}$ |
| $sech x$ | $\frac{1}{\sqrt{1 + u^2}}$ | $\frac{1}{u}$ | $\sqrt{1 — u^2}$ | $\frac{\sqrt{u^2 — 1}}{u}$ | $u$ | $\frac{u}{\sqrt{1 + u^2}}$ |
| $esch x$ | $\frac{1}{u}$ | $\frac{1}{\sqrt{u^2 — 1}}$ | $\frac{\sqrt{1 — u^2}}{u}$ | $\sqrt{u^2 — 1}$ | $\frac{u}{\sqrt{1 — u^2}}$ | $u$ |
ГРАФИКИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
y = sh xy = ch x
y = th x
y = cth x

Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.
Определения гиперболических функций, их области определений и значений
- sh x – гиперболический синус
, –∞ < x < +∞; –∞ < y < +∞.- ch x – гиперболический косинус
, –∞ < x < +∞; 1 ≤ y < +∞.- th x – гиперболический тангенс
, –∞ < x < +∞; – 1 < y < +1.- cth x – гиперболический котангенс
, x ≠ 0; y < –1 или y > +1.
Графики гиперболических функций
График гиперболического синуса y = sh x
График гиперболического косинуса y = ch x
График гиперболического тангенса y = th x
График гиперболического котангенса y = cth x
Формулы с гиперболическими функциями
Связь с тригонометрическими функциями
sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i2 = –1.
Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.
Четность
sh(–x) = – sh x; ch(–x) = ch x.
th(–x) = – th x; cth(–x) = – cth x.
Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные.
Разность квадратов
ch2 x – sh2 x = 1.
Формулы суммы и разности аргументов
sh(x ± y) = sh x ch y ± ch x sh y,
ch(x ± y) = ch x ch y ± sh x sh y,
,
,
sh 2x = 2 sh x ch x ,
ch 2x = ch2 x + sh2 x = 2 ch2 x – 1 = 1 + 2 sh2 x,
.
Формулы произведений гиперболического синуса и косинуса
,
,
,
,
,
.
Формулы суммы и разности гиперболических функций
,
,
,
,
.
Связь гиперболического синуса и косинуса с тангенсом и котангенсом
, ,
, .
Производные
,
Интегралы от sh x, ch x, th x, cth x
,
,
.
Разложения в ряды
.
,
,
.
Обратные функции
Ареасинус
При – ∞ < x < ∞ и – ∞ < y < ∞ имеют место формулы:
,
.
Ареакосинус
При 1 ≤ x < ∞ и 0 ≤ y < ∞ имеют место формулы:
,
.
Вторая ветвь ареакосинуса расположена при 1 ≤ x < ∞ и – ∞ < y ≤ 0 :
.
Ареатангенс
При – 1 < x < 1 и – ∞ < y < ∞ имеют место формулы:
,
.
Ареакотангенс
При – ∞ < x < – 1 или 1 < x < ∞ и y ≠ 0 имеют место формулы:
,
.
Автор: Олег Одинцов. Опубликовано:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Производная функции. Понятие производной. Геометрический смысл производной. Физический смысл производной. Правила дифференцирования. Производная сложной функции. Достаточное условие монотонности функции. Необходимое и достаточное условия экстремума. Поделиться:
| |||||||||||||||||||||||||||||||||
Производная e в степени x и показательной функции
Основные формулы
Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) ( e x )′ = e x.
Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a:
(2) .
Экспонента – это показательная функция, у которой основание степени равно числу e, которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.
Вывод формулы производной экспоненты
Рассмотрим экспоненту, e в степени x:
y = e x.
Эта функция определена для всех . Найдем ее производную по переменной x. По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
А) Свойство экспоненты:
(4) ;
Б) Свойство логарифма:
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь – некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .
Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.
Сделаем подстановку . Тогда ; .
В силу непрерывности экспоненты,
.
Поэтому при , . В результате получаем:
.
Сделаем подстановку . Тогда . При , . И мы имеем:
.
Применим свойство логарифма (5):
. Тогда
.
Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.
Тем самым мы получили формулу (1) производной экспоненты.
Вывод формулы производной показательной функции
Теперь выведем формулу (2) производной показательной функции с основанием степени a. Мы считаем, что и . Тогда показательная функция
(8)
Определена для всех .
Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма.
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.
Находим производную. Выносим постоянную за знак производной:
.
Применяем формулу производной сложной функции:
.
Здесь .
Тем самым, мы нашли производную показательной функции с произвольным основанием степени:
.
Другие способы вывода производной экспоненты
Пусть нам известна формула производной натурального логарифма:
(9) .
Тогда мы можем вывести формулу производной экспоненты, учитывая, что экспонента является обратной функцией к натуральному логарифму.
Перепишем формулу (9) в следующем виде:
,
где .
Переменные можно обозначать любыми буквами. Поменяем местами x и y:
(10) ,
где .
Теперь рассмотрим экспоненту (e в степени x):
(11) .
Применим формулу производной обратной функции:
(12) .
Обратной функцией к экспоненте является натуральный логарифм. Подставим значение производной натурального логарифма (10):
.
И, наконец, выразим y через x по формуле (11):
.
Формула доказана.
Теперь докажем формулу производной экспоненты, применяя формулу производной сложной функции. Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x:
(13) .
Производная от икса равна единице:
.
Применим формулу производной сложной функции:
.
Здесь . Подставим в (13):
.
Отсюда
.
Пример
Найти производные от e в степени 2x, e в степени 3x и e в степени nx. То есть найти производные функций
y = e 2x, y = e 3x и y = e nx.
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = e nx. Затем подставим n = 2 и n = 3. И из общей формулы найдем выражения для производных от e 2x, e 3x и e nx.
Итак, имеем исходную функцию
.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции , зависящей от переменной : ;
2) Функции , зависящей от переменной : .
Тогда исходная функция составлена из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции.
.
Здесь мы подставили .
Итак, мы нашли:
.
Подставляем n = 2 и n = 3.
Ответ
; ; .
См. также
Все примеры вычисления производных с решениями > > >
Производные высших порядков от e в степени x
Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
Мы нашли ее производную первого порядка:
(1) .
Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.
Отсюда видно, что производная n-го порядка также равна исходной функции:
.
Производные высших порядков показательной функции
Теперь рассмотрим показательную функцию с основанием степени a:
.
Мы нашли ее производную первого порядка:
(15) .
Дифференцируя (15), получаем производные второго и третьего порядка:
;
.
Мы видим, что каждое дифференцирование приводит к умножению исходной функции на . Поэтому производная n-го порядка имеет следующий вид:
.
Автор: Олег Одинцов. Опубликовано:
Резюме:
Функция sh позволяет в режиме онлайн вычислять гиперболический синус числа.
Ш онлайнОписание:
Калькулятор позволяет использовать большинство гиперболических функций , есть возможность рассчитать гиперболический косинус (отметил ч или сп), гиперболический синус (принято к сведению ш или зп ), тангенс гиперболический (принято к сведению го или TANH ), и гиперболический котангенс (принято к сведению COTH или cotanh ).
Функция гиперболического синуса записывается в sh, она определяется следующим формула:
`Ш (х) = (ехр (х) ехр (-x)) / 2`
опыта это обозначение экспоненциальный функция.
- Расчет гиперболического синуса
- Производная от гиперболического синуса
- Антипроизводное гиперболического синуса
- Пределы гиперболического синуса
Калькулятор гиперболического синуса позволяет через функцию sh до вычислить онлайн гиперболический синус числа.
Чтобы вычислить гиперболический синус числа, просто введите число и примените функция ш . Для расчета гиперболический синус следующего числа 0, введите sh (`0`) или непосредственно 0, если кнопка sh уже появляется, результат 0 возвращается.
Производная гиперболического синуса равна ch (x).
Антипроизводное гиперболического синуса равно ch (x).
- Границы гиперболического синуса существуют в `-oo` и` + oo`:
- Функция гиперболического синуса имеет предел в -oo, который равен -oo.
- Функция гиперболического синуса имеет предел в «+ oo», который равен «+ oo».
Функция sh позволяет в режиме онлайн вычислить гиперболический синус числа.
Синтаксис:
sh (x), x это число.
Иногда используются другие обозначения: sinh
Примеры:
sh (`2`), возвращает 3.62686040785Производные гиперболического синуса:
Чтобы дифференцировать функцию гиперболического синуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции гиперболического синуса
Производная от sh (x) является производной (`sh (x)`) = `ch (x)`
Антидеривативные гиперболические синусы:
Антидеривативный калькулятор позволяет рассчитать антипроизводное функции гиперболического синуса.
Анти-производное для sh (x) является анти-производным (`sh (x)`) = `ch (x)`
Предел гиперболического синуса:
Калькулятор пределов позволяет вычислять пределы функции гиперболического синуса.
Предел для sh (x) — это предел (`sh (x)`)
Графический гиперболический синус:
Графический калькулятор способен отображать гиперболическую функцию синуса в интервале определения.
Свойство функции гиперболического синуса:
Гиперболическая функция синуса является нечетной функцией.Рассчитать онлайн с sh (гиперболический синус) ,Калькулятор
— sh (0) — Solumaths
Резюме:
Описание:
Калькулятор позволяет использовать большинство гиперболических функций , есть возможность рассчитать гиперболический косинус (отметил ч или сп), гиперболический синус (принято к сведению ш или зп ), тангенс гиперболический (принято к сведению го или TANH ), и гиперболический котангенс (принято к сведению COTH или cotanh ).
Функция гиперболического синуса записывается в sh, она определяется следующим формула:
`Ш (х) = (ехр (х) ехр (-x)) / 2`
опыта это обозначение экспоненциальный функция.
- Расчет гиперболического синуса
- Производная от гиперболического синуса
- Антипроизводное гиперболического синуса
- Пределы гиперболического синуса
Калькулятор гиперболического синуса позволяет через функцию sh до вычислить онлайн гиперболический синус числа.
Чтобы
Производная гиперболического синуса равна ch (x).
Антипроизводное гиперболического синуса равно ch (x).
- Границы гиперболического синуса существуют в `-oo` и` + oo`:
- Функция гиперболического синуса имеет предел в -oo, который равен -oo.
- Функция гиперболического синуса имеет предел в «+ oo», который равен «+ oo».
Функция sh позволяет в режиме онлайн вычислить гиперболический синус числа.
Синтаксис:
sh (x), x это число.
Иногда используются другие обозначения: sinh
Примеры:
sh (`2`), возвращает 3.62686040785Производные гиперболического синуса:
Чтобы дифференцировать функцию гиперболического синуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции гиперболического синуса
Производная от sh (x) является производной (`sh (x)`) = `ch (x)`
Антидеривативные гиперболические синусы:
Антидеривативный калькулятор позволяет рассчитать антипроизводное функции гиперболического синуса.
Анти-производное для sh (x) является анти-производным (`sh (x)`) = `ch (x)`
Предел гиперболического синуса:
Калькулятор пределов позволяет вычислять пределы функции гиперболического синуса.
Предел для sh (x) — это предел (`sh (x)`)
Графический гиперболический синус:
Графический калькулятор способен отображать гиперболическую функцию синуса в интервале определения.
Свойство функции гиперболического синуса:
Гиперболическая функция синуса является нечетной функцией.Рассчитать онлайн с sh (гиперболический синус) ,
производных — англо-сербохорватский словарь
подражает чужой работе.
(закон, закон об авторском праве) Ссылается на произведение, такое как перевод или адаптация, на основе другого произведения, которое может быть предметом ограничений авторского права.
(финансы) Имеет стоимость, которая зависит от базового актива переменной стоимости.
Не хватает оригинальности.
Что-то выведено.
(лингвистика) Слово, которое происходит от другого.
(финансы) Финансовый инструмент, стоимость которого зависит от оценки базового актива; такие как ордер, опцион и т. д.
(химия) Химическое вещество, полученное из другого.
(исчисление) Производная функция функции.
(исчисление) Значение этой функции для заданного значения ее независимой переменной.
Получено путем деривации; не радикальный, оригинальный или фундаментальный.
подражать чужой работе.
Ссылаясь на произведение, такое как перевод или адаптация, на основе другого произведения, которое может быть предметом ограничений авторского права.
Имеет значение, которое зависит от базового актива переменной стоимости.
Не хватает оригинальности.
Что-то выведено.
Слово, которое происходит от другого.
Финансовый инструмент, стоимость которого зависит от оценки базового актива; например, ордер, опцион и т. д.
Химическое вещество, полученное из другого.
Производная функция функции.
Значение этой функции для заданного значения ее независимой переменной.
что-то производное
слово, которое происходит от другого финансового инструмента
, стоимость которого зависит от оценки базового инструмента
химическое вещество, полученное в результате анализа
: значение
производное(акция)
В математике мгновенное скорость изменения функции.
В лингвистике слово, которое происходит от другого.
производное (слово)
(химическое) производное
(химия) Вещество или соединение, полученное из другого вещества или соединения или полученное из него.
в результате или с использованием деривации; «производный процесс»; «стиль прозы с высокой производной»
соединение, полученное из другого соединения
или считающееся его производным от финансового инструмента, стоимость которого основана на другой ценной бумаге
(лингвистика), слово, производное от другого слова; «электричество» является производной от «электричества»
результат математического дифференцирования; мгновенное изменение одной величины относительно другой; DF (X) / DX
больше.Производное — исчисление
На этой странице перечислены основные термины исчисления. Термин используется широко, и глубокое понимание его определения имеет решающее значение.
См. Полный список основных терминов
Имя
Термин производная используется для понятия, определенного здесь. Тем не менее, существует множество вариаций концепции производной, которые описываются с помощью прилагательных для изменения существительного. Когда говорят об этих вариациях, полезно предоставить аналогичное прилагательное, чтобы указать, что мы говорим о обычном понятии производной.Варианты и соответствующие терминологические пояснения приведены ниже:
| Вариация понятия производной | Модифицированное имя для обычного понятия производной, чтобы подчеркнуть, что это оригинальное понятие, а не вариация |
|---|---|
| односторонняя производная (производная слева и правая производная) — определена на этой странице | двусторонняя производная |
| высшее производное (полученное повторным дифференцированием) | первая производная |
| частная производная (производная функции нескольких переменных по одной из переменных, поддерживающих остальные переменные) | обыкновенная производная |
| дискретный производный (не часто используется) | Непрерывное производное(обычно не используется) |
Определение в точке
Концептуальное определение
Предположим, что  — это функция, определенная для подмножества вещественных чисел, а
— это функция, определенная для подмножества вещественных чисел, а  — это точка внутри области
— это точка внутри области  , т.е.домен
, т.е.домен  содержит открытый интервал, окружающий
содержит открытый интервал, окружающий  . Производная из
. Производная из  в
в  , обозначенная как
, обозначенная как 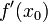 , представляет собой мгновенную скорость изменения из
, представляет собой мгновенную скорость изменения из 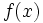 относительно
относительно 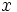 в
в  . Он определяется как предел средней скорости изменения в
. Он определяется как предел средней скорости изменения в  между
между 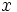 и
и  , когда
, когда 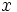 приближается к
приближается к  .
.
В более формальных определениях ниже мы увидим, что:
- Коэффициент разности формализует понятие средней скорости изменения.
- Производная формализует понятие мгновенной скорости изменения и является пределом отношения разности.
алгебраическое определение
Предположим, что  — это функция, определенная для подмножества вещественных чисел, а
— это функция, определенная для подмножества вещественных чисел, а  — это точка внутри области
— это точка внутри области  , то есть область
, то есть область  содержит открытый интервал, окружающий
содержит открытый интервал, окружающий  . Производная (также называемая , первая производная ), равная
. Производная (также называемая , первая производная ), равная  на
на  , обозначаемая
, обозначаемая 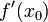 , определяется как предел отношения разности
, определяется как предел отношения разности  между
между  и
и 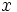 как
как 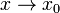 .Явное:
.Явное:
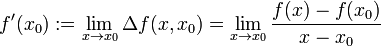
Если этот предел существует, то мы говорим, что производная существует и имеет это значение, и мы говорим, что функция дифференцируема в этой точке. Если предел не существует, то мы говорим, что функция не дифференцируема в точке, а производная не существует.
вычислительно полезная версия алгебраического определения
Это получается из предыдущего определения путем подстановки переменных 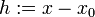 , т. Е.
, т. Е. 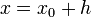 .Явное:
.Явное:
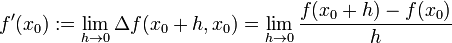
Геометрическое определение
. Предположим, что  — это функция, а
— это функция, а  — это точка внутри области
— это точка внутри области  , то есть область
, то есть область  содержит открытый интервал, окружающий
содержит открытый интервал, окружающий  . Производная из
. Производная из  в
в  — это наклон касательной к графику
— это наклон касательной к графику  через точку
через точку 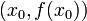 .
.
Алгебраическое определение, разработанное в терминах эпсилон-дельта-определения пределов
Предположим, что  — это функция, определенная для подмножества вещественных чисел, а
— это функция, определенная для подмножества вещественных чисел, а  — это точка внутри области
— это точка внутри области  , т.е.домен
, т.е.домен  содержит открытый интервал, окружающий
содержит открытый интервал, окружающий  . Производная (также называемая первой производной ) с
. Производная (также называемая первой производной ) с  по
по  , обозначенная как
, обозначенная как 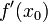 , определяется как действительное число
, определяется как действительное число 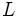 , такое что:
, такое что:
Для каждого
существует, такое что
, если,
, то.
Определение как функция
Предположим, что  — это функция, определенная в подмножестве вещественных чисел. Его производная или первая производная , обозначенная
— это функция, определенная в подмножестве вещественных чисел. Его производная или первая производная , обозначенная 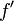 , является функцией, определенной следующим образом:
, является функцией, определенной следующим образом:
БОЛЬШЕ В ПУТИ ЭТОГО ОПРЕДЕЛЕНИЯ ИЛИ ФАКТА ПРЕДСТАВЛЕНО : Сначала мы представляем версию, которая имеет дело с определенной точкой (обычно с нижним индексом) в области соответствующих функций, а затем обсуждаем версию, которая имеет дело с точкой это свободно перемещаться в домене, удалив индекс.Почему мы это делаем?
Цель версии конкретной точки состоит в том, чтобы подчеркнуть, что точка фиксирована на время определения, то есть она не перемещается, пока мы определяем конструкцию или применяем факт. Тем не менее, определение или факт применим не только к одной точке, но и ко всем точкам, удовлетворяющим определенным критериям, и, таким образом, мы можем получить дальнейшие интересные перспективы на , варьируя точку, которую мы рассматриваем. Это цель второй, универсальной версии версии.
Односторонние понятия
Левая производная
Предположим, что  — это функция, определенная в точке
— это функция, определенная в точке 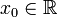 , а также непосредственно слева от
, а также непосредственно слева от  . Левая производная из
. Левая производная из  в
в  определяется как левая граница для отношения разности между
определяется как левая граница для отношения разности между 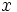 и
и  . Другими словами, это:
. Другими словами, это:
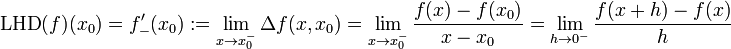
правая производная
Предположим, что  — это функция, определенная в точке
— это функция, определенная в точке 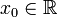 , а также справа от
, а также справа от  .Правая производная от
.Правая производная от  на
на  определяется как правая граница для отношения разности между
определяется как правая граница для отношения разности между 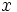 и
и  . Другими словами, это:
. Другими словами, это:
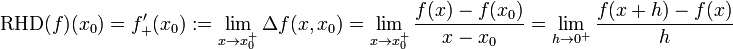
Отношение между односторонними производными и обычной (двусторонней) производной
Производная 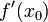 существует тогда и только тогда (как левая, так и правая производные существуют в
существует тогда и только тогда (как левая, так и правая производные существуют в  , и их значения равны). Кроме того, значение производной равно обоим этим значениям.
, и их значения равны). Кроме того, значение производной равно обоим этим значениям.
Лейбниц обозначения для производной
Нотация Лейбница для производной рассматривает производную как относительную скорость изменения двух переменных как и, таким образом, представляет несколько иной взгляд на производную.
Предположим,  — это функция, а
— это функция, а 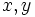 — это переменные, связанные с
— это переменные, связанные с 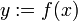 . Здесь
. Здесь 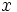 является независимой переменной , а
является независимой переменной , а 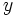 является зависимой переменной (зависимость описывается функцией
является зависимой переменной (зависимость описывается функцией  ).Затем мы определяем:
).Затем мы определяем:
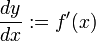
В частности, 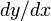 является функцией , из
является функцией , из 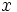 . Его значение на
. Его значение на 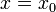 определяется как
определяется как 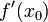 и обозначается следующим образом:
и обозначается следующим образом:
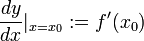
Обратите внимание, что нотация 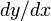 соответствует , а не означает, что число
соответствует , а не означает, что число 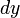 делится на число
делится на число 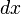 . Один из способов обоснования этой нотации состоит в том, чтобы выразить ее как предел разности:
. Один из способов обоснования этой нотации состоит в том, чтобы выразить ее как предел разности:
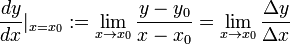
, где 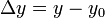 обозначает разницу в значениях
обозначает разницу в значениях 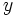 , а
, а 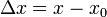 обозначает разницу в значениях
обозначает разницу в значениях 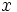 .
.
Частное обозначение вводит в заблуждение, но спасает
Отношение разницы на самом деле является частным из чисел , и производная является пределом этого. Следовательно, многие формальные манипуляции, включающие дроби чисел, работают с этим обозначением, даже если 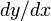 само по себе не является частным чисел (см. Правило цепочки для дифференцирования и теоремы об обратной функции).
само по себе не является частным чисел (см. Правило цепочки для дифференцирования и теоремы об обратной функции).
Выразительное преимущество обозначения Лейбница
Нотация Лейбница выгодна для выполнения вычислений вручную и написания производных выражений, потому что она не требует от нас называть каждую функцию, чтобы дифференцировать ее.С другой стороны, простые обозначения требуют, чтобы мы называли функцию, прежде чем говорить о ее производных.
Таким образом, нотация Лейбница имеет решающее значение для построения сложных выражений с участием производных. Например, рассмотрим выражение:
![\frac{d}{dx}\left[\left(\frac{d}{dx}(x - \cos x)\right)\sin^2\left(\frac{d}{dx}(x^2 \cos(x^3))\right)\right]](/800/600/https/calculus.subwiki.org/w/images/math/1/7/c/17cafeabd60eca7d7bcb13b0c4db6a0b.png)
Чтобы написать это выражение с простыми обозначениями, нам сначала нужно дать имена функциям 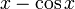 и
и 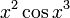 , затем дать имя всему выражению в квадратных скобках, а затем поговорить о его дифференцировании.
, затем дать имя всему выражению в квадратных скобках, а затем поговорить о его дифференцировании.
Выразительный недостаток обозначения Лейбница
Нотация Лейбница не является бессмысленной , т. Е. Мы должны использовать символ для обозначения точки, в которой применяется функция. Напротив, с простыми обозначениями мы можем делать такие утверждения, как 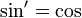 .
.
Физические приложения
Примечание по единицам
В приложениях к естественным и общественным наукам единиц , используемых для измерения 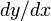 , представляют собой единицы измерения
, представляют собой единицы измерения 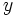 , деленные на единицы измерения
, деленные на единицы измерения 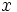 .Это связано с тем, что производная является пределом разностного отношения, которое является величиной, измеренной в единицах
.Это связано с тем, что производная является пределом разностного отношения, которое является величиной, измеренной в единицах 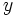 , деленной на величину, измеренную в единицах
, деленной на величину, измеренную в единицах 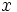 .
.
Если измерения выражены с использованием основы, такой как основа MLT для физических величин, то показатели MLT вычитаются.
| Контекст | Пример производной от реального мира приложения | Функционально зависимая переменная, дифференцируемая | Независимая переменная, с точки зрения которой происходит дифференциация | Соотношение соответствующих разностей | Термин для числителя разностного отношения | Термин для знаменателя отношения разностей | Комментарий | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| кинематика (классическая механика, физика) | мгновенная скорость измеряется в единицах длины / времени | позиция измеряется в единицах длины | время измеряется в единицах времени | средняя скорость | Смещениепрошедшее время | Строго говоря,, это вектор-производная, но мы можем использовать исчисление одной переменной, если ограничимся движением по прямой.2 | скорость измеряется в единицах длины / времени | время измеряется в единицах времени | среднее ускорение | изменение скорости | прошедшее время | Строго говоря,, это вектор-производная, но мы можем использовать исчисление одной переменной, если ограничимся движением по прямой. | |
| химическая реакция (химия) | скорость изменения концентрации конкретного продукта реакции , измеренная в единицах (концентрация) / (время). | концентрация Подходящей мерой концентрации может быть молярность (для реакций в растворе) или парциальное давление (для газообразных реакций) | время измеряется в единицах времени | Средняя скорость изменения концентрации продукта измеряется в единицах (мера концентрации) / (время). | изменение концентрации продукта | прошедшее время |
Родственные понятия
| Понятие | Как это относится к производным |
|---|---|
| высшее производное | снова дифференцирует функцию, полученную дифференцированием определенной функции, и применяет этот процесс повторно.В частности, производная 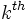 является функцией, полученной путем применения операции дифференцирования является функцией, полученной путем применения операции дифференцирования 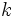 раз. раз. |
| антипроизводных | функция, которая имеет данную производную. Антидифференциация является обратной дифференциацией. Общее выражение для антипроизводного также называется неопределенным интегралом . |
| частная производная | функция более чем одной переменной дифференцируется по отношению к одной из переменных, сохраняя остальные постоянными. |
| высшее частное производное | , полученный путем применения операции частичного дифференцирования к функции более чем одной переменной. Чистые с более высокими частями — это те, в которых все операции частичного дифференцирования относятся к одной и той же переменной. Смешанные с более высокими частями — это те, в которых операции частичного дифференцирования относятся к более чем одной переменной. |
| дифференциал | Заполните это позже |
Значение
Значение знака на интервалах
Производная представляет скорость изменения , и, грубо говоря, знак производной представляет направление изменения .Мы перечисляем свободные и точные утверждения ниже:
Значение знака в точках
Это очень похоже на значение на интервале, но поведение в отдельных точках может быть аномальным и также может представлять переходы между разными типами интервалов.
Вычисление производной
Полный список см. В разделе Категория: Правила дифференцирования.

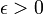
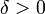 , такое что
, такое что 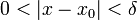 ,
, 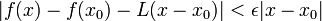 .
. ) в области соответствующих функций, а затем обсуждаем версию, которая имеет дело с точкой это свободно перемещаться в домене, удалив индекс.Почему мы это делаем?
) в области соответствующих функций, а затем обсуждаем версию, которая имеет дело с точкой это свободно перемещаться в домене, удалив индекс.Почему мы это делаем?