Производная уравнение касательной к графику функции: Уравнение касательной к графику функции — урок. Алгебра, 11 класс.

Содержание

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с.

В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике.

СЛОВО К УЧАЩИМСЯ
ГЛАВА I. ЧИСЛА
§ 1. Натуральные числа
2. Арифметические действия над натуральными числами.
3. Деление с остатком.
4. Признаки делимости.
5. Разложение натурального числа на простые множители.
6. Наибольший общий делитель нескольких натуральных чисел.
7. Наименьшее общее кратное нескольких натуральных чисел.

8. Употребление букв в алгебре. Переменные.
§ 2. Рациональные числа
10. Равенство дробей. Основное свойство дроби. Сокращение дробей.
11. Приведение дробей к общему знаменателю.
12. Арифметические действия над обыкновенными дробями.
13. Десятичные дроби.
14. Арифметические действия над десятичными дробями.
15. Проценты.
16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь.
17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь.
18. Координатная прямая.
19. Множество рациональных чисел.
§ 3. Действительные числа
21. Действительные числа. Числовая прямая.
22 Обозначения некоторых числовых множеств.
23. Сравнение действительных чисел.
25. Числовые промежутки.
26. Модуль действительного числа.
27. Формула расстояния между двумя точками координатной прямой.
28. Правила действий над действительными числами.
29. Свойства арифметических действий над действительными числами.

30. Пропорции.
31. Целая часть числа. Дробная часть числа.
32. Степень с натуральным показателем.
33. Степень с нулевым показателем. Степень с отрицательным целым показателем.
34. Стандартный вид положительного действительного числа.
35. Определение арифметического корня.
36. Корень нечетной степени из отрицательного числа.
37. Степень с дробным показателем.
38. Свойства степеней с рациональными показателями.
39. Приближенные значения чисел. Абсолютная и относительная погрешности.
40. Десятичные приближения действительного числа по недостатку и по избытку.
41. Правило извлечения квадратного корня из натурального числа.
42. Понятие о степени с иррациональным показателем.
43. Свойства степеней с действительными показателями.
§ 4. Комплексные числа
45. Арифметические операции над комплексными числами.
46. Алгебраическая форма комплексного числа.
47. Отыскание комплексных корней уравнений.
ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
49.

3.
112. Построение графика функции y = f(x-m)+n
113. График квадратичной функции.
114. Способы построения графика квадратичной функции
115. Построение графика функции y = f(kx).
116. Сжатие и растяжение графиков тригонометрических функций.
117. График гармонического колебания
ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ
§ 12. Преобразование выражений, содержащих переменную под знаком логарифма
119. Определение логарифма положительного числа по данному основанию.
120. Свойства логарифмов.
121. Переход к новому основанию логарифма.
122. Логарифмирование и потенцирование.
123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма.

§ 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений
125. Формулы сложения и вычитания аргументов.
126. Формулы приведения.
127. Соотношения между тригонометрическими функциями одного и того же аргумента.
128. Формулы двойного угла.
129. Формулы понижения степени.

130. Преобразование суммы тригонометрических функций в произведение.
131. Преобразование произведения тригонометрических функций в сумму.
132. Преобразование выражения a cos t + b sin t к виду A sin (t + a).
133. Примеры преобразований выражений, содержащих обратные тригонометрические функции.
ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
§ 14. Уравнения с одной переменной
135. Равносильность уравнений.
136. Линейные уравнения.
137. Квадратные уравнения.
138. Неполные квадратные уравнения.
139. Теорема Виета.
140. Системы и совокупности уравнений.
141. Уравнения, содержащие переменную под знаком модуля.
142. Понятие следствия уравнения. Посторонние корни.
143. Уравнения с переменной в знаменателе.
144. Область определения уравнения.
145. Рациональные уравнения.
146. Решение уравнения p(x) = 0 методом разложения его левой части на множители.
147. Решение уравнений методом введения новой переменной.
148. Биквадратные уравнения.

149. Решение задач с помощью составления уравнений.
150. Иррациональные уравнения.
151. Показательные уравнения.
152. Логарифмические уравнения.
153. Примеры решения показательно-логарифмических уравнений.
154. Простейшие тригонометрические уравнения.
155. Методы решения тригонометрических уравнений.
156. Универсальная подстановка (для тригонометрических уравнений).
157. Метод введения вспомогательного аргумента (для тригонометрических уравнений).

158. Графическое решение уравнений.
159. Уравнения с параметром.
§ 15. Уравнения с двумя переменными
161. График уравнения с двумя переменными.
162. Линейное уравнение с двумя переменными и его график.
§ 16. Системы уравнений
164. Решение систем двух уравнений с двумя переменными методом подстановки.
165. Решение систем двух уравнений с двумя переменными методом сложения.
167. Графическое решение систем двух уравнений с двумя переменными.
168. Исследование системы двух линейных уравнений с двумя переменными.

169. Решение систем двух уравнений с двумя переменными методами умножения и деления.
170. Системы показательных и логарифмических уравнений.
171. Системы тригонометрических уравнений с двумя переменными.
172. Системы трех уравнений с тремя переменными.
173. Решение задач с помощью составления систем уравнений.

Глава VI. НЕРАВЕНСТВА
§ 17. Решение неравенств с переменной
175. Графическое решение неравенств с одной переменной.
176. Линейные неравенства с одной переменной.
177. Системы неравенств с одной переменной.
178. Совокупность неравенств с одной переменной.
179. Дробно-линейные неравенства.
180. Неравенства второй степени.
181. Графическое решение неравенств второй степени.
182. Неравенства с модулями.
183. Решение рациональных неравенств методом промежутков.
184. Показательные неравенства.
185. Логарифмические неравенства.
186. Иррациональные неравенства.
187. Решение тригонометрических неравенств.
188.

Неравенства и системы неравенств с двумя переменными.
§ 18. Доказательство неравенств
190. Синтетический метод доказательства неравенств.
191. Доказательство неравенств методом от противного.
192. Использование неравенств при решении уравнений.

ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
§ 19. Числовые последовательности
194. Способы задания последовательности.
195. Возрастание и убывание последовательности.
196. Определение арифметической прогрессии.
197. Свойства арифметической прогрессии
198. Определение геометрической прогрессии.
199. Свойства геометрической прогрессии.
200. Понятие о пределе последовательности.
201. Вычисление пределов последовательностей.
202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции
204. Вычисление пределов функции при х->оо.
205. Предел функции в точке. Непрерывные функции.
206. Вертикальная асимптота.
207. Вычисление пределов функций в точке.
§ 21.

Производная и ее применения
209. Определение производной.
210. Формулы дифференцирования. Таблица производных.
211. Дифференцирование суммы, произведения, частного.
212. Сложная функция и ее дифференцирование.
213. Физический смысл производной.
214. Вторая производная и ее физический смысл.
215. Касательная к графику функции.
216. Применение производной к исследованию функций на монотонность.
217. Применение производной к исследованию функций на экстремум.
218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке.
219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке.
220. Задачи на отыскание наибольших или наименьших значений величин.
221. Применение производной для доказательства тождеств.
222. Применение производной для доказательства неравенств.
223. Общая схема построения графика функции.
§ 22. Первообразная и интеграл
225. Таблица первообразных.
226.

Правила вычисления первообразных.
227. Интеграл.

228. Связь между интегралов и первообразной (формула Ньютона—Лейбница).
229. Правила вычисления интегралов.
230. Использование интеграла для вычисления площадей плоских фигур.
ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ
2. Точка. Прямая.
3. Определения. Аксиомы. Теоремы.
§ 2. Основные свойства простейших геометрических фигур
5. Луч.
6. Окружность. Круг.
7. Полуплоскость.
8. Угол. Градусная мера угла.
9. Смежные и вертикальные углы.
10. Центральные и вписанные углы.
11. Параллельные прямые.
12. Признаки параллельности прямых.
13. Перпендикулярные прямые.
14. Касательная к окружности.
15. Треугольники.
16. Равенство треугольников.
17. Равнобедренный треугольник.
18. Сумма углов треугольника.
19. Прямоугольный треугольник. Теорема Пифагора.
20. Окружности, вписанные в треугольник и описанные около треугольника.
§ 3. Геометрические построения на плоскости
22.

Простейшие задачи на построение.
23. Геометрическое место точек на плоскости.
§ 4. Четырехугольники
25. Параллелограмм.
26. Прямоугольник. Ромб. Квадрат.
27. Трапеция.
§ 5. Многоугольники
29. Выпуклые многоугольники.
30. Правильные многоугольники.
31. Длина окружности.
§ 6. Решение треугольников
33. Соотношения между сторонами и углами в прямоугольном треугольнике.
34. Теорема косинусов. Теорема синусов.
35. Решение треугольников.
§ 7. Площади плоских фигур
37. Площади многоугольников.
38. Площади подобных фигур.
39. Площадь круга.
ГЛАВА II. Прямые и плоскости в пространстве
§ 9. Параллельность прямых и плоскостей
42. Параллельность прямой и плоскости.
43. Параллельные плоскости.
§ 10. Перпендикулярность прямых и плоскостей
45. Перпендикуляр и наклонная к плоскости.
46. Перпендикулярность плоскостей.
ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ
§ 11. Многогранники
48. Многогранные углы. Многогранники.

49. Призма. Параллелепипед. Куб.
50. Пираприда.
51. Правильные многогранники.
§ 12. Тела вращения
53. Конус.
54. Шар.
§ 13. Изображение пространственных фигур на плоскости
56. Ортогональное проектирование.
57. Геометрическое место точек в пространстве.
§ 14. Объемы тел
59. Объем параллелепипеда, призмы и пирамиды.
60. Объем цилиндра и конуса.
61. Общая формула объемов тел вращения.
§ 15. Площади поверхностей тел
63. Понятие площади поверхности.
64. Площади поверхностей тел вращения.
ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ
§ 16. Координаты на плоскости и в пространстве
66. Координаты середины отрезка.
§ 17. Уравнения фигур на плоскости
68. Пересечение двух окружностей.
69. Уравнение прямой.
70. Пересечение прямой и окружности.
§ 18. Уравнения фигур в пространстве
72. Уравнение сферы.
73. Взаимное расположение сферы и плоскости.
74. Пересечение двух сфер.
ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР
76.

Понятие движения.
§ 20. Подобие фигур
78. Подобные фигуры.
ГЛАВА VI. ВЕКТОРЫ
80. Понятие вектора.
81. Координаты вектора.
§ 22. Операции над векторами
83. Умножение вектора на число. Коллинеарные векторы.
84. Скалярное произведение векторов.
ПРИЛОЖЕНИЯ
ГЕОМЕТРИЯ

[Зачет 85] Определение производной функции в точке и на множестве. Геометрический смысл производной. Уравнения касательной и нормали к графику функции в точке.

Определение производной функции в точке и на множестве.

Пусть функция определена в точке и некоторой ее окрестности. Придадим аргументуприращение такое, что точка попадает в область определения функции. Функция при этом получит приращение .

ОПРЕДЕЛЕНИЕ 1. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при (если этот предел существует и конечен), т. е.

Обозначают: .

Понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке.

Пусть дано топологическое пространство и последовательность Тогда, если существует элемент такой, что

где — открытое множество, содержащее , то он называется пределом последовательности . Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент такой, что

где — метрика, то называется пределом .

Геометрический смысл производной.

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.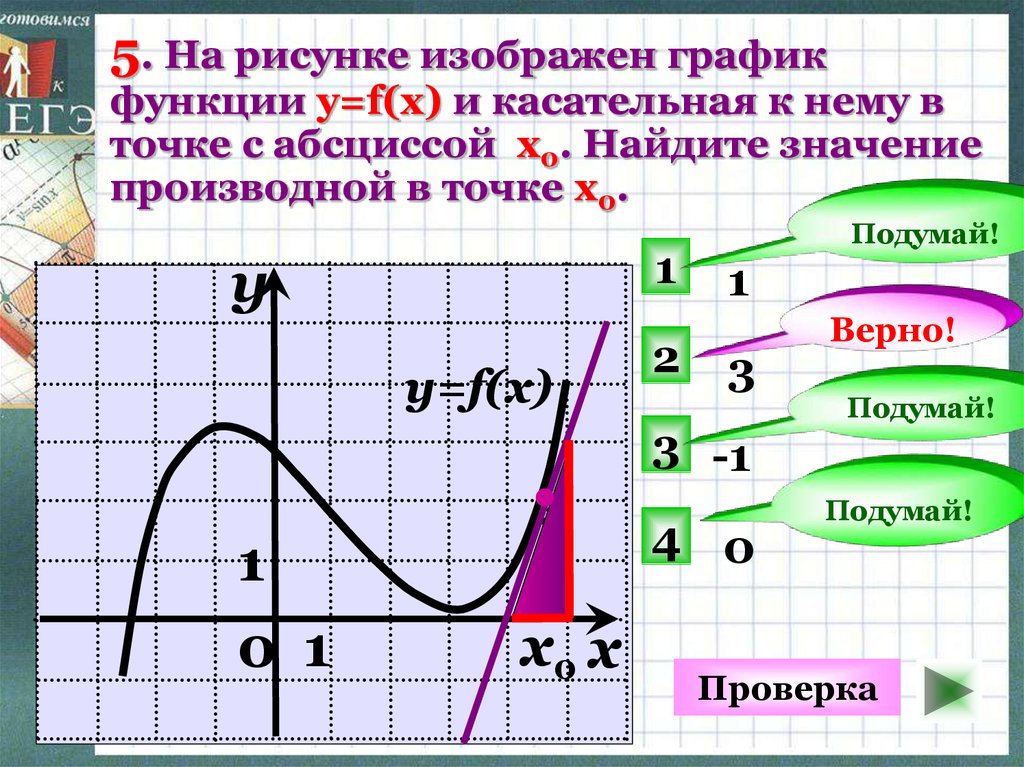

Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции:

xf(x0+x)−f(x0)=tg

, где — угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то

неограниченно уменьшается и приближается к 0, а секущая АВприближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

Уравнения касательной и нормали к графику функции в точке.

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:

y/(x)=limΔx→0ΔxΔy

Δy=f(x+Δx)−f(x).

Уравнение касательной к графику функции:

y=kx+b (k,b=const)
. Из геометрического смысла производной:
f/(x0)=tgα=k
Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.

Уравнение нормали
Нормаль — это перпендикуляр к касательной (см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали — это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка
(x0,f(x0))∈
нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
Примеры.
Напишите уравнение касательной к графику функции y=0,5x^2–3x+1, проходящей под углом 45° к прямой y=0. 3. Составить уравнение касательной к графику этой функции в точке x0=2. Смотреть решение…
Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2. Смотреть решение…
3.2.3 Уравнение касательной Карточки Ирины Солошенко
Уравнение касательной
• Чтобы найти уравнение линии, касательной к кривой, возьмите производную, оцените производную в точке касания, чтобы найти наклон, и подставьте наклон и точку касания в форму точка-наклон линии. • Чтобы найти, где линия, касательная к кривой, является горизонтальной, приравняйте производную к нулю и найдите x.
Чтобы найти уравнение касательной к кривой, начните с вычисления производной.
Помните, производная, вычисленная в точке, дает вам наклон линии, касательной к кривой в этой точке.
Подставьте точку касания в производную. Результатом является наклон касательной.
Уравнение линии требует двух частей информации: наклона и точки на линии. Найдите координату y точки касания, подставив значение x в функцию f.
Помните, что точка касания находится на касательной, потому что это точка, где линия касается кривой.
Подставьте наклон и координаты x и y в форму точки-наклона линии, чтобы получить уравнение касательной линии.
Горизонтальные касательные приводят ко многим приложениям исчисления.
Производная — это функциональная машина, производящая уклоны. Если вы хотите знать, где наклон линии, касательной к кривой, равен нулю, вы должны установить производную равной нулю и найти значение x, которое делает это утверждение верным.
Предположим, вам сказали, что уравнение касательной к графику функции g(x) в точке (−1,−2) равно y=1/2x−3/2. Найдите g′(−1). 92 — 5 в (2, -1).
у = 4х — 9
Производные, касательные и скорости изменения
Производные, касательные и скорости изменения
Исчисление с одной переменной можно разделить на дифференциальное исчисление и интегральное исчисление . Дифференциальное исчисление производные и их приложения. Исследования интегрального исчисления интегралы и их приложения. Два части соединены Основная теорема Расчет ; грубо говоря, что производные и интегралы равны «противоположности».
Я начну обсуждение производных с геометрического вопроса. Учитывая функцию, как найти наклон касательная к графику в точке ?
(Я думаю о касательной линии как о линии который просто просматривает график в , не переходя через график в этой точке. Это расплывчатое описание, но оно пока сделаю)
Вот идея. Выберите точку поблизости и нарисуйте линия, соединяющая с. (А Линия, соединяющая две точки на графике, называется . секущая линия .)
Таким образом, h представляет, сколько вы «переместились» в x-направление. Линия имеет наклон
Если сдвинуть вторую точку по графику по направлению к P секущая линия становится все ближе и ближе к касательной. Алгебраически это равносильно принятию предела как . Таким образом, наклон касательной при
Пример. Пусть .
а) Найдите наклон секущей, соединяющей .
(b) Найдите наклон касательной к точке .
(а)
(b) В этом случае я ввожу уравнение для и вычисляю предел:
Другая форма формулы касательной линии:
Вы можете получить эту формулу из предыдущей, поставив . Тогда, так дает.
Пример. Найдите наклон касательной к в .
График представляет собой прямоугольную гиперболу. Уведомление что, не введя конкретный номер для a, я получил формула, которую я могу использовать для любого a. Например, наклон касательная в (т.е. в точке ) равна
Существует и другая интерпретация наклонов секущей и касательная линия. Наклон секущей, соединяющейся с
Это изменение в f, деленное на изменение в x, поэтому он представляет собой среднюю скорость изменения f при переходе x от a к b (т.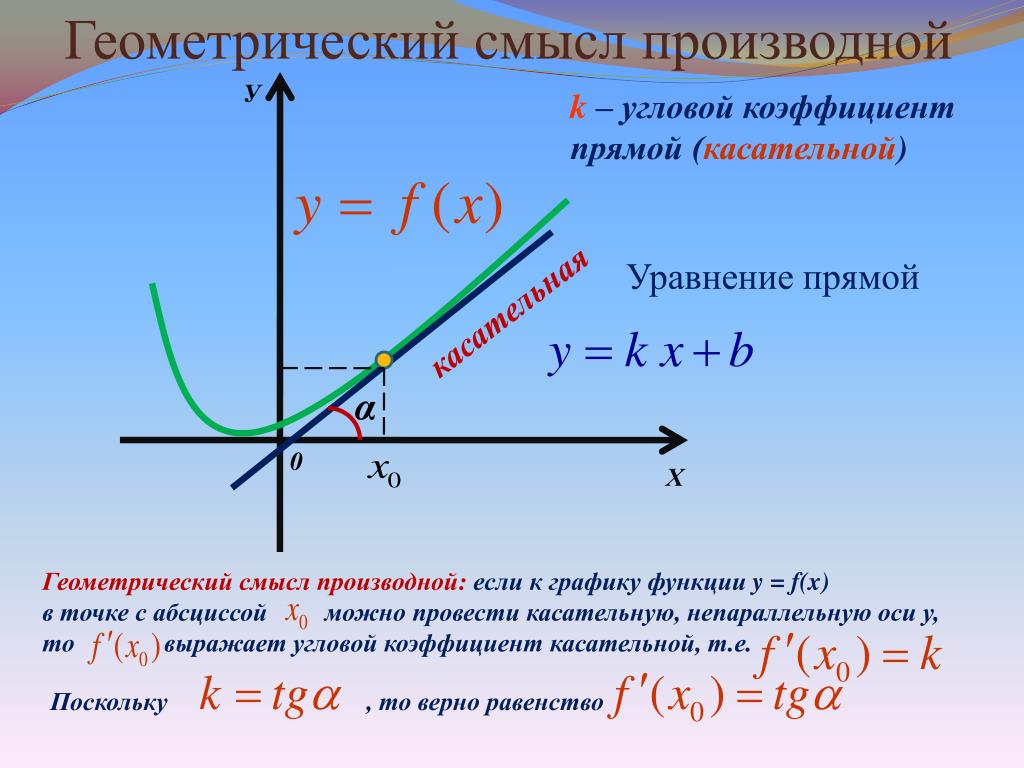 е. на интервале ).
Каков наклон касательной в точке а? Он представляет мгновенную скорость изменения при . (Иногда люди ленятся и просто говорят «оцените изменения» означает » мгновенную скорость изменять».)
Пример. Пусть
а) Найдите среднюю скорость изменения на интервале .
б) Найдите мгновенную скорость изменения при .
(а)
(b) Мгновенная скорость изменения at равна at . я буду использовать вторая формула для:
Я устанавливаю и вычисляю предел:
Таким образом, мгновенная скорость изменения at равна . Это означает что если бы f продолжало изменяться с той же скоростью, то для каждых 4 единиц, что x увеличилось, функция увеличилась бы на 1 единицу.
Конечно, функция , а не продолжает изменяться в такая же ставка. На самом деле меняется скорость изменения функции! — скорость изменения функции сама по себе является функцией.
Предположим, что исследуемая функция дает положение объекта, движущегося в одном измерении. (Представьте, что что-то движется влево или вправо по оси x или предмет, который подбрасывают прямо вверх и который в конце концов падает обратно на землю.) Например, предположим, что это положение объекта в момент времени t.
средняя скорость объекта от до представляет собой изменение положения, деленное по прошедшему времени:
Обратите внимание, что это то же самое, что и наклон секущей к кривая, или средняя скорость изменения.
Мгновенная скорость ат.
Это наклон касательной к кривой или мгновенная скорость изменения. Вы также можете использовать вторую формулу
Грубо говоря, мгновенная скорость показывает, насколько быстро объект движется в определенный момент.
Пример. Положение объекта в момент времени t является
а) Найдите среднюю скорость от до .
б) Найдите среднюю скорость от до .
в) Найдите мгновенную скорость при .
(а)
(б)
Что это значит? Обратите внимание на это и . Другими словами, объект перемещался из в в , но возвращался туда, где находился. начал. Поскольку чистое изменение позиции на равнялось 0, среднее скорость была 0.
(с) я вошел
я получил
Люди, которые видели исчисление раньше, знают, что это обычно называется . производная at a. Он обозначается
То есть производная от at определяется выражением
дает мгновенную скорость изменения f при a, или наклон касательной к графику при .
Производная является функцией сама по себе. Поскольку х обычно используется для обозначения входной переменной для функции, это обычно для запишите определение производной в таком виде:
f равно дифференцируемой в точке x, если существует — то есть, если указанный выше предел определен.
Пример. Вычислить для .
Пример. Предположим
Является ли f дифференцируемым в ?
Однако определение зависит от того, является ли h положительное или отрицательное. Мне нужно взять левый и правый пределы в 1.
Правый предел равен
Левый предел равен
Поскольку левый и правый пределы совпадают, двусторонний предел существует. Таким образом,
Это показывает, что f дифференцируема при .
В этом примере функция была построена путем «склейки» две части и вместе в . Тот факт, что был определен, означает что кусочки были «гладко склеены». По аналогии, если две части функции подобны двум кускам дерева, склеены, можно было провести рукой по стыку и не почувствовать «угол» или «конек».
Геометрически дифференцируемая функция имеет касательную в каждой точка его графика. Вы подозреваете, что это исключит пробелы, скачки, или вертикальные асимптоты — типичные разрывы. Фактически, требование, чтобы дифференцируемая функция имела касательную в точке каждая точка означает, что ее график не имеет «углов» — все кривые и повороты «гладкие».
Теорема. Дифференцируемая функция непрерывный.
Доказательство. Предположим, дифференцируем в точка в. По определению,
Затем
С одной стороны, так левая сторона равна 0. С другой стороны, произведение пределов равно предел произведения, поэтому
Я могу переписать это как
Это говорит о том, что f непрерывна в точке c.
Пример. На рисунке ниже показан этот график функция . Нарисуйте график.
Я буду делать каждую часть отдельно слева направо. Часть левой руки начинается с небольшого положительного наклона. Наклон увеличивается до тех пор, пока велика и положительна на асимптоте.
Кусок в середине начинается с большого положительного наклона в конце. левая асимптота. Уменьшается до 0 — есть горизонталь касательная в верхней части «выпуклости». Продолжает снижаться, становится большим и отрицательным в правой асимптоте.
Наконец, правая часть начинается с большого отрицательного наклона. вблизи асимптоты. По мере того, как вы уходите вправо, наклон продолжается быть отрицательным, но кривая выравнивается — то есть наклон приближается к 0.
Если сложить эти наблюдения вместе, получится такая картина:
Предшествующее обсуждение предлагает следующее эмпирическое правило: если граф непрерывен в точке, но имеет там «угол», производная в углу не определена.
Это не единственный случай, когда производная может быть неопределенной: Например, производная не определена в точке, где график имеет вертикальная касательная .
No related posts.