94. Производная обратной функции.
Производная обратной функции:
y = f(х) с областью определения Д и значений Е. Если
обратное ей соответствие таково, что
для каждого у є Е, определяется единственное значение х є Д, то
мы получим обратную функцию. Обратная – х = f -1 (у)
Пусть y = f(х) имеет в точке хО производную f (xO) = lim x0 y / х.
Чтобы найти производную
обратной функции нужно найти предел lim x0 х / у = (f -1 (yO))
Вследствие непрерывности функции y = f(х) при x0 у0,
тогда
lim x0 х
/ у
= 1 / f
(хO).
Производные обратных функций обратны по величине:
х (уO) = 1 / f (хO) f (хO) 0
у (хO) = 1 / f (уO) f (уO) 0
sin и, соз и, tg и, ctg и, и», а», е“,
In и, logau, arcsin и , arcos и , arctg и , arcctg и, где и = и(х).
1. ,9.
2. 10.
3. 11.
4. 12.
5. 13.
6. 14.
7. 15.
8.
96. Гиперболические функции и их дифференцирование.
Гиперболические функции: Встречаются различные комбинации показательных
функций. Их рассматривают как новые функции:
Гип. синус – Sh — (e x – e—x) /2
Гип.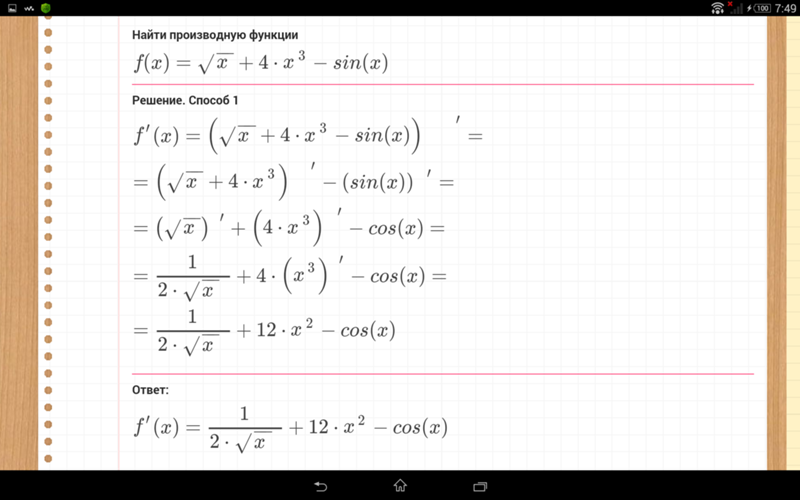 косинус — Ch
– (ex + e—x)
/ 2
косинус — Ch
– (ex + e—x)
/ 2
Гип. тангенс – th — (ex – e-x / 2) / (ex + e-x / 2)
Гип. котангенс – cth — (ex + e-x / 2) / (ex – e-x / 2)
(Sh x) = Ch x (Ch x) = — Sh x
(th x) = 1 / Ch2 x (cth x) = — 1/ Sh2 x
97. Дифференцирование функции, заданной неявно.
Пусть функция y f x = ( ) задана уравнением F x y ( , ) = 0 .
В этом случае говорят, что функция задана неявно .
Для нахождения производной считаем, что в уравнении
y зависит от x ,иначе
. Другими словами дифференцируем уравнение , считая
сложной функцией, зависящей от
F x y x , ( ) = 0 F x y x , ( ) = 0
y x .
98. Дифференцирование
функции, заданной параметрически.
. Диф. функции заданной параметрически:
Функция заданная в виде х = (t) и y = (t) — параметрическая.
предполагается
что х = (t) имеет себе обратную t = x -1 (x).
Предположим что в некоторой области изменения параметра t функции
х = (t) и y = (t) имеют
производные и не обращаются в 0. Тогда у(t) может быть представлена
как сложная функция: у = у(t) и t = х -1 (х)
ух = у (t) = уt(1/х t) = уt / хt
99.Дифференциал функции. Его связь с производной.
Дифференциал функции — это произведение производной f ’( x0 ) и
приращения аргумента :
df = f ’( x0 ) · .
100. Применение дифференциала в приближенных вычислениях.
Если приращение delt x аргумента мало по абсолютной величине,то delt y
приблизительно равно dy
и получаем формулу приближенных вычеслений с помошью дифферинциалов
f (xO +delt x) приблизительно равно f (xO) +
101. Геометрический смысл дифференциала.
Геом. смысл: y = f (xO) + f (xO)(x — xO) x — xO = х
y – f(xO) = dy dy = y – yO – приращение ординаты касательной в точке МО при
переходе
из точки МО с
абсциссой хО в точку М с абсциссой хО + х.
102. Основные правила и формулы нахождения дифференциала (таблица дифференциалов, дифференциал постоянной, суммы, произведения, частного).
103. Инвариантность формы дифференциала первого порядка.
104. Производные и дифференци Определение.
Пусть существует такое множество X, что для .
Тогда может получиться, что
производная имеет производную в некотрой точке. Такая производная называется
второй производной или производной второго порядка. Обозначается
или .
В общем виде . Переходя к дифференциалам, получаем:
. .
Не следует путать обозначения: ,.
Второй дифференциал от x равен 0 только тогда, когда x — независимая переменная
или линейная функция
от
независимой переменной. В этом случае
любой дифференциал .
То есть для
алы
высших порядков.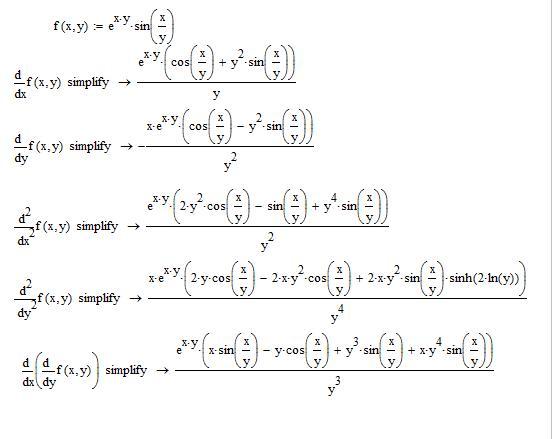
Тест по теме Производная
Тест по алгебре 11 класс
подготовила Шустова Наталия Владимировна
Уровень (базовый)
Поверяемые элементы содержания и виды деятельности:
Умение находить производную функции
1. Найдите производную функции y = ex — x7 .
2. Найдите производную функции у = ех – sinx.
1) = ех + cosx; 2) = ех — cosx; 3) = ½ е2x — cosx; 4) = е 2x — cosx.
3. Вычислите значение производной функции у=3ех+cos2x в точке хо=0.
1) 3; 2) -1; 3) 1; 4) 2.
4. Вычислите значение производной функции у=в точке хо=2. 1) 11,5; 2)10,5; 3) 11; 4) 9,5.
5. Вычислить значение производной функции у=ех sinx + x2 в точке xo=0.
1) 0; 2) 1; 3) 2; 4) 3.
6. Найдите у´(1), если y(х) = + 4ex.1) 9; 2) –5 +4е; 3) 5; 4) 5 + 4e.
7. Найдите производную функции у = x2
1) p2 -1; 2) 2p + 1; 3) 2p -1; 4) 2p.
8. Вычислите значение производной функции у = cos2x + 4x в точке хо= .
1) 2; 2) -2; 3) 4; 4) 0.
9. Вычислите значение производной функции в точке хо=2.
1) 10; 2) 12; 3) 8; 4) 6.
10. Вычислите значение производной функции у= — ln2x в точке хо = 2.
1) 3; 2) 4; 3) 2; 4) 1.
11. Найдите производную функции y = e —x -2x7 .1) y´= — e—x -14x6; 2) y´= — e—x – ; 3) y´= —e—x –2x6; 4) y´= e—x -14x6.
12. Найдите производную функции у=4х3+ е -х.
1) у´=12х2+е -х ; 2) у´=12х2 – е -х ; 3) у´=х4 — е
13. Вычислите значение производной функции у=5х — х5 в точке хо=1.
1) 0; 2)4; 3) ln5 -1; 4) 5(ln5 -1).
14. Вычислите значение производной функции в точке хо = е.
1) sin e; 2) cos e; 3) ; 4) .
15. Вычислите значение производной функции у= -5х3+ 25x2 – 24x +23 в точке хо = 1. 1) 15; 2)11; 3) 17; 4) 9.
1) 15; 2)11; 3) 17; 4) 9.
16. Найдите значение производной функции у = 5cos x – 7x в точке хо = 0.
1) -14; 2) -7; 3) -9; 4) -2.
17. Найдите производную функции .
1) ; 2) ; 3) ; 4) .
18. Найдите производную функции .
1) ; 2) ; 3) ; 4) .
19. Найдите производную функции .
1) 4х – 6+ ; 2) (2х — 3)2+ ; 3) 8х – 12 + ; 4) 4х – 6 — .
20. Найдите производную функции у = sin ex – 9x3.
1) cos ex – 27x2; 2) ex cos ex – 27x2; 3) ex-1 cos x – 27x2; 4) ex cos x – 9x2.
