Конспект открытого урока «Признаки возрастания и убывания функции. Исследование функции на экстремум»
В результате изучения темыстуденты должны
- знать: признаки возрастания и убывания функции, алгоритм исследования функции на промежуткимонотонности. Определения точек максимума и минимума функции; необходимое и достаточное условие существования экстремума, алгоритм исследования функции на экстремум.
- уметь: исследовать несложные функции на промежутки монотонности, находить экстремумы функции.
Тип урока: комбинированный.
Техническое обеспечение: интерактивная доска, компьютер.
В приложении даны варианты тестовых заданий.
Цели урока:
- Научить исследовать функцию на промежутки монотонности , находить экстремумы функции.
- Развитие мыслительных способностей, обеспечивающих анализ ситуации и разработку адекватных способов действия (анализ, синтез, сравнение).

- Формирование интереса к предмету.
На доскеназвание темы урока (Презентация. Слайд1).
Сегодня мы продолжаем изучать приложение производной и рассмотрим вопрос о её применениик исследованию функций.
Какой бы ни была ваша специальность в будущем, вы все изучаете различные объектыи процессы (физические, экономические, общественные и другие). Чтобы изучить любой процесс (будь то распад ядер, движение транспорта, изменение производительности труда) необходимо пройти следующие этапы:
- Создать математическую модель процесса или объекта, т.е. отыскать функцию, составить уравнения, описывающие процесс.
- Исследовать созданную модель, т.е. выяснить как хорошо она описывает данный объект.
- Предсказать на основе полученных результатов развитие процесса или объекта.
Сегодня на уроке мы рассмотрим небольшой элемент работы второго этапа изучения процесса, исследование одного из свойств функции — определение промежутков монотонности и экстремумов функции.
Для решения поставленной задачи, нам необходимо вспомнить некоторые вопросы, рассмотренные ранее.
Итак, внимание! Проводится фронтальный опрос
- Что называется функцией?
- Что называется областью определения функции?
- Какая функция называется возрастающей на промежутке?
- Какая функция называется убывающей на промежутке
- Что называется приращением аргумента?
- Что называетсяприращением функции?
- Что называется первой производной функции?
Определение промежутков монотонности, значит, определение тех промежутков, где функция возрастает или убывает. Давайте рассмотрим это свойство на конкретных примерах.
- Что происходит с давлением газа в цилиндре под поршнем, если увеличить объём газа при постоянной температуре? . Какая это функция? Убывающая. (Слайд 2)
- Что происходит с силой постоянного тока при увеличении напряжения на участке цепи? — вольтамперная характеристика.
 Возрастающая функция. (Слайд 3)
Возрастающая функция. (Слайд 3) - Что происходит с силой тока при размыкании цепи? Какая это функция? Убывающая. функция. (Слайд 4)
- Что происходит с давлением газа при увеличении температуры?Увеличивается (летом шины автомобиля накачивают меньше, чем зимой). (Слайд 5)
В приведённых примерах функция на всей области определения возрастает или убывает. Но может быть иначе. Если мы возьмём графики переменного тока, то эти функции (сила тока, напряжение, эдс) на разных промежутках области определения ведут себя по-разному (возрастание сменяется убыванием и наоборот (Слайд 6).
Вопрос о возрастании и убывании функции очень важен для всех областей познания. Изучив его, можно решить множество практических задач: рассчитать параметры электрической цепи, разработать график движения транспорта, при котором сумма расходов будет наименьшей, экономия труда, материалов, энергоресурсов и многие другие.
Итак, запишем тему сегодняшнего урока: Признаки возрастания и убывания функции.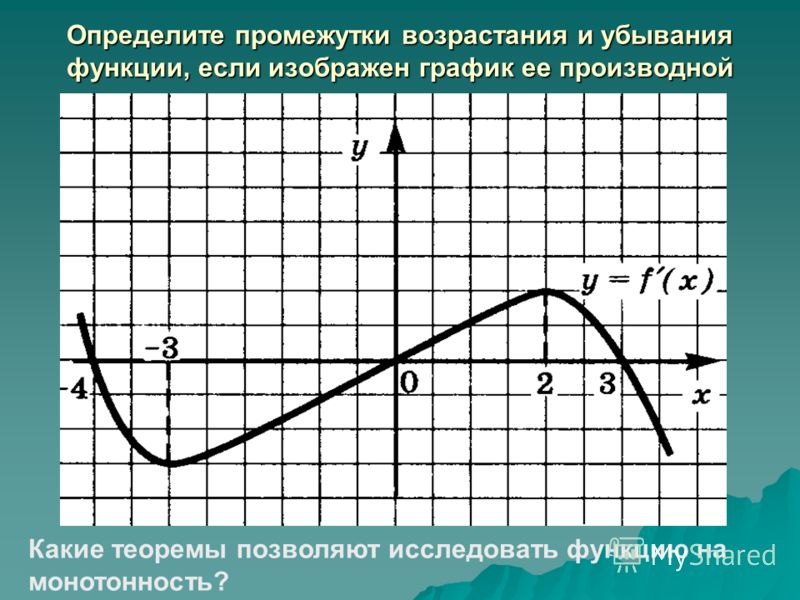 Исследование функции на экстремум.
Исследование функции на экстремум.
На уроке рассмотрим следующиевопросы: (Слайд 7)
План:
- Признаки возрастания и убывания функции.
- Максимум и минимум функции (экстремум), необходимое и достаточное условие существования максимума и минимума функции.
- Исследование функции на экстремум.
Переходим к первому вопросу.
1.
а) (Слайд 8)
>0; >0
>0; >0
>0; >0
функция возрастает
б ) (Слайд 9)
>0; >0
<0; <0.
<0; <0
функция убывает
а) Если в некотором промежутке первая производная функции больше нуля, то функция возрастает на этом промежутке;
б) Если в некотором промежутке первая производная функции меньше нуля, то функция убывает на этом промежутке.
Промежутки, на которых функция только возрастает или только убывает, называются промежутками монотонности.
Переход от возрастания к убываниюи обратно возможен лишь в точках, при переходе через которые, производная меняет свой знак. Такими точками являются те, в которых производная равна нулю или не существует, они называются критическими.
Порядок нахождения промежутков монотонности:
- Найти область определения функции.
- Найти первую производную функции.
- Найти критические точки, исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции.
Рассмотрим несколько примеровисследования функции на возрастание и убывание.
Найти промежутки монотонности функций:
1)
а) область определения ,
б) найдем первую производную:,
в)найдем критические точки: ; , и
Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.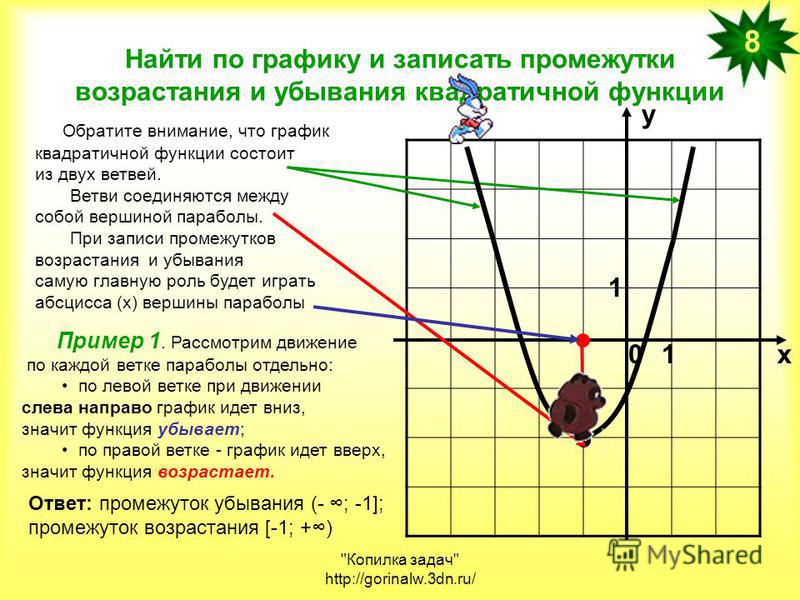
| 0 | 2 | ||||
| + | 0 | — | 0 | + | |
| ↑ | ↓ | ↑ |
Итак, в промежутках функция возрастает, в промежутке убывает.
2)
а) областьопределения ,
б) найдем первую производную: ,
в) найдем критические точки:; ,
Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.
| 0 | |||
| — | 0 | — | |
| ↓ |
Функция убывает на всей области определения.
3) .
а) область определения ,
б) найдем первую производную: ,
в) найдем критические точки:; ;
Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.
| 2,5 | |||
| — | 0 | + | |
| ↓ | ↑ |
Функция возрастает на промежутке , убывает на промежутке
Самостоятельно найти промежутки монотонности функции .
Переходим ко второму вопросу.
2. а) Пусть график некоторой функции имеет вот такой вид. (Слайд 10)
Если рассмотреть значение функции в точке , то оно будет наименьшим (минимальным), чем в любой другой из близлежащей окрестности.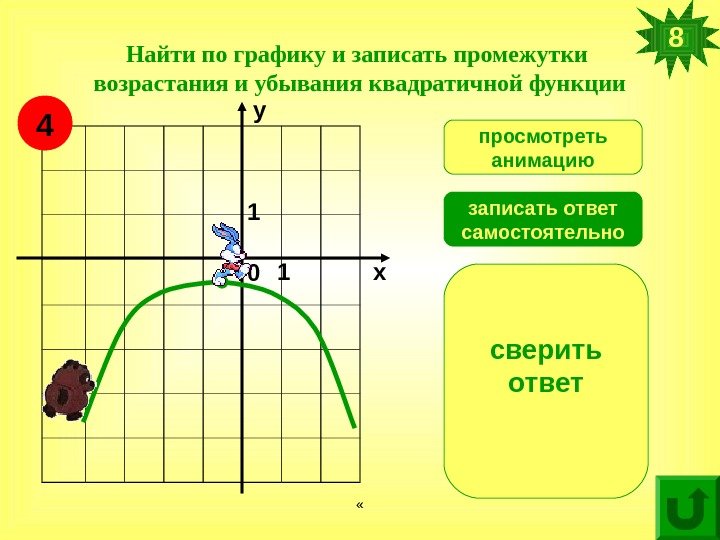 В этом случае говорят, что — точка минимума.
В этом случае говорят, что — точка минимума.
Точка из области определения функции называется точкой минимума, если для любого изокрестноститочки выполняется неравенство > .
б) Если рассмотреть значение функции в точке
Точка из области определения функции называется точкой максимума, если для любого изокрестноститочки выполняется неравенство <
Максимум и минимум функции объединяют словом экстремум ( с латинского — крайний), а точки максимума и минимума называют точками экстремума (экстремальными точками)
Не следует считать, что максимум является наибольшим на всей области определения этой функции; он является наибольшим лишь по сравнению со значениями, взятыми в некоторой окрестности точки максимума. На данном интервале функция может иметь несколько максимумов, причём некоторые из максимумов могут быть меньше некоторых минимумов (Слайд 12).
На данном интервале функция может иметь несколько максимумов, причём некоторые из максимумов могут быть меньше некоторых минимумов (Слайд 12).
При каких же условиях функция имеет экстремум? Исследуем поведение функции в окрестности точек экстремума. Видно, что точкамаксимума служит границей перехода от возрастания к убыванию функции, а точка минимума — от убывания к возрастанию.
Необходимое условие существования экстремума функции в точке: Если -точка экстремума функции и в этой точке функция дифференцируема, то производная в этой точке равна нулю.
(Точками экстремума могут служить лишь критические точки, в которых производная равна нулю или не существует).
Необходимое условие не является достаточным, т.е. из того факта, что производная равна нулю в некоторой точке, не следует, что функция в этой точке имеет экстремум(например, функция ).
Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с «+» на «-«, а для минимума с «-» на «+».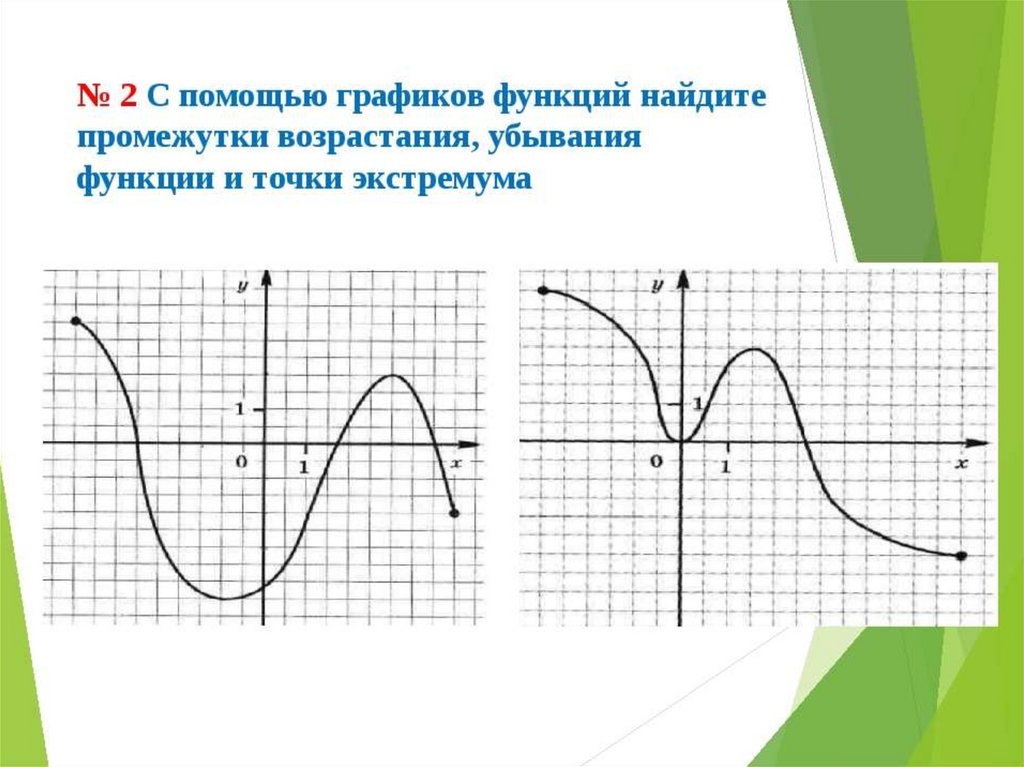 Если при переходе через критическую точкусмены знака производной не происходит, то в данной точке экстремума нет .
Если при переходе через критическую точкусмены знака производной не происходит, то в данной точке экстремума нет .
Переходим к третьему вопросу.
3. План исследования функции на экстремум:
- Найти область определения функции.
- Найти производную.
- Найти критические точки, в которых производная равна нулю или не существует. Расположить их в порядке возрастания.
- Исследовать знак производной в полученных промежутках.
- Вычислить значение функции в точках максимума и минимума.
Найти экстремумы функций:
а);
- область определения ,
- найдем первую производную: ,
- найдем критические точки: ; ;
Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.
| -1 | 0 | 1 | |||||
| — | 0 | + | 0 | — | 0 | + | |
| ↓ | Минимум 0,5 |
↑ | Максимум 0 |
↓ | Минимум 0,5 |
↑ |
б);
- область определения ,
- найдем первую производную ;
- найдем критические точки: ; ;
Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.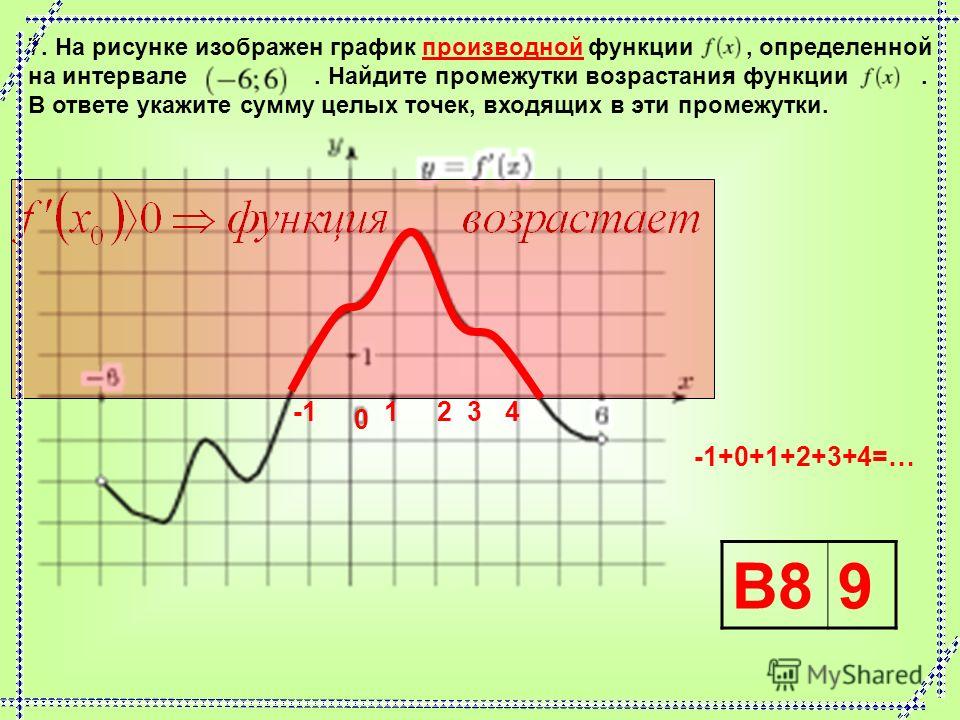
| 2,5 | |||
| — | 0 | + | |
| ↓ | Минимум 1,25 |
↑ |
в)
- область определения ,
- найдем первую производную6
- найдем критические точки: ; ,
Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.
| -2 | 2 | ||||
| — | 0 | + | 0 | — | |
| ↓ | Минимум -11 |
↑ | Максимум 21 |
↓ |
В конце урока , в качестве проверки усвоения нового материала проводится тестирование. (Слайды 13-17)
(Слайды 13-17)
— Что такое формула экспоненциального распада? Примеры
Прежде чем узнать формулу экспоненциального убывания, сначала давайте вспомним, что понимается под экспоненциальным убыванием. При экспоненциальном распаде величина сначала медленно убывает, а затем быстро убывает. Мы используем формулу экспоненциального распада, чтобы найти убыль популяции (амортизацию), и мы также можем использовать формулу экспоненциального распада, чтобы найти период полураспада (количество времени, в течение которого население становится вдвое меньше своего размера). Давайте узнаем больше о формуле экспоненциального распада вместе с решенными примерами
Что такое формулы экспоненциального распада?
Формула экспоненциального затухания помогает найти быстрое уменьшение в течение определенного периода времени, то есть экспоненциальное уменьшение. Формула экспоненциального распада используется для определения распада населения, периода полураспада, распада радиоактивности и т. д. Общая форма: f(x) = a (1 — r) x .
д. Общая форма: f(x) = a (1 — r) x .
Где
a = начальное количество
1-r = коэффициент затухания
x= период времени
Формула экспоненциального затухания
Количество медленно уменьшается, после чего скорость изменения и скорость роста быстро уменьшаются в течение определенного периода времени. Это уменьшение роста рассчитывается с использованием формулы экспоненциального затухания. Формула экспоненциального распада может быть представлена в одной из следующих форм:
f(x) = ab x
f(x) = a (1 — r) x
P = P\(_0\) e — k t
Где,
- a (или) P\(_0\) = Начальная сумма
- b = коэффициент затухания
- r = скорость затухания (для экспоненциального затухания)
- x (или) t = временные интервалы (время может быть в годах, днях или (или) месяцах, все, что вы используете, должно быть одинаковым во всей задаче).

- k = константа пропорциональности
- e- постоянная Эйлера
Примечание. При экспоненциальном затухании всегда 0 < b < 1. Здесь b = 1 - r ≈ e — k .
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Забронируйте бесплатный пробный урок
Примеры использования формул экспоненциального распада
Пример 1. Крис купил новую машину за 20 000 долларов. Стоимость автомобиля уменьшается экспоненциально (амортизируется) со скоростью 8% в год. Тогда какова стоимость автомобиля через 5 лет? Решите это с помощью экспоненциальных формул и округлите ответ до ближайших двух знаков после запятой.
Решение:
Начальная стоимость автомобиля P = 20 000 долларов.
Скорость распада r = 8% = 0,08.
Время t = 5 лет.
Используя формулу экспоненциального распада:
A = P (1 — r) t
A = 20000 (1 — 0,08) 5 = 13181,63
2 = 13181,63
2 .
Пример 2. Джейн купила новый дом за 350 000 долларов. Стоимость дома уменьшается экспоненциально (амортизируется) со скоростью 5 % в год. Тогда какова стоимость дома через 2 года? Решите это с помощью экспоненциальных формул и округлите ответ до ближайших двух знаков после запятой.
Решение:
Начальная стоимость дома = 3 500 000 долларов США
Скорость разрушения, r = 5% = 0,05
Время, t = 2 года
A = P (1 — R) T
A = 350000 (1 — 0,05) 2
A = 315 875
Следовательно, значение дома через 2 года = 315 875 долл. США
Пример 3: Период полураспада углерода-14 составляет 5730 лет. Найдите модель экспоненциального распада углерода-14. Решите его, используя формулу экспоненциального распада, и округлите константу пропорциональности до 4 знаков после запятой.
Решение:
Используя данные, мы можем сказать, что углерод-14 распадается, и поэтому мы используем формулу экспоненциального распада.
P = P\(_0\) e — k t
Здесь P\(_0\) = начальное количество углерода
Известно, что период полураспада углерода-14 составляет 5730 лет. Это означает, что
P = P\(_0\) / 2 = половина исходного количества углерода при t = 5, 730.
Подставим все эти значения в формулу экспоненциального распада:
P\(_0\) / 2 =P\(_0\) e — k (5730)
Разделив обе части на P\(_0\),
0,5 = e — k (5730)
Взяв «ln» с обеих сторон,
ln 0,5 = -5730k
Разделив обе стороны на -5730,
k = ln 0,5 / (-5730) ≈ 1,2097
модель углеродно-экспоненциального распада 14: P = P\(_0\) e — 1,2097k
Часто задаваемые вопросы о формулах экспоненциального распада
Что такое формула экспоненциального распада?
Количество медленно уменьшается через равные промежутки времени на фиксированный процент. Это уменьшение роста рассчитывается по формуле экспоненциального затухания. Общая форма: f(x) = a (1 — r) x ,
Это уменьшение роста рассчитывается по формуле экспоненциального затухания. Общая форма: f(x) = a (1 — r) x ,
, где
- a = начальная сумма
- r = скорость распада
- x = временной интервал
Формула экспоненциального распада используется для определения распада населения, периода полураспада, радиоактивного распада и т. д.
Что такое формула для нахождения экспоненциального распада?
Формула экспоненциального затухания помогает найти быстрое уменьшение за определенный период времени, то есть экспоненциальное уменьшение. Это уменьшение роста рассчитывается с использованием формулы экспоненциального затухания. Формула экспоненциального распада может быть представлена в одной из следующих форм:
f(x) = a (1 — r) x (общая форма)
P = P\(_0\) e — k t (для непрерывного экспоненциального затухания)
где
- a (или) P\(_0\) = исходное количество
- b = коэффициент затухания
- r = скорость распада
- x (или) t = интервалы времени
- k = константа пропорциональности
- e- постоянная Эйлера
Как рассчитать экспоненциальное затухание?
Экспоненциальная формула: y = ab x .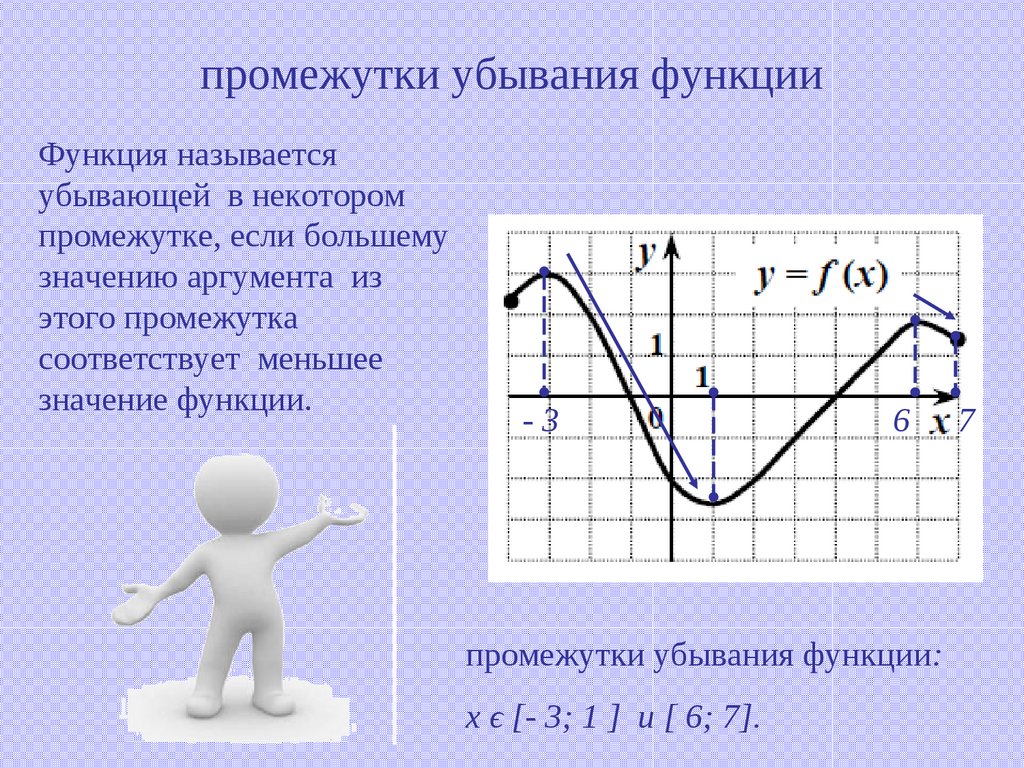 Здесь b — коэффициент затухания. Распад рассчитывается как (1-r), где r = скорость распада. Теперь у — функция затухания. у = а (1-r) х .
Здесь b — коэффициент затухания. Распад рассчитывается как (1-r), где r = скорость распада. Теперь у — функция затухания. у = а (1-r) х .
Как найти скорость затухания экспоненциальной функции?
Формула экспоненциального затухания: f(x) = a b x , где b — коэффициент затухания. Скорость затухания в экспоненциальной функции затухания выражается в виде десятичной дроби. Скорость затухания указана в процентах. Мы преобразуем его в десятичное число, просто отбросив % и разделив его на 100. Затем найдем коэффициент затухания b = 1-r. Например, если скорость затухания составляет 12%, то скорость затухания экспоненциальной функции равна 0,12, а коэффициент затухания b = 1-0,12 = 0,88
Сравнение роста и затухания — экспоненциальные функции
В реальных условиях существуют явления, при которых количества либо растут, либо затухают по экспоненте. Как правило, это такие ситуации, как неконтролируемый рост населения, радиоактивный распад или сложные проценты. Изучение их с точки зрения роста и распада помогает понять их поведение в долгосрочной перспективе.
Изучение их с точки зрения роста и распада помогает понять их поведение в долгосрочной перспективе.
Экспоненциальный рост происходит, когда количество увеличивается на на то же самое за равные промежутки времени. Это приводит к , где в показателе степени t есть время.
г=a⋅bt
Поскольку количество увеличивается на с течением времени, постоянный множитель b должен быть на больше , чем 1. Таким образом, коэффициент роста b может быть выражен как b=1+r, где r — некоторое положительное число. Полученная функция называется функцией экспоненциального роста .
Тогда константа r может быть интерпретирована как скорость роста в десятичной форме. Например, значение 0,06 означает, что количество увеличивается на 6% за каждую единицу времени. Как и в случае со всеми экспоненциальными функциями, a — это координата y точки .
Поскольку коэффициент роста больше 1, количество растет все быстрее и быстрее, без ограничений.
Аналогом экспоненциального роста является экспоненциальный спад; когда величина уменьшается на на один и тот же коэффициент за равные промежутки времени, постоянный множитель экспоненциальной функции затухания меньше 1. Этот коэффициент может быть выражен как (1−r) и известен как коэффициент затухания . .
Тогда константу r можно интерпретировать как скорость распада , в десятичной форме. Например, значение 0,12 будет означать, что количество уменьшается на 12% в каждую единицу времени.
Поскольку коэффициент затухания меньше 1, величина со временем уменьшается до 0.
В идеальной среде популяции бактерий растут экспоненциально и могут быть смоделированы с помощью функции экспоненциального роста. Бактерии Lactobacillus acidophilus размножаются примерно раз в час. Одна бактериальная клетка находится в идеальной среде. Сформулируйте и интерпретируйте константы a и r для роста, который произойдет. Затем напишите функциональное правило, описывающее этот рост.
Затем напишите функциональное правило, описывающее этот рост.
Показать решение expand_more
Константа a — это начальное значение количества, в данном случае количества бактерий. В окружающую среду была помещена только одна бактерия, поэтому a равно 1. Константа r — это скорость роста. Поскольку бактерии размножаются каждый час, количество бактерий удваивается каждый час. Это соответствует увеличению на 100%. Таким образом, r равно 1. Подстановка этого правила в правило экспоненциальной функции роста дает
P(t)=1⋅(1+1)t,
который можно упростить как
P(t)=2t.
Поскольку это экспоненциальная функция роста, население будет расти все быстрее и быстрее, без ограничений. В реальной среде этого бы не произошло, так как доступное пространство и питание должны были бы быть бесконечными. В какой-то момент окружающая среда перестанет быть идеальной, поэтому рост замедлится или остановится.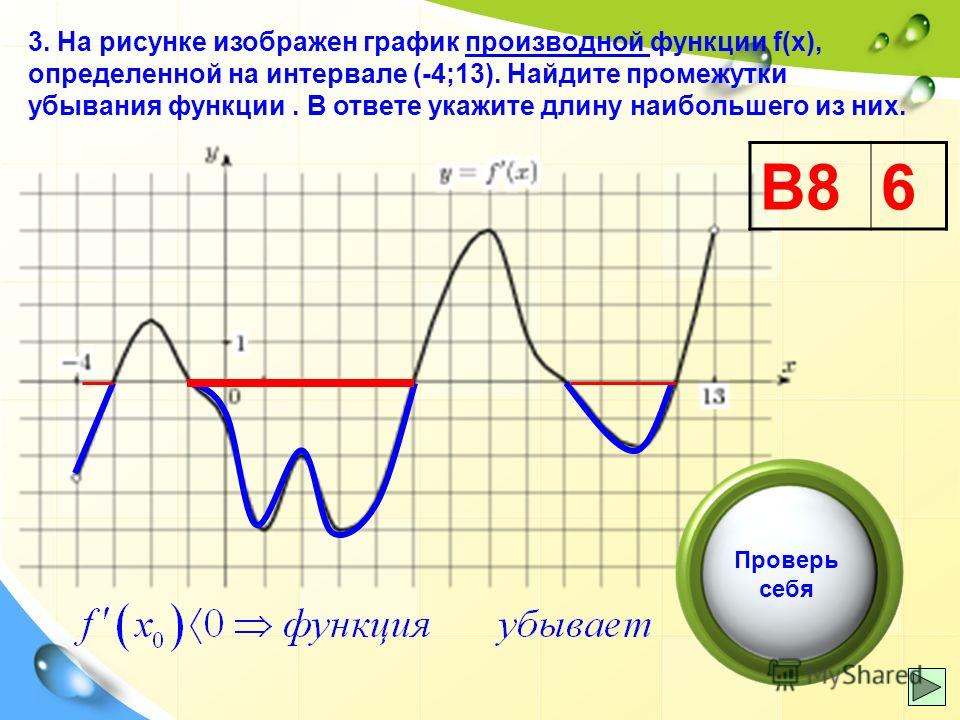
Для экспоненциальной функции роста, записанной как
у=а⋅(1+r)т,
количество (1+r) называется фактор роста. Аналогично, для ,
у=а⋅(1−r)т,
(1−r) называется коэффициентом затухания . В контексте часто указывается скорость роста или распада, r. Используя r, можно оценить соответствующий коэффициент роста или распада. Например, рост на 10% в каждую единицу времени дает фактор роста
(1+r)=(1+0,1)=1,1.
Точно так же может быть необходимо использовать коэффициент роста или затухания, чтобы найти скорость роста или затухания. Например, коэффициент 0,85 указывает на распад. Таким образом, r можно найти, приравняв 0,85 коэффициенту затухания (1−r) и решив уравнение.
(1−r)=0,85⇔r=0,15
Численность карпа в небольшом озере за некоторый период времени можно смоделировать функциейН(т)=800⋅0,88т,
где t — время в годах.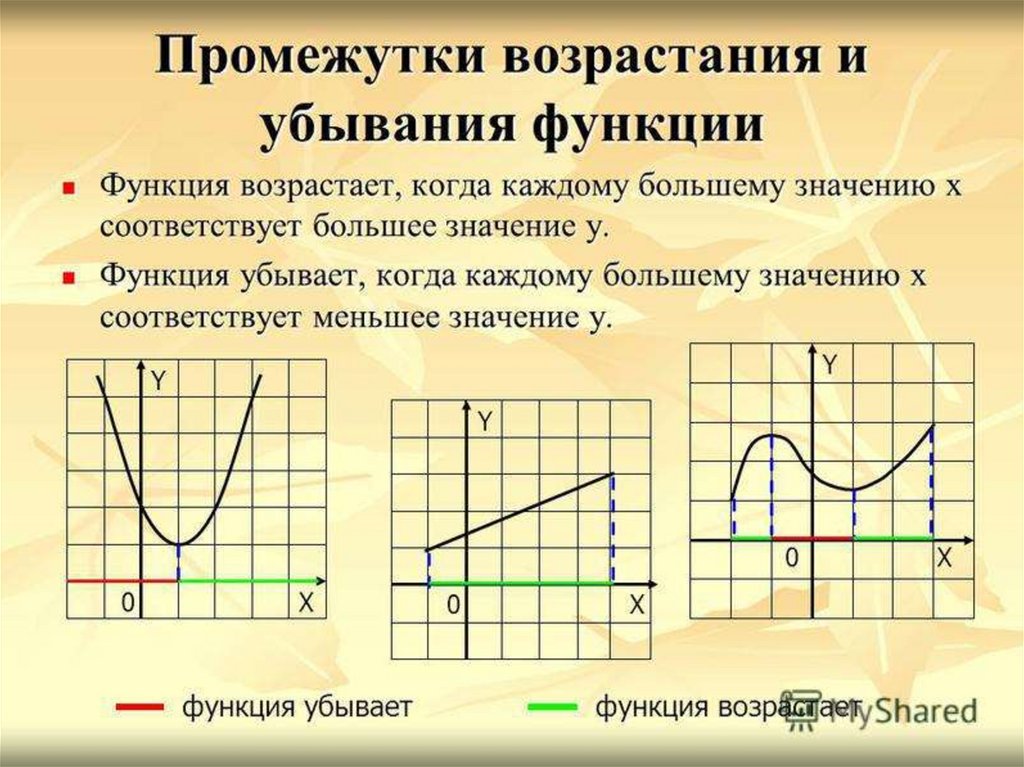 Укажите, показывает ли функция рост или убывание, а затем найдите скорость роста или убывания r. Наконец, нарисуйте график функции.
Укажите, показывает ли функция рост или убывание, а затем найдите скорость роста или убывания r. Наконец, нарисуйте график функции.Показать решение expand_more
Для начала проанализируем данное правило функции. Он записывается в виде y=a⋅bx, где a — начальное значение, а b — постоянный множитель/коэффициент роста. Постоянный множитель 0,88 меньше 1, поэтому это коэффициент затухания. Следовательно, функция показывает затухание. Поскольку коэффициент затухания всегда равен 1−r, мы можем написать уравнение.
0,88=1−r,
которое можно решить относительно r.
0,88=1−r
0,88+r=1
r=0,12
Таким образом, скорость распада составляет 0,12, или 12%, в год. Начальное значение равно 800, а постоянный множитель равен 0,88. Используя эту информацию, мы можем построить несколько точек, лежащих на H, и соединить их плавной кривой.
Когда деньги вносятся на сберегательный счет, накапливаются, часто ежегодно — разные виды процентов работают по-разному. Сложные проценты — это когда полученные проценты добавляются к первоначальной сумме, а будущие проценты начисляются на большую сумму. Чтобы узнать баланс счета в любой момент времени, можно использовать . Когда проценты начисляются ежегодно, баланс можно смоделировать с помощью функции.
Сложные проценты — это когда полученные проценты добавляются к первоначальной сумме, а будущие проценты начисляются на большую сумму. Чтобы узнать баланс счета в любой момент времени, можно использовать . Когда проценты начисляются ежегодно, баланс можно смоделировать с помощью функции.
y=P(1+r)t
В этом контексте P обозначает основную сумму , которая является начальной суммой денег, а r представляет собой процентную ставку в десятичной форме. Если проценты не начисляются ежегодно, функция выглядит немного иначе.
y=P(1+nr)nt
Константа n – это число начислений сложных процентов в год, а r – это по-прежнему годовая процентная ставка. Для счета с основной суммой 100 долларов и годовой процентной ставкой 15%, начисляемой два раза в год, функция роста выглядит следующим образом:
Б(т)=100(1+20,15)2т
Обратите внимание, что эта функция постоянно растет, тогда как на самом деле баланс счета увеличивается только во время начисления.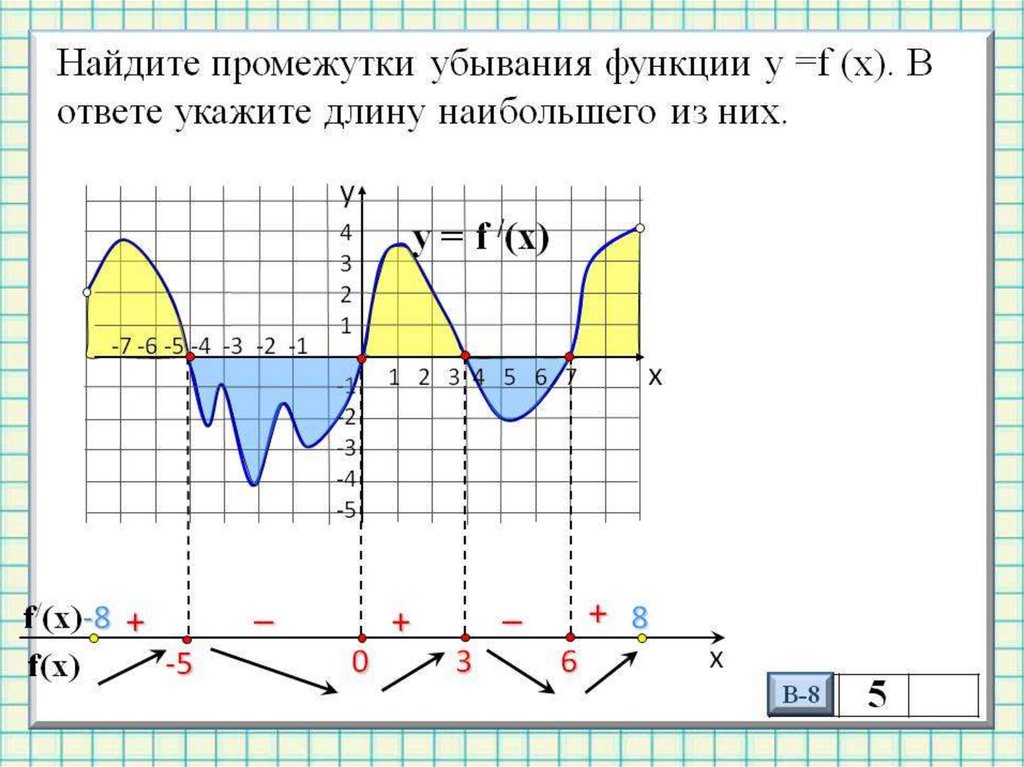 График функции вместе с фактическим балансом счета покажет, как ее можно использовать на практике.
График функции вместе с фактическим балансом счета покажет, как ее можно использовать на практике.
Каждый раз, когда проценты начисляются, в данном случае каждые полгода, значение B равно остатку на счете. Однако во всех остальных случаях это не так. Чтобы найти, например, остаток на счете через 1,75 года, следует оценить B(1,5), поскольку это был последний раз, когда проценты начислялись.
Один сберегательный счет с основной суммой $100 предлагает годовую процентную ставку 15%, начисляемую два раза в год. Найдите остаток на счете через 5 лет. Другой сберегательный счет с той же основной суммой будет иметь тот же баланс через 5 лет. Однако проценты начисляются ежемесячно. Найдите процентную ставку по второму счету.
Показать решение expand_more
Сначала найдем правило функции, описывающее рост первого счета. Дано, что P=100, r=0,15 и n=2. Подстановка этих значений в формулу сложных процентов дает
B(t)=100(1+20,15)2t.
Прежде чем продолжить, упростим эту функцию.
B(t)=100(1+20,15)2t
B(t)=100(1+0,075)2t
B(t)=100⋅1,0752t
Поскольку проценты будут начисляться в течение 5 лет, t=5. Следовательно, мы можем найти баланс счета, оценив B (5).
B(t)=100⋅1,0752t
B(5)=100⋅1,0752⋅5
B(5)=100⋅1,07510
B(5)=206,10315…
3
3
Баланс счета составляет $ 206,10 через 5 лет. Теперь мы можем рассмотреть второй счет. Мы знаем, что баланс на обоих счетах одинаков, по крайней мере, когда проценты по обоим только что были начислены. Это означает, что B(t) также описывает рост во втором счете. Однако, поскольку проценты по второму счету начисляются ежемесячно, или 12 раз в год, n=12. Таким образом, показатель степени в правиле должен быть равен 12t. Используя равенство
2т=1/6⋅12т
и , мы можем переписать B(t) так, чтобы можно было найти месячную процентную ставку.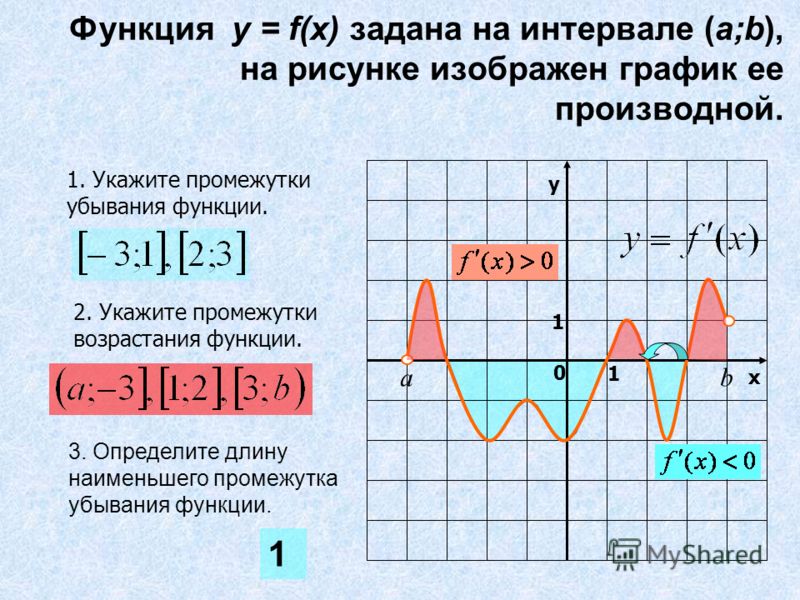


 Возрастающая функция. (Слайд 3)
Возрастающая функция. (Слайд 3)