Простейшие системы уравнений с двумя неизвестными: Системы уравнений. Простейшие системы уравнений с двумя неизвестными

Системы уравнений. Простейшие системы уравнений с двумя неизвестными

Урок 16. Подготовка к ЕГЭ по математике

В данном видеоуроке мы вспомним, что называют системой уравнений, решением системы уравнений и что означает решить систему уравнений. Повторим теоремы о равносильности систем уравнений. Вспомним основные методы решения систем уравнений.

Конспект урока «Системы уравнений. Простейшие системы уравнений с двумя неизвестными»

Напомним, что любое конечное множество уравнений называется системой уравнений.

Систему уравнений принято записывать с помощью фигурной скобки.

Общий вид системы двух уравнений с двумя переменными:

Решением системы двух уравнений с двумя переменными называется пара чисел , при подстановке которых вместо соответствующих переменных  оба уравнения системы обращаются в верные числовые равенства.

Решить систему уравнений – значит найти все её решения или доказать, что решений нет.

Две системы уравнений называются

равносильными, если они имеют одно и то же множество решений. Если обе системы не имеют решений, то они также считаются равносильными.

Теоремы о равносильности систем уравнений.

1. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а второе уравнение заменить равносильным, то полученная система будет равносильна заданной.

2. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а второе заменить суммой или разностью обоих уравнений системы, то полученная система будет равносильна заданной.

3. Если обе части уравнения  ни при каких ,  одновременно не обращаются в нуль, то следующие системы равносильны:

  

Вспомним основные методы решения систем уравнений. Итак, основными методами решения систем уравнений являются метод алгебраического сложения, метод подстановки и метод введения новых переменных.

Метод алгебраического сложения. Сущность этого метода заключается в следующем:

1. обе части первого уравнения умножают на некоторый множитель, обе части второго уравнения умножают на другой множитель (если это требуется). Эти множители подбираются так, чтобы коэффициенты при одной из переменных в обоих уравнениях стали противоположными числами;

2. уравнения почленно складывают и решают полученное уравнение с одной переменной;

3. вторую переменную находят подстановкой найденного значения первой переменной в одно из уравнений системы.

Решите систему уравнений .

Решение.

Решите систему уравнений .

Решение.

Метод подстановки. Сущность этого метода заключается в следующем:

1) выражают из какого-либо уравнения системы одну переменную через другую;

2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;

3) решают получившееся уравнение с одной переменной;

4) находят соответствующие значения второй переменной.

Решите систему уравнений .

Решение.

Решите систему уравнений .

Решение.

Метод введения новых переменных. При сопутствующем выборе вспомогательных переменных иногда решение исходной системы можно свести к решению более простой системы уравнений, чем исходная.

Решите систему уравнений .

Решение.

Решите систему уравнений .

Решение.

Рассмотренные методы решения систем уравнений применяются и к решению систем, содержащих показательную и логарифмическую функции.

Решите систему уравнений .

Решение.

Решите систему уравнений .

Решение.

Предыдущий урок 15 Показательные уравнения. Логарифмические уравнения

Следующий урок 17 Квадратные неравенства. Рациональные неравенства. Иррациональные неравенства

Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ЕГЭ по математике

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Конспект урока «Решение систем уравнений с двумя переменными»

Тема:   Решение сис­те­м ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми

 

Урок №  ___                                 6   класс                               Сиротина Г.В.

Дата:     __ 04,20__    

 

Цель: научить и закрепить умения решать линейные уравнения с двумя переменными разными способами.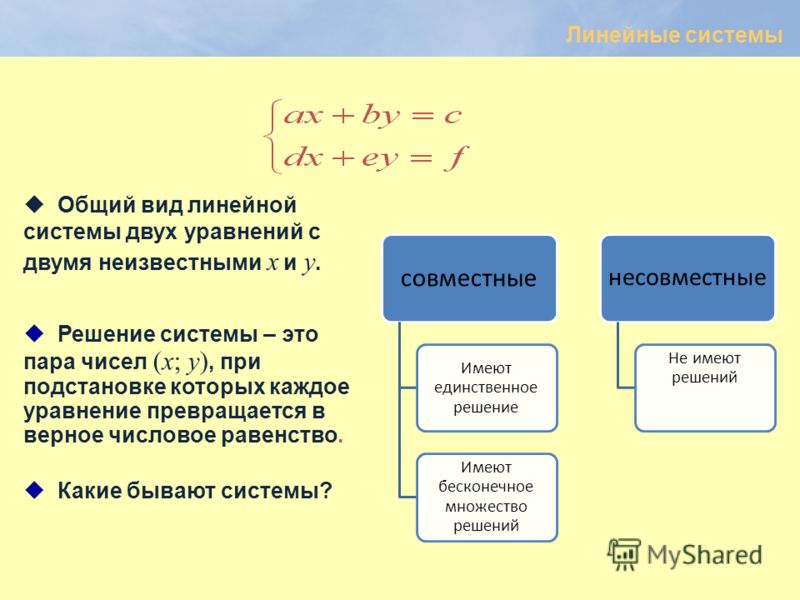

Задачи:

·      Закрепить правила выполнения решения систем уравнений

·      Развивающие – умение преобразовывать выражения, способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, развитию математического кругозора, мышления и речи, внимания и памяти.

·      Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, мобильности, умения общаться, общей культуры.

План урока:

       I.            Оргмомент.(2 мин)

    II.            Проверка домашнего задания.(3 мин)

 III.            Устный счет.(5 мин)

IV.            Систематизация теоретического материала по сложению.(10 мин)

   V.            Закрепление материала.(15)

VI.            Подведение итогов урока.(5 мин)

VII.            Домашнее задание.(5 мин)

Ход урока:

      I.            Оргмомент.(2 мин)

   II.             Проверка домашнего задания.(3 мин)

III.            Устный счет.(5 мин)

IV.            Систематизация теоретического материала

 1. Понятие системы двух линейных уравнений с двумя неизвестными, основные факты

На­пом­ним, что из себя пред­став­ля­ет си­сте­ма двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми. Это си­сте­ма вида:

Из пер­во­го урав­не­ния  можно по­лу­чить ли­ней­ную функ­цию, в слу­чае если : . Гра­фик дан­но­го урав­не­ния – пря­мая линия.

Bто­рое ли­ней­ное урав­не­ние:

, из него также можно по­лу­чить ли­ней­ную функ­цию, при усло­вии, что : . Гра­фик дан­но­го урав­не­ния – также пря­мая линия.

За­пи­шем си­сте­му в дру­гом виде:

Мы знаем, что мно­же­ством ре­ше­ний пер­во­го урав­не­ния яв­ля­ет­ся мно­же­ство точек, ле­жа­щих на со­от­вет­ству­ю­щей ему пря­мой, ана­ло­гич­но и для вто­ро­го урав­не­ния мно­же­ство ре­ше­ний – это мно­же­ство точек на дру­гой пря­мой. Две пря­мые могут пе­ре­се­кать­ся – и тогда у си­сте­мы будет един­ствен­ное ре­ше­ние, един­ствен­ная пара чисел х и у будет удо­вле­тво­рять од­но­вре­мен­но обоим урав­не­ни­ям. Это про­ис­хо­дит, если . Две пря­мые также при неко­то­рых зна­че­ни­ях чис­лен­ных па­ра­мет­ров могут быть па­рал­лель­ны, в таком слу­чае они ни­ко­гда не пе­ре­се­кут­ся и не будут иметь ни одной общей точки, зна­чит в этом слу­чае си­сте­ма не будет иметь ре­ше­ний. Для этого долж­ны вы­пол­нять­ся усло­вия:  и . Кроме того, две пря­мые могут сов­па­дать, и тогда каж­дая точка будет ре­ше­ни­ем обоих урав­не­ний, а зна­чит си­сте­ма будет иметь бес­чис­лен­ное мно­же­ство ре­ше­ний. Для этого долж­ны вы­пол­нять­ся усло­вия:  и .

 2. Способ подстановки

При­мер 1:

На дан­ном урав­не­нии можно про­де­мон­стри­ро­вать сразу несколь­ко спо­со­бов ре­ше­ния си­стем урав­не­ний.

1 спо­соб – спо­соб под­ста­нов­ки: вы­ра­зим во вто­ром урав­не­нии х и под­ста­вим по­лу­чен­ное вы­ра­же­ние в пер­вое урав­не­ние:

Под­ста­вим най­ден­ное зна­че­ние у во вто­рое урав­не­ние и най­дем зна­че­ние х:

 3. Способ алгебраического сложения

2 спо­соб – спо­соб ал­геб­ра­и­че­ско­го сло­же­ния: вы­пол­ним сло­же­ние урав­не­ний:

Из по­лу­чен­но­го урав­не­ния най­дем х:

Те­перь вы­чтем из пер­во­го урав­не­ния си­сте­мы вто­рое:

Таким об­ра­зом, мы по­лу­чи­ли ре­ше­ние си­сте­мы двумя спо­со­ба­ми, и это ре­ше­ние – точка с ко­ор­ди­на­та­ми (2; 1).

 4. Системы уравнений с одним решением

При­мер 2:

В дан­ном слу­чае удоб­нее при­ме­нить спо­соб ал­геб­ра­и­че­ско­го сло­же­ния, вы­чтем из вто­ро­го урав­не­ния пер­вое. По­лу­ча­ем:

Най­дем зна­че­ние у:

Под­ста­вим зна­че­ние у во вто­рое урав­не­ние и най­дем х:

Ответ: (60; 30).

При­мер 3:

В дан­ной си­сте­ме нет пе­ре­мен­ных с оди­на­ко­вы­ми ко­эф­фи­ци­ен­та­ми, но мы можем их урав­нять са­мо­сто­я­тель­но, для этого вы­пол­ним пре­об­ра­зо­ва­ния:

Вы­пол­ним сло­же­ние урав­не­ний:

23y = -46, y = -2

Под­ста­вим по­лу­чен­ное зна­че­ние у в пер­вое урав­не­ние и опре­де­лим зна­че­ние х:

Ответ: (-3; -2).

   V.            Закрепление материала.(15)

При­мер 4:

Раз­де­лим вто­рое урав­не­ние на два:

Вы­чтем из пер­во­го урав­не­ния вто­рое:

Оче­вид­но, что по­лу­чен­ное вы­ра­же­ние не за­ви­сит от зна­че­ний пе­ре­мен­ных си­сте­мы и не яв­ля­ет­ся вер­ным чис­ло­вым ра­вен­ством, зна­чит, си­сте­ма не имеет ре­ше­ний. В дан­ном слу­чае ре­ко­мен­ду­ет­ся гра­фи­че­ски до­ка­зать, что си­сте­ма не имеет ре­ше­ний, для этого из урав­не­ний за­пи­сать ли­ней­ные функ­ции, по­стро­ить их и по­ка­зать, что пря­мые па­рал­лель­ны.

При­мер 5:

Оче­вид­но, что, если раз­де­лить вто­рое урав­не­ние на два, по­лу­чим пер­вое урав­не­ние:

Мы по­лу­чи­ли два оди­на­ко­вых урав­не­ния, зна­чит, чтобы до­ве­сти ре­ше­ние си­сте­мы до конца, можем оста­вить одно: ; это ли­ней­ное урав­не­ние с двумя пе­ре­мен­ны­ми, гра­фик его – пря­мая линия, и оно имеет бес­чис­лен­ное мно­же­ство ре­ше­ний, а зна­чит и си­сте­ма имеет бес­чис­лен­ное мно­же­ство ре­ше­ний. Чтобы за­пи­сать ре­ше­ния, вы­ра­зим у: , таким об­ра­зом, дадим ответ: х – любое число, 

Гра­фи­че­ская ил­лю­стра­ция (рис. 1):

Рис. 1

VI.            Подведение итогов урока.(5 мин)

VII.            Домашнее задание.(5 мин)

Вывод: мы рас­смот­ре­ли си­сте­мы двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми, ва­ри­ан­ты и спо­со­бы их ре­ше­ния. Мы вспом­ни­ли неко­то­рые тер­ми­ны, по­ня­тия и свой­ства и ре­ши­ли при­ме­ры для за­креп­ле­ния тех­ни­ки.

 

Тема: Проценты.

 

Урок №   ____                                5 класс                                         Сиротина Г.В.

Дата: __.04.20__

 

Цель урока:

Ознакомить учащихся с понятием “проценты”;Обозначать, читать и находить процент чисел и некоторых единиц измерения величин;

Задачи:

Образовательные: научить считать проценты

Развивающие: приобретение каждым учеником веры в свои силы, уверенности в своих способностях и возможности , развитие абстрактного мышления, воображения

Воспитательные: воспитание усидчивость, навыков жизни. развитие осознанных мотивов учения, побуждающих учащихся к активной познавательной деятельности

 

Тип урока: объяснение и первичное закрепление учебного материала.

Технологии: учебная мультимедийная презентация.

Оборудование: проектор с экраном для демонстрации презентации, компьютер.

План урока:

1. Организационный момент. (2 мин)

2. Актуализация опорных знаний (5 мин)

3. Работа по теме урока (20 мин)

4. Физкультминутка (2 мин)

5. Самостоятельная работа (9 мин)

6. Заключение (5 мин)

7. Подведение итогов урока (2 мин)

ХОД УРОКА

I. Организационный момент (2 мин.)

Проверка готовности к уроку. Объявление темы и цели урока.

Смена тетрадей.

(СЛАЙДЫ 1-6)

Будь внимательней дружок, 
Начинаем мы урок
Посмотрите все ль в порядке:
Книжка, ручка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.

2. Мотивация урока

— Здравствуйте, ребята! Сегодняшний урок я хочу начать словами французского философа

Ж. Ж. Руссо (1712-1778): “Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошего умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” (СЛАЙД 7)

Я желаю вам сегодня удачи. Вы готовы к работе?

 II. Актуализация опорных знаний.

1.Устные упражнения. (СЛАЙД 8)

Чтобы узнать тему нашего урока вы должны правильно выполнить вычисления и вписать в таблицу буквы, соответствующие найденным ответам. Расположите в порядке убывания.

3.5

3.2

1.5

0.9

0.36

0.25

0. 1

— Итак, ребята, тема сегодняшнего урока – “Проценты”. Это универсальная величина, которая появилась из практической необходимости измерения различных величин. Она очень важная в курсе математики. В этом году мы начнём эту тему. В 6-ом классе мы к ней вернёмся при изучении пропорций.

— Ребята, как вы думаете, где в повседневной жизни встречаются проценты?

Ответы учащихся:

— можно услышать, например, что, в выборах приняли участие 45% избирателей;

— при получении кредитов;

— рейтинг победителя хит-парада 78%;

— успеваемость в классе 100%;

— молоко содержит 5 % жира;

— материал содержит 97% хлопка и т.д.

А также в повседневной жизни встречается очень много задач на нахождение процентного отношения чисел. Полученные знания на уроках математики вам помогут в дальнейшем при решении задач по физике, по химии. При сдаче ЕГЭ дают текстовые задачи на проценты. Поэтому наша цель, научиться решать уже сейчас, и в дальнейшем применять полученные знания.

Повторение изученного материала

— Вспомните:

Правило умножения десятичной дроби на 100;

Правило деления десятичной дроби на 100;

Вопросы: (СЛАЙД 9-10)

1) Сколько килограммов в одном центнере? Какую часть центнера составляет 1 кг?

2) Сколько сантиметров в одном метре? Какую часть метра составляет 1 см?

3) Сколько ар в одном гектаре? Какую часть гектара составляет 1 а?

Учащиеся дают ответы, на экране появляются записи.

1 ц=100 кг; 

1 м=100 см; 

1 га = 100 а; 

Записывают в тетради.

III. Работа по теме урока

1. Объяснение материала

— Ребята, мы рассмотрели соотношения некоторых единиц измерения, которые связаны с одной сотой частью.

Сотая часть любой величины принято называть процентом. (СЛАЙД 11-12)

Предлагается ученикам найти определение процента в учебнике, прочитать и запомнить. В тетради записывается:

Выводы:

·         1 кг – 1% центнера;

·         1 см – 1 % метра;

·         1 а – 1 % га;

·         0,09 – 1 % от 9.

История возникновения процента

Слово “процент” происходит от латинских слов рro centum,что буквально означает “со ста”. Широко начали использовать проценты в Древнем Риме, но идея процентов возникла много раньше- вавилонские ростовщики уже умели находить проценты (но они считали не “со ста”, а “ с шестидесяти”, так как в Вавилоне пользовались шестидесятеричными дробями). А знак % произошел, как предполагают, благодаря опечатке. В рукописях pro centum часто заменяли словом “cento”(сто) и писали его сокращенно — cto. В 1685 году в Париже была напечатана книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %. После этой ошибки многие математики стали употреблять знак % для обозначения процентов. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Денежные расчеты с процентами были особенно распространены в древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню.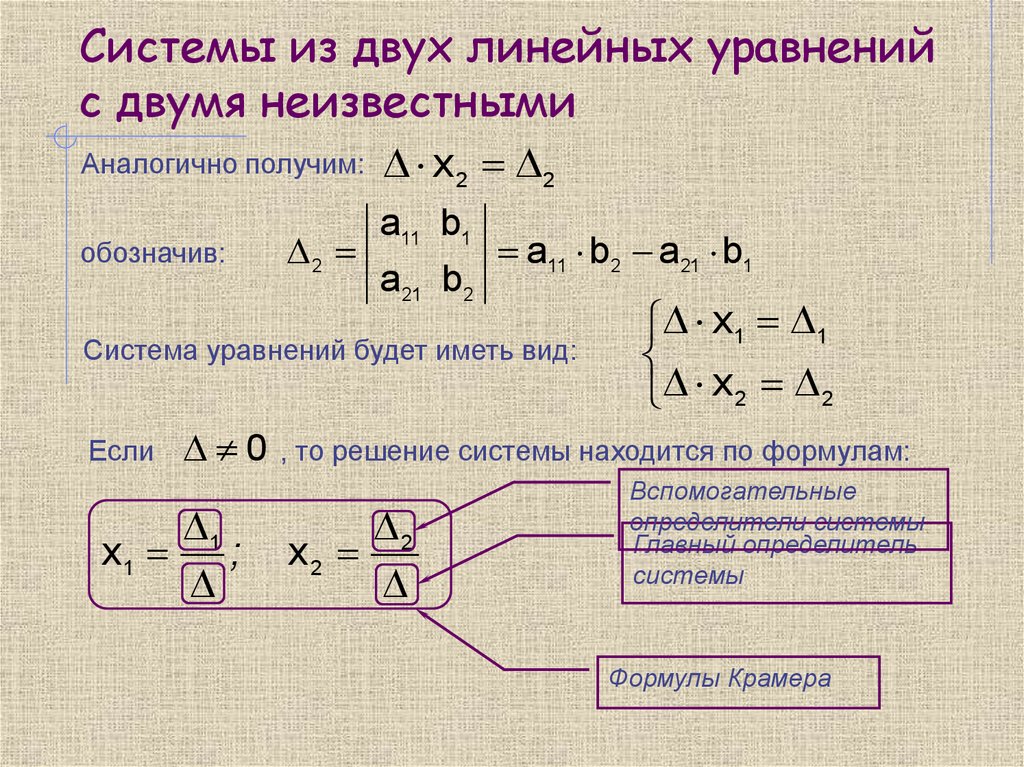 Они брали с должника лихву ( деньги сверх того, что брали в долг). При этом говорили: “ На каждые 100 сестерциев долга заплатишь 16 сестерциев лихвы”. Так как слово “на сто” по латыни звучит “про центум”, то сотую часть и стали называть процентом. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.

В Европе проценты появились на 1000 лет позже. Их ввел бельгийский ученый Симон Стевин, который в1584 году впервые опубликовал таблицы процентов.

Первичное закрепление материала

Задание 1. (СЛАЙД 13)

Как перевести проценты в десятичную дробь?

·         2%=0.02

·         6%=0.06

·         49%=0.49

·         129%=1.29

·         3.9%=0,039

·         0.8%=0.008

Задание 2. (СЛАЙД 14)

Как записать десятичную дробь в процентах?

·         0.87=87%

·         1. 46=146%

·         0,907=90.7%

·         3.456=345.6%

Учитель: Итак, что нужно делать, чтобы десятичную дробь выразить в процентах или проценты представить в виде десятичной дроби?

Выводы: (отвечают ученики)

1) Чтобы обратить десятичную дробь в проценты, надо её умножить на 100.

2) Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

Находят эти правила в учебнике.

3. Решение примеров по учебнику

Решаем № 1561, 1562

Два ученика по очереди на доске показывают решения.

Ответы для проверки:

·         №1532: 0,01; 0,06; 0,45; 1,23; 0,025; 0,004

·         №1533: 87%; 7%; 145%; 3,5%; 267,2%; 90,7%

Решаем задачи (условия задач на экране)

Задача 1. (Слайд 15)

За контрольную работу по математике отметку “5” получили 12 учеников, что составляет 30 % всех учеников. Сколько учеников в классе?

Задача 2. (Слайд 16)

Вини-Пух пошел в лес за медом. Он набрал 4.2 кг меда. По дороге домой Вини-Пух съел 30% меда. Сколько кг меда съел Вини-Пух?

Задача 3. (Слайд 17 )

Из 1800 га колхозного поля 558 га засеяно ячменем. Какой процент поля засеян ячменем?

IV.Физкультминутка (СЛАЙД 18)

·         Раз — подняться на носки и улыбнуться.

·         Два — согнуться, разогнуться.

·         Три — в ладоши три хлопка, головою три кивка.

·         На четыре — руки шире.

·         Пять – руками помахать.

·         Шесть — за парту тихо сесть.

V. Самостоятельная работа учеников

1. Заполнить таблицу (Слайд 19)

2. Решить задачу. (Слайд 20)

Кролик посадил у себя в саду 250 луковиц тюльпанов красного цвета. Но 8% тюльпанов выросло желтыми. Сколько тюльпанов оказалось желтым?

Учащиеся обмениваются тетрадями, проверяют работы, выставляют оценки.

VI. Заключение. Рефлексия

Учитель:

— Оцените свою работу на уроке. Удовлетворены ли вы результатом своей работы?

Итак, ребята, сегодня мы с вами ознакомились с понятием процента. Выяснили, где он применяется. Научились обозначать эту величину, выражать десятичную дробь в процентах и процент представлять в виде десятичной дроби. Рассмотрели, как решаются простейшие задачи на проценты.

Самостоятельная работа показала, как вы усвоили и закрепили этот материал. На следующих уроках мы с вами будем решать более сложные задачи на проценты.

VII. Подведение итогов урока (СЛАЙД 21)

— Что такое процент?

Выставляются оценки за активную работу на уроке, все получают оценку за тест.

Домашнее задание.

— Выучить определение и правила.

Решить № 1598, 1599, 1612(а).

 

Как решать системы, содержащие более двух уравнений

Обновлено: 26 марта 2016 г.

Предварительное исчисление: 1001 практическая задача для чайников (+ бесплатная онлайн-практика)

Исследуйте книгу Купить на Amazon

Большие системы линейных уравнений включают более двух уравнений, которые сопровождаются более чем двумя переменными. Эти более крупные системы можно записать в виде Ax + By + Cz + . . . = K, где все коэффициенты (и K) являются константами. Эти линейные системы могут иметь много переменных, и вы можете решить эти системы, если у вас есть одно уникальное уравнение для каждой переменной. Другими словами, в то время как для трех переменных требуется три уравнения, чтобы найти единственное решение, для четырех переменных требуется четыре уравнения, а для десяти переменных — десять уравнений и так далее. Вам не нужно заниматься более крупными системами нелинейных уравнений. Это было бы слишком сложно для предварительного расчета, а более крупные линейные системы достаточно сложны. Для этих типов систем решения, которые вы можете найти, сильно различаются:

• Вы можете не найти решения.

• Вы можете найти одно уникальное решение.

• Вы можете найти бесконечно много решений.

Количество найденных решений зависит от того, как уравнения взаимодействуют друг с другом. Поскольку линейные системы трех переменных описывают уравнения плоскостей, а не линий (как это делают уравнения с двумя переменными), решение системы зависит от того, как плоскости лежат в трехмерном пространстве относительно друг друга. К сожалению, как и в системах уравнений с двумя переменными, нельзя сказать, сколько решений имеет система, не решая задачу. Относитесь к каждой проблеме так, как будто у нее есть одно решение, и если это не так, вы либо придете к утверждению, которое никогда не будет истинным (нет решений), либо всегда верно (что означает, что существует бесконечное количество решений).

Как правило, вы должны использовать метод исключения более одного раза для решения систем с более чем двумя переменными и двумя уравнениями.

Например, предположим, что проблема требует решения следующей системы:

Чтобы найти решение(я), выполните следующие действия:

1. Посмотрите на коэффициенты всех переменных и решите, какую переменную проще всего исключить.

   С помощью исключения вы хотите найти наименьшее общее кратное (НОК) для одной из переменных, поэтому используйте ту, которая проще всего. В этом случае следует исключить x переменная.

2. Разделите два уравнения и исключите одну переменную.

   Глядя на первые два уравнения, вы должны умножить вершину на -2 и прибавить ко второму уравнению. Сделав это, вы получите следующее:

3. Разделить еще два уравнения и исключить ту же переменную .

   Первое и третье уравнения позволяют снова легко исключить x . Умножьте первое уравнение на 6 и добавьте его к третьему уравнению, чтобы получить следующее:

4. Повторите процесс исключения с двумя новыми уравнениями.

   Теперь у вас должно быть два уравнения с двумя переменными:

   Вам нужно удалить одну из этих переменных. В этом примере вы исключаете переменную y , умножая верхнее уравнение на 4 и нижнее на 7, а затем складывая уравнения. Вот что это дает:

5. Решите окончательное уравнение для оставшейся переменной.

   Если 89 z = –356, z = –4.

6. Подставьте значение решаемой переменной в одно из уравнений, которое имеет две переменные для решения, вместо другого.

   В этом примере используется уравнение –7 y – 11 z = 23. Подстановка дает –7 y – 11(–4) = 23, что упрощается до –7 y + 44. = 23. Теперь закончим работу:

7. Подставьте два значения, которые у вас теперь есть, в одно из исходных уравнений для решения последней переменной.

   В этом примере вы используете первое уравнение исходной системы, которое теперь принимает вид x + 2(3) + 3(–4) = –7. Упростите, чтобы получить окончательный ответ:

   Решениями этого уравнения являются x = –1, y = 3 и z = –4.

Этот процесс называется обратной заменой, потому что вы буквально решаете одну переменную, а затем работаете в обратном направлении, чтобы найти другие. В этом примере вы перешли от решения для одной переменной в одном уравнении к двум переменным в двух уравнениях к последнему шагу с тремя переменными в трех уравнениях. . . всегда двигаться от более простого к более сложному.

Эту статью можно найти в категории:

• Предварительное исчисление,

Руководство для начинающих по системам уравнений | Бретт Берри | Math Hacks

О, основы. Они не случайно называют их фундаментальными. И одним из самых фундаментальных понятий алгебры являются Системы уравнений. Так что, если все эти x и y вызывают у вас косоглазие, не бойтесь. Это краткое руководство поможет вам исправить ситуацию в кратчайшие сроки.

Прежде чем приступить к изучению того, как решать эти неизвестные, важно точно знать, что означают эти решения.

Что такое система уравнений?

Система Уравнений именно то, что написано. Это система, то есть 2 или более уравнений. Когда вы впервые столкнетесь с задачами на систему уравнений, вы будете решать задачи, включающие 2 линейных уравнения. Это означает, что ваши уравнения будут включать максимум переменную x, переменную y и постоянное значение.

В конце концов (возможно, в алгебре 2, предварительном исчислении или линейной алгебре) вы столкнетесь с более сложными системами. Они могут включать функции более высокого порядка, такие как квадратичные уравнения, более двух уравнений в системе или уравнения, включающие переменные x, y и z (эти уравнения представляют плоскости в трехмерном пространстве).

Но какой бы сложной ни была ваша система, ваше решение всегда представляет одну и ту же концепцию: пересечение . Например, решение системы двух линейных уравнений, наиболее распространенный тип системы, представляет собой точку пересечения двух прямых.

Возможные решения

Как вы уже поняли, не все прямые пересекаются ровно в одной точке. Параллельные прямые по определению никогда не пересекаются, поэтому у них нет решения . Вы также можете столкнуться с уравнениями, которые выглядят по-разному, но при сокращении оказываются одним и тем же уравнением. В этом случае у вас будет бесконечно много решений.

Самый простой и наглядный способ найти пересечение системы — нарисовать уравнения в одной координатной плоскости.

Чтобы увидеть примеры того, как решить систему линейных уравнений с помощью графика, а также примеры «нет решения» и «бесконечно много решений», посмотрите мой видеоурок ниже.

Подпишитесь на уроки математики на YouTube

Конечно, построение графиков — не самый эффективный способ решения системы уравнений. Вот почему у нас есть еще пара методов в нашем алгебраическом арсенале.

Первый метод замены . В этом методе вы изолируете переменную в одном из ваших уравнений и подключаете эту связь к другому уравнению. Это даст вам уравнение только с одной переменной, что означает, что вы можете найти переменную. Как только вы узнаете значение одной переменной, вы можете легко найти значение другой переменной путем обратного решения.

Для получения дополнительной информации о том, как решить систему с помощью метода подстановки, ознакомьтесь с этим руководством.

Подпишитесь на математические лайфхаки на YouTube

Если вам не нравится метод подстановки, в вашем распоряжении есть последний метод: метод исключения .

В этом методе вы стратегически исключаете переменную, складывая вместе два уравнения. Чтобы сделать это, вам часто придется умножать одно или оба уравнения на значение, чтобы исключить переменную. После того, как вы добавите уравнения и уберете одну переменную, у вас останется уравнение, в котором есть переменная только одного типа. Это удобно, потому что вы можете найти эту переменную. Найдя одну переменную, вы можете подставить полученное значение в одно из исходных уравнений, чтобы найти значение другой переменной.

Чтобы понять, как именно это работает, посмотрите мое видео об использовании метода исключения для решения системы.