Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
10.18
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Решено
Найти координаты вектора х, если известно, что он перпендикулярен векторам а1=(4,-2,-3) и а2=(0,1,3), образует с ортом j тупой угол и |x|=26.
Решено
Найти расстояние от начала координат до плоскости, проходящей через три заданные точки: А(1;2;-1), В(3;0;1), С(-1;1;3)
Решено
Вершины пирамиды находятся в точках A,B,C,D.Вычислить: а)площадь указанной грани б)площадь сечения, проходящего через середину ребра l и две
Решено
Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1
Основание AD трапеции АВСD лежит в плоскости . Через точки В и С проведены параллельные прямые, пересекающие плоскость в точках Е и Fсоответственно.
Пользуйтесь нашим приложением
Все о перекрестном произведении параллельных векторов
Модуль вектора A, умноженный на модуль вектора B, умноженный на синус угла, образованного векторами n, представляет собой единичный вектор, перпендикулярный плоскости, образованной векторами A и B, и направлен в направлении, перпендикулярном плоскости, образованной векторами A и B.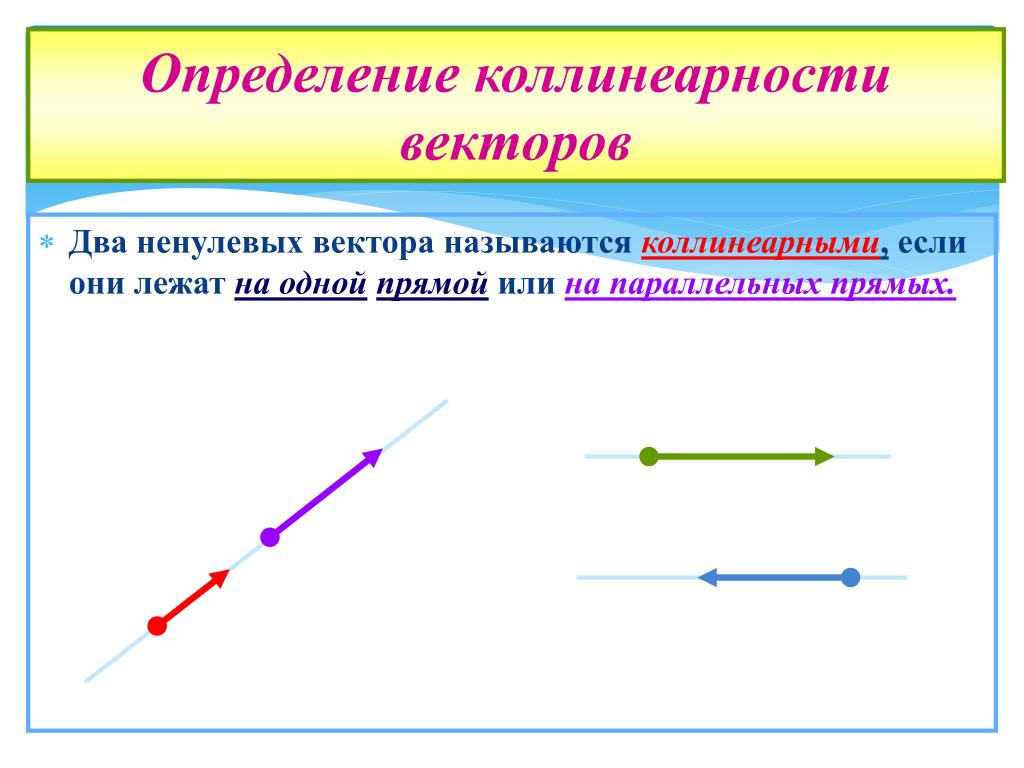
Перекрестное произведение двух векторов является нулевым вектором, перпендикулярным плоскости, образованной двумя векторами, поскольку угол между ними равен нулю. Мы не можем определить плоскость и взять направление вектора, полученного из перекрестного произведения, в соответствии с правым винтом, потому что есть только один вектор. Нулевой вектор, полученный из двух параллельных векторов, не имеет однозначного направления.
Перекрестное произведение антипараллельных векторовАнтипараллельные векторы — это параллельные векторы, направленные в противоположном направлении.
Два направленных отрезка, также называемых векторами в прикладной математике, антипараллельны в евклидовом пространстве, если они поддерживаются параллельными прямыми и имеют противоположные направления. В этом случае один из связанных евклидовых векторов является отрицательным произведением другого.
Нахождение вектора w, перпендикулярного и u, и v в пространстве, по двум непараллельным ненулевым векторам u и v очень полезно.
Для создания такого вектора можно использовать операцию векторного произведения. В этом разделе определяется векторное произведение, прежде чем углубляться в его свойства и использование.
(Если два вектора указывают в одном направлении, они параллельны; если они указывают в противоположных направлениях, они антипараллельны.)
AB/(|A||B|)=0, если A перпендикулярен B, и наоборот, если AB/(|A||B|)=0 , если A и B перпендикулярны.
Перекрестное произведение ортогональных векторовПонятие «ортогональность» имеет решающее значение. Быстрое сканирование вашего текущего окружения, несомненно, обнаружит множество перпендикулярных поверхностей и краев (включая края этой страницы). Быстро проверьте ортогональность с помощью скалярного произведения: векторы u и v перпендикулярны тогда и только тогда, когда u.v=0
Скалярное произведение двух ортогональных векторов равно нулю. Матрицы двух столбцов, которые их представляют, имеют нулевой скалярный продукт.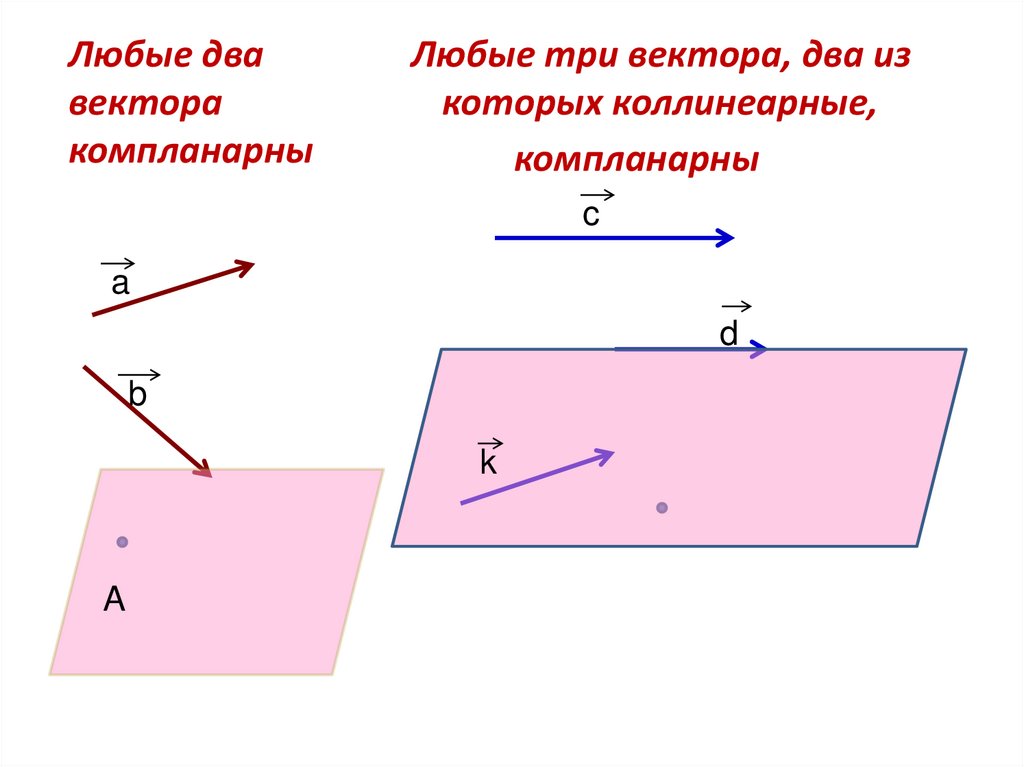
Относительная ориентация — это все, что имеет значение. Скалярное произведение будет равно нулю, если векторы ортогональны.
Скалярное произведение ортогональных векторов равно нулю, а скалярное произведение антипараллельных векторов отрицательно. Векторное произведение двух векторов — это вектор, перпендикулярный обоим векторам. Его величина вычисляется путем умножения величин двух углов на синус угла между ними.
Поскольку направление, перпендикулярное обоим векторам, максимизирует объем, векторное произведение примерно ортогонально к a и b.
Заключение В этой статье мы делаем вывод, что «Параллельные векторы — это векторы, имеющие одинаковое или прямо противоположное направление. Произведение любых двух параллельных векторов является нулевым вектором. Просто возьмите общий множитель из одного вектора и умножьте его на другой вектор, чтобы увидеть, параллельны ли они. Другой вариант — посмотреть, равно ли их векторное произведение нулю.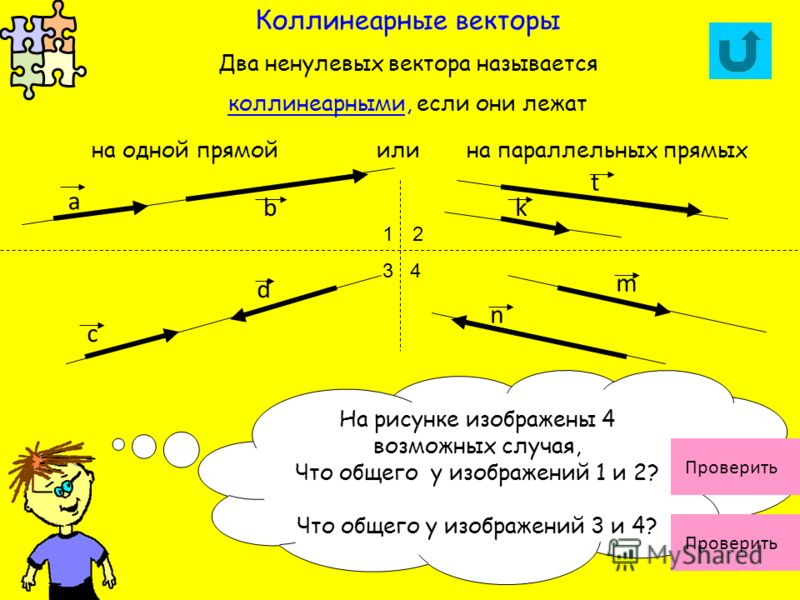
формула коллинеарного вектора — Google
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
b 1 a 1 = b 2 a 2 = b 3 a 3 для коллинеарности векторов. Следовательно, векторы a и b коллинеарны. Следовательно, векторы a и c неколлинеарны.
2. фев. 2023
Коллинеарные векторы: определение, условие, формула с доказательством
testbook.com › учимся › математические коллинеарные векторы
Hervorgehobene Snippets
Ähnliche Fragen
Как найти коллинеарный вектор?
Что такое коллинеарная формула?
Пример коллинеарного вектора?
При каком условии 2 вектора будут коллинеарными?
Коллинеарные векторы — определения, условия, примеры — Cuemath
www.cuemath.com › геометрия › коллинеарные векторы
Рассмотрим два вектора →PP → = (3,4,5), →Q Q → = (6 ,8,10). Два вектора считаются коллинеарными, если отношения их координат равны.
Bilder
ALLE ANLEIGEN
ALLE ANZEIGEN
Проверьте, являются ли два вектора Collinear или нет-Geeksforgeeks
WWW.geekforgeeks.org ›FE-if-if—ve-vectors-are.
. 2021 · Два вектора коллинеарны, если отношения их координат равны, т.е. x1 / x2 = y1 / y2 = z1 / z2. Примечание. Это условие недействительно, если …Типы векторов: коллинеарные и равные векторы, видео … — Toppr
www.toppr.com › гиды › математика › векторная алгебра
Коллинеарные векторы — это два или более векторов, которые параллельны одной и той же прямой независимо от их величины и направления. Равные векторы. Если два вектора \vec …
Предлагаемые видео · Типы векторов
Коллинеарные векторы — OnlineMSchool
onlinemschool.com › библиотека › вектор › коллинеарность
Условие коллинеарности векторов 3. Два вектора коллинеарны, если их пересечение произведение равно нулевому вектору. Н.Б. Условие 3 применимо только к трех- .
..
Как показать, что P, Q и R коллинеарны? | Векторная геометрия
undermathematics.org › решение
Три точки с векторами положения a, b и c коллинеарны тогда и только тогда, когда векторы (a−b) и (a−c) параллельны. Векторы, соединяющие три коллинеарные точки.
Определение коллинеарных векторов. — Веданту
www.vedantu.com › вопрос-ответ › определить-коллин…
Условие-2: Два вектора коллинеарны, если отношение их координат равно. Это неверно, если один из компонентов равен нулю.
Как показать коллинеарность точек — Векторы — YouTube
www.youtube.com › смотреть
20.06.2012 · Краткое руководство по отображению коллинеарности точек, заданных векторными координатамиПОСЕТИТЕ WWW …
Dauer: 4: 29
Прислан: 20.06.2012
Коллинеарные векторы Пример-1 — AtoZmath.com
atozmath.com › пример › Векторы
Два вектора коллинеарны, если отношения их координат равны.