Как определить тупой острый и прямой угол. Виды углов. Как разметить острый угол
Каждый угол, в зависимости от его величины, имеет своё название:
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Острый | Меньше 90° | |
| Прямой | Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой. | |
| Тупой | Больше 90°, но меньше 180° | |
| Развёрнутый | Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла. | |
| Выпуклый | Больше 180°, но меньше 360° | |
| Полный | Равен 360° |
Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны —

Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .
Сумма смежных углов равна 180°.
Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 — вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников.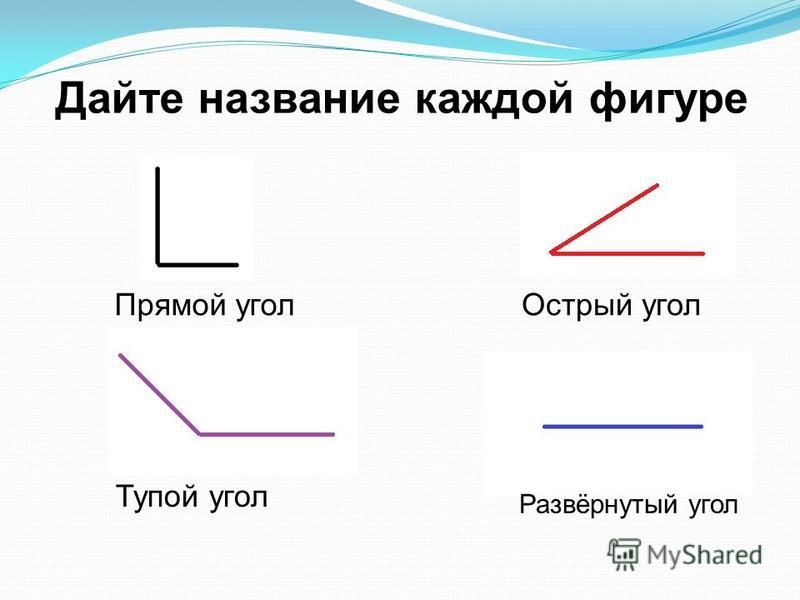 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников.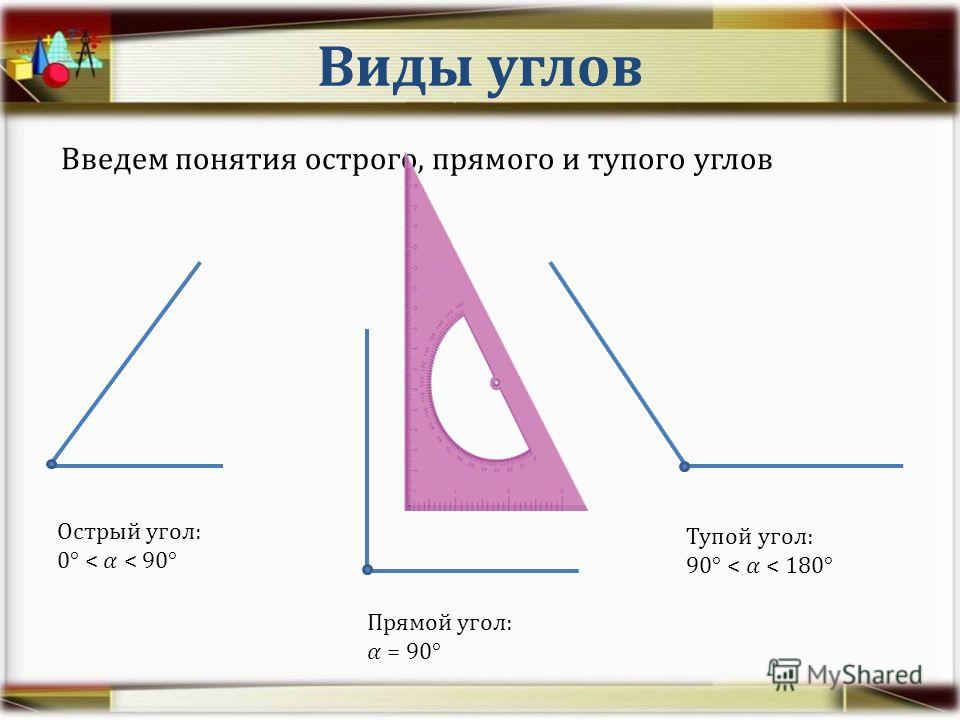 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ.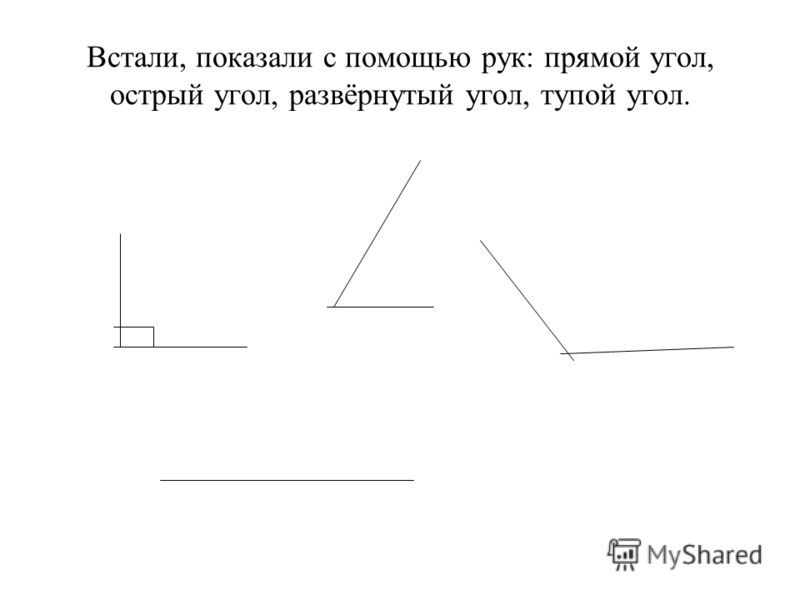 Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников.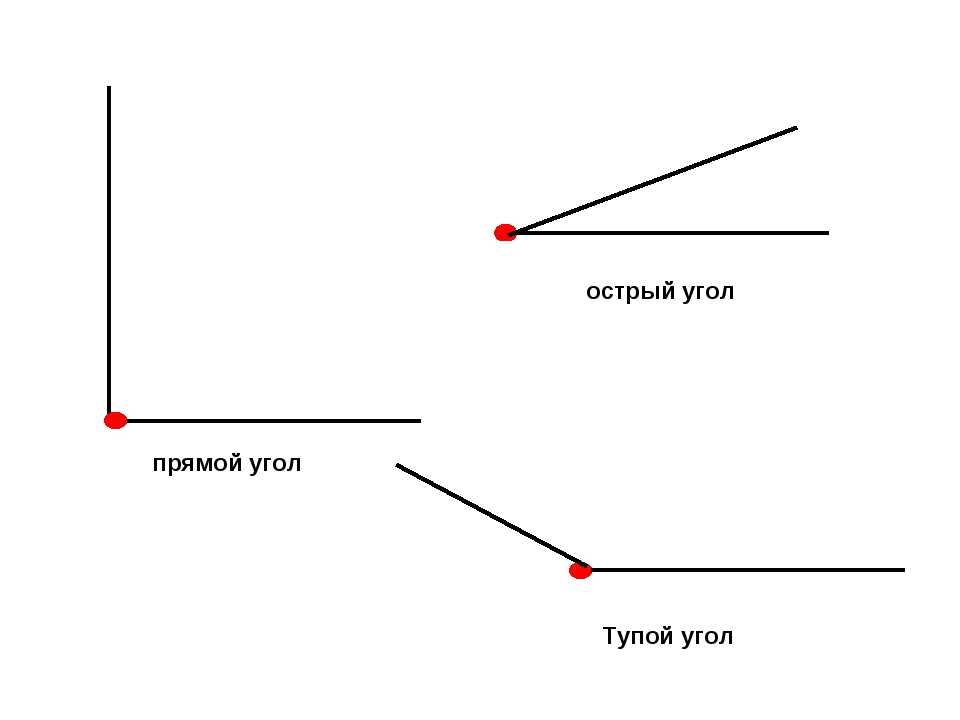 Какое слово спряталось в названии обеих этих фигур?
Какое слово спряталось в названии обеих этих фигур?
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ.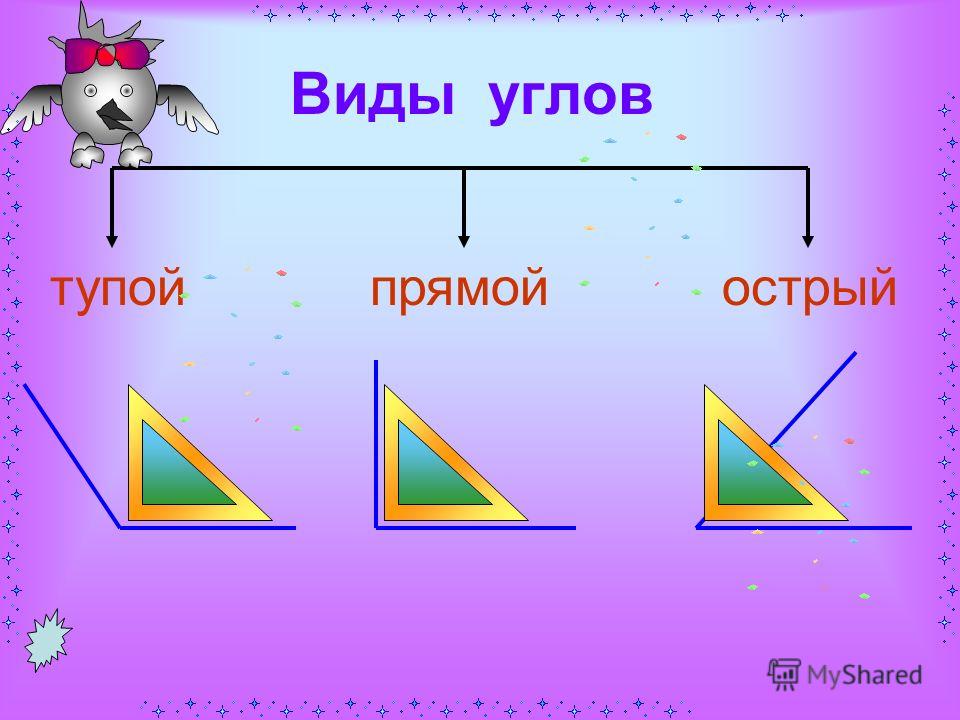
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямШы и прямы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
прямой угол — — Тематики нефтегазовая промышленность EN right angle …
прямой угол — угол, равный своему смежному. * * * ПРЯМОЙ УГОЛ ПРЯМОЙ УГОЛ, угол, равный своему смежному … Энциклопедический словарь
* * * ПРЯМОЙ УГОЛ ПРЯМОЙ УГОЛ, угол, равный своему смежному … Энциклопедический словарь
ПРЯМОЙ УГОЛ — угол, равный своему смежному; в градусном измерении равен 90° … Естествознание. Энциклопедический словарь
Прямой угол — см. Угол … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПРЯМОЙ УГОЛ — 1) угол, равный своему смежному. 2) Внесистемная ед. плоского угла. Обозначение L. 1 L = 90° = ПИ/2 рад 1,570 796 рад (см. Радиан) … Большой энциклопедический политехнический словарь
ПРЯМОЙ — прямая, прямое; прям, пряма, прямо. 1. Ровно вытянутый в каком–н. направлении, не кривой, без изгибов. Прямая линия. «Прямая дорога обрывалась и уж шла вниз.» Чехов. Прямой нос. Прямая фигура. 2. Беспересадочный (ж.–д. и разг.). Прямой маршрут.… … Толковый словарь Ушакова
ПРЯМОЙ — ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямы и прямы. 1. Ровно идущий в каком н. направлении, без изгибов. Прямая линия (линия, образом к рой может служить бесконечная туго натянутая нить). Провести прямую (т. е. прямую линию; сущ.). Дорога идёт… … Толковый словарь Ожегова
Провести прямую (т. е. прямую линию; сущ.). Дорога идёт… … Толковый словарь Ожегова
угол основного профиля витка — (αb) Угол между основным профилем витка эвольвентного червяка и прямой, составляющей с осью червяка прямой угол скрещивания. Примечание Угол прямолинейного основного профиля витка эвольвентного червяка αb равен основному углу подъема… … Справочник технического переводчика
Книги
- Таблицы для численного решения граничных задач теории гармонических функций , Канторович Л. В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи… Купить за 610 руб
- Математика. 2 класс. Учебник. В 2-х частях. Часть 2 , Моро М.И.. Учебник «Математика» входит в образовательную систему» Школа России» . Материал учебника позволяет реализовать системно-деятельностный подход, организовать дифференцированное обучение и…
Конспект урока по Математике «Прямой , тупой и острый углы» 2 класс
Урок математики во 2 классе. «————» ———- 201 —-уч. год
«————» ———- 201 —-уч. год
Тема урока: Прямой , тупой и острый углы.
Цели урока:
различать по видам.
продолжать учить узнавать и называть некоторые буквы латинского алфавита,
продолжать работу по классификации геометрических фигур по различным основаниям,
продолжать работу над формированием вычислительных навыков, знаний названий компонентов,
развивать умения решать задачи изученных видов,
Развивать математическую речь, внимание, память, пространственное воображение.
Формировать графические умения.
Ход урока.
1.Организационный момент.
-Сегодня на уроке мы будем путешествовать по знакомым станциям. С собой в путешествие возьмём хорошее настроение и пожелаем друг другу удачи.
Психологический настрой «Солнышко». Класс делится на 4 группы.
2.Станция «Вспомни-ка!»
Выполнив задания на этой станции, вы откроете первые две буквы в названии темы урока.
В любом путешествии нам необходимо быть внимательными.
Задание на внимание.
(В течение 4-5 секунд я покажу вам картинки, а вы воспроизведёте их в тетради по порядку, сколько запомнили.
После выполнения задания, проверяю у детей правильность выполнения. Открываем первую букву У.
Игра «Истина-ложь».
( Если утверждение истинно, дети большой палец руки поднимают вверх, если ложно – вниз и говорят правильный ответ.)
Сумма чисел 5 и 9 равно 40.
Разность 27 и 3 равно 25.
63 уменьшить на 3 раза будет 8.
От 45 отнять 25 будет 20.
6 увеличить на 30 раз будет 36.
При вычитании из числа на 0 будет 0.
Прямоугольник -это круглая фигура.
Разность чисел 80 и 20 равна 6.
После игры открываем вторую букву Г.
3.Станция «Догадайся!»
Задача на логику.
В комнате 4 угла. В каждом углу по кошке. Напротив каждой кошки — 3 кошки. Сколько всего кошек в комнате?
Напротив каждой кошки — 3 кошки. Сколько всего кошек в комнате?
Открываем букву О.
Сколько треугольников на рисунке?
1) 6; 2) 3; 3) 4;
Покажите все треугольники и откроется буква Л.
4.Изучение нового материала.
Прочитайте тему урока «Угол».
Какие ассоциации возникают у вас в связи с этим словом? Где вы встречались с углами? Где в нашем классе есть углы?
Сценка « Треугольник и квадрат».
Жили-были два брата
Треугольник с квадратом.
Старший — квадратный
Добродушный и приятный.
Младший — треугольный
Вечно недовольный.
Говорит ему квадрат:
-Отчего ты злишься брат?
Тот кричит ему:
-Смотри, ты полней меня и шире.
У меня углов лишь три,
У тебя же их четыре.
И сказал ему квадрат
-Я же старше, я — квадрат
И сказал ещё нежней:
Неизвестно кто нужней.
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя, сказал:
Приятных я тебе желаю снов
Спать ложился – был квадратным,
А проснёшься без углов.
Но наутро младший брат
Страшной мести был не рад.
Поглядел он на квадрата,
Онемел, стоял без слов
Вот так месть! Теперь у брата
Восемь новеньких углов!
— В чём была ошибка прямоугольника?
Угол – геометрическая фигура, он имеет вершину и стороны.
Стороны угла – лучи, исходящие из одной точки, а их общее начало – вершина угла, она обозначается латинскими буквами.
Углы могут быть прямыми и непрямыми.
Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник.
Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол — прямой.
Не совпадут – непрямой.
Непрямые углы делятся на: тупые и острые.
Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
В
На доске чертёж:
Д
А
Читается чертёж так: угол с вершиной в точке А — тупой, угол с вершиной в точке В – острый, угол с вершиной в точке Д – прямой.
Физминутка.
(По стенам кабинета развешаны картинки с изображением изученных геометрических фигур. Учитель называет фигуру, дети находят её взглядом)
Практическая работа по закреплению изученного.
На партах у 1 варианта – салфетки, у 2 варианта – проволока. Сделайте из них прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой.
Работа с учебником.
Работаем на странице 122.
Угол с вершиной в какой точке прямой? Острый? Тупой?
Задание№412 – устно.
Задание№413 – проверить с помощью угольника.
5.Станция «Нарисуй-ка».
Самостоятельно построить в тетради все виды углов, обозначить вершины.
6.Станция «Подумай-ка».
На доске нарисованы углы разные по величине.
15
15
10
10
5
21
5
7
21
— Мы пришли в гости к уголкам. Что мы можем о них сказать, на какие группы разделить? (По цвету, по величине, по числам, которые рядом с ним)
Практическая работа.
При помощи сподручного материала и проволоки сделать различные углы.
(После выполнения задания, каждая группа отчитывается о проделанной работе)
Взаимопроверка: оцените друг друга (звездочка -5, листик -4,цветочек -3 )
7.Итог урока.
-Расскажите мне по схеме о том, что вам дал сегодняшний урок математики?
узнал
представил
смог
8.Рефлексия.
При помощи «солнышка»: красного, жёлтого,и белого лучиков поставьте оценку за урок себе, своему ряду, всему классу. Красное – оценка «5», жёлтое – оценка «4», белый – оценка «3».
Красное – оценка «5», жёлтое – оценка «4», белый – оценка «3».
9.Окончание урока. Домашнее задание.
Работа в печатной тетради.
Урок математики по теме «Виды углов». 2-й класс
Цели:
1. Познакомить учащихся с видами углов, понятиями “прямой угол”, “острый
угол”,“тупой угол”;
2. Учить определять прямые, острые и тупые углы с помощью модели прямого угла
(угольника), обучить сравнению углов;
3. Развивать пространственное воображение, навык работы с чертежными
инструментами, мышление, глазомер;
4. Воспитывать у учащихся отношения делового сотрудничества (доброжелательность
друг другу, уважать мнение других, уметь слушать товарищей), аккуратность,
прививать интерес к предмету.
Планируемые результаты: учащиеся научатся различать виды углов; анализировать и делать выводы; использовать полученные знания в учении и повседневной жизни.
Оборудование: угольник, линейка, веер у каждого ученика, карточки, модели
углов из картона.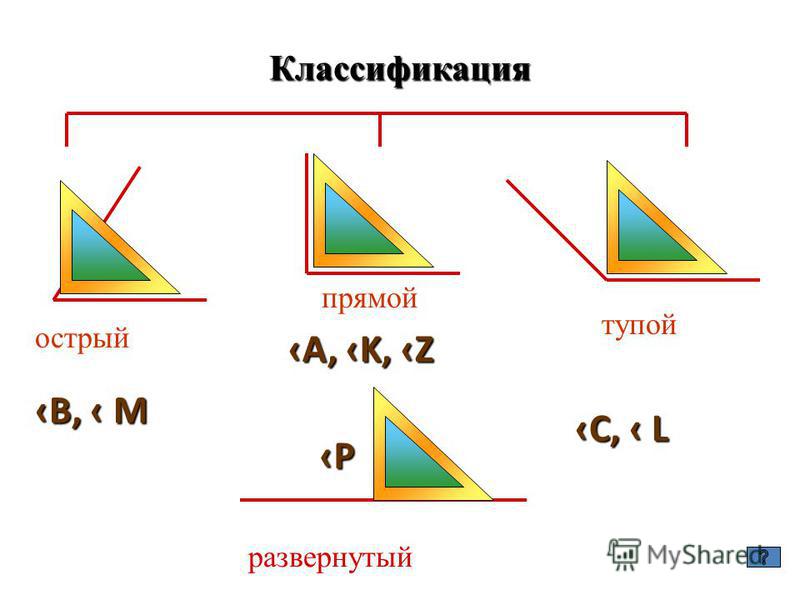
Ход урока
I. Организационный момент.
Урок начинается с приветствия и психологического настроя на работу.
Учитель. Начнем наш урок непременно с улыбки. Пожалуйста, подарите улыбки мне, соседу по парте, гостям
– Проверьте, все ли у вас на рабочем месте. Вы готовы начать урок?
– А с каким настроением вы пришли сегодня на урок, пусть за вас ответит ваш друг
смайлик.
(Учащиеся показывают выбранный ими смайлик, который соответствует их настроению.)
– Я вижу, что у вас хорошее настроение, тогда добро пожаловать на урок математики!
*Чтобы спорилось нужное дело,
*Чтобы в жизни не знать неудач,
*В математики мир отправимся смело,
*В мир примеров и разных задач.
А девизом нашего урока будут такие слова:
*Думать – коллективно!
*Решать – оперативно!
*Отвечать – доказательно!
*Учиться – старательно!
* И открытия – нас ждут обязательно!
II.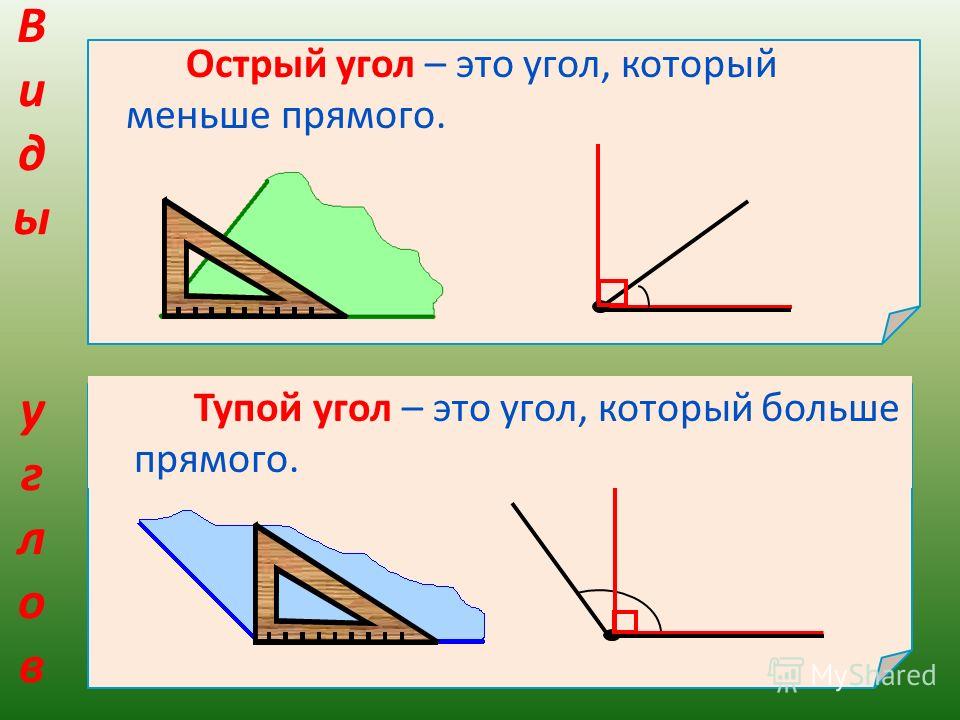 Актуализация опорных знаний . Повторение изученного.
Актуализация опорных знаний . Повторение изученного.
1. – Решите уравнения. Расставьте буквы в порядке убывания соответствующих корней уравнения и расшифруйте слово.
Х – 365 = 274(Р)
х – 32 = 896 (П)
715 – х = 398(О)
273 + х = 500(Й)
502 – х = 99 (Я)
х + 26 = 401(М)
(Ответ: прямой )
2. – Решите примеры и расшифруйте слово.
1х2х6:12х7х2:1(Г)
159х(0х4) (О)
(804:804)х5 (Л)
9х2х1:18х5х2:1 (У)
Ключ:10, 14, 0, 5.
Ответ: угол (учитель записывает слово “угол” на доске).
– Незнайка летом отправился в деревню Простоквашино. Он всерьез решил заняться подсчетами. Помогите ему. После каждого правильного ответа я буду открывать одну букву, из которых потом вы сложите слово.
*Сколько лапок у 5 цыплят? (С)
*Сколько крыльев у 3 гусят? (Ы)
*Сколько пятачков у 14 поросят? (О)
*Сколько копыт у 7 ягнят? (Й)
*Сколько рогов у 7 козлят? (Р)
*Сколько очков у 8 бабушек? (Т)
– Какое слово получилось? (Острый.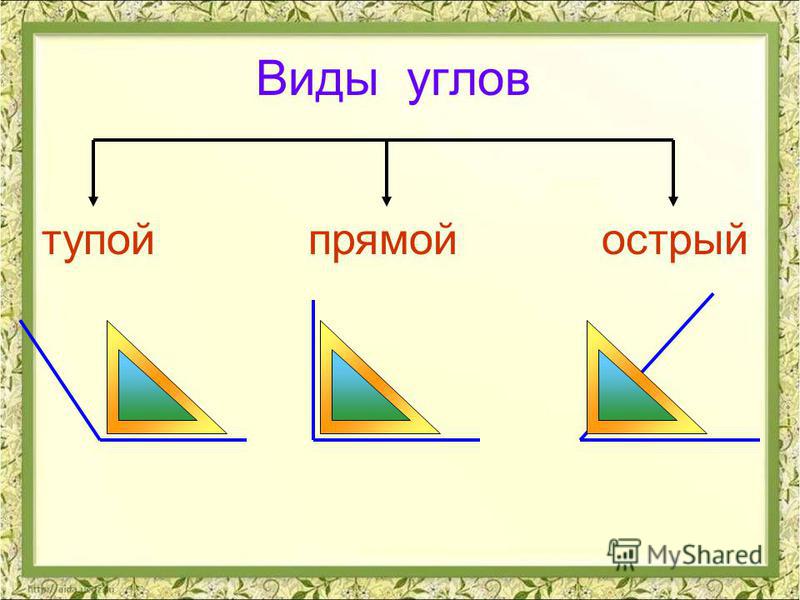 ) (Учитель записывает слово “острый” на
доске.)
) (Учитель записывает слово “острый” на
доске.)
3. – Найди значения выражений. Расставьте буквы в порядке убывания.
60 – 12:2= (О)
36 + 7х2 = (Й)
53 + 5х2 = (П)
100 – 10:2 = (У)
8х2 – 16 = 88 + 6х2= (Т)
– Какое слово получилось? (Тупой.) (Учитель записывает слово на доске.)
– Прочитайте слова на доске и подумайте, как они могут быть связаны между собой
и с нашим сегодняшним уроком. (Прямой, острый и тупой – это виды углов.
Сформулируйте тему нашего урока. Тема нашего урока: “Виды углов”.)
III. Сообщение темы, целей урока.
– Сегодня на уроке мы узнаем,какие бывают углы, научимся их узнавать, сравнивать,различать и строить. Подумайте, какие инструменты нам понадобятся на уроке? (Линейка, угольник, карандаш.)
– Где можно встретить углы в окружающем нас мире? (Крыши домов, угол доски,
угол платочка, книжки, угол стола, полочки, угол в комнате, угол между стрелками
часов, компас, веер и т.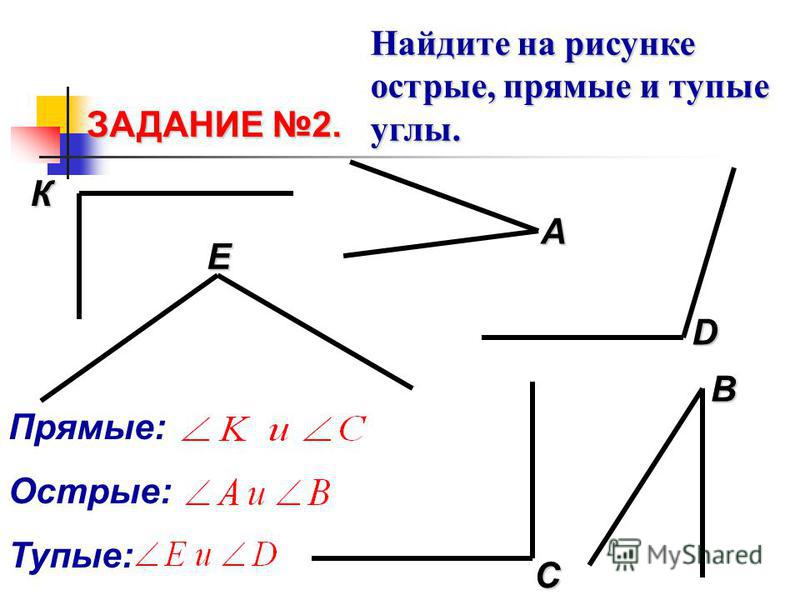 д.)
д.)
IV. Введение новых знаний.
– Что такое угол? Как он получается? (Ответы учащихся.)
Задание 1. – Начертите в тетради два луча с общим началом, которые пересекаются под прямым углом. Можно использовать угольник. (Учащиеся самостоятельно выполняют задание.)
– Сравните угол, начерченный вами, с изображенными на доске углами. (В учебнике.)
(Угол под номером 2 называется прямым.)
А вот как называются угол 1 и 3, узнаете позже.
Задание 2. – Работа в парах. 1. Рассмотрите рисунки.
У кого наконечник копья острый, а у кого тупой? Каким копьем удобнее охотиться?
– Как можно назвать углы, изображенные на рисунке рядом с первобытными охотниками? (Учащиеся называют углы: Острый и тупой. Затем отыскивают на рисунке острый и тупой углы и называют их.)
2. Выполнение задания учебника № 1, с.108.
V. Первичная проверка понимания.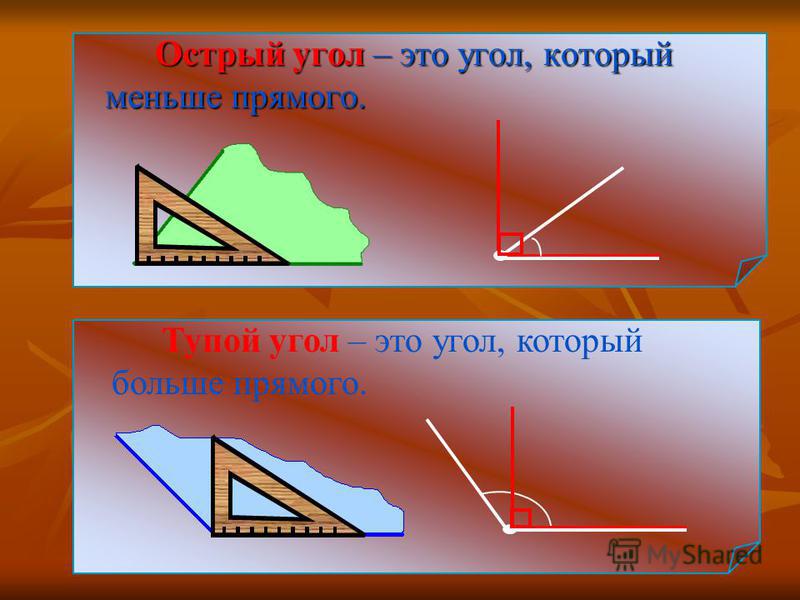
Задание. (На партах у каждого ученика лежит веер. Дети их принесли заранее.) Раскройте веер, изобразите угол. На какой угол раскрыли каждый веер? (Дети по цепочке называют свой угол.)
– Рассмотрите рисунок. На какой угол раскрыт каждый веер на данном рисунке?
– Какой угол вам неизвестен? (Учащиеся получают информацию о развернутом угле.)
Физкультминутка (под музыку)
– Точка – наклоны головы влево – вправо,
– развернутый угол – руки в стороны,
– прямой угол – руки под углом 90*,
– острый угол – руки в стороны – вверх, образуя острый угол;
– тупой угол – руки в стороны, образуя тупой угол.
V. Работа по теме урока. Практическая работа.
Задание 1. Начертить прямой и острый углы, расположив их так, как показано на рисунке. (Образец на доске.) – Луч зеленого цвета.
– Какой угол меньше: острый или прямой?
Вывод: Угол острый меньше прямого, потому что он укладывается в прямом.
– Проведите из общей вершины этих углов несколько лучей так, чтобы с лучём
зеленого цвета они образовывали острые углы. (Задание выполняется в парах.)
– Давайте сделаем вывод о величине прямого и острого углов.
Учащиеся делают вывод: Все острые углы меньше прямого.
Задание 2. Начертите тупой и прямой углы, расположив их так, как показано на рисунке. (Уч-ся самостоятельно выполняют задание по образцу.)
– Луч зеленого цвета.
– Какой угол больше :тупой или прямой?
– Проведите из общей вершины этих углов несколько лучей так, чтобы с зеленым
лучом зеленого цвета они образовывали тупые углы.
(Один ученик выполняет задание у доски, а остальные – в своих тетрадях.)
– Сравните по величине тупой и прямой углы.
Учащиеся делают вывод: Все тупые углы больше прямого.
VI. Закрепление изученного материала.
Задание 1. На чертеже один угол “лишний”. Найди его.
Задание 2. На схеме изображено пересечение шоссейных дорог.
На схеме изображено пересечение шоссейных дорог.
Выпиши получившиеся углы –
А) Прямые:
Б) Острые:
В) Тупые:
Задание 3. Покажи на чертеже прямые углы – красным цветом, острые углы – зеленым, тупые углы – синим. (Работа в группе.)
VII.Обобщение изучаемого на уроке.
– Впишите пропущенные слова.
1) Прямой угол_______________________тупого угла.
2)Тупой угол________________________острого угла.
(Задание выполняется с комментированием.)
VIII. Рефлексия деятельности.
– С какими видами углов вы сегодня познакомились?
Заранее подготовленные дети читают стихи.
Угол.
1. Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется прямым
Если угол уже – острым,
Если шире то – тупым.2.
Я острый – начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим Острый угол мы,
Как острие меча.3. А для угла тупого
Все повторяем снова
Из точки две прямых ведем,
Но их пошире разведем.
На чертеж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
– Как узнать, острый угол или тупой?
– Оцените свою работу на уроке?
– Кто хорошо разобрался в новом материале?
– Кому нужна помощь?
Учитель: Отметьте свое настроение после нашего урока.
IХ. Домашнее задание:
1. При помощи угольника проверьте углы в окружающих нас предметах (у стола, у
шкафа и т.д.).
2. Начертите в тетради фигуры с прямыми, тупыми и острыми углами.
Как определить, острый угол треугольника или тупой?
Геометрия была частью древней истории, а также современного мира. В настоящее время геометрия используется при проектировании, строительных работах, в архитектуре при выборе материала для строительства и т.д. Это в равной степени часть технического мира, поскольку геометрия используется для расчета различных конструкций, производства, создания чертежей, программирования и т. д.
В настоящее время геометрия используется при проектировании, строительных работах, в архитектуре при выборе материала для строительства и т.д. Это в равной степени часть технического мира, поскольку геометрия используется для расчета различных конструкций, производства, создания чертежей, программирования и т. д.
Геометрия — это исследование математики, которое занимается изучением форм и их свойств. Термин происходит от греческих слов «ге» и «материя», что означает землю и измерение соответственно.
Ранний подход к геометрии можно наблюдать в их строительстве и архитектурных работах древних времен с использованием различных форм очень специфическим образом.
Углы
Углы можно определить как пространство между двумя пересекающимися линиями, встречающимися в определенной точке. Компоненты угла включают две стороны, известные как стороны угла, и точку встречи, где образуется угол, называемую вершиной. Углы измеряются в градусах от 0 до 360 градусов.
Первый угол предполагал Карп Антиохийский.
Угол можно просто определить как форму или пространство, образованное в точке встречи двух пересекающихся лучей. Термин «угол» произошел от латинского слова «angulus», что означает «угол».
Уголки делятся на разные типы в зависимости от размера.
Типы уголков
| Уголки | Описание |
|---|---|
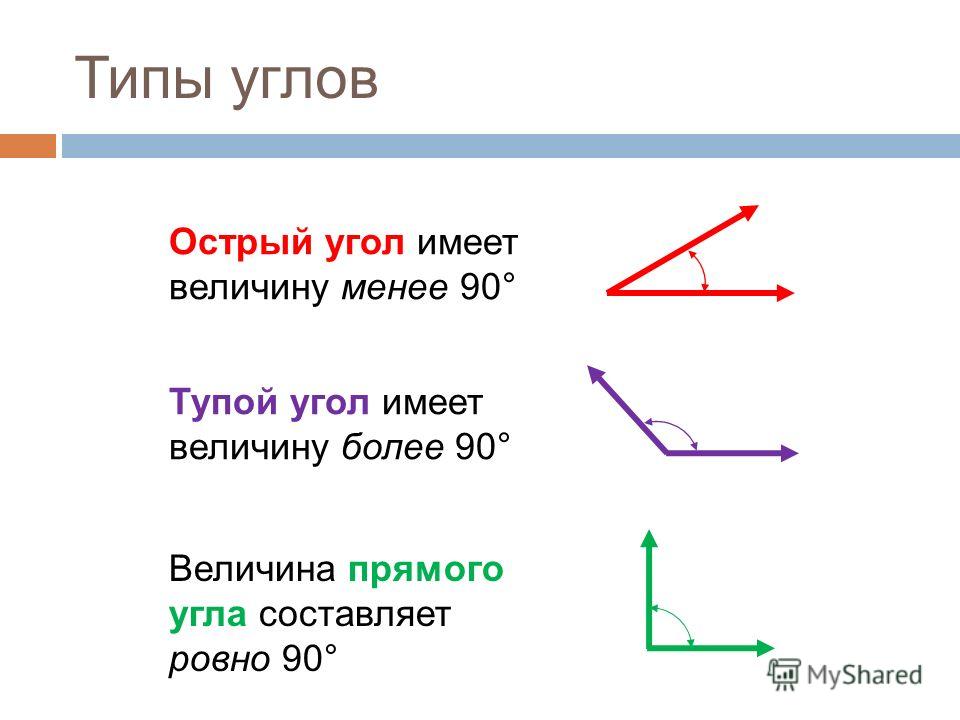
Острый угол | Угол меньше 90 градусов называется острым углом. Градус всегда измеряется в диапазоне от 0 до 90. |
Прямой угол | Угол, равный точно 90 градусам, является прямым углом. Он также считается наполовину прямым углом, так как половина 180 градусов составляет прямой угол. |
Прямой угол | Угол, равный ровно 180 градусам, является прямым углом. Прямые углы образуют прямые линии. Мера прямого угла может быть положительной или отрицательной |
Тупой угол | Угол, величина которого больше 90 градусов и меньше 180 градусов, является тупым углом. Градус всегда лежит между 90 и 180 градусами. Градус всегда лежит между 90 и 180 градусами. |
Угол рефлекса | Угол, который составляет более 180 градусов и меньше 360 градусов, является углом рефлекса. Градус всегда лежит между 180 и 360 градусами. |
Как определить, острый угол треугольника или тупой?
Ответ:
Если треугольник не имеет конкретного упоминания прямого угла. Затем мы можем определить, является ли треугольник остроугольным, прямоугольным или тупоугольным, используя обратную теорему Пифагора.
Как будто сумма квадрата двух самых коротких сторон треугольника больше, чем квадрат самой длинной стороны. Треугольник остроугольный.
a 2 +b 2 >c 2
Давайте рассмотрим это на математическом примере.
Here,
=>a 2 +b 2 =(10) 2 +(12) 2
=>a 2 +b 2 =100+144
=> A 2 +B 2 = 244
=> C 2 = (15) 2
=> C 2 = 225
с 244> 225 и по отношение a 2 +b 2 >c 2 данный треугольник остроугольный.
Аналогично, если сумма квадрата двух более коротких сторон треугольника меньше квадрата самой длинной стороны. Треугольник — тупоугольный треугольник.
A 2 +B 2
2 ЗДЕСЬ,
=> 2 +B 2 = (4) 2 +(3) 2 = (4) 2 +(3) 2
95959595959595959595959595959595959595 = (4).=> A 2 +B 2 = 16 +
=> A 2 +B 2 = 25
=> C 2 = (8) 2
=> c=64
Так как, 64>25, и по соотношению a 2 +b 2
2 данный треугольник тупоугольный.
Примеры вопросов
Вопрос 1. Что такое тупоугольный треугольник?
Ответ:
Тупоугольный треугольник — это треугольник, имеющий один тупой угол (больше 90°) и два острых угла.
Вопрос 2. Сколько острых углов в остроугольном треугольнике?
Ответ:
В остроугольном треугольнике все три внутренних угла треугольника острые, то есть они меньше 90°.
Вопрос 3. Может ли треугольник иметь более одного тупого угла?
Ответ:
Нет, в треугольнике не может быть более одного тупого угла. Так как сумма треугольника равна 180 градусам, то если один из углов тупой, то другой должен быть острым.
Rd_sharma для 6 класса Математика Глава 11
- Решения для учебников
- Класс 6
- Математика
- углы
Rd_sharma Решения для 6 класса по математике Глава 11 Углы представлены здесь с простым пошаговым объяснением. Эти решения для Angles чрезвычайно популярны среди учащихся 6 класса по математике. Angles Solutions пригодится для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Rd_sharma Book of Class 6 Math Chapter 11 предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в Meritnation Rd_sharma Solutions. Все решения Rd_sharma для класса 6 по математике подготовлены экспертами и на 100% точны.
Эти решения для Angles чрезвычайно популярны среди учащихся 6 класса по математике. Angles Solutions пригодится для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Rd_sharma Book of Class 6 Math Chapter 11 предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в Meritnation Rd_sharma Solutions. Все решения Rd_sharma для класса 6 по математике подготовлены экспертами и на 100% точны.
Страница № 11.10:
Вопрос 1:
Приведите по два примера прямого, острого и тупого углов из вашего окружения.
Ответ:
Два примера прямого угла в нашем окружении:
(i) Угол, образованный двумя соседними стенами комнаты, является прямым углом.
(ii) Угол, образованный двумя соседними краями книги, является прямым углом.
Два примера острого угла в нашей среде:
(i) Угол, образованный между двумя соседними пальцами нашей руки.
(ii) Угол между двумя соседними сторонами буквы Z в английском алфавите.
Два примера тупого угла в нашей среде:
(i) Меньший угол, образованный двумя соседними лопастями вентилятора.
(ii) Меньший угол, образованный двумя наклонными сторонами крыши хижины, является тупым углом.
Страница № 11.10:
Вопрос 2:
Угол образован двумя соседними пальцами. Под каким углом он появится?
Ответ:
Угол, образованный двумя соседними пальцами, будет острым.
Страница № 11.10:
Вопрос 3:
Шиха плывет на лодке на северо-восток. В каком направлении она будет грести, если повернет на:
(i) прямой угол
(ii) полный угол
Ответ:
(i) Если Шиха повернется на прямой угол или на 180 градусов, она гребите в юго-западном направлении.
(ii) Если Шикха повернется на полный угол или 360 градусов, она будет грести в своем первоначальном направлении, то есть в северо-восточном направлении.
Страница № 11.10:
Вопрос 4:
Какова мера угла в градусах между:
(i) Север и Запад?
(ii) Север и Юг?
(iii) Север и Юго-Восток?
Ответ:
Мера угла между:
(i) север и запад равны 90 o .
(ii) север и юг равны 180 o .
(iii) север и юго-восток is 135 o .
Номер страницы 11.10:
Вопрос 5:
Корабль, плывущий по реке Джелам, движется на восток. Если он поворачивает на север, под каким углом он поворачивается?
Ответ:
Если корабль плывет в восточном направлении и поворачивает на север, он поворачивается на угол 90 градусов.
Страница № 11.10:
Вопрос 6:
Вы стоите в классе лицом на север. В каком направлении вы смотрите, сделав четверть оборота?
Ответ:
После поворота на четверть или оборота на 90 o ,Я буду смотреть на восток, если повернусь вправо. Точно так же, если я повернусь к левой руке, я буду смотреть на запад.
Страница № 11.10:
Вопрос 7:
Велосипедное колесо делает четыре с половиной оборота. Найдите количество прямых углов, на которые он повернется.
Ответ:
За один оборот колесо велосипеда проходит 360˚.
Если выразить 360˚ в прямых углах, то получим:
360˚90˚ = 4 прямых угла
Таким образом, за четыре с половиной оборота колесо повернется на (4 × 4,5) = 18 прямых углов
Страница № 11.10:
Вопрос 8:
Посмотрите на циферблат. На сколько прямых углов проходит минутная стрелка между 8:00 и 10:30?
Ответ:
Интервал времени между 8:00 и 10:30 составляет 2,5 часа, то есть два с половиной часа.
За 1 час минутная стрелка поворачивается на полный угол, т. е. 360˚ или 360˚/90˚ = 4 прямых угла.
Таким образом, за 2,5 часа минутная стрелка повернется на 2,5 × 4 = 10 прямых углов.
Страница № 11.10:
Вопрос 9:
Если велосипедное колесо имеет 48 спиц, то найдите угол между парой соседних спиц.
Ответ:
В велосипеде центральный угол равен 360˚ и состоит из 48 спиц.
∴ Угол между любыми двумя соседними спицами = 36048 = 7,5 °
Страница № 11.10:
Вопрос 10:
Классифицируйте следующие углы как острые, тупые, прямые, справа, ноль и полный угол:
0005
(i) 118°
(ii) 29°
(iii) 145°
(iv) 165°
(v) 0°
(vi) 75°
(vii) 180°
(viii) 89,5°
(ix) 30°
(x) 90°
(xi) 179°
(xii) 360°
(xiii)
Ответ:
Острый угол измеряется между 0° и 90°; тупой угол составляет от 90° до 180°; прямой угол равен 180°; прямой угол равен 90°; нулевой угол равен 0°, а полный угол равен 360°.
(i) 118° — тупой угол.
(ii) 29° — острый угол.
(iii) 145° — тупой угол.
(iv) 165° — тупой угол.
(v) 0° — нулевой угол.
(vi) 75° — острый угол.
(vii) 180° — прямой угол.
(viii) 89,5° — острый угол.
(ix) 30° — острый угол.
(x) 90° — прямой угол.
(xi) 179° — тупой угол.
(xii) 360 ° — это полный угол.
(xiii) 9012° — тупой угол.
Страница № 11.10:
Вопрос 11:
Используя только линейку, начертите в тетради острый, прямой и тупой углы и назовите их.
ОТВЕТ:
Острый угол ♂ Правой угол секрет.
(i) Восток и запад
(ii) Восток и север
(iii) Север и северо-восток
(iv) Север и юго-восток
Ответ:
(i) Восток и запад образуют угол 180 ˚, который представляет собой прямой угол.
(ii) Восток и север образуют угол 90˚, который является прямым углом.
(iii) Северное и северо-восточное направления образуют угол 45˚, который является острым углом.
(iv) Северное и юго-восточное направления образуют угол 135˚, который является тупым углом.
Страница № 11.11:
Вопрос 13:
Укажите вид каждого из следующих углов:
Ответ:
(i) Острый угол, так как он измеряется между 0˚ и 90˚.
(ii) Тупой угол, поскольку он измеряется между 90˚ и 180˚.
(iii) Прямой угол, так как он равен 180˚.
(iv) Прямой угол, так как он равен 90˚.
(v) Полный угол, так как он равен 360˚.
Страница № 11.11:
Вопрос 1:
Вершина угла лежит
(a) внутри его
(b) снаружи
(c) на углу
(d) внутри угла
Ответ:
(c) на углу
Вершина угла лежит на угле.
Номер страницы 11.11:
Вопрос 2:
Фигура, образованная двумя лучами с одним и тем же началом, известна как
(а) луч
(б) прямая
(в) угол
(г) отрезок
Ответ:
(c) угол
Угол – это фигура, образованная двумя лучами с одной и той же начальной точкой.
Страница № 11.11:
Вопрос 3:
Угол, равный 0°, называется
(a) полным углом
(b) прямым углом
(c) прямым углом
(d) Ни одним из перечисленных
Ответ:
(d) Ни один из этих
Угол измерения 0° называется нулевым углом.
Страница № 11.11:
Вопрос 4:
Угол измерения 90° называется
(a) полным углом
(b) прямым углом
(c) прямым углом
(d) углом отражения
Ответ:
(b) прямой угол
Угол, равный 90°, называется прямым углом.
Страница № 11.11:
Вопрос 5:
Угол измерения 180° называется
(а) нулевой угол
(б) прямой угол
(в) прямой угол
(г) угол отражения
Ответ:
(в) прямой угол
Угол измерения 180° называется прямой угол.
Страница № 11.12:
Вопрос 6:
Угол измерения 360° называется
(a) нулевым углом
(b) прямым углом
(c) углом отражения
(d) полным углом
Ответ:
(d) полный угол
Угол, измеряемый в 360°, называется полным углом.
Страница № 11.12:
Вопрос 7:
Угол измерения 240° равен
(a) острый угол
(b) тупой угол
(c) прямой угол
(d) полный угол
Ответ:
Ни один из предложенных вариантов не является правильным.
Угол измерения 240° называется углом отражения.
Страница № 11.12:
Вопрос 8:
Угол рефлекса измеряется
(a) больше 90°, но меньше 180°
(b) больше 180°, но меньше 270°
(c) больше 180°, но меньше 360°
(d) Ни один из этих
Ответ:
(c) больше 180°, но меньше 360°
Угол рефлекса определяется как угол, который измеряет больше больше 180°, но меньше 360°.
Страница № 11.12:
Вопрос 9:
Количество градусов в 2 прямых углах равно
(a) 90°
(b) 180°
(c) 270°
(d) 360°
5 Ответ :
(b) 180°
∵ 1 прямой угол = 90°
∴ 2 прямых угла = 90° × 2 = 180°
Страница № 11.12:
Вопрос 10:
Количество градусов в 32 прямых углах равно
(a) 180°
(b) 360°
(c) 270°
( г) 90°
Ответ:
Ни один из вариантов не является правильным.
Правильный ответ: 135°.
∵ 1 прямой угол = 90°
∴ 32 прямых угла = 32 × 90° = 135°
Страница № 11.12:
Вопрос 11:
Если колесо велосипеда состоит из 36 пар спиц, то соседних спиц равно
(a) 10°
(b) 15°
(c) 20°
(d) 12°
Ответ:
(a) 10°
Полный центральный угол велосипедного колеса равен 360°.
Следовательно, угол между двумя соседними спицами колеса, содержащего 36 спиц, = 36036 = 10°
Страница № 11.5:
Вопрос 1:
Приведите три примера углов из вашей среды.
Ответ:
Три примера углов из нашей среды:
(i) Угол, образованный минутной и часовой стрелками аналоговых часов
(ii) Угол, образованный двумя соседними стенами комнаты
(iii) Угол, образованный двумя соседними пальцами нашей руки
Страница № 11.5:
Вопрос 2:
Напишите стороны и вершину ∠LMP дано на рис. 11.14.
Ответ:
Руки ∠LMP это MP и ML. Далее, его вершина М.
Далее, его вершина М.
Страница № 11.5:
Вопрос 3:
Сколько углов образовано на рисунках 11.15 (i), (ii) и (iii)? Назови их.
Ответ:
(i) Образуются три угла, а именно ∠ABC, ∠BAC и ∠ACB.
(ii) Образуются четыре угла, а именно ∠ABC, ∠ADC, ∠BCD и ∠BAD.
(iii) Образуются восемь углов, а именно ∠ADC, ∠ACD, ∠DAC, ∠ACB, ∠ABC, ∠BAC, ∠BCD и ∠BAD.
Страница № 11.6:
Вопрос 4:
На рис. 11.16 перечислите точки, которые находятся: (i) внутри ∠ P (ii) снаружи ∠ P и (iii) лежать на ∠ P .
Ответ:
(i) Точки J и C лежат внутри ∠ P .
(ii) Точки D и B лежат снаружи ∠ P .
(iii) Точки A, P и M лежат на ∠ P .
Страница № 11.6:
Вопрос 5:
На рис. 11.17 напишите другое название для:
(i) ∠1
(ii) ∠2
(iii) ∠3
Ответ:
(i) Другое название ∠1 — ∠БПК.
(ii) Другое название ∠2 – ∠BOC.
(iii) Другое название ∠3 – ∠AOC.
(iv) Другое название ∠4 — ∠ AOD.
Страница № 11.6:
Вопрос 6:
На рис. 11.18, Напишите другое имя для:
(i) ∠1
(ii) ∠2
(iii) ∠3
Ответ:
(i) ∠BPE
(ii) ∠PQC
(iii)
Страница № 11.6:
Вопрос 7:
На рис. 11.19, какие из следующих утверждений верны:
(i) Точка B является внутренней частью ∠AOB
(ii) Точка B является внутренней частью ∠ AOC
(iii) Точка A находится внутри ∠AOD 9.0263 (iv) Точка C является внешней стороной ∠AOB
(v) Точка D si является внешней стороной ∠AOC
Ответ:
(ii), (iv) и (v) являются истинными утверждениями.
(i) и (iii) являются неверными утверждениями, поскольку B лежит на ∠AOB, а A лежит на ∠AOD.
Страница № 11.6:
Вопрос 8:
Какие из следующих утверждений верны:
(i) Вершина угла лежит внутри него.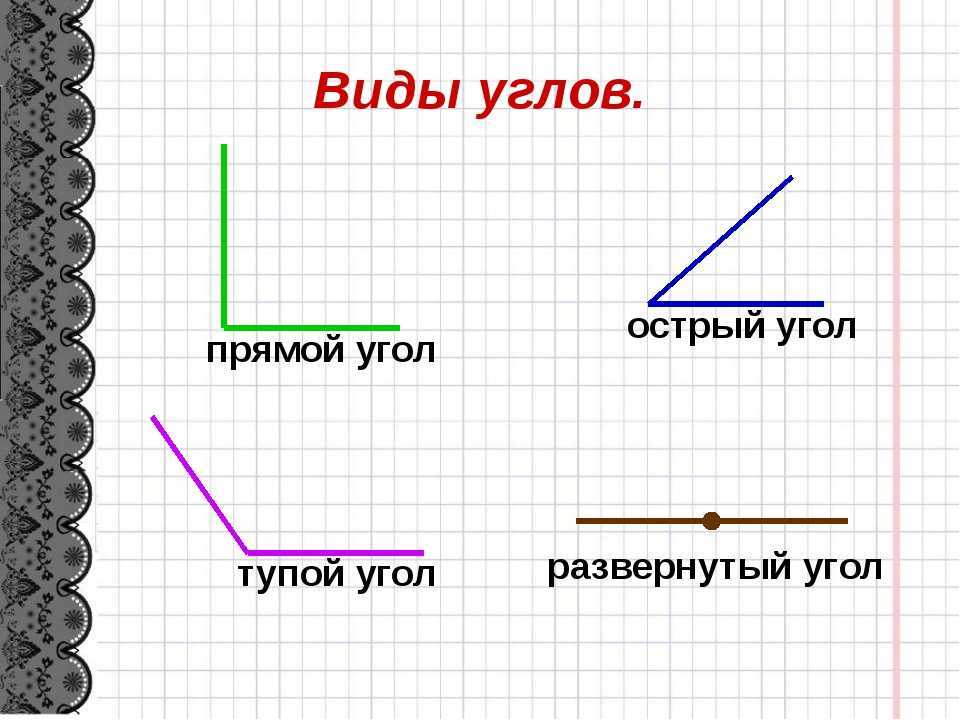
(ii) Вершина угла лежит вне его.
(iii) Вершина угла лежит на нем.
Ответ:
(iii) Вершина угла лежит на нем.
Это единственно верное утверждение.
Страница № 11.6:
Вопрос 9:
Просто взглянув на пару углов, представленных на рис. 11.20, укажите, какой из углов в каждой из пар больше:
Ответ:
(i) ∠AOB больше, чем ∠DEF.
(ii) ∠PQR больше, чем ∠LMN.
(iii) ∠UVW больше, чем ∠XYZ.
Страница № 11.7:
Вопрос 10:
С помощью кальки сравните углы в каждой из пар, приведенных на рис. 11.21.
Ответ:
С помощью кальки получаем, что:
(i)∠PQR больше, чем ∠AOB.
(ii) ∠UVW больше, чем ∠LMN.
(iii) ∠RST больше, чем ∠XYZ.
(iv) ∠PQR больше, чем ∠EFG.
Приведите по два примера прямых острых и тупых углов из вашей среды…
Перейти к
- Углы. Упражнение 11.1.
- Углы.
 Упражнение 11.2.
Упражнение 11.2.
- Зная свои числа
- Игра с числами
- Целые числа
- Действия над целыми числами
- Отрицательное число и целые числа
- Фракции
- Десятичные
- Введение в алгебру
- Соотношение, пропорция и унитарный метод
- Основные геометрические понятия
- Углы
- Треугольники
- Круги
- Пара прямых и поперечная
- Понимание трехмерных форм
- Симметрия
- Основные геометрические инструменты
- Геометрические построения
- Измерение
- Обработка данных Представление данных
- Обработка данных – II
- Гистограммы обработки данных
Главная >
РД Шарма Решения
Класс 6
Математика
>
Глава 11 — Углы
>
Углы.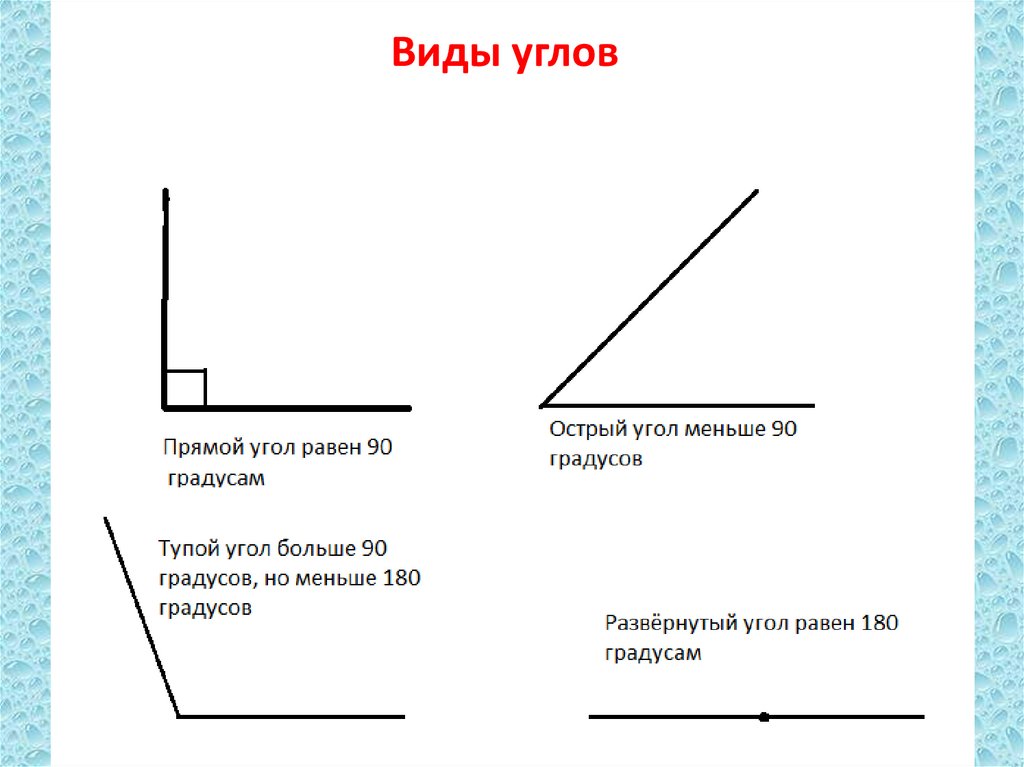 Упражнение 11.2.
>
Вопрос 1
Упражнение 11.2.
>
Вопрос 1
Вопрос 1 Углы Упражнение 11.2
Приведите по два примера прямых, острых и тупых углов из окружающей среды.
Ответ:
Два примера прямого угла:
Две смежные стены комнаты и смежные края книги
Два примера острого угла:
Две смежные стороны буквы Z и два смежных пальца нашей руки.
Два примера тупых углов:
Две наклонные стороны крыши и две смежные лопасти вентилятора
Связанные вопросы
Угол образован двумя соседними пальцами. Под каким углом он появится?
Шиха гребет на лодке на северо-восток. В каком направлении она будет грести, если перевернет ее…
Какова мера угла в градусах между: (i) Севером и Западом? (ii) Севером и Югом? (iii) Нет…
Корабль, плывущий по реке Джелам, движется на восток.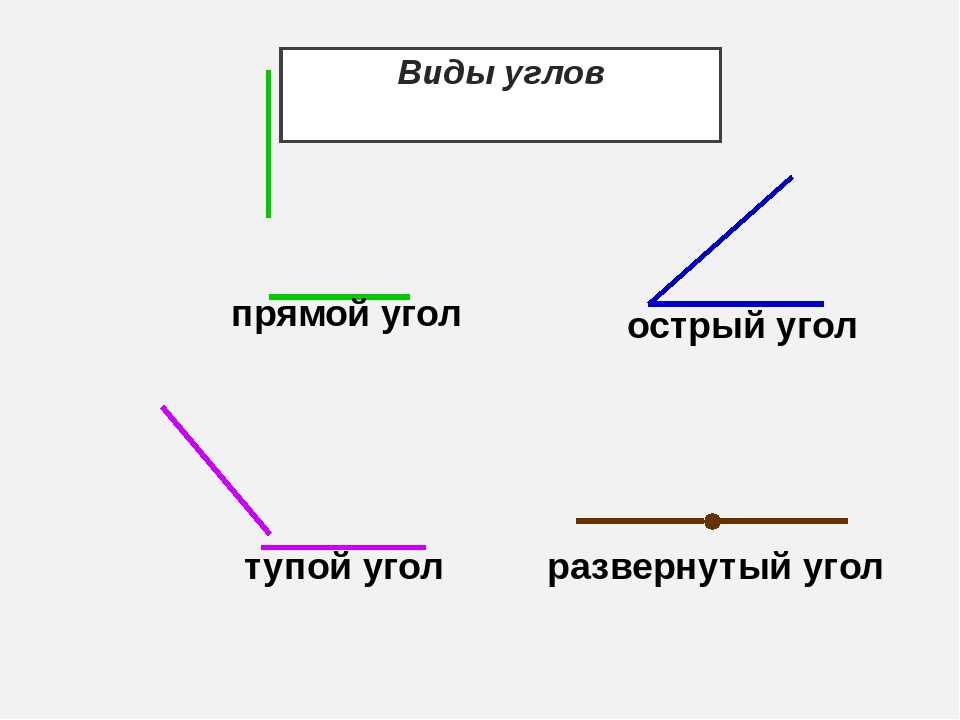 Если она поворачивает на север, под каким углом она…
Если она поворачивает на север, под каким углом она…
Вы стоите в классе лицом на север. В каком направлении вы смотрите после того, как сделаете акварели?
Колесо велосипеда делает четыре с половиной оборота. Найдите количество прямых углов, на которые он повернется.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Углы Упражнения 11.1
Углы Упражнения 11,2
Главы
Знание ваших чисел
Игра с номерами
Целые номера
Операции
Отрицательные номера и целые числа
0202 Decimals
.

 Я острый – начертить хочу,
Я острый – начертить хочу,

 Упражнение 11.2.
Упражнение 11.2.