Урок 11. Площадь прямоугольной трапеции
Площадь прямоугольной трапеции равна произведению полусуммы её оснований на высоту.
или произведению средней линии на высоту:
где
средняя линия.
ЗАДАЧА:
Основания прямоугольной трапеции равны 24 см и 16 см, а диагональ – биссектриса её острого угла. Найдите площадь трапеции.
РЕШЕНИЕ:
Пусть АВСD (АD ∥ ВС, АВ ⊥ АD) – трапеция,АD = 24 см, ВС = 16 см,
DВ – биссектриса кута D,
СК – высота трапеции.
∠ ADB = ∠ CDB, так как
DВ – биссектриса угла D,
∠ ADB = ∠ DBC, так как
АD ∥ ВС и DВ – секущая.
Тогда, ∠ DBC = ∠ CDB и треугольник ВСD – равнобедренный,
СD = СВ = 16 см,
КD = АD – АК =
= АD – ВС =
= 24 – 16 = 8 см.
Из треугольника СКD (∠ К = 90°) получим:
S = 1/2(АD + ВС)× СК
= 1/2(24 + 16)× 8√͞3
= 160√͞3 см2.
ЗАДАЧА:
В прямоугольную трапецию вписана окружность. Точка касания
делит большую боковую сторону на отрезки длиной 4 см и 9 см. Найдите площадь трапеции.
Точка касания
делит большую боковую сторону на отрезки длиной 4 см и 9 см. Найдите площадь трапеции.
Пусть АВСD (АD ∥ ВС, СD ⊥ АD) – прямоугольная трапеция, в которую вписана окружность с центром О.
Е, F, К, Р – точки касания окружности до сторон трапеции.
АР = АЕ = 9 см как касательные к окружности, проведённые из одной точки. Аналогично
ВF = ВЕ = 4 см.
Проведём
ВL ⊥ АD, ОF ⊥ ВС, ОР ⊥ АD
как радиусы, проведённые к касательным.
Поэтому, FР ⊥ АD, откуда
LР = ВF = 4 см,
АL = АР – ВF
= 9 – 5 = 4 см.
Из треугольника АВL:
СD = ВL = 12 см.
ОР = ОF как радиусы окружности.
РОКD і ОFСК – квадраты, у которых общая сторона ОК, поэтому
СК = КD = 1/2 ВL
= 1/2 12 = 6 см.
Откуда
FС = РD = 6 см.
Поэтому,
ВС = ВF + FС
= 4 + 6 = 10 см.
АD = АР + РD
= 9 + 6 = 15 см.
S = 1/2 (ВС + АD)×СD
= 1/2 (10 + 15)×12 =
150 см2.
ЗАДАЧА:
Большая диагональ прямоугольной трапеции делит высоту, проведённую из вершины тупого угла, на отрезки длиной 15 см и 9 см, а большая боковая сторона трапеции равна её меньшему основанию. Найдите площадь трапеции.
РЕШЕНИЕ:
Пусть АВСD – прямоугольная трапеция (АВ ⊥ ВС, АВ ⊥ АD),∠ ВСD – тупой. Тогда СК
СМ = 15 см, МК = 9 см.
Так как по условию ВС = СD, то треугольник ВСD – равнобедренный. Тогда
∠ СВD = ∠ СDВ (1).
Прямые ВС и АD параллельные, поэтому
∠ СВD = ∠ ВDА (2)
как внутренние разносторонние при секущей ВD. Из
равенств (1) и (2) получим, что ∠ СDВ = ∠ ВDА. Поэтому, DВ –
биссектриса ∠ СDА трапеции.
Из
равенств (1) и (2) получим, что ∠ СDВ = ∠ ВDА. Поэтому, DВ –
биссектриса ∠ СDА трапеции.
Пусть СD = 5х, тогда DК = 3х.
Из ∆ СDК (∠ К = 90°):
СD2 = СК2+ КD2,
25х2 = 242 + 9х2,
16х2 = 242, 4х = 24,
х = 6 см.
Получим:
СD = 5 ∙ 6 = 30 (см),
DК = 3 ∙ 6 = 18 (см).
ВС = СD = 30 см,
АD = АК + КD =
= ВС + КD =
= 30 + 18 = 48 (см).
Sтр. = 1/2 (АD + ВС)∙ СК =
= 1/2 (30 + 48) ∙ 24 =
= 78 ∙ 12 = 936 (см2).
ОТВЕТ: 936 см2
ЗАДАЧА:
У прямоугольную трапецию АВСD (АD ∥ ВС, АВ ⊥ АD) вписана окружность с центром в точке О. Найдите площадь трапеции, если
ОС = 6 см, ОD = 8 см.
РЕШЕНИЕ:
Начертим чертёж.
Очевидно, что ∆ СОD прямоугольный с катетами 6 см и 8 см. Тогда СD = 10 см. Точка К – точка касания касательной
СD до окружности.
ОК ⊥ СD, ОК = R,
ВС = R + МС (МС = КС),
АD = R + ND, (ND = КD),
SABCD = ВС∙ АD,
2S∆COD = ОС∙ ОD =
= СD∙ R,
6 ∙ 8 = 10∙ R,
R = 4,8 см.
Воспользуемся следующими соотношениями в прямоугольном ∆ СОD:
ОС2 = СD∙ СК,
36 = 10∙ СК,
СК = МС = 3,6 см.
Тогда КD = ND =
= 10 – 3,6 = 6,4 (см).
SABCD = (4,8 + 3,6) ∙ (4,8 + 6,4) =
= 94,08 (см2).
ОТВЕТ: 94,08 (см2)
Задания к уроку 11
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
все формулы и примеры задач :: SYL.
 ru
ruЗадачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
| Величина | Ее обозначение |
| a | большее основание |
| b | меньшее основание прямоугольной трапеции |
| c, h | перпендикулярная к основаниям боковая сторона, высота |
| d | наклонная боковая сторона |
| α | острый угол |
| β | тупой угол |
| м | средняя линия трапеции |
| д1 | меньшая диагональ |
| д2 | большая диагональ |
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
c = h.
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a — b) * tg α;
c = √ (d2 — (a — b)2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a — b) /cosα;
d = c / sin α;
d = √ (c2 + (а – b)2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.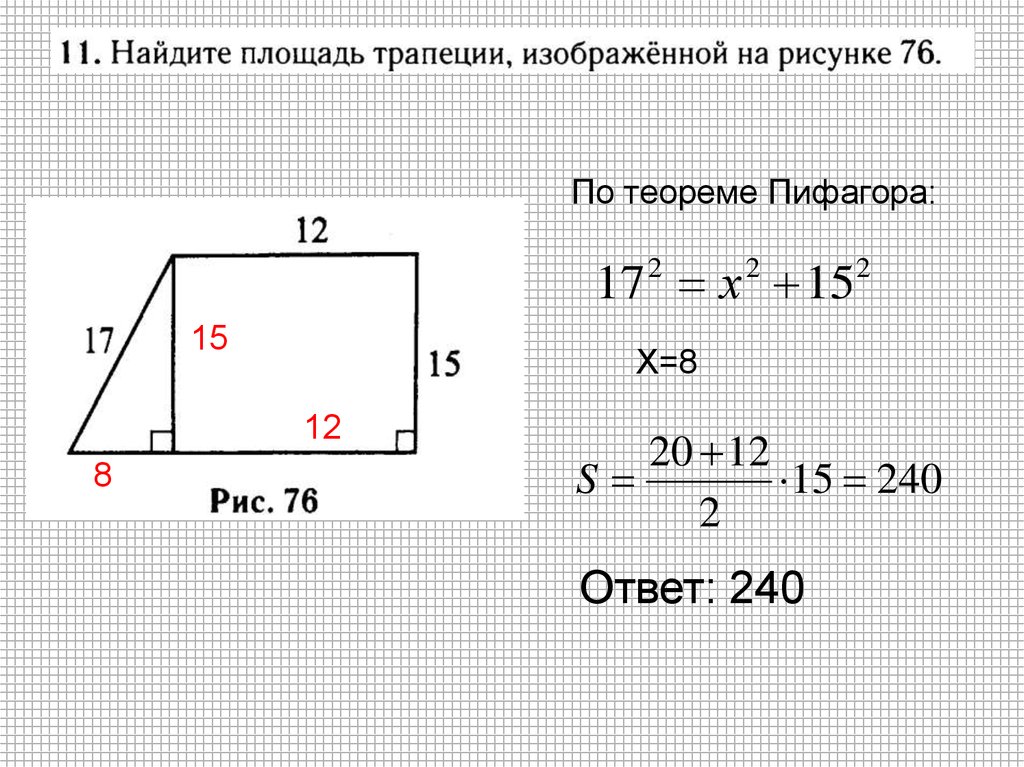
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
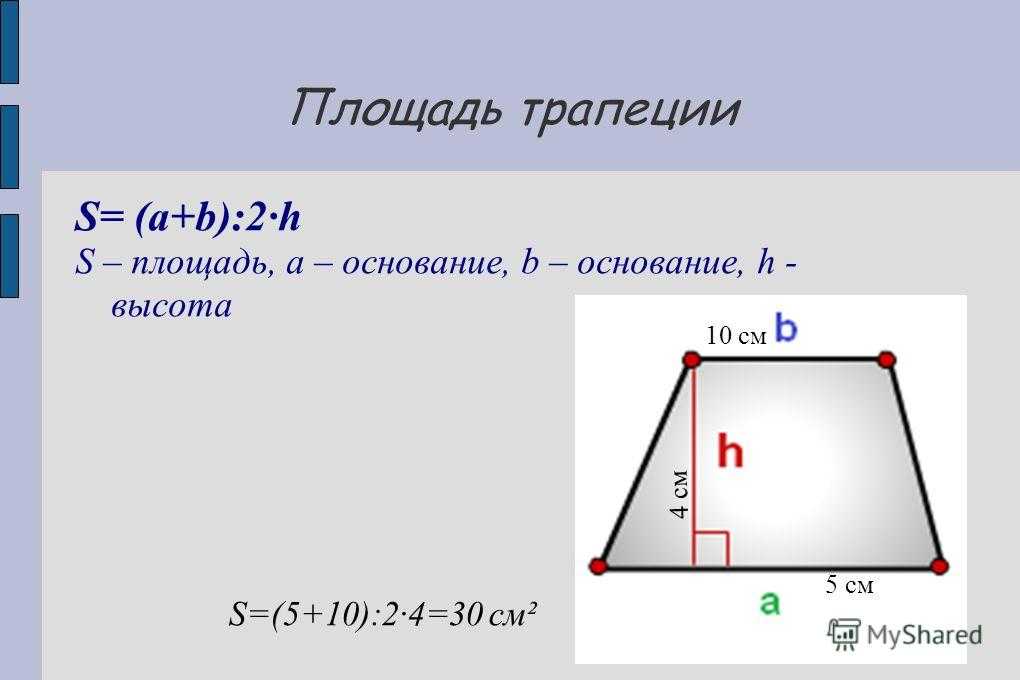
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с2 + b2)
или по-другому, заменив «с» на «h»:
d1 = √ (h2 + b2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с2 + b2) или d2 = √ (h2 + а2).
Задача №1
Условие. Площадь прямоугольной трапеции известна и равна 120 дм2. Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с2 + (а – b)2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а — b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
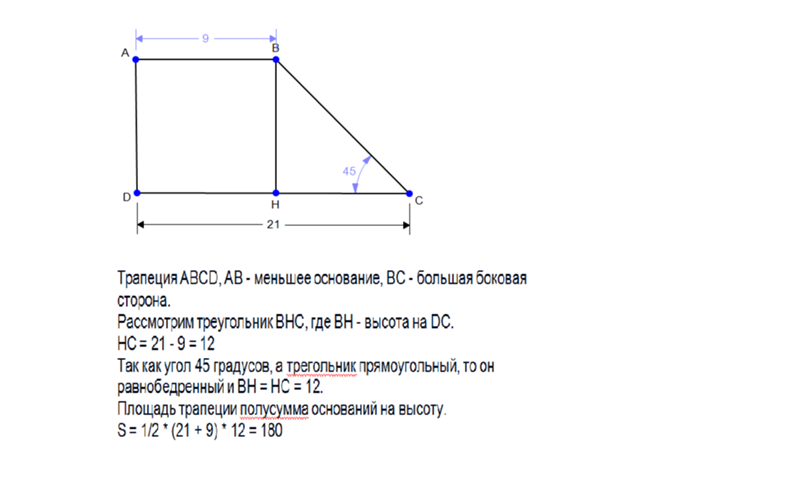
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше.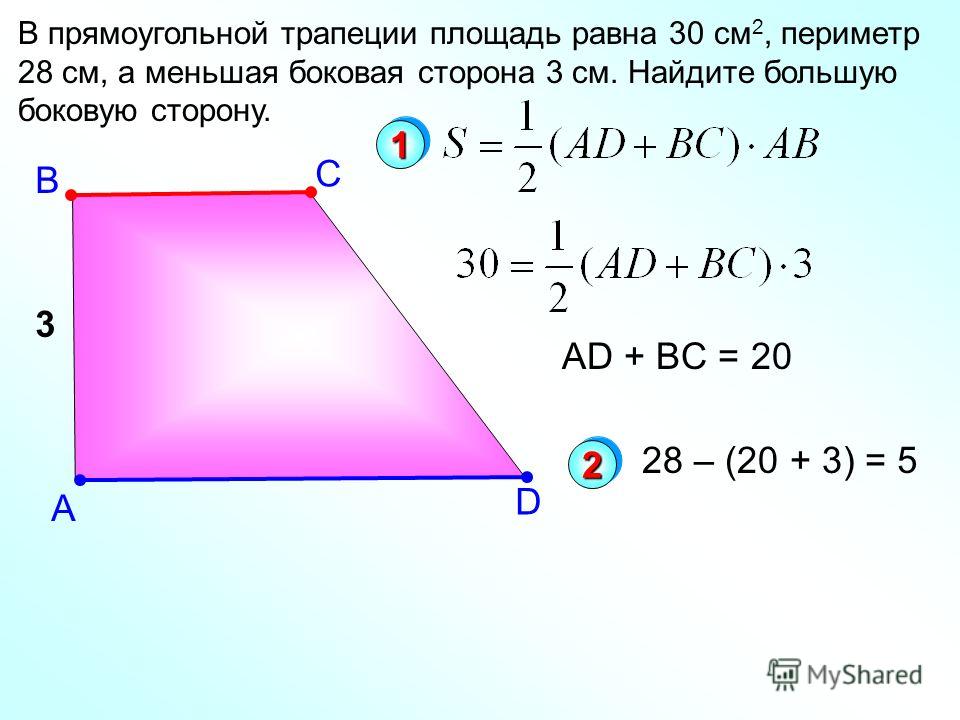 Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Необходимо сделать преобразования, подставив вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см2.
Ответ. Искомая площадь 36 см2.
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
Площадь трапеции — определение, формула и примеры
Этот урок покажет вам, как мы можем найти площадь трапеции, используя два разных метода.
- Разрезание трапеции и перестановка частей, чтобы получились прямоугольник и треугольник.

- Используя формулу для нахождения площади трапеций.
Первый способ поможет понять, почему работает формула нахождения площади трапеций.
Начнем!
Нарисуйте трапецию на миллиметровой бумаге, как показано ниже. Затем разрежьте трапецию на три части и сделайте из них прямоугольник и треугольник.
На рисунке слева показана трапеция, которую нужно разрезать, а на рисунке справа показан прямоугольник и 1 треугольник.
Затем нам нужно сделать следующие четыре важных наблюдения.
1.
Прямоугольник
Основание = 4
Высота = 8
2.
Трапезиоид
Длина нижнего основания = 13
Длина верхнего основания = 4
высота = 8
3.
недавно образованный Triangle (Сделано с голубой)
Длина основания = 9 = 13 — 4 = длина основания трапеции — 4
Высота = 8
4.
Площадь трапеции = площадь прямоугольника + площадь вновь образованного треугольника.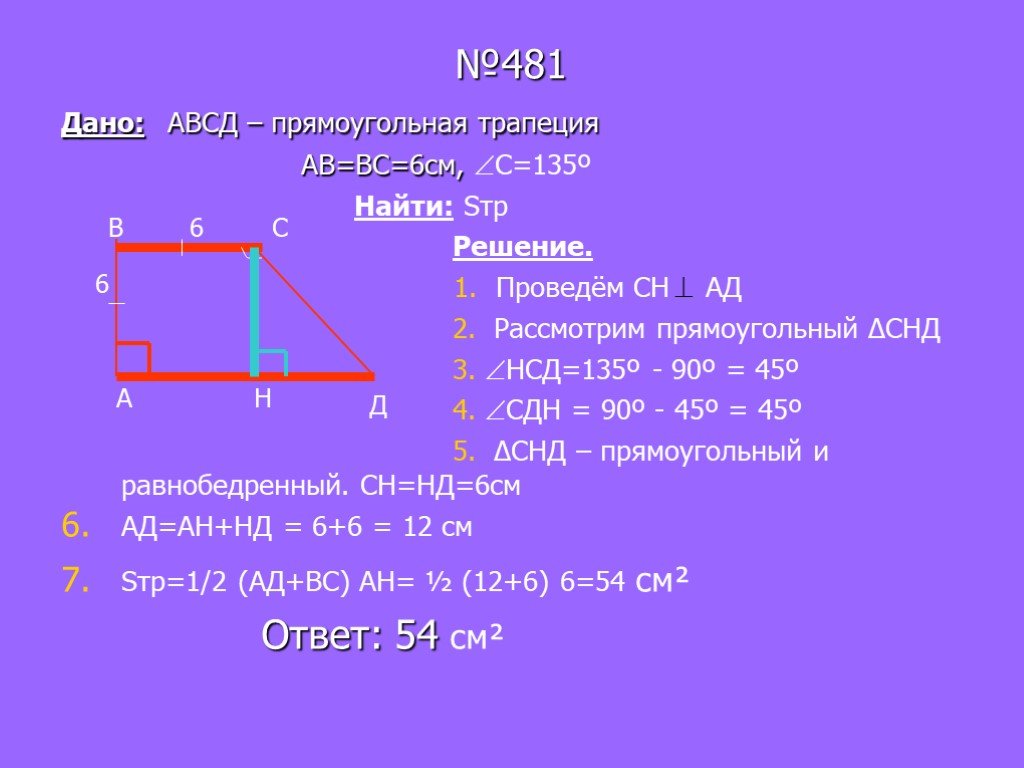
Теперь наша стратегия будет состоять в том, чтобы вычислить площадь прямоугольника и площадь вновь образованного треугольника и посмотреть, сможем ли мы магическим образом вызвать формулу для нахождения площади трапеции.
Площадь прямоугольника = основание × высота = 4 × 8 — 4 × 8] / 2
Площадь треугольника = (13 × 8) / 2 + (- 4 × 8) / 2
Площадь трапеции = 4 × 8 + (13 × 8) / 2 + (- 4 × 8) / 2
Площадь трапеции = 8 × (4 + 13 / 2 + — 4 / 2)
Площадь трапеции = 8 × (4 — 4 / 2 + 13 / 2)
Площадь трапеции = 8 × (8/2 — 4/2 + 13/2)
Площадь трапеции = 8 × (4/2 + 13/2)
Площадь трапеции = (4/2 + 13/2) × 8
Площадь трапеции = 1/2 × (4 + 13) × 8
Пусть b 1 = 4 пусть b 2 = 13, и пусть h = 8
Тогда формула для получения площади трапеции равна 1 / 2 × (b 1 + b 2 ) × h
Формула площади трапеции
В общем случае, если b 1 и b 2 — основания трапеции, а h — высота трапеции, то мы можем использовать приведенную ниже формулу. Площадь трапеции равна половине суммы длин оснований, умноженных на высоту или высоту трапеции.
Площадь трапеции равна половине суммы длин оснований, умноженных на высоту или высоту трапеции.
Основания трапеции — параллельные стороны трапеции. Обратите внимание, что непараллельные стороны не используются для нахождения площади трапеции.
Площадь выражается в квадратных единицах.
- Если основания и высота измеряются в метрах, то площадь измеряется в квадратных метрах или м 2 .
- Если основания и высота измеряются в сантиметрах, то площадь измеряется в квадратных сантиметрах или см 2 .
- Если основания и высота измеряются в футах, то площадь измеряется в квадратных футах или футах 2 .
Примеры, показывающие, как найти площадь трапеции по формуле
Пример №1:
Если b 1 = 7 см, , найдите площадь трапеции
Площадь = 1/2 × (b 1 + b 2 ) × h = 1/2 × (7 + 21) × 2 = 1/2 × (28) × 2
Площадь = 1 / 2 × 56 = 28 квадратных сантиметров или 28 см 2
Пример 2:
Если b 1 = 15 см, см, найдите площадь трапеции
Площадь = 1/2 × (b 1 + b 2 ) × h = 1/2 × (15 + 25) × 10 = 1/2 × (40) × 10
Площадь = 1/2 × 400 = 200 квадратных сантиметров или 200 см 2
Пример №3:
дюймов, b 2 = 15 дюймов и h = 2 дюйма, найдите площадь этой трапеции
Площадь = 1/2 × (b 1 + b 2 ) × h = 1/2 × (9 + 15) × 2 = 1/2 × (24) × 2
Площадь = 1/2 × 48 = 24 квадратных дюйма или 24 дюйма 2
Площадь трапеции, когда высота отсутствует или неизвестна
Предположим, вы знаете только длины параллельных оснований и длины катетов разносторонней трапеции, показанной выше.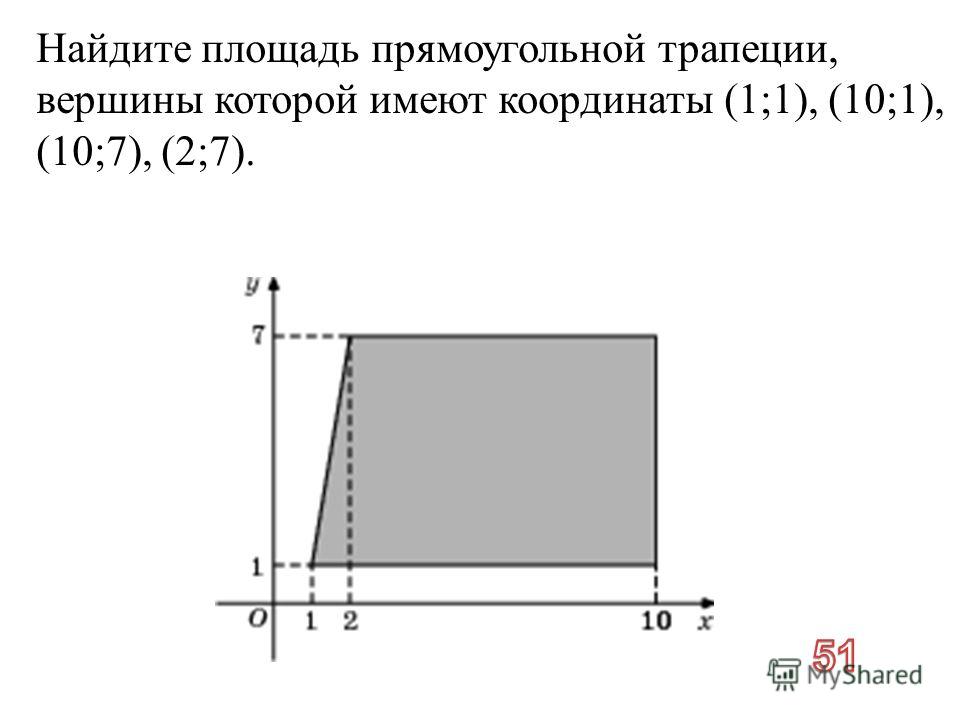 Как найти площадь? Вам нужно сделать прямоугольник и треугольник с трапецией.
Как найти площадь? Вам нужно сделать прямоугольник и треугольник с трапецией.
Разрежьте трапецию на 3 части, прямоугольник и два прямоугольных треугольника. Затем соедините два прямоугольных треугольника и сделайте только 1 треугольник. У вас получится прямоугольник и разносторонний треугольник.
Используйте формулу Герона, чтобы найти площадь разностороннего треугольника.
Площадь = √[s × (s − a) × (s − b) × (s − c)], s = (a + b + c)/2
a = 17, b = 10 и c = 21
с = (17 + 10 + 21)/2 = 48/2 = 24
с — а = 24 — 17 = 7
с — b = 24 — 10 = 14
с − c = 24 − 21 = 3
с × (s − a) × (s − b) × (s − c) = 24 × 7 × 14 × 3 = 7056
√(7056) = 84
Площадь разностороннего треугольника = 84
Используйте площадь разностороннего треугольника, чтобы найти высоту треугольника. Обратите внимание, что основание треугольника равно 21, а высота h разностороннего треугольника также является недостающей стороной прямоугольника.
84 = (21 × высота) / 2
168 = 21 × высота
168 / 21 = высота
Высота = 8
Площадь прямоугольника 8 × 7 = 56
Площадь трапеции = площадь разностороннего треугольника + площадь прямоугольника = 84 + 56 = 140
Площадь трапеции Тест, чтобы узнать, действительно ли вы поняли этот урок.
| Купить полную электронную книгу по геометрическим формулам. Все геометрические формулы объясняются хорошо подобранными текстовыми задачами, чтобы вы могли освоить геометрию. |
Расчет условной вероятности с помощью таблицы непредвиденных обстоятельств
29, 23 марта 10:19
Научитесь рассчитывать условную вероятность с помощью таблицы непредвиденных обстоятельств. Эта таблица непредвиденных обстоятельств может помочь вам разобраться быстро и безболезненно.

Подробнее
Рациональные числа — определение и примеры
15, 23 марта 07:45
Чтобы узнать о рациональных числах, напишите их десятичное представление и распознайте рациональные числа, которые представляют собой повторяющиеся десятичные дроби и завершающие десятичные дроби.
ЧИТАЕТ ДОПОЛНЕНИЕ
Площадь прямоугольной области ABCD Площадь трапеции.
- Количество A больше.
- Количество B больше.
- Обе величины равны.
- Отношения не могут быть определены из предоставленной информации
Итак, вы пытались быть хорошим сдающим экзамен и практиковаться для GRE с помощью PowerPrep онлайн.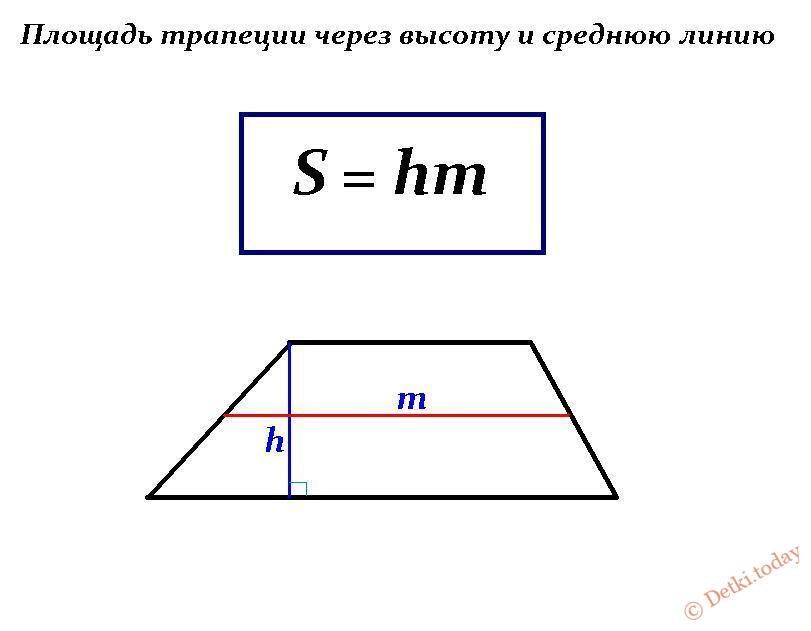
Ответьте на вопрос
Давайте поищем в задаче подсказки относительно того, что она будет тестировать, так как это поможет переключить наши мысли на мысли о том, какой тип математических знаний мы будем использовать для решения этого вопроса. Обратите внимание на любые слова, которые относятся к математике, и на что-нибудь особенное в отношении того, как выглядят числа, и отметьте их на бумаге.
В вопросе есть две четырехсторонние цифры. Мы можем ожидать, что это проверит наши знания о четырехугольниках из геометрии.
Что мы знаем?
Давайте внимательно прочитаем вопрос и составим список того, что мы знаем.
- Нам дан прямоугольник и длины его сторон
- Дана трапеция вместе с длинами ее оснований и высотой
- Мы хотим сравнить площадь квадрата с площадью трапеции
Разработать план
Геометрия! Ну, по крайней мере, они были достаточно любезны, чтобы дать нам поиграть с картинками. Так что мы можем пропустить важный этап создания рисунков для большинства вопросов по геометрии . Тем не менее, мы можем свободно перерисовывать эти цифры на нашем листе бумаги, так как это трудно писать на тестовом экране компьютера (и не одобряется тестовыми прокторами).
Так что мы можем пропустить важный этап создания рисунков для большинства вопросов по геометрии . Тем не менее, мы можем свободно перерисовывать эти цифры на нашем листе бумаги, так как это трудно писать на тестовом экране компьютера (и не одобряется тестовыми прокторами).
Давайте начнем с нисходящего подхода, где мы начнем с того, что мы ищем, и перейдем к деталям того, что нам дано в этом вопросе. Начиная с количества A, мы хотим узнать площадь прямоугольника $ABCD$. Думая об уравнениях на площадей четырехугольников , мы знаем, что:
$$\Area \Rectangle = \Length · \Width$$
Мы видим, что прямоугольник $ABCD$ имеет длину и ширину $3$ и $8$, поэтому мы определенно имеют достаточно информации, чтобы вычислить его площадь.
Переходим к количеству B. Нам нужна площадь трапеции $EFGH$. Ах, мы узнали это, когда узнали о площадях четырехугольников .
$$\Площадь\Трапеция = (\Основание 1 + \Основание 2)/2·\Высота$$
В трапециях два основания должны быть параллельны друг другу, а высота равна стороне , перпендикулярной (образующей угол $90°$) к обоим основаниям. Используя эту информацию, мы видим, что длина двух оснований равна 5$ и 7$ соответственно, а высота равна 4$.
Используя эту информацию, мы видим, что длина двух оснований равна 5$ и 7$ соответственно, а высота равна 4$.
Теперь у нас достаточно информации для решения обеих областей, так что давайте приступим!
Решите вопрос
Во-первых, решив количество А, мы получим:
| $\Площадь\Прямоугольник$ | $=$ | $\Длина · \Ширина$ |
| $\Площадь\Прямоугольник$ | $=$ | $3·8$ |
| $\Площадь\Прямоугольник$ | $=$ | $24$ |
Таким образом, количество A, площадь прямоугольника, имеет значение $24$. Теперь давайте найдем количество B, площадь трапеции.
| $\Площадь\Трапеция$ | $=$ | $(\База 1 + \База 2)/2·\Высота$ |
| $\Площадь\Трапеция$ | $=$ | $(5+7)/2·4$ |
| $\Площадь\Трапеция$ | $=$ | 12/2·4$ |
| $\Площадь\Трапеция$ | $=$ | $24$ |
Ах! Таким образом, обе величины имеют значение $24$, поэтому они равны друг другу.