Пусть f функция истинности: Информатика — Логика. Основные сведения.

Тема 1 Функции алгебры логики

1.1 Логические операции

1.2 Булевы функции

Основным объектом дискретной математики являются булевы функции. Предпосылкой их введения служат высказывания, которые составляют основную базу для построения теории булевых функций.

1.1 Логические операции. Алгебра логики – самый простой раздел математической логики. Язык алгебры логики является одним из простейших языков математики. Основными объектами данного раздела являются высказывания. Понятие «высказывание» является первичным, оно не определяется, а поясняется. Под высказыванием понимают предложение, о котором можно сказать одно из двух: истинно оно или ложно. Например, высказывание «2+3=5» – истинное, высказывание «существует действительное число Х такое, что

Х2 = –1» ложное. Очевидно, не каждое предложение является высказыванием. Например, предложения: «Когда ты был дома?», «Пойдем со мной!» не являются высказываниями. Высказывания будем обозначать малыми латинскими буквами

X, y, z,…, а их значения, т. е. истину и ложь, соответственно 1 и 0. Из двух данных высказываний с помощью связок «не», «и», «или», «если … то», «тогда и только тогда, когда …» можно образовать новые высказывания. Например, из высказываний «число 2 простое», «число 2 четное» с помощью указанных выше связок получаем высказывания «число два простое и четное», «число 2 непростое», «число 2 простое или четное». Высказывание «если π иррационально, то π2 тоже иррационально» получается связыванием двух высказываний связкой «если … то». Эти операции соответствуют упомянутым выше связками, употребляемым в обычной речи.

Рассмотрим примеры логических операций.

1. Логическая операция, соответствующая связке «и», называется Конъюнкцией и обозначается &. В некоторых книгах эту операцию обозначают символом . Пусть X и y – высказывания. Высказывание X×y назовем конъюнкцией X И Y. Данное высказывание истинно тогда и только тогда, когда истинны оба высказывания

X и Y.

Соответствующее определение запишем в виде таблицы истинности

X	Y	Xy
0	0	0
0	1	0
1	0	0
1	1	1

Определение конъюнкции двух высказываний естественным образом распространяется на любое конечное число высказываний.

Конъюнкция X1x2…xn, которую мы кратко обозначим через , истинна тогда и только тогда, когда истинны все высказывания.

2. Логическая операция, соответствующая связке «или», называется Дизъюнкцией и обозначается .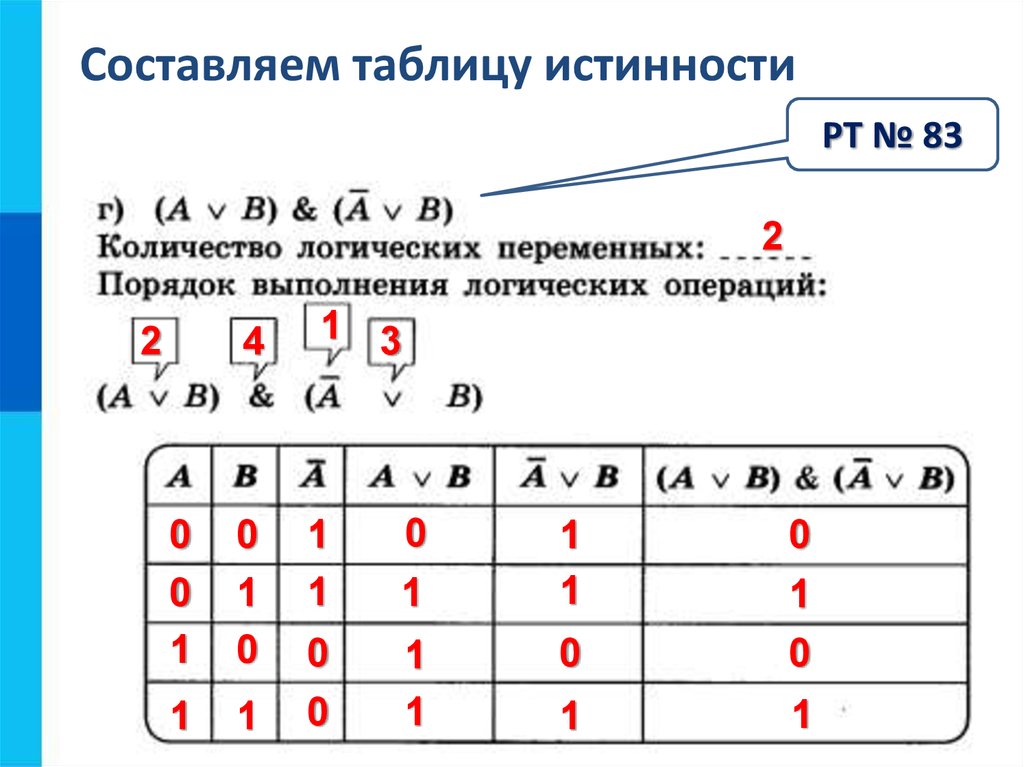

Пусть X и Y – высказывания. Высказывание XÚY назовем дизъюнкцией X и Y. Данное высказывание истинно тогда и только тогда, когда хотя бы одно из высказываний X и Y истинно.

Данное определение запишем в таблицы истинности.

X	Y	XY
0	0	0
0	1	1
1	0	1
1	1	1

Определение дизъюнкции двух высказываний естественным образом распространяется на любое конечное число высказываний. Дизъюнкция X1Ú X2 Ú … Ú XN, которую мы кратко обозначим через , истинна тогда и только тогда, когда хотя бы одно из высказываний X1, X2, …, XN истинно.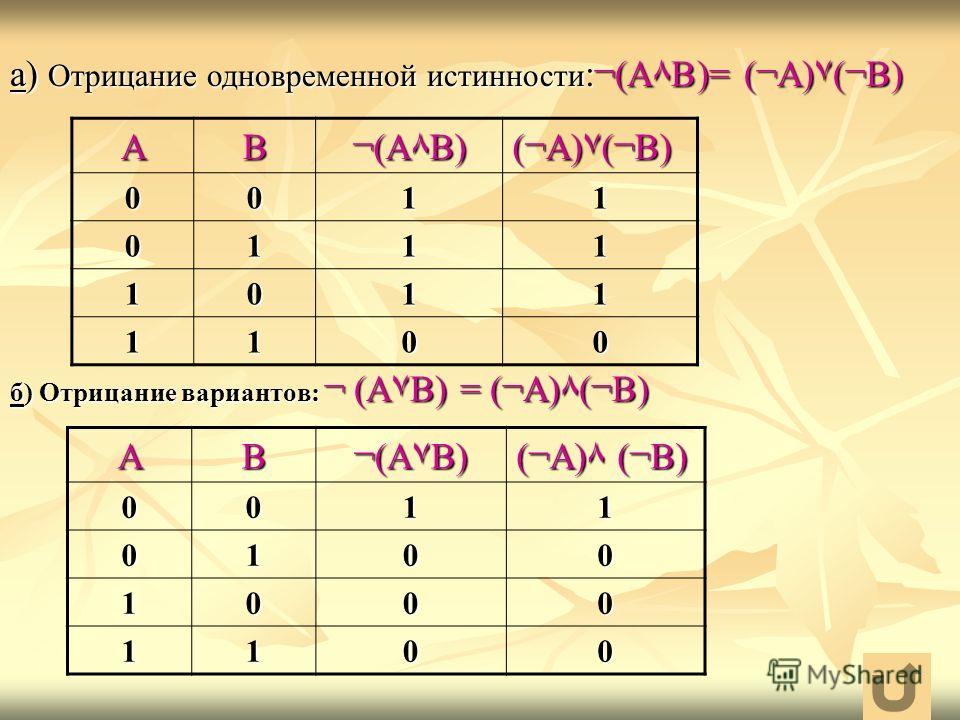

3. Логическая операция, соответствующая связке «не», называется Отрицанием.

Отрицание высказывания X записывается так: и определяется следующей таблицей истинности:

X
0	1
1	0

4. Логическая операция, соответствующая связке «если … то», называется Импликацией. Эту операцию будем обозначать символом _. При этом высказывание «если X, то Y» записывается в виде x_Y. Высказывание X называется посылкой импликации, Y – ее заключением. Импликация двух высказываний X и Y задается следующей таблицей истинности:

X	Y	X_Y
0	0	1
0	1	1
1	0	0
1	1	1

Из определения импликации вытекает, что:

· импликация с ложной посылкой всегда истинна;

· импликация с истинным заключением всегда истинна;

· импликация ложна тогда и только тогда, когда посылка истинна, а заключение ложно.

5. Логическая операция, соответствующая связке «тогда и только тогда, когда …» называется Эквивалентностью и обозначается символом n.

Пусть X и Y – высказывания. Высказывание XNY назовем эквивалентностью X и Y. Данное высказывание истинно тогда и только тогда, когда оба высказывания X и Y или истинны или ложны.

Данное определение запишем в виде таблицы истинности:

X	Y	XNY
0	0	1
0	1	0
1	0	0
1	1	1

1. 2 Булевы функции. Пусть исходный алфавит переменных.

Функцией алгебры логики От переменных называется функция, принимающая значения 1, 0 и аргументы которой также принимают значения 1, 0.

Обычно функции алгебры логики называют булевыми функциями. Название «булевы функции» возникло в связи с использованием функций рассматриваемого типа в алгебре логики, начало которой было положено трудами ирландского ученого 19 века Дж. Буля. Областью определения булевой функции от n переменных служат совокупность всевозможных n-мерных упорядоченных наборов , где .

Следует отметить, что любой такой набор можно рассматривать как представление некоторого целого неотрицательного числа в двоичной системе счисления. Например, набору (0,1,0,1) соответствует число , а набору (1,1,1) – число .

Все наборы размерности n нумеруются целыми числами от 0,2n-1. Отсюда нетрудно заметить, что число таких наборов равно 2n.

Всякая булева функция от n переменных может быть задана с помощью таблицы истинности:

Таблица 1

X1	X2	…	XN-1	XN	F(X1,X2,…,XN-1,XN)
0	0	…	0	0	F (0,0,…,0,0)
0	0	…	0	1	F (0,0,…,0,1)
0	0	…	1	0	F (0,0,…,1,0)
…	…	…	…	…	…
1	1	…	1	1	F (1,1,…,1,1)

Данная таблица состоит из 2n строк, причем в ней все наборы расположены в порядке возрастания их номеров.

Очевидно, что булевы функции от n переменных однозначно определяются своими последними столбцами из таблицы 1, т. е. наборами из 2n нулей и единиц. Следовательно, различных булевых функций от n переменных будет столько, сколько имеется различных наборов длины 2n, а их число равно . Итак, мы доказали следующую теорему:

Теорема 1. Имеется точно Булевых функций от Переменных.

В алгебре логики особое значение имеют следующие булевы функции, которые называют элементарными булевыми функциями.

— константа 0;

— константа 1;

— тождественная функция;

— отрицание х;

— конъюнкция X и y;

— дизъюнкция х и у;

— импликация х и у;

— эквивалентность х и у;

— сложение х и у по mod2;

— функция Шеффера;

— стрелка Пирса.

Последние три функции задаются следующими таблицами истинности:

0	0	0	1	1
0	1	1	1	0
1	0	1	1	0
1	1	0	0	0

Введенное понятие булевой функции несовершенно тем, что оно не позволяет рассматривать функцию от меньшего числа аргументов как функцию от большего числа аргументов. Для устранения этого недостатка введем понятие фиктивной переменной.

Переменная XI в функции называется Фиктивной, если = при любых значениях остальных переменных. В этом случае функция , по существу, зависит от (n-1) – переменной, т. е. представляет собой функцию от (n-1) переменной. Говорят, что функция g получается из функции f удалением фиктивной переменной, а функция f получается из g введение фиктивной переменной, причем эти функции являются равными.

Благодаря введению фиктивных переменных любую булеву функцию от Переменных можно считать функцией от любого большего числа переменных. Поэтому любую конечную совокупность булевых функций можно считать зависящими от одного и того же числа переменных.

< Предыдущая		Следующая >

НОУ ИНТУИТ | Лекция | Какие у Вас корни? Часть 1

Аннотация: В этом уроке будем заниматься решением логических уравнений.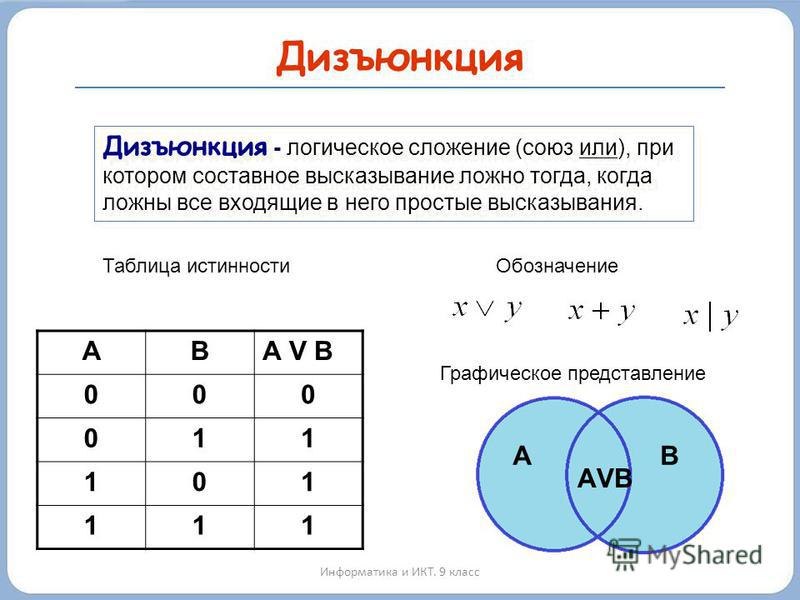 Нас будет интересовать, сколько решений имеет уравнение, какие у него корни.

Смотреть на youtube || на ИНТУИТ в качестве: низком | среднем | высоком

Решение уравнений является одной из основных задач, рассматриваемых в школьном курсе математики. В алгебре, тригонометрии рассматриваются алгебраические и тригонометрические функции, аргументы которых являются вещественными числами, и сами функции принимают вещественные значения. Основным предметом изучения в школе являются функции F(x) от одной переменной. В области вещественных чисел таких функций бесконечно много, в отличие от логических функций от одной переменной, пересчитать которые достаточно пальцев одной руки, а интерес представляет только одна функция – отрицание.

Как связаны функции и уравнения?

intuit.ru/2010/edi»>Пусть F(x) – вещественная функция с вещественным аргументом. Если она задана, то можно, например, построить график этой функции y = F(x), вычисляя значение функции y для заданных значений аргументов.

Уравнением называют запись:

F(x) = a,

Где а – некоторое число.

Решить уравнение означает найти такое значение x*, при котором уравнение превращается в тождество, другими словами, функция F, вычисленная в точке x*, имеет значение a: F(x*) = a.

Уравнение может не иметь корней, может иметь один или несколько корней. Если a равняется нулю, то корнями являются те значения x, в которых функция обращается в нуль, то есть точки, в которых график функции пересекается с осью абсцисс.

Уравнение:

intuit.ru/2010/edi»>F(x) = a

Всегда можно привести к каноническому виду, перенеся значение а в левую часть уравнения:

Ф(x) = 0

Если рассматривать одно уравнение от нескольких переменных:

F(x1, x2, …xk) = 0,

То заниматься поиском корней обычно не имеет смысла, поскольку в общем случае их бесконечно много. Можно конечно, зафиксировать значения всех аргументов, кроме одного, прийти к уравнению с одной переменной и искать его корни.

Поиск корней становится осмысленным, когда мы имеем дело с системой уравнений.

Как меняется ситуация, когда речь идет о логических функциях?

Рассмотрим уравнение:

intuit.ru/2010/edi»>F(x) = a

Пусть F – логическая функция, а x – логическая переменная. Прежде всего, заметим, что параметр a может принимать только 2 значения – 0 или 1, поскольку логическая функция имеет только эти два возможных значения.

Рассматривать уравнение с одним неизвестным для логических функций не имеет смысла, поскольку, как уже говорилось, их всего-то четыре, все они элементарны, о них все известно.

Но зато для логических функций становится осмысленным решение уравнения:

F(x1, x2, …xk) = a

Осмысленно потому, что область определения такой функции содержит конечное число элементов, каждый из которых можно рассматривать как кортеж из k значений аргументов, как слово длины k в двоичном алфавите. На некоторых кортежах функция принимает значение 0, на других – 1.

Что значит найти решение такого уравнения? Решением являются те наборы аргументов из таблицы истинности функции F, на которых функция принимает значение a – 0 или 1.

Канонической записью логического уравнения является запись:

F(x1, x2, …xk) = 1,

Решением являются те кортежи аргументов, на которых функция принимает значение 1 (Истина).

Уравнение, записанное в дополняющей форме:

F(x1, x2, …xk) = 0,

всегда можно привести к каноническому виду, применив операцию отрицания:

F(x1, x2, …xk) = 0

эквивалентно уравнению:

!F(x1, x2, …xk) = 1

intuit.ru/2010/edi»>Под корнем уравнения будем понимать тот набор аргументов, тот кортеж, на котором функция принимает истинностное значение, — значение 1.

Рассмотрим уравнение с k переменными:

F(x1, x2, …xk) = 1

Число всех возможных наборов равно 2^k. Пусть F имеет n корней, то есть принимает значение 1 на n наборах. Тогда остальные наборы, на которых функция равна 0, являются корнями уравнения:

F(x1, x2, …xk) = 0

Число корней этого уравнения равно m = 2^k – n.

Задача решения уравнения сводится, по сути, к построению таблицы истинности функции F. Имея таблицу истинности нетрудно сказать, сколько корней уравнения и какие это корни.

Рассмотрим пример:

intuit.ru/2010/edi»>Задача. Найти число корней и сами корни уравнения:

X₁ | X₂ & X₃ ∧ !X₁ ⇒ X₂ ≡ !X₁ | X₂ & X₃ = 1

Для решения задачи достаточно построить таблицу истинности функции, заданной левой частью уравнения, и определить те наборы аргументов, на которых функция равна 1.

Формула, задающая функцию, включает все основные базисные операции:

! – отрицание;

& — конъюнкцию;

| — дизъюнкцию;

∧ — исключающее или;

⇒ — импликацию;

≡ — тождество.

intuit.ru/2010/edi»>Определение этих операций, надеюсь, известно. При вычислении значения функции, заданной формулой следует следить за порядком выполнения операций, определяемого приоритетом операций. В приведенном выше списке операции следуют в соответствии с их приоритетом. Две операции «Или» — дизъюнкция и исключающее или имеют одинаковый приоритет и выполняются в порядке их следования.

С помощью скобок можно менять порядок выполнения операций, поскольку выражение в скобках имеет самый высокий приоритет.

Перепишу нашу формулу, расставив скобки, но не для того чтобы изменить порядок вычисления, а для того чтобы точно указать порядок выполнения действий:

(((X1 | (X2 & X3)) ∧ (!X1 ))⇒; X2 )≡ ((!X1) | (X2 & X3))

Заметьте, последней будет выполняться операция эквивалентности, а до этого вычисляется выражение в скобках слева и справа от знака операции тождества.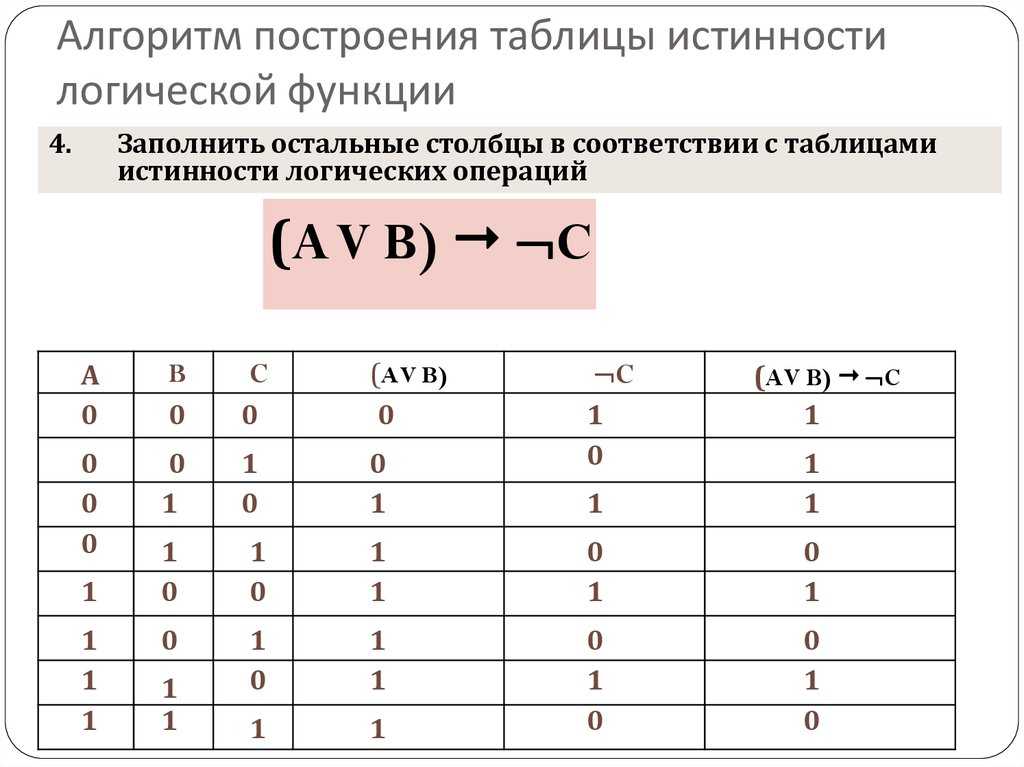 В левой скобке последней будет выполняться операция импликации. Скобки в данной формуле точно указывают порядок вычисления нашей формулы.

Приведу таблицу истинности для функции от трех переменных, заданной нашей формулой. Она определена на восьми наборах. Вот ее вид:

Анализируя нашу таблицу, мы видим, что наше уравнение имеет 5 решений – 5 корней. Первое решение задается набором (0 1 0). Так как наборы можно интерпретировать как числа от 0 до 2ⁿ – 1, записанные в двоичной системе, то все решения можно упорядочить в соответствии с числовым значением набора. Можно считать, что первый корень соответствует набору с числовым значением – 2, последний корень имеет числовое значение – 7. Можно задать все 5 корней как числа – 2, 3, 4, 5, 7. Числа – 0, 1, 6 являются корнями уравнения F(X1, X2, X3) = 0, где F – функция, заданная нашей формулой.

Таков один из возможных способов решения логического уравнения с n переменными. Он хорошо работает, когда n сравнительно мало. Уже при n > 5 утомительно строить таблицу истинности из-за быстрого роста числа строк этой таблицы с ростом n. Правда, можно написать программу, как это сделал я, которая сама будет строить эту таблицу.

операций правды | Заметки Витгенштейна о логике

Фильтр поиска панели навигации Oxford AcademicЗаметки Витгенштейна о логикеФилософия ХХ векаФилософия математики и логикиКнигиЖурналы Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicЗаметки Витгенштейна о логикеФилософия ХХ векаФилософия математики и логикиКнигиЖурналы Введите поисковый запрос

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Подробнее

Укажите

Поттер, Майкл, «Истинные операции», Заметки Витгенштейна по логике (

Oxford

, 2008; онлайн-издание, Oxford Academic, 1 января 2009 г. ), https://doi.org/10.1093/acprof:oso/9780199215836.003 .0018, по состоянию на 8 марта 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicЗаметки Витгенштейна о логикеФилософия ХХ векаФилософия математики и логикиКнигиЖурналы Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicЗаметки Витгенштейна о логикеФилософия ХХ векаФилософия математики и логикиКнигиЖурналы Введите поисковый запрос

Advanced Search

Abstract

Из одного предложения p мы образуем его отрицание не- p .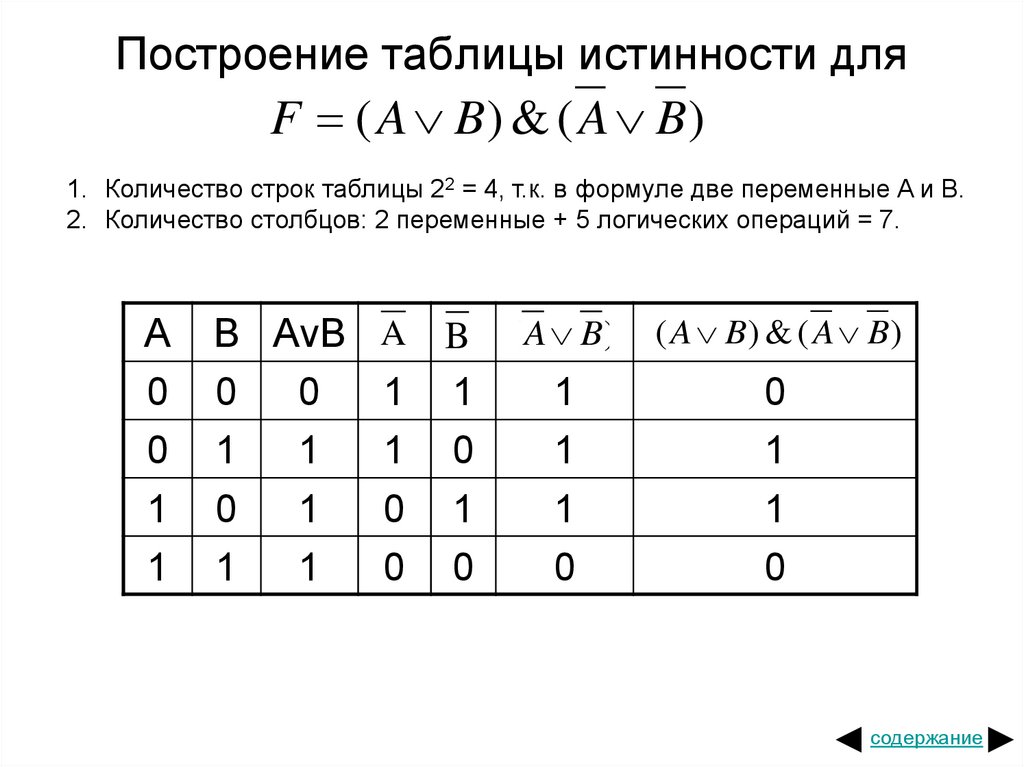 Из двух предложений p и q мы образуем различные дальнейшие предложения, например, p или q , p и q и т. д.; аналогично (хотя и реже) с тремя или более предложениями. Для каждого такого метода формирования предложений принято говорить об определенной функции истинности как о соответствующей ему. С одной стороны, есть функция, которая принимает смысл предложения в качестве входных данных и возвращает смысл предложения в качестве вывода. С другой стороны, существует функция истинности, т. е. функция, принимающая в качестве аргументов некоторое конечное число значений истинности и дающая в качестве значения единственное значение истинности, которое может быть представлено таблицей истинности или диаграммой истинности. В этой главе обсуждается взаимосвязь между ними.

Ключевые слова: таблица истинности, функция истинности, утверждения, диаграмма истинности

Предмет

Философия математики и логики Философия ХХ века

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Щелкните Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Истинно-функциональная полнота

Истинно-функциональная полнота

PL имеет пять операторов: тильда, клин, амперсанд, подкова и тройная черта. Мы знаем, что эти операторы являются функциями истинности. Они принимают значения истинности в качестве входных данных и возвращают значение истинности как выход. Наш вопрос в этом разделе следующий: можем ли мы описать все возможные функции истинности с использованием наших пяти операторов? То есть можем ли мы построить любой функция истинности от входа к выходу с использованием наших операторов? Если ответ да, тогда наша система логики равна правда-функционально полный. Это вопрос в том, что мы называем Металогикой , логикой логики. Спрашивая об этом вопрос мы задаем вопрос о нашей системе логики, и в отвечая на него, мы доказываем что-то о нашей системе логики. Другой металогические вопросы появятся позже в тексте.

Упрощенная версия вопроса, который мы задаем, такова: Можем ли мы построить все возможные таблицы истинности, используя наши пять операторов? Поскольку таблица истинности представляет собой табличное выражение функции от входа к выходу, если мы может построить все возможные таблицы истинности, то наша система функционально полный.

Конечно, существует бесконечное количество таблиц истинности. Итак, как мы можем показать, что можем выразить их все на PL? Мы показываем что у нас есть рецепт построения любой возможной таблицы истинности.

Таблицы истинности бывают разных размеров. Мы помним, что число строк таблицы истинности равно 2 ⁿ , где n — количество отдельные буквы предложений в wff. Начнем с таблицы истинности для п=1. Это имеет две строки:

А	?
Т	?
Ф	?

Здесь «A» может быть T или F. Каковы возможные выходы?

А	?
Т	Т
Ф	Т

Мы могли бы получить все «T» для вывода. Тогда WFF мы потребность — это тавтология. Таким образом, мы можем использовать «(A v ~A)», чтобы получить этот вывод.

А	(А в ~А)
Т	Т
Ф	Т

Теперь рассмотрим возможный результат, при котором мы всегда получаем «Ф»:

А	?
Т	Ф
Ф	Ф

 Тогда нужная нам wff является противоречием. Таким образом, мы можем использовать «(A & ~A)», чтобы дать нам этот вывод.

А	(А и ~А)
Т	Ф
Ф	Ф

 

Далее рассмотрим возможный выход, где выходом является то же, что и ввод:

А	?
Т	Т
Ф	Ф

 Для этого мы просто используем саму букву «А».

А	А
Т	Т
Ф	Ф

Наконец, рассмотрим, что происходит, когда мы переходим от входа «Т» на выход «F» или на вход «F» на выход «T»:

А	?
Т	Ф
Ф	Т

 Это наша старая добрая тильда!

А	~А
Т	Ф
Ф	Т

Мы только что показали, что можем построить все возможные функция от входных значений истинности к выходным значениям истинности для таблиц истинности с одно предложение, отдельная буква. Теперь нам нужно показать, что мы можем сделать это для таблицы истинности с двумя или более различными буквами предложения. Для любого такого таблицы истинности, будет три разновидности: (1) таблицы истинности, которые все «T» в последнем столбце, (2) таблицы истинности, в которых все «F» в последнем столбце столбец и таблицы истинности, в которых есть хотя бы одна буква «Т» и хотя бы одна буква «F». Для в первых двух случаях нам просто нужно построить тавтологии и противоречия. Таким образом, если буква предложения «А» является одной из наших отдельных букв предложения, для таблицы истинности со всеми «Т», мы убеждаемся, что мы отделить «(A v ~A) с другие буквы предложения, и мы получим все буквы «Т» для последнего столбца. Для таблицы истинности со всеми «F», мы соединяем «(A&~A) с буквами предложения и мы получим все «F».

Теперь поговорим о таблицах истинности, где вывод (последний столбец) содержит несколько F и несколько T. Мы формируем wff следующим образом: Начните с первая строка, где все wff оказывается верным: построить соединение следующим образом: для каждого предложения буква, если буква предложения назначена «T», тогда сделайте букву предложения a соединение Если ему присвоено «F», сделайте отрицание буквы предложения a соединение Мы будем называть каждое из этих соединений «ассоциированными соединениями» для тот ряд. Делайте это для в каждой строке, где wff оказывается истинным. Теперь возьмите эти союзы и сформируйте дизъюнкция всех этих союзов, не забудьте использовать только союзы для строки, которые верны в последнем столбце. Результирующий wff является wff с рассматриваемая таблица истинности.

Например, давайте посмотрим на таблицу истинности:

А	Б	?
Т	Т	Ф
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

Следуя нашему рецепту, мы строим связанный союзы (A &~B), для второй строки,   и (~A & B) для третьего ряда.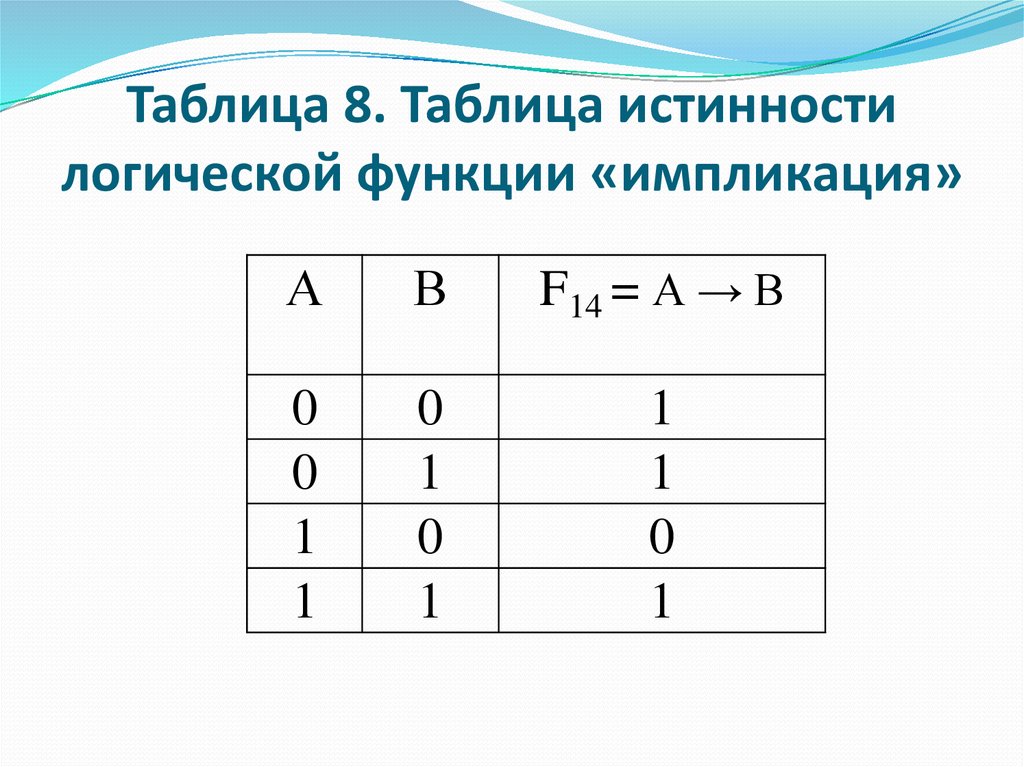 Теперь мы разделяем ассоциированные конъюнкции: (A &~B) v (~A & B). (Не беспокойтесь о группировке здесь.) Эта дизъюнкция имеет рассматриваемую таблицу истинности:

.

А	Б	(А и~В) v (~А и В)
Т	Т	Ф
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

И этот рецепт совершенно общий и будет работать для таблицы истинности любого размера. Итак, мы доказали, что с помощью наших операторов (на самом деле, просто используя отрицание, конъюнкцию и дизъюнкцию — нам не нужно было использовать подкова или тройник) мы можем выразить любой функция истины.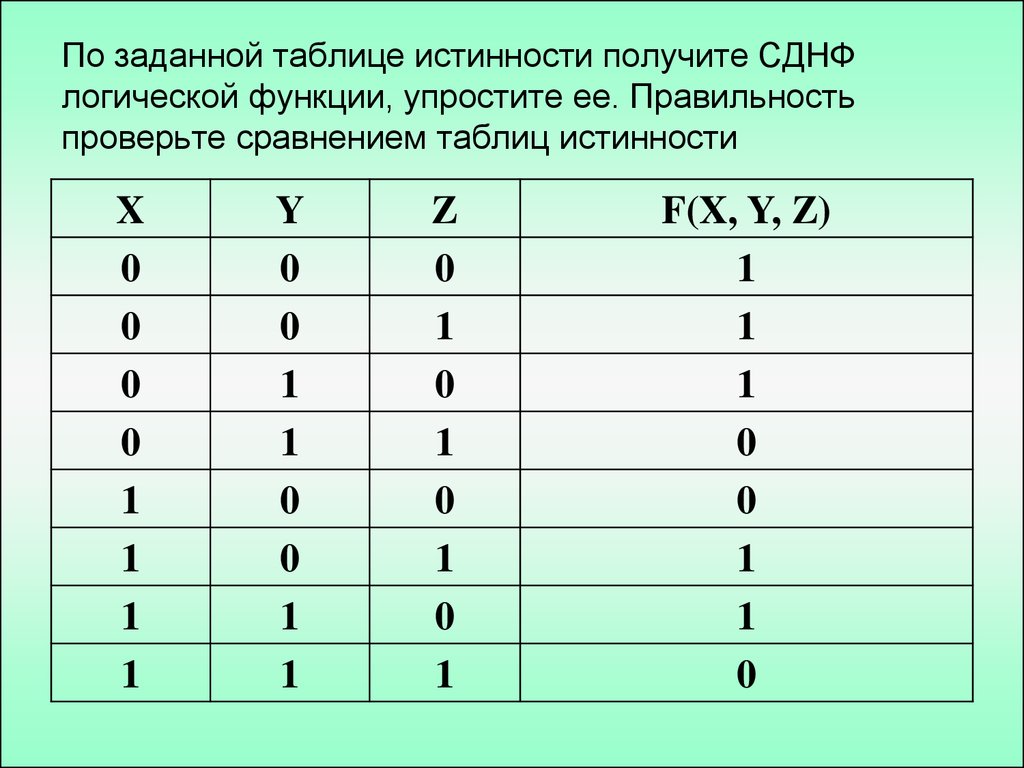 Следовательно, ЯП функционально завершен.

Вот еще. Для чего связан wff:

А	Б	?
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Ф

 

Сначала мы перечисляем связанные союзы. Для первой строки это (A&B), а для третьего (~A & B). Поскольку wff оказывается верным в первой и третьей строках, мы разделяем соединения из этих строк и получить (A & B) v (~A & B).

А	Б	(А и В) v (~А и В)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Ф

 

В качестве упражнения постройте произвольную таблицу истинности и затем создайте wff, который имеет эту таблицу истинности, используя приведенный выше рецепт. Как еще упражнение, объясните, как наше доказательство в этом разделе также является доказательством ненужность подковы и тройки как операторов в PL.