Реальные числа — что это такое, определение и понятие — 2021
Содержание
- Домен действительных чисел
- Реальные числа на реальной линии
- Реальные числа и Матрешка
- Схема действительных чисел
- Классификация действительных чисел
- Примеры действительных чисел
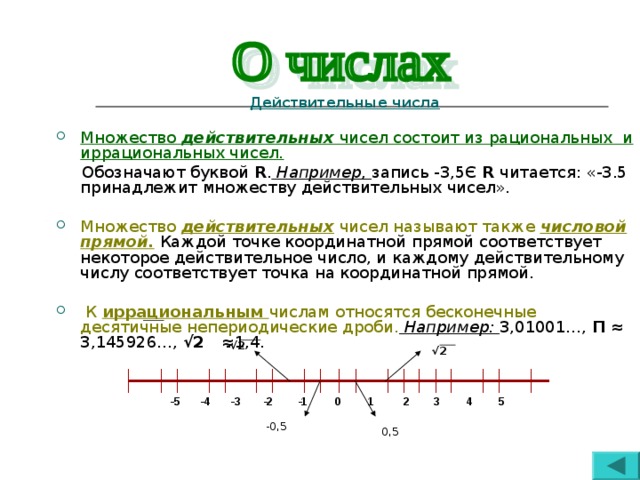
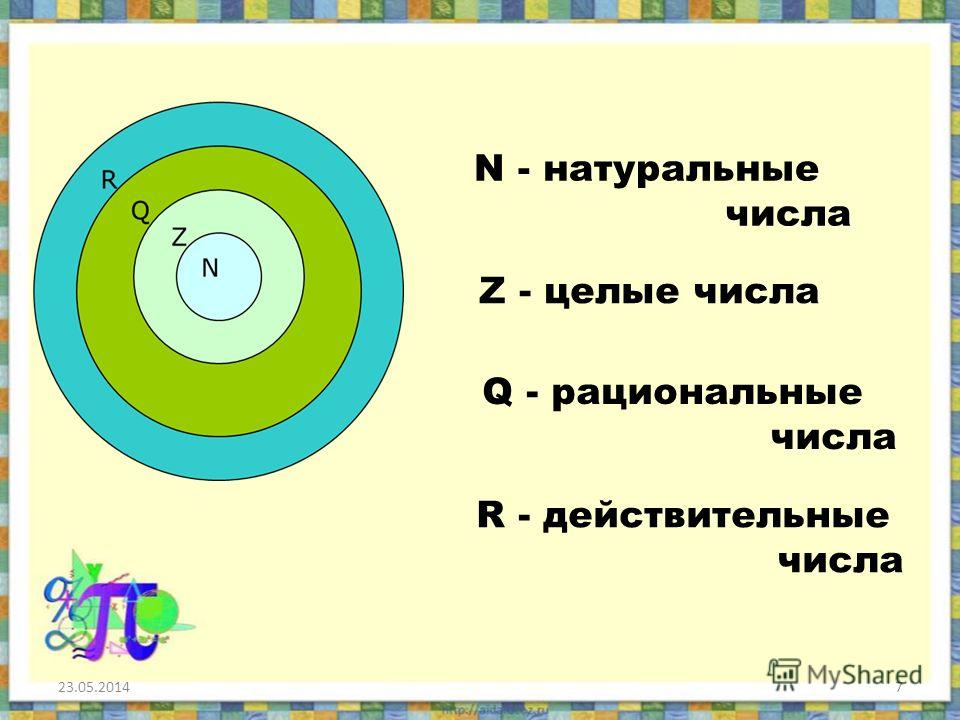
Действительные числа — это любое число, которое соответствует точке на реальной прямой и может быть разделено на натуральные, целые, рациональные и иррациональные числа.
Другими словами, любое действительное число находится между минус бесконечностью и плюс бесконечностью, и мы можем представить его на действительной прямой.
Реальные числа — это все числа, которые мы находим наиболее часто, поскольку комплексные числа не обнаруживаются случайно, а требуют специального поиска.
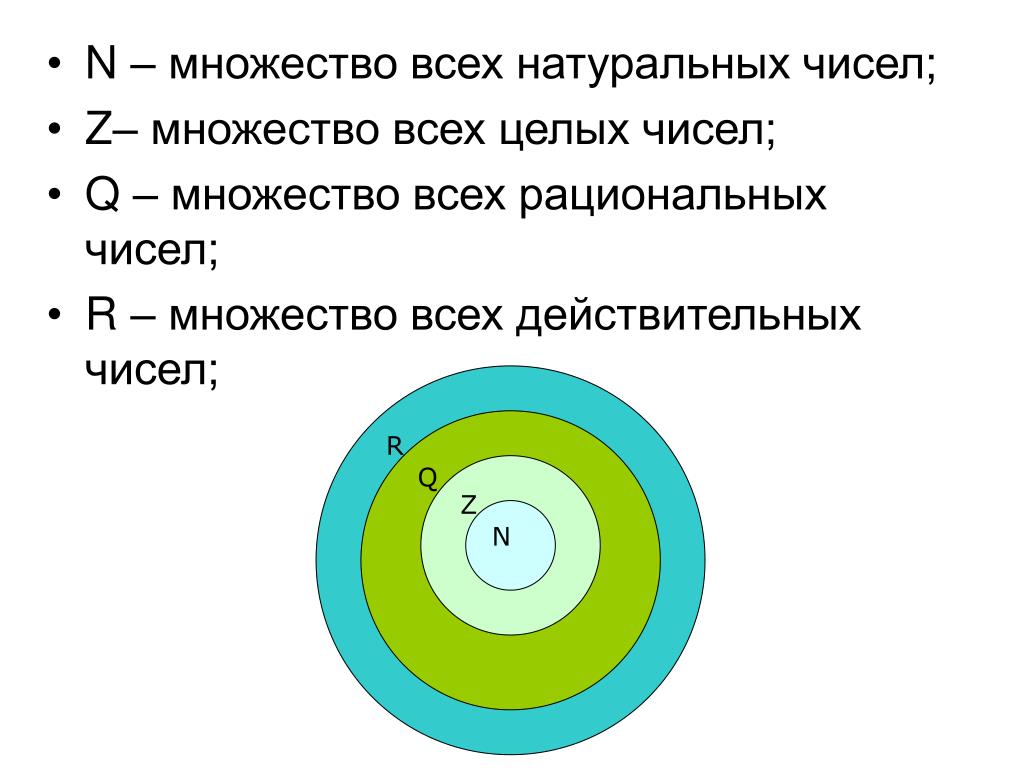
Реальные числа обозначаются буквой R ↓
Домен действительных чисел
Итак, как мы уже сказали, действительные числа — это числа между бесконечными крайностями.
То есть мы не будем включать эти бесконечности в набор.
Реальные числа на реальной линии
Эта линия называется настоящий прямой поскольку мы можем представить в нем все действительные числа.
Реальные числа и Матрешка
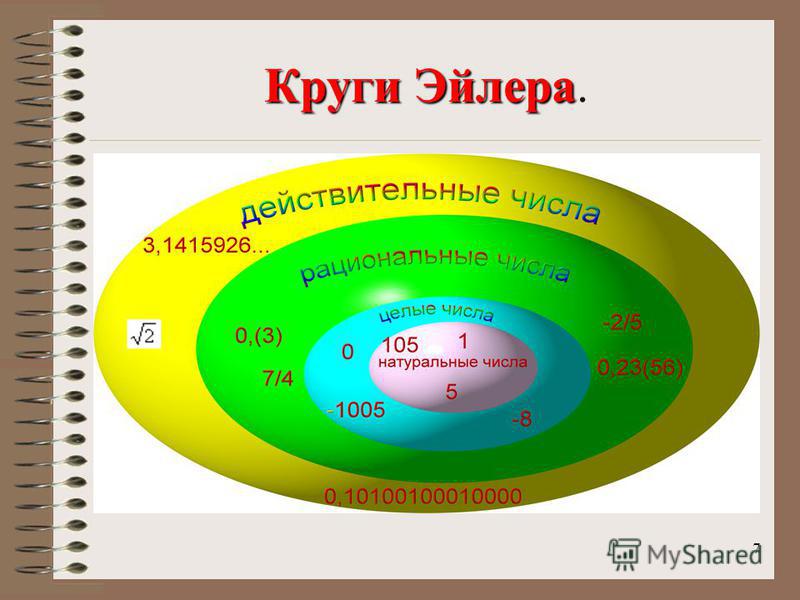
Под матрешкой следует понимать набор реалов, то есть как набор традиционных русских кукол, упорядоченных от самых больших до самых маленьких.
Серия кукол будет такой, чтобы самая большая кукла содержала следующие самые маленькие куклы. Этот набор кукол, собранный внутри самой большой куклы, называется «Матрешка». Схематично:
(Кукла A> Кукла B> Кукла C) = Матрешка
Схема мартиошка
Матрешку мы видим сбоку (рисунок слева от равного), а также сверху или снизу (рисунок справа от равного). Из двух способов мы можем ясно увидеть иерархию измерений, которой следует серия.
Таким же образом, как мы собираем матрешек, мы можем упорядочить действительные числа тем же способом.
Схема действительных чисел
На этой схеме мы можем ясно видеть, что организация реальных чисел похожа на игру в матрешку, видимую сверху или снизу.
Классификация действительных чисел
Как мы видели, действительные числа можно разделить на натуральные, целые, рациональные и иррациональные числа.
- Натуральные числа
Натуральные числа — это первый набор чисел, который мы выучиваем в детстве. Этот набор не принимает во внимание число ноль (0), если не указано иное (нейтральный ноль).
Выражение:
Отслеживать → Мы можем запоминать натуральные числа, думая, что это числа, которые мы «естественно» используем для счета. Когда у нас есть рука, мы игнорируем ноль, то же самое и с натуральными числами.
Первые элементы множества натуральных чисел.
- Целые числа
Целые числа являются натуральными числами и включают ноль (0) и все отрицательные числа.
Выражение:
Пример некоторых элементов множества целых чисел.
Отслеживать: → Мы можем запоминать целые числа, думая, что это все числа, которые мы естественным образом используем для подсчета вместе с их противоположностями, включая ноль (0).
- Рациональное число
Рациональные числа — это дроби, которые могут быть образованы из целых и натуральных чисел. Мы понимаем дроби как частные от целых чисел.
Выражение:
Отслеживать → Мы можем вспомнить рациональные числа, думая, что, будучи дробями целых чисел, «рационально», чтобы результат был целым числом, конечным или полупериодическим десятичным числом.
Пример некоторых элементов множества рациональных чисел.
- Иррациональные числа
Иррациональные числа — это десятичные числа, которые нельзя выразить ни точно, ни периодически.
Выражение:
Отслеживать → Мы можем вспомнить иррациональные числа, думая, что все они — числа, которые не вписываются в предыдущие классификации, и что они также принадлежат к действительной прямой.
Пример некоторых элементов множества иррациональных чисел.
Примеры действительных чисел
В следующем примере с действительными числами убедитесь, что следующие числа соответствуют точкам на действительной прямой.
- Натуральные числа: 1,2,3,4 …
- Целые числа:…, -4, -3, -2, -1, 0, 1, 2, 3, 4…
- Рациональные числа: любая дробь целых чисел.
- Иррациональные числа:
СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
22.01.2023
А в общежитии свой Новый год!
Традиционная «Зимняя сказка» прошла в общежитии.
19.01.2023
Этот старый добрый Новый год…
Группа лицеистов отметила праздник на турбазе.
29.12.2022
Успех во Всероссийском конкурсе учебных судов
Команда СУНЦ УрФУ впервые в истории Свердловской области приняла участие в финальном этапе XVI Всероссийского конкурса учебных судов.
24.12.2022
Победа в первом региональном турнире учебных судов
Команда СУНЦ УрФУ одержала победу в первом в истории Свердловской области региональном турнире XVI Всероссийского конкурса учебных судов.
23.12.2022
Долгожданная награда
Награду из рук губернатора Свердловской области получил победитель Всероссийской олимпиады по искусственному интеллекту.
23.12.2022
Волейбол. Итоги
Команды СУНЦ успешно выступили на первенстве Кировского района Екатеринбурга.
Больше новостей
Видеогалерея:
Новогодние поздравления (декабрь 2022)
СУНЦ.АРТ (ноябрь 2022)
«Горнозаводской Урал» (октябрь 2022)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А.
М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.
Работа с числами · Руководство по программированию R для UC Business Analytics
В этом разделе вы изучите основы работы с числами в R. Это включает в себя понимание
- Как управлять числовым типом (целое или двойное)
- Различные способы генерации неслучайных чисел
- Различные способы генерации случайных чисел
- Как установить начальные значения для воспроизводимой генерации случайных чисел
- Различные способы сравнения чисел
- Как округлить числовые значения
Числовые типы (целые и двойные)
Два наиболее распространенных числовых класса, используемых в R, — целые и двойные (для чисел двойной точности с плавающей запятой). R автоматически выполняет преобразование между этими двумя классами, когда это необходимо для математических целей. В результате можно использовать R и выполнять анализ годами, не указывая эти различия.
Создание целочисленных и двойных векторов
По умолчанию при создании числового вектора с помощью c() , он создаст вектор числовых значений двойной точности.
Чтобы создать вектор целых чисел с помощью c() , вы должны указать явно, поместив L непосредственно после каждого числа.
# создать строку значений двойной точности dbl_var <- c(1, 2.5, 4.5) dbl_var ## [1] 1,0 2,5 4,5 # размещение L после значений создает строку целых чисел int_var <- c(1L, 6L, 10L) int_var ## [1] 1 6 10
Проверка числового типа
Чтобы проверить, состоит ли вектор из целых или двойных значений:
# определяет тип вектора (двойной, целочисленный, логический или символьный) тип (dbl_var) ## [1] "двойной" тип (int_var) ## [1] "целое число"
Преобразование между целыми и двойными значениями
По умолчанию, если вы читаете данные, не содержащие десятичных точек, или создаете числовые значения с использованием метода x <- 1:10 , числовые значения будут закодированы как целые числа. Если вы хотите изменить двойное число на целое или наоборот, вы можете указать одно из следующего:
# конвертирует целые числа в значения двойной точности как.
double(int_var)
## [1] 1 6 10
# идентично as.double()
как.numeric(int_var)
## [1] 1 6 10
# конвертирует двойные числа в целые числа
как.integer(dbl_var)
## [1] 1 2 4
Генерация неслучайных чисел
Есть несколько операторов и функций R, которые особенно полезны для создания векторов неслучайных чисел. Эти функции предоставляют несколько способов создания последовательностей чисел.
Указание номеров в последовательности
Чтобы явно указать числа в последовательности, вы можете использовать оператор двоеточия : , чтобы указать все целые числа между двумя указанными числами, или функцию combo c() , чтобы явно указать все числа в последовательности.
# создать вектор целых чисел от 1 до 10 1:10 ## [1] 1 2 3 4 5 6 7 8 9 10 # создаем вектор, состоящий из 1, 5 и 10 с(1, 5, 10) ## [1] 1 5 10 # сохранить вектор целых чисел от 1 до 10 как объект x х <- 1:10 Икс ## [1] 1 2 3 4 5 6 7 8 910
Создание регулярных последовательностей
Обобщением : является функция seq() , которая генерирует последовательность чисел с заданной арифметической прогрессией.
# генерировать последовательность чисел от 1 до 21 с шагом 2 seq(от = 1 до = 21, по = 2) ## [1] 1 3 5 7 9 11 13 15 17 19 21 # сгенерировать последовательность чисел от 1 до 21, которая имеет 15 равных увеличений # номера seq(0, 21, length.out = 15) ## [1] 0,0 1,5 3,0 4,5 6,0 7,5 9.0 10,5 12,0 13,5 15,0 16,5 18,0 19,5 ## [15] 21,0
Генерация повторяющихся последовательностей
Функция rep() позволяет удобно повторять заданные константы в длинные векторы. Эта функция позволяет использовать сопоставленные и несопоставленные повторения.
# повторяет значения x указанное количество раз с сопоставлением повтор(1:4, раз = 2) ## [1] 1 2 3 4 1 2 3 4 # копирует значения x без сопоставления повтор(1:4, каждый = 2) ## [1] 1 1 2 2 3 3 4 4
Генерация случайных чисел
Моделирование является обычной практикой в анализе данных. Иногда ваш анализ требует реализации статистической процедуры, которая требует генерации случайных чисел или выборки (например, моделирование методом Монте-Карло, выборка начальной загрузки и т.
д.). R поставляется с набором генераторов псевдослучайных чисел, которые позволяют моделировать наиболее распространенные распределения вероятностей, такие как:
- Равномерное
- Обычный
- Биномиальный
- Пуассон
- Экспоненциальный
- Гамма
Равномерные числа
Чтобы сгенерировать случайные числа из равномерного распределения, вы можете использовать функцию runif() . В качестве альтернативы вы можете использовать sample() , чтобы взять случайную выборку с заменами или без них.
# генерировать n случайных чисел между значениями по умолчанию от 0 до 1 руниф (сущ.) # сгенерировать n случайных чисел от 0 до 25 runif(n, минимум = 0, максимум = 25) # сгенерировать n случайных чисел от 0 до 25 (с заменой) образец (0:25, n, заменить = ИСТИНА) # сгенерировать n случайных чисел от 0 до 25 (без замены) образец (0:25, n, заменить = FALSE)
Например, чтобы сгенерировать 25 случайных чисел между значениями от 0 до 10:
runif(25, min = 0, max = 10) ## [1] 9,2494720 1,0276421 9,6061007 7,4582455 8,3666868 0,8090925 7,5638221 ## [8] 4,2810155 2,5850736 9,7962788 6,1705894 0,7037997 9,5056240 4,7589622 ## [15] 7,9750129 5,3932881 5,1624935 1,2704098 8,7064680 8,6649293 0,1049461 ## [22] 1,4827342 2,7337917 7,5236131 3,9803653
Для каждого неравномерного распределения вероятностей доступны четыре основные функции для генерации случайных чисел, плотности (она же функция массы вероятности), кумулятивной плотности и квантилей.
Префиксы для этих функций:
-
r: генерация случайных чисел -
d: плотность или функция массы вероятности -
p: совокупное распределение -
q: квантили
Номера нормального распределения
Нормальное (или Гауссово) распределение является наиболее распространенным и хорошо известным распределением. В R функции нормального распределения записываются как `norm()`.
# генерировать n случайных чисел из нормального распределения с заданным средним и st. разв. rnorm(n, среднее = 0, sd = 1) # генерировать вероятности CDF для значений в векторе q pnorm(q, среднее = 0, sd = 1) # генерируем квантили для вероятностей в векторе p qnorm(p, среднее = 0, sd = 1) # генерировать вероятности функции плотности для значений в векторе x dnorm(x, среднее = 0, sd = 1)
Например, чтобы сгенерировать 25 случайных чисел из нормального распределения со средним значением = 100 и стандартное отклонение = 15 :
x <- rnorm(25, среднее = 100, sd = 15) Икс ## [1] 107.
84214 101.10742 73.67151 113.94035 108.47938 77.48445 73.02016
## [8] 81.02323 101.64169 112.67715 105.28478 92.35393 85.96284 108.83169
## [15] 88.71057 115.13657 141.69830 99.91198 118.69664 110.61667 83.20282
## [22] 113.91008 109.10879 93.45276 109.01996
резюме(х)
## Мин. 1 кв. Медиана Среднее 3-е кв. Максимум.
## 73,02 88,71 105,30 101,10 110,60 141,70
Вы также можете передать вектор значений. Например, предположим, что вы хотите узнать вероятности CDF для каждого значения в векторе x , созданном выше:
pnorm(x, mean = 100, sd = 15) ## [1] 0,69944664 0,52942643 0,03960976 0,82364789 0,71406244 0,06667308 ## [7] 0,03603657 0,10291447 0,54357552 0,80098468 0,63770038 0,30511760 ## [13] 0,17468526 0,72199534 0,22583658 0,84353778 0,99728111 0,49765904 ## [19] 0,89369904 0,76045844 0,13139693 0,82312464 0,72815841 0,33124331 ## [25] 0,72619004
Числа биномиального распределения
Это условно интерпретируется как количество успехов в size = x испытаний и с prob = p вероятностью успеха:
# сгенерировать вектор длины n, отображающий количество успехов из испытание # размер = 100 с вероятностью успеха = 0,5 rbinom(n, размер = 100, вероятность = 0,5) # генерировать вероятности CDF для значений в векторе q pbinom(q, размер = 100, вероятность = 0,5) # генерируем квантили для вероятностей в векторе p qbinom(p, размер = 100, вероятность = 0,5) # генерировать вероятности функции плотности для значений в векторе x dbinom(x, размер = 100, вероятность = 0,5)
Числа распределения Пуассона
Распределение Пуассона — это дискретное распределение вероятностей, выражающее вероятность того, что заданное количество событий произойдет в фиксированный интервал времени и/или в пространстве, если эти события происходят с известной средней частотой и независимо от времени с момента последнего события.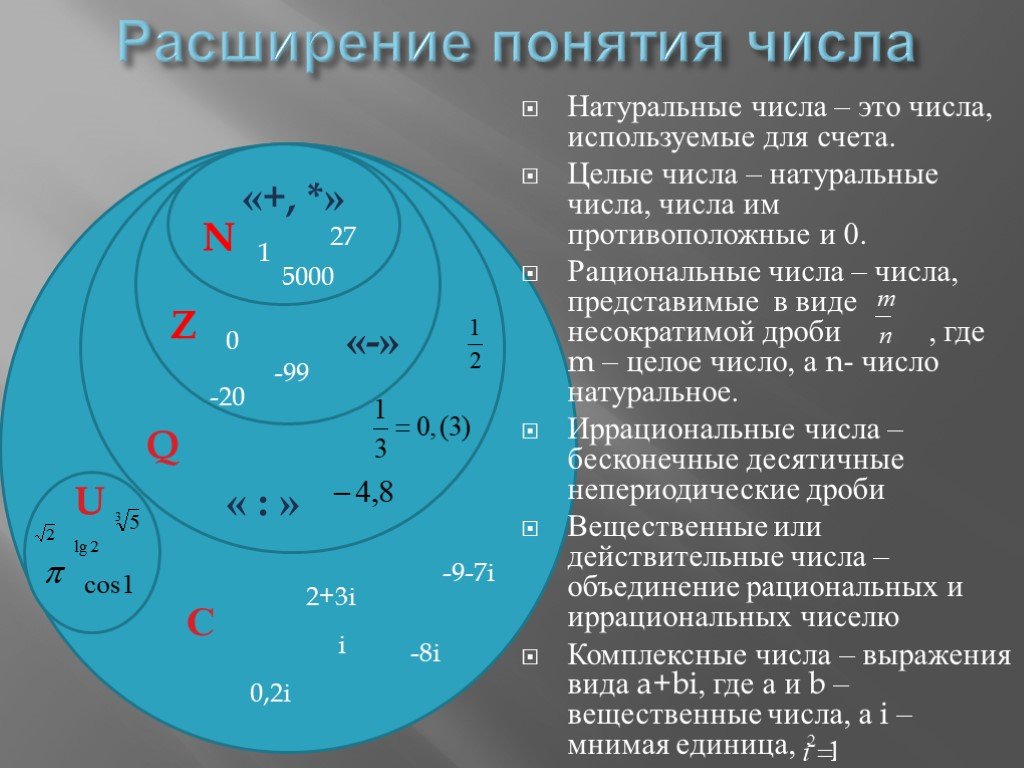
# сгенерировать вектор длины n, отображающий случайное количество происходящих событий # когда лямбда (средняя скорость) равна 4. rpois(n, лямбда = 4) # генерировать вероятности CDF для значений в векторе q, когда лямбда (средняя скорость) # равно 4. ppois(q, лямбда = 4) # генерируем квантили для вероятностей в векторе p, когда лямбда (средняя скорость) # равно 4. qpois(p, лямбда = 4) # генерировать вероятности функции плотности для значений в векторе x, когда лямбда # (средняя скорость) равно 4. dpois(x, лямбда = 4)
Числа экспоненциального распределения
Экспоненциальное распределение вероятностей описывает время между событиями в процессе Пуассона.
# создать вектор длины n со скоростью = 1 reexp(n, скорость = 1) # генерировать вероятности CDF для значений в векторе q, когда rate = 4. pexp(q, скорость = 1) # генерируем квантили для вероятностей в векторе p, когда rate = 4. qexp(p, скорость = 1) # генерировать вероятности функции плотности для значений в векторе x, когда rate = 4.
dexp(x, скорость = 1)
Гамма-распределение Числа
Гамма-распределение вероятности связано с бета-распределением и естественным образом возникает в процессах, для которых важны времена ожидания между событиями с распределением Пуассона.
# создать вектор длины n с параметром формы = 1 rgamma(n, форма = 1) # генерировать вероятности CDF для значений в векторе q, когда параметр формы = 1. pgamma(q, форма = 1) # генерировать квантили для вероятностей в векторе p, когда параметр формы = 1. qgamma (p, форма = 1) # генерировать вероятности функции плотности для значения (значений) в векторе x, когда shape # параметр = 1. dgamma(x, форма = 1)
Установка начальных значений
Если вы хотите сгенерировать последовательность случайных чисел, а затем воспроизвести ту же самую последовательность случайных чисел позже, вы можете установить генератор начальных чисел с помощью set.seed() . Это критический аспект воспроизводимого исследования.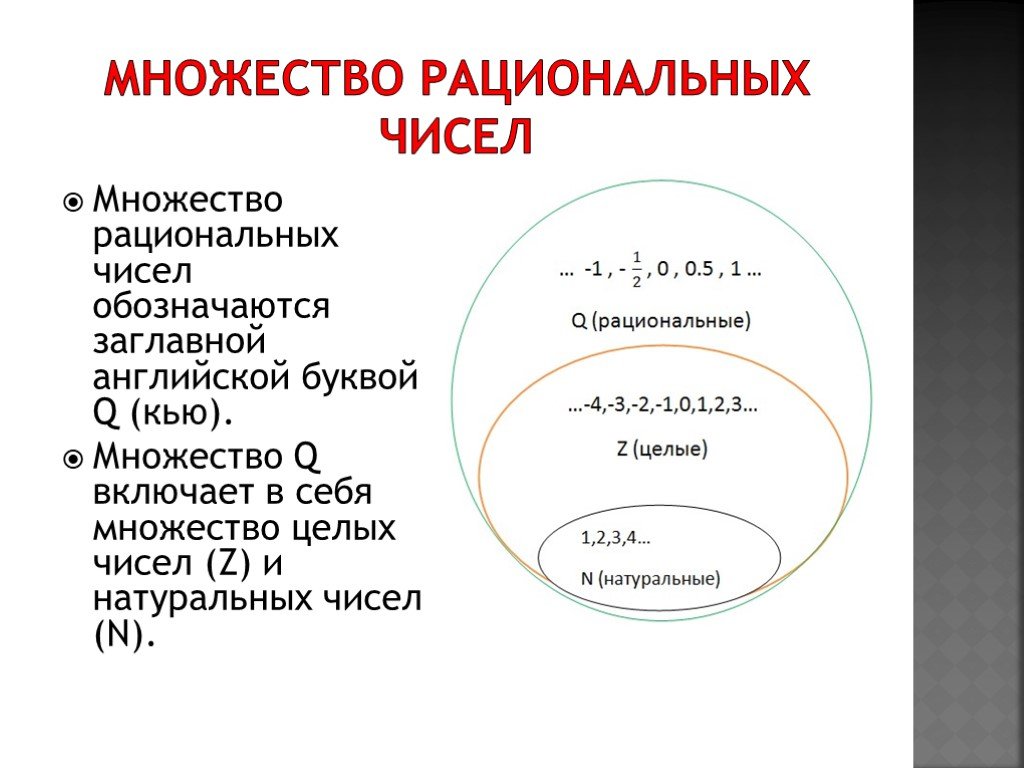
Например, мы можем воспроизвести случайную генерацию 10 значений из нормального распределения:
set.seed(197) rnorm(n = 10, среднее = 0, sd = 1) ## [1] 0,6091700 -1,4391423 2,0703326 0,7089004 0,6455311 0,7290563 ## [7] -0,4658103 0,5971364 -0,5135480 -0,1866703 набор.сид(197) rnorm(n = 10, среднее = 0, sd = 1) ## [1] 0,6091700 -1,4391423 2,0703326 0,7089004 0,6455311 0,7290563 ## [7] -0,4658103 0,5971364 -0,5135480 -0,1866703
Сравнение числовых значений
Существует несколько способов сравнения числовых значений и векторов. Это включает в себя логические операторы, а также проверку на точное равенство, а также почти на равенство.
Операторы сравнения
Обычные бинарные операторы позволяют сравнивать числовые значения и дают ответ в логической форме:
x < y # x меньше y x > y # x больше y x <= y # x меньше или равно y x >= y # x больше или равно y x == y # является ли x равным y x != y # x не равно y
Эти операции можно использовать для сравнения отдельных чисел:
x <- 9 у <- 10 х == у ## [1] ЛОЖЬ
а также для сравнения чисел внутри векторов:
х <- с(1, 4, 9, 12) у <- с(4, 4, 9, 13) х == у ## [1] ЛОЖЬ ИСТИНА ИСТИНА ЛОЖЬ
Обратите внимание, что логические значения ИСТИНА и ЛОЖЬ равны 1 и 0 соответственно.
Итак, если вы хотите определить количество одинаковых значений в двух векторах, вы можете обернуть операцию функцией sum() :
# Сколько попарно равных значений в векторах x и y сумма (х == у) ## [1] 2
Если вам нужно определить расположение попарных равенств в двух векторах, вы можете обернуть операцию в which() function:
# Где находятся попарно равные значения, расположенные в векторах x и y который (х == у) ## [1] 2 3
Точное равенство
Проверка равенства двух объектов:
x <- c(4, 4, 9, 12) у <- с(4, 4, 9, 13) идентичный (х, у) ## [1] ЛОЖЬ
х <- с(4, 4, 9, 12) у <- с(4, 4, 9, 12) идентичный (х, у) ## [1] ИСТИНА
Сравнение с плавающей запятой
Иногда требуется проверить «почти равенство». Функция all.equal() позволяет проверить равенство с допуском разницы 1,5e-8.
х <- с(4,00000005, 4,00000008) у <- с(4.00000002, 4.00000006) все.равно(х, у) ## [1] ИСТИНА
Если разница превышает допустимый уровень, функция вернет среднюю относительную разницу:
x <- c(4,005, 4,0008) у <- с(4,002, 4,0006) все.
равно(х, у)
## [1] "Средняя относительная разница: 0,0003997102"
Округление числовых значений
Существует множество способов округления до ближайшего целого числа, вверх, вниз или до указанного десятичного разряда. Предположим, что у нас есть следующий вектор x :
x <- (1, 1,35, 1,7, 2,05, 2,4, 2,75, 3,1, 3,45, 3,8, 4,15, 4,5, 4,85, 5,2, 5,55, 5,9)
Ниже показаны распространенные способы округления x :
# Округление до ближайшего целого числа круглый (х) ## [1] 1 1 2 2 2 3 3 3 4 4 4 5 5 6 6 # Округлять потолок(х) ## [1] 1 2 2 3 3 3 4 4 4 5 5 5 6 6 6 # Округлить вниз этаж(х) ## [1] 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 # Округлить до указанного десятичного числа округлить (х, цифры = 1) ## [1] 1,0 1,4 1,7 2,0 2,4 2,8 3,1 3,4 3,8 4,2 4,5 4,8 5,2 5,5 5,9
Коронавирус: что такое число R и как оно рассчитывается?
Опубликовано
000Z"> 26 марта 2021 г. Комментарии
Комментарии
Связанные темпы
- изображение 9000. Великобритания, судя по числу R, продолжает стабилизироваться.
Последняя оценка R правительственной научной консультативной группы Sage составляет от 0,7 до 0,9., немного выше, чем неделей ранее.
Это означает, что в среднем каждые 10 человек с Covid заражают от семи до девяти других людей.
Что такое R?
Число R — это способ оценки способности коронавируса или любого другого заболевания распространяться.
R — количество людей, которым в среднем передается вирус от одного зараженного человека.
Корь имеет число R 15 в популяциях без иммунитета.
Это означает, что в среднем один человек заразит корью 15 человек.
Коронавирус, официально известный как Sars-CoV-2, имел бы число репродукции около трех, если бы не были предприняты действия, чтобы остановить его распространение.
Как рассчитывается R?
Нельзя запечатлеть момент заражения людей. Вместо этого ученые работают в обратном направлении.
Данные, такие как количество людей, умерших, госпитализированных или положительных на вирус с течением времени, используются для оценки того, насколько легко распространяется вирус.
Почему число больше единицы опасно?
Если значение R больше единицы, количество случаев продолжает увеличиваться.
Но если число R ниже, болезнь в конечном итоге перестанет распространяться, потому что для поддержания вспышки заражается недостаточно новых людей.
Image caption,Если значение R выше единицы, то число кумулятивных случаев увеличивается, но если оно ниже единицы, то в конечном итоге вспышка прекращается. Чем дальше ниже единицы, тем быстрее это происходит.
Правительства повсюду хотят снизить число R примерно с трех (число R, если мы не предпримем никаких действий) до меньше одного.
Какой номер R в Великобритании?
Номер R не фиксирован. Вместо этого он меняется по мере изменения нашего поведения или развития иммунитета.
Специалисты по математическому моделированию из Имперского колледжа Лондона попытались отследить, как число изменилось после того, как весной 2020 года были введены изоляция, социальное дистанцирование и полная блокировка. созрел для большой вспышки. Последовательные ограничения снизили его, но только после полной изоляции он упал ниже единицы.
Хотя число R в настоящее время в Великобритании составляет от 0,7 до 0,9, существуют региональные различия.
Расчетное число R для Шотландии составляет от 0,8 до 1,0, что немного выше, чем на предыдущей неделе.
В Уэльсе число находится между 0,6 и 0,9, в то время как в Северной Ирландии оно остается между 0,75 и 0,95.
В Англия число немного увеличено до 0,8-1,0.
- Каковы последние правила социального дистанцирования?
- Сколько подтвержденных случаев в вашем районе?
- Вакцинные паспорта могут быть дискриминационными, предупреждают эксперты
Это самый важный номер?
Номер R входит в большую тройку.
