Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеГЛАВА I. ЧИСЛА3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре.  Переменные.11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа § 4. Комплексные числа ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ § 6. Целые рациональные выражения 52. Многочлены. Приведение многочленов к стандартному виду. § 7. Дробные рациональные выражения Глава III. ФУНКЦИИ И ГРАФИКИ § 9. Свойства функций § 10. Виды функций 95. Обратная функция. График обратной функции. 96. Логарифмическая функция. 96. Определение тригонометрических функций. § 11. Преобразования графиков ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12.  Преобразование выражений, содержащих переменную под знаком логарифма§ 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной § 15. Уравнения с двумя переменными § 16. Системы уравнений Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной § 18. Доказательство неравенств ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности § 20. Предел функции § 21. Производная и ее применения § 22. Первообразная и интеграл ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ § 1. О строении курса геометрии § 2. Основные свойства простейших геометрических фигур § 3. Геометрические построения на плоскости § 4. Четырехугольники § 5. Многоугольники § 6. Решение треугольников 34. Теорема косинусов. Теорема синусов. 38. Площади подобных фигур. ГЛАВА II. Прямые и плоскости в пространстве § 8.  Аксиомы стереометрии и некоторые следствия из них§ 9. Параллельность прямых и плоскостей § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники § 12. Тела вращения § 13. Изображение пространственных фигур на плоскости § 14. Объемы тел § 15. Площади поверхностей тел ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве § 17. Уравнения фигур на плоскости § 18. Уравнения фигур в пространстве ГЛАВА V. ПРЕОБРАЗОВАНИЯ ФИГУР § 19. Движение § 20. Подобие фигур ГЛАВА VI. ВЕКТОРЫ § 21. Введение понятия вектора § 22. Операции над векторами ОСНОВНЫЕ ФОРМУЛЫ И СООТНОШЕНИЯ I. Основные законы алгебры ГЕОМЕТРИЯ |
Представление действительных чисел
Представление действительных чиселПредставление дробных чисел в двоичной системе счисления
Дробные числа можно записывать не только в виде десятичных дробей, но и в системах счисления с произвольным основанием.
{-2}\). Поскольку целая часть у нормализованного представления числа всегда (кроме числа 0) равна 1, то целая часть не хранится, а хранится только дробная часть мантиссы. Количество значащих знаков мантиcсы, которое хранится, может быть различным для различных способов представления действительных чисел. Например, в типе данных двойной точности, который в языке Python соответствует типу float, в языке C — типу double, в языке Pascal — типу double, хранится 52 бита дробной части мантиcсы.
Стандарт IEEE754 определяет несколько типов представления действительных чисел, основными из которых являются числа одинарной точности (для их хранения требуется 4 байта), двойной точности (8 байт) и расширенной точности (10 байт).
Точность | Размер (байт) | C, C++ | Pascal | Python | Количество знаков мантиссы | Точность, десятичных цифр | Максимальное значение | Минимальное положительное значение |
одинарная | 4 | float | single | — | 23 | \(\approx 7{,}2\) | \(3{,}4\cdot10^{38}\) | \(1{,}4\cdot10^{-45}\) |
двойная | 8 | double | double | float | 52 | \(\approx 15{,}9\) | \(1{,}7\cdot10^{308}\) | \(5{,}0\cdot10^{-324}\) |
расширенная | 10 | long double (только в gnu gcc/g++) | extended | — | 63 | \(\approx 19{,}2\) | \(1{,}1\cdot10^{4932}\) | \(1{,}9\cdot10^{-4951}\) |
Неточность при представлении действительных чисел
Рациональные числа, которые не могут быть представлены в виде дроби со знаменателем, являющимся степенью двойки, не могут быть точно представлены в виде конечной двоичной дроби, а, значит, не могут быть в точности представлены в памяти компьютера.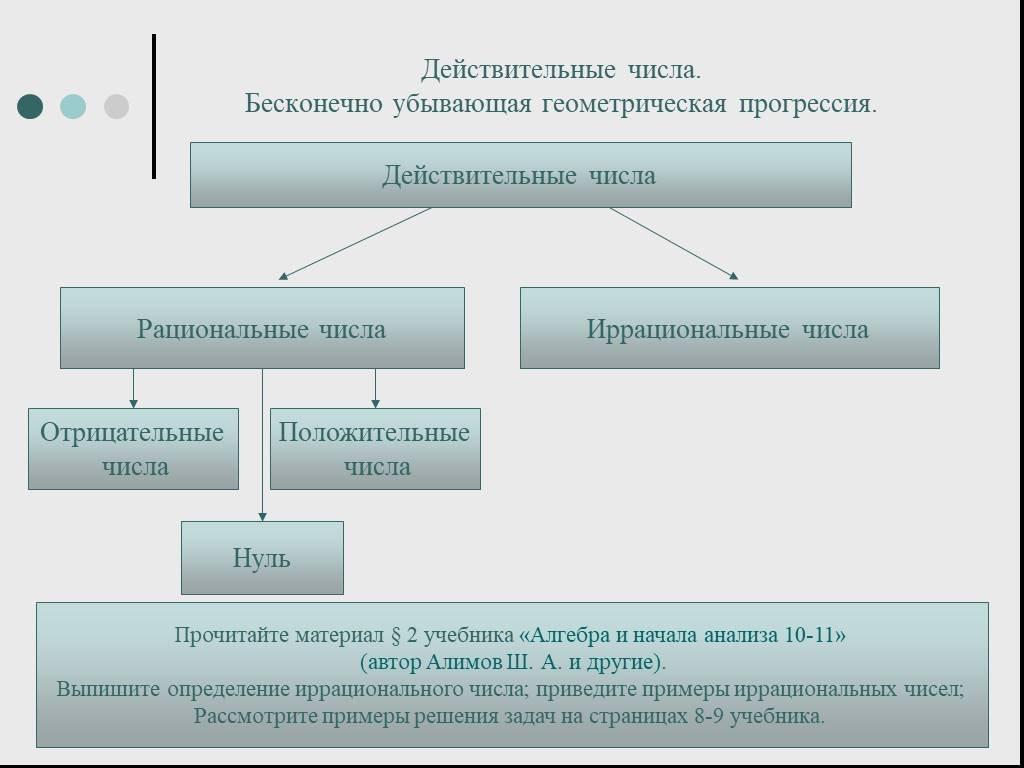
{-2}\) и хранятся только 52 цифры дробной части мантиссы числа. Дальнейшие цифры отбрасываются, поэтому вместо числа \(\frac{1}{3}\), которое непредставимо в действительных типах данных, хранится другое ближайшее к нему представимое число. В случае с числом \(\frac{1}{3}\) записывается меньшее число, также меньшее число записывается и при записи в переменную двойной точности значений \(\frac{1}{10}\) и \(\frac{2}{10}\), а вот вместо числа \(\frac{3}{10}\) уже будет записано большее представимое число. Поэтому если записать в две переменные значения \(0{.}1\) и \(0{.}2\) (десятичные), а в третью переменную записать их сумму, то результат окажется меньше, чем
\(\frac{3}{10}\), в то время как при записи в переменную значения \(\frac{3}{10}\) явно в виде \(0{.}3\), получится результат, больший чем \(\frac{3}{10}\). То есть при вычислении суммы чисел \(0{.}1\) и \(0{.}2\) результат получится отличным от значения \(0{.}3\), записанного в переменную явно, то есть с точки зрения компьютерной арифметики
\(0{.
}1 + 0{.}2 \ne 0{.}3\). Эту проблему (неточное представление действительных чисел и выполнение арифметических операций с действительными числами) всегда следует иметь в виду.
Использование эпсилон при сравнении действительных чисел
Таким образом, сравнивать действительные числа в компьютерных программах на точное равенство нельзя. Вместо этого если нужно сравнить два числа \(a\) и \(b\) на равенство, правильным будет проверка условия, что эти два числа не сильно различаются, то есть что модуль их разности не превосходит некоторого небольшого значения \(\varepsilon\), то есть что \(|a-b|<\varepsilon\). Значение \(\varepsilon\) как правило определяется для каждой задачи исходя из той точности, с которой необходимо получить результат.
В следующей таблице указано, как нужно проверять различные сравнения действительных чисел с использованием \(\varepsilon\).
Условие | Как нужно проверять |
\(a=b\) | \(|a-b|\lt\varepsilon\) |
\(a\ne b\) | \(|a-b|\ge \varepsilon\) |
\(a\lt b\) | \(a \le b — \varepsilon\) |
\(a \le b\) | \(a \lt b + \varepsilon\) |
\(a\gt b\) | \(a \ge b + \varepsilon\) |
\(a\ge b\) | \(a \gt b — \varepsilon\) |
Специальные значения действительных типов
При работе с действительными числами, как правило, в результате алгоритмических ошибок, возникают некоторые специальные значения, например, inf и nan.
Значение inf (от infinity) возникает при переполнении действительной переменной, когда результат становится очень большим. Например, если взять положительное число и умножать его на два в цикле, то довольно скоро получится значение inf. Максимальное значение, которое может быть сохранено до получения переполнения, различается для разных типов действительных чисел.
Значение inf отличается тем, что после получения результата inf из него уже нельзя получить «обычное» действительное число. При прибавлении и вычитании к inf любого действительного (неспециального) числа, умножении и делении inf на положительное число, в результате всегда получается inf. То есть inf считается «очень большим», настолько, что сложение, умножение и деление все равно оставляет результат «очень большим». Значение inf считается больше любого действительного неспециального числа.
Также есть отрицательное значение -inf, которое считается «минус бесконечностью».
При ряде операций со значением inf может возникнуть другое специальное значение nan (от not a number — не число).
Примеры операций, дающих в результате nan:
- \(inf — inf\)
- \(inf \times 0\)
- \(inf / inf\)
nan означает, что результат может быть «чем угодно», то есть это непредсказуемая величина и работать с ней невозможно. Любые арифметические операции c nan будут давать в результате nan. Более того, при любом сравнении nan с любым действительным числом при помощи любой из операций ==, <, <=, >, >= в результате будет получаться false. А при сравнении nan с любым действительным числом при помощи операции != всегда будет получаться true. И даже если значения двух переменных a и b оба равны nan, то сравнение a == b будет давать false, а сравнение a != b будет давать true.
В заголовочном файле cmath определены две константы INFINITY и NAN, которые принимают значения inf и nan соответственно, а также две функции bool isinf(x) и bool isnan(x), которые возвращают true, если аргумент x равен inf и nan соответственно или false в противном случае.
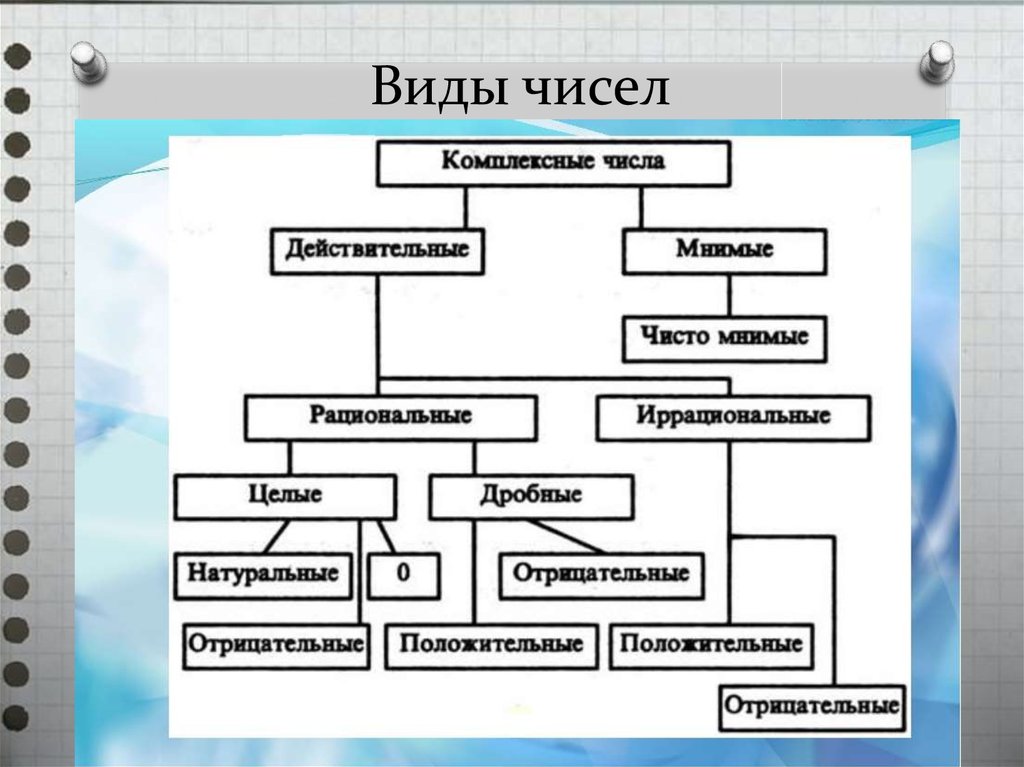
Вещественные числа — Рациональные, иррациональные, корневые и способные
Вещественное число — это любое число, которое может быть представлено точкой на числовой прямой.
Числа 3,5, -0,003, 2/3, π и √2 — все действительные числа.
Действительные числа включают в себя рациональные числа, которые могут быть выражены как отношение двух целых чисел , и иррациональные числа, которые не могут быть выражены. (В приведенном выше списке все числа, кроме pi и квадратного корня из из 2 рациональны.)
Считается, что первое действительное число, признанное иррациональным, было открыто пифагорейцами в шестом веке B . С . До этого открытия люди считали, что каждое число может быть выражено как отношение двух натуральных чисел ( отрицательных чисел еще не были открыты). Однако пифагорейцы смогли показать, что гипотенуза равнобедренного прямоугольного треугольника не может быть точно измерена никакими весами, какими бы тонкими они ни были, которые точно измеряли бы катеты.
Чтобы понять, что это значит, представьте себе числовую прямую с нарисованным на ней равнобедренным прямоугольным треугольником, как на рис.
Пифагорейцы смогли показать, что независимо от того, насколько точно каждая единица была разделена (равномерно), точка P попадет где-то внутри одного из этих подразделений. Даже если бы было миллион, миллиард, миллиард и один или любое другое число однородных подразделений, точка Р была бы пропущена каждым из них. Это попадет внутрь подразделения, а не в конец. Точка P представляет собой действительное число, потому что это определенная точка на числовой прямой, но она не представляет никаких 9.0003 рациональный номер а/б.
Точка P не единственная иррациональная точка. Квадратный корень из любого простого числа иррационален. Так же кубический корень, или любой другой корень. Фактически, используя бесконечные десятичные дроби для представления действительных чисел, математик Кантор смог показать, что число действительных чисел несчетно. Бесконечное множество чисел считается «счетным», если существует способ их перечисления, который позволяет добраться до любого конкретного из них, прочитав список достаточно далеко.
Вещественные числа имеют много известных счетных подмножеств. К ним относятся натуральные числа, целые числа, рациональные числа и алгебраические числа (алгебраические числа — это те, которые могут быть корнями полиномиальных уравнений с интеграл коэффициент). Реальные числа также включают числа, которые не являются «ни одним из вышеперечисленных». Это трансцендентных числа
За исключением редких случаев, таких как √2 ÷ √8 , вычисления можно производить только с рациональными числами. Если кто-то хочет использовать иррациональное число , такое как π, √3 или e, в вычислениях, он должен заменить его рациональным приближением , таким как 22/7, 1,73205 или 2,718.
Результат никогда не бывает точным. Однако всегда можно подобраться к точному вещественному ответу сколь угодно близко. Если Рисунок 1. Иллюстрация Hans & Cassidy. Предоставлено Гейл Групп.
приближение 3,14 для π недостаточно близко для этой цели, тогда можно использовать 3,142, 3,1416 или 3,14159. Каждый дает более близкое приближение.
Плотность рациональных/иррациональных чисел
Плотность рациональных/иррациональных чисел — MathonlineПлотность рациональных/иррациональных чисел
Сгиб СодержаниеПлотность рациональных/иррациональных чисел |
Теперь мы рассмотрим теорему о плотности рациональных чисел в действительных числах, а именно, что между любыми двумя действительными числами существует рациональное число.
Теорема 1 (Плотность рациональных чисел): Пусть $x, y \in \mathbb{R}$ — любые два действительных числа, где $x < y$. Тогда существует рациональное число $r \in \mathbb{Q}$ такое, что $x < r < y$. |
- Доказательство: Предположим, что $x > 0$. Поскольку $x < y$, мы имеем, что $y > 0$, и, кроме того, мы имеем, что $y — x > 0$. Теперь мы знаем по архимедовым свойствам, что поскольку $y — x > 0$, то существует натуральное число $n \in \mathbb{N}$ такое, что $\frac{1}{n} < y - x$.
- Если мы умножим это, то получим, что $1 < ny - nx$ или, скорее, $nx + 1 < ny$. Теперь мы знаем, что поскольку $n >
- Следовательно, $nx ≤ A ≤ nx + 1 ≤ ny$ и, значит, $nx < A < ny$, а значит, рациональное число $r = \frac{A}{n}$ работает при $x < r < y$ . $\blacksquare$
Наш следующий вопрос может состоять в том, чтобы выяснить, всегда ли между любыми двумя действительными числами существует иррациональное число.