найти центр и радиус окружности : Геометрия
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Maryvsev |
| |||||
10/03/11 |
| |||||
| ||||||
| Алексей К. |
| ||
29/09/06 |
| ||
| |||
| Maryvsev |
| ||
10/03/11 |
| ||
| |||
| Nacuott |
| ||
20/04/12 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 4 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Геометрия поворота / Этюды // Математические этюды
Геометрия поворота / Этюды // Математические этюдыМатематические этюды
К списку
Параллельны ли друг другу передние колёса автомобиля при повороте?
Оказывается, что именно геометрия и механика определяют то, как надо поворачивать колёса автомобиля.
Если продолжение оси колёс направлено в центр поворота, то колесо оставляет чёткий след. Чёткая картинка будет, и если несколько осей направлены в центр поворота. Однако, если продолжение оси колеса направлено не в центр поворота, то колесо катится с проскальзыванием. След будет стёртым, а самое главное, управляемость транспорта с таким колесом будет тем хуже, чем выше скорость. Итак, для хорошей управляемости продолжения осей колес должны быть направлены в центр поворота. Что же это значит для четырёхколёсного автомобиля?
Научимся для начала проходить простой поворот — дугу окружности.
Так как задние колёса в большинстве машин не поворачиваются, то центр окружности поворота должен лежать на продолжении оси этих колёс. Передние колёса необходимо повернуть так, чтобы продолжение оси каждого колеса смотрело в этот же центр. А значит, для хорошей управляемости передние колёса необходимо поворачивать на разные углы, и они будут непараллельны!
Вы скажете, что повороты не всегда являются дугой какой-либо окружности, и уж тем более машина не останавливается для того, чтобы повернуть колёса. Это, конечно, правда, но оказывается, что при любом повороте в каждый момент времени можно считать, что машина едет по дуге некоторой окружности
(радиус и центр которой зависят от момента времени).
Это, конечно, правда, но оказывается, что при любом повороте в каждый момент времени можно считать, что машина едет по дуге некоторой окружности
(радиус и центр которой зависят от момента времени).
Рассмотрим произвольную дорогу. Чтобы по ней можно было ездить, у неё не должно быть острых углов, т.е. средняя линия будет, как говорят в математике, гладкой кривой.
Зафиксируем синюю точку на средней линии и подумаем, каким более простым геометрическим объектом можно заменить кривую в небольшой окрестности нашей точки.
Возьмём произвольную красную точку недалеко от синей. Две точки на плоскости определяют единственную прямую, которую и проведём. Будем двигать красную
точку по кривой к синей. В момент, когда они совпадут, прямая, ими определяемая, будет касательной прямой. Она даёт линейное приближение кривой дороги
в небольшой окрестности зафиксированной точки. Однако при увеличении видно, что дорога и касательная прямая рядом идут на очень маленьком участке.
Справа и слева от синей точки возьмём по красной. Три точки, не лежащие на одной прямой, определяют единственную окружность, которую и проведём. Будем двигать красные точки к синей. В момент, когда они совпадут, получим окружность, которая называется соприкасающейся. Это приближение уже второго порядка, и на увеличении видно, насколько оно лучше. Заметим, что на монотонном участке (возрастания или убывания кривой) соприкасающаяся окружность всегда пересекает кривую, в отличие от касательной, расположенной на таких участках по одну сторону от кривой.
Так как соприкасающаяся окружность для нашей задачи хорошо приближает дорогу и может быть построена в любой её точке, то движение по изгибам дороги
можно рассматривать в каждый момент времени как движение по дуге некоторой окружности. Мгновенные радиус и центр этой окружности зависят, конечно,
от той точки, в которой находится машина.
Таким образом, при движении в произвольном повороте можно считать, что в каждый момент времени машина движется по небольшой дуге некоторой окружности. И наш первый случай — поворот машины по дуге окружности — основной, который и нужно изучать.
Но как достичь того, чтобы при любом повороте колёс продолжение осей смотрело в мгновенный центр поворота?
Оказывается, и здесь на помощь приходит геометрия, а именно известная со школы равнобокая трапеция — четырёхугольник, у которого две стороны, называемые основаниями, параллельны между собой, а боковые стороны равны друг другу. Если правильно подобрать размеры сторон трапеции, то достигается небоходимое для хорошего управления условие — продолжение осей передних колёс пересекается в точке, лежащей на продолжении оси задних колёс. Эта точка и есть мгновенный центр поворота машины.
Придумал такое управление передними колёсами француз, каретных дел мастер Шарль Жанто (Charles Jeantand). Однако для карет, передвигавшихся с малыми скоростями,
это было не так существенно, как для машин, и изобретение Жанто было забыто. Лишь почти через три четверти века два отца автомобилестроения, два немца,
два инженера — Готтлиб Даймлер (Gottlieb Wilhelm Daimler) и Карл Бенц (Karl Friedrich Michael Benz) — изобретая свои автомобили, возвращаются к трапеции Жанто.
В 1889 году Даймлер получает патент на «способ независимого управления передними колёсами с разновеликими радиусами поворота».
А в 1893 году Бенц получает патент на «устройство управления экипажей с тангенциальными к колёсам окружностями управления».
Решив задачу управления передними поворотными колёсами и другие важные технические вопросы, Карл Бенц строит свой первый знаменитый
четырёхколёсный автомобиль «Виктория».
Однако для карет, передвигавшихся с малыми скоростями,
это было не так существенно, как для машин, и изобретение Жанто было забыто. Лишь почти через три четверти века два отца автомобилестроения, два немца,
два инженера — Готтлиб Даймлер (Gottlieb Wilhelm Daimler) и Карл Бенц (Karl Friedrich Michael Benz) — изобретая свои автомобили, возвращаются к трапеции Жанто.
В 1889 году Даймлер получает патент на «способ независимого управления передними колёсами с разновеликими радиусами поворота».
А в 1893 году Бенц получает патент на «устройство управления экипажей с тангенциальными к колёсам окружностями управления».
Решив задачу управления передними поворотными колёсами и другие важные технические вопросы, Карл Бенц строит свой первый знаменитый
четырёхколёсный автомобиль «Виктория».
С точки зрения строгой математики, трапеция не позволяет достичь необходимого условия — чтобы продолжение осей передних колес при любом повороте пересекалось
в точке, лежащей на продолжении задней оси. При использовании трапеции эта точка будет всегда лежать чуть-чуть в стороне от линии задней оси. Зачем же мы столько
обсуждали трапецию, скажете вы? Расстраиваться рано — просто не надо бездумно переносить математическую строгость в технические вопросы. Чтобы точка
пересечения линий передних осей всегда лежала на линии задней оси, необходимо, чтобы длина меньшего основания трапеции немного менялась.
При общей длине этого основания более метра необходимые изменения длины составляют всего около одного сантиметра, а это меньше чем люфты в соединениях
и разрешённые допуски при изготовлении.
При использовании трапеции эта точка будет всегда лежать чуть-чуть в стороне от линии задней оси. Зачем же мы столько
обсуждали трапецию, скажете вы? Расстраиваться рано — просто не надо бездумно переносить математическую строгость в технические вопросы. Чтобы точка
пересечения линий передних осей всегда лежала на линии задней оси, необходимо, чтобы длина меньшего основания трапеции немного менялась.
При общей длине этого основания более метра необходимые изменения длины составляют всего около одного сантиметра, а это меньше чем люфты в соединениях
и разрешённые допуски при изготовлении.
Со времён изобретения первых автомобилей скорости передвижения сильно возросли. Увеличились и требования к управлению передними колёсами.
Кроме того, трапеция — это плоская геометрическая фигура. И такой способ управления передними колёсами может использоваться только при зависимой
передней подвеске — когда колёса жёстко связаны друг с другом и прямая, соединяющая их центры, всегда параллельна плоскости трапеции. Сейчас такое можно встретить на грузовых автомобилях. На современных легковых автомобилях подвеска колёс независима, т.е. они могут ходить
по высоте друг относительно друга. Для управления в повороте такими колёсами применяются более сложные, уже неплоские шарнирные механизмы,
чаще всего с центральным звеном в виде рулевой рейки. Но их расчёт — это тоже задача математиков и механиков.
А исторически они так по-прежнему и называются — рулевой трапецией.
Сейчас такое можно встретить на грузовых автомобилях. На современных легковых автомобилях подвеска колёс независима, т.е. они могут ходить
по высоте друг относительно друга. Для управления в повороте такими колёсами применяются более сложные, уже неплоские шарнирные механизмы,
чаще всего с центральным звеном в виде рулевой рейки. Но их расчёт — это тоже задача математиков и механиков.
А исторически они так по-прежнему и называются — рулевой трапецией.
При повороте автомобиля возникает ещё один вопрос, связанный с геометрией. Длина окружности радиуса R равна, как вы помните, 2πR. Соответственно,
длина дуги, опирающейся на угол α окружности радиуса R, равна αR. При повороте автомобиля по дуге окружности внешнее переднее колесо едет по дуге
окружности большего радиуса, чем внутреннее переднее. Точно так же и заднее внешнее колесо описывает дугу большего радиуса, чем внутреннее заднее. А раз радиусы различаются, то, значит, пути, проходимые внутренним и внешним колёсами одной оси, должны быть тоже различны.
В противном случае колесо будет проскальзывать, и управляемость автомобиля снизится.
А раз радиусы различаются, то, значит, пути, проходимые внутренним и внешним колёсами одной оси, должны быть тоже различны.
В противном случае колесо будет проскальзывать, и управляемость автомобиля снизится.
В случае, когда ось неведущая, т.е. её колёса не толкают автомобиль вперёд, всё просто: каждое колесо вертится со своей скоростью, необходимой для прохождения нужного пути без проскальзывания.
А как же сделать так, чтобы колёса ведущей оси, в нашем случае задней, с одной стороны, постоянно толкали автомобиль вперёд, а с другой стороны, могли вращаться с разными скоростями?
Помогает в этом дифференциал — представитель планетарных механизмов. Планетарным называется механизм, у которого есть сателлиты — шестерни, крутящиеся вокруг подвижных осей.
Вал от мотора, пройдя через коробку передач, отдаёт вращение на «бочку». Бочка же через сателлиты передаёт вращение на левую и правую полуоси ведущей оси. Как бы ни вращались колёса, скорость бочки всегда в два раза медленнее вращения вала, а сумма скоростей полуосей равна удвоенной скорости вала.
Как бы ни вращались колёса, скорость бочки всегда в два раза медленнее вращения вала, а сумма скоростей полуосей равна удвоенной скорости вала.
Если машина едет по прямой и под обоими ведущими колёсами одинаковое покрытие — с одинаковым коэффициентом трения, то колёса забирают от бочки одинаковое количество вращения, и полуоси вращаются (колёса и их полуоси) с одинаковой скоростью.
Но если коэффициенты трения различаются, например, одна сторона машины выезжает с асфальта на грунтовую обочину или попадает на лёд, то… Как же будут себя вести колёса при прохождении этого участка? У колёс неведущей оси всё просто: они независимы друг от друга, им не надо толкать машину, и когда одно из них выкатывается на лёд, то перестаёт крутиться, так как трение с дорогой очень маленькое.
Вот и под левое колесо ведущей оси попадает лёд. Справа трение с асфальтом большое, а слева — со льдом — почти отсутствует. Соответственно, левому
колесу вращаться гораздо проще, и оно начинает забирать на себя всё вращение, отдаваемое бочкой на обе полуоси. При этом сумма скоростей полуосей,
как было отмечено выше, всегда постоянна, но одна полуось не крутится, а вторая — вращается очень быстро. Начать движение из такого положения, когда
одно колесо ведущей оси потеряло связь с дорогой (например, находится на льду), а другое нет — невозможно.
Соответственно, левому
колесу вращаться гораздо проще, и оно начинает забирать на себя всё вращение, отдаваемое бочкой на обе полуоси. При этом сумма скоростей полуосей,
как было отмечено выше, всегда постоянна, но одна полуось не крутится, а вторая — вращается очень быстро. Начать движение из такого положения, когда
одно колесо ведущей оси потеряло связь с дорогой (например, находится на льду), а другое нет — невозможно.
Казалось бы, одни неудобства от этого дифференциала, зачем он тогда нужен? Как раз для решения задачи одновременного толкания ведущей осью машины вперёд и прохождения в поворотах ведущими колесами путей разной длины. Каждое колесо берёт от дифференциала количество движения пропорционально длине его пути, а в сумме всю энергию вала они затрачивают на движение машины вперёд.
Инженеры постоянно пытаются улучшить дифференциал, сохранив его основное свойство, пытаются уменьшить неприятные эффекты — каким-либо способом не давать
крутиться полуосям со слишком большой разницей скоростей. Но по сути, всё и сегодня остаётся таким же, ибо законы геометрии никто не отменял.
Но по сути, всё и сегодня остаётся таким же, ибо законы геометрии никто не отменял.
Смотри также
Поворот передних колёс автомобиля // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 54—55, 306.
Млодзеевский Б. К. К теории управления в автомобилях // Вестник инженеров. 1917. 15 января. Т. 3, № 2. С. 37—41.
Другие этюды раздела «Математика и техника»
Колёсная пара Уголковый отражатель Глубина заложенияМатематические этюды
Радиус, окружность и площадь в неевклидовой геометрии
Опубликовано от John
Как длина окружности зависит от ее радиуса? Что с районом? Ответы просты и привычны в евклидовой геометрии, но не так просты и не так привычны в неевклидовой геометрии.
В этом посте будет показано, как окружность и площадь изменяются в зависимости от радиуса в трех пространствах: поверхность с постоянной кривизной 1 (т. е. единичная сфера), поверхность постоянной кривизны 0 (т. е. плоскость) и поверхность постоянная кривизна -1 (гиперболическая поверхность). Радиус в каждом случае представляет собой расстояние от центра до окружности, измеренное на поверхности.
Сферический корпус
В сферическом случае круг радиуса R имеет окружность
C ( R ) = 2π Sin ( R )
и область
A ( и Area A ( и Area A ( и Area A ( и Area A ( и Area A ) = 2π (1 – cos( r )). Формула длины окружности действительна для 0 ≤ r ≤ π, а формула площади действительна для 0 ≤ r ≤ π/2. В гиперболическом случае круг радиусом R имеет окружность C ( R ) = 2π Sinh ( R ) и область A ( R ) = 2π (Cosh ( R ) — 1). Эти формулы справедливы для 0 ≤ r < ∞. Давайте построим пару графиков, чтобы проиллюстрировать приведенные выше уравнения. Во-первых, окружность как функция радиуса. Верхний сюжет поначалу кажется удивительным. Может ли длина окружности уменьшаться при увеличении радиуса? Да, на сфере. Представьте круг вокруг северного полюса. Когда мы тянем этот круг вниз от полюса, длина окружности увеличивается до тех пор, пока круг не станет экватором. За этой точкой окружность круга уменьшается по мере того, как круг спускается дальше на юг. Использование одного и того же диапазона r для всех трех подграфиков скрывает тот факт, что длина окружности в гиперболическом случае экспоненциально растет с радиусом. Теперь давайте посмотрим на площадь как на функцию радиуса. В каждом случае площадь растет примерно квадратично с радиусом. Но опять же рост в гиперболическом случае экспоненциальный, так как r увеличивается дальше, чем это возможно в сферическом случае. Последнее замечание: на плоскости отношение площади к окружности пропорционально р . В гиперболическом случае это же отношение асимптотически постоянно, независимо от r . Вот график C( r ) / r . А вот и участок A ( r ) / r ². Категории : Математика Метки : Дифференциальная геометрия Добавить в закладки постоянную ссылку Если вы учитель, пожалуйста, посетите мой новый сайт: intermathematics. Классическая геометрическая головоломка: нахождение радиуса Это еще один вариант головоломки от Mind Your Decisions. Задача состоит в том, чтобы найти радиус следующего круга: Нам говорят, что линии AD и BC перпендикулярны и длины некоторых частей хорд, но не намного! Сначала я рассмотрю свою попытку решить эту проблему. Это не так «хорошо», как решение в видео, так как требует использования калькулятора, но все же делает свою работу. Метод 1, дополнительные линии построения: Это дополнительные линии построения, необходимые для решения этой задачи. Вот пошаговый мыслительный процесс: Способ 2, создание системы координат Это действительно красивое решение, не требующее калькулятора (и которое обсуждается в видео выше). Начнем с создания системы координат вокруг точки G в точке (0,0). Поскольку у нас есть перпендикулярные линии, мы можем создать координаты для A, B и C. Сначала мы начнем с уравнения центра окружности (p.q): Затем мы создадим 3 уравнения, подставив в наши координаты: Затем мы можем сделать уравнение (3) – уравнение (1) для дать: Затем мы можем подставить это значение для p в уравнения (1) и (3) и приравнять, чтобы получить: Наконец, мы можем подставить оба значения для p и q в уравнение (1), чтобы найти r : Мы получаем тот же ответ, что и раньше, хотя это определенно похоже на «более чистое» решение. Есть и другие способы решить эту проблему, но некоторые из них требуют использования уравнений, которые вы, возможно, еще не знаете (например, закон синусов в описанной окружности или уравнение для перпендикулярных хорд и радиуса). Возможно, изучите любые другие методы решения этой проблемы — каковы относительные достоинства каждого подхода? Основные ресурсы для преподавателей IB 1) Intermathematics. Если вы учитель , пожалуйста, также посетите мой новый сайт. Это было разработано специально для учителей математики в международных школах. Контент теперь включает более 2000 страниц содержимого в формате PDF для всей учебной программы SL и HL Analysis, а также учебной программы SL Applications. Некоторое содержимое включает: Есть и многое другое. Я думаю, что это может сэкономить учителям более 200 часов времени на подготовку к курсу IB по математике, поэтому его стоит изучить! Необходимые ресурсы как для преподавателей, так и для студентов IB 1) Руководства по исследованию и документы 3 Ресурсы Я составил 168-страничное руководство Super Exploration Guide, чтобы рассказать студентам и преподавателям обо всех аспектах подготовки отличной курсовой работы. Студенты всегда делают одни и те же ошибки при выполнении своей курсовой работы — получите внутреннюю информацию от модератора IB! Я также сделал пакетов Paper 3 для HL Analysis, а также студентов, изучающих приложения, чтобы помочь им подготовиться к экзаменам Paper 3. Гиперболический случай
Графики
Обновление
Похожие сообщения
Классическая геометрическая головоломка: нахождение радиуса
 com, где вы найдете более 2000+ страниц ресурсов в формате pdf для обучения математике IB!
com, где вы найдете более 2000+ страниц ресурсов в формате pdf для обучения математике IB! Теперь мы можем использовать Пифагор, чтобы найти длину BD.
Теперь мы можем использовать Пифагор, чтобы найти длину BD. Мы также помечаем центр круга как (p, q).
Мы также помечаем центр круга как (p, q). com
com


 Подскажите пожалуйста идею, что делать дальше?
Подскажите пожалуйста идею, что делать дальше? .. на…
.. на…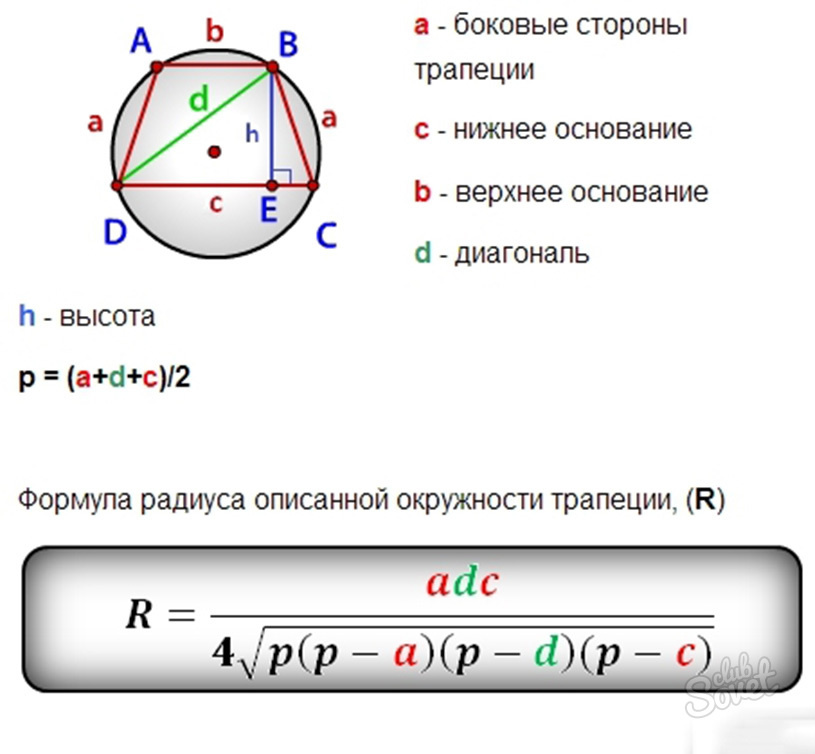
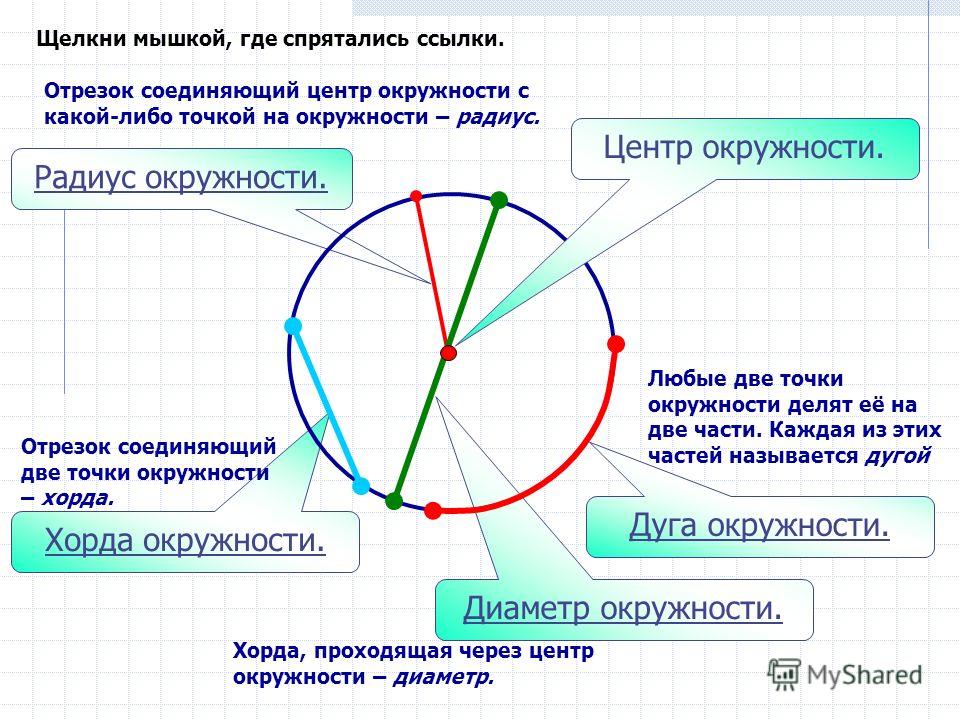 Получим параметрическое (ие) уравнение окружности, а оттуда найти координаты центра, как серединную точку крайних точек полуокружности и радиус, как полурасстояние между крайними точками полуокружности .
Получим параметрическое (ие) уравнение окружности, а оттуда найти координаты центра, как серединную точку крайних точек полуокружности и радиус, как полурасстояние между крайними точками полуокружности .