Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .
как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз
Решено
100 учащихся построеныв шеренгу по росту. Можно ли, меняя местами двух учащихся, стоящих через одного, построить их в обратном порядке?
Решено
По одной и той же кольцевой трассе движутся два велосипедиста в одну и ту же сторону. Длина кольцевой дороги равна 2400 м. Один велосипедист проходит
как решить задачу за 4 класс часть 2 автор муравьёва и урбан на странице129 №2
Пользуйтесь нашим приложением
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
| Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости | Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 | |
| Каждая из окружностей лежит вне другой | Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 | |
| Внешнее касание двух окружностей | Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 | |
| Внутреннее касание двух окружностей | Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 | |
| Окружности пересекаются в двух точках | Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 | |
| Одна из окружностей лежит внутри другой | Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
| Две окружности на плоскости | |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 | |
| Каждая из окружностей лежит вне другой | |
Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 | |
| Внешнее касание двух окружностей | |
Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 | |
| Внутреннее касание двух окружностей | |
Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 | |
| Окружности пересекаются в двух точках | |
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 | |
| Одна из окружностей лежит внутри другой | |
Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 | |
| Две окружности на плоскости |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 |
| Каждая из окружностей лежит вне другой |
Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 |
| Внешнее касание двух окружностей |
Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 |
| Внутреннее касание двух окружностей |
Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 |
| Окружности пересекаются в двух точках |
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 |
| Одна из окружностей лежит внутри другой |
Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
Общие касательные к двум окружностям
| Фигура | Рисунок | Свойства |
| Внешняя касательная к двум окружностям | Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. | |
| Внутренняя касательная к двум окружностям | Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой. | |
| Внутреннее касание двух окружностей | Существует единственная общая внешняя касательная. Других общих касательных нет. | |
| Окружности пересекаются в двух точках | Существуют две общих внешних касательных. Других общих касательных нет. | |
| Внешнее касание двух окружностей | Существует единственная общая внутренняя касательная, а также | |
Каждая из окружностей лежит вне другой | Существуют две общих внешних касательных, а также две общих внутренних касательных. | |
| Внешняя касательная к двум окружностям | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. | |
| Внутренняя касательная к двум окружностям | |
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой. | |
| Внутреннее касание двух окружностей | |
Существует единственная общая внешняя касательная. Других общих касательных нет. | |
| Окружности пересекаются в двух точках | |
Существуют две общих внешних касательных. | |
| Внешнее касание двух окружностей | |
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет. | |
| Каждая из окружностей лежит вне другой | |
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет | |
| Внешняя касательная к двум окружностям |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. |
| Внутренняя касательная к двум окружностям |
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой. |
| Внутреннее касание двух окружностей |
Существует единственная общая внешняя касательная. Других общих касательных нет. |
| Окружности пересекаются в двух точках |
Существуют две общих внешних касательных. Других общих касательных нет. |
| Внешнее касание двух окружностей |
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет. |
| Каждая из окружностей лежит вне другой |
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет |
Формулы для длин общих касательных и общей хорды двух окружностей
| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям | Длина общей внешней касательной к двум окружностям вычисляется по формуле Посмотреть доказательство | |
| Внутренняя касательная к двум окружностям | Длина общей внутренней касательной к двум окружностям вычисляется по формуле Посмотреть доказательство | |
| Общая хорда двух пересекающихся окружностей | Длина общей хорды двух окружностей вычисляется по формуле Посмотреть доказательство |
| Внешняя касательная к двум окружностям | |
Длина общей внешней касательной к двум окружностям вычисляется по формуле Посмотреть доказательство | |
| Внутренняя касательная к двум окружностям | |
Длина общей внутренней касательной к двум окружностям вычисляется по формуле Посмотреть доказательство | |
| Общая хорда двух пересекающихся окружностей | |
Длина общей хорды двух окружностей вычисляется по формуле Посмотреть доказательство | |
| Внешняя касательная к двум окружностям |
Длина общей внешней касательной к двум окружностям вычисляется по формуле Посмотреть доказательство |
| Внутренняя касательная к двум окружностям |
Длина общей внутренней касательной к двум окружностям вычисляется по формуле Посмотреть доказательство |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле где Посмотреть доказательство |
Доказательства формул для длин общих касательных и общей хорды двух окружностей
Утверждение 1.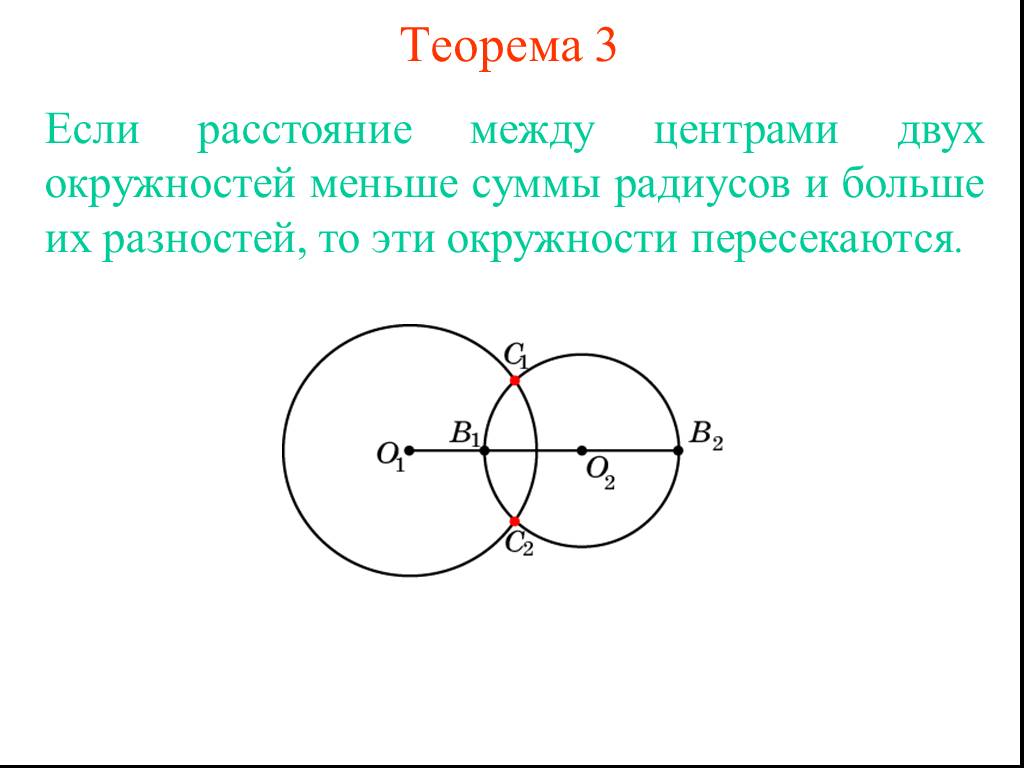 Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
Доказательство. Для того, чтобы найти длину отрезка K1K2, опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.1).
Рис.1
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K2 , K1K3 = r2 , O1K3 = r1 – r2 .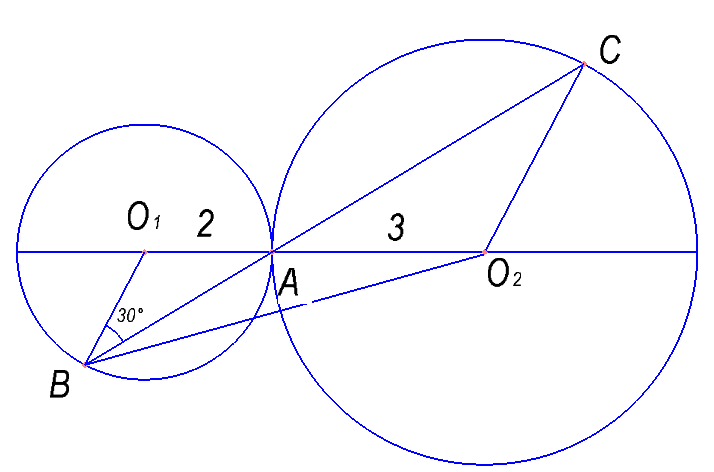
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:
Следовательно,
что и требовалось доказать.
Утверждение 2. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей внутренней касательной к этим окружностям вычисляется по формуле
Доказательство. Для того, чтобы найти длину отрезка K1K2 , опустим из точки O2перпендикуляр O2K3 на прямую O1K1 (рис.2).
Рис.2
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K3 , K1K3 = r2 , O1K3 = r1 + r2 .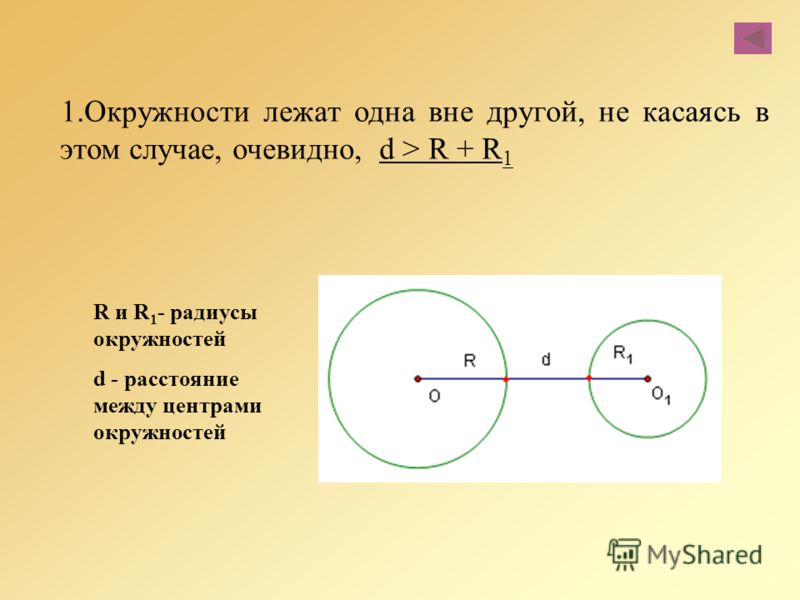
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:
Следовательно,
что и требовалось доказать.
Утверждение 3. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей хорды AB этих окружностей вычисляется по формуле
где
Доказательство. Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,
Рис.3
следующие обозначения:
O2C = y, CB = x .
Тогда, воспользовавшись теоремой Пифагора для треугольников O1CB и O2CB, получим
Поэтому
Таким образом, справедлива формула:
где
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Сумма радиусов двух окружностей равна 7 см, а разница их окружностей 8 см Найти…
Перейти к
- Площадь сектора круга и сегмента. Упражнение 16А.
- Площадь сектора круга и сегмента Упражнение 16B
- Вещественные числа
- Линейные уравнения с двумя переменными
- Координатная геометрия
- Треугольники
- Круги
- Конструкции
- Тригонометрические отношения
- T-коэффициенты некоторых конкретных углов
- Тригонометрические отношения дополнительных углов
- Тригонометрические тождества
- Высота и расстояние
- Периметр и площадь плоских фигур
- Площадь сектора круга и сегмента
Главная >
Решения RS Aggarwal
Класс 10
Математика
>
Глава 16. Площадь сектора круга и сегмента
>
Площадь сектора круга и сегмента
>
Вопрос 6 Площадь круга Сектор и сегмент Упражнение 16A
Сумма радиусов двух окружностей равна 7 см, а разница их окружностей равна 8 см. Найдите длины окружностей.
Ответ:
Сумма радиусов двух окружностей равна 7 см (дана)
Разность длин двух окружностей равна 8 см (дана)
Пусть радиусы окружностей равны х и (7-х)
Тогда
2πx — 2π(7 — x) = 8
2πx — 14π + 2πx = 8
2πx = 26 …..(1)
Это длина окружности одного круга. 92.Тот самый провод…
Найдите площадь кольца, внешний и внутренний радиусы которого равны 23 см и 12 см соответственно.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Area Of Circle Sector And Segment Exercise 16A
Area Of Circle Sector And Segment Exercise 16B
Chapters
Real Numbers
Linear Equations In Two Variables
Coordinate Geometry
Triangles
Circles
Constructions
Тригонометрические отношения
Т-отношения некоторых частных углов
Тригонометрические отношения дополнительных углов
Тригонометрические тождества
Высота и расстояние
Периметр и площадь плоских фигур
Площадь сектора и сегмента окружности
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены .
Для всех этих случаев рассмотрим две окружности с центрами C 1 и C 2 и радиусами r 1 и r 2 соответственно.
Две окружности, соприкасающиеся друг с другом снаружи
Я немного рассказывал об этом случае в предыдущем уроке. Взгляните на рисунок ниже.
У нас есть два круга, внешне соприкасающиеся друг с другом. И совершенно очевидно, что расстояние между центрами двух окружностей равно сумме их радиусов. то есть C 1 C 2 = r 1 + r 2 , что будет требуемым условием внешнего касания двух кругов друг друга. Имеет смысл?
Две окружности, лежащие вне друг друга
В предыдущем случае, что если мы немного отодвинем одну из окружностей от другой? Два круга больше не будут касаться друг друга и лежат вне друг друга.
Поскольку, разделив их, мы увеличили расстояние между их центрами, расстояние C 1 C 2 станет больше, чем r 1 + r 2 . Следовательно, искомое условие будет C 1 C 2 > r 1 + r 2
Две окружности, соприкасающиеся друг с другом внутренне
Посмотрите на рисунок.
В этом случае расстояние между центрами равно разности радиусов окружностей, т.е.0143 2 . Вы видите это?
Один круг лежит внутри другого
Теперь давайте немного сдвинем меньший круг вправо, чтобы он полностью лежал внутри большего круга.
Смещая круг, мы делаем C 1 C 2 меньше, чем в предыдущем случае. Значит, искомое условие для этого случая будет C 1 C 2 < r 1 – r 2 .
Две окружности, пересекающиеся в двух точках
Снова рассмотрим третий случай.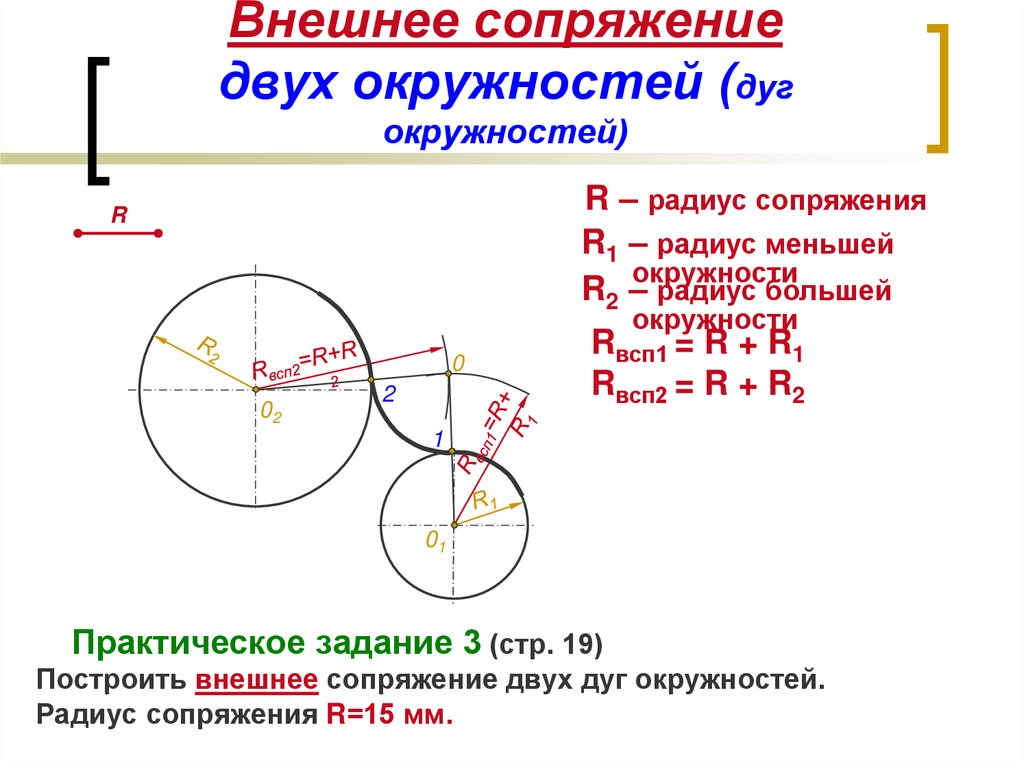 Что, если мы сдвинем меньший круг влево? (Или больший справа?). Окружности теперь будут пересекаться в двух точках. И теперь мы увеличиваем расстояние между их центрами, подразумевая C 1 C 2 > r 1 – r 2 .
Что, если мы сдвинем меньший круг влево? (Или больший справа?). Окружности теперь будут пересекаться в двух точках. И теперь мы увеличиваем расстояние между их центрами, подразумевая C 1 C 2 > r 1 – r 2 .
Но мы не можем толкать его бесконечно влево, потому что возникла бы ситуация, когда C 1 C 2 станет равным r 1 + r 2 , и окружности снова соприкоснутся, но внешне. Это означает, что если мы хотим, чтобы окружности пересекались в двух точках, мы должны сохранить расстояние между их центрами меньше суммы их радиусов.
Учитывая все это, получаем требуемое условие для этого случая:0002
Обратите внимание, что в последних трех случаях я предполагал, что r 1 > r 2 (иначе r 1 – r 2 оказалось бы отрицательным). Для любых двух заданных окружностей вы всегда можете считать, что больший радиус равен r 1 , или же вы можете использовать абсолютное значение их разницы.

 Имеют, т.к. 3+4>5/
Имеют, т.к. 3+4>5/
 Других общих касательных нет
Других общих касательных нет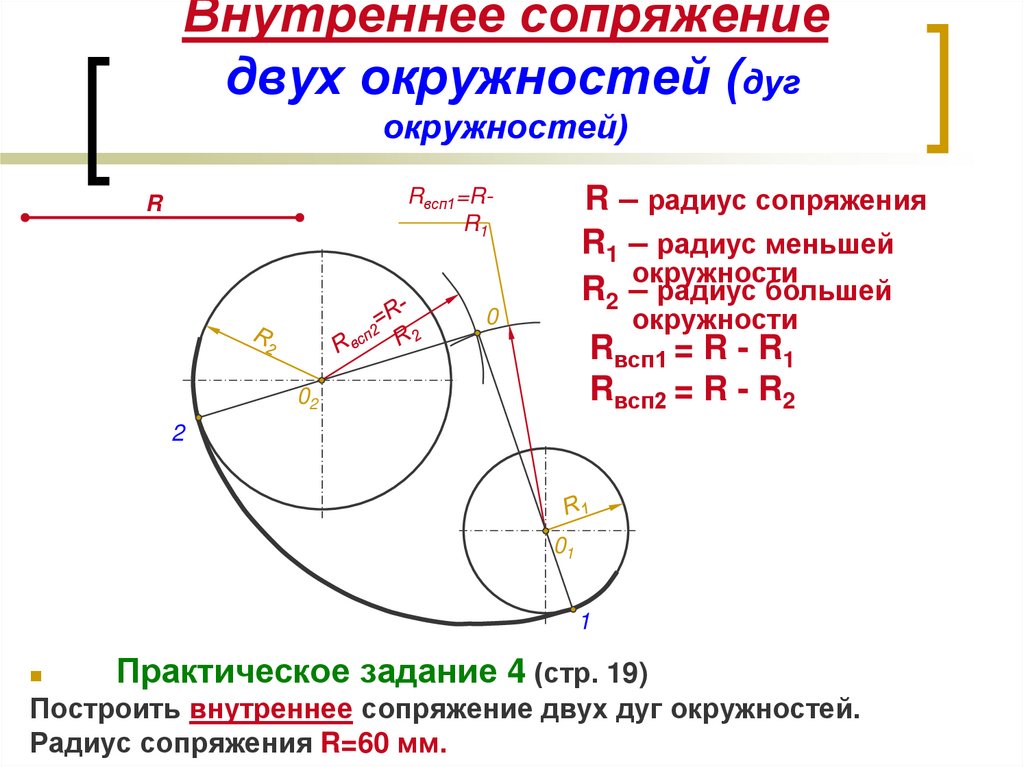 Других общих касательных нет.
Других общих касательных нет.