Расчет объема формула: Формулы объема и программы для расчета объема

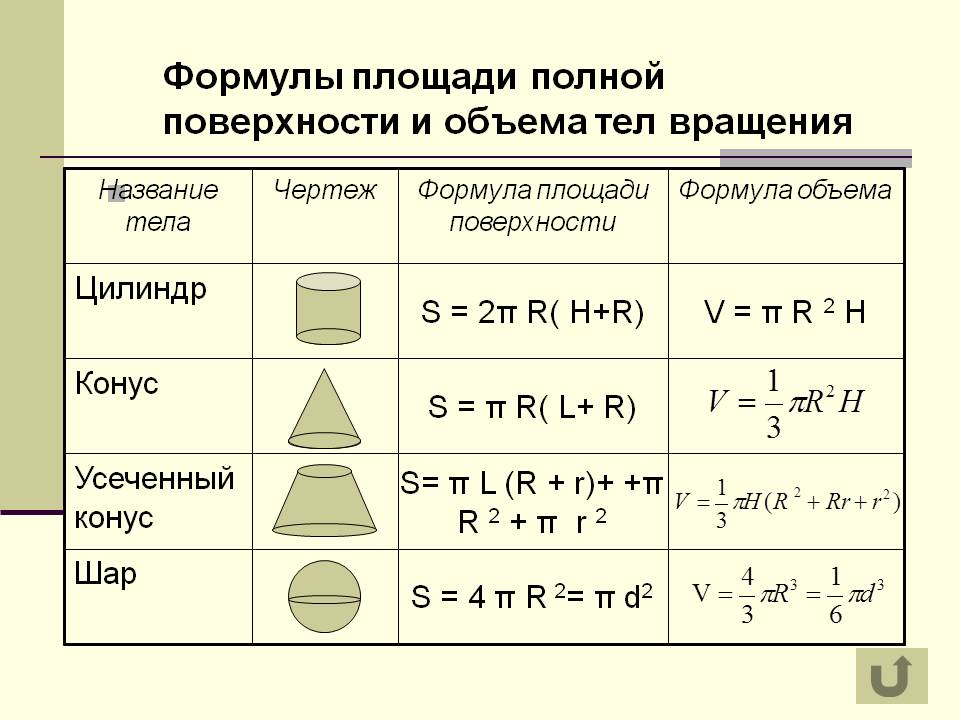
Как рассчитать объём — онлайн калькулятор объёма воды

Онлайн калькуляторы / 1 комментарий

Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.

1. Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …

2. Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …

3. Единицы измерения объёма

3.1. Соотношение единиц объёма

4. Конвертер единиц объёма

5. Заключение

6. Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …

Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …

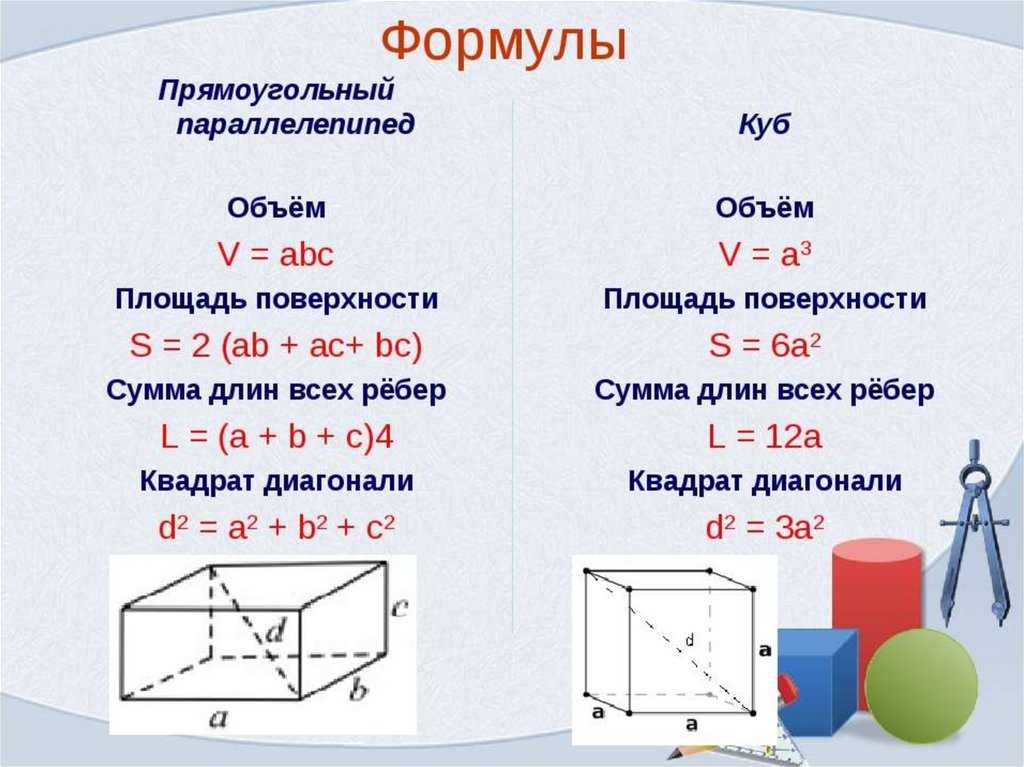
Как рассчитать объём по формуле — формула расчёта объёма прямоугольной ёмкости

V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).

При этом мы помним, что у куба все стороны равны — X=Y=Z . Соответственно формула объёма куба имеет такой вид — V = X³ , где X — длина стороны куба.

Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.

Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →

Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …

Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →

Как рассчитать объём по формуле — формулы расчёта объёма цилиндра

Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.

Вначале рассчитываем площадь основания (площадь внутреннего сечения) по формуле — S = π * R²
Где, R — радиус трубы, π — число ПИ равное 3,1415926535 .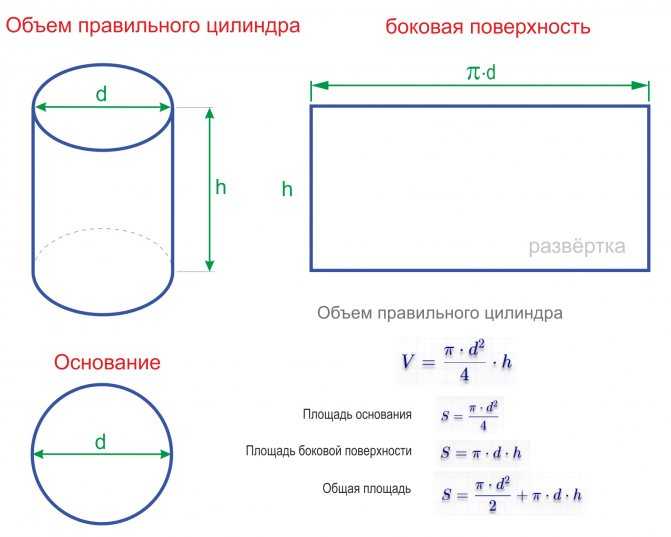

Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).

Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.

Единицы измерения объёма

Вначале кратко ознакомимся с единицами измерения объёма как таковыми.

Официальной единицей измерения объема в системе СИ является м³ — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм³ — кубические дециметры, см³ — кубические сантиметры, литры …

Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.

Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C

Соотношение единиц объёма

1 м3 = 1000 дм³ = 1 000 000 см³ = 1 000 000 000 мм³ = 1000 литров
1 литр = 0,001 м³ = 1 дм³ = 1 000 см³ = 1 000 000 мм³

Конвертер единиц объёма

Конвертация кубических метров ( м

³ ) в кубические сантиметры ( см³ ) и литры

Конвертация литров в метры кубические ( м

³ ) и кубические сантиметры ( см³ )

Конвертация кубических сантиметров ( см

³ ) в кубические метры ( м³ ) и литры

Заключение

Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта. Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.

 

Поделись с друзьями 🙂

Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …

Статья опубликована: 2023-04-12 Автор: Waterman

Калькулятор расчета объема груза — Avrora Logistic

• На главную
• Расписание
  движения
• КАЛЬКУЛЯТОР
  ТАМОЖЕННЫХ
  ПЛАТЕЖЕЙ
• КАЛЬКУЛЯТОР
  СБОРНЫХ
  ГРУЗОВ
• КАЛЬКУЛЯТОР
  ЦЕЛЫХ
  КОНТЕЙНЕРОВ
• РАСЧЕТ ОБЪЕМА
  ГРУЗА

Рассчитайте объем вашего груза

РАСЧЕТ ОБЪЕМА ГРУЗА

ШИРИНА (W) *

ДИАМЕТР (D) *

РАСЧЕТ ОБЪЕМА КоробкиЦилиндр

ВЫСОТА (H) * ЕДИНИЦА ИЗМЕРЕНИЯ * ммсмм

ДЛИНА (L) *

КОЛИЧЕСТВО КОРОБОК *

КОЛИЧЕСТВО ЦИЛИНДРОВ *

ИТОГО:

Объем одной коробки Объем одного цилиндра	0 м³
Общий объем	0 м³

ИСПОЛЬЗУЙТЕ ПОЛУЧЕННЫЕ РАСЧЕТЫ
ДЛЯ ОФОРМЛЕНИЯ ЗАЯВКИ

Далее

• На главную
• Расписание
  движения
• РАСЧЕТ ОБЪЕМА
  ГРУЗА
• КАЛЬКУЛЯТОР
  ТАМОЖЕННЫХ
  ПЛАТЕЖЕЙ
• КАЛЬКУЛЯТОР
  СБОРНЫХ
  ГРУЗОВ
• КАЛЬКУЛЯТОР
  ЦЕЛЫХ
  КОНТЕЙНЕРОВ

Возникли вопросы?

Я согласен на обработку персональных данных в порядке и на условиях, указанных по ссылке

Прикрепить файл (максимальный размер 20 Мб)

Расчет объема

Расчет объема

ДЕП Дом	Вода/сточные воды Математический калькулятор Танк Калькулятор объема Возврат в информационный центр оператора
Формула: Д х Ш x D = кубические футы *** Кубический футов x 7,47 = галлонов	Объем квадратного или прямоугольного резервуара или отстойника Пожалуйста введите данные о длине, ширине и глубине боковой воды. Бак Д Длина (футы) введите длину Бак Ш ширина (футы) введите ширину Боковой Вода D Высота (фут) введите глубину Нажмите на кнопку для расчета кубических футов Нажмите на кнопку для расчета галлонов
Формула: 3. 1417 x R x D = кубические футы **** Кубический футов х 7,47 = Галлоны	Объем круглого бака или очистителя Пожалуйста введите данные для радиуса резервуара (радиус составляет 1/2 диаметра) и стороны глубина воды. Бак R радиус (фут): введите радиус (1/2 диаметра) Бак Боковая вода D epth (ft): введите глубину Нажмите на кнопку, чтобы рассчитать куб. футов Нажмите на кнопка для расчета объема воды (галлоны)

 

Объем – формула, определение, расчет, примеры

Объем – это мера емкости, которую держит объект. Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой.

В этом можно убедиться с помощью простого упражнения дома:

• Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
• Соедините противоположные стороны листа бумаги, не сгибая лист.
• Вы создали трехмерный объект, который заключает в себе пространство, из двухмерного листа.

1.	Определение тома
2.	Объем трехмерных фигур
3.	Список формул объема
4.	Как рассчитать объем?
5.	Единицы объема
6.	Калькулятор объема
7.	Часто задаваемые вопросы о томе

Определение тома

Объем определяется как объем, занимаемый трехмерной твердой формой. В любой форме это трудно визуализировать, но можно сравнить между формами. Например, объем ящика компаса больше объема помещенного в него ластика. Для вычисления площади любой двумерной фигуры мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.

Объем 3D-фигур

Каждый предмет в нашем окружении имеет свойство занимать пространство. Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.

Объем кубоида

Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если мы сложим их один поверх другого до высоты ‘h’ , мы получим прямоугольный параллелепипед размерности л, б, з . Это можно увидеть на следующем рисунке, на котором показаны длина, ширина (ширина) и высота образованного таким образом прямоугольного параллелепипеда.

Чтобы вычислить объем пространства, заключенного в этот прямоугольный параллелепипед, мы используем формулу: Объем кубоида = l × b × h

Объем куба

Куб является частным случаем прямоугольного параллелепипеда, где все три стороны равны по мере. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³. Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.

Объем цилиндра

Точно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.

Цилиндр представляет собой трубчатую конструкцию с двумя параллельными круглыми основаниями, соединенными изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как объем цилиндра = π r² h

Объем пирамиды

Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине.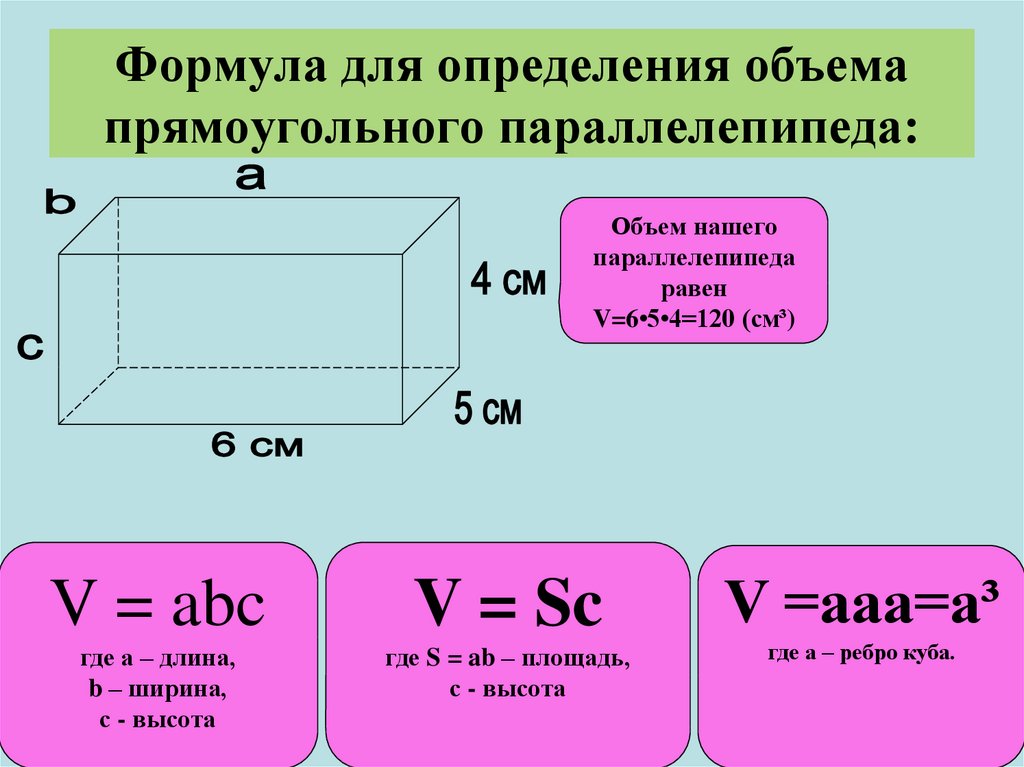 Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать в виде 1/3 × площадь основания многоугольника × высота пирамиды.

Объем конуса

Разница между конусом и пирамидой заключается в том, что основание конуса круглое, тогда как основание пирамиды представляет собой многоугольник. Объем конуса рассчитывается по формуле: 1/3 × πr ² ч.

Объем шара

Объем шара – это занимаемое им пространство.

Объем сферы, радиус которой r равен 4/3 πr³.

Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте взглянем на различные единицы объема.

Список формул объема

Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (твердых) форм.

Как рассчитать объем?

Вот шаги для расчета объема любой твердой формы:

• Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема. Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т. д.
• Убедитесь, что все параметры имеют одинаковые единицы измерения.
• Подставьте значения в формулу объема соответствующих фигур.
• Запишите единицы измерения в кубических единицах.

Давайте разберемся с шагами на примере.

Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3,142.

Решение:

Радиус цилиндра r = 25 м.
Его высота h = 1 метр.
Объем цилиндра V = πr ² h = (3,142)(25) ² (1) = 1963,75 м ³ .
Объем баллона 1963,75 куб.м.

единиц объема

Единицей объема в системе СИ является кубический метр (м ³ ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью. Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.

Боковой блок	Единица объема	Метрический эквивалент
Дюйм	кубических дюймов (в 3 )	1 куб. дюйм = 16,387064 мл
Ножка	кубических футов ( 3 футов)	1 куб.фут = 28,316846592 л
см	Кубический сантиметр (см 3 )	1 кубический сантиметр = 1 мл
Двор	Кубический ярд (ярд 3 )	1 куб.ярд = 764,554857984 л 1 куб.ярд = 0,764554857984 м 3

В то время как стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции. В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.

Блок	Эквивалентное преобразование
1 пинта (pt)	2 чашки
1 кварта	2 балла
1 галлон	3,78 литра
1 литр	1000 кубических сантиметров

Калькулятор объема

Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы. Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.

☛Также проверьте:

• Калькулятор объема цилиндра
• Калькулятор объема сферы
• Калькулятор объема куба
• Калькулятор объема прямоугольного параллелепипеда

☛Статьи по теме

Ознакомьтесь со статьями, посвященными объему различных объемных форм.

• Объем конуса
• Объем цилиндра
• Объем прямоугольного параллелепипеда
• Объем пирамиды

 

Примеры томов

1. Пример 1: У Эдвина есть конический сосуд радиусом 6 дюймов и высотой 7 дюймов. Каков объем сосуда? Используйте π = 22/7.

   Раствор.
   Сосуд имеет форму конуса.
   Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 6 × 6 × 7 = 264 дюйма³
   ∴ Объем сосуда 264 куб. дюйм

2. Пример 2: Джо любит играть со строительными блоками. Он построил конструкцию из 15 кубов. Если длина (ребро) каждого куба равна 3 дюймам, каков будет объем его конструкции?

   Раствор.
   Рассчитаем объем одного куба. Объем куба = ребро × ребро × ребро = 3 × 3 × 3 = 27 дюймов³
   В его структуре 15 кубиков. Итак, объем всей конструкции:
   Объем конструкции = 15 × объем одного куба = 15 × 27 = 405 дюймов³
   ∴ Объем конструкции 405 дюймов³.

3. Пример 3: Если диаметр мяча составляет 14 дюймов, сколько воздуха может вместить мяч? Используйте π = 3,14

   Решение.
   Количество воздуха внутри шара займет все пространство в шаре. Итак, нам нужно найти объем шара.
   Радиус шара 14/2 дюйма = 7 дюймов
   Объем шара = 4/3 πr³
   = [4/3 × 3,14 × (7)³]
   = 1436,02 дюйма³
   ∴ Мяч содержит 1436,02 дюйма³ воздуха.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы в томе

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по тому

Что означает объем?

Объем — это мера емкости, которую содержит объект. Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.

☛Загрузите прямо сейчас, чтобы попрактиковаться.

• Объемные листы
• Объем кубов Рабочие листы
• Объем конуса Рабочие листы
• Объем цилиндра Рабочие листы

Какая формула объема частичного конуса?

Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» — радиус верхней поверхности.

☛ Прочтите основы здесь:

• Объем правого кругового конуса
• Объем частичного конуса
• Объем конуса в единицах числа Пи

Как найти объем пирамид?

Объем пирамиды рассчитывается по формуле: V = 1/3 × Площадь основания × Высота.

☛ Также проверьте:

• Объем прямоугольной пирамиды
• Объем треугольной пирамиды
• Объем прямоугольной пирамиды

Как найти объем конуса?

Объем конуса составляет 1/3 объема цилиндра той же высоты и такого же основания. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.

Как найти объем цилиндра?

Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.

В чем разница между объемом и площадью?

Объем фигуры или твердого тела — это пространство, занимаемое им, которое также включает его высоту или глубину. Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.

☛ Проверьте список важных математических формул:

• Формулы площади
• Формулы площади поверхности
• Геометрические формулы
• Формулы измерения

Каков объем мяча?

Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.

Какая формула объема цилиндра?

Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.

Как найти объем призмы?

Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» — это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).

☛Чек:

• Объем призмы
• Объем призм. Рабочие листы

Как найти объем бака?

Объем резервуара зависит от его формы. В зависимости от размера мы можем использовать приведенные ниже формулы:

• Объем параллелепипеда = l × b × h; где «l» — длина прямоугольного параллелепипеда, «b» — ширина (ширина) прямоугольного параллелепипеда, а «h» — высота прямоугольного параллелепипеда.
• Объем куба = a ³ , где «a» — ребро куба.

  No related posts.