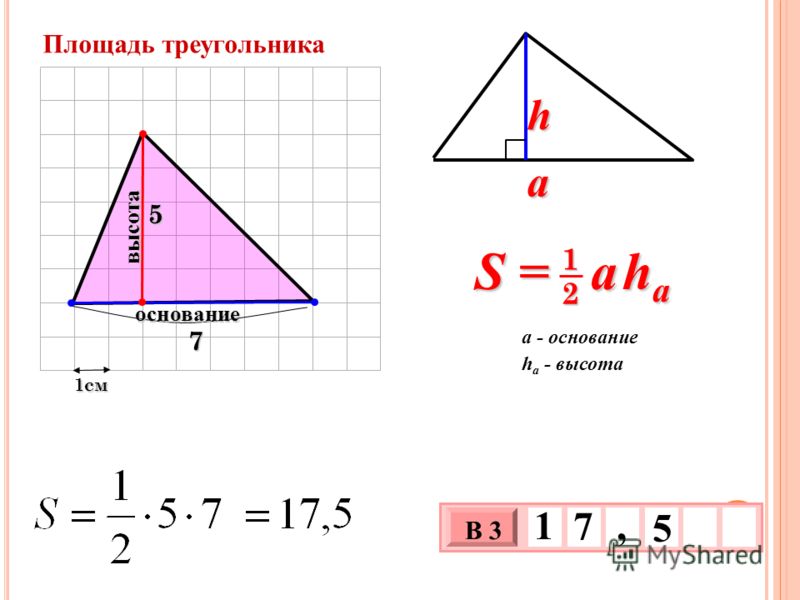
Расчет площади треугольника на примере участка треугольной формы по формуле Герона
Наверно, даже тот, кто в школе был отъявленным троечником, ответит на этот вопрос утвердительно. И в самом деле – формула проста и легко запоминается: нужно лишь длину основания умножить на длину опущенного до этого основания из противолежащего угла перпендикуляра (высоты), и затем разделить на два. С прямоугольным треугольником – вообще красота: перемножай длины катетов – и половина от полученного произведения как раз и будет площадью фигуры.
Ответ почти на «пятерку»! Ну а прочему – «почти»? Потому что это не единственный способ, а зачастую – и весьма труднореализуемый.
Вы полностью уверены, что знаете, как рассчитывается площадь треугольника?Мнение эксперта:
Афанасьев Е.В.
Главный редактор проекта Stroyday.ru. Инженер.
Задать вопрос эксперту
Например, при работе на местности, в условиях, когда треугольник – явно не прямоугольный, а без специального геодезического инструмента сложно отбить точный перпендикуляр
 Вы полностью уверены, что знаете, как рассчитывается площадь треугольника в таких условиях? Нет ли какого-нибудь метода, что позволял бы избежать дополнительных построений или вычерчиваний схем в масштабе? Скажем, можно было бы обойтись только промером длин сторон с помощью рулетки?
Вы полностью уверены, что знаете, как рассчитывается площадь треугольника в таких условиях? Нет ли какого-нибудь метода, что позволял бы избежать дополнительных построений или вычерчиваний схем в масштабе? Скажем, можно было бы обойтись только промером длин сторон с помощью рулетки?Да, такой метод тоже существует, вот только помнят о нем не все. По все видимости потому что лежащая в его основе формула Герона — довольно-таки «тяжеловесная», не располагающая к быстрому и четкому запоминанию.
Многим может показаться, что расчет площади треугольника – вообще мало кому нужное занятие. Ведь на практике при строительстве, проведении ремонта, при работах на территории участка чаще приходится иметь дело с четырёхугольниками.
Возможно, это и так, но треугольник тоже очень часто может пригодиться.
- Ну, во-первых, не надо делать категоричных заключений. Нечасто, но встречаются и треугольные территории. А если говорить о разбивке этой территории на зоны, особенно при использовании радиального принципа, то есть от центра по расходящимся к периферии лучам – треугольников может получиться больше чем достаточно.
 Нельзя совсем исключить треугольники и в области архитектуры — тому тоже немало примеров.
Нельзя совсем исключить треугольники и в области архитектуры — тому тоже немало примеров.
- А во-вторых, и это главное, знание этого вопроса поможет вам «бороться» и с куда более сложными фигурами. Ведь любой многоугольник, независимо от количества его вершин, можно воображаемыми секущими линиями разбить на совокупность прилегающих друг к другу треугольников различной формы и размеров.
Правда, формула одним своим видом быстро развеивает оптимизм:
Формула Герона:
S = √ (p × (p – а) × (p – b) × (p – c))
S — площадь треугольника;
a b c — длины сторон треугольника;
p — полупериметр треугольника, то есть
p = (a + b + c) / 2
М-да,, так просто, в уме – и не подсчитаешь, Тем более что в формуле присутствует еще и квадратный корень…
А в уме и не надо – это очень точно и быстро сделает за вас онлайн-калькулятор, размещенный ниже.
Перейти к расчётам
Введите промеренные длины всех трех сторон треугольника (в метрах) и нажмите
«РАССЧИТАТЬ ПЛОЩАДЬ ТРЕУГОЛЬНОГО УЧАСТКА»
ДЛИНА СТОРОНЫ А (метров)
ДЛИНА СТОРОНЫ В (метров)
ДЛИНА СТОРОНЫ С (метров)
Тот редкий случай, когда никаких пояснений по расчету, должно быть, и не требуется. Знай себе, подставляй промеренные длины сторон – и получай готовый результат.
А как быть с остальными фигурами?
С многоугольными – понятно. А если присутствуют ещё и округлые формы? Приходится разбираться с каждым случаем индивидуально, и очень часто для этого отыскивается то или иное приемлемое решение. Разбор интересных с точки зрения геометрии вариантов проведен в специальной статье нашего портала, посвященной именно
расчету площадей.
Понравилась статья?
Сохраните, чтобы не потерять!
Оцените:
- 5
- 4
- 3
- 2
- 1
5
Площадь треугольника 21 способ
Калькулятор площади треугольника онлайн подробно опишет как находить площадь любого треугольника.
Различные формулы для вычисления площади треугольников подскажут как это сделать самостоятельно или просто введите данные вашего треугольника и получите подробное решение с ответом.
Выберите тип треугольника
ПрямоугольныйРавнобедренныйРавностороннийПроизвольный
Способ расчета площади треугольника
По высоте и основаниюПо двум сторонам и углу между нимиПо радиусу вписанной окружности и трем сторонамПо радиусу описанной окружности и трем сторонамПо трем сторам (формула Герона)По стороне и двум прилежащим угламСторона a: Сторона b: Угол α°:
Треугольник — это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).
Формула площади треугольника:
где а и b — стороны, α — угол между ними.
Решение:
S =
· a · b · sin(α)
=
· 15 · 19.5 · sin(45º)
=
· 292.5 · 0.707
=
103.414
Ответ: площадь треугольника сo сторонами 15 и 19.5 и углом 45º равна 103.414
Треугольник — это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).
Прямоугольный треугольник — это треугольник, в котором один угол прямой (составляет 90 градусов).
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а другая — основанием.
Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.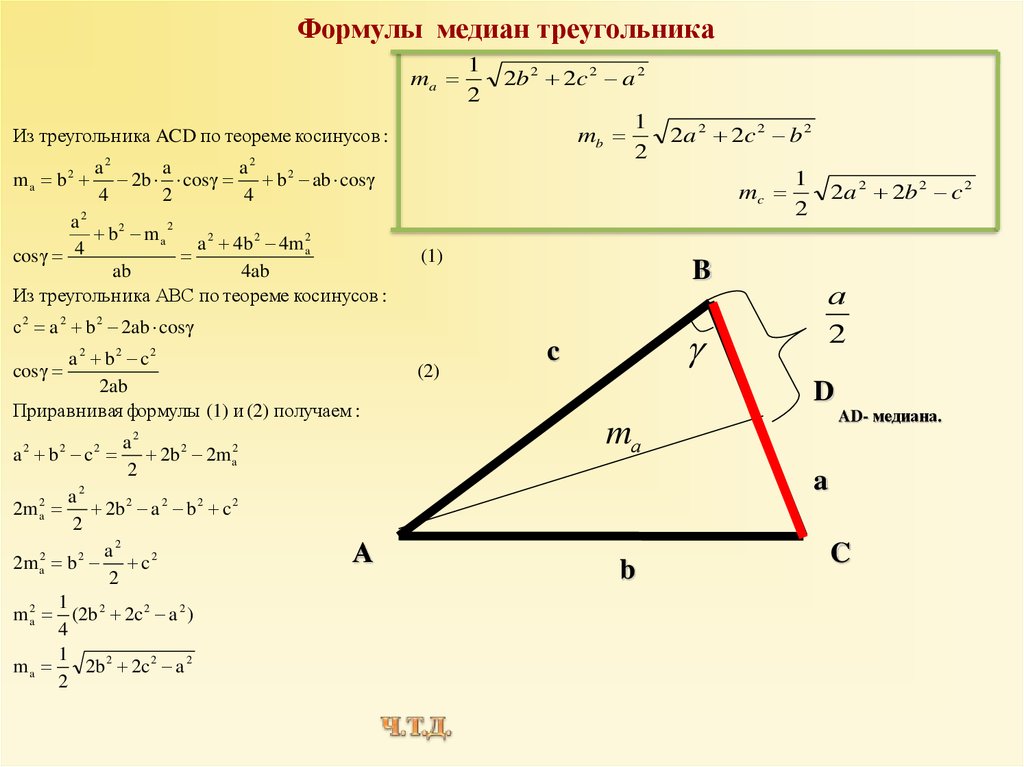
Скачать все формулы в формате Word
Похожие калькуляторы
Сторона треугольника 14 формул расчет онлайн
Периметр треугольника 8 формул
Площадь ромба онлайн калькулятор (7 способов)
Площадь трапеции онлайн калькулятор (5 способов)
Площадь параллелограмма онлайн калькулятор (4 способа)
Калькуляторы других категорий
Перевод чисел из одной системы счисления в любую другую онлайн
Сложение, умножение и деление чисел в различных системах счисления
Деление в столбик онлайн. Калькулятор наглядного деления.
Умножение в столбик онлайн. Калькулятор наглядного умножения.
Площадь поверхности призмы онлайн калькулятор
| Ваша оценка? |
— периметр, площадь, пример решения и часто задаваемые вопросы
Что такое треугольник?
Многоугольник с тремя сторонами и тремя вершинами является треугольником. В геометрии это одна из фундаментальных тем геометрии. Треугольник с вершинами A, B и C представлен как △ ABC. В евклидовой геометрии любые три точки, не лежащие на одной прямой, определяют уникальный треугольник и уникальную плоскость одновременно. В треугольнике три угла. Каждый угол образуется, когда любые две стороны треугольника встречаются в общей точке, называемой вершиной.
В геометрии это одна из фундаментальных тем геометрии. Треугольник с вершинами A, B и C представлен как △ ABC. В евклидовой геометрии любые три точки, не лежащие на одной прямой, определяют уникальный треугольник и уникальную плоскость одновременно. В треугольнике три угла. Каждый угол образуется, когда любые две стороны треугольника встречаются в общей точке, называемой вершиной.
Формула периметра треугольника
Периметр любого многоугольника представляет собой сумму длин сторон.
В треугольнике
Периметр = сумма трех сторон
Площадь треугольника
Площадь треугольника — это общая область, заключенная между тремя сторонами любого конкретного треугольника. Он равен половине высоты основных периодов. Следовательно, мы должны знать его основание и высоту, чтобы найти поле трехстороннего многоугольника.
Найдем площади различных типов треугольников.
В равнобедренном треугольнике две стороны равны по длине.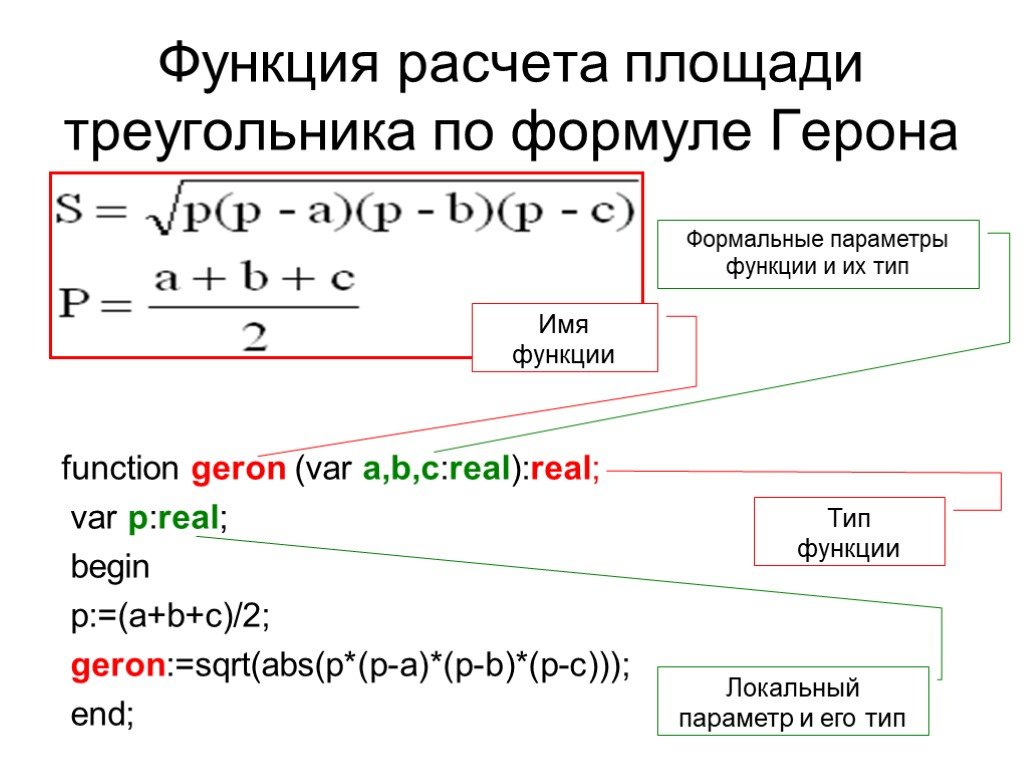 Также равны друг другу два угла, противоположные двум равным сторонам.
Также равны друг другу два угла, противоположные двум равным сторонам.
Если даны основание и высота, используем следующую формулу:
A = ½ × высота × основание
2 − б 2 /4) × б]
Используя 2 стороны треугольника и угол между ними:
A = ½ × b × c × sin(α)
Используя два угла между двумя сторонами и их длину:
- A
- = [c 2 × sin(β) × sin(α)/ 2 × sin(2π−α−β)]
Разносторонний треугольник — это тип треугольника, в котором все три стороны имеют разные измерения. стороны. Из-за этого три угла отличаются друг от друга.
стороны. Из-за этого три угла отличаются друг от друга.
A = ½ × высота × основание
Все три стороны равностороннего треугольника равны друг другу. Как следствие, все внутренние углы равны градусам, то есть каждый угол равен 60°.
A = (√3)/4 × сторона 2
Где
A — площадь треугольника.
а — длина треугольника.
b — основание треугольника.
c — третья сторона треугольника.
h — высота треугольника.
α и β — углы между двумя сторонами.
Пример решена
Определить площадь треугольника с основанием 12см и высотой 10см.
Решение:
Площадь треугольника = ½ × высота × основание
= ½ × 12 × 10
= 6 × 10
= 60 см 2
Заключение
С ТРИНЕРС многоугольника, поэтому, чтобы найти периметр треугольника, мы должны найти сумму трех сторон. Точно так же, чтобы найти площадь треугольника, мы должны сначала узнать о длинах сторон треугольника.
Точно так же, чтобы найти площадь треугольника, мы должны сначала узнать о длинах сторон треугольника.
How to Find the Area of a Triangle (Formula, Video, & Examples)
Written by
Malcolm McKinsey
Fact-checked by
Paul Mazzola
Area and base
Во-первых, давайте рассмотрим несколько определений, которые помогут нам найти площадь треугольника.
Площадь треугольника – это внутреннее пространство, ограниченное тремя его прямыми сторонами. Хотя он всегда имеет форму треугольника, он измеряется в квадратных единицах.
основание треугольника — это сторона, используемая для создания высоты или высоты.
Нарисуйте косой треугольник △RCK\треугольник RCK△RCK, где ∠R=31° , ∠C=47° , ∠K=102°. Расположите треугольник так, чтобы сторона RC , равная 8 см , была вертикальной и располагалась слева.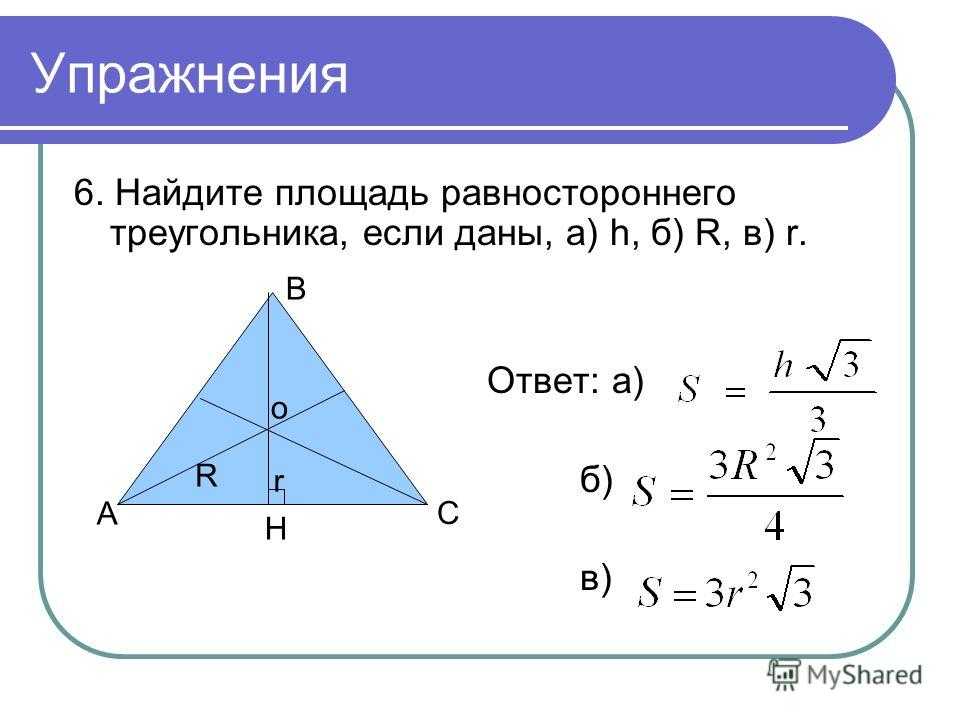 Другие стороны, сторона RK должны быть 5,98 см и сторона КС должны быть 4,21 см.
Другие стороны, сторона RK должны быть 5,98 см и сторона КС должны быть 4,21 см.
Обычно авторы учебников по геометрии дают вам треугольник с горизонтально расположенным основанием, но это обман! Здесь нет обмана — любая сторона может быть базовой!
Высота или высота над уровнем моря
Добавьте перпендикуляр со стороны RC на ∠K\угол K∠K. Этот перпендикуляр является высотой или высотой треугольника от этого основания. Мы знаем, что длина стороны RC составляет 8 см , и мы можем вычислить высоту, которая будет примерно 3,08 см . Обозначьте точку пересечения высоты с RC как Point O . Этот треугольник РОК с!
Обратите внимание, что наша высота перпендикулярна стороне RC , даже если сторона RC вертикальна, как на нашем рисунке. Основание не обязательно рисовать горизонтально для вас.
Для того же треугольника мы можем выбрать другую сторону в качестве основания. Возьмем сторону RK , 5,98 см и построим высоту ∠C\угол C∠C. Эта высота равна 4,12 см .
Возьмем сторону RK , 5,98 см и построим высоту ∠C\угол C∠C. Эта высота равна 4,12 см .
Попробуйте последнюю сторону и постройте высоту со стороны KC , 4,21 см в длину, и чтобы он пересекался ∠R\угол R∠R. Эта высота составляет 5,85 см высоты.
Косой треугольник
Вы хорошо потрудились, чтобы вспомнить равносторонний, равнобедренный и разносторонний треугольники. Они названы по длине их сторон. Потом кто-то рассказал вам о прямоугольных, остроугольных и тупоугольных треугольниках. Они названы по своим внутренним углам. Например, в прямоугольном треугольнике есть один прямой угол.
Теперь мы должны открыть вам секрет об остроугольных и тупоугольных треугольниках.
Оба типа наклонных треугольников или треугольников без прямых углов. Остроугольные треугольники имеют три острых внутренних угла (каждый меньше 90° ). Равносторонний треугольник является примером остроугольного треугольника.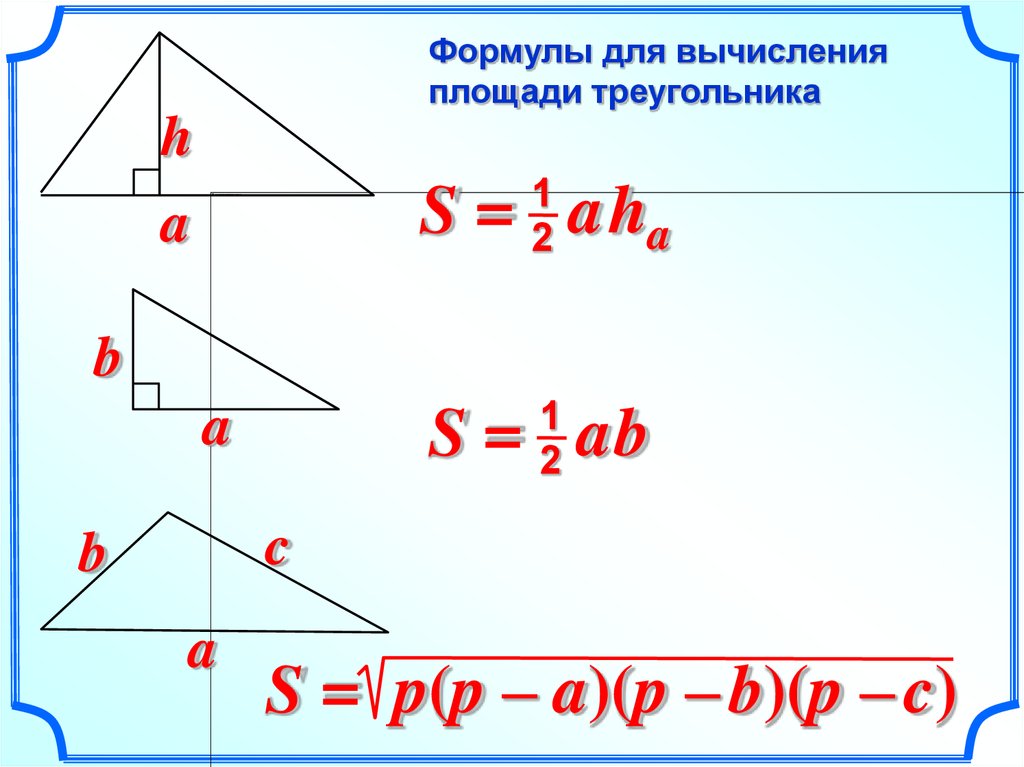 В тупоугольных треугольниках один угол больше 90° и два острых угла.
В тупоугольных треугольниках один угол больше 90° и два острых угла.
Вы понимаете, почему у никогда не может быть треугольник с двумя внутренними углами больше, чем 90° ? Две из трех сторон расходятся или удаляются друг от друга, а не сходятся.
Теперь мы готовы разблокировать нашу формулу!
Формула площади треугольника
Удобная формула позволяет вычислить площадь любого треугольника в квадратных единицах.
У нас уже есть △RCK\треугольник RCK△RCK , готовый к использованию, поэтому давайте попробуем на нем формулу:
Но мы также нашли высоту, взяв за основу две другие стороны. Итак, давайте посмотрим, работает ли формула для всех трех сторон:
То есть в пределах 0,0019 нашего первого расчета!
То есть в пределах 0,0065 первой! Это незначительные простые ошибки округления с более точными измерениями, чем вы могли бы получить с помощью линейки.
Итоги урока
Теперь, когда вы прошли этот урок, вы теперь знаете, как определить прямоугольный треугольник (имеющий один прямой угол), косоугольный треугольник (не имеющий прямых углов), основание треугольника и высота или высота треугольника.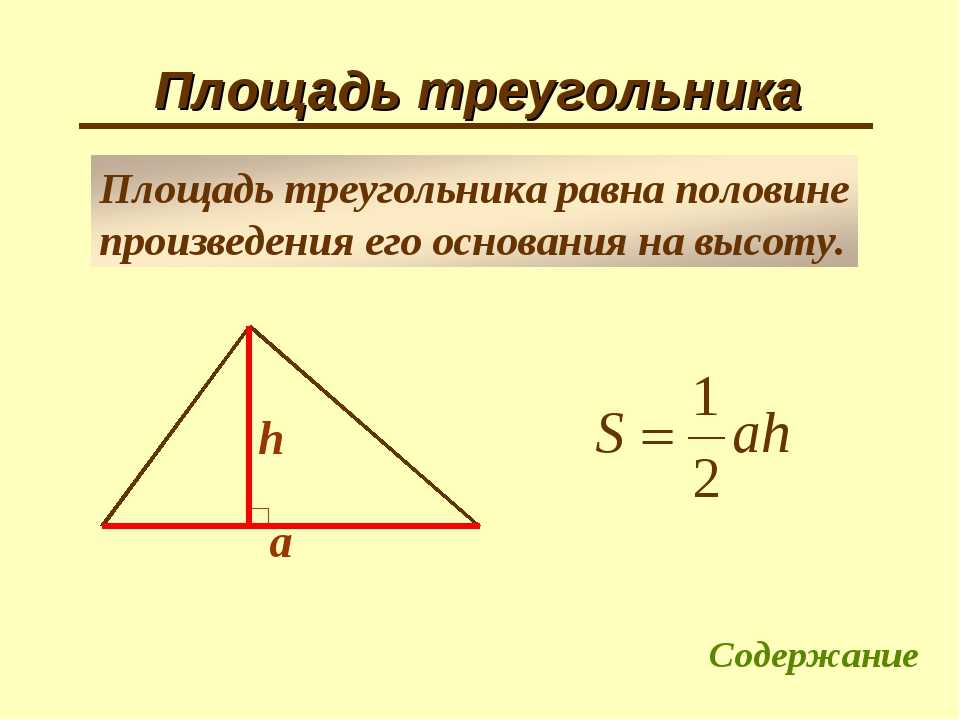

 Нельзя совсем исключить треугольники и в области архитектуры — тому тоже немало примеров.
Нельзя совсем исключить треугольники и в области архитектуры — тому тоже немало примеров.