Точки 1 и 2 базовые, размещаются с определенным задаваемым шагом. В скрипте Scilab это переменная step. Координаты точки 3 будем вычислять таким образом, чтобы в ней было максимальное отклонение синуса ( или косинуса ) от отрезка 1-2.
Ниже приведены скрипты на Scilab для расчета коэффициентов полинома второй степени на интервале [ 0 … pi /2] и графики отклонений для от функций синуса и косинуса .
Расчет коэффициентов для синуса на Scilab
/// синус
function [a,b,c]= koef_parabola(x1,y1,x2,y2,x3,y3)
/// расчет коэффициентов параболы по 3 точкам
a1= y3 - ( x3*(y2-y1)+ x2*y1 -x1*y2 )/( x2-x1)
a2= x3*( x3-x1-x2 ) + x1*x2
a= a1 /a2
b =( y2-y1)/( x2-x1) - a*( x1+x2)
c=( x2*y1 - x1*y2) / (x2-x1) + a * x1*x2
endfunction
kol_int =12 /// количество интервалов на отрезке 0 ... %pi/ 2
kol_funct =kol_int+1
step =%pi/ ( 2*kol_int) /// шаг
point0_x =0:step:%pi/ 2
point0_sin = cos(point0_x)
aa_sin =1:1:(kol_int)
bb_sin =1:1:(kol_int)
cc_sin =1:1:(kol_int)
xx1=0
yy1=1
for ii=1:1:kol_int
xx2=xx1+step
yy2=cos(xx2)
wsp1 =(yy2-yy1)/(xx2-xx1) /// наклон
xx3=asin(-wsp1) /// координаты центральной точки
yy3= sqrt( 1- wsp1^2) /// cos(xx3)
[aa,bb,cc]=koef_parabola( xx1,yy1,xx2,yy2,xx3,yy3)
aa_sin(ii)=aa
bb_sin(ii)=bb
cc_sin(ii)=cc
xx1=xx2
yy1=yy2
end
///вывод шага и коэффициентов
disp( step,aa_sin,bb_sin,cc_sin)
xx1=0
xx2=step
for ii=1:1:kol_int
int01=[xx1:0. 2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end
2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
endПример отклонений для синуса
график отклонений полинома второй степени от синуса на интервале 0 … Пи/ 2 при разбиении на 8 интервалов ( размер интервала =Пи/ 16 примерно = 0.196 )
Расчет коэффициентов для косинуса на Scilab
function [a, b, c]=koef_parabola(x1, y1, x2, y2, x3, y3)
/// расчет коэффициентов параболы по 3 точкам
a1= y3 - ( x3*(y2-y1)+ x2*y1 -x1*y2 )/( x2-x1)
a2= x3*( x3-x1-x2 ) + x1*x2
a= a1 /a2
b =( y2-y1)/( x2-x1) - a*( x1+x2)
c=( x2*y1 - x1*y2) / (x2-x1) + a * x1*x2
endfunction
kol_int =12 /// количество интервалов на отрезке 0 ... %pi/ 2
kol_funct =kol_int+1
step =%pi/ ( 2kol_int) /// шаг
point0_x =0:step:%pi/ 2
point0_sin = cos(point0_x)
aa_sin =1:1:(kol_int)
bb_sin =1:1:(kol_int)
cc_sin =1:1:(kol_int)
xx1=0
yy1=1
for ii=1:1:kol_int
xx2=xx1+step
yy2=cos(xx2)
wsp1 =(yy2-yy1)/(xx2-xx1) /// наклон
xx3=asin(-wsp1) /// координаты центральной точки
yy3= sqrt( 1- wsp1^2) /// cos(xx3)
[aa,bb,cc]=koef_parabola( xx1,yy1,xx2,yy2,xx3,yy3)
aa_sin(ii)=aa
bb_sin(ii)=bb
cc_sin(ii)=cc
xx1=xx2
yy1=yy2
end
///вывод шага и коэффициентов
disp( step,aa_sin,bb_sin,cc_sin)
xx1=0
xx2=step
for ii=1:1:kol_int
int01=[xx1:0. 2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end
2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
endПример отклонений для косинуса
график отклонений полинома второй степени от синуса на интервале 0 … Пи/ 2 при разбиении на 12 интервалов
Синус таблица коэффициентов полинома степени 2 для 8 интервалов
( шаг Пи / 16 )
Я не привожу кода на каком либо языке или псевдокода, дабы не засорять публикацию, каждый желающий может подобрать себе коэффициенты полинома степени 2 для аппроксимации и написать свою функцию. По значению аргумента x вычисляем номер интервала, запоминаем коэффициенты и подставляем из в формулу полинома
соз(х) | функция косинуса
cos(x), функция косинуса.
- Определение косинуса
- График косинуса
- Правила косинуса
- Функция арккосинуса
- Таблица косинусов
- Калькулятор косинуса
Определение косинуса
В прямоугольном треугольнике ABC синус α, sin(α) равен определяется как отношение между стороной, примыкающей к углу α, и сторона, противоположная прямому углу (гипотенуза):
cos α = B / C
Пример
B = 3 «
C = 5″
COS α = B / C = 3 /5 = = B / C = 3 /5 = B / C = 3 /5 = B / C = 3 /5 = B / C = 3 /5 = B / C = 3 /5 = B / CS = . TBD Арккосинус x определяется как функция арккосинуса x, когда -1≤x≤1. Когда косинус y равен x: cos y = x Тогда арккосинус x равен функции арккосинуса x, которая равна y: arccos5 x = cos -1 х = у arccos 1 = cos -1 1 = 0 рад = 0° См.: Функция Arccos 7 (рад) Создано Артуро Баррантесом Отзыв от доктора медицинских наук, кандидата наук Доминики Смялек Последнее обновление: 05 октября 2022 г. Мощный калькулятор косинуса треугольника (также «вычисление косинуса») — это инструмент, который определяет косинус угла, который может быть выражен в градусах, радианах или пи-радианах. Интересно, как вы решите домашнее задание по тригонометрии? Не волнуйся. В этой статье мы объясним, что такое косинус, как его вычислить, и покажем несколько примеров. Косинус угла — это тригонометрическая функция, которая связывает обе стороны треугольника, образующие угол. Лучше пояснить на картинке: Как видите, α\alphaα — это угол между стороной bbb и стороной ccc треугольника. Тогда косинус альфы — это деление между bbb и ccc. Обратите внимание, что ccc — это гипотенуза треугольника. Таким образом, определение косинуса можно выразить следующим образом: В прямоугольном треугольнике косинус — это тригонометрическая функция, которая делит одну сторону угла и гипотенузу. Эта сторона и гипотенуза составляют угол, о котором мы говорим. Вычислить косинус довольно просто. Вы можете использовать наш калькулятор косинуса или сделать следующее: cos(α)=bccos(\alpha)=\frac{b}{c}cos(α)=cb Это 0,866. Кроме того, это квадратный корень из трех, разделенный на 2. Как? Попробуйте калькулятор косинусного треугольника Omnicalculator или сделайте следующее: Поскольку вы уже знаете, как использовать этот калькулятор косинуса, вы можете взглянуть на другие калькуляторы: Попробуйте инструмент Omnicalculator калькулятор косинуса треугольника или сделайте следующее: График косинуса
График косинуса Правила косинуса
Название правила Правило Симметрия Симметрия cos(90°- θ ) = грех θ Пифагорейское тождество грех 2 (α)
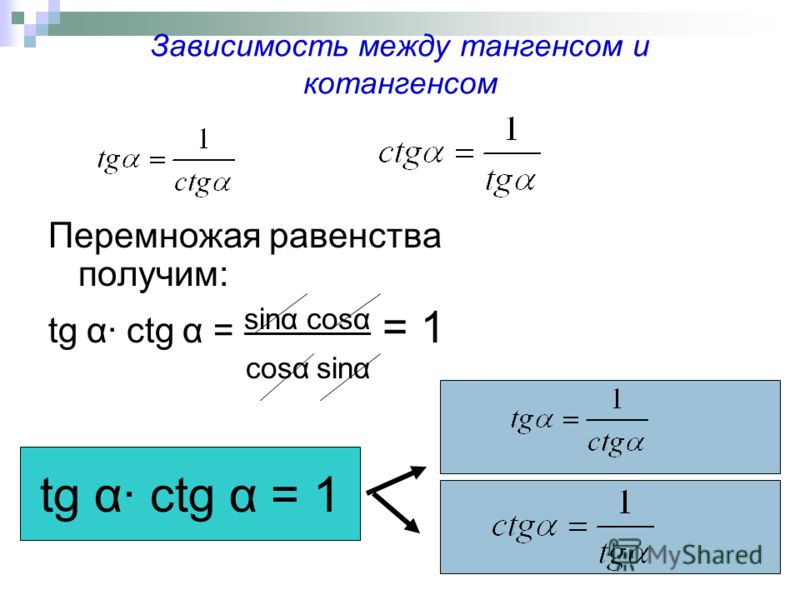
+ cos 2 (α) = 1 cos θ = sin θ / тангенс θ cos θ = 1/сек θ Двойной уголок cos 2 θ = cos 2 θ — sin 2 θ Сумма углов cos( α+β ) = cos α cos β — грех α грех β Разница углов cos( α-β ) = cos α cos β + sin α грех β Сумма к произведению cos α + cos β = 2 cos
[( α+β )/2] cos [( α-β )/2] Отличие от продукта cos α — cos β = — 2 sin
[( α+β )/2]
грех [( α-β )/2] Закон косинусов Производная cos’ x = — sin x Интеграл ∫ cos x d x = sin x + C Формула Эйлера , потому что х = ( e ix + e — ix ) / 2 Функция арккосинуса

Пример
Таблица косинусов
x 90
x соз х 180° № -1 150° 5π/6 -√3/2 135° 3π/4 -√2/2 120° 2π/3 -1/2 90° №/2 0 60° №/3 1/2 45° №/4 √2/2 30° №/6 √3/2 0° 0 1 См.
 также
также Калькулятор косинуса треугольника
Что такое косинус в тригонометрии?
Как вычислить косинус угла?
 Результат — косинус угла. Значение ноты никогда не может превышать 1.
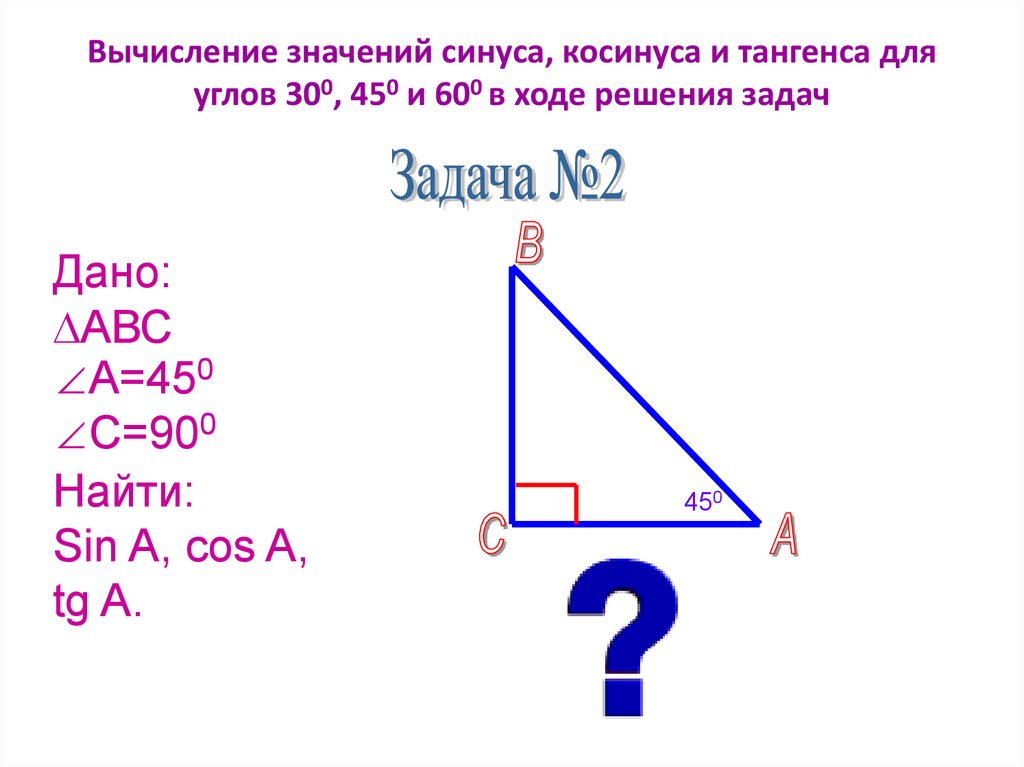
Результат — косинус угла. Значение ноты никогда не может превышать 1. Пример косинусного треугольника. Чему равен косинус 30 градусов?
Другие полезные инструменты, такие как калькулятор косинуса треугольника
Часто задаваемые вопросы
Как получить косинус угла?

 2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end
2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end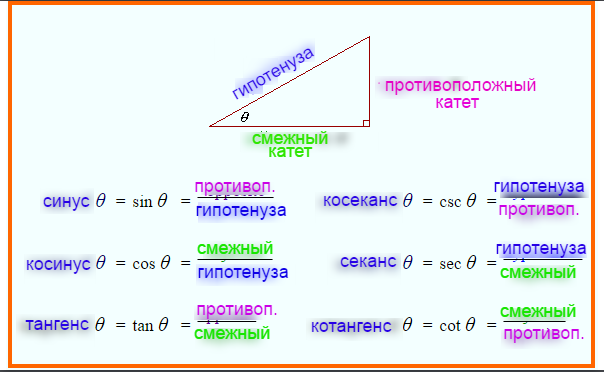 2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end
2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end