Разложение вектора по двум неколлинеарным векторам
Автор Ольга Андрющенко На чтение 6 мин. Просмотров 127 Опубликовано
Вы узнаете в этой статье что значит разложить вектор по двум неколлинеарным векторам.
Представление вектора \vec{c} в виде \vec{c}=x \vec{a}+y \vec{b}, где векторы \vec{a} и \vec{b} являются неколлинеарными векторами, называется разложением вектора по двум неколлинеарным векторам.
Теорема (о разложении вектора по двум неколлинеарным векторам)
Теорема. Любой вектор с можно единственным образом представить в виде \vec{c}=x \vec{a}+y \vec{b}, где \vec{a} и \vec{b} — неколлинеарные векторы, х и у — числа.
Коллинеарные вектора \vec{m} и \vec{n} — это такие вектора, где один из векторов параллелен другому и связан с ним соотношением
\vec{m}=k\vec{n}
Доказательство:
Пусть даны векторы \vec{c}=\overrightarrow{AB}, \vec{a} и \vec{b}. Проведем через точки A и B прямые, параллельные векторам \vec{a} и \vec{b}, и обозначим точку C их пересечения. Тогда \overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}.
Проведем через точки A и B прямые, параллельные векторам \vec{a} и \vec{b}, и обозначим точку C их пересечения. Тогда \overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}.
К теореме о разложении вектора по двум коллинеарным векторам
Так как векторы \vec{a} и \overrightarrow{AC} коллинеарные, то существует такое число х, что \overrightarrow{AC} =х\vec{a}. Векторы \vec{b} и \overrightarrow{CB} тоже коллинеарные, следовательно, существует такое число у, что \overrightarrow{CB} =y\vec{b}.
Таким образом, \vec{c}=x \vec{a}+y \vec{b}.
Докажем единственность такого представления вектора с способом от противного. Допустим, что имеется другое разложение вектора, например, такое:
\vec{c}=n \vec{a}+m \vec{b}, тогда два разложения вектора \vec{c} можно приравнять:
n \vec{a}+m \vec{b}=x \vec{a}+y \vec{b} (если равны левые части равенств, то равны и правые).
Перенесем все в левую часть равенства:
n \vec{a}+m \vec{b}-x \vec{a}-y \vec{b}=0
(n-x)\vec{a}+(m-y) \vec{b}=0
\displaystyle \vec{a}=\frac{y-m}{n-x} \vec{b}
То есть векторы \vec{a} и \vec{b} получаются коллинеарными. А у нас условие — векторы \vec{a} и \vec{b} — неколлинеарные вектора.
А у нас условие — векторы \vec{a} и \vec{b} — неколлинеарные вектора.
Таким образом, возможно только единственно возможное представление вектора \vec{c} в виде \vec{c}=x \vec{a}+y \vec{b}, где векторы \vec{a} и \vec{b} являются неколлинеарными векторами.
Теорема доказана.
Если вектор \vec{c} коллинеарен какому-либо из векторов \vec{a} и \vec{b}, то либо число x, либо число y равно нулю.
Базис векторов и разложение вектора по базису
В декартовой системе координат Oxy вектор с координатами (x, y) можно разложить по единичным векторам \vec{e_1}(1;0) и \vec{e_2}(0;1).
Тогда, например, вектор \vec{c}(3; -1) можно представить в виде разложения:
\vec{c}=x \vec{e_1}+y \vec{e_2}=3 \vec{e_1}-1 \vec{e_2}
Действительно:
\begin{cases} 3=3 \cdot 1+(-1)\cdot 0, \\ — 1=3 \cdot 0+(-1)\cdot 1. \end{cases}
Система векторов, по которым можно разложить вектор с коэффициентами разложения равными его координатам, называется базисом вектора.
Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.
Однако, это не отменяет тот факт, что вектор можно разложить и по другим векторам, то есть по новому базису. Тогда говорят о переходе к новому базису векторов.
Обычно в декартовой системе координат базисные векторы на плоскости обозначают так: \vec{i}(1;0) и \vec{j}(0;1).
В пространственной декартовой системе координат базис векторов будет: \vec{i}(1; 0; 0), \vec{j}(0;1; 0), \vec{k}(0;0;1)
В то же время на любых векторах можно построить свою систему отсчета, тогда данные вектора будут считаться базисом этой системы и в этой системе можно найти координаты любого вектора. То есть любой вектор можно разложить по базису, конечно, если при этом базисные вектора не являются коллинеарными.
Примеры разложения вектора
Пример 1. Разложить вектор \vec{c}(0; 1) по двум векторам \vec{a}(3; 6) и \vec{b}(4; 9).
Решение:
Для разложения вектора \vec{c} запишем:
\vec{c}=x \vec{a}+y \vec{b}
Нам нужно найти коэффициенты разложения x и y, для этого разложим каждую координату вектора \vec{c}:
- Для абсциссы: 0=x \cdot 3+y \cdot 4
- Для ординаты: 1=x \cdot 6+y \cdot 9
Получаем систему из двух уравнений с двумя неизвестными, которую решаем:
\begin{cases} 3x+4y=0, \\ 6x+9y=1. \end{cases}
Решая, получаем: \displaystyle x=\frac{-4}{3} и y=1
И разложение вектора \vec{c} будет иметь вид: \displaystyle \vec{c}=-\frac{4}{3} \vec{a}+\vec{b}
Пример 2. Найти координаты вектора \vec{a} в базисе, если известно разложение вектора по базису \vec{e_1} и \vec{e_2}:
\vec{a}=7 \vec{e_1}+5 \vec{e_2}
Решение: Координаты вектора в базисе векторов \vec{e_1} и \vec{e_2} будут равны коэффициентам разложения, то есть \vec{a}(7; 5)
Ответ: \vec{a}(7; 5)
Пример 3. Разложить вектор \vec{b}(1; 2) по базису \vec{e_1}(2; 3) и \vec{e_2}(2; 5).
Разложить вектор \vec{b}(1; 2) по базису \vec{e_1}(2; 3) и \vec{e_2}(2; 5).
Решение:
Запишем разложение вектора по базису:
\vec{b}=b_1 \vec{e_1}+b_2 \vec{e_2}
Получим систему уравнений:
\begin{cases} 1=2b_1+4b_2, \\ 2=2b_1+5b_2. \end{cases}
От второго уравнения системы отнимем первое, получим:
\begin{cases} 1=b_2, \\ 2=2b_1+5b_2. \end{cases}
Тогда:
\begin{cases} b_2=1, \\ b_1=-1,5. \end{cases}
И разложение вектора будет иметь вид: \vec{b}=-1,5 \vec{e_1}+\vec{e_2}
Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)
Помощь в написании работы
О чем статья
Базис векторов
Система линейно независимых векторов пространства, за которыми можно разложить произвольный вектор – это и есть базис векторов или этого пространства.
Так, согласно доказательству (3), произвольные три некомпланарные векторы , , , образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор пространства. Векторы , , , которые образуют базис называются базисными.
Векторы , , , которые образуют базис называются базисными.
Будем считать, что базисные векторы , , сведены к точке .
Числ , про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:
.
Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.
Базисным вектором на прямой линии может быть любой ненулевой вектор.\Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:
- .
- .
- .
Обратите внимание!
Векторы равны, когда у них одинаковые соответствующие координаты.
Линейные действия над векторами аналитическим путём
Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:
Давайте вспомним и сформулируем линейные действия:
Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть:
Приведём пример:
Пример 1
Найти сумму векторов и , заданных на плоскости .
Решение:
Согласно правилу 1 у нас получается:
= (6, 3).
Построим эти векторы: .
Рис. 3
Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.
Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:
Пример 2
Дан вектор Найти
Решение:
Согласна правилу 2 у нас получается:
Геометрическое изображение смотрите на рис. 4.
4.
Рис. 4
Два вектора равны, если у них равны соответствующие координаты:
.
Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.
Как найти базис вектора, пример
Пример 1
В некотором базисе заданы своими координатами векторы и Разложить вектор по базису, который образовался из векторов и
Решение:
Разложение вектора по базису и имеет такой вид:
где числа и – неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов и , а тогда воспользуемся свойствами 1 и 2:
Согласно свойству 3 про равенство векторов, получим систему уравнений:
Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:
.
Значит, ответ у нас выходит:
Средняя оценка 0 / 5. Количество оценок: 0
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
5818
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Помощь в написании работы
Проекция на подпространство
Рисунок 1
Пусть S — нетривиальное подпространство векторного пространства V , и предположим, что v — вектор в V , не лежащий в S .
60010 параллелен S и v ⊥ S ортогонален S ; см. рисунок .
Vector V ‖ S , который фактически находится в в S , называется Projection из В на S , также обозначал Proj S 1 V . Если v 1 , v 2 , …, v r образуют ортогональный базис для S , тогда проекция v на S является суммой проекций v на отдельные базисные векторы, факт, который критически зависит от ортогональные базисные векторы:
На рисунке геометрически показано, почему эта формула верна в случае двумерного подпространства S в R 3 .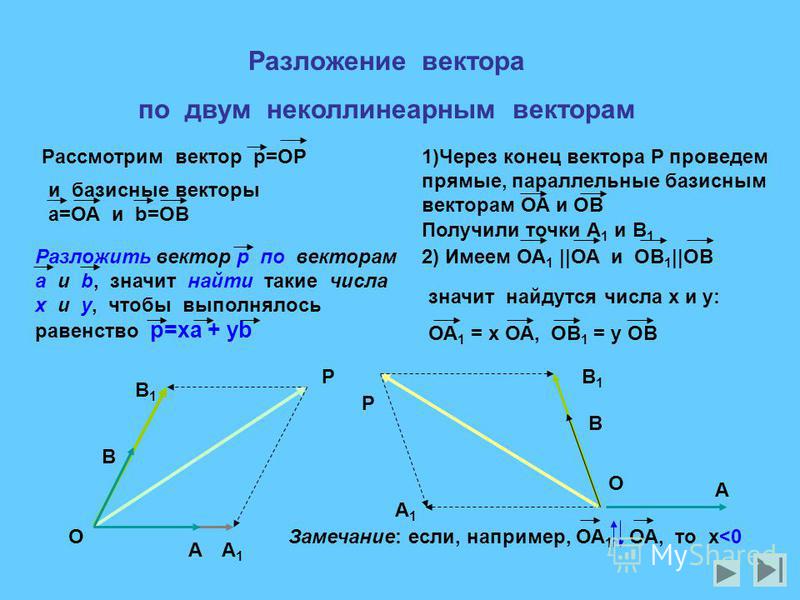
Рисунок 2
Пример 1 : Пусть S будет двумерным подпространством R 3 , натянутым на ортогональные векторы v 1 = (1, 2, 1) и 6
1, −1, 1). Запишите вектор v = (−2, 2, 2) как сумму вектора в S и вектора, ортогонального S .Из (*) проекция v на S есть вектор
Следовательно, v = v ‖ S где v ‖ S = (0, 2, 0) и
То, что v ⊥ 6 и 2 : Таким образом, уникальное представление вектора v как сумма вектора в S и вектора, ортогонального S , читается следующим образом: См. Пример 2 : Пусть S будет подпространством евклидова векторного пространства V . Набор всех векторов в V , которые ортогональны каждому вектору в S , называется ортогональным дополнением к S : ( S ⊥ читается как «S perp.») Покажите, что S ⊥ также является подпространством V . Доказательство . Во-первых, заметим, что S ⊥ не пусто, поскольку 0 ∈ S ⊥ . Чтобы доказать, что S ⊥ является подпространством, необходимо установить замыкание относительно векторного сложения и скалярного умножения. Пусть v 1 и v 2 быть векторами в S ⊥ ; v 1 · s = v 2 · s = 0 для каждого вектора s в S , 3  рис.
рис.
Рисунок 3
доказывает, что v 1 + v 2 ∈ S ⊥ . Следовательно, S ⊥ замкнуто относительно сложения векторов. Наконец, если
Следовательно, S ⊥ замкнуто относительно сложения векторов. Наконец, если
Пример 3 : Найти ортогональное дополнение плоскости x−y в R 3 .
На первый взгляд может показаться, что плоскость x−z является ортогональным дополнением плоскости x−y , так же как стена перпендикулярна полу. Однако не каждый вектор в плоскости x−z ортогонален каждому вектору в плоскости x−y : например, вектор v = (1, 0, 1) в плоскости x−z .

Рисунок 4
Пример 4 : Пусть P будет подпространством R 3 , заданным уравнением 2 x + y = 2 z = 0. Найдите расстояние между 0 90 P и 9000 точкой. д = (3, 2, 1).
Подпространство P явно является плоскостью в R 3 , а q является точкой, не лежащей в P . Из рисунка видно, что расстояние от q 9От 0006 до P — это длина компонента q , ортогонального к P .
Рисунок 5
Один из способов найти ортогональный компонент q ⊥ P состоит в том, чтобы найти ортогональный базис для P , использовать эти векторы для проецирования вектора q на P , а затем сформировать разность 9 − proj P q для получения q ⊥ P . Здесь проще спроецировать q на вектор, который, как известно, ортогонален P . Поскольку коэффициенты x, y и z в уравнении плоскости обеспечивают компоненты вектора нормали к P , n = (2, 1, −2) ортогонален P . Теперь, с
Здесь проще спроецировать q на вектор, который, как известно, ортогонален P . Поскольку коэффициенты x, y и z в уравнении плоскости обеспечивают компоненты вектора нормали к P , n = (2, 1, −2) ортогонален P . Теперь, с
расстояние между P и точкой q равно 2.
Алгоритм ортогонализации Грама-Шмидта . Преимущество ортонормированного базиса очевидно. Компоненты вектора относительно ортонормированного базиса очень легко определить: достаточно простого вычисления скалярного произведения. Вопрос в том, как получить такую основу? В частности, если  ключ к алгоритму.
ключ к алгоритму.
Пример 5 : Преобразование базиса B = { v 1 = (4, 2), v 2 = (1, 2)} для R 2 в ортонормированный .
Первый шаг — сохранить v 1 ; позже нормализуется. Второй шаг — проект V 2 на подпространство, охватываемое V 1 , а затем сформируйте разницу V 2 — Proj V1 V 2 = v1 V 2 = V1 V 2 = V1 V 2 . ⊥1 Начиная с
компонент вектора v 2 ортогональный к v 1 это
, как показано на рисунке .
Рисунок 6
Векторы v 1 и v ⊥1 теперь нормализованы:
Таким образом, базис B = { v 1 = (4, 2), v 2 = (1, 2)} преобразуется в ортонормированный базис
, показанный на рисунке .
Рисунок 7
Предыдущий пример иллюстрирует алгоритм ортогонализации Грама-Шмидта для базиса B , состоящего из двух векторов. Важно понимать, что этот процесс не только создает ортогональный базис B ′ для пространства, но также сохраняет подпространства . То есть подпространство, натянутое на первый вектор в B ′, совпадает с подпространством, натянутым на первый вектор в B ′ и пространство, натянутое на два вектора в B ′ , такое же, как подпространство, натянутое на два вектора в B .
В целом, алгоритм ортогонализации грамм -шмидта, который преобразует базис, B = { V 1 , V 2 ,…, V R , …, V R , Aче пробел V в ортогональный базис, B ′ { w 1 , w 2 ,…, w r }, для V — при сохранении подпространств по пути — действует следующим образом:
Шаг 1. Установите w 1 равным v 1
Установите w 1 равным v 1
Шаг 2. Спроектируйте v 2 на S 1 , пространство охватывает w 1 ; затем сформируйте разницу v 2 − proj S 1 v 2 Это w 2 .
Шаг 3. Спроектируйте v 3 на S 2 , пространство между w 1 и w 2 ; затем образуем разность v 3 − proj S 2 v 3 . Это w 3 .
Шаг и . Проект v i на S i −1, пространство охватывает w 1 , …, w − 90; Затем сформируйте разницу V I — Proj S I −1 V I . Этот процесс продолжается до этапа r , когда w r сформировано и ортогональный базис завершен. Если требуется ортонормированный базис , нормализуйте каждый из векторов w i . Пример 6 : Пусть H будет трехмерным подпространством R 4 с базой Найдите ортогональный базис для H , а затем — путем нормализации этих векторов — ортонормированный базис для Н . Каковы компоненты вектора x = (1, 1, −1, 1) относительно этого ортонормированного базиса? Что произойдет, если вы попытаетесь найти компоненты вектора y = (1, 1, 1, 1) относительно ортонормированного базиса? Первым шагом является установка w 1 равным v 1 . компонент вектора v 2 ортогональный w 1 равен Теперь последний шаг: проект v 3 на подпространство S 2 , натянутое на w 1 и w  Это w i .
Это w i .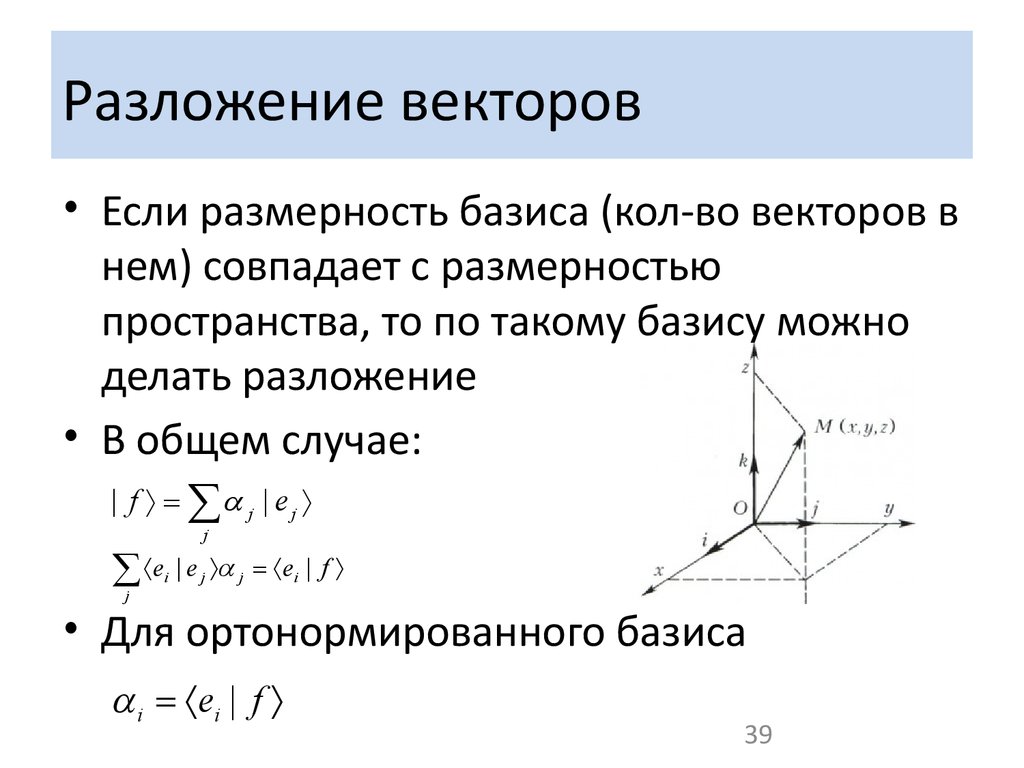 Второй шаг состоит в том, чтобы спроецировать v 2 на подпространство, натянутое на w 1 , а затем сформировать разность 9. С
Второй шаг состоит в том, чтобы спроецировать v 2 на подпространство, натянутое на w 1 , а затем сформировать разность 9. С С
С
и
и { w 1 , w 2 } является ортогональным базисом для S 2 , проекция v 3 на S 2 равна
Это дает
Таким образом, процесс Грама-Шмидта дает из B следующий ортогональный базис для H :
Вы можете убедиться, что эти векторы действительно ортогональны, проверив, что w 1 · w 2 = w 1 · w 3 = w 2 · w 3 = 0 и что подпространства сохраняются по пути:
Ортонормированный базис для H получается путем нормализации векторов w 1 , w 2 и w 3 :
Относительно ортонормированного базиса B » = { х 1 , х 2 , х 3 }, вектор x = (1, 1, −1, 1) имеет компоненты
Из этих расчетов следует, что
результат, который легко проверить.
Если компоненты y = (1, 1, 1, 1) относительно этого базиса желательны, вы можете действовать точно так же, как указано выше, находя
Из этих расчетов следует, что
Проблема, однако, в том, что это уравнение неверно, как показывает следующий расчет:
Что пошло не так? Проблема в том, что вектор y не находится в H , поэтому никакая линейная комбинация векторов в любом базисе для H не может дать y . Линейная комбинация
дает только проекцию y на H .
Пример 7 : Если строки матрицы образуют ортонормированный базис для R n , то говорят, что матрица равна ортогональный . (Термин ортонормированный был бы лучше, но терминология теперь слишком устоялась.) Если A является ортогональной матрицей, покажите, что A −1 = A T .
let B = { Vˆ 1 , Vˆ 2 ,…, Vˆ N } Будь ортонормальной базой для R 9009 n и CART MATRIC 110 и.0009 A , строки которого являются этими базисными векторами:
Матрица A T имеет следующие базисные векторы в качестве столбцов:
Поскольку векторы vˆ 1 , vˆ 2 , …, vˆ n ортонормированы,
Теперь, поскольку запись ( i, j ) произведения AA T является скалярным произведением строки i в A и столбец j в A T ,
Таким образом, A −1 = A T . [На самом деле утверждение A −1 = A T иногда принимают за определение ортогональной матрицы (из чего затем видно, что строки A образуют ортонормированный базис для ). Р п ).]
[На самом деле утверждение A −1 = A T иногда принимают за определение ортогональной матрицы (из чего затем видно, что строки A образуют ортонормированный базис для ). Р п ).]
Теперь легко следует дополнительный факт. Предположим, что A является ортогональным, поэтому A −1 = A T . Обратное значение обеих частей этого уравнения дает
, из чего следует, что A T ортогонален (поскольку его транспонирование равно его инверсии). Заключение
означает, что , если строки матрицы образуют ортонормированный базис для R n , , то и столбцы .
python — Смена базы в numpy
Задай вопрос
спросил
Изменено 1 месяц назад
Просмотрено 11 тысяч раз
Даны две базисные матрицы base_old и base_new в numpy, есть ли где-нибудь в библиотеке функция для получения матрицы преобразования для преобразования вектора vec в base_old в его представление в base_new ?
Например, если у меня есть вектор vec = [1,2,3] в стандартном базисе [1,0,0], [0,1,0], [0,0,1] , как мне преобразовать его в другую базу, скажем,
e1 = [1 0 0] е2 = [0 0 1] е3 = [0 1 0] base_new = np.array([e1, e2, e3]) # Я хочу что-то вроде этого vec_new = np.linalg.change_of_basis (vec_old, base_old, base_new) # Или это: transform_matrix = np.linalg.basis_change (базис_старый, базис_новый)
Редактировать: изменено basic_new, чтобы быть линейно независимым
- python
- numpy
- линейная алгебра
5
Вспомните, что означает, что набор векторов w1, w2, w3 является базисом R3.
w должны быть линейно независимыми . Это означает, что единственным решением для x1 w1 + x2 w2 + x3 w3 = 0 должно быть x1 = x2 = x3 = 0. Но в вашем случае вы можете убедиться, что x1 = 1, x2 = -2, x3 = 1 является другим решением . Итак, ваш
base_newнедействителен.Матрица W = [w1, w2, w3] должна быть обратимой.
Для каждого вектора в R3 должен быть уникальный способ записать его как линейную комбинацию w.


 Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.
Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.