Краткий курс высшей математики
Краткий курс высшей математики
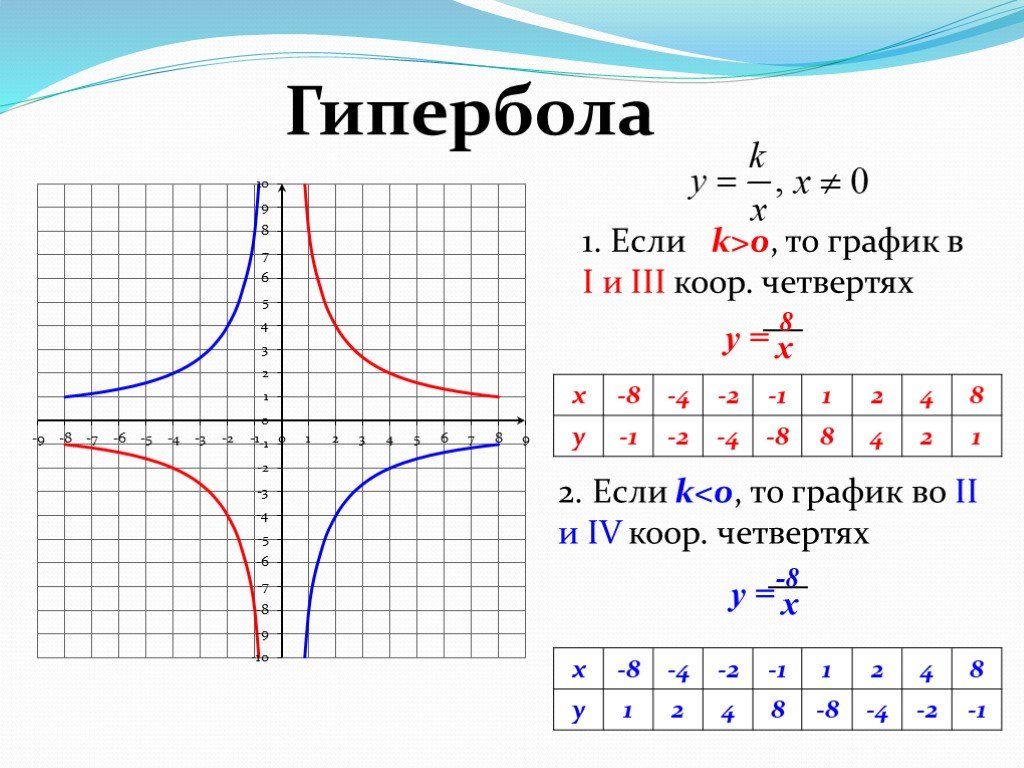
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа  Расстояние между двумя точками на прямой§ 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4.  Общее уравнение прямой и его частные случаи5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8. Пучок прямых 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3.  Понятие об определителях высших порядков§ 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2.  Равенство матриц. Действия над матрицами3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. 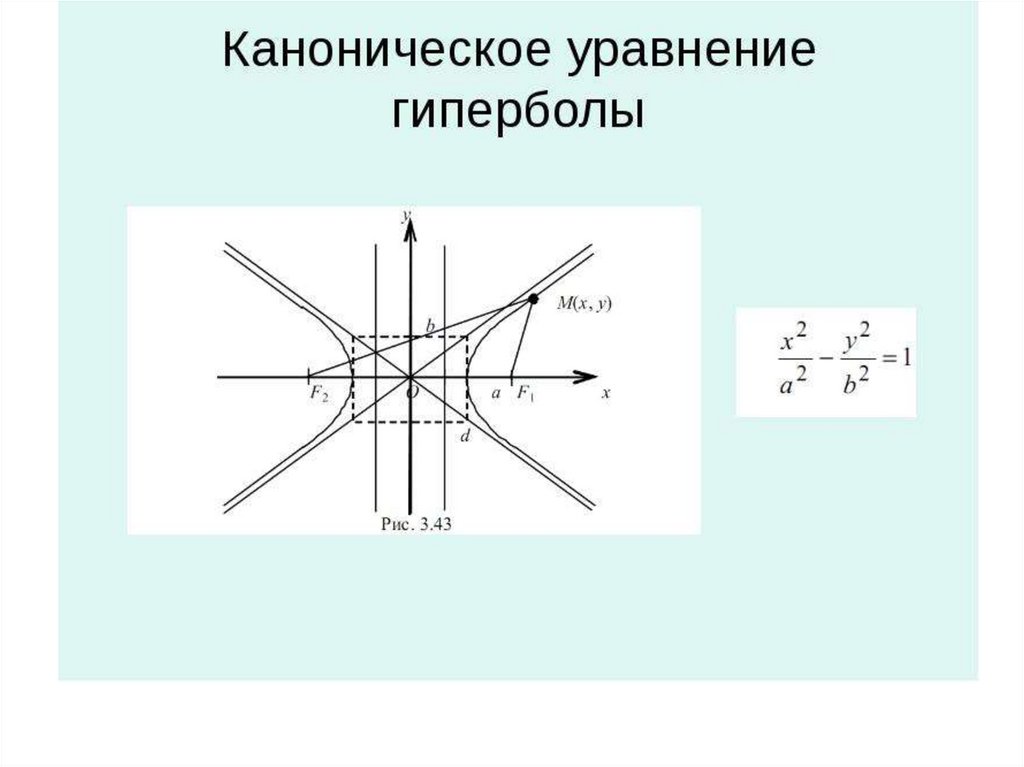 Прямая и плоскость в пространстве2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. 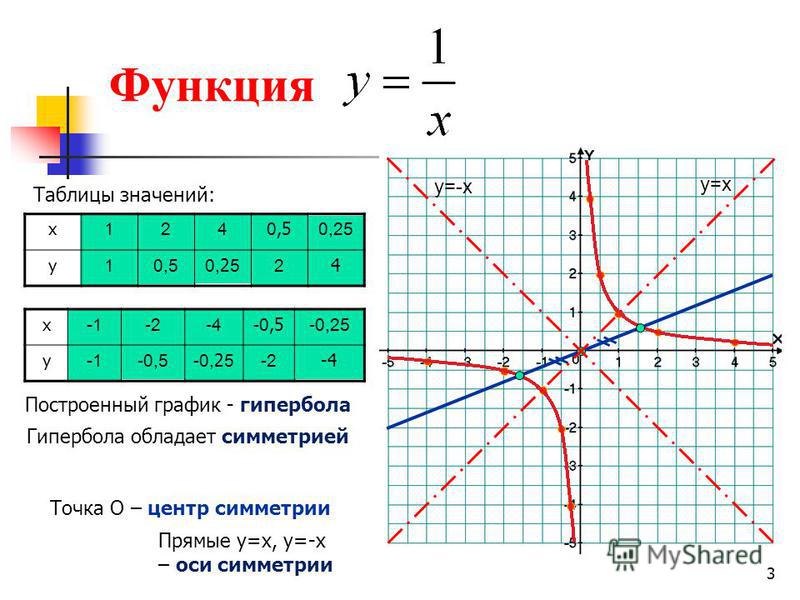 Понятие о гиперболических функцияхГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 4. Определение производной и ее механический смысл 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2.  Механический смысл второй производной§ 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 4.  Отыскание наибольшего и наименьшего значений функции5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5.  Метод неопределенных коэффициентов6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. 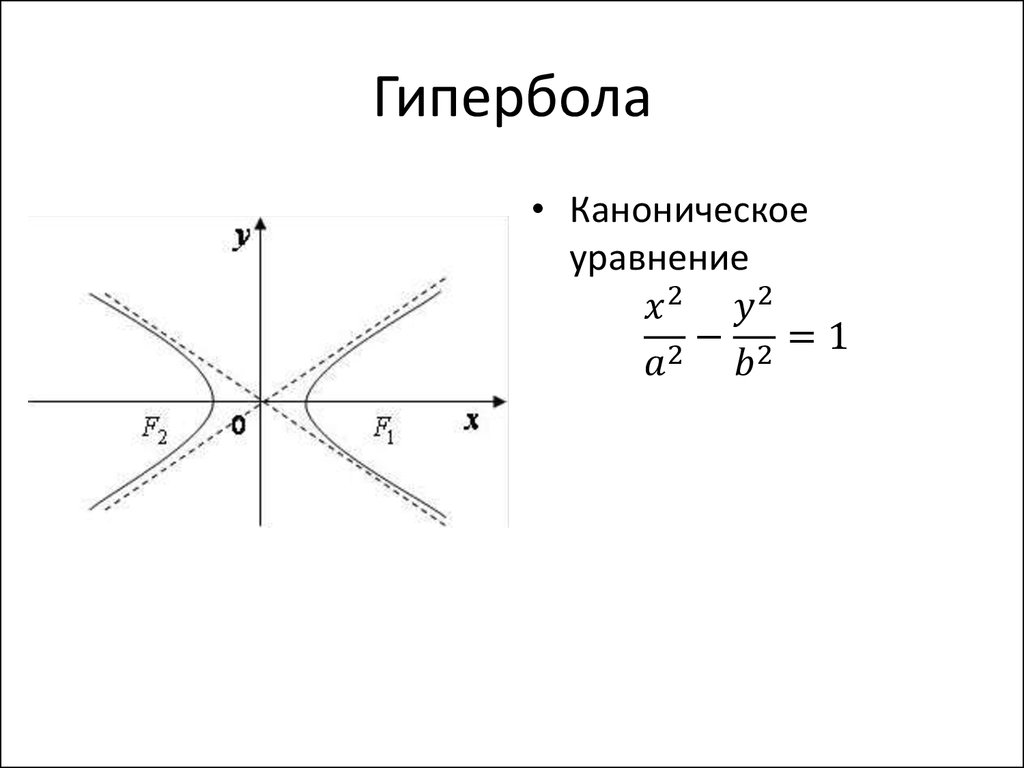 Вычисление объема тела по известным поперечным сечениям4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4.  Точки разрыва5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4.  Вычисление двойного интеграла в декартовых координатах5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2.  ФУНКЦИОНАЛЬНЫЕ РЯДЫ2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7.  Особые решения8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6.  ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ§ 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ |
«Гипербола» перешла на EDI.Контур с 80 % поставщиков — Контур.EDI — СКБ Контур
Сегодня гипермаркет работает через систему электронного заказа EDI.Контур со 154 из 190 поставщиков. До конца 2016 года «Гипербола» намерена перевести в электронный вид взаимоотношения с 95 % поставщиков.
Предпосылки
«Гипербола» — это уникальный для Урала проект. Сегодня он включает два крупных продуктовых гипермаркета в Екатеринбурге, при создании которых учтен лучший мировой опыт ритейла. У «Гиперболы» 193 поставщика. Документы гипермакета формируются в товароучетной системе Gestori. До внедрения EDI «Гипербола» использовала автозаказ.
Он базировался на фиксированном перечне товаров, сформированном на основе номенклатуры Gestori. При необходимости категорийный менеджер менял количество товара в заказе, и эта информация отправлялась поставщику. Стороны согласовывали номенклатуру, цены и количество. Четкой системы при этом не было. Времени уходило много, на приемке товара неизбежно появлялись расхождения, документооборот увеличивался, так как документы приходилось переделывать. Чтобы решить эти проблемы, в конце 2014 года было принято решение о переходе на электронный заказ EDI.
Задачи
С помощью EDI «Гипербола» планировала:
- выстроить четкий бизнес-процесс заказа: с момента его отправки до приемки товара и формирования закрывающих документов;
- обеспечить согласованные действия всех участников процесса заказа и приемки товара;
- сократить и упростить приемку товара;
- контролировать заказ и поставку на каждом этапе.
Дмитрий Рогулькин, руководитель отдела информационных технологий торговой сети «Гипербола»: «Выбирая провайдера, мы в первую очередь оценивали опыт: число и уровень реально запущенных и работающих решений документооборота.
Также для нас было важно, сколько в целом поставщиков успешно работают через данного провайдера. Выбор почти сразу пал на СКБ Контур. Он соответствовал нашим требованиям, у нас уже был положительный опыт взаимодействия на примере системы электронной отчетности Контур.Экстерн. Центральный офис СКБ Контур, как и наш, расположен в Екатеринбурге, это ускоряет и облегчает контакты наших IT-специалистов с разработчиками СКБ Контур».
Решение
Главная техническая часть проекта была реализована за три месяца. Большую часть этого времени IT-специалисты «Гиперболы» дорабатывали и тестировали терминалы сбора данных. Нужно было научить их и Gestori работать с заказами в новом формате.
Дмитрий Рогулькин: «При EDI поставка принимается по черновику товарной накладной. А раньше мы принимали товар по заказу. Нужно было доработать и настроить наше программное обеспечение. В частности, мы научили Gestori формировать заказ по новому принципу и обмениваться информацией с поставщиком через провайдера.
И мы доработали программное обеспечение терминалов сбора данных, чтобы они работали с новым типом заказов, подтвержденных поставщиком».
Полное техническое внедрение EDI.Контур в документооборот «Гиперболы» заняло полгода. Сейчас гипермаркет использует цепочку ORDERS-ORDRSP-DESADV-RECADV — [INVOIC] ЭСФ+ЭТОРГ12.
Категорийный менеджер отправляет поставщику заказ напрямую из Gestori, в которую загружены цены по договору поставки. Поставщик получает заказ, подтверждает или корректирует его и отправляет категорийному менеджеру «Гиперболы», чтобы он подтвердил. Весь обмен информацией происходит через товароучетные системы поставщика и сети, поэтому расхождения в номенклатуре, пропуски информации или ошибки сводятся практически к нулю.
Пилот
В пилотном проекте «Гиперболы» участвовали Хладокомбинат № 3, ТД «Сыробогатов», ООО «Прометей» и Уктусский молочный завод. С этими поставщиками, которые находятся в одном регионе с гипермаркетом, было удобно тестировать EDI.
Во время пилота сеть столкнулась с проблемами при отправке заказа по EDI и при получении подтверждения от поставщика. Чтобы их решить, пришлось исправлять алгоритм обработки EDI-сообщений в Gestori.
Также в этот период наглядно проявились ошибки, связанные с человеческим фактором на стороне поставщиков: нарушался регламент обмена, возникали сбои и т.д. Чтобы избежать этого, «Гипербола» внесла в договор дополнительный пункт о штрафных санкциях для поставщиков.
Дмитрий Рогулькин: «Большинство крупных и средних поставщиков приветствовали новый формат взаимодействия. С EDI им самим проще согласовывать заказы и отгружать товар. Но некоторые отреагировали негативно. Думаю, во многом это связано с тем, что автоматизация процессов повышает уровень ответственности сторон. Человеческим фактором уже не оправдаешься. Кроме того, мы заключили с поставщиками дополнительное соглашение о штрафных санкциях на случай, если поставка не соответствует заказу. Команда СКБ Контур плотно работала с поставщиками, поэтому их сотрудники довольно быстро научились работать с системой, не провоцировать сбои и соблюдать регламент».
После завершения пилота в течение 1,5 месяцев было подключено сразу около 70 поставщиков. Сейчас их число уже достигло 154.
Результаты
С помощью системы EDI.Контур «Гипербола» решила все задачи, которые поставила на старте проекта:
- Товар принимается быстро за счет того, что расхождения почти исчезли. Если раньше акты расхождений по причинам «отсутствует в заказе», «отсутствует в товароучетной системе», «недовоз» или «излишки» составляли 50 % все актов расхождений, то теперь причины «отсутствует в заказе» и «отсутствует в товароучетной системе» сократились до нуля. Число актов расхождений из-за «недовоза» и «излишков» сократилось более чем в три раза.
Дмитрий Рогулькин: «Надо понимать, что EDI — не средство от всех болезней, оно не избавит от спорных моментов, связанных с браком, боем или потерей товарного вида на этапе приемки. Также надо понимать, что даже после всех согласований не исключено, что грузчик на складе поставщика банально может что-то перепутать.
Но расхождения после внедрения EDI сокращаются очень значительно, прежде всего за счет того, что поставщик и заказчик при согласовании поставки говорят на одном языке. Если можно так выразиться, на формализованном языке обмена EDI-сообщениями».
- Нагрузка на штат приемщиков и операторов снижена, персонал переориентирован на другие задачи.
- В разы сократилось время, которое затрачивает бухгалтерия на сверку первичных документов с поставщиками.
Сейчас «Гипебола» завершает цепочку — внедряет электронные счета-фактуры и ТОРГ-12 — с теми поставщиками, которые уже четко и без сбоев работают с ней через EDI. Параллельно идет привлечение оставшихся поставщиков к работе через EDI.
retailer.ru
задач гиперболы | Superprof
Упражнение 1
Определите и постройте координаты фокусов и вершин и рассчитывайте эксцентричность следующих гиперболов:
1
2
3
4
Лучшие наставники математики.
go
Упражнение 2
Определите и начертите координаты фокусов и вершин и вычислите эксцентриситет следующих гипербол:
1
2
Упражнение 3
Вычислите уравнение гиперболы с поперечной осью 8 и фокусным расстоянием 10.
Упражнение 4
точка P = (8, 14). Найдите его уравнение.
Упражнение 5
Вычислите уравнение гиперболы с центром в точке (0, 0), фокусное расстояние которой равно 34, а расстояние от одного фокуса до ближайшей вершины равно 2,
Упражнение 6
Определите уравнение гиперболы с центром в точке (0, 0), проходящей через точки: и . .
Упражнение 7
Определите уравнение гиперболы с центром в точке (0, 0), которая проходит через точку и имеет эксцентриситет .
Упражнение 8
Определите уравнение гиперболы с центром в точке (0, 0), зная, что один фокус находится на расстоянии 2 единиц от одной вершины и 50 от другой.
Упражнение 9
Определите координаты точки (точек) пересечения прямой x + y − 1 = 0 и гиперболы .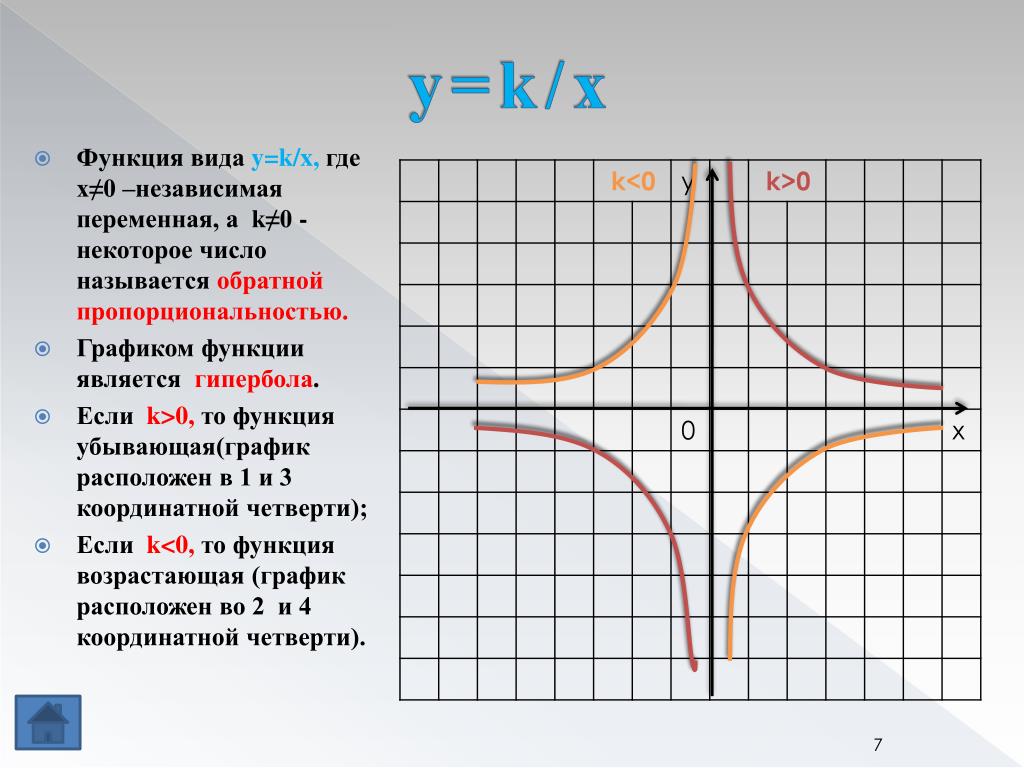
Упражнение 10
Прямоугольная гипербола проходит через точку . Найдите его уравнение и определите координаты вершин и фокусов.
Упражнение 11
Поперечная ось гиперболы равна 12, а эксцентриситет равен . Вычислите уравнение этой гиперболы.
Упражнение 12
Рассчитайте уравнение прямоугольной гиперболы, зная, что ее фокусное расстояние равно .
Упражнение 13
Длина сопряженной оси гиперболы равна 8, а уравнения асимптот таковы: . . Вычислите уравнение гиперболы, ее фокусы и вершины.
Решение упражнения 1
Определить и построить координаты фокусов и вершин и рассчитать эксцентриситет следующих гиперболов:
1
0003
2
3
Divide by 30:
4
Divide на 1296:
Раствор упражнения 2
Определение и график координат ски гиперболы:
1
2
Solution of exercise 3
Calculate the equation гиперболы с поперечной осью 8 и фокусным расстоянием 10,
Решение упражнения 4
Поперечная ось гиперболы составляет 12, а кривая проходит через точку P = (8, 14).
Найдите его уравнение.
Решение упражнения 5
Рассчитайте уравнение гиперболы, центрированное на (0, 0), фокусное расстояние, 34, а расстояние от одного фокуса до ближайшего вершины — 2 — 2
Решение упражнения 6
Определите уравнение гиперболы с центром в точках (0, 0), проходящей через точки (0, 0).
Решение упражнения 7
Определите уравнение гиперболы с центром в точке (0, 0), проходящей через точку ec.
Решение упражнения 8
Определить уравнение гиперболы, сосредоточенное на (0, 0).
Решение упражнения
Определите координаты точки (ы) пересечения между линией x + y — 1 = 0 и гиперболой x² — 2y² = 1.
Решение упражнения 10
Прямоугольная гипербола проходит через точку (4, 1/2).
Найдите его уравнение и определите координаты вершин и фокусов.
Решение упражнения 11
. Поперечная ось гиперболы составляет 12, а эксцентричность — 4/3. Вычислите уравнение этой гиперболы.
Решение упражнения 12
Рассчитайте уравнение прямоугольной гиперболы, зная, что его фокусное расстояние составляет /.
Найдите различных репетиторов по математике на SuperProf.
Решение упражнения 13
Длина сопряженной оси гиперболы равна 8, а уравнения асимптот таковы: . Вычислите уравнение гиперболы, ее фокусы и вершины.
Пять способов остановить гиперболу, разрушая вашу жизнь
Стрэттон Крэйг
Преувеличение часто безвредно; сказать другу, что он выглядит потрясающе, когда все в порядке, точнее никогда не повредит.
Однако в мире рекламы все иначе. Хотя может показаться убедительным немного раздуть ваши утверждения, расширенные заявления могут вызвать недоумение. Действительно ли гипербола разрушит вашу жизнь? Нет. Но это может нанести непоправимый ущерб авторитету вашего бренда.
Гипербола, буквально происходящая от греческого слова, означающего «излишество», представляет собой крайнее преувеличение, используемое для того, чтобы подчеркнуть точку зрения. Он разработан именно для того, чтобы привлечь к себе внимание, и эта тактика, которую лингвист Клаудия Кларидж называет «эмоциональным убеждением». Римский ритор Квинтилиан настаивал на том, что это не лживая ложь, а скорее «элегантное превосходство истины».
Найти лучший способ описать чувство, место или продукт часто бывает сложно, а слова позволяют передать четко различимое значение. Преувеличение делает намерение утверждения безошибочным, а тонкая гипербола сохраняет связь, которую могут потерять чрезмерно амбициозные метафоры и запутанные аналогии.
Литература — это место, где гипербола наиболее уместна, где ее можно довести до абсурда для художественного эффекта. Возьмите вступительные слова Пола Баньяна в американской народной сказке «Малыш, Синий Бык»:
«Ну, однажды зимой было так холодно, что все гуси отлетели назад, и даже снег стал синим. Поздно ночью стало так холодно, что все произносимые слова замерзали, прежде чем их можно было услышать. Людям приходилось ждать до восхода солнца, чтобы узнать, о чем люди говорили накануне вечером».
Когда этого следует избегать… как чумыХотя гипербола процветает в литературе и речи, бывают случаи, когда ее использование отталкивает. При продаже продукта или услуги у организаций возникает соблазн зайти слишком далеко. Если вы заставите читателей ориентироваться в преувеличенных прилагательных и страстных оборотах фразы, вы можете оттолкнуть их, вместо того, чтобы привлечь их внимание.
Да, у вас есть продукт для продажи, и да, это конкурентный рынок.
Но если вы можете уверенно стоять за свой бизнес, преувеличение не должно быть необходимым для привлечения клиентов.
Вот несколько советов, как справляться с гиперболами:
1) Избегайте абсолютов, превосходных степеней и клишеИзбегайте таких слов, как «никогда», «всегда» и «лучше». Или «наиболее», «последний», «бесспорный» и «непревзойденный». Вместо этого будьте честны, скромны и прямолинейны. Самые лучшие заявления трудно доказать, и если вы установите планку слишком высоко, легко не оправдаться. Гиперболические клише также могут заставить вас чувствовать себя на миллион долларов, но они также ненадежны и в некоторых случаях смешны.
2) Используйте числа и определите количествоТакие выражения, как «многочисленные», «несколько», «различные» и «немногие», неоднозначны и неясны. Дайте количественную оценку, когда сможете, или укажите относительный контекст.
3) Докажи это! Будьте конкретны, всегда указывайте свой источник и предлагайте подтверждение всего, что вы говорите.