Решение игры в смешанных стратегиях: Решения игр в смешанных стратегиях

Содержание

Решение игр в смешанных стратегиях

Лекция 5.

Тема: «Решение игр в смешанных стратегиях»

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией игрока А называется применение чистых стратегий с вероятностями , причем сумма вероятностей равна 1: = 1. Смешанные стратегии игрока А записываются в виде матрицы:

или в виде строки Аналогично смешанные стратегии игрока В обозначаются:

или , где сумма вероятностей появления стратегий равна 1: .

Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1 соответствует чистой стратегии. На основании принципа минимакса определяется оптимальное решение (или решение) игры: это пара оптимальных стратегий в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству:

где и — нижняя и верхняя цены игры.

Справедлива следующая основная теорема теории игр — теорема Неймана. Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.

Пусть и — пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое практическое значение — она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.

Рассмотрим игру размера 2х2, которая является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение — это пара чистых стратегий, соответствующих этой точке.

Игра, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий и .

Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии , то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался игрок В. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) — случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная стратегия) будет равен v и для 1-й, и для 2-й стратегии противника.

Пусть игра задана платежной матрицей:

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию , а игрок B – чистую стратегию(это соответствует 1-му столбцу платежной матрицы Р), равен цене игры v: .

Тот же средний выигрыш получает игрок А, если 2-й игрок применяет стратегию , т.е. . Учитывая, что , получаем систему уравнений для определения оптимальной стратегии и цены игры v:

(1)

Решая эту систему, получим оптимальную стратегию

(2)

, (3)

и цену игры

. (4)

Применяя теорему об активных стратегиях при отыскании— оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А (или ) средний проигрыш игрока В равен цене игры v, т. е.

(5)

Тогда оптимальная стратегия определяется формулами:

(6)

(7)

Применим полученные результаты для отыскания оптимальных стратегий для игры «Поиск», рассмотренной в предыдущей лекции. Найти оптимальные стратегии игры «Поиск».

Решение. Игра «Поиск» задана платежной матрицей без седловой точки:

Поэтому ищем решение в смешанных стратегиях; для игрока А средний выигрыш равен цене игры v (при и ), для игрока В средний проигрыш равен цене игры v (при и ). Системы уравнений в данном случае имеют вид:

Решая эти системы, получаем

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью 1/2, при этом средний выигрыш равен 0.

Геометрическая интерпретация игры 2х2

Решение игры 2х2 допускает наглядную геометрическую интерпретацию. Пусть игра задана платежной матрицей По оси абсцисс отложим единичный отрезок ; точка (x=0) изображает стратегию , а все промежуточные точки этого отрезка — смешанные стратегии первого игрока, причем расстояние от до правого конца отрезка — это вероятность стратегии , расстояние до левого конца — вероятность стратегии. На перпендикулярных осях 1—1 и II—II откладываем выигрыши при стратегиях и соответственно. Если 2-й игрок примет стратегию , то она дает выигрыши и на осях 1—1 и II—II, соответствующие стратегиям и . Обозначим эти точки на осях 1—1 и II—II буквой . Средний выигрыш , соответствующий смешанной стратегии , определяется по формуле математического ожидания и равен ординате точки , которая лежит на отрезке и имеет абсциссу (рис.1).

рис. 1. рис.2.

Аналогично строим отрезок , соответствующий применению вторым игроком стратегии (рис.2). При этом средний выигрыш — ордината точки .

В соответствии с принципом минимакса оптимальная стратегия такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис.3), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке— против стратегии на участке — против стратегии ). Оптимальную стратегию

определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры v. На рис3 обозначены также верхняя и нижняя цены игры и.

Пример 2.

Применим геометрический метод для решения следующей задачи. Решить графически игру, заданную платежной матрицей:

Рис. 3 Рис.4

Решение. Откладываем по оси абсцисс (рис.4) единичный отрезок . На вертикальной оси 1—1 откладываем отрезки: = 1,5, соответствующий стратегии и = 3, соответствующий стратегии . На вертикальной оси II—II отрезок ⁼ 2 соответствует стратегии , отрезок ⁼ 1 соответствует стратегии ( рис.4). Нижняя цена игры . Верхняя цена игры , седловая точка отсутствует. Из рис.4 видно, что абсцисса точки N определяет оптимальную стратегию , а ордината — цену игры v. Точка N является точкой пересечения прямых и . Уравнение прямой , проходящей через точки (0; 1,5) и (1; 2):

или

Уравнение прямой , проходящей через точки (0; 3) и (1;1):

или

Точка пересечения прямых является решением системы:

или х = 0,6; у == 1,8, т.е. N (0,6; 1,8).

Рис.5

Таким образом, ;оптимальная стратегия=(0,6;0,4), цена игры v=1,8

Геометрически можно также определить оптимальную стратегию игрока В, если поменять местами игроков А и В и вместо максимума нижней границы в соответствии с принципом минимакса (рис.5) рассмотреть минимум верхней границы.

Абсцисса точки М определяет в оптимальной стратегии игрока В, ордината этой точки -цена игры. Прямая проходящая через точки (0; 1,5) и (1; 3), удовлетворяет уравнению

Прямая , проходящая через точки (0; 2) и (1; 1), удовлетворяет уравнению у = —х +2.

Координаты их точки пересечения М — это решение системы уравнений:

откуда х = 0,2; у = 1,8, т.е. =0,8,

Оптимальное решение игры найдено.

Вместе с этой лекцией читают «Протокол межсетевого взаимодействия IP».

Рис. 6 Рис. 7

Из решения задачи следует, что геометрически можно определять оптимальную стратегию как игрока А, так и игрока B, в обоих случаях используется принцип минимакса, но во втором случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум. Если платежная матрица содержит отрицательные числа, то для графического решения задачи лучше перейти к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число. Решение игры при этом не изменится, а цена игры увеличится на это число. В задаче платежная матрица не имела седловой точки ().

При наличии седловой точки графическое решение дают варианты, изображенные на рис.6 и рис.7. На рис.6 наибольшей ординатой на ломаной обладает точка , поэтому оптимальной является чистая стратегия для игрока А ( — для игрока В), т. е. оптимальное решение: = (0; 1), = (0; 1). Игра имеет седловую точку = v.

Чистая стратегия (рис.7) не выгодна для игрока В, поскольку при любой стратегии игрока А она дает последнему больший выигрыш, чем чистая стратегия . На основании принципа минимакса выделим прямую и на ней точку с наибольшей ординатой на оси I-I. Чистая стратегия является оптимальной для игрока А, а чистая стратегия — для игрока В. Оптимальное решение: цена игры , т.е. имеется седловая точка.

Графический метод можно применить также при решении игры 2 и m

15. Решение игры в смешанных стратегиях.

Задача теории игр – нахождение оптимальных стратегий игроков в предположении одинаковой «разумности» противников.

Рассмотрим игру (модель конфликтной ситуации), в которой участвует два игрока A и B, имеющие прямо противоположные интересы.

Процесс игры заключается в последовательных ходах (личных – сознательных и случайных) противников, а совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации называется стратегией игрока.

При конечном числе стратегий игра будет конечной. Пусть у игрока A имеется m возможных стратегий A₁, A₂…A_m, а у игрока B – n возможных стратегий B₁, B₂…B

n. Пусть также известны величины a_ij– выигрыши игрока A при использовании A_i с его стороны и B_i со стороны противника.

Тогда игра, называемая игрой m×n, может быть представлена таблицей, называемой платежной матрицей или просто матрицей игры.

По матрице игры определяются нижняя α и верхняя β цены игры.

Принцип выбора противниками стратегий, соответствующих получению ими выигрышей α и β называется принципом минимакса, а сами стратегии – минимаксными. Известно, что минимаксные стратегии устойчивы по отношению к информации о поведении другой стороны только в случае, если α = β.

В случае α ≠ β для получения наибольшего выигрыша игроку выгодно

применять не одну (чистую) стратегию, а чередовать случайным образом несколько стратегий.

Такие стратегии, состоящие в случайном чередовании чистых стратегий, называются смешанными и задаются соответствующими вероятностными векторами.

Пусть S_A — смешанная стратегия игрока A, а S_B— смешанная стратегия игрока B. Тогда S_A=(p₁, p₂… p_m), S_B=(q₁, q₂… q_n), где p_i— вероятность применения игроком A стратегии A_i

, q_i — вероятность применения игроком B стратегии B_i, причем

Чистая стратегия – частный случай смешанной.

Если допустить применение смешанных стратегий, то для каждой конечной игры можно найти хотя бы одно решение, т.е. пару устойчивых оптимальных стратегий игроков (S_A^*, S_B^*), обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступить от своей.

Выигрыш, соответствующий решению, называется ценой игры и в общем случае (при применении смешанной стратегии) лежит в интервале α ≤ γ ≤ β.

α – нижняя цена игры

γ – выигрыш

β – верхняя цена игры

Рассмотрим игру 2×2.

Ее матрица имеет вид:

Если в матрице 2×2 седловой точки нет и α ≠ β, то необходимо искать решение в смешанных стратегиях.

Пара оптимальных смешанных стратегий S_A= (p₁, p₂), S_B= (q₁, q₂), и цена игры в этом случае определяются по формулам:

Игра 2×2 и ее решение имеют простую геометрическую интерпретацию.

Пусть точки A₁ и A₂ соответствуют применению одноименных стратегий, а любая точка внутри этого отрезка соответствует некоторой смешанной стратегии

S_A^*= (p₁, p₂).

Рисунок 1 – геометрическая интерпретация задачи 2×2

Ординаты прямой B₁B₁, проведенной так, как показано на рис.1, соответствуют выигрышу игрока A при применении им любой стратегии (чистой или смешанной) при условии, что B применяет B₁. Прямая B₂B₂ также отражает выигрыш игрока A в случае, когда B применяет B₂. Жирной линией отмечена нижняя граница выигрыша B₁NB₂ – минимальный выигрыш игрока A при любой его смешанной стратегией. Очевидно, решение достигается в точке максимума нижней границы (на рис.1 в точке

N). Геометрические построения легко осуществляются по элементам матрицы игры, которые откладываются на вертикальных осях.

По рисунку легко находятся α, β, γ и проводится анализ игры.

Геометрическим способом также легко анализируются и решаются игры 2×n.

Они задаются матрицей игры:

Например, геометрическая интерпретация игры 2×4, в которой число наклонных линий получается равным 4, по числу стратегий игрока B. имеет вид:

Рисунок 2 – геометрическая интерпретация задачи 2×4

Нижняя граница игры может в данном случае уже представлять сложную ломаную линию, максимум которой, как и ранее, определяет решения игры.

Т.е. находим, самую нижнюю кривую и самая верхняя точка пересечения в этой кривой и есть решение игры.

Из рис. 2 видно, что нижняя граница выигрыша – прямая B₁

MNB₂, ее максимум достигается в точке N, которая определяет оптимальную стратегию S_A^*= (p₁, p₂).

Следует отметить, что стратегия B₃ вообще может не рассматриваться как заведомо невыгодная игроку B, а значения p₁и p₂можно найти по формулам игры 2×2, учитывая, что в точке N активных стратегий игрока B только две B₂ и B₄.

Смешанные стратегии

Цель обучения

Какие игры требуют или допускают рандомизацию как часть своего решения?

Давайте снова рассмотрим игру с сопоставлением монет, как показано на рис. 16.13 «Снова сопоставление монет».

Рис. 16.13 Повторное совпадение монет

Предположим, что Строка считает, что Столбец играет орлом с вероятностью p . Тогда, если Строка играет орлом, она получает 1 с вероятностью p и –1 с вероятностью (1 – p ), для ожидаемого значения 2 p – 1. Аналогично, если Строка играет решкой, Строка получает –1 с вероятностью p (когда Столбец играет орлом) и 1 с вероятностью (1 – p ), для ожидаемого значения 1 – 2 p . Это обобщено на рис. 16.14 «Смешанная стратегия сопоставления пенни».

Если 2 p – 1 > 1 – 2 p , то в среднем Роу лучше играть орлом, чем решкой. Аналогично, если 2 p – 1 < 1 – 2 p , то Роу лучше играть решкой, чем решкой. Если, с другой стороны, 2 p – 1 = 1 – 2 p , то Строка получает один и тот же выигрыш независимо от того, что делает Строка. В этом случае Роу может сыграть орлом, решкой или подбросить монету и сделать ход Роу случайным.

Смешанная стратегия Равновесие по Нэшу Равновесие по Нэшу, при котором по крайней мере один игрок использует случайную стратегию, и ни один из игроков не может увеличить свой ожидаемый выигрыш, играя по альтернативной стратегии. предполагает, что по крайней мере один игрок использует рандомизированную стратегию, и ни один игрок не может увеличить свой ожидаемый выигрыш, играя альтернативную стратегию. Равновесие по Нэшу, в котором ни один игрок не рандомизирует, называется чистой стратегией. Равновесие Нэша, в котором ни один игрок не рандомизирует.0009

Рисунок 16.14. Смешанная стратегия сопоставления монет

Обратите внимание, что рандомизация требует равенства ожидаемых выплат. Если предполагается, что игрок рандомизирует стратегию A

или стратегию B , то обе эти стратегии должны давать один и тот же ожидаемый выигрыш. В противном случае игрок предпочел бы одну из них и не стал бы играть в другую.

Вычисление смешанной стратегии имеет один элемент, который часто сбивает с толку. Предположим, что Row собирается рандомизировать. Тогда выигрыши строки должны быть одинаковыми для всех стратегий, которые использует строка с положительной вероятностью. Но это равенство в выигрышах Строки не определяет вероятности, с которой Строка играет различные ряды. Вместо этого это равенство в выигрышах Строки будет определять вероятности, с которыми Столбец играет с различными столбцами. Причина в том, что именно вероятности столбца определяют ожидаемые выигрыши для строки; если Строка собирается рандомизировать, то вероятности Столбца должны быть такими, чтобы Строка была готова рандомизировать.

Таким образом, например, мы вычислили выигрыш для ряда выпадения орла, который составил 2 p – 1, где p — вероятность того, что столбец выпал орлом. Точно так же выигрыш Row при игре в «Решку» составил 1 – 2 p . Строка готова рандомизировать, если они равны, что дает p = ½.

Теперь давайте рассмотрим более сложный пример и вернемся к битве полов. Рисунок 16.15 «Смешанная стратегия в битве полов» еще раз иллюстрирует выигрыши.

Рисунок 16.15 Смешанная стратегия в битве полов

В этой игре есть две чистые стратегии равновесия Нэша: (Бейсбол, Бейсбол) и (Балет, Балет). Существует ли смешанная стратегия? Чтобы вычислить смешанную стратегию, пусть женщина идет на игру в бейсбол с вероятностью p , а мужчина идет на игру в бейсбол с вероятностью q . На рис. 16.16 «Полное вычисление смешанной стратегии» показано вычисление выигрышей смешанной стратегии для каждого игрока.

Рисунок 16.16 Полный расчет смешанной стратегии

Например, если Мужчина (игрок ряда) идет на бейсбольный матч, он получает 3, когда женщина идет на бейсбольный матч (вероятность p ), а в противном случае получает 1 при ожидаемом выигрыше 3 p + 1 (1 – p ) = 1 + 2 p . Остальные расчеты аналогичны, но обязательно нужно пробежаться по логике и проверить каждый расчет.

Смешанная стратегия в игре «Битва полов» требует, чтобы обе стороны выполняли рандомизацию (поскольку чистая стратегия одной из сторон предотвращает рандомизацию другой). Безразличие мужчины между походом на бейсбол и на балет требует 1 + 2 p = 2 – 2 p , что дает p = ¼. То есть Мужчина будет готов рандомизировать, какое мероприятие он посещает, если Женщина будет ходить на балет 3/4 времени, а в противном случае — на игру в бейсбол. Это делает мужчину безразличным между двумя событиями, потому что он предпочитает быть с женщиной, но ему также нравится быть на бейсбольном матче. Чтобы компенсировать преимущество, которое дает ему игра, Женщине приходится чаще бывать в Балете.

Аналогичным образом, для того, чтобы Женщина могла быть выбрана случайным образом, Женщина должна получить равные выплаты от посещения игры в бейсбол и от посещения балета, что требует 2 q = 3 – 2 q или q = ¾.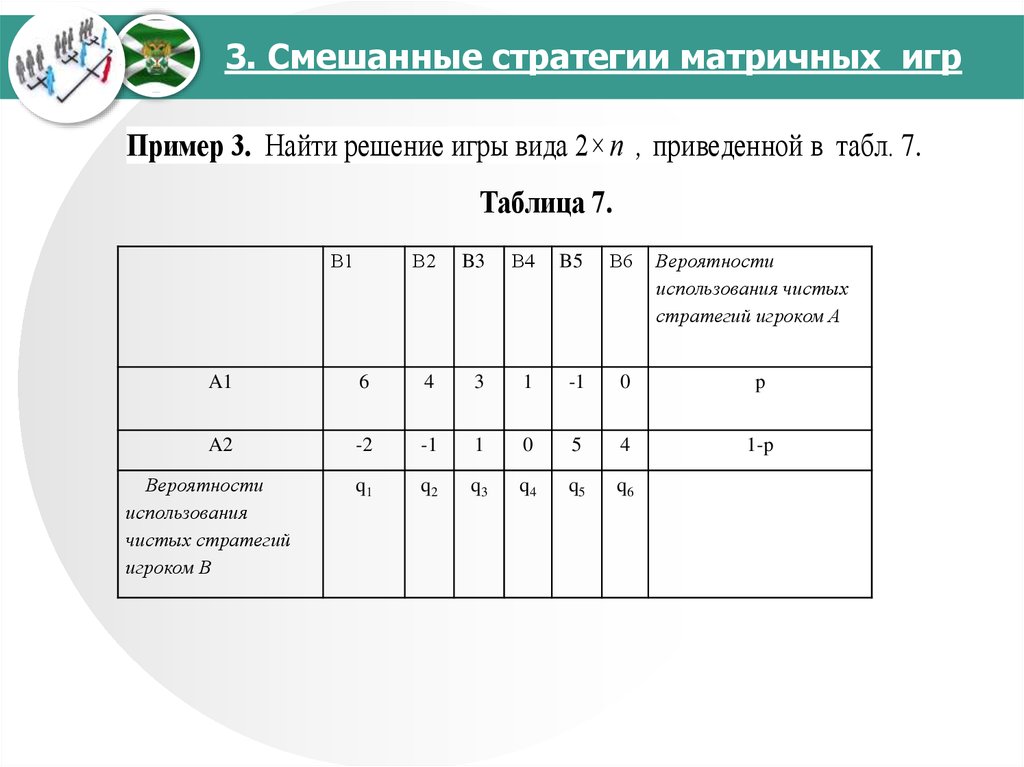 Таким образом, вероятность того, что мужчина пойдет на бейсбол, составляет ¾, а на балет – ¼ всего времени. Это независимые вероятности, поэтому, чтобы получить вероятность того, что оба пойдут на игру в бейсбол, мы умножаем вероятности, что дает 3/16. На рис. 16.17 «Вероятности смешанной стратегии» показаны вероятности всех четырех возможных исходов.

Рис. 16.17 Вероятности смешанной стратегии

Обратите внимание, что более половины времени (бейсбол, балет) является результатом смешанной стратегии, и два человека не вместе. Это отсутствие координации обычно является признаком равновесия смешанной стратегии. Ожидаемые выигрыши для обоих игроков также легко вычисляются. Выигрыш игрока 1 + 2 p = 2 – 2 p , а так как p = ¼, то Человек получает 1½. Аналогичный расчет показывает, что выигрыш женщины такой же. Таким образом, оба делают хуже, чем координируя свои менее предпочтительные результаты. Но это равновесие по Нэшу со смешанной стратегией, каким бы нежелательным оно ни казалось, является равновесием по Нэшу в том смысле, что ни одна из сторон не может улучшить свой собственный выигрыш при заданном поведении другой стороны.

В битве полов смешанная стратегия равновесия Нэша может показаться маловероятной; и мы могли бы ожидать, что пара будет координировать свои действия более эффективно. Действительно, простой звонок по телефону должен исключить смешанную стратегию. Итак, давайте рассмотрим еще одну игру, связанную с битвой полов, где нарушение координации имеет больше смысла. Это игра «курица». В этой игре два игрока едут навстречу друг другу, пытаясь убедить другого уступить и в конечном итоге свернуть в канаву. Если оба сворачивают в канаву, мы объявляем результат ничьей, и оба получают ноль. Если один сворачивает, а другой нет, водитель, который сворачивает, проигрывает, а другой водитель выигрывает, и мы даем победителю одно очко. Обратите внимание, что добавление константы к выигрышам игрока или умножение выигрышей этого игрока на положительную константу , не влияет на равновесие Нэша — чистое или смешанное. Следовательно, мы всегда можем считать, что один исход для каждого игрока равен нулю, а другой исход равен единице. Остается только один вопрос: что произойдет, если ни один из них не даст результатов, и в этом случае произойдет сбой. В этой версии выигрыш был установлен в четыре раза больше проигрыша при отклонении, как показано на рис. 16.18 «Цыпленок», но вы можете изменить игру и посмотреть, что произойдет.

Рис. 16.18 Цыпленок

В этой игре есть два равновесия в чистой стратегии: (Отклоняйся, не отклоняйся) и (Не отклоняйся, отклоняйся). Кроме того, у него смешанная стратегия. Предположим, что столбец отклоняется с вероятностью p . Тогда Строка получает 0 p + –1(1 – p ) за отклонение, 1 p + (–4)(1 – p ) за отсутствие отклонения, и Строка рандомизирует, если они равны, что требуется p = ¾. То есть вероятность того, что столбец отклонится в равновесии со смешанной стратегией, равна 3/4. Вы можете проверить, что у игрока в ряду одинаковая вероятность, установив вероятность того, что ряд отклонится, равной 9.0013 q и расчет ожидаемых выплат Колонки. Таким образом, вероятность столкновения составляет 1/16 в равновесии смешанной стратегии.

Равновесие смешанной стратегии в некотором смысле более вероятно в этой игре: если бы игроки уже знали, кто уступит, им не нужно было бы играть в игру. Весь смысл игры в том, чтобы узнать, кто уступит, а значит, заранее неизвестно. Это означает, что равновесие смешанной стратегии в некотором смысле является более разумным равновесием.

Рисунок 16.19 Камень, ножницы, бумага

«Камень, ножницы, бумага» — детская игра, в которой двое детей одновременно выбирают бумагу (рука плоская), ножницы (рука с двумя оттопыренными пальцами, похожими на ножницы). ), или рок (рука в кулак). Природа выигрышей такова, что бумага побеждает камень, камень побеждает ножницы, а ножницы побеждают бумагу. Эта игра имеет структуру, показанную на рис. 16.19 «Камень, ножницы, бумага».

Ключевые выводы

Смешанная стратегия Равновесие по Нэшу предполагает, что по крайней мере один игрок использует случайную стратегию, и ни один игрок не может увеличить свой ожидаемый выигрыш, играя альтернативную стратегию.
Равновесие Нэша без рандомизации называется равновесием Нэша чистой стратегии.
Если предполагается, что игрок рандомизирует две стратегии, то обе стратегии должны давать один и тот же ожидаемый выигрыш.
В игре с сопоставлением монет используется смешанная стратегия, а не чистая стратегия.
Игра Битва полов имеет смешанную стратегию и две чистые стратегии.
Игра в курицу похожа на битву полов и, как и она, имеет две чистые стратегии и одну смешанную стратегию.

Упражнения

Пусть q будет вероятностью того, что Строка сыграет решкой. Покажите, что столбец готов к рандомизации тогда и только тогда, когда q = ½. (Подсказка: сначала вычислите ожидаемый выигрыш Столбца, когда Столбец играет орлом, а затем вычислите ожидаемый выигрыш Столбца, когда Столбец играет решкой. Они должны быть равны, чтобы Столбец мог рандомизировать. )
Покажите, что в игре «камень-ножницы-бумага» не существует равновесия в чистой стратегии. Покажите, что выполнение всех трех действий с равной вероятностью является равновесием смешанной стратегии.
Найдите все равновесия следующих игр:
Рисунок 16.20
Если умножить выигрыш игрока на положительную константу, равновесие в игре не изменится. Правда это или ложь и почему?

микроэкономика — Игра с равновесием в чистых, но без равновесия в смешанных стратегиях?

$\begingroup$

Мне попалась такая игра:

Вопрос заключается в нахождении потенциальных равновесий в смешанных и чистых стратегиях. Решение говорит о том, что в чистых стратегиях (B,N) существует равновесие, а в смешанных стратегиях – нет. Математически это имеет для меня смысл, так как если вы решаете для равновесия смешанной стратегии, вы получаете решение, что игрок 2 должен будет играть в стратегию L «-100%» времени, чтобы сделать игрока 1 безразличным между стратегией A и стратегия Б. Однако я не понимаю, как этот результат согласуется с теоремой Нэша, которая утверждает, что каждая игра с конечным числом игроков и конечным числом чистых стратегий имеет по крайней мере одно равновесие в смешанных стратегиях. В данном случае мы действительно имеем конечное число игроков и чистых стратегий. Так как же возможно, что не существует равновесия смешанных стратегий?

микроэкономика
теория игр
доминирующая стратегия

$\endgroup$