Калькулятор Пределов — Решение Пределов Онлайн
Этот калькулятор пределов вычисляет положительные или отрицательные пределы для заданной функции в любой точке. Вы должны попробовать этот решатель пределов, чтобы определить, как легко решать пределы. Кроме того, калькулятор правил l’hopital помогает вычислять предельные задачи \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \) и поддерживает вычисление пределов онлайн на положительной и отрицательной бесконечности. Что ж, читайте дальше, чтобы понять, как найти предел онлайн функции с помощью этого решение пределов онлайн. Начнем с основ!
Что такое предел (математика)?
Обозначение пределов представляет собой математическое понятие, основанное на идее близости. Его также можно определить как значение, к которому функция «приближается», когда вход «приближается» к некоторому значению. Необходимо оценить Предел в исчислении и математическом анализе, чтобы определить непрерывность, производные и интегралы. калькулятор пределов онлайн присваивает значения определенным функциям в точках, где значения не определены, таким образом, чтобы они согласовывались с ближайшими или близкими значениями. В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда. С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.
В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда. С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.
Что ж, пределы онлайн калькулятор производной – лучший способ вычислить предел производную функции по заданным значениям и показывает дифференцирование.
Что такое формула предела?
Формула предела будет следующей:
$$ \ lim_ {x \ to a} f (x) = L $$
Пример:
Если у вас есть функция «\ (\ frac {(x2 – 1)} {(x – 1)} \)», тогда необходимо найти пределы, когда \ (x \) равно \ (1 \), как деление по нулю не является законной математической операцией. С другой стороны, для любого другого значения \ (x \) числитель может быть учтен, а также разделен на \ ((x – 1) \), чтобы получить \ (x + 1 \). Таким образом, это частное будет равно \ (x + 1 \) для всех значений \ (x \), за исключением 1, которая не имеет значения. Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисление пределов онлайн упростить с помощью калькулятор пределов онлайн правил Лопиталя.
Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисление пределов онлайн упростить с помощью калькулятор пределов онлайн правил Лопиталя.
Для нахождения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Кроме того, бесплатный пределы онлайн калькулятор интегралов позволяет вам определить интегралы функции, соответствующие задействованной переменной, и показать вам пошаговую работу.
Лимитные законы:
Для нахождения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Эти законы можно использовать для оценки предела полиномиальной или рациональной функции. Кроме того, для некоторых правил существуют определенные условия, и если они не выполняются, то правило не может использоваться для проверки оценки лимита.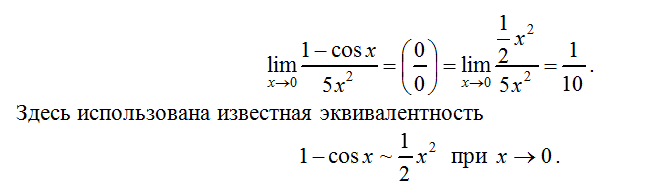 Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент.
Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент.
В следующей таблице приведены вычислить предел законы и некоторые основные свойства.
| Предельный закон в символах | Предел закон на словах | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | \( \lim_{x \to a} [f(x) + g(x)] = \lim_{x \to a}f(x) + \lim_{x \to a}g(x)\) | Сумма Лимитов равна лимиту суммы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | \(\lim_{x \to a}[ f(x) – g(x)]= \lim_{x \to a} f(x) – \lim_{x \to a} g(x)\) | Разница лимитов равна лимиту разницы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | \( \lim_{x \to a} cf (x) = c \lim_{x \to a} f (x) \) | Постоянный предел функции равен пределу постоянного времени функции. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | \(\lim_{x \to a}[ f(x)g(x)] = \lim_{x \to a} f(x) × \lim_{x \to a} g(x)]\) | Произведение лимитов равно лимиту продукта. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | \(\lim_{x \to a} \frac {f(x)} {g(x)} = \frac {\lim_{x \to a} f(x)} {\lim_{x \to a} g(x) }\) | Частное пределов равно пределу частного. 2} $$ 2} $$мы можем найти предел онлайн 0, Inf, -Inf или вычисление пределов онлайн коэффициентам. Формальный метод:Речь идет о доказательстве того, как мы можем максимально приблизиться к ответу, сделав «\ (y \)» близким к «\ (a \)». Как калькулятор лимитов вычисляет лимиты?Этот калькулятор лимитов позволяет вам оценить лимит данных переменных. Что ж, искатель решение пределов онлайн помогает найти пределы, выполнив следующие действия: Вход:
Выход:
Часто задаваемые вопросы:Как узнать, что лимит не существует?Чтобы найти предел на графике, если существует вертикальная асимптота, и одна сторона идет в сторону бесконечности, а другая – в направлении отрицательной бесконечности, тогда предел не существует. Точно так же, если на графике есть дыра при значении x c, то двусторонний предел не будет существовать. Тем не менее, поиск пределов может помочь вам более точно оценить пределы. Каковы правильные обозначения пределов?По сути, предельная запись – это способ сформулировать тонкую идею, чем просто сказать \ (x = 5 \) или \ (y = 3 \). \ (\ lim_ {x \ to a} f (x) = b \). С другой стороны, калькулятор пределов онлайн избавляет от беспокойства об обозначении пределов, поскольку он определяет пределы и указывает их неточное форматирование. Можно ли применить правило L‘Hopital к каждому пределу?Правило L’Hôpital используется с неопределенными пределами, имеющими форму \ (0/0 \) или бесконечность. Он не решает всех ограничений. Иногда даже повторяющиеся применения правила не могут помочь найти предел онлайн значения. Итак, для удобства калькулятор правил l’hopital – лучший способ решить бесконечные вычислить предел функций. Может ли 0 быть пределом?Если мы просто оцениваем уравнение, предел \ (0/0 \) будет неопределенным. Однако, если мы получим \ (0/0 \), то может быть серия ответов. Теперь единственный способ определить точный ответ – это использовать решатель пределов для точного определения проблем с предельными значениями. Как используются лимиты в расчетах?Пределы определяют, как функция будет действовать рядом с точкой, как альтернатива в этой точке. Эта идея лежит в основе исчисления. Например, предел «\ (f \)» при \ (x = 3 \) и \ (x = 3 x = 3 \) – это значение f по мере того, как мы приближаемся к \ (x = 3 \). Конечное примечание:Этот пределы онлайн калькулятор пределов находит пределы и специально предназначен для определения пределов в отношении переменной. Пределы можно оценивать как с положительной, так и с отрицательной стороны. Он обслуживает все вычислить предел задачи, которые невозможно решить алгебраически. Таким образом, здорово помочь студентам и профессионалам решить и проверить ваши ограничения в мгновение ока. Other Languages: Limit Calculator, Limit Hesaplama, Kalkulator Limit, Grenzwertrechner, Kalkulačka Limit, Calculadora De Limites, Calculateur De Limite, Calculadora De Limites, Calcolatore Limiti.
калькулятор пределов (решатель) — с шагамиКалькулятор лимита с шагамионлайн калькулятор пределов поможет вам найти предел функции по отношению к переменной. Калькулятор пределов с шагами показывает пошаговое решение пределов вместе с графиком и расширением ряда. Он использует все предельные правила, такие как сумма, произведение, частное и правило Лопиталя, для расчета точного значения. Вы можете оценить пределы относительно \(\text{x, y, z, v, u, t}\) и \(w\) с помощью этого калькулятора пределов. Это не то. С помощью этого инструмента вы также можете найти,
Как работает калькулятор лимитов?Чтобы оценить предел с помощью этого решателя пределов, выполните следующие шаги.
| возведение в степень | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| solve | решение уравнений, неравенств, систем уравнений и неравенств | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| expand | раскрытие скобок | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor | разложение на множители | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sum | вычисление суммы членов последовательности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| derivative | дифференцирование (производная) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| integrate | интеграл | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| lim | предел | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| inf | бесконечность | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| plot | построить график функции | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| log (a, b) | логарифм по основанию a числа b | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin, cos, tg, ctg | синус, косинус, тангенс, котангенс | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sqrt | корень квадратный | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | число «пи» (3,1415926535. 2), {x, 0.5, 2} 2), {x, 0.5, 2}Калькулятор предела (решатель) — С шагамиКалькулятор предела с шагамиКалькулятор предела поможет вам найти предел функции по отношению к переменной. Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению. Калькулятор пределов с шагами показывает пошаговое решение пределов вместе с графиком и расширением ряда. Он использует все предельные правила, такие как сумма, произведение, частное и правило Лопиталя, для вычисления точного значения. Вы можете вычислить ограничения по отношению к \(\text{x , y, z , v, u, t}\) и \(w\) , используя этот калькулятор пределов. Это не так. Используя этот инструмент, вы также можете найти:
Как работает калькулятор предела? Чтобы оценить предел с помощью этого решателя пределов, выполните следующие шаги.
Вы найдете ответ под инструментом. Щелкните Show Steps , чтобы просмотреть пошаговое решение. Что такое предел в исчислении?Предел функции — это значение, к которому f(x) приближается по мере того, как x приближается к некоторому числу. Пределы можно использовать для определения производных, интегралов и непрерывности, находя предел данной функции. Это записывается как: \(\lim _{x\to a}\:f\left(x\right)=L\) действительное число, то приведенное выше выражение читается как предел f x 9x приближается к 0 равно 1. Каков предел, когда x приближается к бесконечности ln(x)? Предел при приближении x к бесконечности ln(x) равен + ∞ . Предел этого натурального логарифма может быть доказан доведением до абсурда.
Калькулятор рядов Тейлора — Найдите разложение Тейлора с шагамиКалькулятор рядов Тейлора с шагами Онлайн-калькулятор рядов Тейлора используется для решения ряда Тейлора заданной функции вокруг центральной точки. Что такое серия Тейлора? «В математике ряд Тейлора — это выражение функции, для которой дифференцирование всех порядков существует в точке « 9n\left(a\right)\) — n-й порядок данной функции, « a » — конкретная точка или центр функции, а « n » — порядок. Как рассчитать ряд Тейлора?Вот пример, решенный нашим калькулятором разложения Тейлора. Пример 9п\) |
Серия Taylor | Encyclopdia Britannica, Inc. (nd)
Пример ряда Тейлора | Tutorial.math.lamar.edu (n.d.)
Калькулятор интегралов с шагами
Калькулятор интегралов с шагами
Калькулятор первообразных (интегралов) — это онлайн-инструмент, используемый для расчета первообразных с шагами. Этот интегральный калькулятор интегрирует функции относительно переменной, т. е. x, y, z, u или t.
Этот интегральный калькулятор вычисляет выражения неопределенного интеграла, а также определенного интеграла с шагом.
В случае определенного интеграла этот интегральный калькулятор использует верхний и нижний пределы заданной функции. Верхний и нижний пределы – это максимальное и минимальное значения интервалов.
Как работает первообразный калькулятор
?
Вы можете вычислить интегралы, выполнив следующие действия.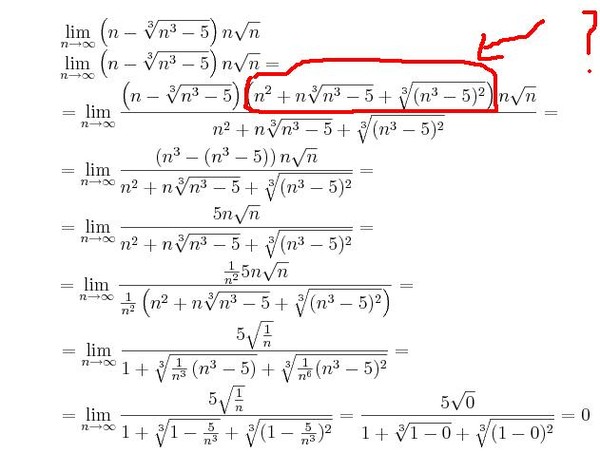
- Выберите метод, т. е. определенный или неопределенный.
- Выберите переменную.
- Заполните поля верхнего и нижнего пределов в случае определенного интеграла.
- Запишите функцию в поле ввода.
- Используйте значок клавиатуры для ввода математических ключей.
- Нажмите кнопку вычислить . Вы получите вывод данной функции с пошаговым расчетом.
- Нажмите показать больше , чтобы увидеть пошаговое решение.
- Нажмите кнопку сброса , чтобы войти в новую функцию.
Что такое интеграл?
В математике интеграл присваивает числа функциям таким образом, который описывает площадь, объем, перемещение и другие понятия, возникающие при объединении бесконечно малых данных. Процесс нахождения интеграла называется интегрированием.
В уравнении интеграла используются три члена:
- Знак интегрирования
- Интеграл (функция, подлежащая интегрированию)
- Переменная интегрирования
Уравнение интеграла приведено ниже.
\(\int f\left(x\right)dx\)
Типы интегралов:
- Двойной интеграл
- Тройной интеграл
- Несобственный интеграл
4 Правила интегрирования 903 перечислены в таблице.
| Имена | Правила |
Как вычислять интегралы?
Используя определенные и неопределенные интегралы, мы можем легко вычислить первообразные заданных функций. Ниже приведены некоторые примеры, которые оцениваются нашим интегральным калькулятором. Пример 1: Для неопределенного интеграла . 92x
Ссылки
- Wikimedia Foundation | Что такое интеграл? Википедия.
- Правила интеграции | Исследование.com | Пройдите онлайн-курсы. Заработайте кредит колледжа.
Калькулятор пределов (решение) — Con pasos
Калькулятор пределов с расчетом
Калькулятор пределов le ayuda encontrar el límite de una función con respecto a una Variable.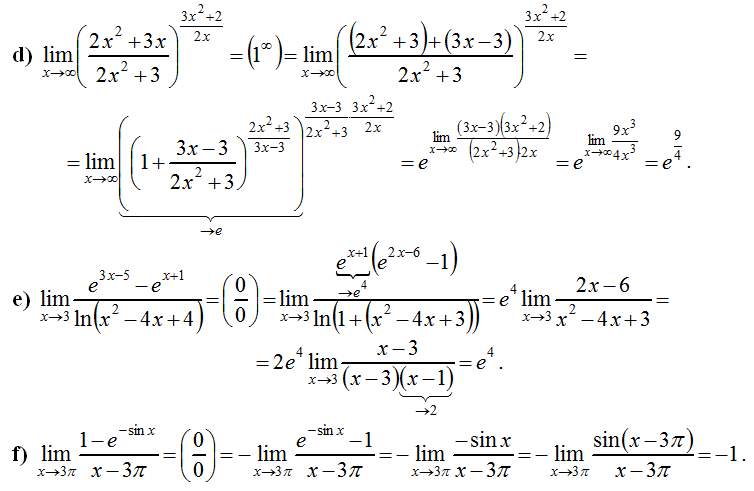 Es уна herramienta ан línea дие ло ayuda исчисление эль доблесть де уна función cuando уна entrada себе acerca ип доблесть específico.
Es уна herramienta ан línea дие ло ayuda исчисление эль доблесть де уна función cuando уна entrada себе acerca ип доблесть específico.
La Calculadora de limites con pasos muestra la solucion paso a paso de los límites junto con una grafica y una expansión en serie. Emplea todas las reglas de límite, como la suma, el producto, el cociente y la regla de L’hopital para calcular el valor correcto.
Вы можете оценить ограничения, связанные с \(\text{x, y, z, v, u, t}\) y \(w\), которые используются для расчета ограничений.
Нет ЕСО. Mediante el uso de esta herramienta, también puede encontrar,
- Предельный предел (+)
- Предельный предел (-)
- Двусторонний предел
¿Cómo funciona la Calculadora de limites?
Para evaluar el límite usando este solucionador de límites, siga los pasos a continuación.
- Ingrese la función en el cuadro de entrada Dado.
- Выбор корреспонденции переменной.

- Introduzca el valor límite.
- Элиге-эль-ладо-дель-лимит. es decir, izquierda, derecha o de dos caras.
- Pulse el botón Расчетный пункт для получения результатов.
- Используйте el botón Reiniciar para ingresar nuevos valores y el icono de teclado para ingresar valores adicionales.
Encontrará la respuesta debajo de la herramienta. Haga clic en Mostrar pasos para ver la solución paso a paso.
¿Qué es un limit en cálculo?
El limite de una función es el valor al que f(x) se acerca a medida que x se acerca a algún número. Los límites себе pueden usar para definir las derivadas, lasintegres y la continuidad al encontrar el límite de una función Dada. Está escrito como: 9x tiende a 0 es 1.
¿Cuál es el límite cuando x tiende al infinito de ln(x)?
Ограничение, которое может длиться до бесконечности, как ln(x) es +∞. El límite de este logaritmo natural puede demostrarse por reductio ad absurdum.
• Si x >1ln(x) > 0, el límite debe ser positivo.
• Como ln(x2) − ln(x1) = ln(x2/x1). Si x2>x1, la diferencia es positiva, por lo que ln(x) siempre es creciente.
• Si lim x→∞ ln(x) = M ∈ R, тенемос ln(x)
Калькулятор пределов со свободными шагами
Этот калькулятор пределов серии вычисляет положительные или отрицательные пределы для заданной функции в любой точке. Вы должны попробовать этот решатель лимитов, чтобы определить, как легко решать лимиты. Кроме того, этот калькулятор правила Лопиталя помогает вычислять предельные задачи \(\frac{0}{0}\) и \(\frac{\infty}{\infty}\) и поддерживает вычисление пределов на положительных и отрицательных бесконечностях.
Что ж, читайте дальше, чтобы получить представление о том, как найти предел функции с помощью этого оценщика пределов. Начнем с основ!
Что такое предельная математика?
Его можно определить как:
«Значение, к которому функция «приближается» как входное «приближается» к некоторому значению».
Предельное обозначение представляет собой математическую концепцию, основанную на идее близости. Необходимо оценить предел в исчислении либо калькулятором предела исчисления, либо вручную. Калькулятор определения пределов присваивает значения определенным функциям в точках, где значения не определены. Все это делается таким образом, чтобы соответствовать ближайшим или близким значениям.
В большинстве курсов исчисления мы работаем с пределом, что означает, что легко начать думать, что предел исчисления всегда существует. С другой стороны, это также помогает решить предел по правилу Лопиталя, что будет объяснено ниже.
Что ж, онлайн-калькулятор производной — лучший способ вычислить производную функции по заданным значениям и показать дифференцирование, что является важным аспектом калькулятора l’hopital при нахождении пределов.
Уравнение ограничения:
Теперь вы можете легко вычислить пределы любых функций, используя формулу, которая также используется калькулятором пределов и приведена ниже:
$$ \lim_{x \to a}f(x)=L $$
Пример Описание:
Если у вас есть функция \(\frac {(x2 − 1)} {(x − 1)}\), то необходимо найти пределы, когда x равно 1, так как деление на ноль не является законным математическим операция. С другой стороны, для любого другого значения x числитель можно учесть, а также разделить на (x-1), чтобы получить x+1. Таким образом, это частное будет равно x+1 для всех значений x, кроме 1, которая не имеет значения. Однако 2 можно присвоить функции \(\frac {(x2 − 1)} {(x − 1)}\) в качестве ее предела, когда x приближается к 1. Если предел x приближается к 0 или бесконечности, такие вычисления могут быть упрощается с помощью калькулятора правила Лопиталя с шагами.
С другой стороны, для любого другого значения x числитель можно учесть, а также разделить на (x-1), чтобы получить x+1. Таким образом, это частное будет равно x+1 для всех значений x, кроме 1, которая не имеет значения. Однако 2 можно присвоить функции \(\frac {(x2 − 1)} {(x − 1)}\) в качестве ее предела, когда x приближается к 1. Если предел x приближается к 0 или бесконечности, такие вычисления могут быть упрощается с помощью калькулятора правила Лопиталя с шагами.
Для определения пределов существуют определенные законы и калькуляторы пределов, которые используют правила исчисления для определения предела функции. Кроме того, бесплатный онлайн-калькулятор интегралов позволяет определить интегралы функции, соответствующей задействованной переменной, и показывает пошаговую работу.
Законы лимита:
Этот лучший калькулятор лимов с шагами работает, анализируя различные операции лимитов. Эти законы можно использовать для оценки предела полиномиальной или рациональной функции. Кроме того, для некоторых правил существуют определенные условия, и если они не выполняются, правило нельзя использовать для проверки оценки ограничения. Однако использование оценщика пределов — лучший способ оценить пределы функции в любой точке.
Кроме того, для некоторых правил существуют определенные условия, и если они не выполняются, правило нельзя использовать для проверки оценки ограничения. Однако использование оценщика пределов — лучший способ оценить пределы функции в любой точке.
В следующей таблице приведены предельные законы вместе с некоторыми основными свойствами.
| Предельный закон в символах | Предельный закон прописью | |
| 1 | \( \lim_{x \to a} [f(x) + g(x)] = \lim_{x \to a}f(x) + \lim_{x \to a}g(x)\) | Сумма лимитов равна лимиту суммы. |
| 2 | \(\lim_{x \to a}[ f(x) – g(x)]= \lim_{x \to a} f(x) – \lim_{x \to a} g(x)\) | Разность пределов равна пределу разности. |
| 3 | \( \lim_{x \to a} cf (x) = c \lim_{x \to a} f (x) \) | Постоянное время предел функции равен пределу постоянного времени функции. |
| 4 | \(\lim_{x \to a}[ f(x)g(x)] = \lim_{x \to a} f(x) × \lim_{x \to a} g(x)]\) | Произведение пределов равно пределу произведения. |
9н\) | Где значение \( n\) является положительным целым числом, а если \( n \) четным. |
Как оценить лимиты?
Существуют различные способы определения лимитов, одним из лучших из которых является бесплатный калькулятор l’hopital. Но здесь мы будем разрабатывать каждый из них один за другим. Пойдем!
Метод подстановки:
В этом методе нам необходимо подставить значение лимита в функцию для оценки лимита. Вы также можете сделать это быстро, воспользовавшись этим онлайн-калькулятором лимита оценки. Как это звучит для вас?
Метод факторинга:
В этом методе вам нужно сделать множители, чтобы одинаковые условия можно было аннулировать. И когда есть оставшиеся термины, вы должны применить к ним ограничения в соответствии с правилом.
Правило Лопиталя:
Это действительно один из наиболее важных методов, используемых для оценки пределов в форме \(\frac{0}{0}\) или \(\frac{\inf}{ \инф}\). Чтобы применить этот метод, необходимо учитывать следующие моменты:
- Во-первых, следуйте методу замены, чтобы оценить предел. Если это приводит к \(\frac{0}{0}\) или \(\frac{\inf}{\inf}\), вам необходимо применить это правило. Еще одна легкость здесь заключается в том, что этот бесплатный калькулятор правил больниц занимает пару минут, чтобы распознать, является ли данная функция неопределенной или нет.
- Теперь, когда вы получите форму, как определено выше, вам нужно дифференцировать функцию.
После этого вы должны применить метод подстановки, чтобы найти предел данной функции.
Для лучшего приближения мы узнаем, как находить пределы, используя этот конкретный способ в примере позже.
Метод сопряжения:
В этом методе чаще всего встречаются комплексные числа. Теперь наш совет заключается в том, чтобы определить сопряжение данного числа. После того, как вы это сделаете, вам нужно упростить его и использовать этот калькулятор бесконечных пределов для определения границ любой функции.
Теперь наш совет заключается в том, чтобы определить сопряжение данного числа. После того, как вы это сделаете, вам нужно упростить его и использовать этот калькулятор бесконечных пределов для определения границ любой функции.
Бесконечный предел и рациональная функция:
Функция, которую можно записать в виде отношения двух многочленов:
$$ f(x) = \frac {P(y)} {Q(y)} $$
Мы можем найти предел функции 0, Inf, -Inf или вычислить по коэффициентам.
Как рассчитать пределы?
Как насчет решения нескольких примеров, чтобы понять, как вы используете различные методы для упрощения ограничений? Давайте погрузимся в это!
Пример № 01:
Оцените предел функции ниже:
$$ \lim_{x \to 13} \frac {x} {5} $$
Решение:
Здесь мы будем использовать метод подстановки:
$$ \lim_{x \to 13 } \frac {x} {5} $$
Положим x = 3;
$$ \lim_{x \to 13} \frac {x} {5} = \frac{13}{5} $$
$$ \lim_{x \to 13} \frac {x} {5 } = 2. 2} {y-2} $$ 92 – 4 } {y – 2} $$
2} {y-2} $$ 92 – 4 } {y – 2} $$
$$ = \lim_{y \to 2} \frac {(y-2) (y + 2)} {(y-2)} $$
Теперь подставляя у = 2;
$$ \lim_{y \to 2} ( y + 2 ) $$
$$ 2+2 = 4 $$
Вы также можете перепроверить все ответы, используя этот лучший калькулятор поиска предела в мерцание мгновений.
Пример № 03:
Как ограничить функцию, указанную ниже:
$$ \lim_{x \to 0} \left(\frac{sin x}{x}\right) $$
Решение:
Используя метод подстановки:
$$ \lim_{x \to 0} \left(\frac{sin x}{x}\right) $$
$$ = \frac{sin 0 {0} $$
$$ = \frac{0}{0} $$
Это неопределенная форма. Итак, здесь мы будем применять правило Лопиталя:
Прежде чем двигаться дальше, мы должны проверить, являются ли обе функции выше и ниже винкулума дифференцируемыми или нет.
$$ \frac{d}{dx} \left(sin x\right) = cos x $$
$$ \frac{d}{dx} \left(x\right) = 1 $$
Двигаемся дальше:
$$ \lim_{x \to 0} \left(\frac{cos x}{1}\right) $$
$$ = \frac{cos 0}{1} $$
$$ = 1 $$
Чтобы ускорить вычисления, попробуйте воспользоваться калькулятором правил l’Hospital.
Пример #04:
Как найти предел следующей функции:
$$ \lim_{z \to 9} \frac {3 – \sqrt {z}} {9 – \sqrt {z }} $$
Решение:
Если значение z равно 92} {( 9 – z ) (3 + \sqrt {z})} $$
$$ = \frac {( 9 – z )} {( 9 – z ) (3 + \sqrt {z})} $$
$$ = \frac {1} { 3 + \sqrt {z} } $$
$$ \lim_{z \to 9} \frac { 3 + \sqrt {z} } { 9 – z } $$
После отмены 9-z;
$$ \lim_{z \to 9} \frac {1} { 3 + \sqrt {z} } $$
$$ = \frac {1} { 3 + \sqrt {9} } $$
$$ = \frac {1} { 3 + 3 } $$
$$ = \frac {1} {6} $$
Как калькулятор лимитов вычисляет лимиты?
Графический калькулятор пределов позволяет оценить предел заданных переменных. Что ж, искатель пределов помогает найти пределы, выполнив указанные шаги:
Ввод:
- Прежде всего, введите уравнение или функцию.
- Выберите из раскрывающегося списка переменную, для которой необходимо оценить предел.
 Это может быть x,y,z,a,b,c или n.
Это может быть x,y,z,a,b,c или n. - Укажите число, по которому вы хотите рассчитать лимит. В этом поле вы также можете использовать простое выражение, такое как inf=∞ или pi =π.
- Теперь выберите направление ограничения. Может быть как положительным, так и отрицательным
- После того, как вы введете значения в данные поля, калькулятор выдаст вам предварительный просмотр уравнения.
- Нажмите кнопку расчета.
Вывод:
Калькулятор оценки свободных пределов выполняет следующие вычисления:
- Определяет пределы заданной функции
- Показать пошаговые расчеты
- Представляет разложение в ряд Тейлора для заданной функции
Часто задаваемые вопросы:
Как узнать, что ограничения не существует?
Чтобы найти предел на графике, если есть вертикальная асимптота и одна сторона стремится к бесконечности, а другая — в направлении отрицательной бесконечности, то предела не существует. Точно так же, если в графе есть дыра при значении x c, двустороннего предела не будет. Тем не менее, определитель пределов может помочь вам более точно оценить пределы.
Точно так же, если в графе есть дыра при значении x c, двустороннего предела не будет. Тем не менее, определитель пределов может помочь вам более точно оценить пределы.
Что такое правильное обозначение предела?
По сути, предельное обозначение — это способ сформулировать деликатную идею, а не просто сказать, что x=5 или y=3 \(\lim_{x \to a} f(x)=b\) С другой стороны, единица Калькулятор двусторонних пределов избавляет от беспокойства по поводу обозначений пределов, поскольку он решает пределы и указывает их неточное форматирование.
Можно ли применить правило Лопиталя ко всем пределам?
Правило Лопиталя используется с неуказанными пределами, которые имеют форму 0/0 или бесконечность. Это не устраняет все виды ограничений. Иногда даже повторное применение правила не может помочь найти предельные значения. Итак, для удобства калькулятор правила Лопиталя — лучший способ решения бесконечных пределов функций.
Может ли 0 быть пределом?
Если мы просто вычисляем предел уравнения 0/0, он не будет определен. Однако, если мы получим 0/0, тогда может быть ряд ответов. Теперь единственный способ определить точный ответ — использовать решатель пределов для точного определения предельных задач.
Однако, если мы получим 0/0, тогда может быть ряд ответов. Теперь единственный способ определить точный ответ — использовать решатель пределов для точного определения предельных задач.
Как пределы используются в расчетах?
Пределы определяют, как функция будет действовать вблизи точки, а не в этой точке. Эта идея лежит в основе исчисления. Например, пределом «f» при x=3 является значение f по мере того, как мы все ближе и ближе приближаемся к x=3. Это также можно было бы получить, подвергнув это лучшему калькулятору пределов.
Заключение:
Этот онлайн-калькулятор лимитов находит лимиты и, в частности, работает для решения лимитов по отношению к переменной. Пределы можно оценивать как с положительной, так и с отрицательной стороны. Он обслуживает все предельные задачи, которые невозможно решить алгебраически. Таким образом, здорово помочь студентам и профессионалам решить и проверить свои пределы в мгновение ока.
Ссылки:
Из официального источника Википедии: Предел (математика), функция, последовательность, стандартные детали и многое другое!
Источник Академии Хана предоставляет: Лучшая стратегия в поиске пределов
Из источника tutorial. math: Все, что вам нужно знать о приближении к пределу
math: Все, что вам нужно знать о приближении к пределу
Другие языки: Предел Hesaplama, Предел калькулятора, Гренцвертрехнер, Предел Калкулачка, Калькулятор пределов, Калькулятор пределов, Калькулятор пределов, Калькулятор пределов, Калькулятор Пределов.
Исчисление I. Пределы вычислений
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-5: Расчетные ограничения
В предыдущем разделе мы видели, что существует большой класс функций, который позволяет нам использовать
. \[\ mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left(a \right)\]
для вычисления лимитов. Тем не менее, есть также много ограничений, для которых это не будет легко работать. Цель этого раздела — разработать методы работы с некоторыми из этих ограничений, которые не позволят нам просто использовать этот факт.
Давайте сначала вернемся и посмотрим на один из первых пределов, которые мы рассмотрели, вычислим его точное значение и проверим наше предположение относительно предела. 92} — 2x}} & = \mathop {\lim }\limits_{x \to 2} \frac{{\left({x — 2} \right)\left({x + 6} \right)}} {{x\left( {x — 2} \right)}}\\ & = \mathop {\lim }\limits_{x \to 2} \frac{{x + 6}}{x}\end{align *}\]
Итак, разложив на множители, мы увидели, что можем сократить \(x — 2\) как в числителе, так и в знаменателе.
Обратите внимание, что на самом деле это то, что мы предполагали.
Прежде чем закончить этот пример, давайте обсудим тот факт, что мы не могли подставить \(x = 2\) в наш первоначальный предел, но как только мы сделали упрощение, мы просто подставили \(x = 2\), чтобы получить ответ. На первый взгляд может показаться, что это противоречие.
В исходном пределе мы не могли подставить \(x = 2\), потому что это давало нам ситуацию 0/0, с которой мы ничего не могли сделать. Сделав упрощение, мы можем заметить, что 92} — 2x}} = \frac{{x + 6}}{x}\hspace{0,25 дюйма}{\mbox{при условии}}x \ne 2\]
Другими словами, два уравнения дают одинаковые значения, за исключением точки \(x = 2\), а поскольку пределы касаются только того, что происходит вокруг точки \(x = 2\), предел двух уравнений будет равен равный.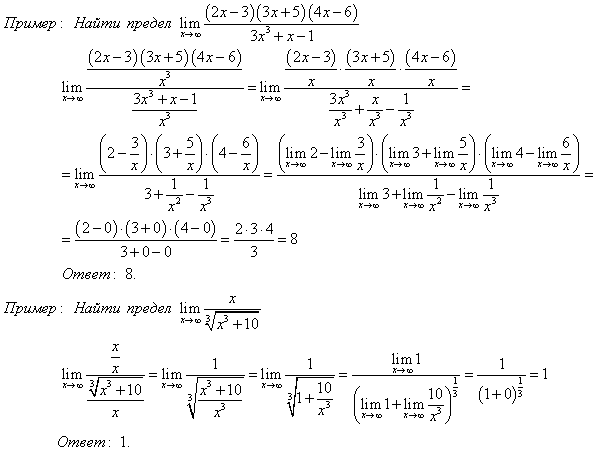 Что еще более важно, в упрощенной версии мы получаем «достаточно хорошее» уравнение, и поэтому то, что происходит вокруг \(x = 2\), идентично тому, что происходит при \(x = 2\).
Что еще более важно, в упрощенной версии мы получаем «достаточно хорошее» уравнение, и поэтому то, что происходит вокруг \(x = 2\), идентично тому, что происходит при \(x = 2\).
Таким образом, мы можем взять предел упрощенной версии, просто подставив \(x = 2\), даже если мы не смогли подставить \(x = 2\) в исходное уравнение, а значение предела упрощенной версии уравнение будет таким же, как предел исходного уравнения.
Кстати, 0/0, которое мы изначально получили в предыдущем примере, называется неопределенной формой . Это означает, что мы на самом деле не знаем, что это будет, пока не проделаем дополнительную работу. Как правило, ноль в знаменателе означает, что он не определен. Однако это будет верно только в том случае, если числитель не равен нулю. Кроме того, ноль в числителе обычно означает, что дробь равна нулю, если только знаменатель также не равен нулю. Точно так же все, что делится само на себя, равно 1, если только мы не говорим о нуле.
Итак, здесь действительно три конкурирующих «правила», и непонятно, какое из них победит. Также возможно, что ни один из них не выиграет, и мы получим что-то совершенно отличное от undefined, нуля или единицы. Мы могли бы, например, получить из этого значение 4, чтобы выбрать число совершенно случайно.
Также возможно, что ни один из них не выиграет, и мы получим что-то совершенно отличное от undefined, нуля или единицы. Мы могли бы, например, получить из этого значение 4, чтобы выбрать число совершенно случайно.
При простом вычислении уравнения 0/0 не определено. Однако, принимая предел, если мы получаем 0/0, мы можем получить множество ответов, и единственный способ узнать, какой из них правильный, — это фактически вычислить предел. 92}}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{h\left( { — 12 + 2h} \right)}}{h}\\ & = \ mathop {\ lim} \ limit_ {h \ to 0} \, \, — 12 + 2h = — 12 \ end {align *} \]
Пример 3 Оцените следующий предел. \[\ mathop {\lim }\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}}\]
Показать решение
Этот предел требует немного больше работы, чем два предыдущих. Однако еще раз обратите внимание, что мы получаем неопределенную форму 0/0, если пытаемся просто оценить предел. Также обратите внимание, что ни один из двух примеров здесь не поможет, по крайней мере, на начальном этапе. Мы не можем разложить уравнение на множители и не можем просто что-то умножить, чтобы упростить уравнение. 92}\]
Также обратите внимание, что ни один из двух примеров здесь не поможет, по крайней мере, на начальном этапе. Мы не можем разложить уравнение на множители и не можем просто что-то умножить, чтобы упростить уравнение. 92}\]
Итак, если в первом и/или втором члене есть квадратный корень, рационализация устранит корень(и). Этот может помочь в оценке предела.
Попробуем рационализировать числитель в этом случае.
\[\ mathop {\lim }\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}} = \mathop {\lim }\limits_{t \ до 4} \frac{{\left( {t — \ sqrt {3t + 4}} \right)}}{{\left( {4 — t} \right)}}\,\frac{{\left( {t + \sqrt {3t + 4}} \right)}}{{\left( {t + \sqrt {3t + 4}} \right)}}\] 92} — 3t — 4}}{{\left( {4 — t} \right)\left( {t + \sqrt {3t + 4} } \right)}}\end{align*}\]
Обратите внимание, что мы также не умножали знаменатель. Большинство студентов заканчивают занятия по алгебре с вбитой в голову мыслью всегда умножать этот материал. Однако в этом случае умножение сделает задачу очень сложной, и в конце концов вы все равно просто разложите ее на множители.
Однако в этом случае умножение сделает задачу очень сложной, и в конце концов вы все равно просто разложите ее на множители.
На этом этапе мы почти закончили. Обратите внимание, что мы можем разложить числитель на множители, так что давайте сделаем это.
\[\ mathop {\lim }\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}} = \mathop {\lim }\limits_{t \ до 4} \frac{{\left( {t — 4} \right)\left( {t + 1} \right)}}{{\left( {4 — t} \right)\left( {t + \sqrt {3t + 4} } \справа)}}\]
Теперь все, что нам нужно сделать, это заметить, что если мы вычитаем «-1» из первого члена в знаменателе, мы можем сделать некоторое сокращение. В этот момент проблема деления на ноль исчезнет, и мы сможем оценить предел.
\[\begin{align*}\mathop {\lim}\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}} & = \mathop {\ lim }\limits_{t \to 4} \frac{{\left( {t — 4} \right)\left( {t + 1} \right)}}{{ — \left( {t — 4} \ right)\left( {t + \sqrt {3t + 4} } \right)}}\\ & = \mathop {\lim }\limits_{t \to 4} \frac{{t + 1}}{{ — \left( {t + \sqrt {3t + 4} } \right)}}\\ & = — \frac{5}{8}\end{align*}\]
Заметим, что если бы мы умножили знаменатель, мы бы не смогли сделать это сокращение и, по всей вероятности, даже не увидели бы, что какое-то сокращение можно было бы сделать. 92} + 5 & \hspace{0.25in}{\mbox{if }}y < - 2\\ 1 - 3y & \hspace{0.25in}{\mbox{if }}y \ge - 2\end{align *} \Правильно.\]
92} + 5 & \hspace{0.25in}{\mbox{if }}y < - 2\\ 1 - 3y & \hspace{0.25in}{\mbox{if }}y \ge - 2\end{align *} \Правильно.\]
Вычислите следующие пределы.
- \(\ mathop {\lim }\limits_{y \to 6} g\left( y \right)\)
- \(\ mathop {\lim }\limits_{y \to — 2} g\left( y \right)\)
Показать все решения Скрыть все решения
a \(\mathop {\lim }\limits_{y \to 6} g\left( y \right)\) Показать решение
В этом случае делать особо нечего. При выполнении ограничений помните, что мы всегда должны смотреть на то, что происходит по обе стороны от рассматриваемой точки, когда мы приближаемся к ней. В этом случае \(y = 6\) полностью находится внутри второго интервала функции, поэтому по обе стороны от \(y = 6\) есть значения \(y\), которые также находятся внутри этого интервала. Это означает, что мы можем просто использовать этот факт для оценки этого предела.
\[\begin{align*}\mathop {\lim}\limits_{y \to 6} g\left(y\right) & = \mathop {\lim}\limits_{y \to 6}( 1 — 3y )\\ & = — 17\end{align*}\]
b \(\mathop {\lim }\limits_{y \to — 2} g\left( y \right)\) Показать решение
Эта часть является реальной причиной этой проблемы. В этом случае точка, для которой мы хотим взять предел, является точкой отсечки для двух интервалов. Другими словами, мы не можем просто подставить \(y = — 2\) во вторую часть, потому что этот интервал не содержит значений \(y\) слева от \(y = — 2\) и нам нужно знать, что происходит по обе стороны точки.
Чтобы выполнить эту часть, нам нужно вспомнить факт из раздела об односторонних пределах, в котором говорится, что если два односторонних предела существуют и одинаковы, то нормальный предел также будет существовать и иметь то же значение.
Обратите внимание, что оба односторонних ограничения могут быть выполнены здесь, так как мы будем смотреть только на одну сторону рассматриваемой точки. 2} + 5 & \hspace{0.25in}{\mbox{if}}y < - 2\\ 3 - 3y & \hspace{0.25in}{ \mbox{if }}y \ge - 2\end{align*} \right.\]
9+ }{\mbox{ подразумевает }}y > — 2\\ & = 9\end{align*}\]
2} + 5 & \hspace{0.25in}{\mbox{if}}y < - 2\\ 3 - 3y & \hspace{0.25in}{ \mbox{if }}y \ge - 2\end{align*} \right.\]
9+ }{\mbox{ подразумевает }}y > — 2\\ & = 9\end{align*}\]
Односторонние пределы одинаковы, поэтому мы получаем
\[\ mathop {\lim}\limits_{y \to — 2} g\left( y \right) = 9\]
Есть еще один предел, который нам нужно сделать. Однако нам понадобится новый факт о пределах, который поможет нам в этом.
Факт
Если \(f\left( x \right) \le g\left( x \right)\) для всех \(x\) на \([a, b]\) (за исключением, возможно, \ (x = c\)) и \(a \le c \le b\), тогда
\[\ mathop {\lim }\limits_{x \to c} f\left( x \right) \le \ mathop {\lim }\limits_{x \to c} g\left(x \right)\]
Обратите внимание, что этот факт должен иметь для вас некоторый смысл, если мы предположим, что обе функции достаточно хороши. Если обе функции «достаточно хороши», чтобы использовать факт вычисления предела, то мы имеем
. \[\ mathop {\lim}\limits_{x \to c} f\left(x\right) = f\left(c\right) \le g\left(c\right) = \mathop {\lim} \limits_{x \to c} g\left( x \right)\]
\[\ mathop {\lim}\limits_{x \to c} f\left(x\right) = f\left(c\right) \le g\left(c\right) = \mathop {\lim} \limits_{x \to c} g\left( x \right)\]
Неравенство верно, потому что мы знаем, что \(c\) находится где-то между \(a\) и \(b\), и в этом диапазоне мы также знаем \(f\left( x \right) \le g\ влево( х \вправо)\).
Обратите внимание, что на самом деле нам не нужно, чтобы две функции были достаточно хорошими, чтобы факт был правдой, но он обеспечивает хороший способ дать быстрое «обоснование» факту.
Также обратите внимание, что мы сказали, что предполагали, что \(f\left( x \right) \le g\left( x \right)\) для всех \(x\) на \([a, b]\ ) (за исключением, возможно, точки \(x = c\)). Поскольку пределы не заботятся о том, что на самом деле происходит в \(x = c\), нам на самом деле не нужно, чтобы неравенство выполнялось в этой конкретной точке. Нам нужно только, чтобы он держался вокруг \(x = c\), так как это то, о чем заботится предел.
Мы можем развить этот факт еще на один шаг, чтобы получить следующую теорему.
Теорема сжатия
Предположим, что для всех \(x\) на \([a, b]\) (кроме, возможно, на \(x = c\)) имеем
\[f\влево( x \вправо) \le h\влево( x \вправо) \le g\влево( x \вправо)\]
Также предположим, что
\[\ mathop {\ lim} \ limit_ {x \ to c} f \ left ( x \ right) = \ mathop {\ lim } \ limits_ {x \ to c} g \ left ( x \ right) = L \ ]
для некоторых \(a \le c \le b\). Затем
\[\ mathop {\lim}\limits_{x \to c} h\left( x \right) = L\]
Как и в случае с предыдущим фактом, нам нужно только знать, что \(f\left( x \right) \le h\left( x \right) \le g\left( x \right)\) верно вокруг \( x = c\), потому что мы работаем с ограничениями, а они касаются только того, что происходит вокруг \(x = c\), а не того, что на самом деле происходит в \(x = c\).
Теперь, если мы снова предположим, что все три функции достаточно хороши (опять же, это не требуется, чтобы сделать теорему о сжатии верной, это только помогает с визуализацией), тогда мы можем получить быстрый набросок того, что говорит теорема о сжатии. нас. На следующем рисунке показано, что происходит в этой теореме.
нас. На следующем рисунке показано, что происходит в этой теореме.
Из рисунка видно, что если пределы \(f(x)\) и \(g(x)\) равны в \(x = c\), то значения функции также должны быть равны в \ (x = c\) (здесь мы используем тот факт, что мы предполагали, что функции «достаточно хороши», что на самом деле не требуется для теоремы). Однако, поскольку \(h(x)\) «зажато» между \(f(x)\) и \(g(x)\) в этой точке, то \(h(x)\) должно иметь то же значение . Следовательно, предел \(h(x)\) в этой точке также должен быть таким же.
Теорема сжатия также известна как 92} \ cos \ влево ( {\ гидроразрыва {1} {х}} \ вправо) \]
Показать решение
В этом примере ни один из предыдущих примеров нам не поможет. Здесь нет факторинга или упрощения. Мы не можем рационализировать, и односторонние ограничения не сработают. Возникает даже вопрос, будет ли существовать этот предел, поскольку у нас есть деление на ноль внутри косинуса при \(x=0\).



 .
. Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению.
Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению. x приближается к 0, равен 1.
x приближается к 0, равен 1. Эта неопределённость обозначается символом ∞. Когда её упоминают, то имеют в виду как бесконечно малое число, так и большое. Для записи предела функций используется знак лимита, например, lim 0k (y). В нижней части указывается аргумент со стрелочкой, обозначающей, к чему именно стремится неопределённость. Если предел известный, то он называется конечным, в ином случае — бесконечным.
Эта неопределённость обозначается символом ∞. Когда её упоминают, то имеют в виду как бесконечно малое число, так и большое. Для записи предела функций используется знак лимита, например, lim 0k (y). В нижней части указывается аргумент со стрелочкой, обозначающей, к чему именно стремится неопределённость. Если предел известный, то он называется конечным, в ином случае — бесконечным. Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞.
Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞. То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a.
То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a. Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L.
Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L. Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя.
Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя.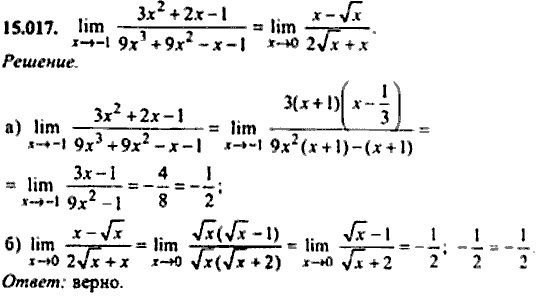 В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ .
В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ . Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень.
Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень. Таким образом, решение будет равняться минус единице.
Таким образом, решение будет равняться минус единице.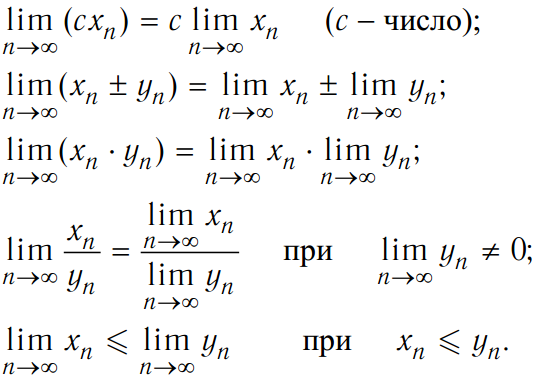 Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0. Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности.
Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0. Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности.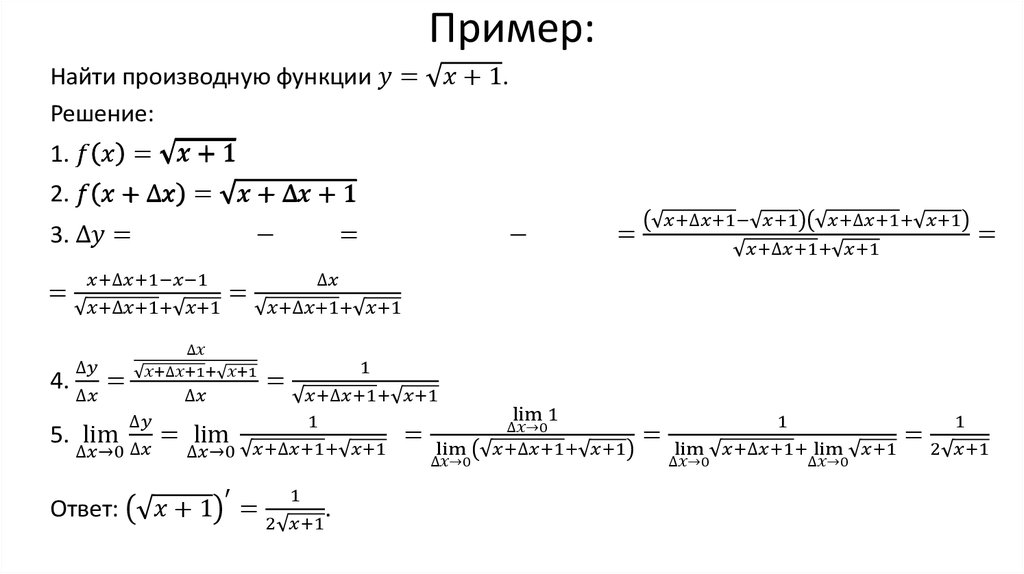 Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению.
Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению.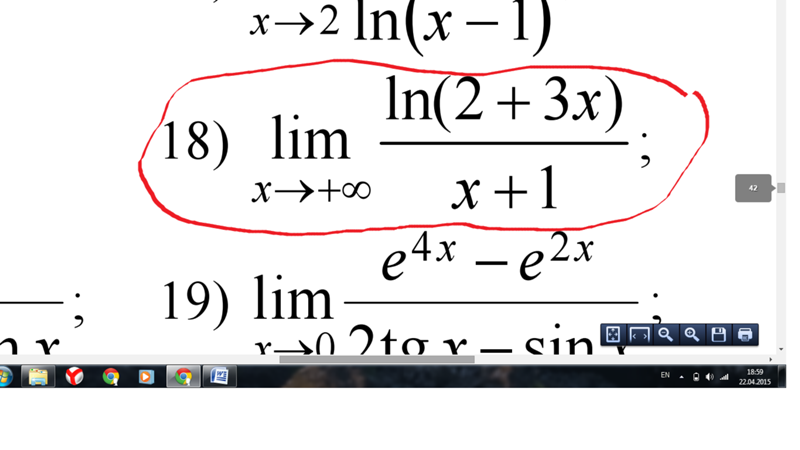 semestr.
semestr.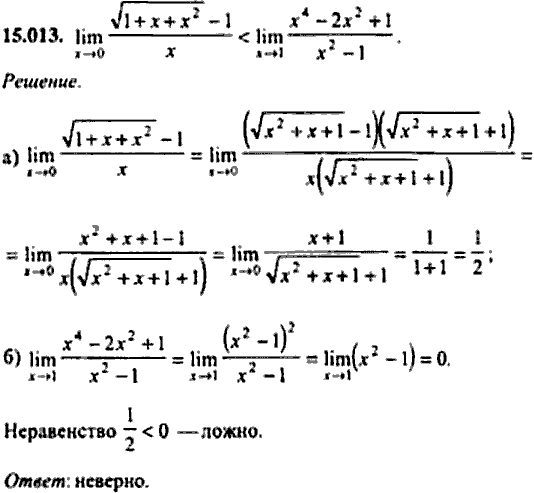 Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).
Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).
 В других выражениях, например в суммах, делать такую замену нельзя.
В других выражениях, например в суммах, делать такую замену нельзя.
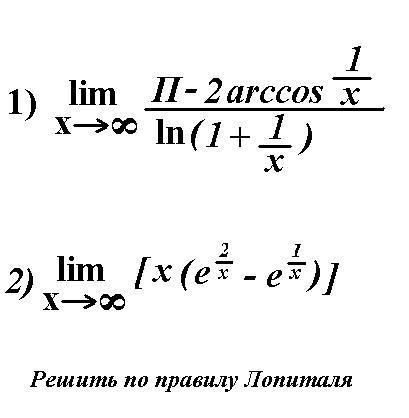




 Наш калькулятор Тейлора предоставляет пошаговое решение для заданной функции. Этот калькулятор разложения в ряд Тейлора также используется для указания порядка многочлена Тейлора. 9x и т. д.
Наш калькулятор Тейлора предоставляет пошаговое решение для заданной функции. Этот калькулятор разложения в ряд Тейлора также используется для указания порядка многочлена Тейлора. 9x и т. д.

 Это может быть x,y,z,a,b,c или n.
Это может быть x,y,z,a,b,c или n.