Решение линейных уравнений методом гаусса калькулятор онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Содержание

Решение СЛАУ методом Гаусса — онлайн калькулятор, бесплатный сервис

Компания Zaochnik предлагает воспользоваться нашим сервисом для решения уравнений. Это сэкономит ваше время на расчеты, поможет избежать ошибки в преобразованиях и получить точный результат. Многоступенчатые вычисления основаны на математических формулах. Поэтому промежуточные ответы не теряются, а используются в следующих действиях.

В автоматизации процесса последовательно выполняются необходимые действия. Записывается расширенная матрица системы, происходят элементарные преобразования, в процессе удаляются нулевые строки. После этого матрица имеет ступенчатый вид и подвергается обратному ходу метода Гаусса.

Рассмотрим несколько примеров решений СЛАУ с помощью онлайн-калькулятора

Онлайн-калькулятор позволяет находить решение СЛАУ, когда свободные члены, переменные и коэффициенты при них являются вещественными числами. Максимальное количество неизвестных – 6.

Важно: калькулятор не работает с комплексными числами!

Пример 1.

Возьмем простую систему уравнений с двумя неизвестными:

x1+2×2=113×1-x2=12

Для того, чтобы решить ее методом Гаусса с помощью онлайн-калькулятора:

Укажем количество неизвестных в системе:
Впишите коэффициенты при переменных в соответствующие поля:
Нажмите «Рассчитать»
Калькулятор сам произведет все вычисления, а вы сможете не только получить ответ, но и ознакомиться подробным решением:

Пример 2.

Рассмотрим более сложную систему с большим количеством неизвестных:
2×1+10×2-3×3=38-3×1-24×2+5×3=-86×1+x2-5×3=27

По аналогии с первым примером, укажем количество неизвестных, введем в поля соответствующие коэффициенты, и нажмем «Рассчитать»:

Калькулятор выдаст ответ с ходом решения и промежуточными выкладками:

Заметьте, если вы вдруг введете неверные коэффициенты или запишите такую систему, которая не имеет решения, калькулятор выдаст соответствующее сообщение:

Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:

Решение квадратных уравнений: формула корней, примеры
Уравнение и его корни: определения, примеры
Теорема Виета, формулы Виета
Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
Квадратные неравенства, примеры, решения
Решение квадратных неравенств методом интервалов

Ответ:

Решение

Ответ:

list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

Решение квадратных уравнений
Решение систем линейных уравнений методом Крамера
Решение систем линейных уравнений матричным методом
Решение систем линейных уравнений методом подстановки

Решение биквадратных уравнений

Калькулятор с решением систем линейных уравнений методом Гаусса

В наш раздел с калькуляторами часто заходят учащиеся школ и университетов при подготовке к занятиям и во время контрольных работ.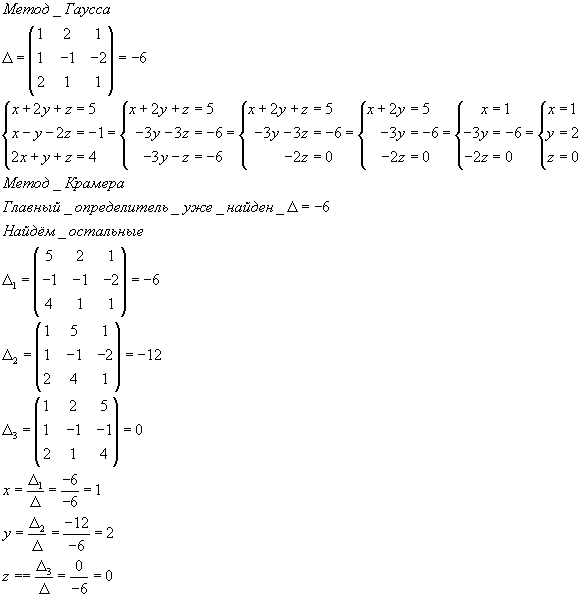 Также производят вычисления преподаватели для экономии времени при проверке большого количества заданий.

Применяйте метод Гаусса в решении систем линейных уравнений онлайн. Для этого следуйте инструкции:

задайте число неизвестных в системе;
введите условие в соответствующие поля;
воспользуйтесь кнопкой «Рассчитать».

После отправки задачи на расчет вы мгновенно получаете ответ. При этом вам видны все действия. Глядя на готовые вычисления легче разбирать используемый математический метод. Для следующего аналогичного примера вы можете применить известный алгоритм и самостоятельно найти ответ к задаче.

Если процесс решения на калькуляторе вам непонятен, обратитесь за индивидуальной помощью. Специалист компании решит ваши задания с подробным введением в тему. Напишите консультанту или оформите заказ.

Понравился калькулятор? Поделись с друзьями!

Решение уравнений методом Гаусса онлайн калькулятор

Карл Фридрих Гаусс — немецкий математик, механик, физик, астроном и геодезист.

Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса позволяет максимально легко и быстро решить систему линейных алгебраических уравнений (СЛАУ). Успех данного метода заключается в последовательном исключении неизвестных из уравнений. Сегодня решить систему алгебраических уравнений онлайн методом Гаусса можно с помощью специальных решательов, но ниже мы разберем решение системы линейных уравнений, чтобы наглядно на примере увидеть все его достоинства.

Так же читайте нашу статью «Решить уравнение матричным способом онлайн решателем»

Допустим, дана система линейных уравнений:

\[\left\{\begin{matrix} 2\cdot x_1+4\cdot x_2+1\cdot x_3 = 36\\ 5\cdot x_1 + 2 \cdot x_2 +1 \cdot x_3 =47\\ 2\cdot x_1 + 3\cdot x_2 + 4 \cdot x_3 = 37 \end{matrix}\right. \]

Представим ее в матричной форме:

\[\begin{bmatrix} 2 & 4 & 1\\ 5 & 2 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 36\\ 47\\ 37 \end{bmatrix}\]

Выберем строку с максимальным коэффициентом \[a_i1\] и меняем ее с первой.

\[\begin{bmatrix} 5 & 2 & 1\\ 2 & 4 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 47\\ 36\\ 37 \end{bmatrix}\]

Нормируем уравнения относительно коэффициента при \[x_1\]:

\[\begin{bmatrix} 1 & \frac{2}{5} & \frac{1}{5}\\ 2 & \frac{4}{2} & \frac{1}{2}\\ 2 & \frac{3}{2} & \frac{4}{2} \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} \frac{47}{5}\\ \frac{36}{2}\\ \frac{37}{2} \end{bmatrix} \]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 1 & 2 & 1\\ 1 & 1.5 & 2 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9. 4\\ 9.6\\ 9.1 \end{bmatrix}\]

Вычитаем 1 уравнение из 2 и 3:

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Выбираем строку с наибольшим коэффициентом при \[a_i2\] (уравнение 1 не рассматривается) и перемещаем ее на место 2.

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Нормируем 2 и 3 уравнения относительно коэффициента при \[x_2\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 1 & 1.636 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 8.272 \end{bmatrix}\]

Вычитаем уравнение 2 из 3

\[\begin{bmatrix} 1 & 0.4 & 0. T\].

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Решение системы линейных уравнений методом Гаусса-Жордана

Укажите количество уравнений в системе m=2345678910

метод Гаусса–Жордана – один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0.

Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.

Алгоритм метода Гаусса

На основании системы линейных уравнений составляем расширенную матрицу системы;
Приводим матрицу к “треугольному” виду;
Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через
переменные которые могут принимать произвольные значения;

Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

Рассматриваем строку i(начиная с первой). Если, элемент aⁱ_i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a¹₁ отличен от нуля – переходим к следующему шагу;
Для каждой строки j, ниже i-й находим значение коэффициента K_j=a^j_i/aⁱ_i;
Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a^j_kнов. =a^j_k-K_j*aⁱ_k;
После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n – размерность матрицы A
В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пaⁱ_i, которое и будет являтся определителем;

Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.

Комментарий к шагу 3 Метода Гаусса. Рангом матрицы A размера m × n называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы A обозначается через r(A) = rangA = rankA.
Минором M (от латинского “minor” меньший) k-го порядка матрицы A называется определитель некоторой матрицы, составленной из элементов матрицы A, стоящих на пересечении произвольно выбранных k
строк и k столбцов с сохранением их порядка. Если номера столбцов, в которых расположен минор M, совпадают с номерами строк, то этот минор называется главным. Каждая матрица A порядка n имеет
(C^k_n)2 миноров k-го порядка. Минорами 1-го порядка являются сами элементы матрицы A.

Основываясь на сравнении полученных значений рангов для основной и расширенной матрицы можно сделать следующие выводы о разрешимости системы:

если ранг основной системы равен рангу расширенной и равен числу уравнений системы (rangA=rangA’=n), то система совместна и имеет единственное решение;
если ранг основной системы равен рангу расширенной, но меньше числа уравнений в системе (rangA=rangA’
если ранг основной системы меньше ранга расширенной (rangA

Подробнее

Финансовая математика. 12 задач решены с помощью финансовых функций MS EXCEL

Решение задач, Финансовый менеджмент

Выполнил: user387341

Экономико-математические методы Задача 16 (решение через поиск решения в Excel)

Решение задач, Высшая математика

Выполнил: Мудрый Тушканчик

Так же вы можете купить уже выполненные похожие работы. Для удобства покупки работы размещены на независимой бирже. Подробнее об условиях покупки тут.

Решение систем линейных уравнений алгоритмы общих и частных методов нахождения корней, основные правила и теоремы и примеры их использования, онлайн калькулятор

Совокупность математических записей, из которых каждая является линейным алгебраическим равенством первой степени, называется системой линейных уравнений. Её решение — это классическая задача алгебры, определяющая объекты и методы. Существует несколько принципиально разных способов нахождения ответа. Каждый из них имеет достоинства и недостатки, но выбор метода зависит лишь только от личных предпочтений решающего.

Понятия и обозначения

Для измерения геометрических или физических величин в математике используют действительное число — вещественное. В уравнении под ним понимают все свободные члены или неизвестные переменные. Вычисление линейных алгебраических уравнений играет важную роль в различных математических задачах: численных методах, программировании, эконометрике.

Общий вид системы линейных уравнений (СЛАУ) в классическом понимании представляют следующим образом:

a11 * n 1 + a 12 * n 2 + …+a 1x n x = c 1.

a21 * n 1 + a 22 * n 2 + …+a 2x n x = c 2.

as1 * n 1 + a 12 * n 2 + …+a 1x n x = c s.

В этой записи s — это количество уравнений, x — число переменных, а n — переменная которую необходимо вычислить. Предполагается что a и b это известные свободные члены. Индексы обозначают порядковый номер уравнения. Первый символ — расположение строчки, а второй — позиция произведения переменной и свободного члена.

Если эти члены отличные от нуля, то система называется неоднородной, в ином же случае однородной. Квадратной системой называется совокупность уравнений, когда их число совпадает с количеством неизвестных. Существует понятие и неопределённой системы. Это совокупность, при которой неизвестных больше числа уравнений. Если наоборот, то система считается переопределенной. В литературе её ещё часто называют прямоугольной.

Система считается решаемой, когда множество членов X соответствует такому набору чисел, что при их подстановке вместо n вся система обратится в тождество. Если существует хотя бы одно решение, система называется совместной. Ответы, превращающие уравнения в равенства, при которых переменные не совпадают, считаются различными.

Существует четыре способа развязывания системы уравнений:

способ подстановки;
использование новых переменных;
алгебраическое сложение;
матричный метод.

Вид используемого алгоритма зависит от типа примера. Метод алгебраического сложения применяют, когда в задании лишь одно неизвестное, а коэффициенты противоположны или равны. Если же хотя бы в одной из формул коэффициент равен единице, то удобнее будет решить систему уравнений методом подстановки. В иных случаях используют матрицы.

Алгебраическое сложение

Способ заключается в сложении или вычитании выражений. Это довольно простой способ и в то же время эффективный. Алгоритм нахождения ответа для равенств с двумя переменными n и m сводится к следующему:

уравниванию модулей коэффициентов при любом из неизвестных;
сложению или вычитанию равенства;
вычисления составленного выражения;
прогонки каждого найденного корня через первую или вторую строчку системы уравнений;
нахождению второго неизвестного.

То есть после выполнения арифметических действий с уравнениями должно получиться одно выражение с одним неизвестным. Затем находят значение этой переменной и в него подставляют полученный корень. Например, нужно узнать, какие корни системы, состоящей из двух строчек, превращают её в тождество:

n2 – m2 = 21.

n2 + m2 = 29.

В первую очередь необходимо сложить равенства между собой. В итоге получится:

2 * n 2 = 50;
n 2 = 25;
n = +5 (-5).

Подставив поочерёдно в каждое равенство найденные корни можно найти второе неизвестное. Для корня n = – 5 ответом будет:

(-5)2 + m2 = 29;
25 + m2 = 29;
m2 = 29 – 25;
m2 = 4.

Соответственно, корнями будут числа два и минус два. Аналогичные действия необходимо выполнить и для корня другого знака n = 5. В итоге получится, что пары (− 5; − 2), (− 5; 2), (5; − 2), (5 ; 2) являются нужным ответом. При достаточном опыте подробно описывать решение не обязательно.

Существуют системы, требующие подготовительного этапа. Например, такого вида:

3 * n – 4 * m = 5.

2 * n + 3 * m = 7.

Исключить здесь сразу переменную не выйдет. Если умножить все члены первой строчки на тройку, а второй на четвёрку, получится запись:

9 * n – 12 * m = 15.

8 * n + 12 * m = 28.

Теперь равенства можно сложить, тем самым исключив переменную m. Затем система решается по базисному алгоритму. Чтобы понять, можно ли решить систему этим методом, следует предварительно её проанализировать. Необходимое условие заключается в том, что коэффициенты второй переменной должны быть одинаковыми по модулю, но противоположными по знаку.

Метод подстановки

Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:

через n в одном из уравнений выражают m;
подставляют полученное равенство вместо n в другое тождество;
решают уравнение и находя m;
поочерёдно подставляют найденные корни и получают ответ.

Например, нужно проверить, все ли целые корни могут быть у системы:

8 * n – 5 * m = -16.

10 * n + 3 * m = 17.

Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.

Использование матриц

Для систем с произвольным числом уравнений и неизвестных используют другие методы. Если система состоит из нелинейных дифференциальных уравнений с постоянными коэффициентами, то используют матричный способ. Этот метод предполагает применение обратной матрицы.

Пусть дана система с тремя неизвестными х1, х2, х3. Нужно найти значения, при которых равенства станут верными. Для нахождения решений используют три матрицы:

Коэффициент системы. При этом её определитель не должен быть равным нулю.
Вектора неизвестных. Именно его понадобится найти.
Столбца свободных членов.

Базисное решение строят на произведении первой и второй матрицы. В результате получают матрицу размером три на один. То есть вектор-столбец с тремя элементами. После выполнения действия получится, что системный вектор будет равен левой части системы и соответствовать третьей матрице. Таким образом, обозначив матрицы буквами А, Б, В, можно записать выражение А * Б = В и найти необходимую Б.

При умножении на А-1 (обратную матрицу) получают равенство: Е * Б = А-1 * В, где Е – единичная матрица получена из совместимости прямой и обратной. Так как при произведении с единичной матрицей значения не изменяются, то решением системы будет формула: Б = А-1 * В.

Способ Гаусса-Жордана

Частным случаем решения системы является Метод Гаусса — Жордана. Суть решения основана на составлении специальной таблицы. В первый столбец заносятся известные значения, то есть величины, расположенные после равно, а в три других коэффициенты, стоящие после неизвестных. Чтобы приступить к решению, необходимо выполнить три шага:

выбрать ключевой элемент из первых трёх столбцов;
переписать строчку с ключевым значением, предварительно разделив все элементы на это значение;
переписать оставшиеся элементы, при этом вычитая из него произведение соответствующих ему чисел.

В полученной новой матрице снова выбирают ключевой элемент и выполняют все действия снова. Шаги повторяют до тех пор, пока не получится матрица, состоящая из нулей и единиц. Значения корней системы будут находиться на пересечении столбцов со строчками напротив единиц.

Этот метод используют только при выполнении условия совместности. Его ещё называют способом простой итерации. Он был доказан и оптимизирован Зейделем. С помощью итерационного метода можно посчитать систему А* Б = В с точностью “е”. Составляют n уравнение на сходимость, а затем на точность. Затем из первого уравнения выражают n1, второго n2, третьего n3 и так далее. Новые n с индексом i +1 считаются через старые i. Зейдель предложил расширить решение и добавить снова для счёта индекс i+1.

Это фундаментальные способы решения сложных систем уравнений. Они трудные, требуют опыта и внимательности. Поэтому существуют специальные онлайн-калькуляторы по методу Гаусса с подробным решением, помогающие исследовать систему любой численности.

Теорема Кронекера — Капелли

Применяется она при проведении исследований без непосредственного решения. То есть для записи эквивалентной совокупности алгебраических уравнений с их минимальным числом. Теорема говорит о следующем: система уравнений А * Б = В имеет решение только тогда, когда ранг А равен (А, В), где последнее расширенная матрица, полученная из первого члена путём приписывания столбца В.

Это утверждение обобщает различные виды СЛАУ:

Несовместные – которые определяют при условии, что их ранг меньше ранга расширенной матрицы. Существование корней невозможно.
Совместные неопределённые – системы, имеющие бесконечное множество решений. В этом случае ранги равны, а количество неизвестных будет меньше.
Совместно определённые – в этом случае ранг равен расширенной матрице и количеству неизвестных. Точное решение будет одно.

Выводом из этой теоремы является то, что число главной переменной совокупности будет всегда равно рангу системы. При этом столбец свободных членов представляет собой линейную комбинацию столбцов матрицы А.

Решение Крамера

Пожалуй, это один из самых простых способов нахождения корней уравнений. Для решения строят несколько матриц. Основная получается из коэффициентов, стоящих при неизвестных. Она обозначается символом дельта. Вторую, дельта-икс, образуют из основной матрицы заменой первого столбца на ответы уравнений. Следующая, дельта-игрек, строится с заменой в основной матрице второго столбца на значения ответов и так далее.

Затем вычисляют дискриминант этих матриц, то есть их определитель. Для его поиска можно использовать способ треугольника или разложения. Первый подходит для простых матриц. Находят его как разницу умножения чисел, стоящих в матрице крест-накрест. Второй же применим для матриц, содержащих три и более строк. При нахождении выбирают одну из них и раскладывают матрицу.

Как только все дискриминанты найдены, используют правило Крамера: n = Δn/ Δ. Подставляют значения, находят ответ. Стоит отметить, что много интернет-порталов, предлагающих услугу расчётов СЛАУ, используют для вычислений онлайн-метод Крамера.

Удобные онлайн-калькуляторы

В некоторых случаях решение СЛАУ онлайн будет хорошим подспорьем для того, чтобы разобраться в различных правилах, используемых при решениях. Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.

Для выполнения расчёта необходимо ввести параметры системы и нажать кнопку «Рассчитать». При этом можно выбрать метод, на базе которого будут проводиться вычисления. Удобным является и то, что полученный расчёт сопровождается объяснениями.

На этих порталах также можно посмотреть примеры и правила решений. Некоторые калькуляторы могут построить и график системы. Например, kontrolnaya-rabota. Для этого на сайте нужно выбрать раздел «Графическое решение уравнений онлайн» и ввести исследуемую систему равенств.

Система комплексных линейных уравнений

Египетские дроби. Часть вторая
Египетские (аликвотные) дроби
По сегменту определить радиус окружности
Круг и площадь, отсекаемая перпендикулярами
Деление треугольника на равные площади параллельными
Определение основных параметров целого числа
Свойства обратных тригонометрических функций
Разделить шар на равные объемы параллельными плоскостями
Взаимосвязь между организмами с различными типами обмена веществ
Аутотрофные и миксотрофные организмы
Рассечение круга прямыми на равные площади
Период нечетной дроби онлайн. Первые полторы тысяч разложений.
Представить дробь, как сумму её множителей
Решение системы из двух однородных диофантовых уравнений
Расчет основных параметров четырехполюсника
Цепочка остатков от деления в кольце целого числа
Система счисления на базе ряда Фибоначчи онлайн
Уравнение пятой степени. Частное решение.
Рассчитать площадь треугольника по трем сторонам онлайн
Общее решение линейного диофантового неоднородного уравнения
Частное решение диофантового уравнения с несколькими неизвестными
Онлайн разложение дробно рациональной функции
Корни характеристического уравнения
Имя пользователя при работе с Excel
Распределение частот появления букв русского алфавита в текстах

Элементы комплексной системы линейных уравнений

77 acos(i-8) -i -2i (4+2i)/3 10+3

Вы ввели следующую систему уравнений

Решение системы следующее

Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:

— иметь только одно верное решение;

— иметь бесконечное множество корней;

— иметь несовместный тип (когда решений быть не может).

Метод Гаусса, используемый нашим АБАК-ботом — самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.

Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т.н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами — ровно то же самое, что и элементарные преобразования матриц в переложении для строк.

Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!

Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей а также в множестве специализированных задач. 3&2\\-11&5&-7\end{pmatrix}*\begin{pmatrix}x_0\\x_1\\x2\end{pmatrix}=\begin{pmatrix}10\\i\\100\end{pmatrix}\)

Решение системы следующее

$x_0=-0.2912700033-0.49464964882i\\x_1=13.2727837191-8.78277932011i\\x_2=-4.34744448116-5.49610720908i$

Успехов в расчетах !

Скалярное произведение двух матриц >>

Поиск по сайту

Русский и английский алфавит в одну строку
Часовая и минутная стрелка онлайн. Угол между ними.
Универсальный калькулятор комплексных чисел онлайн
Перемешать буквы в тексте онлайн
Массовая доля химического вещества онлайн
Декoдировать текст \u0xxx онлайн
Частотный анализ текста онлайн
Поворот точек на произвольный угол онлайн
Площадь многоугольника по координатам онлайн
Остаток числа в степени по модулю
Расчет процентов онлайн
Обратный и дополнительный код числа онлайн
Как перевести градусы в минуты и секунды
Поиск объекта по географическим координатам
Расчет пропорций и соотношений
Время восхода и захода Солнца и Луны для местности
DameWare Mini Control. Настройка.
Растворимость металлов в различных жидкостях
Калькулятор географических координат
Теория графов. Матрица смежности онлайн
Географические координаты любых городов мира
Расчет значения функции Эйлера
Перевод числа в код Грея и обратно
Онлайн определение эквивалентного сопротивления
Произвольный треугольник по заданным параметрам
НОД двух многочленов. Greatest Common Factor (GCF)
Площадь пересечения окружностей на плоскости
Калькулятор онлайн расчета количества рабочих дней
Непрерывные, цепные дроби онлайн
Построить ненаправленный граф по матрице
Расчет заряда и разряда конденсатора через сопротивление
Месторождения золота и его спутники
Расчет понижающего конденсатора
Сообщество животных. Кто как называется?
Система комплексных линейных уравнений
Из показательной в алгебраическую. Подробно
Дата выхода на работу из отпуска, декрета онлайн
Проекция точки на плоскость онлайн
Определение формулы касательной к окружности
Расчет параметров конденсатора онлайн


Онлайн расчеты


Подписаться письмом

Онлайн калькулятор.

Решение систем линейных уравнений … — Orașul Löbau Онлайн калькулятор. Решение систем линейных уравнений … — Orașul Löbau — document PDF

liblib.ro

Онлайн калькулятор. Метод Гаусса. Детальное пошаговое решение системы линейных уравнений (СЛУ) методом Гаусса.

Онлайн калькулятор. Решение систем линейных уравнений …

Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) методом Крамера, вы сможете очень просто и быстро найти решение системы.

Онлайн калькулятор. Решение систем линейных уравнений …

Метод Крамера решения систем линейных уравнений

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не …

Метод Гаусса решения системы линейных уравнений — E–maxx

11 июн. 2008 г. … Алгоритм Гаусса. Строго говоря, описываемый ниже метод правильно называть методом «Гаусса-Жордана» (Gauss-Jordan elimination), поскольку он …

Решение системных уравнений методом гаусса. Метод Гаусса …

28 нояб. 2021 г. … Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, …

Калькулятор симплекс-метода | Решение основной задачи …

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве …

Водафон онлайн-чат: решение проблем в режиме online

Чат Водафон – это специальная форма связи с консультантами через официальный сайт или личный кабинет. Он позволяет решить вопросы, которые вызывают у …

Симплекс метод онлайн. Шаг за шагом — Решение задач по …

позволяет решить произвольную задачу линейного программирования. Конечно, симплекс метод не является самым наглядным, как и все аналитические методы решения. Но …

Литры в кубы | Онлайн калькулятор

Онлайн конвертер для перевода литров в кубические метры м3 и обратно, калькулятор имеет высокий класс точности, историю вычислений и пишет число прописью, …

Простой калькулятор онлайн — Ipipip.ru

В настоящее время, в связи с тем, что в английском языке используется только термин «калькулятор» (calculator), термин «микрокалькулятор» вышел из обращения …

Декалитры в литры | Онлайн калькулятор

Онлайн калькулятор переводит декалитры в литры и обратно, данный конвертер имеет высокий класс точности, историю вычислений и поможет прочитать число.

Число Пи в Excel — Калькулятор онлайн

Для работы с числом Пи в Excel существует всторенная функция Пи(), которая позволяет получить число Pi с точностью до 9 знаков после запятой.

Totul.online – решение для увеличения ваших онлайн-продаж

11 сент. 2020 г. … Как работает Marketplace Totul.online? По сути, после того как вы загрузили товар на Totul. online, все, что вам нужно сделать – это получать …

Порт 389 (tcp/udp) — Бесплатный онлайн-калькулятор подсети …

389/TCP — Известные назначения портa (3 зап. найдено). Сервис. Детали. Источник. ldap. Lightweight Directory Access Protocol.

Закон Ома онлайн — формулы и калькулятор — Многоформул.ру

I = U R {I= dfrac{U}{R}} I=RU, где I — сила тока, U — напряжение, R — сопротивление.

Онлайн калькулятор группы крови ребенка

Бесплатный онлайн сервис для расчета группы крови ребенка. Группа крови мамы: I (O), II (A), III (B), IV (AB). Группа крови папы:.

Кредитный калькулятор онлайн, рассчитать потребительский …

Рассчитать потребительский кредит, ежемесячный платеж и процентную ставку. ✓Калькулятор погашения кредита — расчет платежа по кредиту в ОТП Банке.

Калькулятор кредита онлайн — ОТП Банк — Выберу.ру

Кредитный калькулятор ОТП Банка. Чтобы не тратить время на поиск нужной программы кредитования в ОТП Банке, воспользуйтесь расчетом калькулятора по кредитам . ..

Уравнение идеального газа | Онлайн калькулятор

Рассчитывается все это дело по следующей формуле: pV = nRT, где n – молекулы газа, R – газовая постоянная.

Онлайн калькулятор поля зрения (FOV) для ArmA от Hi,A3

Введите значение горизонтального угла поля зрения (FOV) (должно быть > 70° и

Онлайн-калькулятор для облачного майнинга HashFlare.io

Калькулятор позволяющий максимально полно оценить возможный заработок с помощью облачного майнинга от Hashflare.io.

калькулятор онлайн, конвертер валют из лея в рубли (mdl-rub)

Конвертировать, lei. Стоимость, ₽. График отношения молдавского лея к … По состоянию на 21 мая 2022 года при продаже 1 mdl вы получаете 3 рубля 7 копеек.

Онлайн калькулятор постройки бани и стоимости.

[email protected] г. Санкт-Петербург, шоссе Революции, 88ж. РАСЧИТАТЬ БАНЮ ДЛЯ СЕБЯ. Наши телефоны. Общий: 8 (921) 840-22-68.

онлайн калькулятор обмена валют | Альта-Софт

USD Доллар США (840), EUR Евро (978), CNY Китайский юань (156), RUB Российский рубль (643), AMD Армянский драм (51), AUD Австралийский доллар (36) . ..

калькулятор онлайн, конвертер валют из евро в доллары (eur-usd)

Калькулятор валют онлайн – быстрый и точный перевод из евро (eur) в доллары США (usd). Моментальная конвертация по актуальному курсу ЦБ РФ.

Кредитный калькулятор ОТП Банка — рассчитать кредит онлайн

Умный кредитный калькулятор ОТП Банка 2022 — рассчитывает график ежемесячных платежей, срок, проценты, сумму переплат. Узнайте какая часть выплат идет на …

калькулятор онлайн, конвертер валют из доллара в евро (usd-eur)

Калькулятор валют онлайн – быстрый и точный перевод из доллара США (usd) в евро (eur). Моментальная конвертация по актуальному курсу ЦБ РФ.

калькулятор онлайн, конвертер валют из драма в рубли (amd-rub)

Калькулятор валют онлайн – быстрый и точный перевод из армянского драма (amd) в российские рубли (rub). Моментальная конвертация по актуальному курсу ЦБ РФ.

Онлайн калькулятор. Конвертер единиц объёма. Литр.

Литр — внесистемная метрическая единица измерения объёма и вместимости, равная 1 кубическому дециметру. Этот онлайн конвертер позволит вам очень просто …

калькулятор онлайн, конвертер валют из рубля в евро (rub-eur)

Калькулятор валют онлайн – быстрый и точный перевод из российского рубля (rub) в евро (eur). Моментальная конвертация по актуальному курсу ЦБ РФ.

калькулятор онлайн, конвертер валют из биткоина в евро (btc-eur)

Конвертер биткоина к евро. Покупка. 1 BTC = 31532,7 EUR. Обновлен. 20.05.

калькулятор онлайн, конвертер валют из евро в левы (eur-bgn)

Калькулятор валют онлайн – быстрый и точный перевод из евро (eur) в болгарские левы (bgn). Моментальная конвертация по актуальному курсу ЦБ РФ.

Бесплатный онлайн-калькулятор подсети IPv4 — adminsub.net

IP-Aдрес. 192.168.1.0. 11000000.10101000.00000001.00000000 · Маска. 255.255.255.128 = 25. 11111111.11111111.11111111.10000000 · Вилдкард. 0.0.0.127.

калькулятор стоимости КАСКО онлайн от угона и тотала

Выберите лучшие условия по КАСКО от угона в 2022 году на Сравни! Онлайн расчет стоимости КАСКО от хищения по 29-ти предложениям в 6-ти самых популярных . ..

онлайн калькулятор расчета стоимости доставки — DHL Express

Если вы являетесь корпоративным клиентом и у вас есть клиентский счет DHL – рассчитайте тариф здесь. Откуда забрать? Страна *.

Онлайн калькулятор расчета стоимости имплантации зубов …

Лечение аппаратом VECTOR (1 зуб) · Лечение аппаратом VECTOR (2 челюсти) · Лазерное лечение десен · Лечением аппаратом FotoSan. Хирургическая стоматология.

Коэфициент Бонус — Малус. КБМ., калькулятор онлайн, конвертер

Коэффициент Бонус-Малус, классы и коэффициенты водителя и страхования ОСАГО,база КБМ РСА по ОСАГО, таблица коэффициентов ОСАГО.

калькулятор онлайн, конвертер валют из рубля в доллары (rub …

Московский Кредитный Банк. 12,00%. Ставка в год. от 1 ₽. На срок от 1 дня. Без капитализации. Без частичного снятия. Без пополнения. Перейти. Лиц. № 1978.

Онлайн калькулятор ОСАГО 2018 — бесплатный расчёт стоимости

У вас отключён JavaScript: часть функций сайта будет недоступна! Бонус-малус. ру. Меню. справочник страхователя. Калькулятор ОСАГО. расчёт стоимости полиса в …

Онлайн калькулятор стоимости бани из бревна — Сруб-Строй

Наглядный калькулятор онлайн для получения предварительного расчета стоимости бревенчатой бани.

Prin utilizarea site-ului nostru, sunteți de acord cu utilizarea cookie-urilor pentru o experiență mai bună.

Калькулятор исключения Гаусса с шагами

Эта бесплатная матрица калькулятора исключения Гаусса специально разработана, чтобы помочь вам в решении систем уравнений. Да, теперь получить максимально точное решение уравнений можно всего за пару кликов.

Давайте двигаться дальше и понять концепцию этого алгоритма, чтобы найти решение матричных уравнений.

Сосредоточьтесь!

Что такое алгоритм исключения Гаусса?

В свете математического анализа:

«Конкретный метод, который используется для нахождения решения линейных уравнений путем составления расширенной матрицы чисел их коэффициентов, известен как алгоритм Гаусса»

Расширенная матрица:

который состоит из всех констант линейных уравнений».

Общая форма:

$$ A = \begin{bmatrix} a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3 \\\end{bmatrix} \hspace{0.25in} B = \begin{bmatrix}d_1\\d_2\\ d_3\\\end{bmatrix} $$

$$ \text{Расширенная матрица} = \left[\begin{array}{ccc|c}a_1&b_1&c_1&d_1\\a_2&b_2&c_2&d_2\\a_3&b_3&c_3&d_3\\\end{array}\right] $$

Лучший калькулятор расширенных матриц также отображает окончательный ответ в том же формате, что и выше.

Если мы запишем систему линейных уравнений с использованием коэффициентов расширенной матрицы, то получим:

$$ a_{1}x + b_{1}y + c_{1}z = d_{1} $$

$$ a_{2}x + b_{2}y + c_{2}z = d_{2} $$

$$ a_{3}x + b_{3}y + c_{3}z = d_{3} $$

Окончательный ответ, который также определяется бесплатным калькулятором исключения Гаусса, представлен в следующем формате:

$$ \left[\begin{array}{ccc|c}1&0&0&k\\0&1&0&l\\0&0&1&m\\\end{array}\right] $$

Свойства расширенной матрицы:

Расширенная матрица обладает следующие свойства:
Итак, здесь у нас есть следующий формат матрицы, которая окончательно оформлена как нижняя форма матрицы:

Прямоугольная расширенная матрица
Переменные в линейных уравнениях и постоянный член определяют количество столбцов.
Количество систем уравнений равно количеству строк.
Строки расширенной матрицы можно менять местами.
Константа может использоваться для умножения или деления элементов определенной строки.
Конкретную строку матрицы можно добавлять и удалять из других строк.
Кратность строки матрицы может быть применена к другой строке матрицы.

Как применить алгоритм исключения Гаусса?

Здесь мы собираемся применить эту теорему на примере ниже. Поэтому для лучшего понимания просто оставайтесь сосредоточенными!

Пример № 01:

Найдите решение следующей системы уравнений следующим образом: } = 34 $$

Решение:

Без сомнения, наш широко используемый калькулятор исключения Гаусса с шагами покажет подробные вычисления для упрощения этих уравнений, но нам нужно проанализировать сценарий вручную.

Эквивалентная расширенная матричная форма приведенных выше уравнений выглядит следующим образом:

$$ \begin{bmatrix} 3&6&23 \\ 6&2&34 \\\end{bmatrix} $$

Шаги исключения Гаусса:

Шаг № 01:

Разделить нулевую строку на 3.

$$ \left[\begin{array}{cc|c}1&2& \frac{23}{3} \\6&2&34 \\\end{array}\right] $ $

Шаг #02:

Умножьте первую строку на 6, а затем вычтите ее из нулевой строки.

$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&-10&-12 \\\end{array}\right] $$

Шаг # 03:

Перейти к делению первой строки на -10.

$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&1&\frac{6}{5}\\\end{array}\right] $$

Шаг № 04:

Приступаем к нахождению произведения нулевой строки и 2. После этого вычитаем результат из первой строки.

$$ \left[\begin{array}{cc|c}1&0&\frac{26333333334}{5000000000}\\0&1& \frac{6}{5}\\\end{array}\right] $$

Как вы видите в левой части матрицы, мы получаем единичную матрицу. Таким образом, ответом в правой части уравнения будут значения переменных в уравнениях.

Итак, окончательные результаты следующие:

$$ b_{1} = 5,266 $$

$$ b_{2} = 1,2 $$

калькулятор ликвидации.

Как работает калькулятор исключения Гаусса?

Познакомьтесь с тем, как этот бесплатный алгоритм уменьшения строки матрицы решения с методом исключения Гаусса упрощает системы уравнений.

Ввод:

Сначала настройте порядок матрицы из выпадающих списков
После этого нажмите кнопку «Установить матрицы», чтобы получить нужный формат матрицы
Теперь получить числа в своих полях
После того, как вы закончите с материалом, нажмите кнопку расчета

Вывод:

Лучший калькулятор исключения Гаусса Джордана с шагами выполняет следующие вычисления:

Показывает коэффициенты переменных
Отображает шаги исключения Гаусса

Часто задаваемые вопросы:

В чем разница между методом исключения Гаусса и методом Гаусса-Жордана?

Между ними существует только одно различие. Там, где исключение Гаусса генерирует редуцированную ступенчатую форму данной матрицы, Гаусс Джордан действительно производит только ступенчатую форму. А наш лучший гаусс-калькулятор позволит вам определить приведенную форму, которая более эффективна, чем получение только ступенчатого формата матрицы.

Почему мы используем метод исключения Гаусса?

Стратегия сокращения строк для решения систем линейных уравнений известна в математике как метод исключения Гаусса. Он состоит из серии операций над связанной матрицей коэффициентов. Этот подход также можно использовать для оценки следующего:

Ранг предоставленной матрицы.
Определитель квадратной матрицы
Обратная обратимая матрица

Что эффективнее Жордан Гаусса или Исключение Гаусса?

Поскольку он пропускает процесс обратной замены, метод Гаусса-Жордана более эффективен, чем методы исключения Гаусса. И именно поэтому наш бесплатный калькулятор метода Джордана Гаусса использует именно этот метод для немедленного отображения результатов.

Для чего в реальной жизни используется метод исключения Гаусса?

Надежное улучшение изображения отпечатков пальцев является важным применением исключения Гаусса. Изображение усилено фильтром Гаусса. В процессорах, подключенных к сетке, метод SGE также может использоваться для решения линейных уравнений. В алгоритмах планирования также используется подход Гаусса.

Когда используется метод исключения Гаусса?

Метод исключения Гаусса чаще всего используется для решения ряда задач линейной алгебры.

Каковы преимущества метода исключения Гаусса?

Эта процедура полностью надежна и справедлива.
Может решать множество линейных уравнений одновременно.

Какие подводные камни метода исключения Гаусса?

Определитель, близкий к нулю Указывает на отсутствие или неограниченное количество решений. Однако определить, насколько близок должен быть определитель к нулю, чтобы указать на плохую обусловленность, проблематично.

Что является ключевым в исключении Гаусса?

Поворот имеет целью превратить элемент выше или ниже ведущей единицы в ноль. «Поворотный элемент» или «поворотный элемент» — это левая часть матричного элемента, для которого компоненты выше и ниже должны быть равны нулю. Ошибки округления уменьшаются за счет поворота.

Что такое точка опоры в матрице?

В ступенчато-строковой форме матрицы опорной точкой является положение ведущей записи. Сводная колонка — это колонка, в которой есть точка опоры.

Заключение:

Матрицы Гаусса Джордана находят широкое применение в различных областях образования и технологий. Из-за такой важности мы разработали эту лучшую матрицу калькулятора исключения Гаусса, чтобы помочь любому, кто анализирует этот конкретный метод, решать уравнения.

Ссылки:

Из источника википедии: Исключение Гаусса, Операции со строками, Эшелонная форма, Вычисление определителей, обращение матрицы, Ранги0003

Из источника изучения люмена: исключение Гаусса, расширенная матрица, система уравнений, приложения

3.3: Решающие системы с исключением Гаусса-Жордана

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 40127

OpenStax
OpenStax

Цели обучения

Написать расширенную матрицу системы уравнений.
Напишите систему уравнений из расширенной матрицы.
Решите систему линейных уравнений с помощью матриц и графического калькулятора.
Решайте финансовые задачи с помощью матриц и графического калькулятора.

Предварительные навыки

Прежде чем начать, пройдите этот предварительный тест.

Введите в калькулятор следующие матрицы и выполните указанные операции. Если операция не может быть выполнена, укажите причину.

$A=\begin{bmatrix} 5 & 1 & -2\\2 & 6 & 7\\4 & 1 & −5 \end{bmatrix} $, $B=\begin{bmatrix} 3 & -7\\0 & 1\\2 & −8 \end{bmatrix} $, $C=\begin{bmatrix} 9 & 4\\6 & -5\\7 & −1 \end{bmatrix } $

а. $A \cdot B$

б. $B \cdot A$

c. $4B-2C$

д. $A+C$

Нажмите здесь, чтобы проверить свой ответ

а. $\begin{bmatrix} 11 и -18\\20 и -64\\2 и 13 \end{bmatrix} $

б. Не определено, так как количество столбцов в матрице $B$ не соответствует количеству строк в матрице $A$.

в. $\begin{bmatrix} -6 и -36\\-12 и 14\\-6 & −30 \end{bmatrix} $ 9{го}\) века, но он до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика, среди прочих. Его открытия, касающиеся теории матриц, изменили то, как математики работали последние два столетия.

Рисунок $\PageIndex{1}$: немецкий математик Карл Фридрих Гаусс (1777–1855).

Ранее в этой главе мы рассмотрели методы решения систем уравнений. В этом разделе мы изучим еще один метод решения систем, на этот раз с использованием матриц.

Расширенные матрицы

Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства. Когда система записывается в такой форме, мы называем ее расширенной матрицей .

Например, рассмотрим следующую $2 × 2$ систему уравнений.

\[\begin{align*} 3x+4y&= 7\\ 4x-2y&= 5 \end{align*}\]

Мы можем записать эту систему в виде расширенной матрицы:

$\left[ \ begin{array}{cc|c} 3&4&7\\4&-2&5\end{array} \right]$

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .

$\begin{bmatrix}3&4\\4&−2\end{bmatrix}$

Система уравнений три на три , такая как

\[\begin{align*} 3x- y-z&= 0\\ x+y&= 5\\ 2x-3z&= 2 \end{align*}\]

имеет матрицу коэффициентов

$\begin{bmatrix}3&−1&−1\\1&1&0\\2&0&−3\end{bmatrix}$

и представлен расширенной матрицей

$\left [ \begin{array}{ccc|c}3&-1&-1&0\\1&1&0&5\\2&0&-3&2\end{array} \right]$

Обратите внимание, что матрица записана таким образом, что переменные выстраиваются в собственные столбцы: $x$-термы идут в первом столбце, $y$-термы во втором столбце и $z$-термы в третьем столбце. Очень важно, чтобы каждое уравнение было записано в стандартной форме $ax+by+cz=d$, чтобы переменные совпадали. Когда в уравнении отсутствует переменный член, коэффициент равен $0$.

Как: Записать расширенную матрицу по системе уравнений

Записать коэффициенты при $x$-членах в виде чисел в первом столбце.
Запишите коэффициенты $y$-членов в виде чисел во втором столбце.
Если есть $z$-члены, запишите коэффициенты в виде чисел в третьем столбце.
Нарисуйте вертикальную линию и запишите константы справа от линии.

Пример $\PageIndex{1}$: запись расширенной матрицы для системы уравнений

Запишите расширенную матрицу для данной системы уравнений.

\[\begin{align*} x+2y-z&= 3\\ 2x-y+2z&= 6\\ x-3y+3z&= 4 \end{align*}\]

Решение

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

$\left[ \begin{array}{ccc|c}1&2&−1&3\\2&−1&2&6\\1&−3&3&4\end{array} \right]$

Упражнение $\PageIndex{1} $

Запишите расширенную матрицу данной системы уравнений.

\[\begin{align*} 4x-3y&= 11\\ 3x+2y&= 4 \end{align*}\]

Ответ: $\left[ \begin{массив}{cc|c} 4&−3&11\\3&2&4\end{массив} \right]$

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы для решения систем уравнений, поскольку они упрощают операции, когда системы не перегружены переменными. Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Пример $\PageIndex{2}$: запись системы уравнений из расширенной матрицы

Найдите систему уравнений из расширенной матрицы.

$\left[ \begin{array}{ccc|c}1&−3&−5&-2\\2&−5&−4&5\\−3&5&4&6 \end{array} \right]$

Решение

Когда столбцы представляют переменные $x$, $y$ и $z$,

\[\left[ \begin{array}{ccc|c}1&-3&-5&- 2\\2&-5&-4&5\\-3&5&4&6 \end{массив} \right] \rightarrow \begin{align*} x-3y-5z&= -2\\ 2x-5y-4z&= 5\\ -3x+ 5y+4z&= 6 \end{align*}\]

Упражнение $\PageIndex{2}$

Напишите систему уравнений из расширенной матрицы.

$\left[ \begin{array}{ccc|c}1&−1& 1&5\\2&−1&3&1\\0&1&1&-9\end{массив}\right]$

Ответ: $\begin{align*} x-y+z&= 5\\ 2x-y+3z&= 1\\ y+z&= -9 \end{align*}$

Сокращенная ступенчатая форма

Чтобы решить систему уравнений, мы хотим преобразовать ее матрицу в уменьшенная форма строки-эшелона , в которой единицы расположены вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции выше и ниже главной диагонали, как показано.

Сокращенная ступенчатая форма $\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$

Следующие расширенные матрицы представлены в сокращенной ступенчатой форме.

$\left[ \begin{array}{cc|c}1 & 0 & -2 \\ 0 & 1 & 5\end{array} \right]$, $\left[ \begin{array }{ccc|c}1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2\end{массив} \right]$

Следующие расширенные матрицы не имеют редуцированной ступенчатой формы.

$\left[ \begin{array}{cc|c}2 & 4 & -6 \\ 4 & 0 & 7\end{array} \right]$, $\left[ \begin{array }{ccc|c}0 & 2 & 3 & 3 \\ 1 & 5 & 0 & 2 \\ 0 & 0 & 1 & 0\end{массив} \right]$

Пример $\PageIndex{3 }$: Матрицы в редуцированной ступенчатой форме

Запишите систему уравнений из каждой из матриц в редуцированной ступенчатой форме сверху. В чем преимущество этой формы?

а. $\left[ \begin{массив}{cc|c}1 & 0 & -2 \\ 0 & 1 & 5\end{массив} \right]$

b. $\left[ \begin{array}{ccc|c}1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2\end{массив} \right]$

Раствор

а. $\begin{align*} x=-2\\ y=5 \end{align*}$

b. $\begin{align*} x=4\\ y=3\\z=2 \end{align*}$

Преимущество редуцированной строчно-эшелонной формы состоит в том, что решение системы уравнений дано в правой колонке.

ИСКЛЮЧЕНИЕ ГАУССА-ЖОРДАНА

Метод исключения Гаусса-Жордана относится к стратегии, используемой для получения сокращенной формы строки-эшелона матрицы. Цель состоит в том, чтобы написать матрицу $A$ с номером $1$ в качестве записи вниз по главной диагонали и со всеми нулями сверху и снизу.

$A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33 }\end{bmatrix}\xrightarrow{После\пробел Гаусса-Жордана\исключение пробела} A=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$

Мы можем выполнить операций со строками над матрицей, таких как сложение, умножение на константу и перестановка строк, чтобы создать сокращенную форму строки-эшелона. Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.

Решение систем уравнений с исключением Гаусса-Жордана

Для целей этого курса мы продемонстрируем, как найти уменьшенную форму строки-эшелона в графическом калькуляторе.

Как: Данную систему уравнений решить с помощью матриц с помощью калькулятора

Сохранить расширенную матрицу как матричную переменную $[A], [B], [C],. ..$
1. Нажмите 2 ^и МАТРИЦА. На экране отобразится меню Matrix. Дважды используйте клавишу со стрелкой вправо, чтобы выбрать меню EDIT. В меню EDIT используйте стрелку вниз, чтобы переместить курсор, чтобы выбрать желаемое имя матрицы из меню, и нажмите ENTER. Появится экран ввода матрицы.
2. Введите размеры общего размера матрицы в виде строк $\times$ столбцов. Введите количество строк, нажмите клавишу ВВОД, введите количество столбцов и снова нажмите клавишу ВВОД. Форма матрицы изменяется на экране, чтобы показать запрошенное количество строк и столбцов. Убедитесь, что форма соответствует нужной матрице; если нет, то вернитесь к верхнему ряду и скорректируйте размеры. Если матрица слишком велика и не помещается на экране, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы просмотреть оставшиеся строки и столбцы.
3. Введите элементы матрицы, после каждого нажимайте ENTER. Курсор прокручивает матрицу, перемещаясь по каждой строке слева направо, а затем вниз к следующей строке. Использование клавиш со стрелками для перемещения курсора вместо нажатия клавиши ENTER может привести к тому, что значение не будет сохранено в памяти калькулятора.
4. Нажмите 2 ^и ВЫХОД, чтобы завершить процесс сохранения и вернуться на главный экран.
Используйте функцию rref( в калькуляторе, чтобы найти сокращенную ступенчатую форму матрицы.
1. На главном экране нажмите 2 ^nd MATRIX. Используйте стрелку вправо один раз, чтобы перейти в меню MATH.
2. Прокрутите вниз (или вверх) до rref(, стараясь не выбирать ref(, и нажмите ENTER.
3. Нажмите 2 ^nd MATRIX еще раз и с помощью стрелки вниз (при необходимости) выберите имя матрицы и нажмите ENTER.
4. Нажмите ENTER для завершения операции.
Если существует сокращенная форма строки-эшелона матрицы, калькулятор отобразит ее на главном экране. ×

Пример $\PageIndex{4}$: Решение системы уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

\[\begin{align*} 6x+4y+3z&= -6\\ x+2y+z&=\dfrac{1}{3}\\ -12x-10y-7z&= 11 \end{align*} \]

Решение

Запишите расширенную матрицу системы уравнений.

$\left[ \begin{array}{ccc|c} 6&4&3&-6\\1&2&1&\dfrac{1}{3}\\-12&-10&-7&11\end{массив} \right]$

На странице матрицы калькулятора введите указанную выше расширенную матрицу в качестве переменной матрицы $[A]$.

$[A]=\left[ \begin{array}{ccc|c} 6&4&3&-6\\1&2&1&\dfrac{1}{3}\\-12&-10&-7&11\end{массив} \right ]$

Используйте функцию rref( в калькуляторе, вызвав матричную переменную $[A]$.

rref([A])

представить элементы матрицы в виде дробей

Вычислить

\[\begin{array}{cc} {\left[ \begin{array}{ccc|c} 1&0&0&-\dfrac{2}{3}\\ 0&1&0&\dfrac{5}{2}\\0&0&1&-4\end{массив} \right] \rightarrow} & {\begin{align*} x+0y+0z &= -\dfrac{2}{3} \ \ y+0z &= \dfrac{5}{2} \\ z &= -4 \end{align*}} \end{array}\]

Таким образом, решение, которое легко читается из правого столбца редуцированной строчно-эшелонной формы матрицы, равно $\left(-\dfrac{2}{3},\dfrac{5}{2} ,−4\справа)$.

Упражнение $\PageIndex{3}$

Решите систему уравнений.

\[\begin{align*} 4x-7y+2z&= -5\\ -x+3y-8z&= -10\\ -5x-4y+6z&= 19 \end{align*}\]

Ответ

Напишите расширенную матрицу для системы уравнений.

$\left[ \begin{array}{ccc|c} 4&-7&2&-5 \\ -1&3&-8&-10 \\ -5&-4&6&19\end{массив} \right]$

$[A]=\left[ \begin{array}{ccc|c} 4&-7&2&-5 \\ -1&3&-8&-10 \\ -5&-4&6&19\end{массив} \right]$

Используйте функцию rref( в калькуляторе, вызывая матричную переменную $[A]$.

rref([A])

Используйте параметр MATH —> FRAC в калькуляторе, чтобы выразить элементы матрицы в виде дробей.

Оценка

\[\begin{array}{cc} {\left[ \begin{array}{ccc|c} 1&0&0&-2\\0&1&0&0\\0&0&1&\dfrac{3}{2}\end{array} \right] \rightarrow} & {\begin{align*} x+0y+0z &= -2 \\ y+0z &= 0 \\ z &= \dfrac{3}{2} \end{align*}} \end {массив}\]

Таким образом, решение, которое легко читается из правого столбца редуцированной построчно-ступенчатой формы матрицы, равно $\left(-2, 0,\dfrac{3}{2}\right)$.

Пример $\PageIndex{5}$: применение матриц $2×2$ к финансам 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил $$1335$. Сколько было вложено по каждой ставке?

Решение

У нас есть система двух уравнений с двумя переменными. Пусть $x=$ сумма, вложенная под 10,5 %, и $y=$ сумма, вложенная под 12 %.

\[\begin{align*} x+y&= 12,000\\ 0,105x+0,12y&= 1,335 \end{align*}\]

В качестве матрицы мы имеем

$\left[ \begin{ array}{cc|c} 1&1&12 000\\0,105&0,12&1,335\end{массив} \right]$

Введите эту матрицу как переменную матрицы $[A]$. Используйте функцию rref( , вызывающую переменную матрицы $[A]$. \0&1&5000\конец{массив} \право]\)

Таким образом, $7000 долларов США$ было инвестировано под 10,5% годовых, а $5000 долларов США$ под 12% годовых.

Пример $\PageIndex{6}$: применение матриц $3×3$ к финансам

Ava инвестирует в общей сложности $10 000 долларов США$ в три счета, один из которых приносит 5 % годовых, другой – 8 %. проценты, а третий платит 9 % годовых. Годовой процент, полученный по трем инвестициям в прошлом году, составил $$770$. Сумма, вложенная под 9%, вдвое превышала сумму, вложенную под 5%. Сколько было вложено по каждой ставке?

Решение

У нас есть система из трех уравнений с тремя переменными. Пусть $x$ будет суммой, инвестированной под 5 % процентов, пусть $y$ будет суммой, инвестированной под 8 % процентов, и пусть $z$ будет суммой, инвестированной под 9 % процентов. Таким образом,

\[\begin{align*} x+y+z &= 10 000 \\ 0,05x+0,08y+0,09z &= 770 \\ 2x−z &= 0 \end{align*}\]

В качестве матрицы у нас есть

$\left[ \begin{array}{ccc|c} 1&1&1&10,000\\0,05&0,08&0,09&770\\2&0&-1&0\end{array} \right]$

Введите эту матрицу как переменную матрицы $[A]$. Используйте функцию rref( , вызывающую переменную матрицы $[A]$.

rref([A])

$\left[ \begin{array}{ccc|c} 1&0&0&3000\ \0&1&0&1000\\0&0&1&6000\end{array} \right]$

Ответ: $3000$$ инвестировано под 5%, $1000$$ инвестировано под 8% и $6000$$ инвестировано под 9 % процентов.

Упражнение $\PageIndex{4}$

Небольшая обувная компания взяла кредит в размере $$1 500 000$ для расширения своего ассортимента. Часть денег была взята в долг под 7 %, часть – под 8%, а часть была заимствована под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7 %, а годовой процент по всем трем кредитам составлял $130 500 долларов США$. Используйте матрицы, чтобы найти сумму займа под каждая ставка

Ответить: $$150,000$ под 7%, $$750,000$ под 8%, $$600,000$ под 10%

Медиа

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практических занятий по решению систем линейных уравнений методом исключения Гаусса.

Решение системы двух уравнений с помощью расширенной матрицы
Решение системы трех уравнений с помощью расширенной матрицы
Расширенные матрицы на калькуляторе

Ключевые понятия

Расширенная матрица содержит коэффициенты и константы системы уравнений. См. пример $\PageIndex{1}$.
Матрица, дополненная постоянным столбцом, может быть представлена в виде исходной системы уравнений. См. пример $\PageIndex{2}$.
Мы можем использовать метод исключения Гаусса-Жордана для решения системы уравнений. См. Пример $\PageIndex{4}$.
Многие реальные проблемы можно решить с помощью расширенных матриц. См. Пример $\PageIndex{5}$ и Пример $\PageIndex{6}$.

Авторы и авторство

Эта страница под названием 3.3: Solving Systems with Gauss-Jordan Elimination распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Показать страницу TOC
да
Метки
1. расширенная матрица
2. Исключение Гаусса
3. операции со строками
4. рядно-эшелонная форма
5. источник@https://openstax. org/details/books/precalculus
6. источник[1]-math-15092
7. источник[2]-math-3101
8. источник[3]-math-15092

Алгебра — расширенные матрицы

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 7-3: Расширенные матрицы

В этом разделе нам нужно рассмотреть третий метод решения систем уравнений. Для систем двух уравнений это, вероятно, немного сложнее, чем методы, которые мы рассмотрели в первом разделе. Однако для систем с большим количеством уравнений это, вероятно, проще, чем использовать метод, который мы видели в предыдущем разделе.

Прежде чем мы перейдем к методу, нам сначала нужно разобраться с некоторыми определениями.

Расширенная матрица для системы уравнений представляет собой матрицу чисел, в которой каждая строка представляет константы из одного уравнения (и коэффициенты, и константа по другую сторону от знака равенства), а каждый столбец представляет все коэффициенты для одной переменной.

Давайте рассмотрим пример. Вот система уравнений, которую мы рассмотрели в предыдущем разделе.

\[\begin{align*}x — 2y + 3z & = 7\\ 2x + y + z & = 4\\ — 3x + 2y — 2z & = — 10\end{align*}\]

Вот расширенная матрица для этой системы.

\[\left[ {\begin{array}{rrr|r}1&{- 2}&3&7\\2&1&1&4\\{- 3}&2&{- 2}&{- 10}\end{array}} \right] \]

Первая строка состоит из всех констант из первого уравнения с коэффициентом при $x$ в первом столбце, коэффициентом при $y$ во втором столбце, коэффициентом при $z $ в третьем столбце и константа в последнем столбце. Вторая строка — это константы из второго уравнения с тем же размещением и аналогично для третьей строки. Пунктирная линия показывает, где в исходной системе уравнений стоял знак равенства, и он не всегда включается. Это в основном зависит от инструктора и/или используемого учебника.

Далее нам нужно обсудить элементарных операций со строками . Их три, и мы дадим как обозначение, используемое для каждого, так и пример с использованием расширенной матрицы, приведенной выше.

Замена двух рядов . С помощью этой операции мы поменяем местами все записи в строке $i$ и строке $j$. Здесь мы будем использовать обозначение ${R_i} \leftrightarrow {R_j}$. Вот пример. \[\left[ {\begin{array}{rrr|r}1&{- 2}&3&7\\2&1&1&4\\{- 3}&2&{- 2}&{- 10}\end{array}} \right] \begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}{ — 3 }&2&{ — 2}&{ — 10}\\2&1&1&4\\1&{ — 2}&3&7\end{массив}} \right]\]
Итак, мы делаем именно то, что говорит операция. Каждая запись в третьей строке перемещается вверх в первую строку, а каждая запись в первой строке перемещается вниз в третью строку. Убедитесь, что вы переместили все записи. Одна из наиболее распространенных ошибок — забыть переместить одну или несколько записей.
Умножение строки на константу. В этой операции мы умножим строку $i$ на константу $c$ и будем использовать обозначение $c{R_i}$. Обратите внимание, что мы также можем разделить строку на константу, используя обозначение $\frac{1}{c}{R_i}$. Вот пример. \[\left[ {\begin{array}{rrr|r}1&{- 2}&3&7\\2&1&1&4\\{- 3}&2&{- 2}&{- 10}\end{array}} \right] \begin{array}{*{20}{c}}{ — 4{R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ — 2}&3&7 \\2&1&1&4\\{12}&{ — 8}&8&{40}\end{массив}} \right]\]
Итак, когда мы говорим, что будем умножать строку на константу, это на самом деле означает, что мы будем умножать каждую запись в этой строке на константу. Следите за знаками в этой операции и убедитесь, что вы умножаете каждую запись.
Добавить несколько строк в другую строку . В этой операции мы заменим строку $i$ суммой строки $i$ и константы $c$, умноженной на строку $j$. Для этой операции мы будем использовать обозначение ${R_i} + c{R_j} \to {R_i}$. Чтобы выполнить эту операцию, мы возьмем запись из строки $i$, добавим к ней $c$ умножить на соответствующую запись из строки $j$ и поместим результат обратно в строку $i$. Вот пример этой операции. \[\left[ {\begin{array}{rrr|r}1&{- 2}&3&7\\2&1&1&4\\{- 3}&2&{- 2}&{- 10}\end{array}} \right] \begin{array}{*{20}{c}}{{R_3} — 4{R_1} \to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr| r}1&{ — 2}&3&7\\2&1&1&4\\{ — 7}&{10}&{ — 14}&{ — 38}\end{массив}} \right]\]
Давайте пройдемся по отдельным вычислениям, чтобы убедиться, что вы все сделали правильно.
\[\begin{align*} — 3 — 4\left( 1 \right) & = — 7\hspace{0.25in}\\ 2 — 4\left( { — 2} \right) & = 10\\ — 2 — 4\влево( 3 \вправо) & = — 14\\ — 10 — 4\влево( 7 \вправо) & = — 38\end{align*}\]
Будьте очень осторожны со знаками здесь. Мы будем выполнять эти вычисления в нашей голове по большей части, и очень легко перепутать знаки и добавить один, который не принадлежит, или потерять тот, который должен быть там.
Очень важно, чтобы вы могли выполнить эту операцию, так как именно эту операцию мы будем использовать чаще, чем две другие вместе взятые.

Итак, как мы можем использовать расширенные матрицы и операции со строками для решения систем? Начнем с системы двух уравнений и двух неизвестных.

\[\begin{align*}ax + by & = p\\ cx + dy & = q\end{align*}\]

Сначала запишем расширенную матрицу для этой системы,

\[\ влево [ {\ begin {массив} {rr | r} a & b & p \\ c & d & q \ end {массив}} \ right] \]

и с помощью элементарных операций со строками преобразуйте его в следующую расширенную матрицу.

\[\ влево [ {\ begin {массив} {rr | r} 1 & 0 & h \\ 0 & 1 & k \ end {массив}} \ right] \]

Как только мы получим расширенную матрицу в этой форме, мы закончим. Решением системы будут $x = h$ и $y = k$.

Этот метод называется Gauss-Jordan Исключение .

Пример 1. Решите каждую из следующих систем уравнений.

$\begin{align*}3x — 2y & = 14\\ x + 3y & = 1\end{align*}$
$\begin{align*} — 2x + y & = — 3\\ x — 4y & = — 2\end{align*}$
$\begin{align*}3x — 6y & = — 9\\ — 2x — 2y & = 12\end{align*}$

Показать все решения Скрыть все решения

a $\begin{align*}3x — 2y & = 14\\ x + 3y & = 1\end{align*}$ Показать решение

Первым шагом здесь является запись расширенной матрицы для этой системы.

\[\require{color}\left[ {\begin{array}{rr|r} {\color{Red} 3}&{- 2}&{14}\\1&3&1\end{массив}} \right] \]

Чтобы преобразовать его в окончательную форму, мы начнем с верхнего левого угла и будем работать против часовой стрелки, пока первые два столбца не станут такими, какими они должны быть.

Итак, первый шаг — преобразовать красную тройку в расширенной матрице выше в 1. Мы можем использовать любые операции со строками, какие захотим. Однако мы всегда должны стараться свести к минимуму работу, насколько это возможно.

Итак, поскольку в первом столбце уже есть единица, она просто не в правильной строке, давайте воспользуемся операцией первой строки и поменяем две строки местами.

\[\require{color}\left[ {\begin{array}{rr|r}3&{ — 2}&{14}\\1&3&1\end{array}} \right]\begin{array}{*{ 20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{массив}\left[ {\begin{array}{rr|r}1&3&1\\{\color{Red} 3} &{ — 2}&{14}\end{массив}} \right]\]

Следующим шагом будет получение нуля ниже единицы, которую мы только что получили в верхнем левом углу. Это значит, что нам нужно поменять красную тройку на ноль. Это почти всегда потребует от нас использования операции третьей строки. Если мы добавим -3 строки 1 к строке 2, мы можем преобразовать эти 3 в 0. Вот эта операция.

\[\require{color}\left[ {\begin{array}{rr|r}1&3&1\\3&{ — 2}&{14}\end{array}} \right]\begin{array}{*{ 20}{c}}{{R_2} — 3{R_1} \to {R_2}}\\ \to\end{array}\left[ {\begin{array}{rr|r}1&3&1\\0&{\ цвет {Красный} — 11}&{11}\end{массив}} \right]\]

Далее нам нужно поставить 1 в нижний правый угол первых двух столбцов. Это означает изменение красного -11 на 1. Обычно это достигается с помощью операции второй строки. Если мы разделим вторую строку на -11, мы получим 1 в том месте, которое нам нужно.

\[\require{color}\left[ {\begin{array}{rr|r}1&3&1\\0&{ — 11}&{11}\end{array}} \right]\begin{array}{*{ 20}{c}}{ — \frac{1}{{11}}{R_2}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&{\color{ Красный} 3}&1\\0&1&{ — 1}\end{массив}} \right]\]

Итак, мы почти закончили. Последний шаг — превратить красную тройку в ноль. Опять же, для этого почти всегда требуется операция третьей строки. Вот операция для этого последнего шага.

\[\require{color}\left[ {\begin{array}{rr|r}1&3&1\\0&1&{ — 1}\end{array}} \right]\begin{array}{*{20}{c }}{{R_1} — 3{R_2} \to {R_1}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&0&4\\0&1&{ — 1}\end {массив}} \справа]\]

У нас есть расширенная матрица в нужном виде, и все готово. Решением этой системы являются $x = 4$ и $y = — 1$.

b $\begin{align*} — 2x + y & = — 3\\ x — 4y & = — 2\end{align*}$ Показать решение

В этой части мы не будем подробно объяснять каждый шаг. Следующее число, которое нам нужно изменить, мы отметим красным цветом, как мы это делали в предыдущей части.

Сначала мы запишем расширенную матрицу, а затем приступим к операциям со строками.

\[\require{color}\left[ {\begin{array}{rr|r}{\color{Red} — 2}&1&{- 3}\\1&{- 4}&{- 2}\end{ array}} \right]\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{array}\left[ {\begin{array}{rr |r}1&{ — 4}&{ — 2}\\{\color{Red} — 2}&1&{ — 3}\end{array}} \right]\begin{array}{*{20}{c }}{{R_2} + 2{R_1} \to {R_2}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&{- 4}&{-2} \\0&{\color{Red} — 7}&{ — 7}\end{массив}} \right]\]

Прежде чем перейти к следующему шагу, заметим, что во второй матрице у нас были единицы в обоих местах, которые нам были нужны. Тем не менее, единственный способ изменить -2 на ноль, который мы также должны были иметь, заключался в том, чтобы также изменить 1 в правом нижнем углу. Это хорошо. Иногда это произойдет, и попытка сохранить оба вызовет только проблемы.

Давайте закончим задачу.

\[\require{color}\left[ {\begin{array}{rr|r}1&{-4}&{-2}\\0&{\color{Red}-7}&{-7}\end {массив}} \right]\begin{массив}{*{20}{c}}{ — \frac{1}{7}{R_2}}\\ \to \end{массив}\left[ {\begin {array}{rr|r}1&{\color{Red} — 4}&{- 2}\\0&1&1\end{array}} \right]\begin{array}{*{20}{c}}{ {R_1} + 4{R_2} \to {R_1}}\\ \to \end{массив}\left[ {\begin{array}{rr|r}1&0&2\\0&1&1\end{массив}} \right] \]

Тогда решением этой системы является $x = 2$ и $y = 1$.

c $\begin{align*}3x — 6y & = — 9\\ — 2x — 2y & = 12\end{align*}$ Показать решение

Сначала запишем расширенную матрицу для этой системы.

\[\require{color}\left[ {\begin{array}{rr|r}{\color{Red} 3}&{- 6}&{- 9}\\{- 2}&{- 2} &{12}\end{массив}} \right]\]

В этом случае в первом столбце нет единицы, поэтому мы не можем просто поменять местами две строки в качестве первого шага. Однако обратите внимание, что, поскольку все записи в первой строке имеют 3 в качестве множителя, мы можем разделить первую строку на 3, что даст 1 в этом месте, и мы не будем вводить дроби в задачу.

Вот работа для этой системы.

\[\require{color}\left[ {\begin{array}{rr|r}{\color{Red} 3}&{- 6}&{- 9}\\{- 2}&{- 2} &{12}\end{array}} \right]\begin{array}{*{20}{c}}{\frac{1}{3}{R_1}}\\ \to \end{array}\ слева [ {\ begin {массив} {rr | r} 1 & { — 2} & { — 3} \\ {\ color {Red} — 2} & { — 2} & {12} \ end {массив}} \ right]\begin{array}{*{20}{c}}{{R_2} + 2{R_1} \to {R_2}}\\ \to \end{array}\left[ {\begin{array}{ rr|r}1&{ — 2}&{ — 3}\\0&{\color{Red} — 6}&6\end{массив}} \right]\] \[\require{color}\left[ {\begin{array}{rr|r}1&{- 2}&{- 3}\\0&{\color{Red} — 6}&6\end{array}} \right]\begin{array}{*{20}{c}}{ — \frac{1}{6}{R_2}}\\ \to \end{array}\left[ {\begin{array}{ rr|r}1&{\color{Red} — 2}&{ — 3}\\0&1&{ — 1}\end{array}} \right]\begin{array}{*{20}{c}}{ {R_1} + 2{R_2} \to {R_1}}\\ \to \end{массив}\left[ {\begin{array}{rr|r}1&0&{ — 5}\\0&1&{- 1}\ конец{массив}} \справа]\]

Решением этой системы является $x = — 5$ и $y = — 1$.

Важно отметить, что путь, который мы выбрали, чтобы привести расширенные матрицы в этом примере к окончательной форме, не единственный путь, который мы могли бы использовать. Есть много разных путей, по которым мы могли бы пойти. Однако все пути пришли бы к одной и той же окончательной расширенной матрице, поэтому мы всегда должны выбирать путь, который, по нашему мнению, является самым простым путем. Обратите также внимание на то, что разные люди могут чувствовать, что разные пути проще, и поэтому могут решать системы по-разному. Однако они получат то же решение.

Для двух уравнений и двух неизвестных этот процесс, вероятно, немного сложнее, чем простой процесс решения, который мы использовали в первом разделе этой главы. Этот процесс становится полезным, когда мы начинаем рассматривать более крупные системы. Итак, давайте взглянем на пару систем с тремя уравнениями в них.

В этом случае процесс в основном идентичен, за исключением того, что нужно сделать больше. Как и в случае с двумя уравнениями, мы сначала создадим расширенную матрицу, а затем с помощью операций со строками приведем ее к форме 9.0003

\[\ влево [ {\ begin {массив} {rrr | r} 1 & 0 & 0 & p \\ 0 & 1 & 0 & q \\ 0 & 0 & 1 & r \ end {массив}} \ right] \]

Если расширенная матрица приведена в такой форме, решение имеет вид $x = p$, $y = q$ и $z = r$. Как и в случае с двумя уравнениями, на самом деле нет никакого заданного пути для приведения расширенной матрицы к этой форме. Обычный путь состоит в том, чтобы получить 1 в правильных местах и 0 под ними. Как только это будет сделано, мы попытаемся получить нули выше единиц.

Давайте рассмотрим пару примеров, чтобы увидеть, как это работает.

Пример 2. Решите каждую из следующих систем уравнений.

$\begin{align*}3x + y — 2z & = 2\\ x — 2y + z & = 3\\ 2x — y — 3z & = 3\end{align*}$
$\begin{align*}3x + y — 2z & = — 7\\ 2x + 2y + z & = 9\\ — x — y + 3z & = 6\end{align*}$

Показать все решения Скрыть все решения

a $\begin{align*}3x + y — 2z & = 2\\ x — 2y + z & = 3\\ 2x — y — 3z & = 3\end{align*}$ Показать решение

Сначала запишем расширенную матрицу для этой системы.

\[\ требуется {цвет} \ влево [ {\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & { — 2} & 2 \\ 1 & { — 2} & 1 & 3 \\ 2 & { — 1} &{ — 3}&3\end{массив}} \right]\]

Как и в предыдущих примерах, мы будем отмечать числа, которые мы хотим изменить на данном шаге, красным цветом. Первым шагом здесь является получение 1 в верхнем левом углу, и опять же, у нас есть много способов сделать это. В этом случае мы заметим, что если мы поменяем местами первую и вторую строку, мы можем получить 1 в этом месте с относительно небольшими усилиями.

\[\require{color}\left[ {\begin{array}{rrr|r}{\color{Red} 3}&1&{- 2}&2\\1&{- 2}&1&3\\2&{- 1} &{ — 3}&3\end{массив}} \right]\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{массив}\left [ {\ begin {массив} {rrr | r} 1 & { — 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & { — 2} & 2 \\ {\ color {Red} 2} & { — 1} & { — 3}&3\конец{массив}} \справа]\]

Следующим шагом является преобразование двух чисел ниже этой 1 в 0. Также обратите внимание, что для этого почти всегда требуется операция третьей строки. Кроме того, мы можем сделать оба из них за один шаг следующим образом.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 2}&1&3\\{\color{Red} 3}&1&{- 2}&2\\{\color{Red } 2}&{ — 1}&{ — 3}&3\end{массив}} \right]\begin{массив}{*{20}{c}}{{R_2} — 3{R_1} \to {R_2 }}\\{{R_3} — 2{R_1} \to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{- 2}&1&3\\ 0&{\color{Red} 7}&{ — 5}&{ — 7}\\0&3&{ — 5}&{ — 3}\end{массив}} \right]\]

Далее мы хотим превратить 7 в 1. Мы можем сделать это, разделив вторую строку на 7.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 2}&1&3\\0&{\color{Red} 7}&{- 5}&{- 7}\\ 0&3&{ — 5}&{ — 3}\end{массив}} \right]\begin{массив}{*{20}{c}}{\frac{1}{7}{R_2}}\\ \to \end{массив}\left[ {\begin{массив}{rrr|r}1&{- 2}&1&3\\0&1&{-\frac{5}{7}}&{-1}\\0&{\color {Красный} 3}&{ — 5}&{ — 3}\end{массив}} \right]\]

Итак, здесь появилась дробь. Это будет происходить время от времени, так что не волнуйтесь по этому поводу. Следующий шаг — изменить 3 под этой новой 1 на 0. Обратите внимание, что мы пока не собираемся возиться с -2 над ней. Иногда так же легко превратить это в 0 на том же шаге. Однако в этом случае, вероятно, так же легко сделать это позже, как мы увидим.

Итак, с помощью операции третьей строки получаем

\[\require{color}\left[ {\begin{array}{rrr|r}1&{ — 2}&1&3\\0&1&{ — \frac{5}{7}}&{ — 1}\\0&{ \color{Red} 3}&{ — 5}&{ — 3}\end{array}} \right]\begin{array}{*{20}{c}}{{R_3} — 3{R_2} \ to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ — 2}&1&3\\0&1&{ — \frac{5}{7}}&{ — 1}\\0&0&{\color{Red} — \frac{{20}}{7}}&0\end{массив}} \right]\]

Далее нам нужно преобразовать число в правом нижнем углу в 1. Мы можем сделать это с помощью операции второй строки.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{ — 2}&1&3\\0&1&{ — \frac{5}{7}}&{ — 1}\\0&0&{ \color{Red} — \frac{{20}}{7}}&0\end{array}} \right]\begin{array}{*{20}{c}}{ — \frac{7}{{ 20}}{R_3}}\\ \to \end{массив}\left[ {\begin{array}{rrr|r}1&{- 2}&{\color{Red} 1}&3\\0&1&{\ color{Red} — \frac{5}{7}}&{ — 1}\\0&0&1&0\end{array}} \right]\]

Теперь нам нужны нули над этой новой единицей. Таким образом, использование операции с третьей строкой дважды, как показано ниже, сделает то, что нам нужно.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 2}&{\color{Red} 1}&3\\0&1&{\color{Red}-\frac{5 {7}}&{ — 1}\\0&0&1&0\end{массив}} \right]\begin{массив}{*{20}{c}}{{R_2} + \frac{5}{7}{ R_3} \to {R_2}}\\{{R_1} — {R_3} \to {R_1}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{\ цвет {Красный} — 2}&0&3\\0&1&0&{ — 1}\\0&0&1&0\end{массив}} \right]\]

Обратите внимание, что в этом случае последний столбец не изменился на этом шаге. Это произошло только потому, что последняя запись в этом столбце была нулевой. В общем, этого не будет.

Последним шагом будет превращение -2 над 1 во втором столбце в ноль. Это легко сделать с помощью операции третьего ряда.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{\color{Red} — 2}&0&3\\0&1&0&{- 1}\\0&0&1&0\end{array}} \right ]\begin{array}{*{20}{c}}{{R_1} + 2{R_2} \to {R_1}}\\ \to \end{array}\left[ {\begin{array}{rrr |r}1&0&0&1\\0&1&0&{ — 1}\\0&0&1&0\end{массив}} \right]\]

Итак, у нас есть расширенная матрица в окончательном виде и решение будет,

\[x = 1,\,\,\,y = — 1,\,\,\,z = 0\]

Это можно проверить, подставив их во все три уравнения и убедившись, что все они удовлетворяются.

b $\begin{align*}3x + y — 2z & = — 7\\ 2x + 2y + z & = 9\\ — x — y + 3z & = 6\end{align*}$ Показать решение

Опять же, первый шаг — записать расширенную матрицу.

\[\require{color}\left[ {\begin{array}{rrr|r}{\color{Red} 3}&1&{- 2}&{- 7}\\2&2&1&9\\{- 1}&{ — 1}&3&6\end{массив}} \right]\]

На этот раз мы не можем получить 1 в верхнем левом углу, просто поменяв местами ряды. Мы могли бы поменять местами первую и последнюю строку, но для этого потребуется еще одна операция, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы могли бы использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.

\[\require{color}\left[ {\begin{array}{rrr|r}{\color{Red} 3}&1&{- 2}&{- 7}\\2&2&1&9\\{- 1}&{ — 1}&3&6\end{массив}} \right]\begin{array}{*{20}{c}}{{R_1} — {R_2} \to {R_1}}\\ \to \end{массив} \left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\{\color{Red} 2}&2&1&9\\{\color{Red} — 1 }&{ — 1}&3&6\end{массив}} \right]\]

Теперь мы можем использовать операцию с третьей строкой, чтобы превратить два красных числа в нули.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\{\color{Red} 2}&2&1&9\\{ \color{Red} — 1}&{ — 1}&3&6\end{array}} \right]\begin{array}{*{20}{c}}{{R_2} — 2{R_1} \to {R_2 }}\\{{R_3} + {R_1} \to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ — 1}&{ — 3 }&{ — 16}\\0&{\color{Red} 4}&7&{41}\\0&{ — 2}&0&{ — 10}\end{массив}} \right]\]

Следующий шаг — поставить 1 на место, занятое красной 4. Мы могли бы сделать это, разделив всю строку на 4, но это привело бы к паре неприятных дробей. Итак, вместо этого мы собираемся поменять местами второй и третий ряд. Причина этого станет очевидной достаточно скоро.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\0&{\color{Red} 4}&7&{41 }\\0&{ — 2}&0&{ — 10}\end{массив}} \right]\begin{массив}{*{20}{c}}{{R_2} \leftrightarrow {R_3}}\\ \to \end{массив}\left[ {\begin{array}{rrr|r}1&{- 1}&{-3}&{-16}\\0&{\color{Red}-2}&0&{-10 }\\0&4&7&{41}\end{массив}} \right]\]

Теперь, если мы разделим вторую строку на -2, мы получим 1 в нужном месте.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\0&{\color{Red} — 2}&0&{ — 10}\\0&4&7&{41}\end{массив}} \right]\begin{массив}{*{20}{c}}{ — \frac{1}{2}{R_2}}\\ \to \end{массив}\left[ {\begin{массив}}{rrr|r}1&{- 1}&{- 3}&{- 16}\\0&1&0&5\\0&{\color{Red} 4}&7&{ 41}\end{массив}} \right]\]

Прежде чем перейти к следующему шагу, давайте подумаем, обратите внимание на пару вещей. Во-первых, нам удалось избежать дробей, что всегда хорошо, а во-вторых, этот ряд теперь готов. В конечном итоге нам бы понадобился ноль на третьем месте, и мы получили его бесплатно. Мало того, это не изменится ни в одной из последующих операций. Это не всегда происходит, но если это произойдет, это облегчит нашу жизнь.

Теперь воспользуемся операцией третьей строки, чтобы заменить красную цифру 4 на ноль.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\0&1&0&5\\0&{\color{Red} 4} &7&{41}\end{массив}} \right]\begin{array}{*{20}{c}}{{R_3} — 4{R_2} \to {R_3}}\\ \to \end{массив }\left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\0&1&0&5\\0&0&{\color{Red} 7}&{21}\end {массив}} \справа]\]

Теперь мы можем разделить третью строку на 7, чтобы число в правом нижнем углу стало единицей.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 1}&{- 3}&{- 16}\\0&1&0&5\\0&0&{\color{Red} 7} &{21}\end{array}} \right]\begin{array}{*{20}{c}}{\frac{1}{7}{R_3}}\\ \to \end{array}\ влево [ {\ begin {массив} {rrr | r} 1 & { — 1} & {\ color {Red} — 3} & { — 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {массив}} \ right] \]

Далее мы можем использовать операцию с третьей строкой, чтобы преобразовать -3 в ноль.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{- 1}&{\color{Red}-3}&{-16}\\0&1&0&5\\0&0&1&3\end{ array}} \right]\begin{array}{*{20}{c}}{{R_1} + 3{R_3} \to {R_{\kern 1pt} }}\\ \to \end{array}\ слева [ {\ begin {массив} {rrr | r} 1 & {\ color {Red} — 1} & 0 & { — 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {массив}} \ right] \]

Последним шагом является преобразование -1 в 0, используя операцию третьей строки снова.

\[\require{color}\left[ {\begin{array}{rrr|r}1&{\color{Red} — 1}&0&{- 7}\\0&1&0&5\\0&0&1&3\end{array}} \right ]\begin{array}{*{20}{c}}{{R_1} + {R_2} \to {R_{\kern 1pt}}}\\ \to \end{array}\left[ {\begin{ array}{rrr|r}1&0&0&{ — 2}\\0&1&0&5\\0&0&1&3\end{массив}} \right]\]

Тогда решение этой системы

\[x = — 2,\,\,\,y = 5,\,\,\,z = 3\]

Использование исключения Гаусса-Жордана для решения системы из трех уравнений может потребовать больших усилий, но часто это не больше работы, чем непосредственное решение, и во многих случаях работы меньше. Если бы мы составили систему из четырех уравнений (чего мы делать не собираемся), то в этот момент устранение Гаусса-Жордана, по всей вероятности, потребовало бы меньше усилий, чем если бы мы решали ее напрямую.

Кроме того, как мы видели в последнем примере, работавшем в этом разделе, на самом деле не существует единого пути решения этих проблем. Каждая система уникальна, и для ее выполнения может потребоваться другой путь и набор операций. Кроме того, путь, который один человек считает самым легким, может не совпадать с путем, который другой человек считает самым легким. Однако независимо от пути окончательный ответ будет одинаковым.

Дифференциальные уравнения — Обзор: Системы уравнений

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / Системы ЦЭ / Обзор : Системы уравнений

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Раздел 5-1: Обзор: Системы уравнений

Поскольку мы будем работать почти исключительно с системами уравнений, в которых количество неизвестных равно количеству уравнений, мы ограничим наш обзор системами такого типа.

Все, что мы будем здесь делать, может быть легко распространено на системы с большим количеством неизвестных, чем уравнений, или с большим количеством уравнений, чем неизвестных, если это необходимо.

Начнем со следующей системы $n$ уравнений с $n$ неизвестными, $x_{1}$, $x_{2}$,…, $x_{n} $.

\[\begin{equation}\begin{aligned}{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots + {a_{1n}}{x_n} & = {b_1}\ \ {a_{21}}{x_1} + {a_{22}}{x_2} + \cdots + {a_{2n}}{x_n} & = {b_2}\\ \vdots \hspace{0,8in} & \ \ {a_{n1}}{x_1} + {a_{n2}}{x_2} + \cdots + {a_{nn}}{x_n} & = {b_n}\end{выровнено}\label{eq:eq1} \конец{уравнение}\]

Обратите внимание, что в нижних индексах коэффициентов в этой системе, $a_{ij}$, $i$ соответствует уравнению, в котором находится коэффициент, а $j$ соответствует неизвестному, что умножается на коэффициент.

Чтобы использовать линейную алгебру для решения этой системы, мы сначала запишем расширенную матрицу для этой системы. Расширенная матрица — это просто все коэффициенты системы и числа для правой части системы, записанные в матричной форме. Вот расширенная матрица для этой системы.

\[\left( {\begin{array}{*{20}{r}}{{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}& {{b_1}}\\{{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}&{{b_2}}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\{{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}}&{{b_n}}\end{массив} } \Правильно)\]

Чтобы решить эту систему, мы будем использовать элементарные операции со строками (которые мы определим чуть позже), чтобы переписать расширенную матрицу в треугольной форме. Матрица будет иметь треугольную форму, если все элементы ниже главной диагонали (диагональ, содержащая $a_{11}$, $a_{22}$, …, $a_{nn}$) равны нулю .

После этого мы можем вспомнить, что каждая строка в расширенной матрице соответствует уравнению. Затем мы преобразуем нашу новую расширенную матрицу обратно в уравнения, и на этом этапе решение системы станет очень простым.

Прежде чем работать с примером, давайте сначала определим элементарные операции со строками. Их три.

Поменяйте местами два ряда. Это именно то, что он говорит. Мы поменяем местами строку $i$ на строку $j$. Обозначение, которое мы будем использовать для обозначения этой операции: ${R_i} \leftrightarrow {R_j}$
Умножить строку $i$ на константу $c$. Это означает, что каждая запись в строке $i$ будет умножена на константу $c$. Обозначение этой операции: $c{R_i}$
Добавить число, кратное строке $i$, к строке j. В уме мы умножим строку $i$ на соответствующую константу, а затем добавим результат к строке $j$ и поместим новую строку обратно в строку $j$, оставив строку $i$ в матрица без изменений. Обозначение этой операции: $c{R_i} + {R_j}$

Всегда немного легче понять эти операции, если мы увидим их в действии. Итак, давайте решим пару систем.

Пример 1. Решите следующую систему уравнений. \[\begin{align*} — 2{x_1} + {x_2} — {x_3} & = 4\\ {x_1} + 2{x_2} + 3{x_3} & = 13\\ 3{x_1} + { x_3} & = — 1\конец{выравнивание*}\]

Показать решение

Первый шаг — записать расширенную матрицу для этой системы. Не забывайте, что коэффициенты отсутствующих членов равны нулю.

\[\require{color} \left( {\begin{array}{*{20}{r}}{\color{Red} — 2}&1&{- 1}&4\\1&{\color{Red} 2 }&3&{13}\\3&0&{\color{Red} 1}&{ — 1}\end{массив}} \right)\]

Теперь мы хотим, чтобы записи ниже главной диагонали были равны нулю. Главная диагональ окрашена в красный цвет, чтобы мы могли следить за ней в этом первом примере. По причинам, которые со временем станут очевидными, мы бы предпочли, чтобы все элементы главной диагонали также были единицами.

Мы можем получить единицу в самом верхнем месте, заметив, что если мы поменяем местами первый и второй ряд, мы получим единицу в самом верхнем месте бесплатно. Итак, давайте сделаем это.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} — 2}&1&{- 1}&4\\1&{\color{Red} 2 }&3&{13}\\3&0&{\color{Red} 1}&{ — 1}\end{array}} \right)\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\{ — 2}& {\color{Red} 1}&{ — 1}&4\\3&0&{\color{Red} 1}&{- 1}\end{array}} \right)\]

Теперь нам нужно, чтобы две последние записи (-2 и 3) в первом столбце были равны нулю. Мы можем сделать это, используя операцию третьей строки. Обратите внимание, что если мы возьмем первую строку в 2 раза и добавим ее во вторую строку, мы получим ноль во второй записи в первом столбце, а если мы возьмем -3 раза первую строку в третью строку, мы получим 3 в быть нулем. Мы можем выполнить обе эти операции одновременно, так что давайте сделаем это.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\{ — 2}&{\color{Red} 1}&{ — 1}&4\\3&0&{\color{Red} 1}&{ — 1}\end{array}} \right)\begin{array}{*{20}{c}}{2{ R_1} + {R_2}}\\{ — 3{R_1} + {R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color {Красный} 1}&2&3&{13}\\0&{\color{Красный} 5}&5&{30}\\0&{ — 6}&{\color{Красный} — 8}&{ — 40}\end{массив }} \Правильно)\]

Прежде чем перейти к следующему шагу, убедитесь, что вы выполнили то, что мы только что сделали. Давайте посмотрим на первую операцию, которую мы выполнили. Эта операция требует умножить запись в строке 1 на 2 и добавить ее к соответствующей записи в строке 2, а затем заменить старую запись в строке 2 этой новой записью. Ниже приведены четыре отдельные операции, которые мы выполнили для этого.

\[\begin{align*}2\left( 1 \right) + \left( { — 2} \right) & = 0\\ 2\left( 2 \right) + 1 & = 5\\ 2\left ( 3 \right) + \left( { — 1} \right) & = 5\\ 2\left( {13} \right) + 4 & = 30\end{align*}\]

Ладно, следующий шаг необязательный, но опять-таки удобный. Технически 5 во втором столбце можно оставить. Тем не менее, это облегчит нашу жизнь в будущем, если это будет 1. Мы можем использовать операцию второй строки, чтобы позаботиться об этом. Мы можем разделить всю строку на 5. Это даст

. \[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 5}&5&{ 30}\\0&{ — 6}&{\color{Red} — 8}&{ — 40}\end{array}} \right)\begin{array}{*{20}{c}}{\frac {1}{5}{R_2}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\ \0&{\color{Red} 1}&1&6\\0&{ — 6}&{\color{Red} — 8}&{ — 40}\end{array}} \right)\]

Следующим шагом будет использование операции с третьей строкой, чтобы преобразовать -6 во втором столбце в ноль.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 1}&1&6\ \0&{ — 6}&{\color{Red} — 8}&{ — 40}\end{array}} \right)\begin{array}{*{20}{c}}{6{R_2} + {R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{ Красный} 1}&1&6\\0&0&{\color{Красный} — 2}&{ — 4}\end{массив}} \right)\]

Итак, официально мы закончили, но опять же, удобно разместить все единицы на главной диагонали, поэтому мы сделаем последний шаг.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 1}&1&6\ \0&0&{\color{Red} — 2}&{ — 4}\end{array}} \right)\begin{array}{*{20}{c}}{ — \frac{1}{2}{ R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red } 1}&1&6\\0&0&{\color{Red} 1}&2\end{массив}} \right)\]

Теперь мы можем вернуться к уравнениям.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 1}&1&6\ \0&0&{\color{Red} 1}&2\end{массив}} \right)\hspace{0,25in} \Rightarrow \hspace{0,25in}\begin{aligned}{x_1} + 2{x_2} + 3{ x_3} &= 13\\{x_2} + {x_3} &= 6\\{x_3} &= 2\end{выровнено}\]

На данный момент решить довольно просто. Мы получаем $x_{3}$ бесплатно, и как только мы получаем это, мы можем подставить это во второе уравнение и получить $x_{2}$. Затем мы можем использовать первое уравнение, чтобы получить $x_{1}$. Обратите также внимание, что наличие единиц вдоль главной диагонали несколько помогло в этом процессе.

Решение этой системы уравнений:

\[{x_1} = — 1\hspace{0,25 дюйма}\hspace{0,25 дюйма}{x_2} = 4\hspace{0,25 дюйма}\hspace{0,25 дюйма}{x_3} = 2\]

Процесс, используемый в этом примере, называется Исключение по Гауссу . Давайте посмотрим на другой пример.

Пример 2. Решите следующую систему уравнений. \[\begin{align*}{x_1} — 2{x_2} + 3{x_3} & = — 2\\ — {x_1} + {x_2} — 2{x_3} & = 3\\ 2{x_1} — {x_2} + 3{x_3} & = 1\конец{выравнивание*}\]

Показать решение

Сначала запишите расширенную матрицу.

\[\left( {\begin{array}{*{20}{r}}1&{ — 2}&3&{ — 2}\\{ — 1}&1&{ — 2}&3\\2&{ — 1}&3&1 \конец{массив}} \справа)\]

Мы не будем вводить столько слов при работе с этим примером. Вот работа для этой расширенной матрицы.

\[\left( {\begin{array}{*{20}{r}}1&{ — 2}&3&{ — 2}\\{ — 1}&1&{ — 2}&3\\2&{ — 1}&3&1 \end{array}} \right)\begin{array}{*{20}{c}}{{R_1} + {R_2}}\\{ — 2{R_1} + {R_3}}\\ \to \ конец {массив} \ left( {\ begin {массив} {* {20} {r}} 1 & { — 2} & 3 & { — 2} \\ 0 & { — 1} & 1 & 1 \\ 0 & 3 & { — 3} & 5 \ конец {массив}} \справа)\] \[\begin{array}{*{20}{r}}{ — {R_2}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}1& { — 2}&3&{ — 2}\\0&1&{ — 1}&{ — 1}\\0&3&{ — 3}&5\end{массив}} \right)\begin{массив}{*{20}{c }}{ — 3{R_2} + {R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2} \\0&1&{ — 1}&{ — 1}\\0&0&0&8\end{массив}} \right)\]

В этом примере мы не будем идти дальше. Вернемся к уравнениям, чтобы понять, почему.

\[\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2}\\0&1&{- 1}&{- 1}\\0&0&0&8\end{массив} } \right) \Rightarrow \begin{align}{x_1} — 2{x_2} + 3{x_3} & = — 2\\{x_2} — {x_3} & = — 1\\0 & = 8\end{ выровнено}\]

Последнее уравнение должно вызвать некоторое беспокойство. Тут один из трех вариантов. Во-первых, нам каким-то образом удалось доказать, что 0 равно 8, и мы знаем, что это невозможно. Во-вторых, мы допустили ошибку, но, проанализировав нашу работу, не видно, что мы допустили ошибку.

Остается третий вариант. Когда мы получаем что-то вроде третьего уравнения, которое просто не имеет смысла, мы сразу понимаем, что решения нет. Другими словами, не существует набора из трех чисел, который одновременно делает все три уравнения верными.

Давайте рассмотрим еще один пример. Мы собираемся получить систему для этого нового примера, внеся очень небольшое изменение в систему по сравнению с предыдущим примером.

Пример 3. Решите следующую систему уравнений. \[\begin{align*}{x_1} — 2{x_2} + 3{x_3} & = — 2\\ — {x_1} + {x_2} — 2{x_3} & = 3\\ 2{x_1} — {x_2} + 3{x_3} & = — 7\end{align*}\]

Показать решение

Итак, единственная разница между этой системой и системой из второго примера в том, что мы заменили 1 справа от знака равенства в третьем уравнении на -7.

Теперь запишите расширенную матрицу для этой системы.

\[\left( {\begin{array}{*{20}{r}}1&{ — 2}&3&{ — 2}\\{ — 1}&1&{ — 2}&3\\2&{ — 1}&3& { — 7}\end{массив}} \right)\]

Действия для этой задачи идентичны действиям для второй задачи, поэтому мы не будем их все записывать. Выполнив те же действия, мы придем к следующей матрице.

\[\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2}\\0&1&{- 1}&{- 1}\\0&0&0&0\end{массив} } \Правильно)\]

На этот раз последнее уравнение сокращается до

\[0 = 0\]

и в отличие от второго примера это не проблема. Ноль на самом деле равен нулю!

Мы могли бы остановиться здесь и вернуться к уравнениям, чтобы получить решение, и в этом случае решение есть. Однако, если мы сделаем еще один шаг и получим ноль над единицей во втором столбце, а также под ней, наша жизнь станет немного проще. Выполнение этого дает,

\[\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2}\\0&1&{- 1}&{- 1}\\0&0&0&0\end{массив} } \right)\begin{array}{*{20}{c}}{2{R_2} + {R_1}}\\ \Rightarrow \end{array}\left( {\begin{array}{*{20 }{r}}1&0&1&{ — 4}\\0&1&{ — 1}&{ — 1}\\0&0&0&0\end{массив}} \right)\]

Если мы теперь вернемся к уравнению, мы получим следующие два уравнения.

\[\left( {\begin{array}{*{20}{r}}1&0&1&{- 4}\\0&1&{- 1}&{- 1}\\0&0&0&0\end{массив}} \right)\ hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\begin{array}{*{20}{r}}{{x_1} + {x_3} = — 4}\\{{x_2} — {x_3} = — 1}\\{}\конец{массив}\]

У нас есть два уравнения и три неизвестных. Это означает, что мы можем решить для двух переменных с точки зрения оставшейся переменной. Поскольку $x_{3}$ входит в оба уравнения, мы будем решать с их помощью.

\[\begin{align*}{x_1} & = — {x_3} — 4\\ {x_2} & = {x_3} — 1\end{align*}\]

Это решение означает, что мы можем выбрать значение $x_{3}$ как угодно, а затем найти значения $x_{1}$ и $x_{2} $. В этих случаях мы обычно записываем решение следующим образом:

. \[\begin{align*}{x_1} & = — t — 4\\ {x_2} & = t — 1\hspace{0.25in}\hspace{0.25in}t = {\mbox{любое действительное число}} \\ & {x_3} = t\end{align*}\]

Таким образом, мы получаем бесконечное число решений, по одному для каждого значения $t$.

Эти три примера подводят нас к интересному факту о системах уравнений.

Факт

Учитывая систему уравнений $\eqref{eq:eq1}$, у нас будет одно из трех возможных значений количества решений.

Нет решения.
Ровно одно решение.
Бесконечно много решений.

Прежде чем перейти к следующему разделу, нам нужно рассмотреть еще одну ситуацию. Система уравнений в $\eqref{eq:eq1}$ называется неоднородной системой, если хотя бы одно из b _i ’ s не равно нулю. Однако если все $b_{i}$ равны нулю, мы называем систему однородной, и система будет иметь вид

. \[\begin{equation}\begin{aligned}{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots + {a_{1n}}{x_n} & = 0\\ { a_{21}}{x_1} + {a_{22}}{x_2} + \cdots + {a_{2n}}{x_n} & = 0\\ \vdots \hspace{0,8in} & \\ {a_{ n1}}{x_1} + {a_{n2}}{x_2} + \cdots + {a_{nn}}{x_n} & = 0\end{выравнивание}\label{eq:eq2}\end{equation}\ ]

Теперь заметьте, что в однородном случае мы гарантированно имеем следующее решение.

\[{x_1} = {x_2} = \cdots = {x_n} = 0\]

Это решение часто называют тривиальным решением .

Для гомогенных систем приведенный выше факт можно изменить на следующий.

Факт

Учитывая однородную систему уравнений, $\eqref{eq:eq2}$, у нас будет одна из двух возможностей для количества решений.

Ровно одно решение, тривиальное решение
Бесконечное множество ненулевых решений в дополнение к тривиальному решению.

Во второй возможности мы можем сказать, что решение ненулевое, потому что если будет бесконечно много решений и мы знаем, что одно из них является тривиальным решением, то все остальные должны иметь хотя бы одно из $x_{i }$ не равно нулю, и, следовательно, мы получаем ненулевое решение.

Система линейных уравнений и обращение матриц

Этот учебный объект JavaScript E-labs предназначен для поиска решения систем линейных уравнений до трех уравнений с тремя неизвестными. Это также позволяет нам найти обратную матрицу.
Другие учебные объекты JavaScript для принятия решений из этой серии относятся к разным областям применения в разделе МЕНЮ на этой странице.
Профессор Хоссейн Аршам
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода.
Инструкции и приложения:

Имена неизвестных переменных: X1, X2, X3,.. и X10, в зависимости от того, есть ли у вас одно уравнение, два уравнения или три уравнения с одной неизвестной, двумя неизвестными или тремя неизвестными переменными соответственно.
Начиная с левого верхнего угла, замените столько нулей в матрице данных коэффициентами неизвестных переменных в уравнениях вместе с их правыми значениями, сколько необходимо. Матрица коэффициентов должна представлять собой квадратную матрицу, расположенную в верхнем левом углу матрицы данных, поэтому не оставляйте пустых строк между ними.
JavaScript основан на операциях строки Gauss-Jordan (GJ). Требование для операций GJ состоит в том, что первый элемент в матрице коэффициентов должен быть ненулевым. Поэтому сначала введите коэффициент всех уравнений, имеющих ненулевой коэффициент X1; затем введите все остальные уравнения. То есть любое уравнение с нулевыми коэффициентами для X1 должно стоять в конце таблицы ввода данных.
Численный пример 1. Рассмотрим следующую систему уравнений:
Х2 + Х3 = 5
3Х1 + Х3 = 6
-Х1 + Х2 = 1
Матрица коэффициентов переменных:
0    1    1
3    0    1
-1    1    0
Первая запись первого столбца равна нулю, хотя в нем всегда есть хотя бы один ненулевой элемент. Следовательно, мы должны перестроить систему уравнений таким образом, чтобы любое уравнение с нулевым коэффициентом X1 оказалось среди последнего набора уравнений. То есть, рассматривая эквивалентную систему уравнений:
3Х1 + Х3 = 6
-Х1 + Х2 = 1
Х2 + Х3 = 5
Решите эту эквивалентную систему уравнений, введя ее коэффициент и значения RHS в таблицу ввода данных, затем нажмите кнопку «Рассчитать». Выходом является решение: X1 = 1, X2 = 2 и X3 = 3, что можно проверить подстановками.
Нахождение обратной матрицы с помощью System of Equations Solver: Чтобы найти обратную квадратную матрицу размера n, решите n систем уравнений с единичным вектором в правой части. Следующий числовой пример иллюстрирует этот процесс:
Численный пример 2. Предположим, мы хотим найти обратную (A ^-1 ) следующую матрицу (если она существует) A:
2 1
А =
1 -1
В общем найти А ^-1 , столбец за столбцом, решить n систем уравнений, имеющих матрицу коэффициентов A, но с n различными векторами идентичности в качестве их правых значений.
Для этого числового примера мы должны решить следующие две системы уравнений:
2Х1 + Х1 = 1
Х1 — Х2 = 0
а также
2Х1 + Х1 = 0
Х1 — Х2 = 1
Обратите внимание, что коэффициенты переменных X1 и X2 являются матрицей A в обеих системах уравнений, однако RHS являются двумя единичными векторами в n = 2-мерном пространстве.
Решения первой и второй систем уравнений в соответствии с приведенной выше инструкцией дают первый и второй столбцы матрицы A ^-1.
Чтобы найти первый столбец A ^-1, решите:
2Х1 + Х1 = 1
Х1 — Х2 = 0
Это дает X1 = 1/3, X2 = 1/3. Чтобы найти второй столбец A ^-1, решите:
2Х1 + Х1 = 0
Х1 — Х2 = 1
Это дает X1 = 1/3, X2 = -2/3. Следовательно, A ^-1 p равно
1/3 1/3
А ^-1 =
1/3 -2/3
Примечание: Матрица, имеющая обратную, называется неособый или обратимый. Матрица называется вырожденной, если она не имеет обратной. Например, следующая матрица является сингулярной:
1    6    4
2    4   -1
-1    2    5
Поэтому при применении описанной выше процедуры обращения матрицы, если матрица вырожденная, то по крайней мере из систем уравнений не имеет решения.
Для редактирования ваших данных, включая добавление/изменение/удаление, вам не нужно нажимать на кнопку «очистить», а заново вводить свои данные заново. Вы можете просто добавить, изменить число на другое в той же ячейке или удалить число из ячейки, установив его значение равным нулю. После редактирования нажмите кнопку «Рассчитать».
Это полезно, например. найти обратную матрицу A _10×10, где мы должны изменить только значения RHS.
Для расширенного редактирования или использования JavaScript для нового набора данных используйте кнопку «Очистить».

Х1	Х2	X3	X4	Х5	Х6	Х7	Х8	Х9	x 10













Решение Есть:
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10

Для получения технических сведений вернуться к:
Темы линейной алгебры
Пожалуйста, отправьте ваши комментарии по адресу:
Профессор Хоссейн Аршам

МЕНЮ

Инструменты принятия решений в экономике и финансах

Классификация инвентаризации ABC
Авторегрессионный временной ряд
Расчеты бета и ковариации
Двумерные дискретные распределения
Анализ безубыточности и прогнозирование
Категории вероятностных и статистических инструментов
Обнаружение тренда и автокреляции
Определение выбросов
Прогнозирование сглаживанием
Модели управления запасами
Решатели линейной оптимизации для загрузки
Линейная оптимизация с чувствительностью
Денежная математика: анализ сложных процентов
Матричная алгебра и цепи Маркова
Оценка среднего и дисперсии
Измерение точности прогноза
Другие полиномиальные регрессии
Оптимальный возраст для замены
Параметрическая система линейных уравнений
Показатели эффективности для портфелей
График временного ряда
Прогнозы по регрессии
Оценка доли
Квадратичная регрессия
Регрессионное моделирование
Сезонный указатель
Инвентаризационный анализ за один период
Обобщите свои данные
Система уравнений и обращение матриц
Тест на случайные колебания
Тест на сезонность
Тест для стационарных временных рядов
Статистика временных рядов

Вероятностное моделирование

Байесовский вывод для среднего
Пересмотренная вероятность Байеса
Двумерные дискретные распределения
Сравнение двух случайных величин
Принятие решений в условиях неопределенности
Определение полезной функции
Принятие рискованных решений
Измерьте качество вашего решения
Полиномиальные распределения
Игры с нулевой суммой для двух человек

Статистика

Ковариационный анализ
Дисперсионный анализ для сжатых наборов данных
Дисперсионный анализ для зависимых групп населения
ANOVA: проверка средств
Байесовский статистический вывод
Статистика двумерной выборки
Хи-квадрат Тест на родство
Совместимость нескольких счетчиков
Доверительные интервалы для двух совокупностей
Описательная статистика
Определение выбросов
Эмпирическая функция распределения
Равенство многовариантности
Оценки с уверенностью
Согласие для дискретных переменных
Тестирование идентичных популяций
Номера индексов с приложениями
Тест K-S на равенство двух совокупностей
Тест Лиллифорса для экспоненциального
Множественные регрессии
Процент: оценка и тестирование
Тест парной пропорции
Полиномиальные регрессии
Объединение средних и отклонений
P-значения для популярных дистрибутивов
Квадратичная регрессия
Определение объема выборки
Пересмотр среднего значения и дисперсии
Рассеянная диаграмма и выбросы
Простая линейная регрессия
Субъективная оценка оценок
Субъективность при проверке гипотез
Проверка нескольких коэффициентов корреляции
Проверка однородности совокупности
Тест на нормальность
Испытание на равномерное распределение
Тестирование процесса Пуассона
Тест на случайность
Тестирование нескольких пропорций
Проверка среднего значения
Тестирование медиан
Проверка коэффициента корреляции
Тестирование двух популяций
Проверка дисперсии
Тест «до и после»
Другие средства
Двухфакторный дисперсионный анализ
Двухфакторный дисперсионный анализ с повторениями

Заявление об авторских правах. Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях.
Этот сайт может быть переведен и/или зеркально отображен в неизменном виде (включая эти уведомления) на любом сервере с общедоступным доступом. Все файлы доступны по адресу http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.
Пожалуйста, пришлите мне по электронной почте ваши комментарии, предложения и проблемы. Спасибо.
Профессор Хоссейн Аршам
Вернуться к:
Домашняя страница доктора Аршама

ЕОФ: 1994-2015 гг.

(Сокращенный) Калькулятор формы эшелона строк

Вспомните систему уравнений, которую мы имели в втором разделе, но прямо перед тем, как мы начали играть с элементарными операциями над строками:

x + y + z = 32 ,

-х + 2у = 25 и

-y + 2z = 16 .

Прежде чем мы перейдем к пошаговым расчетам, давайте быстро скажем несколько слов о том, как мы можем ввести такую систему в наш калькулятор сокращенной ступенчатой формы. Во-первых, у нас в системе три строки, поэтому нам нужно сообщить об этом калькулятору вверху, в поле количества уравнений. Это покажет нам символическую картину произвольной системы трех линейных уравнений.

Нам нужно определить, какое число соответствует какому символу из калькулятора rref. На рисунке первое уравнение имеет символы a₁ , b₁ , c₁ и d₁ , которые находятся соответственно рядом с x , с y , с 9 z справа и с 929808 сторона знака = . Это числа, которые мы ищем в нашей системе. Глядя на первое из наших уравнений, мы определяем, что a₁ = 1 , b₁ = 1 , c₁ = 1 и d₁ = 32 ( помните, что отсутствие числа перед переменной означает, что коэффициент равен 1 ).

Аналогично, для следующих двух строк мы получаем A₂ = -1 , B₂ = 2 , C₂ = 0 , D₂ = 25 и A₃ = 0 , B₃ = -1 , A₃ = 0 , B₃ = -1 , . c₃ = 2 , d₃ = 16 ( помните, что если в уравнении нет какой-либо переменной, то коэффициент рядом с этой переменной равен 0 ). Если ввести все эти данные в калькулятор формы сокращенного эшелона строк, вы получите спойлер ответа . Также обратите внимание, что наш калькулятор rref не позволяет использовать нелинейные (например, квадратичные) уравнения .

Теперь мы будем следовать инструкциям по сокращению строк матрицы, заданным методом исключения Гаусса , чтобы преобразовать ее в эшелонированную форму строк. Наконец, мы сделаем дополнительный шаг из исключения Гаусса-Джордана , чтобы превратить его в сокращенную версию, которая используется по умолчанию в калькуляторе rref.

По алгоритму начинаем с выбираем уравнение с первой переменной (в нашем случае это x ) и помещаем его в верхнюю строку. Обратите внимание, что наша система уже находится в таком виде, поэтому нам не нужно ничего менять. Затем, , мы используем первое уравнение, чтобы исключить x из двух других строк . Обратите внимание, что нам нужно иметь дело только со вторым уравнением, так как третье уравнение не имеет x . чтобы избавиться от -x в средней строке, нам нужно добавить к этому уравнению кратное первому уравнению, чтобы x компенсировали друг друга. Поскольку -x + x = 0 , нам нужно иметь x с коэффициентом 1 в том, что мы добавляем во вторую строку. К счастью, это именно то, что мы имеем в верхнем уравнении. Следовательно, мы добавляем первую строку ко второй , чтобы получить

-x + 2y + (x + y + z) = 25 + 32 ,

что равно

3y + z = 57 .

Вместе с двумя другими уравнениями это дает

x + y + z = 32

3y + z = 57

-y + 2z = 16 .

Отлично! Теперь у нас есть две последние строки без x в них . Правда, второе уравнение получило z , которого раньше не было, но это просто цена, которую мы должны заплатить.

Теперь нам нужно что-то сделать с y в последнем уравнении, и мы будем использовать для него вторую строку. Тем не менее, это будет не так просто, как в прошлый раз - у нас есть 3y в нашем распоряжении и -y , с которым нужно разобраться. Что ж, инструменты, которые нам дали, пригодятся.

Чтобы исключить -y из третьего уравнения, нам нужно получить y (т.е. y с коэффициентом 1 ) из второго, так как -y + y = 0 . Чтобы получить его от 3y достаточно разделить на 3 . Другими словами, на языке сокращения строк матрицы, мы добавим кратное 1/3 (эквивалентно делению на 3 ) второго уравнения к нижней строке . Это дает

-y + 2z + (1/3) * (3y + z) = 16 + (1/3) * 57 .

Обратите внимание, что 1/3 также появился справа от с 57 . После упрощения это дает

(7/3)z = 35 ,

, что вместе с двумя другими уравнениями равно

x + y + z = 32 ,

3y + z = 7/ 3 (

`8 3 ,`

`8 3)z = 35`

Вуаля! Это эшелонированная форма строк, заданная методом исключения Гаусса . Обратите внимание, что такие системы получаются в нашем калькуляторе rref ответом « No » на вопрос показывать ли сокращенную форму вверху калькулятора.

Чтобы получить сокращенную форму эшелона строки, мы следуем шестому шагу, упомянутому в разделе выше — мы делим каждое уравнение на коэффициент его первой переменной . Это значит, что нам нужно первую строку разделить на 1 (коэффициент х ), вторую на 3 (коэффициент y ), а третью на 7/3 (коэффициент z ). Это дает

x + y + z = 32 ,

y + (1/3)z = 19. ,

z = 15 ,

и отмечают конец алгоритма исключения Гаусса-Жордана . Мы можем получить такие системы в нашем калькуляторе формы сокращенного ряда, ответив « Да » на верхний вопрос (как это делается по умолчанию).

Заметьте, что теперь легко найти решение нашей системы . Из последней строки мы знаем, что z = 15 , поэтому мы можем подставить его во второе уравнение, чтобы получить

y + (1/3) * 15 = 19. .

Отсюда мы получаем y = 14 , и мы можем подставить это и z = 15 в первую строку, чтобы получить

x + 14 + 15 = 32 ,

что дает 8 93080 .

Решение СЛАУ методом Гаусса — онлайн калькулятор, бесплатный сервис

Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:

Калькулятор с решением систем линейных уравнений методом Гаусса

Решение уравнений методом Гаусса онлайн калькулятор

Решение системы линейных уравнений методом Гаусса-Жордана

Алгоритм метода Гаусса

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

Решение систем линейных уравнений алгоритмы общих и частных методов нахождения корней, основные правила и теоремы и примеры их использования, онлайн калькулятор

Понятия и обозначения

Алгебраическое сложение

Метод подстановки

Использование матриц

Способ Гаусса-Жордана

Теорема Кронекера — Капелли

Решение Крамера

Удобные онлайн-калькуляторы

Система комплексных линейных уравнений

Онлайн калькулятор.

Калькулятор исключения Гаусса с шагами

Что такое алгоритм исключения Гаусса?

Расширенная матрица:

Общая форма:

Свойства расширенной матрицы:

Как применить алгоритм исключения Гаусса?

Как работает калькулятор исключения Гаусса?

Часто задаваемые вопросы:

В чем разница между методом исключения Гаусса и методом Гаусса-Жордана?

Почему мы используем метод исключения Гаусса?

Что эффективнее Жордан Гаусса или Исключение Гаусса?

Для чего в реальной жизни используется метод исключения Гаусса?

Когда используется метод исключения Гаусса?

Каковы преимущества метода исключения Гаусса?

Какие подводные камни метода исключения Гаусса?

Что является ключевым в исключении Гаусса?

Что такое точка опоры в матрице?

Заключение:

Ссылки:

3.3: Решающие системы с исключением Гаусса-Жордана

Расширенные матрицы

Написание системы уравнений из расширенной матрицы

Сокращенная ступенчатая форма

Решение систем уравнений с исключением Гаусса-Жордана

Ключевые понятия

Авторы и авторство

Алгебра — расширенные матрицы

Раздел 7-3: Расширенные матрицы

Дифференциальные уравнения — Обзор: Системы уравнений

Раздел 5-1: Обзор: Системы уравнений

Факт

Факт

Система линейных уравнений и обращение матриц

(Сокращенный) Калькулятор формы эшелона строк

8 3 ,

8 3)z = 35

Добавить комментарий Отменить ответ

`8 3 ,`

`8 3)z = 35`