Решение логарифмических выражений онлайн с подробным решением: Решение логарифмических уравнений | Онлайн калькулятор

Курсовая работа на тему «Методика изучения логарифмических уравнений и неравенств.»

Министерство просвещения Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования «Чеченский государственный

педагогический университет»

                            

Физико-математический факультет

_{(факультет/институт)}

Геометрии и методики преподавания математики

_{(кафедры)}

 

_{КУРСОВАЯ РАБОТА}

 

 

                                                                         по дисциплине: «Методика обучения математики»                                        .

..

на тему: «Методика изучения логарифмических уравнений и неравенств»

 

 

	Выполнена студенткой 4 курса МИ1 группы
	очной формы обучения
	Профиль «Математика» и «Информатика»   __________               Тепсуркаева Хава Адаовна               Подпись                                                                 ФИО студента
	Руководитель_______________________________                                                                                      (Ученая степень и звание)
	___________          Багашева Аймани Бураевна               подпись                                                        ФИО руководителя
Работа защищена «___» _________2021г.   протокол №______
	Оценка________________________________

_{___________________________________________________________________}

 

 

 

Грозный – 2021

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………..………………3

ГЛАВА 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ………………………………………5

1.1.          Методические     особенности изучения логарифмических уравнений и неравенств…..………………………………………………………….………….5

1.2.          Анализ заданий на решение логарифмических уравнений в составе ЕГЭ……………………………………………………………………………..…..8

ГЛАВА 2. ВИДЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ И МЕТОДЫ ИХ РЕШЕНИЯ……………………………….11

2. 1.    Метод решения по определению логарифма………………..…………..11

2.2.    Метод потенцирования………………………………………..………….11

2.3.   Метод замены переменной………………………………………..………13

2.4.    Графический метод…………………………………………………………15

2.5.    Метод логарифмирования обеих частей уравнения……………..………16

2.6.    Метод приведения логарифмов к одному и тому же основанию……….17

2.7.  Методическая разработка урока по теме «Решение логарифмических уравнений»……………………………………………………………………….18

ЗАКЛЮЧЕНИЕ……………………………………………………………..….24

СПИСОК ЛИТЕРАТУРЫ………………………………………………………26

 

ВВЕДЕНИЕ

 

Актуальность работы. В школьном курсе математики важное место занимает решение показательных и логарифмических уравнений и неравенств. В зависимости от авторов учебника эта тема изучается в 10 или 11 классе. Показательные и логарифмические уравнения, неравенства встречаются в заданиях ЕГЭ. Поэтому, изучению методов решения показательных и логарифмических уравнений и неравенств должно быть уделено особое внимание. Из вышеуказанного следует актуальность выбранной темы, необходимость рассмотрения этой темы для будущего учителя математики.

При решении логарифмических уравнений часто возникают трудности, связанные со следующими особенностями:

—                     незнание четкого алгоритма решения логарифмических уравнений;

—                     при решении логарифмических уравнений, ученики производят преобразования, которые не равносильны исходным уравнениям;

—                     при решении логарифмического уравнения введением новой переменной забывают возвращаться к обратной замене.

Цель данной работы: изучить теоретический материал по теме «Логарифмические уравнения в школьном курсе», провести анализ этой темы в учебниках алгебра и начала анализа, рассмотреть основные методы решения логарифмических уравнений, систематизировать и обобщить основные особенности этой темы.

Для достижения поставленной цели необходимо решить следующие задачи:

—                     изучить требования государственных стандартов по теме «Логарифмические уравнения»;

—                     проанализировать материал по теме в учебниках алгебры и начала анализа;

—                     систематизировать методы решения логарифмических уравнений;

—                     систематизировать и обобщить методические особенности изучения данной темы.

Объектом исследования является процесс обучения математики в старших классах.

Предметом исследования являются методические особенности изучения показательных и логарифмических уравнений, неравенств.

Методы исследования:

−                  анализ психолого-педагогической литературы по проблеме исследования;

−                  методы статистической обработки полученной информации.

Структура работы: введение, две главы, заключение, список литературы. Объем работы: 27 стр.

 

 

ГЛАВА 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ.

 

1.1          Методические          особенности изучения логарифмических уравнений и неравенств.

 

Первоначально в курсе алгебры изучались такие функции, вычисление значений которых сводилось к четырем арифметическим действиям и возведению в степень. Для вычисления значений логарифмической функции нужно уметь находить логарифмы чисел, т.е. выполнять новое для учащихся действие – логарифмирование. До появления компьютеров логарифмы широко использовались для выполнения вычислений и детально изучались в школе. Теперь же их роль стала вспомогательной, а изучение в школе не стало столь подробным.

Знакомство с логарифмами чисел и их свойствами для многих учащихся достаточно сложно. Поэтому полезны подробные и наглядные объяснения. Обычно логарифм определяется как показатель степени, в которую нужно возвести основание, чтобы получить данное число: , т.к. . Следует обратить внимание на то, что  является корнем уравнения , а поэтому . Таким образом, получается основное логарифмическое тождество  , где  Это равенство является краткой символической записью определения логарифма.

Доказательство свойств логарифма опирается на его определение. Т.к., например, по определению логарифма , , то, перемножая эти равенства и используя свойство умножения степеней, получаем  ,  . Последнее равенство показывает, что  отсюда и следует свойство логарифма произведения

На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10 (десятичный логарифм) и по основанию  (- натуральный логарифм), отсюда возникает необходимость формулы перехода от логарифма по одному основанию к логарифму по другому основанию: , где

Т.к. на микрокалькуляторе есть клавиши  и , то для вычисления логарифма по основаниям, отличным от 10 и , нужно использовать формулу перехода.

Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением.

Простейшим логарифмическим уравнением является уравнение вида

 (1)

Утверждение 1. Если , уравнение (1) при любом действительном b имеет единственное решение 

Пример 1. Решить уравнения:

Решение. Используя утверждение 1, получим

Приведем основные свойства логарифма.

. Основное логарифмическое тождество:

где 

 Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:

Замечание. Если  тогда свойство  примет вид

 Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя:

 

Замечание. Если , тогда свойство  примет вид

, 

 Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:

. Формула перехода к другому основанию:

,  в частности, если  , получим,

Используя свойства , легко получить следующие свойства

и, если в (5) c — четное число  ), имеет место

 [1 c.214]

Перечислим и основные свойства логарифмической функции  :

1. Область определения логарифмической функции есть множество положительных чисел.

2. Область значений логарифмической функции — множество действительных чисел.

3. При  логарифмическая функция строго возрастает а при , — строго убывает

4.

5. Если , то логарифмическая функция отрицательна при x (0;1) и положительна при  а если , то логарифмическая функция положительна при и отрицательна при.

6. Если то логарифмическая функция выпукла вверх, а если  — выпукла вниз [1 c.217].

Важнейшей частью школьного курса математики является обучение методам решения уравнений. Для успешного решения уравнений  необходимо знать и использовать свойства показательной и логарифмической функций, свойства действий со степенями, определение логарифма, основные логарифмические тождества.

Цель темы – обучение учащихся методам решения логарифмических уравнений.

Для передачи теоретического материала наиболее эффективна исследовательская работа учеников, которая сопровождается беседами учителя с учащимися. Для закрепления материала используются задания из учебника, дополнительной литературы.

Особое место отводится самостоятельной работе – решению уравнений, подготовка сообщений, проработке теоретического материала. При изучении темы «логарифмические уравнения» учащиеся должны уметь:

1. Определять методы решения логарифмических уравнений.

2. Решать логарифмические уравнения.

 

1.2          Анализ заданий на решение логарифмических уравнений в составе ЕГЭ.

 

Рассмотрим задания из состава ЕГЭ, содержащие примеры на решение логарифмических выражений уравнений:

1.  Найдите корень уравнения.

Решение.

Последовательно получаем:

Ответ: −124.

2. Найдите корень уравнения 

Решение.

Последовательно получаем:

Ответ: 21.[2 c.40]

3. Решите уравнение 

Если, уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение.

На ОДЗ перейдем к уравнению на основание логарифма:

Итак, на ОДЗ уравнение имеет только один корень.

Ответ: 12.

4.а) Решите уравнение.

б) Укажите корни этого уравнения, принадлежащие отрезку.

Решение.

а) Запишем исходное уравнение в виде:

б) Посколькуотрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

5. а) Решите уравнение 

б) Укажите корни этого уравнения, принадлежащие отрезку.

Решение.

а) Из уравнения получаем:

б) Заметим, что. 

Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2. [2 c.30]

Анализируя задания ЕГЭ, можно сделать вывод о том, что задачи на решение логарифмических уравнений могут встречаться в любой части заданий ЕГЭ. В первойчасти обычно предлагают решить простейшие логарифмические  уравнения. Во второй части можно встретить более сложные логарифмические уравнения, решение которых обычно является одним из этапов выполнения задания. Уравнения в части «С» могут быть и комбинированные, т.е. быть логарифмическими, иррациональными, тригонометрическими и показательными и т.д.

В части «С» предложены не только логарифмические уравнения, но и системы уравнений. Задание «С-1» заключается в том, чтобы решить уравнение и выбрать подходящий корень из определенного промежутка [10 c.162].

 

 

ГЛАВА 2. ВИДЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ И МЕТОДЫ ИХ РЕШЕНИЯ.

 

2.1.   Метод решения по определению логарифма

 

Решение уравнений, основанных на определении логарифма.

Пример 1

Решение: По определению логарифма

корень уравнения.

Ответ:

Пример 2.

ОДЗ

Используем определение логарифма: 

Ответ:

 

2.2.   Метод потенцирования

 

Решение логарифмических уравнений типа  сводится к решению уравнения 

Это следует из монотонности логарифмической функции.

Потенцирование — это переход от уравнения вида  к  уравнению, где  — отличное от единицы положительное число,   — элементарные алгебраические функции, 

Для решения рассматриваемого типа уравнений достаточно найти все решения уравнения .Среди полученных выбрать те, которые принадлежат ОДЗ уравнения 

В случае, если уравнение  решений не имеет, то их не имеет и исходное логарифмическое уравнение.[3 c.168]

Пример:

Решение:Находим ОДЗ:

Решаем уравнение:

 принадлежит интервалу значит, является корнем исходного логарифмического уравнения.

Ответ: 

Пример:

Решение:

ОДЗ:

значит,  −5,5 не является корнем исходного уравнения.
Ответ: [4 c.87].

 

2.3.   Метод замены переменной

 

Теория:

Уравнения вида  решаются с помощью подстановки , которая приводит уравнение к виду 

Если t — корень уравнения , то после возвращения к подстановке  можно найти корень исходного логарифмического уравнения, т. е.  (аналогично находятся и другие корни, если они есть) [1 c.219].

Пример:

Решение:

Отвеет: .

 

2.7. Методическая разработка урока по теме «Решение логарифмических уравнений»

 

План — конспект урока по теме:

«Решение логарифмических уравнений»

Цель  урока: повторить понятие и свойства логарифма; изучить способы решения логарифмических уравнений и закрепить их при выполнении упражнений.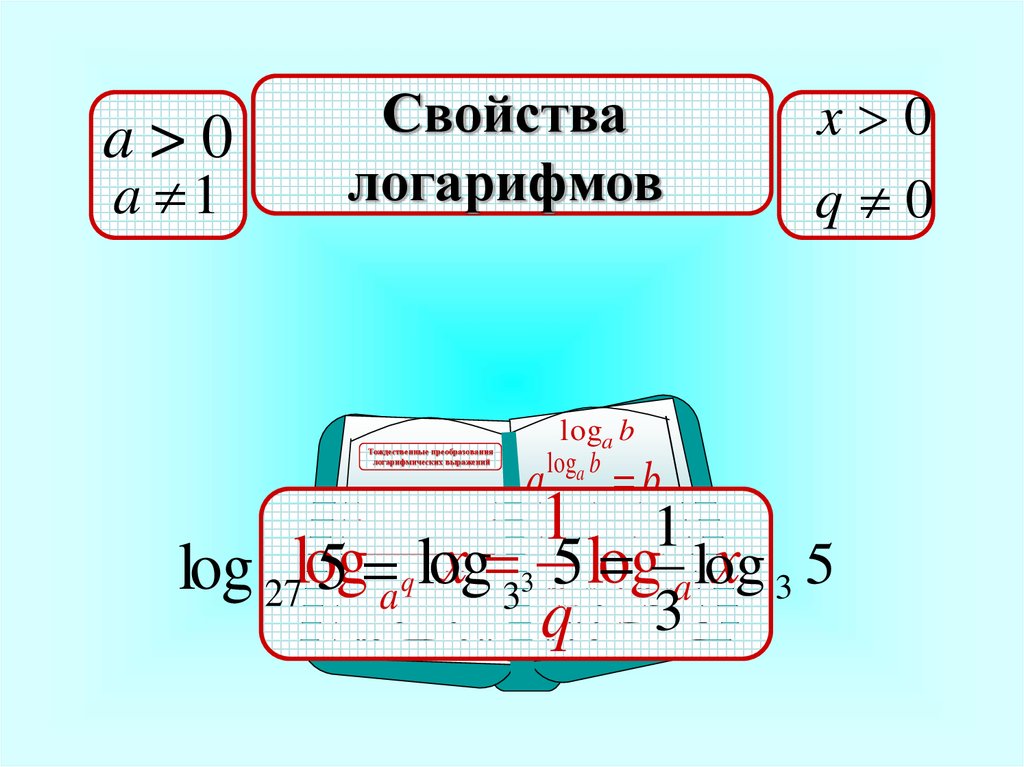

Задачи:

— обучающие: повторить определение и основные свойства логарифмов, уметь применять их в вычислении логарифмов, в решении логарифмических уравнений;

-развивающие: развить память, внимание, умение работать самостоятельно;

-воспитательные: воспитывать настойчивость, самостоятельность; прививать интерес к предмету.

Тип урока:  урок изучения нового материала. 

Педагогические технологии: информационно-коммуникационные, коллективная система обучения – вариационная пара.

Необходимое техническое оборудование: компьютер, проектор, экран.

Структура и ход  урока:

I.                  Организационный момент.

Проверка готовности обучающихся и кабинета к занятию. Объявление темы.        

II.              Устная работа.

Закрепление понятия логарифма, повторение его основных свойств и свойств логарифмической функции:

1. Разминка по теории:

1. Дайте определение логарифма.

2. От любого ли числа можно найти логарифм?

3. Какое число может стоять в основании логарифма?

4.  Функция  является возрастающей или убывающей? Почему?

5.  Какие значения может принимать логарифмическая функция?

6. Какие логарифмы называют десятичными, натуральными?

7. Назовите основные свойства логарифмов.

8. Можно ли перейти от одного основания логарифма к другому? Как это сделать?

2. Работа по карточкам:

Карточка №1:  Вычислить: Решить уравнение:

Карточка №2:  Вычислить: Решить уравнение:

 

3. Фронтальный опрос класса (сопровождается слайдами презентации)

Вычислить:

ЕГЭ 2009. Математика. Справочник / А. М. Титаренко, И. В. Третьяк, Т. М. Виноградова. – М: Эксмо, 2018. – 448 с.  3.                 Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений /А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2014. –                   384 с. 4.                 Дидактические материалы по алгебре и началам анализа для 11 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2013. – 143 с. 5.                 Система тренировочных задач и упражнений по математике./ Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др. – М.:Просвещение, 2015. – 208 с.  6.                 Мордковича А.Г. Алгебра и начала анализа. 10-11 классы: задачник /А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.-М.: Мнемозина, 2017. – 315 с.  7.                 Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных учреждений:  базовый уровень/ Ш. А. Алимов, Ю.М. Колягин, М.В. Ткачева и др., 2012. – 464 с.  8.                 ЕГЭ – 2012. Математика: типовые экзаменационные варианты: 30 вариантов/ под редакцией А.В. Семенова, И.В. Ященко. – М.: Национальное образование, 2015. – 192 с. 9.                 Алгебраический тренажер: пособие для школьников и абитуриентов/ под редакцией Мерзляк А.Г., Полонский В.Б., Якир М.С. –                   М.: Илекса, 2017. – 320 с. 10.     Математика. Репетитор. ЕГЭ-2009. Авторы: В.В.Кочагин; М.Н.Кочагина. — М.: Эксмо, 2019. – 272 с.  11.    Тригонометрические, показательные и логарифмические уравнения и неравенства: учебное пособие/ Севрюков П.Ф., Смоляков А.Н. М.: Илекса; Народное образование; Ставрополь: Сервисшкола, 2018. – 352 с.  12.     Математика для поступающих в вузы: учебное пособие/ И.Ф. Шарыгин. М.: Дрофа, 2016. – 479 с.  13.     Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 2017. – 416 с.

Математика в школе.

Тесты онлайн

Skip to main content

Skip available courses

Видео объяснения, интерактивные задания, тематические тесты из обширной и постоянно обновляющейся базы — обеспечат пятиклассникам прочные и уверенные знания по математике. Курс составлен в полном соответствии с требованиями ФГОС, утвержденными приказом Министерства образования и науки РФ. Уважаемые родители и педагоги, этот курс поможет вам лучше отслеживать и корректировать степень понимания детьми учебного материала, а также позволит своевременно выявлять и восполнять пробелы в знаниях учащихся. 

Содержание

Требования к уровню математической подготовки учащихся в 5 классе

Определение и свойства натуральных чисел (видео)

Тест «Определение натуральных чисел»

Запись и чтение натуральных чисел (видео)

Тест «Запись и чтение натуральных чисел»

Геометрические фигуры на плоскости (видео)

Тест «Геометрические фигуры»

Шкалы и координаты (видео)

Тест «Шкалы и координаты»

Компоненты и свойства арифметических действий (видео)

Тест «Компоненты и свойства арифметических действий»

Тест «Сложение и вычитание натуральных чисел»

Тест «Умножение и деление натуральных чисел»

Математические выражения

Тест «Математические выражения»

Уравнение

Тест «Уравнение». Вариант 1

Тест «Уравнение». Вариант 2

Для того, чтобы записаться на курс «Математика 5 онлайн» напишите нам по адресу:  [email protected]

Курс рассчитан на учащихся 5-11 классов, желающих научиться решать любые задачи на проценты и отлично подготовиться к экзаменам.  Курс содержит видео материалы, задачи с подробным решением и множество разнообразных тестов. Из нашего курса каждый учащийся, в каком бы классе он ни учился, найдёт для себя нужные материалы. Запись на этот курс по адресу: [email protected] 

Содержание

Что такое 1%. 2 видео. 10 тестовых вопросов.

Как найти проценты от числа. Видео

Тест 1. Проценты от числа (10 заданий)

Как найти число по его процентам. Видео

Тест 2. Число по его процентам (10 заданий)

Изменение величины в процентах. Видео

Тест 3. Изменение величины в процентах (10 заданий)

Как решать задачи на проценты с помощью пропорции

Напутственная задача. Видео

Условия и ответы задач 1А — 64А. 4 видео

Решения задач 1А — 64А

Тест. Проценты 1А-10А (10 заданий)

Тест. Проценты 11А-16А (6 задач)

Тест. Проценты 17А-30А (8 задач)

Тест. Проценты 31А-46А (6 задач)

Тест. Проценты 47А-56А (5 задач)

Тест. Проценты в диаграммах 57А-64А (8 задач)

Итоговый тест. Проценты. Уровень А (10 заданий)

Условия и ответы задач 1В — 33В. 2 видео

Решения задач 1В — 33В

Тест. Проценты 1В-12В (5 задач)

Тест. Проценты 13В-17В (10 задач)

Тест. Растворы. Уровень В (5 задач)

Итоговый тест. Уровень В (10 задач)

Условия и ответы задач 1С — 31С. 2 видео

Решения задач 1С — 31С. Видео

Тест. Сплавы и растворы. Уровень С (5 задач)

Тест. Вклады и комиссии. Уровень С (5 задач)

Итоговый тест. Уровень С (10 задач)

Обобщающий тест. Уровни А, В и С (10 задач)

15 января планируется взять кредит в банке. Видео (схема: разбор задачи-самостоятельное решение, всего 16 задач)

Тест. 15 января взять кредит (4 задачи)

В июле планируется взять кредит (задачи 1-5)

Тест. Кредит в июле по задачам 1-5 (3 задачи)

В июле планируется взять кредит (задачи 6-11)

Тест. Кредит в июле по задачам 6-11 (3 задачи)

В июле планируется взять кредит (задачи 12+)

Тест. Взять кредит в июле (5 задач)

Кредит в декабре (задачи 1-7)

Тест. Кредит в декабре (3 задачи)

Логарифмические выражения и pH — Математические модули Ohlone Biotechnology

• Различные экспоненциальные основания
• Десятичный логарифм
• Определение pH и [H+]
• Решения

Связь логарифмов и показателей степени

Давайте начнем знакомство с логарифмами с нескольких вопросов о показателях степени. В течение минуты заполните поля ниже:

2 5=32

3 3=27

10 4=100 

Правильные ответы: 5, 3 и 2.

Вам может быть интересно: если этот модуль посвящен логарифмам, почему мы задаем вопросы о показателях степени?

Экспоненты и логарифмы очень тесно связаны. Фактически, показатели степени и логарифмы на самом деле являются обратными функциями друг друга. Что такое инверсия? Обратная функция — это «обратная» другая функция. Поскольку логарифмы и показатели степени обратны, мы можем переключаться между логарифмическим выражением и экспоненциальным выражением, как показано здесь:

ax=y ⟷ logay = x

Для того чтобы понять логарифмы, давайте рассмотрим различные части логарифма и то, что мы называем «десятикратным логарифмом» (строчным логарифмом).

Это очень важное соотношение  – обратная зависимость между логарифмами и показателями: x дает нам аргумент y. Чем раньше вы запомните и вспомните это соотношение, тем легче вам будет вычислять логарифмы.

Давайте быстро вернемся к вопросам в начале этого раздела и применим наше новое соотношение:

• 2 ⁵  = 32 ⟷ log ₂ ⁡ 32 = 5
• 3 ³  = 27 ⟷ log ₃ ⁡ 27 = 3
• 10 ²  = 100 ⟷log ₁₀  ⁡100 = 2

Видите связь между двумя обозначениями? Может потребоваться некоторая практика, чтобы привыкнуть к преобразованию между экспоненциальной записью ( ^x  = y) и логарифмической записью (log _a  y = x).

Давайте потренируемся вычислять несколько логарифмов ниже. Используйте приведенное выше соотношение и свое знание показателей. Примечание: мы используем термин оценить вместо решить при работе с функциями.

Проверка понимания #1: Логарифмические выражения

Оцените следующие логарифмические выражения. Используйте соотношение выше. Решения находятся в конце этого руководства.

1. Журнал оценки ₄ ⁡64
2. Журнал оценки ₁₀  ⁡0,001
3. Журнал оценки ₃  ⁡9
4. Журнал оценки ₁₀  ⁡80

Давайте перейдем к разговору о логарифмах с точки зрения «логарифма». Хотя в качестве основания логарифмического выражения можно использовать любое число, есть одно основание, которое вы будете встречать гораздо чаще, чем другие.

Наиболее распространенное основание логарифмического выражения — 10. Когда основание равно 10, логарифм называется «десятичным логарифмом» или просто «десятичным логарифмом». Общий журнал записывается просто как «журнал» и имеет подразумеваемое, но не показанное основание 10.

Давайте рассмотрим несколько примеров общих журналов, чтобы лучше понять эту концепцию:

1. log⁡ 100 000 = 5 , потому что 10 ⁵ = 100 000– База 10 подразумевается — также писай также журнал ₁₀ 100 000 000 000 000 000. = 5, но это не пишется в общем формате журнала
2. log ⁡0,001 = -3 , потому что 10 ^-3  = 0,001
3. log ⁡87 ≈ 1,94 , потому что 10 ^1,94 ≈ 87

Опять же, логарифмы могут сбивать с толку. Чтобы привыкнуть к ним, потребуется время и практика.

Рассмотрим последний пример. Наш последний пример не содержит точного ответа, и на самом деле его легче найти с помощью калькулятора, хотя вы можете приблизиться к ответу и без калькулятора, если очень хорошо знаете свои квадраты. (В данном случае мы этого делать не будем.)

Вместо того, чтобы работать над получением «близкого» числа, давайте посмотрим, как использовать калькулятор для нахождения общего логарифма числа. Далее в этом руководстве мы будем использовать общий журнал для расчета pH, поэтому важно понимать, как найти журналы с помощью калькулятора.

Поиск общего журнала с помощью калькулятора

На фотографии ниже показан простой научный калькулятор TI-30XIIS (слева) и более продвинутый графический калькулятор TI-84 Plus (справа). Скорее всего, у вас есть калькулятор, похожий на один из этих. Найдите научный калькулятор или графический калькулятор для этого упражнения. Найдите функцию журнала на своем собственном калькуляторе. Фотография может помочь вам найти ключ от журнала.

Чтобы использовать функцию журнала: Найдите и нажмите клавишу «журнал». Введите число, которое вы хотите взять в общий журнал после круглых скобок. Скобки закрывать не нужно. Нажмите Enter, и вы получите ответ. В некоторых калькуляторах вам нужно будет сначала ввести число,  , затем  нажмите кнопку журнала.

Попробуйте оценить некоторые распространенные журналы с помощью приведенного ниже калькулятора.

Проверка понимания #2: поиск общего журнала с помощью калькулятора

Оцените следующие общие журналы с помощью калькулятора. Округлите ответы до 4 знаков после запятой. Решения находятся в конце этого руководства.

• лог⁡24,435
• лог⁡0,4327
• лог⁡8.4288
• лог⁡0,0035

Все, что мы рассмотрели до сих пор в этом руководстве, привело к применению логарифмов для определения pH и концентрации ионов водорода [H+], что является обычной практикой в ​​области биотехнологии.

Давайте быстро обсудим концентрацию ионов водорода и pH:

Концентрация ионов водорода (написано [H+] – скобки означают «концентрация») обычно колеблется между 1,0 M и 1 × 10 ^-14  M. (Подсказка: «M является молярным или «моль/литр».) Эта шкала рН может показаться знакомой:

В биотехнологии мы можем применить использование логарифмов для определения рН и концентрации ионов водорода [H+]. Мы можем сделать это, используя любой из этих две формулы:

pH = -log [H ⁺ ]     и     [H ⁺ ] = 10 ^-pH

Помните, когда мы рассматривали отношения между показателями степени и логарифмами, где ^x a a -= log4 54  = y может быть повторно выражено как 9004 54  = log00 = х? Здесь используется то же соотношение, и именно так мы можем определить pH по концентрации ионов водорода, и наоборот.

Если у вас возникли проблемы с пониманием этой зависимости, попробуйте еще раз записать экспоненциальную и логарифмическую зависимость и заменить a, y и x частями этих формул.

Давайте рассмотрим несколько примеров. Когда мы используем здесь «журнал», мы имеем в виду общий журнал.

Пример 1 и 2 – определение pH

1) Каков pH раствора с концентрацией ионов водорода 2,75 × 10 ^-4   M ?

Дано [H+] = 2,75 x 10 ^-4 моль/литр

Формула: pH = -log ⁡[H ⁺ ]

pH = -log[2,75 x 10 ^-4 ,03 ≈0,03

2) Раствор имеет [H ⁺ ] 6,72 x 10 ^-2 М. Каков его рН?

pH = -log6,72 x 10 ^-2 M ≈ 1,17

Пример 3 и 4 – Определение pH

3) Какова концентрация ионов водорода в растворе с pH 5,43?

Указанный pH = 5,43

[H ⁺ ] = 10 ^-PH

[H ⁺ ] = 10 ^-5,43 = 3,7 x 10 ^-6 M

4) Что является [Н ⁺ ] раствора с рН = 9,8?

pH = 9,8

[H ⁺ ] = 10 ^-PH

[H ⁺ ] = 10 ^-9,8 = 1,6 x 10 ^-10 M

Проверьте для понимания #3: Поиск PH и водородного концентрации

Найдите концентрацию ионов водорода или pH в следующих вопросах:

1. Чему равно [H+] кислого раствора с pH 3?
2. Каков pH раствора с [H+] 8,34 × 10 ^-5  моль/литр? Является ли этот раствор кислотным или щелочным?
3. Какова концентрация ионов водорода в растворе кислоты с рН 6,5?
4. Каков рН раствора с концентрацией ионов водорода 0,5М? Является ли этот раствор кислотным или щелочным?

Проверка понимания #1: Логарифмические выражения

1. Вычислить log ₄ ⁡64
   log ₄ ⁡64 = 3; 4 ³  = 64
2. Журнал оценки ₁₀  ⁡0,001
   log ₁₀  ⁡0,001 = -3; 10 ^-3  = 0,001
3. Журнал оценки ₃ ⁡9
   log ₃  ⁡9 = 2; 3 ²  = 9
4. Лог оценки _10⁡  80
   log ₁₀  ⁡80 ≈ 1,9; 10 ^1,9 ≈ 80

Проверка понимания #2: Поиск общего журнала с помощью калькулятора

1. log⁡ 24,435 ≈ 1,3880
2. log ⁡0,4327 ≈ -0,3638
3. лог⁡ 8,4288 ≈ 0,9258
4. log⁡ 0,0035 ≈ -2,4559

Проверка понимания #3: pH и концентрация ионов водорода

1. Чему равно [H+] кислого раствора с pH 3?

   10 ^-3  = 0,001  М

2. Каков pH раствора с [H+] 8,34 x 10 ^-5   моль/литр ? Является ли этот раствор кислотным или щелочным?

   pH = -log⁡(8,34 x 10 ^-5 ) = 4,08; кислая

3. Какова концентрация ионов водорода в растворе кислоты с рН 6,5?

   [H ⁺ ] = 10 ^-6,5  = 3,16 x 10 ^-7   M

4. Каков рН раствора с концентрацией ионов водорода 0,5М? Является ли этот раствор кислотным или щелочным?

   pH  = -log⁡(0,5) = 0,30; кислый

Калькулятор вычислений логарифмов x – Googlesuche0002 www.

symbolab.com › … › Алгебра › Уравнения

Бесплатный калькулятор логарифмических уравнений — пошаговое решение логарифмических уравнений.

Ln (x)+ln (x-1)=ln (3x+12) · Ln (x)+ · Решить логарифмические уравнения… · 4+log _3(7x)=10

Калькулятор логарифмических уравнений & Solver — SnapXam

www.snapxam.com › калькуляторы › логарифмическое уравнение…

Калькулятор логарифмических уравнений онлайн с решением и шагами. Подробные пошаговые решения ваших задач с логарифмическими уравнениями онлайн с помощью нашей математики …

Калькулятор логарифмов — Mathway

www.mathway.com › Калькулятор › калькулятор логарифмов

Бесплатный калькулятор логарифмов — пошаговые решения, помогающие упростить логарифмические выражения.

Калькулятор решения для x — Mathway

www.mathway.com › Калькулятор › Калькулятор решения для x

Калькулятор решения для x позволяет ввести задачу и решить уравнение, чтобы увидеть результат. Решите в одной переменной или много.

Ähnliche Fragen

Есть ли калькулятор, который может найти x?

Калькулятор уравнения логарифма

www.calculatorsoup.com › Алгебра

Этот калькулятор решит основное уравнение логарифма logbx = y для любой одной из переменных, если вы введете две другие. Логарифмическое уравнение решено …

Калькулятор логарифмов | Калькулятор log(x) — RapidTables.com

www.rapidtables.com › calc › math › Log_Calculator

Калькулятор логарифмов онлайн. Основание 2, основание e, основание 10. Логарифмы сложения/вычитания/умножения/деления.

Решить — Экспоненциальная и логарифмическая функции Шаг за шагом … — QuickMath

quickmath.com › … › Экспоненциальная функция

Дан график функции натурального логарифма, определяемой выражением f ( x )= ln x на рисунке 5.12. Натуральные логарифмы можно найти с помощью калькулятора с клавишей In …

Онлайн-калькулятор логарифмических уравнений

mathforyou.

No related posts.