Решение матриц в маткаде: MathCAD — это просто! Часть 4. Системы линейных алгебраических уравнений

MathCAD — это просто! Часть 4. Системы линейных алгебраических уравнений

Итак, мы с вами продолжаем изучать MathCAD — самую дружелюбную к пользователю математическую среду из существующих в настоящее время. Пока мы занимались тем, что изучали способы решения уравнений — трансцендентных и алгебраических, и теперь вы знаете, как их решать с помощью MathCAD’а в общем виде или численно. Как вы могли убедиться из материала третьей части, численное решение уравнений — не такая простая задача, как может показаться с первого взгляда, однако и не такая сложная, если построить график уравнения. Но просто уравнения — это, согласитесь, довольно скучно, потому что в жизни, как правило, уравнения по одиночке не встречаются. Поэтому сегодня мы перейдем к более сложной, а значит, и более интересной, теме — попробуем решать системы уравнений. Я сказал «попробуем»? Простите, пожалуйста — я, наверное, оговорился. Конечно, не попробуем, а научимся — потому что благодаря MathCAD’у можно быть уверенным в том, что подобные попытки увенчаются успехом.

Готовы? Ну что же, тогда вперед.

Решение систем с помощью функции lsolve

Системы уравнений многие просто-таки ненавидят еще со школы — прямо как русскую литературу. Что ж, школа может привить отвращение ко многим вещам, которые без нее могли бы оказаться гораздо более интересными. Как и любая обязаловка, она убивает романтику изучения чего-то нового. Но теперь, когда вас никто не заставляет изучать решение систем уравнений, вы можете взглянуть на них с совершенно новой для себя стороны. И поможет в этом, конечно же, MathCAD.

Для обозначения систем линейных алгебраических уравнений у математиков есть своя аббревиатура — СЛАУ. Ее используют намного чаще, чем полное название, что, в общем-то, вполне естественно — эта аббревиатура и произносима легко, и не перекрывается с другими математическими аббревиатурами. Так что и мы с вами тоже будем ее применять. СЛАУ называется система уравнений следующего вида:
k11x1 + k12x2 + … + k1nxn + l1 = 0

k12x1 + k22x2 + … + k2nxn + l2 = 0
…
kn1x1 + kn2x2 + … + knnxn + ln = 0

Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные. Такие уравнения обычно записывают также с помощью матриц:
KX + L = 0

Здесь K — матрица (kij), составленная из коэффициентов при переменных величинах, где i — номер строки матрицы, а j — номер столбца. X и L — это, соответственно, векторы, составленные из переменных и свободных членов. Собственно, при решении СЛАУ с помощью MathCAD мы будем записывать СЛАУ именно в таком виде, потому что решение СЛАУ в MathCAD реализовано именно с помощью матричных методов. Возможно, вы что-нибудь слышали о методах решения СЛАУ Гаусса и Крамера, но даже если и нет, ничего страшного в этом нет — MathCAD тем и удобен, что с его помощью можно решать уравнения, не задумываясь над тем, каким именно алгоритмом пользуется математическая система при их решении.

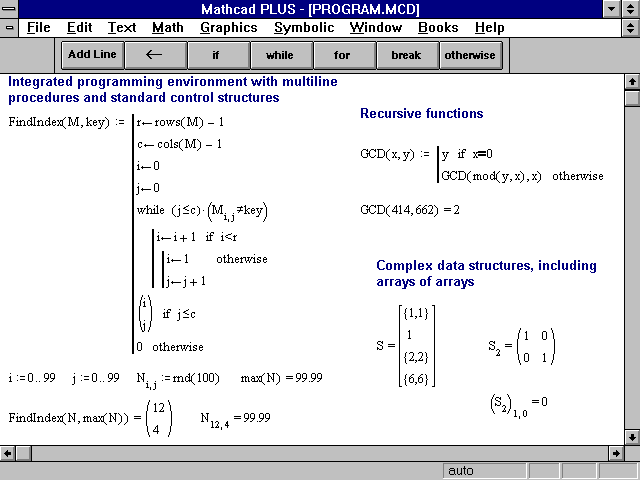
Итак, для начала давайте посмотрим, каким именно образом в MathCAD’е нужно задавать матрицы. Для этого на панели инструментов Matrix нажмите кнопку Matrix or Vector, а в появившемся окне задайте количество столбцов и строк в матрице. Мы с вами попробуем решать для начала СЛАУ из четырех уравнений, и, соответственно, нам нужна будет матрица размером четыре на четыре элемента. Только, поскольку мы будем присваивать значение, записанное в этой матрице, переменной, обозначающей матрицу коэффициентов, то сначала лучше записать «K_:=», а потом уже вставлять матрицу. Обратите внимание на то, что мы будем обозначать матрицу не просто буквой К, а еще добавлять подчеркивание. Делается это специально для того, чтобы не переобозначать встроенные переменные среды MathCAD. Аналогичным образом теперь нужно задать вектор свободных членов — только его размер уже будет не 4х4, а 1х4. Для решения СЛАУ после того, как мы ввели коэффициенты (вы можете ввести их произвольно, а можете

воспользоваться теми, которые приведены на скриншоте — с ними цифры в ответе получаются довольно ровными и красивыми), нужно для решения СЛАУ использовать функцию lsolve. У нее есть два параметра: первый — это матрица коэффициентов уравнений, а второй — вектор свободных членов. То есть для получения результата нам нужно написать:
lsolve(K_, L_) =

Ну, а после знака равенства MathCAD нам уже нарисует результат.

С помощью функции lsolve можно получать и аналитические решения СЛАУ. Давайте попробуем заменить одно из чисел в матрице коэффициентов на букву — например, «а». Функция lsolve сразу выдаст ошибку, но не нужно этого пугаться — нужно просто заменить знак равенства на стрелку (ее можно найти на панели инструментов Symbolic или же записать комбинацией клавиш Ctrl + .). Дело в том, что знак «равно» в MathCAD’е используется для численных вычислений, а стрелка — для символьных, то есть при решении систем уравнений в общем виде нужно применять именно стрелку.

Решение с помощью solve

В общем-то, решать такую систему можно было бы и используя уже знакомый нам с вами оператор solve. Для этого достаточно записать уравнения в виде матрицы, а затем применить к ней оператор solve точно так же, как если бы мы с вами решали не целую систему, а всего лишь одно- единственное уравнение. «Записать уравнения в виде матрицы» в данном случае означает не запись матричного уравнения KX + L = 0, а просто запись в каждой строке одностолбцовой матрицы (т.е. вектор-столбца) одного уравнения из системы. Напомню на всякий случай, что оператор solve находится на панели Symbolic, а для записи знака равенства нужно использовать не просто клавишу «=», а ее комбинацию с клавишей Ctrl. Еще хочу добавить, что в данном случае, как, впрочем, и во многих других, которые мы с вами уже обговорили, это может вполне успешно использоваться для получения не только символьных, но и для численных решений.

Решение СЛАУ с помощью solve поначалу кажется не таким уж привлекательным, однако, по сути, оно ничем не отличается от использования функции lsolve. Например, если вы замените какой-нибудь из числовых коэффициентов в одном из уравнений на букву, чтобы получить аналитическое решение, solve справится с этим точно так же быстро и хорошо, как и функция lsolve. Так что, в общем-то, выбор при решении СЛАУ в пользу функции lsolve или в пользу оператора solve — дело скорее вкуса, причем вкуса в плане записи самой системы уравнений, а не оператора или функции, у которых, в общем-то, даже названия очень и очень похожи.

Пожалуй, один из немногих случаев, когда все же предпочтительнее использовать именно оператор solve — это когда уравнений у нас больше, чем неизвестных, содержащихся в них. В этом случае матрица системы будет выглядеть не так, как хотелось бы, а вот с solve все будет нормально. Даже если решение найти не удастся, solve любезно об этом сообщит. Аналогичным образом можно попытаться решить СЛАУ и в том случае, когда соотношение между уравнениями и неизвестными, напротив, не в пользу уравнений (правда, как говорится, не с разгромным счетом, а то решение заведомо найти не удастся). Но даже в случае, когда мы пытаемся решить систему с тремя уравнениями и четырьмя неизвестными, оставив после solve только две из них, у нас это далеко не всегда может получиться — в этом вы можете убедиться воочию.

Численное решение СЛАУ

Что ж, давайте теперь посмотрим, как решать СЛАУ с использованием численных методов их решения. Это тоже вовсе не так сложно, как может с самого начала показаться, поскольку MathCAD имеет в своем арсенале ряд средств и на этот случай. Как и в случае с одиночными уравнениями, сначала нужно задать начальное приближение (на то оно и начальное, чтобы задавать его сначала). Только, поскольку переменная у нас теперь не одна, а их несколько, то и начальное приближение необходимо будет задать для каждой из них. В тех случаях, когда переменных в СЛАУ много, это будет совсем не просто. После того, как вы задали начальные приближения для каждой из нужных переменных, запишите сами уравнения — только сделайте это так, чтобы их и начальные приближения разделяло специальное слово «Given» (оно, конечно же, в рабочей области MathCAD’а должно быть записано безо всяких кавычек). После того, как вы записали начальные приближения, слово «Given» и сами уравнения, можно смело воспользоваться функцией find, которая найдет точные значения решений системы. Поскольку в СЛАУ каждая из переменных в итоге будет иметь только одно значение, над подбором максимально точного начального приближения можно особо и не страдать — в конечном итоге в случае СЛАУ оно скорее просто формальность, нежели реальная необходимость, и, как вы сами имели возможность убедиться, есть методы, которые прекрасно решают СЛАУ и без него.

Теперь, когда вы знаете уже столько разных способов решения СЛАУ, вполне логично было бы задаться вопросом: а какой из них лучше при прочих равных условиях? В литературе, как правило, рекомендуется использовать функции lsolve или find, дающие точность до 15 знаков после запятой — однако на самом деле, учитывая тот факт, что такая точность бывает нужна не так уж часто, данным советом можно пренебречь, потому что точность решения системы намного больше зависит от нее самой, нежели от используемого метода ее решения в MathCAD’е. Так что используйте пока что смело тот, который показался вам наиболее удобным, а о погрешностях при решении СЛАУ мы с вами еще поговорим, но только, пожалуй, немного попозже.

SF, spaceflyer@tut.by

Компьютерная газета. Статья была опубликована в номере 16 за 2008 год в рубрике soft

МЕТОД ОБРАТНОЙ МАТРИЦЫ В MATHCAD

Пример 1. Данасистемалинейныхалгебраических уравнений

Решить СЛАУ методом обратной матрицы

1. Задаем массив коэффициентов СЛАУ и вектор правых

	частей: 1		2	3	4		30
	A	1 2		3	4	f	10
			1	1
		0			1		3
		1	1	1	1		10

6

МЕТОД ОБРАТНОЙ МАТРИЦЫ В MATHCAD

2. Находим определитель det A:

3. Находим обратную матрицу A–1:

				1			1			3
A	1		0.75				1.25			4
				0.5			0.5			1
4. Находим решение:			0. 25				0.75			2
								1
		x A			1		f	2
									3
						30		4
5. Проверка решения:
			A x			10
							3
						10

A 4

3

21

1

7

РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА

Пусть det A 0

Построим m вспомогательных матриц

	a	11	. ..	f	1	…
A i	a	21	…	f 2		…
			…	…		…
	…							i-й столбец
			…	f m		…
	am1

Решения находим по формулам:

	xi	det Ai	i=1,2,…m.
		det A

Метод используется для решения небольших систем, т.к. нахождение определителей –

трудоемкая операция

8

МЕТОД КРАМЕРА В MATHCAD

Пример 2. Данасистемалинейныхалгебраических уравнений

Решить СЛАУ методом Крамера

1.По умолчанию элементы массива нумеруются с нуля. Для того, чтобы элементы нумеровались с единицы:

ORIGIN 1

9

Работа с массивами и решение систем уравнений в Mathcad (стр. 1 из 2)

Содержание

Введение

3. Решение систем линейных уравнений

4. Решение нелинейных уравнений

5. Решение систем нелинейных уравнений

Заключение

Библиографический список

Введение

Одна из задач ЭВМ — автоматизация труда, повышение эффективности научных исследований. Основная особенность ЭВМ — ориентация на применение пользователями, не владеющими языками программирования. Такой подход позволяет преодолевать языковой барьер, отделяющий человека от машины. С этой целью разрабатываются пакеты прикладных программ, рассчитанные на широкие круги специалистов. К подобным пакетам относится MATHCAD.

MATHCAD — универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета — естественный математический язык, на котором формируются решаемые задачи.

Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.

Цель работы: изучение выполнения основных операций с массивами, решения систем линейных и нелинейных уравнений в Mathcad.

В математике часто возникает необходимость в задании некоторого ряда значений. Например, при вычислении

нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Для создания таких рядов в Mathcad используются ранжированные переменные. В простом случае для создания ранжированной переменной используется выражение

Name:=Nbegin…Nend,

Где Name – имя переменной, Nbegin – начальное значение переменной, Nend – ее конечное значение. Символ «…» (он вводится с клавиатуры знаком точка с запятой «;») указывает на изменение переменной в заданных границах. Если Nbegin<Nend, то шаг изменения переменной будет равен +1, в противном случае –1. Например, выражение a:=1…10 описывает ранжированную переменную a со значениями от 1 до 10.

Для создания ранжированной переменной общего вида используется выражение

Name:=Nbegin, (Nbegin+Step)…Nend,

где Step— заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend и отрицательным в противном случае).

Например, выражение a:=1, 1.5, …10 описывает ранжированную переменную a со значениями от 1 до 10 с шагом 0,5.

Ранжированные переменные широко применяются для представления функций в виде таблиц вывода, а также для построения их графиков.

Если после некоторого выражения с ранжированной переменной поставить знак равенства, то после щелчка мышью на экране будет выведена таблица значений этого выражения. Такие таблицы называются таблицами вывода.

Необходимо учитывать следующее свойство таблиц вывода: если количество значений ранжированной переменной и, соответственно, строк в таблице вывода больше 16, то выводятся первые 16 строк. Если указатель мыши находится в пределах таблицы, то щелчок левой кнопкой мыши приводит к появлению вертикальной полосы прокрутки, позволяющей просмотреть все строки таблицы.

Помните, что задание ранжированных переменных эквивалентно заданию конечных циклов.

Примеры использования ранжированных переменных приведены на рисунке 1. 1.

Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.

Местоположение элемента массива задается одним индексом для вектора и двумя для матрицы. Индексы могут быть только положительными целыми числами. Для ввода индекса используется знак « [ » – прямая открывающая скобка.

Для задания массивов можно либо воспользоваться командой Matrices меню Math, либо нажать комбинацию клавиш Ctrl+V, либо щелкнуть на значке с изображением шаблона матрицы. Любое из этих действий вызывает появление диалогового окна, в котором надо указать количество строк m и столбцов n в массиве. При m=1 получим вектор-столбец, а при n=1 – вектор-строку.

В отношении массивов действуют те же правила присваивания и вывода, что и для обычных переменных. В частности, с помощью оператора присваивания можно создать массив заданного размера и заданного типа без ручного заполнения шаблона (рисунок 2.1.).

Рис. 2.1 Пример создания матриц без использования шаблонов матриц

Для работы с массивами Mathcad содержит ряд операторов и функций. Ниже представлены операторы для работы с векторами и матрицами. В таблице используются следующие обозначения: V – для векторов, M – для матриц, Z – для скалярных величин.

Существует ряд встроенных векторных и матричных функций. Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц.

length(V)	возвращает число элементов вектора
last(V)	возвращает номер последнего элемента вектора
max(V)	возвращает максимальный по значению элемент вектора или матрицы
min(V)	возвращает минимальный по значению элемент вектора или матрицы
augment(M1,M2)	объединяет в одну две матрицы, имеющие одинаковое число строк (объединение идет бок о бок)
identity(n)	создает единичную квадратную матрицу размером n*n
stack(M1,M2)	объединяет в одну две матрицы, имеющие одинаковое число столбцов, располагая М1 над М2
submatrix(A,ir,jr,ic,jc)	возвращает субматрицу, состоящую из всех элементов содержащихся в строках от ir по jr и столбцов с ic по jc (ir£jr и ic£jc)
diag(V)	создает диагональную матрицу, элементы главной диагонали которой равны элементам вектора V
matrix(m,n,f)	создает матрицу, в которой (i, j) элемент равен f(i,j), где i=0, 1, …, m и j=0, 1, …, n; f(i,j) — некоторая функция
cols(M)	возвращает число столбцов матрицы M
rows(M)	возвращает число строк матрицы M
rank(M)	возвращает ранг матрицы M
tr(M)	возвращает след (сумму диагональных элементов) матрицы M
mean(M)	возвращает среднее значение элементов матрицы M

Примеры работы с матрицами приведены на рисунке 2. 2.

Рис. 2.2. Примеры работы с матрицами

3. Решение систем линейных уравнений

Векторные и матричные операторы и функции позволяют решать широкий круг задач линейной алгебры.

Например, если задана матрица A и вектор B для системы линейных уравнений в матричной форме

, то вектор решения X можно получить из уравнения

.

Поскольку решение систем линейных уравнений довольно распространенная задача, то в Mathcad введена специальная функция lsolve(A,B), которая возвращает вектор X для системы линейных уравнений

при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A — n´n.

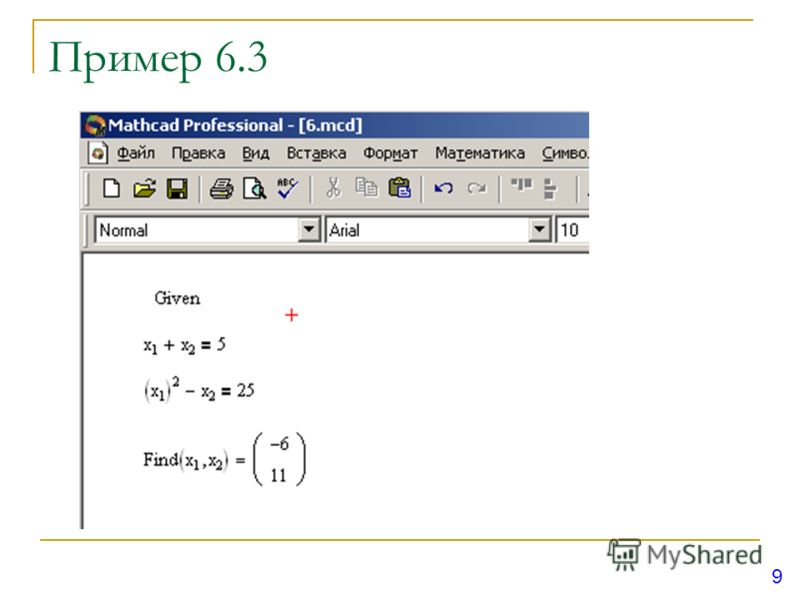
Пусть необходимо решить систему уравнений

.

Решение задачи анализа цепей — векторы и матрицы в MATLAB

Матрица — очень универсальный математический инструмент, используемый в различных областях, таких как робототехника, машинное обучение, механика, электроника и так далее. В этой статье мы увидим различные операции, которые мы можем выполнять с векторами и матрицами в MATLAB.

MATLAB расшифровывается как MAT rix LAB ораторское искусство. Все переменные MATLAB являются массивами. Каждая переменная может содержать несколько чисел. Большинство функций MATLAB работают с несколькими значениями одновременно.

Типы векторов и матриц

Давайте рассмотрим различные типы массивов, используемых в MATLAB
Матрица — это массив с несколькими строками и несколькими столбцами.
Скаляр означает матрицу с одним элементом. Скаляр — это одно число, которое по сути является массивом один за другим.
Вектор-столбец — это матрица из одного столбца и нескольких строк.
Вектор-строка — это матрица с одной строкой и несколькими столбцами.

Матрица и скалярные векторы строк и столбцов

Создание векторов вручную

Мы можем создать матрицу или массив, используя квадратные скобки. Если числа в квадратных скобках разделены пробелом или запятой, то MATLAB создает вектор-строку. Если числа разделены точкой с запятой, то MATLAB создает вектор-столбец.

>> Строка1 = [1 2 3 4 5]

>> Строка2 = [10,20,30,40,50]

>> Столбец1 = [1;2;3;4; 5]

Пробелы и точки с запятой объединены для создания матрицы. Матрица вводится построчно, где каждая строка отделяется точкой с запятой.

>> м = [1 2 3; 4 5 6; 7 8 9]

Равномерно расположенные векторы очень распространены. Вводить длинные векторы вручную нецелесообразно. MATLAB предлагает сокращенный метод для создания равномерно расположенных векторов. Используйте оператор двоеточия и укажите начальную и конечную точки.

>> even_row = 5 : 8 создать вектор-строку с элементами 5, 6, 7, 8.

Оператор двоеточия использует интервал по умолчанию, равный 1. Мы можем указать другой интервал, используя оператор двоеточия.

>> even_row = 20 : 2 : 30 создает вектор-строку с элементами 20, 22, 24, 26, 28, 30.

>> even_row = 1 : 0,5 : 5 создает вектор-строку с элементами 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0.

Другим методом создания равномерно расположенных векторов является функция linspace(). Мы должны указать количество элементов, которые мы хотим в векторе.

>> even_row = linspace(0, 1, 5) создает вектор-строку с 5 элементами, равномерно распределенными от 0 до 1.

Пока что мы создали векторы-строки. Как мы можем создать векторы-столбцы? Мы можем создавать векторы-столбцы вручную, вводя элементы и разделяя их точкой с запятой.

>> col1 = [2; 4; 6; 8; 10]

Другой метод состоит в том, чтобы создать вектор-строку, используя один из сокращенных методов, обсуждавшихся ранее, а затем использовать оператор транспонирования для создания вектор-столбца.

>> четный_столбец = четный_ряд'

Функции создания векторов и матриц

Мы можем быстро создать квадратную или неквадратную матрицу, используя случайные числа. Единицы() и нули() можно использовать для создания массива всех единиц и массива всех нулей. Функция eye() используется для создания матрицы идентичности. Функция diag() может использоваться для создания диагональной матрицы или для получения диагональных элементов матрицы.

MATLAB функция rand Функция MATLAB единиц Функция MATLAB нулей MATLAB функция глаза MATLAB функция диагностики MATLAB функция get diag

Функция Size() дает размер вектора или матрицы.

Функция размера MATLAB

Индексирование

Положение элемента в матрице или массиве называется его индексом. Мы можем использовать индекс для извлечения или изменения определенного элемента.
Для Matrix элемент принадлежит строке r и столбцу c, тогда (r,c) становится его индексом.

Индекс вектораИндекс матрицы

Мы можем прочитать или изменить всю строку или весь столбец, используя оператор двоеточия. Используйте ключевое слово end для ссылки на последний элемент.

>> x = v(1, : ) считывает всю 1-ю строку.

>> x = v(: , end) читает весь последний столбец.

Доступ к диапазону значений в массиве или матрице можно получить с помощью оператора двоеточия.

>> x = v(2:4, 3) считывает элементы со 2 по 4 в 3-м столбце.

Арифметика массивов

Операции с массивами выполняются поэлементно. Мы можем добавить или вычесть скалярное значение к каждому элементу матрицы. Умножить или разделить массив на скалярное значение. Поэлементное произведение матрицы A и матрицы B выполняется оператором поэлементного умножения «.*».

если два массива/матрицы имеют одинаковый размер, то каждый элемент в первом операнде сопоставляется с соответствующим элементом во втором операнде для выполнения арифметических операций. например, мы можем добавить два вектора одинакового размера.

>> А = [1 2 3] ;

>> B = [2 2 2] ;

>> A+B

>> ans =

3 4 5

матрица. например,

>> А = [1 2 3; 4 5 6];

>> 4.* A

>> ANS =

4 8 12

16 20 24

, если размер двух матриц.

В таблице ниже приводится сводка арифметических операций с массивами, доступных в MATLAB.

Оператор	Функция	Описание
+	Сложение	Добавляет две матрицы одинакового размера. например, A+B добавляет A и B.
+	Унарный плюс	Возвращает ту же матрицу. например, +A возвращает A.
–	Вычитание	Вычитает вторую матрицу из первой. например, AB вычитает B из A.
–	Унарный минус	Возвращает отрицательную матрицу. например -A отрицает элементы A. 9B возводит каждый элемент A в соответствующую степень B .
./	Правое деление массива	A ./ B делит каждый элемент A на соответствующий элемент B .
.\	Левое деление массива	B .\ A делит каждый элемент A на соответствующий элемент B .
.’	Транспонирование массива	A .’ возвращает несопряженное транспонирование A , то есть меняет местами индекс строки и столбца для каждого элемента.

Арифметика матриц

Операции с матрицами выполняются в соответствии с правилами линейной алгебры. Требуемый размер входной матрицы зависит от операции. Для умножения матриц с помощью оператора умножения матриц «*» матрицы должны иметь общие внутренние размеры. Это означает, что количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Чтобы разделить матрицу A на матрицу B с помощью оператора деления вправо «/», матрицы A и B должны иметь одинаковое количество столбцов.

В таблице ниже приводится сводка матричных операторов, доступных в MATLAB.

Оператор	Функция	Описание
*	MALRIX	*	MATRIX	*	. Если A  – это матрица размера m на p, а B  – матрица размера p на n, то C  – матрица размера m на n, определяемая формулой. Для нескалярных A и B количество столбцов A должно равняться количеству строк B . Умножение матриц — это 90 304, а не 90 305, универсально коммутативное для нескалярных входных данных. То есть A*B обычно не равно B*A .
\	Матрица левого деления	A \ B решает систему линейных уравнений A*x = B . Матрицы A и B должны иметь одинаковое количество строк. 9B вычисляет A в степени B .
‘	комплексно-сопряженное транспонирование	Комплексно-сопряженное транспонирование матрицы меняет местами индекс строки и столбца для каждого элемента, отражая элементы по главной диагонали. Операция также инвертирует мнимую часть любых комплексных чисел.

Применение матрицы в анализе цепей

Теперь давайте рассмотрим одно применение матрицы.
Проанализируйте цепь и найдите токи, протекающие через различные сопротивления.

Проблема цепи

Здесь мы будем использовать законы Кирхгофа, которые утверждают, что

1. полное изменение электрического потенциала вокруг замкнутого контура равно нулю.
2. Сумма всех токов в любом узле цепи равна нулю.

Разность потенциалов на резисторе R1 равна i1R1, а разность потенциалов на регистре R2 равна i2R2.
Тогда по 1-му закону получаем
i ₁ R1 + i ₂ R2 = V

Кирхгофа 1-й закон

В узле N втекающий ток равен i1, а вытекающий ток равен i2 и i3.
Тогда согласно второму закону получаем
i ₁ – i ₂ – i ₃ = 0

Кирхгофа 2 закон

Разность потенциалов на резисторе R2 равна сумме разностей потенциалов на резисторах R3 и R4.
I ₂ R2 = I ₃ R3 + I ₃ R4

Следовательно,
-i ₂ R2 + I ₃ R3 + I ₃ R40380 3 R3 + I ₃ R4 = 0

10. эти линейные уравнения можно представить в виде матрицы Z.i = v

поэтому i = Z-1 .v

матрица линейных уравнений

Для решения линейных уравнений в матричном формате используйте функцию linspace().

Matlab Обратная косая черта | Как использовать оператор обратной косой черты в MATLAB?

Оператор обратной косой черты MATLAB используется для решения линейного уравнения вида a*x = b, где «a» и «b» — матрицы, а «x» — вектор. Решение этого уравнения дается как x = a \ b, но оно работает, только если количество строк в «a» и «b» равно. Если количество строк не равно, а «а» не является скаляром, мы получим предупреждение от MATLAB.

Синтаксис оператора обратной косой черты:

x = a \ b

Детали оператора обратной косой черты:

1. x = a \ b будет выполнять левое деление матрицы, также называемое обратной косой чертой
2. Если ‘a’ является скаляром, то оператор обратной косой черты выполнит поэлементное деление

Как использовать оператор обратной косой черты в MATLAB?

Давайте теперь поймем, как использовать оператор обратной косой черты в MATLAB.

Пример #1

В этом примере мы будем использовать оператор обратной косой черты для матрицы 3 x 3. Мы инициализируем две матрицы, одну матрицу 3 x 3, а другую матрицу 3 x 1, чтобы создать и решить линейное уравнение a*x = b

Код:

a = [4 6 12; 1 10 6; 14 4 3] [Инициализация матрицы 3 x 3 в качестве первого ввода] б = [2; 4; 7] [Инициализация матрицы 3 x 1 в качестве второго входа] x = a \ b
[Использование оператора обратной косой черты для решения линейного уравнения, образованного «a» и «b»]

Вот как будут выглядеть наши ввод и вывод в MATLAB:

Ввод:

Вывод:

Как видим, мы получили решение уравнения ax* = b в качестве вывода с использованием оператора обратной косой черты

Пример #2

В этом примере мы будем использовать оператор обратной косой черты на матрице 4 x 4. Здесь также мы инициализируем 2 матрицы, одну матрицу 4 x 4, а другую матрицу 4 x 1, чтобы создать и решить линейное уравнение a*x = b

Код:

а = [6 1 12 2; 1 1 4 5; 4 12 3 11; 2 4 6 1] [Инициализация матрицы 4 x 4 в качестве первого ввода] б = [3; 4; 8; 3] [Инициализация матрицы 4 x 1 в качестве второго входа] x = a \ b
[Использование оператора обратной косой черты для решения линейного уравнения, образованного 'a' и 'b']

Вот как наши ввод и вывод будут выглядеть в MATLAB:

Ввод:

Вывод:

Как мы видим, мы получили решение уравнения a*x = b в качестве вывода с помощью оператора обратной косой черты.

Пример #3

В этом примере мы будем использовать оператор обратной косой черты на разреженной матрице. Обратите внимание, что разреженная матрица — это матрица с небольшим количеством ненулевых элементов. Здесь мы инициализируем две разреженные матрицы для создания и решения линейного уравнения a*x = b.

Код:

a = разреженный ([0 0 1 3 0; 0 1 4 0 0; 1 0 0 0 4; 2 1 0 0 0; 1 0 4 0 0])
[Инициализация 5 x 5 разреженная матрица в качестве первого входа] b = разреженный ([4; -1; -8; 6; 10])
[Инициализация разреженной матрицы 5 x 1 в качестве второго ввода] x = a \ b
[Использование оператора обратной косой черты для решения линейного уравнения, образованного 'a' и 'b']

Вот как наши ввод и вывод будут выглядеть в MATLAB:

Ввод:

Вывод:

Как мы видим, мы получили решение уравнения a*x = b в качестве вывода с помощью оператора обратной косой черты на разреженных матрицах.

В приведенных выше примерах количество строк в обеих матрицах было принято равным. Далее посмотрим, что произойдет, если количество строк во входных матрицах не равно.

Пример #4

В этом примере мы будем использовать оператор обратной косой черты для матрицы 3 x 3 и матрицы 2 x 1. Обратите внимание, что мы берем две матрицы с разным количеством строк.

Код:

а = [1 6 22; 1 0 8; 4 14 3] [Инициализация матрицы 3 x 3 в качестве первого ввода] б = [2; 4] [Инициализация матрицы 2 x 1 в качестве второго входа] x = a \ b
[Использование оператора обратной косой черты для решения линейного уравнения, образованного «a» и «b»]

Вот как будет выглядеть наш ввод и вывод в MATLAB:

Ввод:

Вывод:

Как мы видим, мы получили сообщение об ошибке на выходе, когда число строки во входных матрицах не равны.

Заключение

• Оператор обратной косой черты используется для решения линейного уравнения вида a*x = b, где «a» и «b» — матрицы, а «x» — вектор.
• Используется для вычисления левого деления между двумя матрицами.
• Для работы оператора обратной косой черты обе входные матрицы должны иметь одинаковое количество строк.

Рекомендуемые статьи

Это руководство по обратной косой черте в Matlab. Здесь мы обсуждаем введение, синтаксис, как использовать оператор обратной косой черты в MATLAB? примеры с реализацией кода. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:

1. Nyquist Matlab
2. Предел Matlab
3. Импульсная характеристика Matlab
4. Matlab Saveas

Операции MATRIX – Руководство по MATLAB для ME 160

Введение

MATLAB служит мощным инструментом для решения матриц. Чтобы использовать матрицы в качестве инструмента для решения уравнений или представления данных, необходимо фундаментальное понимание того, что такое матрица и как выполнять с ней арифметические операции.

Что такое матрица?

Матрица представляет собой прямоугольный массив или сетку значений, расположенных в строках и столбцах. Матрицы используются для работы с набором чисел с вариациями традиционных математических операций. Матрицы играют важную роль во многих инженерных и математических задачах благодаря их полезной способности эффективно хранить и организовывать информацию. Понимание матриц оказывается полезным при решении систем уравнений, организации данных, собранных во время экспериментов, вычислении математических операций с большими количествами чисел и сложных приложениях линейной алгебры, машинного обучения и оптимизации.

При описании матриц мы будем называть их по количеству строк и столбцов. Например, следующая матрица представляет собой матрицу 2 × 3, поскольку она имеет две строки и три столбца.

[латекс]\влево[\начало{матрица}2&4&65\\3&2&-8.5\\\конец{матрица}\вправо][/латекс]

И эта матрица представляет собой матрицу 4×3:

[латекс]\влево[\begin{matrix}\begin{matrix}1&-21\\2&25\\\end{matrix}\\\begin{matrix}3&12\\4&-11\\\end{matrix} \\\конец{матрица}\право][/латекс]

Матричная арифметика

Матрицы — это эффективный способ изменить весь набор чисел за одну операцию. Простые способы изменения матриц включают сложение, вычитание, умножение и деление на скаляр или индивидуальное число. При выполнении этих операций завершите расчет с каждым числом в матрице, как указано ниже.

[латекс]\влево[\begin{matrix}1&2\\4&3\\\end{matrix}\right]+2=\left[\begin{matrix}1+2&2+2\\4+2&3+2\ \\end{matrix}\right]=\left[\begin{matrix}3&4\\6&5\\\end{matrix}\right]\gets Answer[/latex]

 

[латекс]\влево[\begin{matrix}2&-4\\1.5&3\\\end{matrix}\right]\ast3=\left[\begin{matrix}2\ast3&-4\ast3\\1.5 \ast3&3\ast3\\\end{matrix}\right]=\left[\begin{matrix}6&-12\\4.5&9\\\end{matrix}\right]\gets Answer[/latex]

 

Матрицы с одинаковыми размерами (т. е. две матрицы 2×2) могут иметь больше математических операций, выполненных с ними. Например, вы можете складывать или вычитать матрицы с одинаковыми размерами, выполняя операции со значениями в каждом соответствующем месте матрицы. Ниже показан шаблон для сложения или вычитания двух матриц.

 

[латекс]\влево[\begin{matrix}a&b\\c&d\\\end{матрица}\right]+\left[\begin{matrix}e&f\\g&h\\\end{matrix}\right]= \left[\begin{matrix}(a+e)&(b+f)\\(c+g)&(d+h)\\\end{matrix}\right][/latex]

 

Умножение матриц сложнее, чем сложение и вычитание, и не соответствует указанному выше формату. Процесс, известный как поэлементное умножение матриц, показан ниже. Этот процесс умножения матриц является фундаментальной концепцией линейной алгебры и возникает при работе с матрицами в MATLAB. Помните об общей форме, показанной ниже, и о том, что ее можно экстраполировать на матрицы разных размеров. Альтернативный метод умножения двух матриц одинакового размера называется покомпонентным умножением, которое будет иметь ту же форму, что и сложение матриц, показанное выше. Процедура их кодирования в MATLAB показана ниже.

Векторы и матрицы в MATLAB

Ввод матриц

В скрипты MATLAB легко вводить матрицы. Чтобы создать стандартную матрицу в командном окне, используйте следующий формат со значениями матрицы, перечисленными с пробелами между каждым значением. Используйте точку с запятой для разделения каждой строки матрицы. Чтобы увидеть, как этот процесс выглядит в MATLAB, обратитесь к примерам в конце этого раздела.

>> [1 2 3;4 5 6;7 8 9]

Что производит [латекс]\left[\begin{matrix}1&2&3\\4&5&6\\7&8&9\\\end{matrix}\right][/latex] в MATLAB.

Обратите внимание, что для создания массива перечислите все числа в строке, разделенные только пробелами. Чтобы перейти к новой строке, используйте точку с запятой. Чтобы сэкономить время при создании большого массива, можно использовать двоеточие для «перечисления» чисел. Например, 1:5 создаст строку, содержащую 1, 2, 3, 4 и 5. Например,

>> [1:3;4:6;7:9]

создает ту же матрицу, что и в первом примере. Если вы хотите создать матрицу, которая рассчитывается в единицах, отличных от единицы, добавьте второе двоеточие, обозначающее, какие числа будут включены. Например,

>> [2:2:10;12:2:20]

создаст следующую матрицу из 2 строк на 5 столбцов, которая считает двойками от 2 до 10 в верхней строке и от 12 до 20 в нижней строке

 

Операции с матрицами и объединение матриц

Примеры

1) Эффективно введите следующую матрицу в MATLAB.

[латекс]\влево[\начало{матрица}1&2&3\\7&8&9\\\конец{матрица}\вправо][/латекс]

2) Эффективно введите следующую матрицу в MATLAB.

[латекс]\влево[\begin{matrix}1&2&3&4&5&6\\7&9&11&13&15&17\\18&18.5&19&19.5&20&20.5\\\end{matrix}\right][/latex]

3) Используйте следующие матрицы в следующих частях.

[латекс]a=\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right][/latex] и [латекс]b=\left[\begin{matrix}2&4\\6&8 \\\конец{матрица}\право][/латекс]

3a) Введите вышеуказанные матрицы в MATLAB. Назначьте каждой переменной указанное имя.

Обратите внимание, что при размещении точки с запятой в конце строки вывод подавляется. В результате настоящие матрицы не печатаются в коде, что в данном случае экономит место.

ИЗОБРАЖЕНИЕ

3b) Сложить матрицы [латекс]а[/латекс] и [латекс]b[/латекс] друг к другу.

ИЗОБРАЖЕНИЕ

3c) Вычтите матрицу [латекс]а[/латекс] из матрицы [латекс]b[/латекс].

ИЗОБРАЖЕНИЕ

3d) Умножьте матрицу [латекс]а[/латекс] и матрицу [латекс]b[/латекс], используя покомпонентное умножение.

ИЗОБРАЖЕНИЕ

3e) Умножьте матрицу [латекс]а[/латекс] и матрицу [латекс]b[/латекс] с помощью умножения матриц.