Однородные дифференциальные уравнения первого порядка
Определение
- Однородное дифференциальное уравнение первого порядка
- – это уравнение вида
, где f – функция.
Как определить однородное дифференциальное уравнение
Для того, чтобы определить, является ли дифференциальное уравнение первого порядка однородным, нужно ввести постоянную t и заменить y на ty и x на tx: y → ty, x → tx. Если t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется.
.
Пример
Определить, является ли данное уравнение однородным
Решение
Делаем замену y → ty, x → tx.
Делим на t 2.
.
Уравнение не содержит t. Следовательно, это однородное уравнение.
Метод решения однородного дифференциального уравнения
Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки y = ux. Покажем это. Рассмотрим уравнение:
(i)
Делаем подстановку:
y = ux,
где u — функция от x. Дифференцируем по x:
y′ = (ux)′ = u′ x + u (x)′ = u′ x + u
Подставляем в исходное уравнение (i).
,
,
(ii) .
Разделяем переменные. Умножаем на dx и делим на x ( f(u) – u ).
При f(u) – u ≠ 0 и x ≠ 0 получаем:
Интегрируем:
Таким образом, мы получили общий интеграл уравнения (i) в квадратурах:
Заменим постоянную интегрирования C на ln C, тогда
Опустим знак модуля, поскольку нужный знак определяется выбором знака постоянной C. Тогда общий интеграл примет вид:
Далее следует рассмотреть случай f(u) – u = 0.
Если это уравнение имеет корни, то они являются решением уравнения (ii). Поскольку уравнение (ii) не совпадает с исходным уравнением, то следует убедиться, что дополнительные решения удовлетворяют исходному уравнению (i).
Всякий раз, когда мы, в процессе преобразований, делим какое либо уравнение на некоторую функцию, которую обозначим как g(x, y), то дальнейшие преобразования справедливы при g(x, y) ≠ 0. Поэтому следует отдельно рассматривать случай g(x, y) = 0.
Пример решения однородного дифференциального уравнения первого порядка
Решить уравнение
.
Решение
Проверим, является ли данное уравнение однородным. Делаем замену y → ty, x → tx. При этом y′ → y′.
,
,
.
Сокращаем на t.
Постоянная t сократилась. Поэтому уравнение является однородным.
Делаем подстановку y = ux, где u – функция от x.
y′ = (ux)′ = u′ x + u (x)′ = u′ x + u
Подставляем в исходное уравнение.
,
,
,
.
При x ≥ 0, |x| = x. При x ≤ 0, |x| = – x. Мы пишем |x| = ± x подразумевая, что верхний знак относится к значениям x ≥ 0, а нижний – к значениям x ≤ 0.
,
Умножаем на ± dx и делим на .
При u2 – 1 ≠ 0 имеем:
Интегрируем:
Интегралы табличные,
.
Применим формулу:
(a + b)(a – b) = a 2 – b 2.
Положим a = u, .
.
Возьмем обе части по модулю и логарифмируем,
.
Отсюда
.
Таким образом имеем:
,
.
Опускаем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C.
Умножаем на x и подставляем ux = y.
,
.
Возводим в квадрат.
,
,
.
Теперь рассмотрим случай, u2 – 1 = 0.
Корни этого уравнения
.
Легко убедиться, что функции y = ± x удовлетворяют исходному уравнению.
Ответ
,
,
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
Однородные дифференциальные уравнения первого порядка
Дифференциальное уравение первого порядка 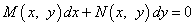 называется однородным, если
называется однородным, если 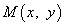 и
и
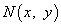 — однородные функции
одной и то же степени.
— однородные функции
одной и то же степени.
Функция 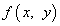 называется однородной функцией k-й степени, если для любого t выполняется равенство
называется однородной функцией k-й степени, если для любого t выполняется равенство
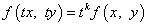 .
.
В частном случае, если однородная функция имеет нулевую степень, то выполняется равенство

Пример 1. Установить, являются ли однородными функции
1) 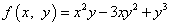 ;
;
2) 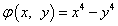 ;
;
Решение. Находим
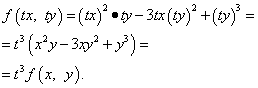
Следовательно, 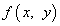 —
однородная функция третьей степени.
—
однородная функция третьей степени.
Аналогично устанавливается, что 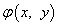 —
однородная функция четвёртой степени:
—
однородная функция четвёртой степени:
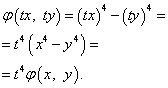
Отношение двух однородных функций одинаковых степеней также есть однородная функция, но
нулевой степени. Пусть 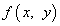 и
и
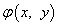 — однородные функции
k-й степени. Это означает, что
— однородные функции
k-й степени. Это означает, что 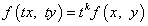 , а
, а
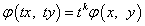 . Их отношение — некоторая функция
. Их отношение — некоторая функция
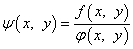 , так как
, так как 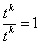 .
.
Как решить однородное дифференциальное уравнение первого порядка?
Решение однородного дифференциального уравнения первого порядка сводится к решению дифференциального уравнения с разделяющимися переменными.
Для этого преобразуем уравнение к виду
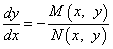 или
или
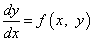 , (1)
, (1)
где 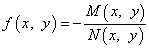
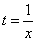 , то
, то
 , или
, или
 , т. е. функция
, т. е. функция
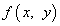 представлена в виде функции
от
представлена в виде функции
от 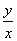 .
.Обозначим это отношение через z, т. е. 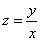 ,
откуда
,
откуда 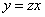 . Тогда
. Тогда
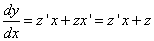
и уравнение (1) преобразуется так:
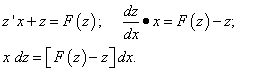
Это уравнение с разделяющимися переменными. Разделив переменные и выполнив почленное интегрирование,
затем следует заменить z на 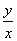 .
.
Пример 5. Решить однородное дифференциальное уравнение
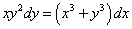
Решение. Поделим почленно уравнение на dx и получим
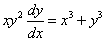 или
или
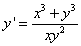 .
.
Произведём подстановку 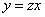 ,
откуда
,
откуда 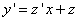 . Тогда уравнение примет вид
. Тогда уравнение примет вид
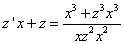 .
.
Путём дальнейших преобразований получаем 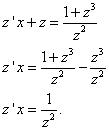
Итак, 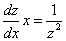 или
или
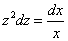 .
.
Почленное интегрирование даёт
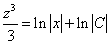 .
.
Заменяя z на 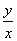 ,
получим
,
получим 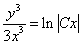
Чтобы избавиться от дробности, умножим обе части выражения на x в кубе и получим 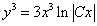
— общий интеграл данного уравнения.
Выводы. Чтобы решать однородные дифференциальные уравнения, необходимо хорошо владеть методами интегрирования — путём замены переменной и по частям. В практических задачах на этот вид дифференциальных уравнений нередко после преобразований получаются выражения, интегрируя которые, требуется применять как один, так и другой метод интегрирования дважды или даже трижды.

Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
Однородное дифференциальное уравнение — Википедия
Материал из Википедии — свободной энциклопедии
Существует два понятия однородности дифференциальных уравнений.
Обыкновенное уравнение первого порядка y′=f(x,y){\displaystyle y’=f(x,y)} называется однородным относительно x и y, если функция f(x,y){\displaystyle f(x,y)} является однородной степени 0:
- f(λx,λy)=λ0f(x,y)=f(x,y){\displaystyle f(\lambda x,\lambda y)=\lambda ^{0}f(x,y)=f(x,y)}.
Однородную функцию можно представить как функцию от yx{\displaystyle {\frac {y}{x}}}:
- f(x,y)=f(1,yx)=g(yx){\displaystyle \ f(x,y)=f\left(1,{\frac {y}{x}}\right)=g\left({\frac {y}{x}}\right)}.
Используем подстановку yx=u{\displaystyle {\frac {y}{x}}=u}, а затем воспользуемся правилом произведения: d(ux)dx=xdudx+udxdx=xdudx+u{\displaystyle {\frac {d(ux)}{dx}}=x{\frac {du}{dx}}+u{\frac {dx}{dx}}=x{\frac {du}{dx}}+u}. Тогда дифференциальное уравнение y′=f(x,y){\displaystyle y’=f(x,y)} сводится к уравнению с разделяющимися переменными:
- u′x+u=g(u)⇒duu−g(u)+dxx=0{\displaystyle u’x+u=g(u)\Rightarrow {\frac {du}{u-g(u)}}+{\frac {dx}{x}}=0}.
Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение F(y,y′,y″,…)=G(x){\displaystyle F(y,y’,y»,\ldots )=G(x)} — однородно, если G(x)≡0{\displaystyle G(x)\equiv 0}.
В случае, если G(x)≠0{\displaystyle G(x)\neq 0}, говорят о неоднородном дифференциальном уравнении.
Именно для решения линейных однородных дифференциальных уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции.
Однородные дифференциальные уравнения 1-ого порядка
Определение и формулы однородных ДУ первого порядка
Уравнение вида (1) заменой
(или ) сводится к уравнению с разделяющимися переменными относительно новой функции :
или
Общий интеграл уравнения:
Интеграл, стоящий в правой части, табличный, тогда:
Необходимо рассмотреть еще особый случай . Если это уравнение имеет корни, то они являются и решением уравнения . Но это уравнение не совпадает с исходным дифференциальным уравнением, поэтому надо убедиться, что решения уравнения удовлетворяют исходному уравнению (1).
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Дифференциальные уравнения первого порядка
Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Как решать дифференциальные уравнения первого порядка
Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .
Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.
Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.
Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.
Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.
Уравнения с разделяющимися переменными
;
.
Делим на и интегрируем. При получаем:
.
Подробнее >>>
Уравнения, приводящиеся к уравнениям с разделяющимися переменными
Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>
Однородные уравнения
Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>
Уравнения, приводящиеся к однородным
Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>
Обобщенные однородные уравнения
Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>
Линейные дифференциальные уравнения
Есть три метода решения линейных уравнений.
1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>
2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:
Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>
Уравнения Бернулли
Подстановкой уравнение Бернулли приводится к линейному уравнению.
Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
Уравнения Риккати
Оно не решается в общем виде. Подстановкой
уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:
оно приводится к виду:
,
где .
Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>
Уравнения Якоби
Решается подстановкой:
.
Подробнее >>>
Уравнения в полных дифференциалах
При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.
Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>
Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция, при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>
Уравнения, не решенные относительно производной y’
Уравнения, допускающие решение относительно производной y’
Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, допускающие разложение на множители
Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;
;
Подробнее >>>
Уравнения, не содержащие x и y
Здесь – постоянная:
,
где – корень уравнения
.
Подробнее >>>
Уравнения, не содержащие x или y
или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .
Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>
Уравнения, разрешенные относительно y
Уравнения Клеро
Такое уравнение имеет общее решение
Подробнее >>>
Уравнения Лагранжа
Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>
Уравнения, приводящиеся к уравнению Бернулли
Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.
Общий вид линейного дифференциального уравнения первого порядка таков:
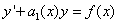 ,
,
где 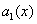 и
и
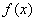 — непрерывные функции от x.
— непрерывные функции от x.
Как решить линейное дифференциальное уравнение первого порядка?
Интегрирование такого уравнения можно свести к интегрированию двух двух дифференциальных уравнений первого порядка с разделяющимися переменными. Великие математики доказали, что нужную функцию, то есть решение уравнения, можно представить в виде произведения двух неизвестных функций u(x) и v(x). Пусть y = uv, тогда по правилу дифференцирования произведения функций
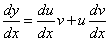
и линейное дифференциальное уравнения первого порядка примет вид
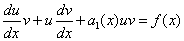
или
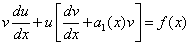 . (*)
. (*)
Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:
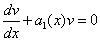 ,
,
то есть в качестве функции v берётся одно из частных решений этого уравнения с разделяющимися
переменными, отличное от нуля. Разделяя в уравнении 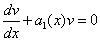 переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v —
решение уравнения, то её подстановка в уравнение
переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v —
решение уравнения, то её подстановка в уравнение 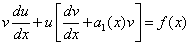 даёт
даёт
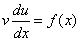 .
.
Таким образом, для нахождения функции u получили дифференциальное уравнение первого порядка с разделяющимися переменными. Найдём функцию u как общее решение этого уравнения.
Теперь можем найти решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций u и v, т. е. y = uv. u и v уже нашли.
Пример 1. Решить линейное дифференциальное уравнение первого порядка
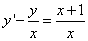 .
.
Решение. Как было показано в алгоритме, y = uv. Подставляя выражения для
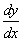 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
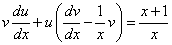 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
 или
или 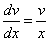 .
.
После разделения переменных это уравнение принимает вид
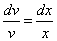 .
.
Почленное интегрирование даёт
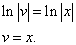
Подставив найденное значение функции v в равенство (* *), получим
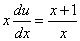 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:
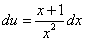
и, интегрируя находим u:
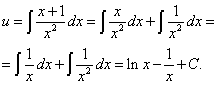
Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:
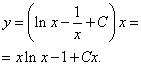
Как видим, всё решение выполняется точным следованием алгоритму, приведённому в начале статьи. Меняются лишь виды функций в уравнениях. Степени, корни, экспоненты и т.д. Это чтобы алгоритм отпечатался в памяти и был готов к разным случаям, которые только могут быть на контрольной и экзамене. А кому стало скучно, наберитесь терпения: впереди ещё примеры с интегрированием по частям!
Важное замечание. При решении заданий не обойтись без преобразований выражений. Для этого требуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Пример 2. Решить линейное дифференциальное уравнение первого порядка
 .
.Решение. Подставляя выражения для
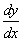 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
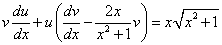 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
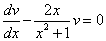 .
.
После разделения переменных это уравнение принимает вид
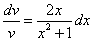 .
.
Почленное интегрирование даёт
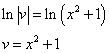
Подставив найденное значение функции v в равенство (* *), получим
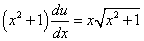
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:
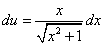
и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:
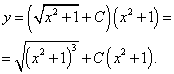
В следующем примере — обещанная экспонента.
Пример 3. Решить линейное дифференциальное уравнение первого порядка
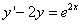 .
.
Решение. Подставляя выражения для
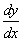
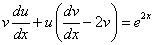 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
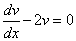 или
или 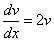 .
.
После разделения переменных это уравнение принимает вид
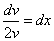 .
.
Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим
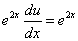 .
.
Это уравнение с разделяющимися переменными для нахождения функции
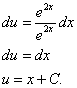
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
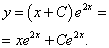
Любители острых ощущений дождались примера с интегрированием по частям. Таков следующий пример.
Пример 4. Решить линейное дифференциальное уравнение первого порядка
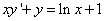 .
.
Решение. В этом случае сначала нужно добиться, чтобы производная «игрека» ни на что не умножалась. Для этого поделим уравнение почленно на «икс» и получим
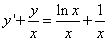 .
.
Подставляя выражения для
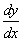 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
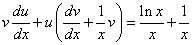 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
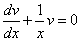 или
или 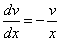 .
.
После разделения переменных это уравнение принимает вид
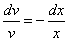 .
.
Почленное интегрирование даёт
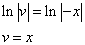
Подставив найденное значение функции v в равенство (* *), получим
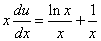 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируем по частям.
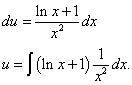
В интеграле 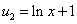 ,
,
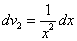 .
.
Тогда 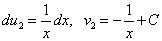 .
.
Интегрируем и находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:
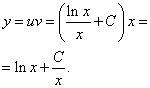
И уж совсем странной статья о дифференциальных уравнениях была бы без примера с тригонометрическими функциями.
Пример 5. Решить линейное дифференциальное уравнение первого порядка
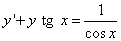 .
.
Решение. Подставляя выражения для
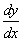 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
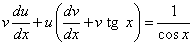 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
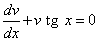 или
или 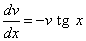 .
.
После разделения переменных это уравнение принимает вид
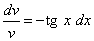 .
.
Почленное интегрирование даёт
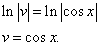
Подставив найденное значение функции v в равенство (* *), получим
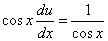 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
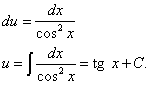
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
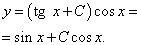
В последних двух примерах требуется найти частное решение уравнения.
Пример 6. Найти частное решение линейного дифференциальное уравнение первого порядка
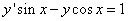 при условии
при условии 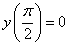 .
.
Решение. Чтобы производная «игрека» ни на что не умножалась, разделим уравнение почленно на
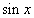 и получим
и получим
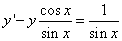
или
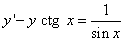 .
.
Подставляя выражения для
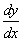 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
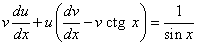 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
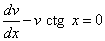 или
или 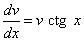 .
.
После разделения переменных это уравнение принимает вид
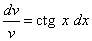 .
.
Почленное интегрирование даёт
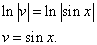
Подставив найденное значение функции v в равенство (* *), получим
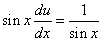 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
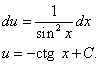
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
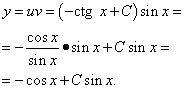
Найдём частное решение уравнения. Для этого в общее решение подставим 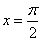 и
и
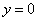 и найдём значение C:
и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:
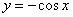 .
.
Пример 7. Найти частное решение линейного дифференциального уравнения первого порядка
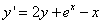 при условии
при условии 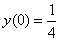 .
.
Перенесём функцию «игрека» в левую часть и получим
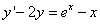 .
.
Подставляя выражения для
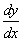 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
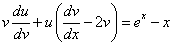 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
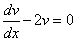 или
или 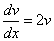 .
.
После разделения переменных это уравнение принимает вид
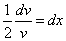 .
.
Почленное интегрирование даёт
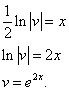
Подставив найденное значение функции v в равенство (* *), получим
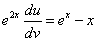 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
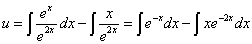 .
.
Первый интеграл равен 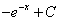 ,
второй находим интегрированием по частям.
,
второй находим интегрированием по частям.
В нём 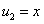 ,
,
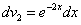 .
.
Тогда 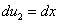 ,
, 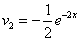 .
.
Находим второй интеграл:
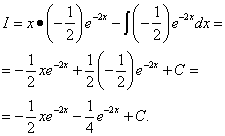 .
.
В результате получаем функцию u:
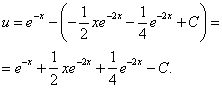
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
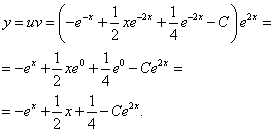
Найдём частное решение уравнения. Для этого в общее решение подставим 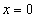 и
и
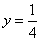 и найдём значение C:
и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:
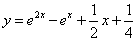 .
.
Выводы. Алгоритм решения линейных дифференциальных уравнений первого порядка достаточно однозначен. Трудности чаще всего возникают при интегрировании и это означает, что следует повторить этот обширный раздел математического анализа. Кроме того, что особенно видно из примеров ближе к концу статьи, очень важно владеть приёмами действий со степенями и дробями, а это школьные темы, и если они подзабыты, то их тоже следует повторить. Совсем простых «демо»-примеров ждать на контрольной и на экзамене не стоит.

Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
Дифференциальные уравнения: виды, методы решения
Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1-го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2-го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y’=dxdy, если y является функцией аргумента x.
Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y’=f(x)
Начнем с примеров таких уравнений.
Пример 1y’=0, y’=x+ex-1, y’=2xx2-73
Оптимальным для решения дифференциальных уравнений f(x)·y’=g(x) является метод деления обеих частей на f(x). Решение относительно производной позволяет нам прийти к уравнению вида y’=g(x)f(x). Оно является эквивалентом исходного уравнения при f(x) ≠ 0.
Пример 2