Решение онлайн матричного уравнения: Умножение матриц онлайн

Содержание

Решение матричных уравнений. Подробные примеры решений

Предварительно рекомендуется изучить основные действия над матрицами.

Даны матричные уравнения

A·X = B, (1)
Y·A = B, (2)

где A и B – заданные матрицы, причем A – невырожденная. Требуется найти матрицы X и Y.
Нельзя ли определить деление матриц?
Вспомним, что в числовой области частное от деления b на a определяется как решение уравнения a∙x=b (или x∙a=b) и существует не всегда. Можно попытаться определить «деление» матриц, рассматривая уравнения (1) и (2), в которых, согласно правилу умножения, матрицы A, B, X, Y не могут иметь произвольную структуру. Так, в первом уравнении матрицы A и B должны иметь одинаковое число строк, а во втором – одинаковое число столбцов. Уже отсюда ясно, что если даже оба эти уравнения однозначно разрешимы (а это далеко не всегда так), то их решения вполне могут быть матрицами не только разными, но и разной структуры.

Таким образом, для матриц оказывается невозможным определить деление с привычными свойствами.
Матричные уравнения вида (1) и (2) решаются следующим образом. Так как A невырожденная матрица, то существует обратная матрица A^-1. Умножим слева обе части уравнения (1) на A^-1: A^-1·A·X = A^-1·B, тогда получим E·X = A^-1·B, или

X = A^-1·B. (3)

Аналогично, умножая справа обе части равенства (2) на A^-1, будем иметь: Y·A· A^-1 = B· A^-1, откуда находим, что

Y = B· A^-1. (4)

Пример 1. Решить матричное уравнение .
Решение. Обозначим , . Тогда матричное уравнение запишется в виде A·X = B. Найдем A^-1: ; A₁¹ = 4; A₂¹ = -3; A₁² = -2; A₂² = 1, . Воспользуемся формулой (3):

Пример 2. Решить матричное уравнение .

Решение. (в силу пропорциональности строк), т.е. матрица A – вырожденная, следовательно уравнение решения не имеет.
Пример 3. Решить уравнение .
Решение. Данное уравнение записываем в виде A∙X∙B = C. Умножаем обе части этого равенства слева на A^-1 и справа на B^-1: A^-1∙A∙X∙B∙B^-1 = A^-1∙C∙B^-1. Так как A∙A^-1 = B∙B^-1 = E и E∙X = X∙E = X, то X = A^-1∙C∙B^-1.

Находим обратные матрицы , , тогда
.
Проверка.

Перейти к онлайн решению своей задачи

Пример 6

Вариантов записей матричных уравнений может быть достаточно много, однако, все их можно свести к двум видам:

A·X = B
Y·A = B

где A и B – заданные матрицы, причем A – невырожденная.

Требуется найти матрицы X и Y. Данные матричные уравнения решаются с помощью онлайн-калькулятора. Далее покажем на примерах, как можно свести все варианты записи матричных выражений к двум классическим.

Перед изучением материала необходимо иметь представление об операциях над матрицами:

умножение матриц (A*B): соответствующие элементы матриц умножаем и складываем: ;
сложение матриц (C+B): складываются соответствующие элементы матриц C и B ;
разница (вычитание) матриц (A-B): из каждого элемента матрицы A вычитается соответствующий элемент матрицы B ;
умножение матрицы на число (2*C): число умножается на каждый элемент матрицы ;

Пример 1. Решить матричные уравнения и сделать проверку.

Запишем данное матричное уравнение в матричной форме: A·X - B = 3C.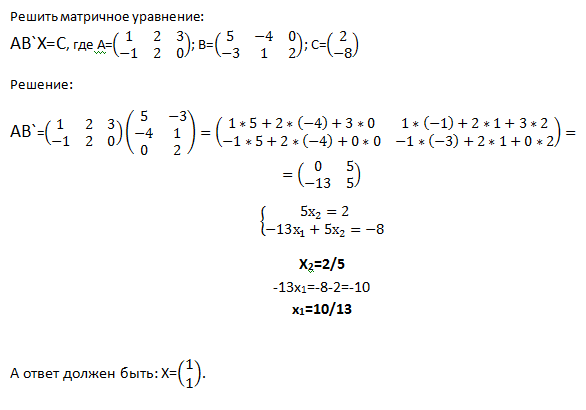

Его можно записать как A·X = 3C + B. Найдем сумму матриц:

3C + B =

-1	2
2	-2
-3	-1

Обозначим:

A =

2	1	1
3	4	-2
3	-2	4

B =

-1	2
2	-2
-3	-1

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 2*(4*4 — (-2)*(-2)) — 3*(1*4 — (-2)*1) + 3*(1*(-2) — 4*1) = -12
Определитель матрицы А равен detA=-12
Так как A невырожденная матрица, то существует обратная матрица A^-1.

Умножим слева обе части уравнения на A^-1: A^-1·A·X = A^-1·B, тогда получим E·X = A^-1·B, или X = A^-1·B.
Найдем обратную матрицу A^-1.
Транспонированная матрица A^T.

A^T =

2	3	3
1	4	-2
1	-2	4

Алгебраические дополнения

A_1,1 = (-1)¹⁺¹

4	-2
-2	4

∆_1,1 = (4*4 — (-2)*(-2)) = 12

A_1,2 = (-1)¹⁺²

∆_1,2 = -(1*4 — 1*(-2)) = -6

A_1,3 = (-1)¹⁺³

∆_1,3 = (1*(-2) — 1*4) = -6

A_2,1 = (-1)²⁺¹

∆_2,1 = -(3*4 — (-2)*3) = -18

A_2,2 = (-1)²⁺²

∆_2,2 = (2*4 — 1*3) = 5

A_2,3 = (-1)²⁺³

∆_2,3 = -(2*(-2) — 1*3) = 7

A_3,1 = (-1)³⁺¹

∆_3,1 = (3*(-2) — 4*3) = -18

A_3,2 = (-1)³⁺²

∆_3,2 = -(2*(-2) — 1*3) = 7

A_3,3 = (-1)³⁺³

∆_3,3 = (2*4 — 1*3) = 5
Обратная матрица A^-1.

A^-1 = ¹/₁₂

12	-6	-6
-18	5	7
-18	7	5

Матрицу Х ищем по формуле: X = A^-1·B

X= ¹/₁₂

12	-6	-6
-18	5	7
-18	7	5

-1	2
2	-2
-3	-1

¹/₂	-3¹/₂
^-7/₁₂	4⁵/₁₂
-1⁵/₁₂	4⁷/₁₂

Ответ:

X =

¹/₂	-3¹/₂
^-7/₁₂	4⁵/₁₂
-1⁵/₁₂	4⁷/₁₂

Пример 2.

Данное выражение в матричной форме имеет вид: X·A - B = 2C. Преобразуем к виду: X·A = 2C + B или X·A = D, где D = 2C + B

Пример 3.

Пример 4.

Здесь имеем следующий тип матричного уравнения: A - X·B = 2C. Сводим его к типу X·B = A + 2C или X·B = D, где D = A + 2C.

A + 2C =

Обозначим:

A =

3	2	2
2	3	1
1	1	3

Тогда матричное уравнение запишется в виде: Y·A = B.
Вычислим определитель матрицы А:
∆ = 3*(3*3 — 1*1) — 2*(2*3 — 1*2) + 1*(2*1 — 3*2) = 12
Определитель матрицы А равен detA=12
Так как A невырожденная матрица, то существует обратная матрица A^-1.

Умножим справа обе части уравнения на A^-1: X·A·A^-1 = B·A^-1, откуда находим, что X = B·A^-1
Найдем обратную матрицу A^-1.
Транспонированная матрица A^T.

A^T =

3	2	1
2	3	1
2	1	3

Алгебраические дополнения

A_1,1 = (-1)¹⁺¹

∆_1,1 = (3*3 — 1*1) = 8

A_1,2 = (-1)¹⁺²

∆_1,2 = -(2*3 — 2*1) = -4

A_1,3 = (-1)¹⁺³

∆_1,3 = (2*1 — 2*3) = -4

A_2,1 = (-1)²⁺¹

∆_2,1 = -(2*3 — 1*1) = -5

A_2,2 = (-1)²⁺²

∆_2,2 = (3*3 — 2*1) = 7

A_2,3 = (-1)²⁺³

∆_2,3 = -(3*1 — 2*2) = 1

A_3,1 = (-1)³⁺¹

∆_3,1 = (2*1 — 3*1) = -1

A_3,2 = (-1)³⁺²

∆_3,2 = -(3*1 — 2*1) = -1

A_3,3 = (-1)³⁺³

∆_3,3 = (3*3 — 2*2) = 5
Обратная матрица A^-1.

A^-1 = ¹/₁₂

8	-4	-4
-5	7	1
-1	-1	5

Матрицу X ищем по формуле: X = B·A^-1

X =

¹/₁₂

8	-4	-4
-5	7	1
-1	-1	5

-3⁵/₁₂

2⁷/₁₂

¹/₁₂

Ответ:

X =

-3⁵/₁₂

2⁷/₁₂

¹/₁₂

Пример 2.

Перейти к онлайн решению своей задачи

Пример №5. Решение матричных уравнений.
Обозначим:

A =

3	-1
5	-2

C =

14	16
9	10

Тогда матричное уравнение запишется в виде: A·X·B = C.
Вычислим определитель матрицы А:
∆ = 3*(-2) — 5*(-1) = -1
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A^-1. Умножим слева обе части уравнения на A^-1:Умножаем обе части этого равенства слева на A^-1 и справа на B^-1: A^-1·A·X·B·B^-1 = A^-1·C·B^-1. Так как A·A^-1 = B·B^-1 = E и E·X = X·E = X, то X = A^-1·C·B^-1
Найдем обратную матрицу A^-1.

Транспонированная матрица A^T.

A^T =

3	5
-1	-2

Алгебраические дополнения
A₁₁ = (-1)¹⁺¹·-2 = -2; A₁₂ = (-1)¹⁺²·-1 = 1; A₂₁ = (-1)²⁺¹·5 = -5; A₂₂ = (-1)²⁺²·3 = 3;
Обратная матрица A^-1.

A^-1 = 1/-1

-2	1
-5	3

Вычислим определитель матрицы B:
∆ = 5*8 — 7*6 = -2
Определитель матрицы B равен detB=-2
Найдем обратную матрицу B^-1.
Транспонированная матрица B^T.
Алгебраические дополнения:
A₁₁ = (-1)¹⁺¹·8 = 8; A₁₂ = (-1)¹⁺²·6 = -6; A₂₁ = (-1)²⁺¹·7 = -7; A₂₂ = (-1)²⁺²·5 = 5;
Обратная матрица B^-1.

B^-1 = 1/-2

8	-6
-7	5

Матрицу X ищем по формуле: X = A^-1·C·B^-1

X = 1/-1

-2	1
-5	3

14	16
9	10

· 1/-2

8	-6
-7	5

Ответ:

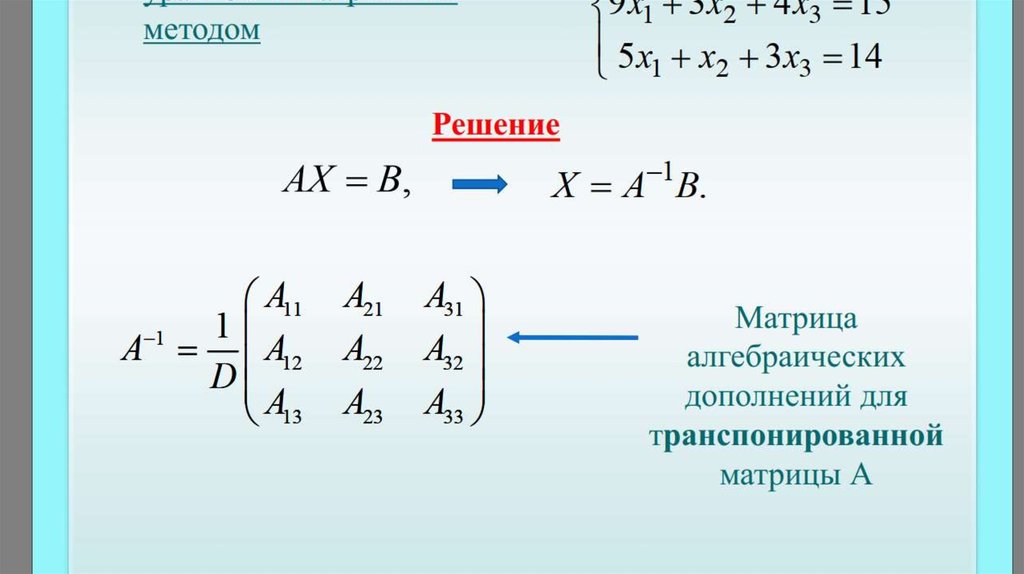
3. Обратная матрица. Решение матричных уравнений

Матрица называется обратной к квадратной матрице , если

где — единичная матрица, имеющая тот же порядок, что и матрица .

Обратная матрица существует только в том случае, если , и ее элементы находятся по формуле

где — алгебраическое дополнение к элементу .

Внимание! Алгебраические дополнения, которые вычисляются к элементам строки, записываются в столбец.

Если , то матрица называется вырожденной, в противном случае невырожденной, т.е. обратная матрица существует только для невырожденных матриц.

Обозначается обратная матрица , т.е.

при этом ее определитель .

Для невырожденных матриц и выполнены соотношения

Введение обратной матрицы позволяет решать матричные уравнения. В конечном счете, матричные уравнения сводятся к двум простейшим уравнениям:

или .

Если матрица — квадратная, невырожденная, то эти уравнения имеют единственное решение, которое можно получить с помощью обратной матрицы. Так как при умножении матриц коммутативный закон не выполняется, они решаются разными способами.

При поиске решения первое из уравнений надо умножать на обратную матрицу слева, а второе справа, т.е.

, (5)

. (6)

►Пример 5. Найти решение матричного уравнения , то есть определить матрицу , если ; .

Решение.

Решение в матричном виде определяется формулой (5), т. е. , если матрица невырожденная. Вычислим определитель матрицы :

Следовательно, матрица невырожденная, и для нее существует обратная матрица. Проведем вычисления, необходимые для построения обратной матрицы. Вычислим алгебраические дополнения:

Составим обратную матрицу и найдем неизвестную матрицу .

При вычислениях множитель рекомендуем оставлять перед матрицей и проводить умножение полученной матрицы на него на последнем этапе вычислений.

►Пример 6. Найти решение матричного уравнения , если .

Решение.

Формулой (5) воспользоваться нельзя, так как матрица не квадратная, следовательно, для нее не существует обратной матрицы. Умножим обе части уравнения на транспонированную матрицу слева, получаем

Матрица − квадратная и, если ее определитель не равен нулю, то решение заданного уравнения имеет вид

Проведем вычисления:

Определитель полученной матрицы . Следовательно, обратная матрица к матрице существует, и можно найти матрицу :.

. ◄

Упражнения.

1. Для заданных матриц найти обратную матрицу:

а) ; б) ; в) ; г) ; д) .

Ответы:

а) ; б) ; в) ;

г) ; д) .

2. Найти неизвестную матрицу из уравнений:

а) ; б) ;

в) ;

г) ; д) .

Ответы:

а) ; б) ; в) ; г) ; д) .

Решение матричных уравнений спросил

3 года 8 месяцев назад

Изменено 3 года, 8 месяцев назад

Просмотрено 407 раз

$\begingroup$

Я новичок в системе Mathematica и пытаюсь применить решение этой задачи. {-1}$. Инверсия $B$: 9{-1}_{i, j}=A_{i, j}$, если $B_{ij} \neq 0$.

Как мне решить эту систему уравнений с помощью Mathematica?

Бонус: Зная, что на самом деле матрица имеет форму 16 на 16 и что есть 64 параметра $b_{i, j}$, можно ли решить эту проблему с помощью Mathematica или мне следует попробовать что-то еще?

Спасибо за помощь 🙂

решение уравнений
матрица
линейная алгебра

$\endgroup$

6 9{-1}$, которые изменяют все элементы на $0$, равные нулю в B.

Используя симметричное определение $B$ (извините за форматирование нижнего индекса)

 B = {{Subscript[b, 11], Subscript[ б, 12], нижний индекс [б, 13],
    0}, {Нижний индекс[b, 12], Нижний индекс[b, 22], 0, 0}, {Нижний индекс[b, 13],
     0, нижний индекс[b, 33], нижний индекс[b, 34]}, {0, 0, нижний индекс[b, 34],
    Индекс[b, 44]}};
Binv = Обратное[B];
Решить[Таблица[
   If[MatchQ[B[[i, j]], Subscript[b, i_]], Binv[[i, j]], 0], {i,
    4}, {j, 4}] ==
  Таблица[If[MatchQ[B[[i, j]], Subscript[b, i_]], A[[i, j]], 0], {i,
    4}, {к, 4}]]
 9{-1}=\left(\begin{array}{cccc}50 & 3 & 10 & \frac{8}{11} \\3 & 60 & \frac{3}{5} & \frac{12} {275} \\10 & \frac{3}{5} & 55 & 4 \\\frac{8}{11} & \frac{12}{275} & 4 & 45 \\\end{массив}\ справа)$$ 
 
    $\endgroup$
 
 




            3
     
 
    $\begingroup$
     
  Матрицы, предоставленные пользователем: 
  мА = {{50, 3, 10, 2}, {3, 60, 7, 1}, {10, 7, 55, 4}, {2, 1, 4, 45 }}
mB = {{b11, b12, b13, 0}, {b12, b22, 0, 0}, {b13, 0, b33, b34}, {0, 0, b34, b44}}
 
 Параметризация  мА , где  мБ  имеет ноль. (См. документы для  Indexed  .)
 mAnext = MapIndexed[
  If[TrueQ[0 == Extract[mB, #2]], Indexed[a, #2], #1] &, mA, {2}]
 
 Извлеките параметры из двух матриц и создайте единый вектор параметров.
 prmsA = Дела[Catenate@mAnext, _Indexed]
prmsB = DeleteCases[Catenate[mB], 0]
prms = Присоединиться[prmsA, prmsB]
 
 Предположим, что обратное значение  мБ  равно  mNext  и решить:
 mI = IdentityMatrix[4]
Решить[mI == mB.mAследующий, prms]
 
 $\endgroup$
 1
 Зарегистрируйтесь или войдите в систему 
 Зарегистрируйтесь с помощью Google
 Зарегистрироваться через Facebook
 Зарегистрируйтесь, используя адрес электронной почты и пароль
 Опубликовать как гость 
 Электронная почта
 Требуется, но никогда не отображается
 Опубликовать как гость 
 Электронная почта
 Требуется, но не отображается
 Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
 линейная алгебра - Решение матричного уравнения над GF (2) в Sage 
 Задавать вопрос
 спросил  7 лет, 3 месяца назад 
 Изменено
 7 месяцев назад
 Просмотрено
 787 раз
 Я пытаюсь решить систему линейных уравнений в Sage. Однако я хочу напечатать решение, только если оно уникально. Я попытался использовать  A.solve_right(y)  , где  A - матрица коэффициентов  ,  y - правая часть (Ax = y)  . Однако это возвращает решение, когда существует несколько решений. Я попытался проверить, равен ли определитель 0, но это работает только при наличии квадратной матрицы.
 Я думал о 2-х способах, но не нашел подходящего способа реализовать свои мысли в Sage:
 Метод решения системы из  n  уравнений  m  переменных. Всякий раз, когда я вызываю A.solve(x), где A - матрица n x m, а x - вектор длины n, я должен получить либо исключение " Нет уникального решения"  (если нет или более одного решения), либо решение, если оно уникально .
 Метод, позволяющий добавлять строки в матрицу  A  . Когда я добавляю новую строку, я проверяю, является ли она линейной комбинацией предыдущих строк, и если да, то я игнорирую эту строку.No related posts.

Решение матричных уравнений. Подробные примеры решений

3. Обратная матрица. Решение матричных уравнений

Решение матричных уравнений спросил

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

линейная алгебра - Решение матричного уравнения над GF (2) в Sage

Добавить комментарий Отменить ответ