Метод решения задач с процентами
Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
которые можно записать в виде пропорции
| все | = | 100% |
| часть | часть в % |
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
Пример 1.
Найти число B составляющее 15% от числа 30.
Решение.
x
соответствует 15%Запишим пропорцию
| 30 | = | 100% |
x | 15% |
решим полученное уравнение
x = | 30 · 15% | = 4. 5 5 |
| 100% |
Ответ: 15% от 30 равно 4.5.
Пример 2.
Найти сколько процентов составляет число 35 от числа 20.
Решение.
x
Запишим пропорцию
| 20 | = | 100% |
| 35 | x |
решим полученное уравнение
x = | 35 · 100% | = 175% |
| 20 |
Ответ: 35 составляет 175% от 20.
Пример 3.
Найти число, 5% которого равны 20.
Решение.
x
соответствует 100%Запишим пропорцию
x | = | 100% |
| 20 | 5% |
решим полученное уравнение
x = | 20 · 100% | = 400 |
| 5% |
Ответ: 400.
Проценты: Вступление и оглавление. Определение процентов и общая информация о процентах Преобразования между десятичной дробью и процентами Метод решения задач с процентами
Наиболее распространенные типы задач на проценты: Вычисление процента от заданного числа. Вычисление исходного числа по известному проценту от числа. Вычисление процентного выражения одного числа от другого. Вычисление числа на заданный процент большего или меньшего от исходного числа. Вычисление числа по значению числа большего или меньшего от исходного на заданный процент. Задачи на смеси. Вычисление сложных процентов.
При изучении процентов вам также будут полезны:
Онлайн калькуляторы для решения задач с процентами
Онлайн задачи и упражнения с процентами
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Карта сайта
Карта сайтаЦвет:C C C
Изображения Вкл. Выкл.
Обычная версия сайта
- Телефон доверия: 8 800 200-01-22
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Решение задач с использованием процентов | Бухгалтерский учет для менеджеров
Результат обучения
- Оценка выражений и текстовых задач с использованием процентов
В этом разделе мы будем решать процентные вопросы, определяя части задачи. Мы рассмотрим обычное применение процентов — чаевые официанту в ресторане — чтобы понять, как настроить базовое приложение процентов.
Мы рассмотрим обычное применение процентов — чаевые официанту в ресторане — чтобы понять, как настроить базовое приложение процентов.
Когда Аолани и ее друзья ужинали в ресторане, счет пришел на [латекс]\текст{\$80}[/латекс]. Они хотели оставить [латекс]20\%[/латекс] чаевых. Какой суммы будут чаевые?
Чтобы решить эту проблему, мы хотим найти сумму [латекс]20\%[/латекс] от [латекс]\$80[/латекс]. [latex]\$80[/latex] называется базой . процентов — это заданный [латекс]20\%[/латекс]. Сумма чаевых будет [латекс]0,20(80)[/латекс] или [латекс]\$16[/латекс] — см. изображение ниже. Чтобы узнать сумму чаевых, мы умножили процент на основание.
Чаевые [латекс]20\%[/латекс] за счет ресторана [латекс]\80[/латекс] составляют [латекс]\16$[/латекс].
Части процентной задачи
процентов. Проблемы включают три количества: Основание (целое), процент и SUNT (часть из SUNT (часть из партии (часть из партии (часть из части полную или частичную сумму).
Сумма в процентах от базовой.
Давайте посмотрим на другой пример:
У Джеффа есть купон Guitar Strings на [латекс]15\%[/латекс] на любую покупку [латекс]$100[/латекс] или больше. Он хочет купить подержанную гитару с ценой [латекс]220 долларов[/латекс]. Джефф задается вопросом, сколько денег купон снимет с первоначальной цены [латекс] в 220 долларов[/латекс]. Задачи, связанные с процентами, будут иметь некоторую комбинацию этих трех величин для работы: процентов , сумма и основание . Процент имеет символ процента (%) или слово процент. В приведенной выше задаче [латекс]15\%[/латекс] — это процент от покупной цены. Базой является вся сумма или первоначальная сумма. В приведенной выше задаче «полная» цена гитары составляет [латекс] 220 долларов[/латекс], что является базовой. Сумма неизвестна и что нам нужно будет рассчитать.
Возможны три случая: недостающая сумма, недостающий процент или недостающая база. Давайте рассмотрим каждую возможность.
Решение суммы
При решении задачи на сумму в процентах вы будете умножать процент (в виде десятичной дроби) на основание. Обычно мы выбираем десятичное значение для процентов.
[латекс]\текст{процент}\cdot{\текст{база}}=\текст{количество}[/латекс]
Пример
Найти [латекс]50\%[/латекс] от [латекс]20 [/latex]
Решение:
Сначала определите каждую часть проблемы:
процентов: [латекс]50\%[/латекс] или [латекс].5[/латекс]
база: [латекс]20[/латекс]
количество: неизвестно
Теперь подставьте их в уравнение [латекс]\текст{процент}\cdot{\текст{база}}=\текст{количество}[/ латекс]
[латекс].5\cdot{20}= ?[/латекс]
[латекс].5\cdot{20}= 10[/латекс]
Следовательно, [латекс]10[/латекс] это количество или часть, которая составляет [латекс]50\%[/латекс] от [латекс]20[/латекс].
Пример
Что такое [латекс]25\%[/латекс] от [латекс]80[/латекс]?
Показать ответ
Попробуй
youtube.com/embed/jTM7ZMvAzsc?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Решение задачи на проценты
При решении задачи на проценты вы будете делить сумму на основание. Вышеупомянутое уравнение перестроено, и проценты вернутся в виде десятичной дроби, которую вы можете указать в форме, которую вам задают.
[латекс]\Large{\frac{\text{amount}}{\text{base}}}\normalsize=\text{percent}[/latex]
Пример
Сколько процентов [латекса]320[ /латекс] это [латекс]80[/латекс]?
Решение:
Сначала определите каждую часть проблемы:
процент: неизвестно
основание: [латекс]320[/латекс]
количество: [латекс]80[/латекс]
Теперь подставьте значения в уравнение [латекс] \Large{\frac{\text{amount}}{\text{base}}}\normalsize=\text{percent}[/latex]
[латекс]\large\frac{80}{320}\normalsize= ?[/latex]
[латекс]\large\frac{80}{320}\normalsize=.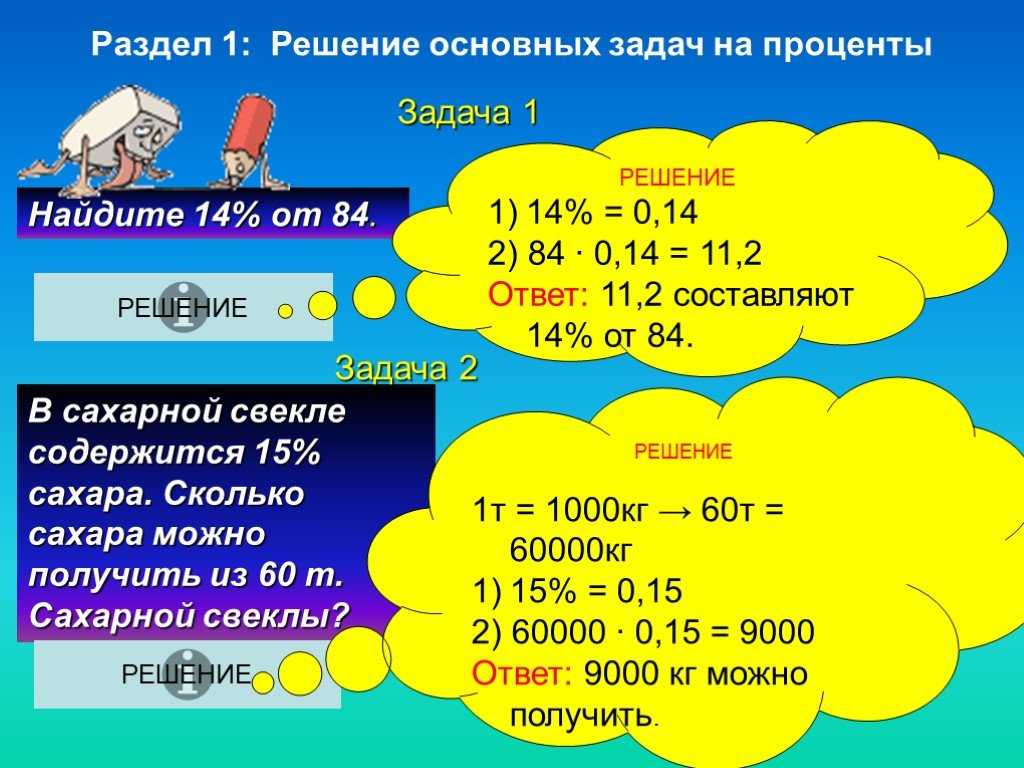 25[/latex]
25[/latex]
Следовательно, [латекс]80[/латекс] равен [латекс]25\%[/ латекс] из [латекс]320[/латекс].
ПОПРОБУЙТЕ
Решение для основания
При решении для основания в задаче на проценты вы разделите сумму на процент (в виде десятичной дроби или дроби). Уравнение выше перестроено, и вы найдете базу после подстановки значений.
[латекс]\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}[/latex]
EXample
[latex]60[/latex] [латекс]40\%[/латекс] от какого числа?
Решение:
Сначала определите каждую часть проблемы:
процентов: [латекс]40\%[/латекс] или [латекс].4[/латекс]
основание: неизвестно
количество: [латекс]60[/латекс]
Теперь подставьте значения в уравнение [латекс]\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}[/latex]
[latex]( 60)\div(. 4)=?[/latex]
4)=?[/latex]
[латекс](60)\div(.4)=150[/latex]
Следовательно, [латекс]60[/латекс] это [латекс] 40\%[/латекс] из [латекса]150[/латекс].
Пример
В статье говорится, что [латекс]15\%[/латекс] пожертвований некоммерческих организаций, около [латекс]30 000 долларов[/латекс] в год, поступают от индивидуальных доноров. Какова общая сумма пожертвований, которые получает некоммерческая организация?
Показать ответ
ПОПРОБУЙТЕ
Вот еще несколько процентных задач, которые вы можете попробовать.
попробуй
попробуй
попробуй
Проценты часто используются в нашей повседневной жизни, например чаевые, налог с продаж, скидки и проценты. Чтобы решить эти приложения, мы переведем базовое уравнение процентов, как и те, которые мы решали в предыдущих примерах в этом разделе. Как только вы переведете предложение в процентное уравнение, вы будете знать, как его решить.
Чтобы решить эти приложения, мы переведем базовое уравнение процентов, как и те, которые мы решали в предыдущих примерах в этом разделе. Как только вы переведете предложение в процентное уравнение, вы будете знать, как его решить.
пример
Дезон и его девушка наслаждались ужином в ресторане, и счет был [латекс]\текст{\$68,50}[/латекс]. Они хотят оставить чаевые [латекс]\текст{18%}[/латекс]. Если чаевые будут составлять [латекс]\текст{18%}[/латекс] от общего счета, сколько должны быть чаевые?
Решение
попробуй
В следующем видео мы покажем еще один пример определения размера чаевых в процентах.
пример
На этикетке хлопьев для завтрака Масао указано, что одна порция хлопьев содержит [латекс]85[/латекс] миллиграммов (мг) калия, что [латекс]\текст{2%}[/латекс] рекомендуемой дневной нормы. Какова общая рекомендуемая суточная доза калия?
Какова общая рекомендуемая суточная доза калия?
Показать ответ
попробуй
попробуй
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Советы по решению задач со словами в процентах
Проблемы со словами проверяют как ваши математические способности, так и навыки понимания прочитанного. Чтобы правильно ответить на них, вам нужно внимательно изучить вопросы. Всегда убедитесь, что вы знаете, о чем спрашивают, какие операции необходимы и какие единицы, если таковые имеются, вам нужно включить в свой ответ.
Удаление посторонних данных
Иногда текстовые задачи включают посторонние данные, которые не нужны для решения задачи. Например:
Ким выиграла 80 процентов игр в июне и 90 процентов игр в июле. Если она выиграла 4 игры в июне и сыграла 10 игр в июле, сколько игр Ким выиграла в июле?
Самый простой способ устранить лишние данные — определить вопрос; в данном случае: «Сколько игр Ким выиграла в июле?» В приведенном выше примере любая информация, не относящаяся к июлю, не нужна для ответа на вопрос. У вас осталось 90 процентов от 10 игр, что позволяет вам сделать простой подсчет:
У вас осталось 90 процентов от 10 игр, что позволяет вам сделать простой подсчет:
0.9*10=9 игр
Вычислить дополнительные данные
Дважды прочтите часть вопроса, чтобы убедиться, что вы знаете, какие данные вам нужны для ответа на вопрос:
В тесте из 80 вопросов Абель дал 4 неправильных ответа. Какой процент вопросов он ответил правильно?
Словесная задача дает вам только два числа, поэтому легко предположить, что вопросы включают эти два числа. Однако в этом случае вопрос требует, чтобы вы сначала вычислили другой ответ: количество вопросов, на которые Абель ответил правильно. Вам нужно будет вычесть 4 из 80, а затем вычислить процент разницы:
80-4=78, а 78/80*100=97,5 процента
Перефразируйте сложные задачи
Помните, что часто можно переставить задачи, чтобы упростить их. Это особенно полезно, если у вас нет под рукой калькулятора:
Джине нужно набрать не менее 92 процентов на выпускном экзамене, чтобы получить пятерку за семестр. Если на экзамене 200 вопросов, сколько вопросов Джине нужно ответить правильно, чтобы получить пятерку?
Если на экзамене 200 вопросов, сколько вопросов Джине нужно ответить правильно, чтобы получить пятерку?
Стандартным подходом было бы умножение 200 на 0,9.2: 200*0,92=184. Хотя это простой процесс, вы можете сделать его еще проще. Вместо того, чтобы находить 92 процента от 200, найдите 200 процентов от 92, удвоив это число:
92*2=184
Этот метод особенно полезен, когда вы имеете дело с числами с известными отношениями. Если, например, задача со словами требует найти 77 процентов от 50, вы можете просто найти 50 процентов от 77:
50 * 0,77 = 38,5 или 77/2 = 38,5
Счет для единиц
ответы в соответствующие единицы:
Кэсси работает с 7 утра до 4 вечера. каждый будний день. Если Кэсси отработала 82 % своей смены в среду и отработала 100 % других смен, какой процент недели она пропустила? Сколько всего времени она работала?
Сначала подсчитайте, сколько часов Кэсси работает в день с учетом полудня, затем за неделю:
4+(12-7)=9 9*5=45
Затем рассчитайте 82 процента от 9 часов:
0,82*9=7,38
Вычтите произведение из 9 для общего количества пропущенных часов:
9-7,38=1,62
Подсчитайте, какой процент недели она пропустила:
1,62/45*100=3,6 процента на временные приращения.

 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Курсы/ Кружки/ Факультативы
Курсы/ Кружки/ Факультативы