Решение системы уравнений примеры: Решение систем уравнений — метод как решить систему линейных уравнений

Решение системы уравнений в Excel

3459 16.10.2022 Скачать пример

Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.

В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:

Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.

Бита дороже мяча на 1 доллар.
Сколько стоит мяч?

Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 🙂 Но весьма скоро, я уверен, вы сообразите, что на самом деле всё не так примитивно и для получения ответа нужно решить простую систему уравнений (здесь b — это бита, а m — это мяч):

Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:

Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.

Способ 1. Матричные функции МУМНОЖ и МОБР

Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач.

В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.

Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).

Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):

Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:

1. Выделить диапазон для результатов — G7:H8
2. Ввести функцию =МОБР(B7:C8) в строку формул
3. Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter

Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т. е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):

Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.

Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:

Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.

Способ 2. Подбор надстройкой «Поиск решения» (Solver)

Принципиально другой способ решения подобных задач — это итерационные методы, т. е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.

В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins). 

Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:

Подготавливаем основу для оптимизации в Excel:

Здесь:

• В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных
  x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column). 
• В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
• В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.

Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:

• Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
• Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
• Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
• В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.

После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:

Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно

Поиск решения и нажав кнопку Параметры (Options).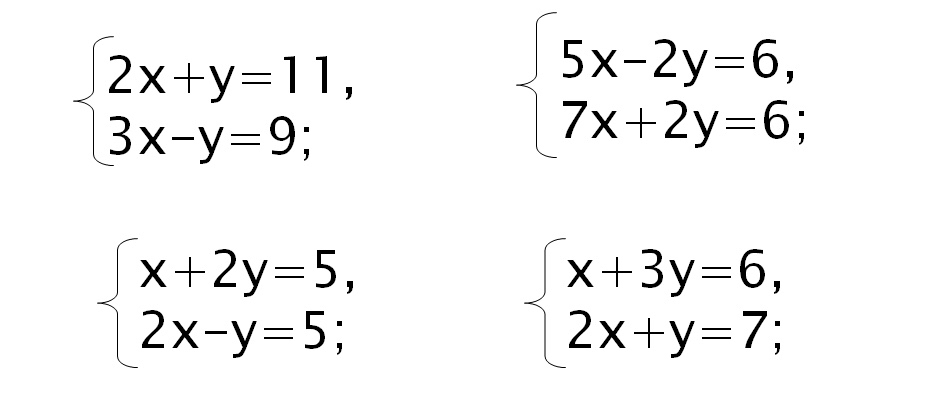

7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.

Комментарии преподавателя

Метод подстановки.

Су­ще­ству­ет несколь­ко ме­то­дов ре­ше­ния си­стем. Один из них метод под­ста­нов­ки. Рас­смот­рим при­мер.

При­мер 1:

Суть ме­то­да под­ста­нов­ки за­клю­ча­ет­ся в том, что в одном из урав­не­ний нужно вы­ра­зить одну пе­ре­мен­ную через вто­рую и под­ста­вить по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние.

В дан­ном слу­чае удоб­но вы­ра­зить х во вто­ром урав­не­нии:

Под­ста­вим по­лу­чен­ное вы­ра­же­ние в пер­вое урав­не­ние:

Пре­об­ра­зу­ем пер­вое урав­не­ние:

,

 ,

 ,

 

Под­ста­вим по­лу­чен­ное зна­че­ние во вто­рое урав­не­ние:

, ,

 

По­лу­ча­ем сле­ду­ю­щее ре­ше­ние си­сте­мы:

При­мер 2:

В дан­ном слу­чае неко­то­рая слож­ность за­клю­ча­ет­ся в том, что ис­ход­ную си­сте­му нужно пре­об­ра­зо­вать, чтобы была воз­мож­ность удоб­но и без оши­бок при­ме­нить метод под­ста­нов­ки. Для этого умно­жим оба урав­не­ния на шесть:

Вы­ра­зим у из пер­во­го урав­не­ния:

Под­ста­вим по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние и вы­пол­ним пре­об­ра­зо­ва­ния:

, ,

 ,

 

 

Под­ста­вим по­лу­чен­ное зна­че­ние в пер­вое урав­не­ние:

По­лу­ча­ем един­ствен­ное ре­ше­ние си­сте­мы, пара чисел:

Вывод:

на дан­ном уроке мы озна­ко­ми­лись с по­ня­ти­ем си­сте­мы двух ли­ней­ных урав­не­ний с двумя неиз­вест­ны­ми и одним из ме­то­дов ее ре­ше­ния – спо­со­бом под­ста­нов­ки. Мы ре­ши­ли при­ме­ры для по­ни­ма­ния и за­креп­ле­ния дан­ной тех­ни­ки.

Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10

Метод сложения.

Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.

Метод ал­геб­ра­и­че­ско­го сло­же­ния, как и метод под­ста­нов­ки, за­клю­ча­ет­ся в том, что из­на­чаль­но из двух урав­не­ний с двумя пе­ре­мен­ны­ми нужно по­лу­чить одно урав­не­ние с одной пе­ре­мен­ной. Рас­смот­рим метод ал­геб­ра­и­че­ско­го сло­же­ния на при­ме­ре:

При­мер 1:

 

За­да­на си­сте­ма двух ли­ней­ных урав­не­ний с двумя неиз­вест­ны­ми, и нужно найти такую пару х и у, чтобы при под­ста­нов­ке ее в урав­не­ния по­лу­чи­лись вер­ные чис­ло­вые ра­вен­ства.

Неслож­но за­ме­тить, что в пер­вом урав­не­нии у стоит с ми­ну­сом, а во вто­ром – с плю­сом, и если сло­жить эти урав­не­ния, то у уни­что­жит­ся, и мы по­лу­чим одно урав­не­ние с одной неиз­вест­ной:

+

По­лу­ча­ем:

Най­дем зна­че­ние х:

, 

Под­ста­вим зна­че­ние х во вто­рое урав­не­ние и най­дем у:

Ответ: (2,4; 2,2)

 

Об­ра­тим вни­ма­ние на то, что мы рас­смат­ри­ва­ем метод ал­геб­ра­и­че­ско­го сло­же­ния, зна­чит, урав­не­ния можно не толь­ко скла­ды­вать, но и вы­чи­тать. Рас­смот­рим при­мер:

При­мер 

При сло­же­нии урав­не­ний по­лу­чим:

, 

По­про­бу­ем вы­честь урав­не­ния, при­чем, вы­чтем пер­вое из вто­ро­го:

, 

Ответ: (5,5; 0,5)

 

Вывод:

на дан­ном уроке мы рас­смот­ре­ли новый метод ре­ше­ния си­стем двух ли­ней­ных урав­не­ний – метод ал­геб­ра­и­че­ско­го сло­же­ния. Мы ре­ши­ли несколь­ко при­ме­ров для за­креп­ле­ния дан­ной тех­ни­ки.

 

• Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
• Если прямые , являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
• Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
•  Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.

Примеры. Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Ответ: (4; 5).

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

Ответ: (-2; 5).

 

Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/metod-algebraicheskogo-slozheniya?konspekt&chapter_id=10

http://www.mathematics-repetition.com/6-klass-mathematics/6-9-1-reshenie-sistem-lineynh-uravneniy-grafitcheskim-sposobom.html

 

Источник видео: https://www.youtube.com/watch?v=VltC62A-Tt4

Решение системы уравнений – методы и примеры

К настоящему моменту вы получили представление о том, как решать линейные уравнения, содержащие одну переменную. Что, если бы вам представили множественных линейных уравнений, содержащих более одной переменной ? Набор линейных уравнений с двумя или более переменными известен как система уравнений .

Существует несколько методов решения систем линейных уравнений.

Эта статья научит , как решать линейные уравнения, используя обычно используемые методы , а именно замена и устранение.

Метод подстановки

Подстановка — это метод решения линейных уравнений, при котором переменная в одном уравнении выделяется, а затем используется в другом уравнении для решения оставшейся переменной.

Общие шаги для замены:

• Составьте подлежащее формулы для переменной в одном из данных уравнений.
• Подставьте значение этой переменной во второе уравнение».
• Решите уравнение, чтобы получить значение одной из переменных.
• Подставьте полученное значение в любое из уравнений, чтобы также получить значение другой переменной.

Решим пару примеров методом подстановки.

Пример 1

Решите приведенные ниже системы уравнений.

b = a + 2

a + b = 4.

Решение

Подставьте значение b во второе уравнение.

а + (а + 2) = 4

Теперь найдем а

Подставьте полученное значение a в первое уравнение.

b = a + 2

b = 1 + 2

b = 3

Следовательно, решение для двух уравнений: a = 1 и b = 3.

Пример 2

Решите следующие уравнения с помощью подстановки.
7x – 3y = 31 ——— (i)

9x – 5y = 41 ——— (ii)

Решение

Из уравнения (i),

7x – 3y = 31 = 31

Вычтите 7x из обеих частей уравнения 7x – 3y = 31, чтобы получить;

– 3y = 31 – 7x

3y = 7x – 31

3y/3 = (7x – 31)/3

Следовательно, y = (7x – 31)/3

Теперь подставим уравнение y = ( 7x – 31)/3 во второе уравнение:9x – 5y = 41

9x – 5 × (7x – 31)/3 = 41

Решение уравнения дает;

27x – 35x + 155 = 41 × 3

–8x + 155 – 155 = 123 – 155

–8x = –32

8x/8 = 32/8

x0 = 7 x в уравнении y = (7x – 31)/3, получаем;

y = (7 × 4 – 31)/3

y = (28 – 31)/3

y = –3/3

y = –1

Следовательно, решением этих систем уравнений является х = 4 и у = –1

Пример 3

Решите следующие системы уравнений:

2x + 3y = 9 и x – y = 3

Решите второе уравнение

x

.

х = 3 + у.

Теперь подставьте это значение x в первое уравнение: 2x + 3y = 9.

⇒ 2(3 + y) + 3y = 9

⇒ 6 + 2y + 3y = 9

y = ⅗ = 0,6

Подставляем полученное значение y во второе уравнение – y =3.

⇒ x = 3 + 0,6

x = 3,6

Таким образом, решение x = 3,6 и y = 0,6

• Приравнять коэффициенты данных уравнений путем умножения на константу.
• Вычесть общие коэффициенты новых уравнений с одинаковыми знаками и сложить, если общие коэффициенты имеют противоположные знаки,
• Решите уравнение, полученное в результате сложения или вычитания.
• Подставьте полученное значение в любое из уравнений, чтобы получить значение другой переменной.

.

4а+3а) +(5b – 5b) = 12 + 9

7а = 21

а = 21/7

а = 3

полученное значение а=3 подставить в уравнение первое уравнение 0

b = 0/5 = 0

Следовательно, решение a = 3 и b = 0.

Пример 5

Решите методом исключения.

2x + 3y = 9 ———–(i)

x – y = 3 ———–(ii)

Решение

Умножьте два уравнения на 2 и выполните вычитание.

2x + 3y = 9

(-)

2x – 2y = 6

-5y = -3

y = ⅗ = 0,6

Теперь подставим полученное значение y во второе уравнение: x – y = 3

x – 0,6 = 3

x = 3,6

Следовательно, решение: x = 3,6 и y = 0,6

 

метод упрощения. Примерка одежды в магазине помогает нам исключить варианты и решить, что купить. Мы исключаем пункты из списка дел в течение дня, чтобы упростить наши графики. В математике мы используем метод исключения для решения систем уравнений, чтобы исключить одну переменную и найти другую.

Этот пост объяснит процесс решения систем уравнений методом исключения.

Решение систем линейных уравнений методом исключения

Замена и исключение — два способа алгебраического решения систем линейных уравнений. В общем, подстановка является лучшим выбором, когда в одном уравнении есть изолированная переменная. Таким образом, при прочих равных условиях мы, вероятно, использовали бы замену, если бы наша система уравнений была:

y=1-x

х-5у=3,5

Итак, когда лучше использовать метод исключения? Мы могли бы использовать метод исключения для решения системы уравнений, если переписать уравнения, чтобы изолировать переменную, более сложно.

Рассмотрим следующую систему:

2x+5y=12,5

6x-5y=3,5

Понятно, что если мы попытаемся решить одно из этих уравнений относительно x или y, то получим дроби. Дроби могут усложнить процесс замены. Итак, с этой системой уравнений лучшим вариантом было бы решить систему уравнений методом исключения.

Заинтересованы в лицензии школы Альберта?

Что такое метод исключения?

Итак, как решать системы уравнений методом исключения? Давайте начнем наш обзор того, как решить систему уравнений методом исключения, со списка шагов.

1. Определите, какая переменная будет исключена. При необходимости перепишите одно или оба уравнения, чтобы коэффициенты этой переменной были обратными.
2. Объедините уравнения, используя сложение. Новое уравнение должно иметь только одну оставшуюся переменную.
3. Решите новое уравнение для оставшейся переменной.
4. Подставьте значение этой переменной в одно из исходных уравнений и решите.
5. Проверьте свою работу с помощью графика или замены.

Посмотрите это видео, чтобы получить полное представление о методе исключения в действии.

Начните заниматься Алгеброй 1 на Альберте прямо сейчас!

Далее давайте применим эти шаги к некоторым примерам метода исключения.

Решение систем уравнений методом исключения Примеры

Давайте подробнее рассмотрим приведенную ниже систему.

2х+5у=12,5

6x-5y=3,5

Во-первых, обратите внимание, что коэффициенты для членов y равны 5 и -5. Эти два числа являются аддитивными инверсиями , а это означает, что их сумма равна 0. Следовательно, если мы сложим эти уравнения, члены по y взаимно компенсируют друг друга.

Но является ли добавление уравнений законным средством решения системы уравнений? Рассмотрим Дополнительное свойство равенства , которое гласит:

  Если a=b, то a+c=b+c  . 

Мы собираемся использовать это свойство для решения систем линейных уравнений методом исключения.

Для начала давайте подумаем о втором уравнении в двух частях. Мы могли бы разделить каждую часть и переписать их следующим образом:

6x-5y=z\quad\text{ и }\quad z=3.5

Мы знаем, что эти утверждения верны, потому что 6x-5y=3,5. Следовательно, если одна часть этого уравнения равна z, то и другая равна z.

Теперь мы можем использовать аддитивное свойство равенства, чтобы переписать первое уравнение в нашей системе, 2x+5y=12,5, как:

2x+5y+{\color{red}{z}}=12,5+{\color {красный} {z}}

… а затем подставим наши значения z, чтобы получить:

2x+5y+{\color{red}{(6x-5y)}}=12,5+{\color{red}{(3,5)}}

Мы только что сложили два наших уравнения! Когда мы упростим наше новое уравнение, мы удалим член y, чтобы мы могли найти x.

2х+5у+6х-5у=12,5+3,5

 8x=16

 \dfrac{8x}{{\color{red}{8}}}=\dfrac{16}{{\color{red}{8}}}

х=2

Затем мы можем заменить x на 2 в одном из наших исходных уравнений и найти y.

6 {\ цвет {красный} {(2)}} -5y = 3,5

12-5лет=3,5

-5у=-8,5

у=1,7

Итак, решение нашей системы (2,1.7). Мы можем проверить нашу работу по графику, как показано ниже.

Заинтересованы в лицензии школы Альберта?

Решение систем уравнений методом исключения с умножением

Что произойдет, если коэффициенты переменной не являются аддитивными обратными в системе уравнений? Например, рассмотрим систему ниже.

4x-2y=5

7x-2y=9

Если мы добавим эти уравнения в том виде, в котором они есть сейчас, члены по оси y станут равными -2y+(-2y)=-4y, а члены по оси x станут равными 4x+7x=11x. Мы не будем исключать какие-либо переменные.

Однако, если мы умножим одно из уравнений на коэффициент -1, мы получим коэффициенты, что являются аддитивными обратными. Давайте попробуем: 

{\color{red}{-1}}(4x-2y)={\color{red}{-1}}(5)

-4x+2y=-5

Теперь мы можем добавить наши уравнения, чтобы исключить переменную y и найти x.

Чтобы решить другие системы уравнений методом исключения, нам нужно переписать оба уравнения, чтобы исключить переменную. Например, рассмотрим систему ниже.

3x-9y=6

2x-2y=8

Мы могли бы умножить первое уравнение на -2, а второе уравнение на 3, чтобы исключить x при сложении уравнений. Давайте используем этот процесс для решения системы методом исключения.

Шаг	Уравнения
1. Определите, какая переменная будет исключена. При необходимости перепишите одно или оба уравнения, чтобы коэффициенты этой переменной были обратными.	{\ color {red} {-2}} (3x-9y) = {\ color {red} {-2}} (6) -6x + 18y = -12 {\ color {red} {3 }}(2x-2y)={\color{red}{3}}(8) 6x — 6y = 24
2. Объедините уравнения, используя сложение. Новое уравнение должно иметь только одну оставшуюся переменную.	-6x + 18y + 6x — 6y = -12 + 24 (-6x + 6x) + (18y — 6y) = 12 12y = 12
3. Решите новое уравнение для оставшейся переменной.	12y \div 12= 12 \div 12 y = 1
4. Подставьте значение этой переменной в одно из исходных уравнений и решите.	2x-2y=8 2x-2({\color{red}{1}})=8 2x-2=8 2x=10 x=5
5. Проверьте свою работу по графику или замена.	3x-9y=6 3({\color{red}{5}})-9({\color{red}{1}})=6 15-9=6 6=6

Начните практиковать Алгебру 1 на Альберте прямо сейчас!

Более сложные системы уравнений с умножением

Наконец, мы столкнемся с системами, в которых необходимо более подробно переписать уравнения, чтобы исключить переменную. Например, рассмотрим систему ниже.

3x=4y-2

5x-2y=6

Перед добавлением этих уравнений нам нужно переместить член Y в противоположную сторону от знака равенства в первом уравнении и умножьте второе уравнение на -2.

3x — 4y =4y-2 — 4y \rightarrow 3x — 4y = -2

-2(5x-2y)=-2(6)\стрелка вправо -10x + 4y = -12

Теперь мы можем исключить y слагаемых и найти x.

Заинтересованы в лицензии школы Альберта?

Подводя итог, можно сказать, что ключом к эффективному переписыванию уравнений является выбор правильного коэффициента для умножения одного или обоих уравнений для создания аддитивных обратных уравнений. Аддитивные инверсии будут компенсировать друг друга и, таким образом, исключат эту переменную при добавлении уравнений.

Используйте ссылку здесь, чтобы получить доступ к большему количеству решений систем линейных уравнений путем исключения практических задач.

Решение систем уравнений методом исключения: ключи для запоминания

• Мы используем исключение, чтобы исключить одну переменную в системе с двумя переменными.

  No related posts.