Вы можете решать здесь все виды трансцендентых уравнений с помощью онлайн калькулятора с подробным решением!
Приведём примеры трансцедентых уравнений, решаемых данным сервисом:
Дано уравнение $$- \sin{\left (x \right )} + \cos^{2}{\left (x \right )} = 1$$ преобразуем $$- \left(\sin{\left (x \right )} + 1\right) \sin{\left (x \right )} = 0$$ $$- \sin^{2}{\left (x \right )} — \sin{\left (x \right )} = 0$$ Сделаем замену $$w = \sin{\left (x \right )}$$ Это уравнение видаa*w^2 + b*w + c = 0
Квадратное уравнение можно решить с помощью дискриминанта.
Корни квадратного уравнения: $$w_{1} = \frac{\sqrt{D} — b}{2 a}$$ $$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$ где D = b^2 — 4*a*c — это дискриминант.
Т.к. $$a = -1$$ $$b = -1$$ $$c = 0$$ , то D = b^2 — 4 * a * c = (-1)^2 — 4 * (-1) * (0) = 1
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b — sqrt(D)) / (2*a)
или
$$w_{1} = -1$$
$$w_{2} = 0$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
Дано уравнение
$$\sin{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
Или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (-1 \right )}$$
$$x_{1} = 2 \pi n — \frac{\pi}{2}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (w_{2} \right )}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (0 \right )}$$
$$x_{2} = 2 \pi n$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (w_{1} \right )} + \pi$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (-1 \right )} + \pi$$
$$x_{3} = 2 \pi n + \frac{3 \pi}{2}$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (w_{2} \right )} + \pi$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (0 \right )} + \pi$$
$$x_{4} = 2 \pi n + \pi$$
Ещё для примера, уравнения содержащие:
являются трансцедентными уравнениями.
Как решить трансцендентные уравнения
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Трансцендентное уравнение представляет собой уравнение, которое состоит из трансцендентной функции (иррациональные, логарифмические, показательные, тригонометрические и обратные тригонометрические) от неизвестного (переменного), например уравнения:
\[\sin x + \log_6 x=x\]
Решить данного рода уравнения означает:
1. Определить все системы значений параметров, при которых данное уравнение имеет решение.
Так же читайте нашу статью «Решить систему двух уравнений онлайн решателем»
2. Определить все решения для каждой определенной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Трансцендентные уравнения с параметрами состоят их множества разнообразных трансцендентных функций, именно поэтому способы решения данных уравнений в большей степени зависят от свойств функций. Проанализировав исходные данные, необходимо проверить уравнения на решение стандартными математическими способами.
Где можно решить трансцендентное уравнение онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Решение квадратных уравнений
Как бы кто ни говорил, но тема квадратных уравнений – это база всей школьной программы. Читая дальше, вы поймете почему.
Решая линейные уравнения, требуется лишь навык применения арифметических операций. Даже решать систему линейных уравнений несложно, все сводится к сложению, вычитанию или раскрытию скобок, когда подставляем одно уравнение в другое. И так далее.
Иное дело, когда возрастает старшая степень неизвестной переменной, и первый вид таких уравнений как раз называется квадратным уравнением, когда неизвестная переменная представлена во второй степени.
Есть прямая связь квадратных уравнений с тем, что мы можем наблюдать вокруг нас. Тема квадратных уравнений легкая, но очень важная и требует полного изучения, однако, этим пренебрегают ученики, да и учителя тоже.
Например, полет снаряда, выпущенного из орудия, летит по траектории, описываемой квадратным уравнением, и называется параболой. Парабола имеет вершину и две ветви, расположенные зеркально, что напоминает подкову.
Где встречаются квадратные уравнения
На практике квадратные уравнения встречаются практически во всех сферах жизненной деятельности человека, от науки до искусства. В школьной программе обязательно в алгебре, геометрии со стереометрией, тригонометрии, при упрощении выражений и так далее. Разумеется, не только в математике. В химии, физике, экономике, биологии и других науках без квадратных уравнений никак не обойтись.
Более того, в некоторых задачах необходимо оперировать со значениями, являющимися корнями квадратного уравнения, и опять-таки требуется находить корни. Если нахождение корней квадратного уравнения является промежуточным действием, например, необходимо использовать только сумму корней или их произведение, то глядя на уравнение, это сразу видно. Но опять же это нужно знать!
График квадратного уравнения
Как вы уже знаете графиком квадратного уравнения является парабола. По виду уравнения можно легко определить расположение ее вершины и направление ветвей относительно системы координат.
Парабола может либо пересекать ось абсцисс (в одной или двух точках), либо не пересекать ее. Во втором случае говорят, что квадратное уравнение не имеет действительных решений (корней). Если же график параболы пересекает ось абсцисс, то корней два или один как минимум.Запомните! У квадратного уравнения всегда имеются либо два разных, либо один кратности два корень, потому что уравнение второй степени. В том случае, когда корни не принадлежат полю действительных чисел, они находятся в поле комплексных чисел. Если вы еще не слышали про комплексные числа, просто примите это к сведению.
Что такое дискриминант
Общий вид квадратного уравнения следующий:
a*x2 + b*x + c = 0
Умножим обе части уравнения на 4*a, прибавим b2 к обеим частям и применим формулу сокращенного умножения «квадрат суммы». Перенесем 4*a*c в правую часть уравнения. В результате получим:
(2*a*x + b)2 = b2
Отсюда очевидно, что при b2 – 4*a*c действительных корней нет, потому что нет такого числа, которое в квадрате давало бы отрицательное.
При b2 – 4*a*c = 0 только один кратный корень.
И третий случай, при b2 – 4*a*c > 0 уравнение имеет два разных корня.
Рассмотрим последний случай, когда уравнение имеет два разных корня x1 и x2. Соответственно график параболы пересекает ось X в двух разных точках.
Координата вершины параболы определяется значением x = –b/2a.
Так как график параболы симметричен, то оба корня равноудалены от линии, проходящей через ее вершину.
Отсюда очевидно, что чем больше значение дискриминанта, тем дальше друг от друга располагаются корни уравнения. В этом заключается геометрический смысл дискриминанта.
Другими словами, значение дискриминанта напрямую указывает на удаленность корней уравнения друг от друга на числовой оси.
Так вот, удаленность корней друг от друга и называются дискриминантом, а формула, которую дают в школе под соусом «дискриминант», всего лишь выражает этот факт.
Как найти корни квадратного уравнения
Самое интересное это поиск корней уравнения. Есть несколько методов их нахождения, перечислим более известные.1. Первый из них, самый известный всем школьникам, описанный выше, – это поиск по формуле квадратного уравнения, используя значение дискриминанта.
2. Принято отдельно считать метод выделения полного квадрата. Но как мы видели из поиска дискриминанта, это вытекает из первого способа.
3. Другой популярный способ – это разложение уравнения на множители, когда его приводят к виду (x+A)*(x+B)=0. Частный случай такого уравнения x*(x+A)=0 с нулевым корнем.
4. Еще один не менее важный способ – графический. В этом методе исследуют график параболы и находят ее пересечение с осями координат.
5. Очень удобный способ определения корней квадратного уравнения и часто применяемый в практических задачах – применение теоремы Виета.
Рассмотрим пример определения корней по теореме Виета
Пусть дано уравнение x2 — 5 x + 6 = 0
Согласно этой теореме, сумма корней есть коэффициент перед x, но с противоположным знаком, а произведение корней – это значение свободного члена квадратного уравнения.
Очевидно, что x1=2, а x2=3, так как x1+x2=2+3=5, а x1*x2=2*3=6
Калькулятор решения квадратных уравнений
С нашим калькуляторе вы без проблем решите любое квадратное уравнение онлайн. Он полезен как для самопроверки, таки и для изучения этой темы, поскольку пошагово покажет весь ход решения до определения корней.
В калькуляторе предусмотрены различные варианты решения квадратного уравнения. Это по формуле через дискриминант, с помощью выделения полного квадрата и методом разложения на множители.
Каждый способ решения хорош по-своему, а главное помогает школьникам лучше усвоить столь важную тему как решение квадратных уравнений.
Желаем успехов!
UPD: Теперь вы можете вводить условия задачи Коши прямо в форму:
Рассмотрим пример решения задачи Коши с помощью онлайн калькулятора «Контрольная-работа.Ру».
Внимание! Следуя этому примеру и подробно и внимательно читая вы сможете решить и свою задачу, просто следуя тем же шагам!
Возьмём задачу из контрольной «Решить задачу Коши для дифференциального уравнения второго порядка
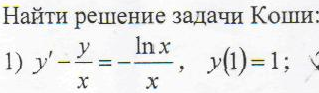
Для того, чтобы решить данную задачу откройте сервис решения дифференциальных уравнений онлайн
и введите в форму левую часть уравнения y’ — y/x
а в правую часть уравнения: -lnx/x
как на картинке:
Нажимаем кнопку «Решить дифференциальное уравнение!«
Видим ответ для этого дифф. ур-ния:
y(x) == C1*x + log(x) + 1
Но как вы знаете, это ещё не решение задачи Коши, это всего лишь решение дифференциального уравнения.
Теперь по начальным условиям y(1) = 1 надо найти C1.
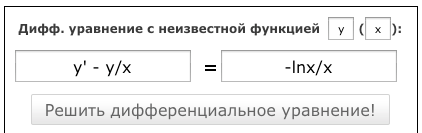
Для этого воспользуемся сервисом по решению обычных уравнений онлайн
Вобъём в форму обычных уравнений в правую часть уравнения c*x + log(x) + 1, а в левую y
А также укажем, что уравнение с неизвестной c=C1
На рис. всё это видно:
Нажимаем кнопку «Решить уравнение!«
Получаем ответ для C1
y - log(x) - 1
──────────────
x Но и это ещё не всё.
Надо указать, что y = 1 и x = 1 (т.к. y(1)=1). Подставляем по той же ссылке как на рис. ниже:
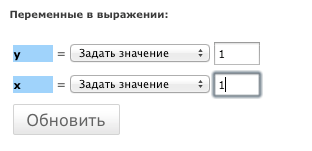
Нажимаем кнопку «Обновить«
И получаем окончательный ответ для C1:
C1 = c = 0
Подставляем это C1 в решение дифф. уравнения и мы получим решение нашей задачи Коши:
y(x) = C1*x + log(x) + 1 = 0*x + log(x) + 1 = log(x) + 1
Данный онлайн калькулятор позволяет вычислять дифференциальные уравнения практически любого типа и порядка: линейные дифференциальные уравнения, с разделяемыми или неразделяемыми переменными, уравнения Бернулли и т.д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям.
По умолчанию в уравнении функция y является функцией от переменной x. Однако вы можете задать своё обозначение переменной, если напишете, например, y(t) в уравнении, то калькулятор автоматически распознает, что y есть функция от переменной t. С помощью калькулятора вы сможете решать дифференциальные уравнения любой сложности и вида: однородные и неоднородные, линейные или нелинейные, первого порядка или второго и более высоких порядков, уравнения с разделяющимися или не разделяющимися переменными и т.д. Решение диф. уравнения даётся в аналитическом виде, имеет подробное описание. Дифференциальные уравнения очень часто встречаются в физике и математике. Без их вычисления невозможно решать многие задачи (особенно в математической физике).
Одним из этапов решения дифференциальных уравнений является интегрирование функций. Есть стандартные методы решений дифференциальных уравнений. Необходимо привести уравнения к виду с разделяющимися переменными y и x и отдельно проинтегрировать разделенные функции. Чтобы это сделать иногда следует провести определенную замену.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
Смотрите также
∫ Решение интегралов онлайн с подробным решением
Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно!
Это онлайн сервис в один шаг:
- Ввести подинтегральное выражение (подинтегральную функцию)
Перейти: Онлайн сервис «Неопределенный интеграл» →
Это онлайн сервис в один шаг:
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний предел для интеграла
- Ввести верхний предел для интеграла
Перейти: Онлайн сервис «Определенный интеграл» →
- Ввести подинтегральное выражение (подинтегральную функцию)
- Введите верхнюю область интегрирования (или + бесконечность)
- Ввести нижнюю область интегрирования (или — бесконечность)
Перейти: Онлайн сервис «Несобственный интеграл» →
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний и верхний пределы для первой области интегрирования
- Ввести нижний и верхний предел для второй области интегрирования
Перейти: Онлайн сервис «Двойной интеграл» →
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний и верхний пределы для первой области интегрирования
- Ввести нижний и верхний предел для второй области интегрирования
- Ввести нижний и верхний предел для третьей области интегрирования
Перейти: Онлайн сервис «Тройной интеграл» →
Данный сервис позволяет проверить свои вычисления на правильность
Возможности
Таблица интегралов
Вы также можете воспользоваться таблицей интегралов, чтобы самостоятельно посчитать любой интеграл, перейти:
90000 Solving of differential equations online for free 90001 90002 90003 90004
90005
90006 90007 Enter the differential equation: 90008 90009
90010
90005
90006
90013 Example: y » + 9y = 7sin (x) + 10cos (3x) 90014
90009
90010
90005
90006 90007 Enter the Cauchy problem (optional): 90008 90009
90010
90005
90006
90025 Example: y (0) = 7, y ‘(6) = — 1
90009
90010
90028 90029 90030
90005
90032 x 90009 90034 y 90009 90036 π 90009 90038 e 90009 90040 90041 1 90009 90043 2 90009 90045 3 90009 90047 ÷ 90009 90040 90050 Trig func 90009
90010
90005
90054 a 90055 2 90056 90009 90058 a 90055 b 90056 90009 90062 a 90063 b 90064 90009 90066 exp 90009 90068 4 90009 90070 5 90009 90072 6 90009 90074 × 90009 90076 90013 delete 90014 90009
90010
90005
90082 (90009 90084) 90009 90086 | a | 90009 90088 ln 90009 90090 7 90009 90092 8 90009 90094 9 90009 90096 — 90009 90098 ↑ 90009 90100 ↓ 90009
90010
90005
90104 √ 90009 90106 90055 3 90056 √ 90009 90110 C 90009 90112 log 90063 a 90064 90009 90116 0 90009 90118.90009 90006 90121 ↵ 90122 90009 90124 + 90009 90126 ← 90009 90128 → 90009
90010
90028 90030
90005
90006 TRIG: 90009 90136 sin 90009 90138 cos 90009 90140 tan 90009 90142 cot 90009 90040 90145 csc 90009 90147 sec 90009 90040 90050 Back 90009
90010
90005
90006 INVERSE: 90009 90156 arcsin 90009 90158 arccos 90009 90160 arctan 90009 90162 acot 90009 90164 acsc 90009 90166 asec 90009 90076 90013 delete 90014 90009
90010
90005
90006 HYPERB: 90009 90176 sinh 90009 90178 cosh 90009 90180 tanh 90009 90182 coth 90009 90032 x 90009 90036 π 90009 90098 ↑ 90009 90100 ↓ 90009
90010
90005
90006 OTHER: 90009 90196 ‘90009 90198, 90009 90034 y 90009 90202 = 90009 90204 <90009 90206> 90009 90126 ← 90009 90128 → 90009
90010
90028 90013 This calculator for solving differential equations is taken from Wolfram Alpha LLC.All rights belong to the owner! 90014
90216 Solving Differential Equations online 90217
90013 This online calculator allows you to solve differential equations online. Enough in the box to type in your equation, denoting an apostrophe ‘derivative of the function and press «Solve the equation». And the system is implemented on the basis of the popular site WolframAlpha will give a detailed solution to the 90219 differential equation 90220 is absolutely free. You can also set the Cauchy problem to the entire set of possible solutions to choose private appropriate given initial conditions.Cauchy problem introduced in a separate field. 90014
90216 Differential equation 90217
90013 By default, the function equation 90007 y 90008 is a function of the variable 90007 x 90008. However, you can specify its marking a variable, if write, for example, y (t) in the equation, the calculator will automatically recognize that 90007 y 90008 is a function of the variable 90007 t 90008. Using a calculator, you will be able 90007 to solve differential equations 90008 of any complexity and types: homogeneous and non-homogeneous, linear or non-linear, first-order or second-and higher-order equations with separable and non-separable variables , etc.The solution diffusion. equation is given in closed form, has a detailed description. Differential equations are very common in physics and mathematics. Without their calculation can not solve many problems (especially in mathematical physics). 90014
90013 One of the stages of solutions of differential equations is integration of functions. There are standard methods for the solution of differential equations. Should be brought to the form of the equation with separable variables x and y, and integrate the separate functions separately.To do this sometimes to be a replacement. 90014
.90000 python — sympy: How to solve this system of transcendental equations? 90001
Stack Overflow 90002
90003
Products
90004 90003
Customers
90004
90003
Use cases
90004
90009
90010
90003
Stack Overflow
Public questions and answers
90004
90003
Teams
Private questions and answers for your team
90004
90003
Enterprise
Private self-hosted questions and answers for your enterprise
90004
90003
Jobs
Programming and related technical career opportunities
90004
90003
Talent
Hire technical talent
90004
90003
Advertising
Reach developers worldwide
90004 90009 .90000 Newest ‘transcendental-equation’ Questions — Stack Overflow 90001
Stack Overflow 90002
90003
Products
90004 90003
Customers
90004
90003
Use cases
90004
90009
90010
90003
Stack Overflow
Public questions and answers
90004
90003
Teams
Private questions and answers for your team
90004
90003
Enterprise
Private self-hosted questions and answers for your enterprise
90004
90003
Jobs
Programming and related technical career opportunities
90004
90003
Talent
Hire technical talent
90004
90003
Advertising
Reach developers worldwide
90004 90009
90024 Loading … 90025 90002
90003 90004 90003
Log in
Sign up 90004 90031
90032
current community
90033
90034
90003
Stack Overflow
help
chat 90004
90003
Meta Stack Overflow 90004
90039 90024
90032
your communities 90033 90025
90004 90009.