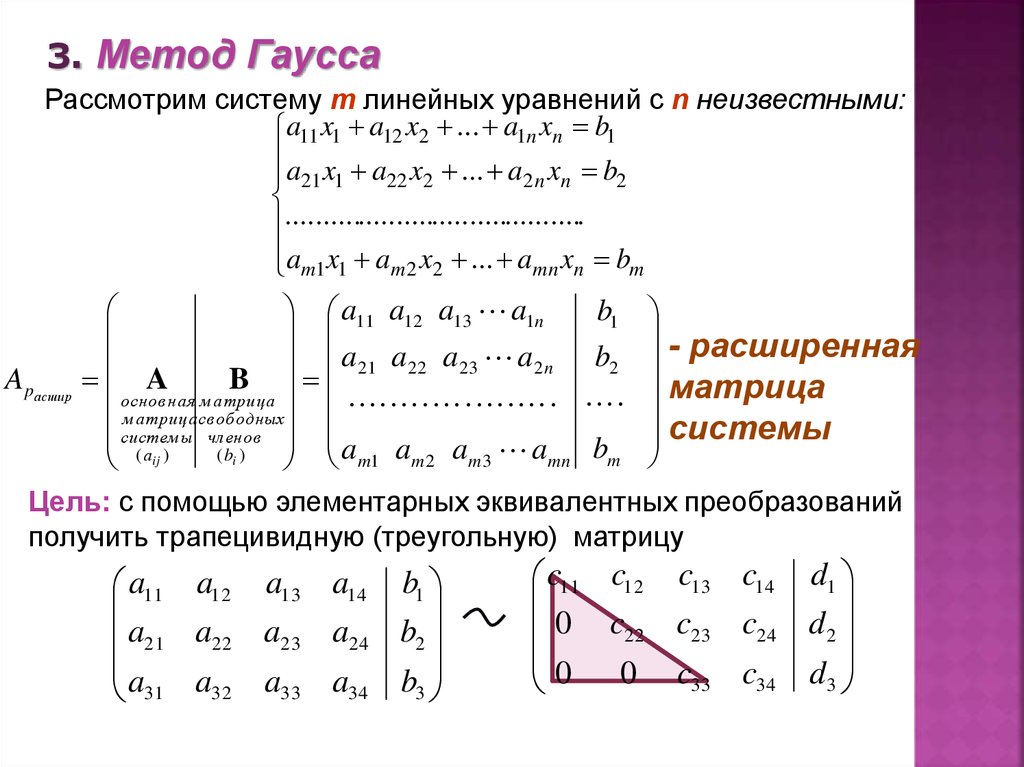
Решение уравнений по гауссу онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Решение уравнений методом Гаусса онлайн калькулятор

Карл Фридрих Гаусс — немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса позволяет максимально легко и быстро решить систему линейных алгебраических уравнений (СЛАУ). Успех данного метода заключается в последовательном исключении неизвестных из уравнений. Сегодня решить систему алгебраических уравнений онлайн методом Гаусса можно с помощью специальных решательов, но ниже мы разберем решение системы линейных уравнений, чтобы наглядно на примере увидеть все его достоинства.

Так же читайте нашу статью «Решить уравнение матричным способом онлайн решателем»

Допустим, дана система линейных уравнений:

\[\left\{\begin{matrix} 2\cdot x_1+4\cdot x_2+1\cdot x_3 = 36\\ 5\cdot x_1 + 2 \cdot x_2 +1 \cdot x_3 =47\\ 2\cdot x_1 + 3\cdot x_2 + 4 \cdot x_3 = 37 \end{matrix}\right.\]

Представим ее в матричной форме:

\[\begin{bmatrix} 2 & 4 & 1\\ 5 & 2 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 36\\ 47\\ 37 \end{bmatrix}\]

Выберем строку с максимальным коэффициентом \[a_i1\] и меняем ее с первой.

\[\begin{bmatrix} 5 & 2 & 1\\ 2 & 4 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 47\\ 36\\ 37 \end{bmatrix}\]

Нормируем уравнения относительно коэффициента при \[x_1\]:

\[\begin{bmatrix} 1 & \frac{2}{5} & \frac{1}{5}\\ 2 & \frac{4}{2} & \frac{1}{2}\\ 2 & \frac{3}{2} & \frac{4}{2} \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} \frac{47}{5}\\ \frac{36}{2}\\ \frac{37}{2} \end{bmatrix} \]

\[\begin{bmatrix} 1 & 0. 4 & 0.2\\ 1 & 2 & 1\\ 1 & 1.5 & 2 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 9.6\\ 9.1 \end{bmatrix}\]

Вычитаем 1 уравнение из 2 и 3:

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Выбираем строку с наибольшим коэффициентом при \[a_i2\] (уравнение 1 не рассматривается) и перемещаем ее на место 2.

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Нормируем 2 и 3 уравнения относительно коэффициента при \[x_2\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 1 & 1.636 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9. 4\\ 5.375\\ 8.272 \end{bmatrix}\]

Вычитаем уравнение 2 из 3

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 0 & 1.4489 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 2.897 \end{bmatrix}\]

Нормируем уравнение 3 относительно коэффициента при \[x_3\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.166\\ 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.333\\ 2 \end{bmatrix}\]

Откуда получаем \[x_3=2\]. Подставляем полученное значение в уравнения 2 и 1 получаем

\[x_2 = 5.333 — 0.1666 \cdot 2 = 5.333 — 0.333 =5\]

\[x_1+0.4 \cdot x_2 = 9.4 — 0.2 \cdot 2 = 9.4 — 0.4=9\]

Подставляя полученное значение \[x_2=5\] в уравнение 1, найдем

\[x_1 = 9 — 0.4 \cdot 5 = 9 — 2 = 7\]

Таким образом, решением системы уравнений будет вектор

\[x =\begin{bmatrix} 7 & 5 & 2 \end{bmatrix}^T\].

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Как решить уравнение Гаусса онлайн с решением

Карл Фридрих Гаусс — немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса идеально подходит для решения систем линейных уравнений, поскольку он имеет большее количество преимуществ по сравнению с другими методами, а именно:

— универсальность;

— не требует проверки системы на совместимость;

— минимальное количество математических операций.

Так же читайте нашу статью «Решить неравенство онлайн решателем»

Если возникли сомнения касательно конечного результата, то всегда можно узнать онлайн решение уравнения методом Гаусса и сравнить ответы.

Решим следующее уравнение методом Гаусса:

\[\left\{\begin{matrix} x_1+2x_2+3x_3-2_x4=1\\ 2x_1-x2-2x_3-3x_4=2\\ 3×1+2x_2-x_3+2x_4=-5\\ 2x_1-3x_2+2x_3+x_4=11 \end{matrix}\right.\]

Составляем расширенную матрицу системы

\[\begin{pmatrix} 1&2&3&-2\\ 2&-1&-2&-3\\ 3&2&-1&2\\ -2&-3&2&1 \end{pmatrix} \begin{pmatrix} 1&2&3&-2\\ 0&-5&-8&1\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\]

Далее необходимо с помощью второго уравнения исключить переменную \[x_2\] из:

\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\]

Сделаем собственно исключение переменной\[ x_2\] из 3 и 4 уравнений. Для этого к третьей строке прибавим вторую, умноженную на \[\frac{1}{4},\] а к четвёртой — вторую, умноженную на\[ \frac{7}{1}.\]

\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix} \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&-18&54 \end{pmatrix}\]

Теперь с помощью третьего уравнения исключим переменную \[x_3\] из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на \[ -\frac{18}{18}=-1\]. Получаем расширенную матрицу трапециевидной формы.

\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&0&18 \end{pmatrix}\]

Заданная система эквивалентна, таким образом, следующей:

\[ \left\{\begin{matrix} x_1+2x_2+3x_3-2x_4=1\\ x_2-2x_3+7x_4=-8\\ -18x_3+36x_4=-40\\ 18x_4-7 \end{matrix}\right.\]

Следовательно, полученная и данная системы являются совместными и определёнными. Искомое решение находим «с конца». Из четвёртого уравнения имеем

\[x_4=-\frac{7}{18}\]

Это значение подставляем в третье уравнение системы и получаем

\[-18x_3+36(-\frac{7}{18})=-40\]

откуда

\[x_3=\frac{13}{9}\]

Далее, подставляем значения\[ x_3\]и \[x_4\] во второе уравнение системы:

\[x_2=2\frac{13}{9}+7(-\frac{7}{18})-8\]

т.е.

\[x_2=-\frac{43}{18},\]

Наконец, подстановка значений

\[x_1+2(-\frac{43}{18})+3(\frac{13}{9})-2(-\frac{7}{18})=1\]

Получаем:

\[x_1=\frac {2}{3}\]

Итак, данная система уравнений имеет единственное решение \[(x_1=\frac {2}{3}, x_2=-\frac{43}{18}, x_3=\frac{13}{9}, x_4=-\frac{7}{18})\].

Решить систему матричных уравнений онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе.

Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Калькулятор функции ошибки

| Калькулятор ERF

Создано Анной Щепанек, доктором философии

Отредактировано Домиником Черниа, доктором философии и Джеком Боуотером

Последнее обновление: 28 октября 2022 г.

Содержание:

• Что такое функция ошибок?
• Обратная функция ошибки
• Как рассчитать erf с помощью этого калькулятора функции ошибки?
• Как рассчитать erf вручную?
• Таблица функций ошибок

Добро пожаловать в калькулятор функций ошибок ! Это поможет вам вычислить значения четырех функций из семейства erf:

• Сама функция ошибки;
• Дополнительная функция ошибки;
• Обратная функция ошибки; и
• Обратная дополнительная функция ошибки.

Если вы не уверены, что такое функция ошибки Гаусса, не волнуйтесь! Если вы прокрутите вниз, вы найдете все необходимые определения и графики, а также краткое объяснение того, почему функция ошибки имеет значение. В качестве бонуса мы покажем вам, как (приблизительно) рассчитать erf вручную! Наконец, в самом низу страницы вы можете найти таблицу функций ошибок. 92)\textrm{d}terf(x)=π

2​∫0x​exp(−t2)dt

На графике ниже мы видим, что erf является нечетной сигмовидной функцией.

Geek3, CC BY 3.0, через Wikimedia Commons. вероятность того, что Z попадает в интервал [−x, x] равно erf(x) , где мы предполагаем, что x неотрицательно. Как следствие, функция ошибок используется во многих различных вычислениях, в частности, в тех, с которыми вы можете столкнуться в следующих инструментах Omni:

• калькулятор p-значения;
• Калькулятор доверительных интервалов; и
• Калькулятор критических значений.

Дополнительная функция ошибки

Дополнительная функция ошибки, чаще всего обозначаемая как erfc 92)\textrm{d}terfc(x)=π

​2​∫x∞​exp(−t2)dt

В статистике дополнительная функция ошибки erfc(x) , где предполагается, что x является неотрицательным, описывает вероятность того, что случайная величина Z , следующая нормальному распределению Гаусса со средним значением 0 и дисперсией 0,5 , попадает за пределы интервала [−x, x].

Обратная функция ошибок

Как видно из графика функции ошибок, если 9{-1}(1-x).erfc-1(x)=erf-1(1-x).

Как рассчитать erf с помощью этого калькулятора функции ошибок?

Поскольку функция ошибок не является элементарной функцией (как и три другие функции, которые мы определили выше с помощью erf ), найти их значения для заданного аргумента x непросто.

К счастью, калькулятор erf от Omni здесь, чтобы помочь!

1. В поле mode выберите, какую из четырех функций из семейства erf вы хотите рассчитать.

2. Введите значение аргумента , при котором вы хотите оценить функцию.

3. Наш калькулятор функции ошибок немедленно возвращает ответ . Наслаждаться!

Как рассчитать erf вручную?

Что, если однажды вам понадобится определить функцию ошибки Гаусса без специального калькулятора под рукой? Ваша ситуация не безнадежна. Есть несколько хороших способов приблизить erf к . Отметим два из них. 97}{42} \!+\! \ldots\! \верно) \end{align*}erf(x)​=π

​2​n=0∑∞​(2n+1)n!(−1)nx2n+1​=π

​2​(x−3x3 ​+10x5​−42x7​+…)​

Справедливо для всех действительных аргументов x . В практических приложениях нужно вычислять частичную сумму этого ряда, т.

е. сумму нескольких начальных членов. Чем больше, тем лучше приближение.

2. Оказывается, что соответствующим образом преобразованная циклометрическая (обратно-тригонометрическая) функция arctan может служить неплохим приближением функции ошибок: 94))erf(x)≈π2​arctan(2x(1+x4))

   На приведенном ниже графике показаны эти две функции, чтобы вы могли видеть, насколько хороша аппроксимация.

   Функция ошибки erf (красный) и ее приближение арктангенса (синий).

   Таблица функций ошибок

   Поскольку erf является специальной функцией и не может быть легко вычислена без специального калькулятора, существует давняя традиция табулирования ее значений. Если вам когда-нибудь понадобится такая таблица, мы приводим ее ниже. Он охватывает споры между 0 и 3 . Для отрицательных аргументов вам нужно использовать тот факт, что erf является нечетной функцией, то есть что erf(-x) = -erf(x) .

   9023 02 0
   9 0,4
   4 0,4 ​​02403 900 4
   7 30220

   002 0,6

   9
   02330 80237 90 3
   3
   0237

   1,3

   7

   43 0,4 7

   0,95228512

   70
   90,2370003
   0 502
   307

   2 0,0000 40

   x	erf(x)	erfc(x)
   0	1
   0,01	0,011283416	0,988716584
   0,02	0,022564575
   0,03	0,033841222	0,966158778	3
   0,045111106	0,954888894
   0,05	0,056371978	0,943628022
   0,06	0,067621594	0,	08 2 4032908 0233
   0,07	0,07885772	0,92114228
   0,0126	0,909921874
   0,09	0,101280594	2 0,098719406
   0,1	0,112462916	0,8875203084 3	0,2 ​​	0,222702589	0,777297411
   30	0, 7 0,328626759	0,671373241
   0,4	0,428392355	0,5451 03
   0,5	0,520499878	0,479500122
   0,603856091	0,396143909
   0,7 3 0,7 3 . 677801194	0,322198806
   0,8	0,742100965	0,2578
   0,9	0,7962	0,203091788
   0,842700793	0,157299207
   1,1	0,11979493
   1,2	0,910313978	0,089686022	0,934007945	0,065992055
   0,04771488
   1,5	2 0,94661002 0,94661002 37 0,033894854
   1,6	0,976348383	0,023651617
   0,9837
   0,016209541
   1,8	0,0108
   1,9	0,9927 209571
   2	0,995322265	0,004677735
   2,5	0,999593048	0,000406952
   3	907 2 7,99	0,00002209
   3,5	0,999999257

   Анна Щепанек , PhD

   erf(x)

   Ознакомьтесь с 40 похожими алгебраическими калькуляторами 🔡

   Уравнение абсолютного значенияНеравенство абсолютного значенияСложение и вычитание многочленов… 37 more

   Гауссовский онлайн калькулятор алгебры бесплатно

   • Выражение
   • Уравнение
   • Неравенство
   • Связаться с нами
   • Упростить0 910 0 Расширить 0
   • GCF
   • LCM
   • Решить
   • График
   • Система
   • Решение
   • График
   • Система
   • Математический решатель на вашем сайте

   Наших пользователей:

   Как ни гордилась моя мама каждый раз, когда я видел, как она подбадривает меня после того, как я пробежал тачдаун с 5 ярдов, она всегда так же беспокоилась о моих оценках.

   Она сказала, что если я не подниму свои оценки, никто никогда не даст мне стипендию, независимо от того, сколько ярдов я наберу. Даже когда мой тренер показал мне вашу программу, я не захотел в ней участвовать. Но это начало обретать смысл. Теперь я занимаюсь алгеброй так же уверенно, как играю в футбол, и мой выпускной год будет моим лучшим!
   Сэм Уиллис, MD

   Я считаю, что программа очень полезна! Спасибо!
   Тина Вашингтон, Техас

   Продолжайте в том же духе, сотрудники Алгебратора! Спасибо!
   Памела Нельсон, MT

   Один из моих студентов принес программу под названием «Алгебратор». Сначала я думал, что это будет отличный инструмент, чтобы помочь всем моим ученикам, которые боролись. Когда я исследовал дальше, я понял, что это также помогает мне подготовить урок в два раза быстрее.
   

   Поль Д'Суза, Северная Каролина

   Я должен сказать, что я очень впечатлен тем, насколько удобным для пользователя является это приложение по сравнению с Personal Tutor. Легко входить в задачи, я получаю объяснения для каждого шага, каждый шаг завершен и т. д.
   A.R., Arkansas

   ---

   Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?

   
   

   Поисковые фразы, использованные 21 августа 2011 г.:

   • математика алгебра 2 помощь
   • бесплатных печатных рабочих листов для начинающих по наибольшим общим делителям и наименьшим общим множителям
   • СКАЧИВАНИЕ ПЗУ ti-84
   • лист триггера кальция
   • математическая справка по коэффициенту масштабирования
   • рациональных выражений ответы
   • Упрощение квадратных корней
   • Шаги кубического корня TI-89
   • есть ли у кого-нибудь ответы на второй семестровый тест по алгебре Гленко 1
   • Упрощение рациональных выражений
   • геометрия пустоши комплексный подход ответы
   • кубические корни для средней школы
   • Учебники по решениям для учащихся по чистой математике 11 класс
   • ответов на тест Алекса Колледжа по математике
   • биномиальные уравнения
   • сложение смешанных чисел с помощью калькулятора
   • заданий по математике для учащихся 11 класса
   Калькулятор факторинга
   • с работой
   • диаграмма Венна наибольший общий делитель ks3
   Калькулятор радикалов
   • дискриминантная таблица онлайн
   • Решатель квадратного корня
   • ответы к алгебре 1 рабочие листы glenco
   • бесплатный онлайн-чат с репетитором по математике
   • Сингапурский экзамен по математике A-level скачать
   • смешанная дробь, преобразованная в проценты
   • Рабочие листы по рационализации подкоренных выражений
   • Использование квадратных уравнений в реальной жизни
   • полиномы планы уроков 8 класс
   • nj спросить 6-й класс по математике прошлый тест
   • бесплатный решатель домашних заданий по алгебре
   • ответы к рабочей тетради по биологии Прентиса Холла
   • граф геометрической последовательности
   • радикальные выражения и решатели функций
   • Pearson Prentice Hall Рабочая тетрадь по алгебре
   • Квадратное уравнение, текстовые задачи, рабочий лист, ответ
   • Рабочие листы итогового теста по концептуальной физике
   • преобразование второго порядка в связанное уравнение первого порядка
   • МАТЕМАТИЧЕСКИЙ КАЛЬКУЛЯТОР НАИМЕНЬШИХ кратных
   • Преобразователь стандартных форм алгебры
   • KS3 бесплатные тестовые листы SAT
   • ПО для алгебры КПК
   • голодный форд, решения абстрактной алгебры, глава 6
   • баллов за решение линейных уравнений
   • Рабочие листы по алгебраическим математическим задачам
   • ti-89 делящие полиномы
   • простых изображений параболы
   • нечетный четный пример функции Algebra2 учитывает
   • Стандартизированная практика тестирования 6-го класса
   • Учебное пособие по начальной алгебре для колледжа
   • вычисление коэффициента растяжения в квадратичных уравнениях
   • бесплатных уроков алгебры для взрослых
   • алгебраические формулы
   • калькулятор у.

     No related posts.