Решение уравнений на ЕГЭ по Математике. Готовимся правильно!
В этом разделе – все основные способы и приемы решения уравнений на ЕГЭ по математике.
А встретиться вам могут всевозможные уравнения – квадратные, а также уравнения высших степеней. Дробно-рациональные уравнения. Уравнения, содержащие знак корня (иррациональные) или знак модуля. Показательные и логарифмические. И для каждого из этих типов – свои методы и секреты решения.
Десятиклассникам будут особенно полезны темы: «Алгебраические уравнения», «Уравнения с модулем», «Иррациональные уравнения», «Системы алгебраических уравнений».
Квадратные уравнения
Алгебраические уравнения
Системы алгебраических уравнений
Показательные уравнения
Логарифмические уравнения
Уравнения с модулем
Иррациональные уравнения
Простейшие тригонометрические уравнения, 1
Простейшие тригонометрические уравнения, 2
Тригонометрические уравнения. Методы решения
Запомним главное – что нужно знать при решении уравнений
— Корень уравнения – это такое число, при подстановке которого в уравнение получается верное равенство.
— Решить уравнение – значит найти все его корни или доказать, что их нет.
— Равносильными называются уравнения, множества решений которых совпадают.
— Если в уравнении есть дроби, корни четной степени, логарифмы – значит, не забываем про область допустимых значений (ОДЗ) уравнения.
— Если в уравнении можно сделать замену переменной – сделайте замену переменной.
— Решение уравнения лучше всего оформлять в виде цепочки равносильных переходов.
— Решив уравнение, сделайте проверку. Действительно ли найденные вами ответы являются корнями уравнения?
— Если слева и справа в уравнении находятся функции разных типов – например, квадратичная и показательная, или логарифм и синус, — значит, оно решается или графически, или с использованием свойств этих функций, или методом оценки
Больше уравнений:
Задание 5 Профильного ЕГЭ по математике
Задание 13 Профильного ЕГЭ по математике
Система уравнений. Подробная теория с примерами.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Для чего нужно уметь решать системы уравнений? Где они они могут пригодиться?
Все, что нужно знать о решении системы уравнений — в этой статье.
Помни, твоя цель — хорошо сдать ОГЭ или ЕГЭ и поступить в институт твоей мечты.
Let’s go… (Поехали!)
СОДЕРЖАНИЕ СТАТЬИ
| Система уравнений |
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
СИСТЕМА УРАВНЕНИЙ И МЕТОДЫ ЕЕ РЕШЕНИЯ
Метод подстановки
Это самый простой метод, но зачастую – самый трудоемкий.
Идея проста – нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной.
Затем точно так же выражаем и подставляем другую переменную и т.д., пока не получим уравнение с одной переменной.
После его решения и нахождения одной из переменных — последовательно возвращаемся к ранее выраженным, подставляя найденные значения.Непонятно?
Давай рассмотрим на примере
Пример 1
Из второго уравнения очень просто выразить :
Теперь подставим то, что получилось вместо в первое уравнение:
Мы получили уравнение с одной неизвестной, которое очень просто решить:
А теперь вернемся к выраженному и подставим в него полученное значение :
.
Итак,
Ответ:
Ответ, кстати, принято записывать как координаты, то есть в таком виде: .
В случае трех неизвестных: , и так далее.
То есть ответ в нашем примере запишется так:
Ответ:
Попробуй сам решить несколько примеров методом подстановки:
Пример 2
1) Здесь проще всего выразить из второго уравнения неравенства –
, а затем подставить в первое.
Ответ:
Пример 3
Выражаем из второго уравнения и подставляем в первое.
Ответ:
Пример 4
Здесь лучше выразить из первого уравнения:
, а затем уже подставлять во второе.
Ответ:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 5
Для этого сперва выразим в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно ):

Видно, что графики пересекаются в точке с координатами .
Графический метод – самый неточный.
Практически его можно применять только для систем линейных уравнений (вида ), графиками которых являются прямые.
Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать графический метод (лучше использовать его только для иллюстраций).
Метод сложения
Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений.
То есть:
Действительно, мы ведь имеем право прибавить к обеим частям уравнения одно и то же число, например, прибавим к первому уравнению число :
Но раз , в правой части можем заменить на :
.
Пример 6
Сложим эти уравнения (левые части друг с другом, и правые – тоже друг с другом):
.
Вот как! просто уничтожился в результате сложения.
Скажу сразу, это и была цель всего действия: складываем уравнения только тогда, когда при этом получим более простое уравнение.
Остается теперь только подставить в любое уравнение вместо число :
Ответ:
Пример 7
Очевидно, здесь сложение ничего не даст.
Придется решать другим методом?
Нет!
Иначе метод сложения был бы полезен слишком редко. Мы ведь можем умножать любое уравнение на любое ненулевое число?
Так давай умножим первое уравнение на такое число, чтобы потом при сложении какая-то переменная исчезла.
Лучше всего умножить на :
Теперь можно складывать:
Теперь подставим в первое уравнение системы:
Ответ:
Теперь порешай сам (методом сложения):
Пример 8
1. На что здесь надо умножить, чтобы коэффициенты при x или y были противоположными?
Хм….
Как из получить или из получить ?
Умножать на дробное число?
Слишком громоздко получится.
Но ведь можно умножить оба уравнения! Например, первое на , второе на :
Теперь, сложив уравнения, мы можем легко найти .
Подставляем в любое из уравнений и находим .
Ответ:
Пример 9
2. Решать нужно аналогично первому примеру – сначала нужно умножить первое уравнение на , а второе на , и сложить.
Ответ: .
3. Первое умножаем на , а второе на и складываем.
Ответ: .
Пример 10
4. Умножать можно и на дроби, то есть делить.
Умножим первое уравнение на , а второе на :
Теперь сложим уравнения:
Подставив в первое уравнение, найдем :
Ответ:
Тренировка без подсказок
Теперь попробуй сам определить наиболее рациональный способ решения, а затем проверь ответы. Подсказок уже не будет!
Примеры 11-16
Как видишь, система уравнений — базовая, но не самая сложная тема!
Используй методы, описанные в этой статье, и ты без труда справишься с решением систем.
Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных:
Методы решения систем уравнений:
1. Решение методом подстановки
Нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной.
Повторять подобную процедуру пока не будут найдены все переменные.
2. Решение графическим методом
Если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Графический метод – самый неточный.
Практически его можно применять только для систем линейных уравнений (вида ), графиками которых являются прямые.
Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать графический метод (только для иллюстраций).
3. Решение методом сложения
Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений.
То есть:
Но ни в коем случае не наоборот:
ТЕПЕРЬ ТЕБЕ СЛОВО…
Мы постарались объяснить что такое системы уравнений и как их решать.
Теперь хотелось бы послушать тебя…
Как тебе статья?
Получается ли у тебя решать системы уравнений?
У тебя есть вопросы? Предложения?
Напиши в комментариях.
Мы читаем все.
И удачи на экзаменах!
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Примеры решения показательных уравнений
Решение показательных уравнений различными способами
методы решения
образцы решения
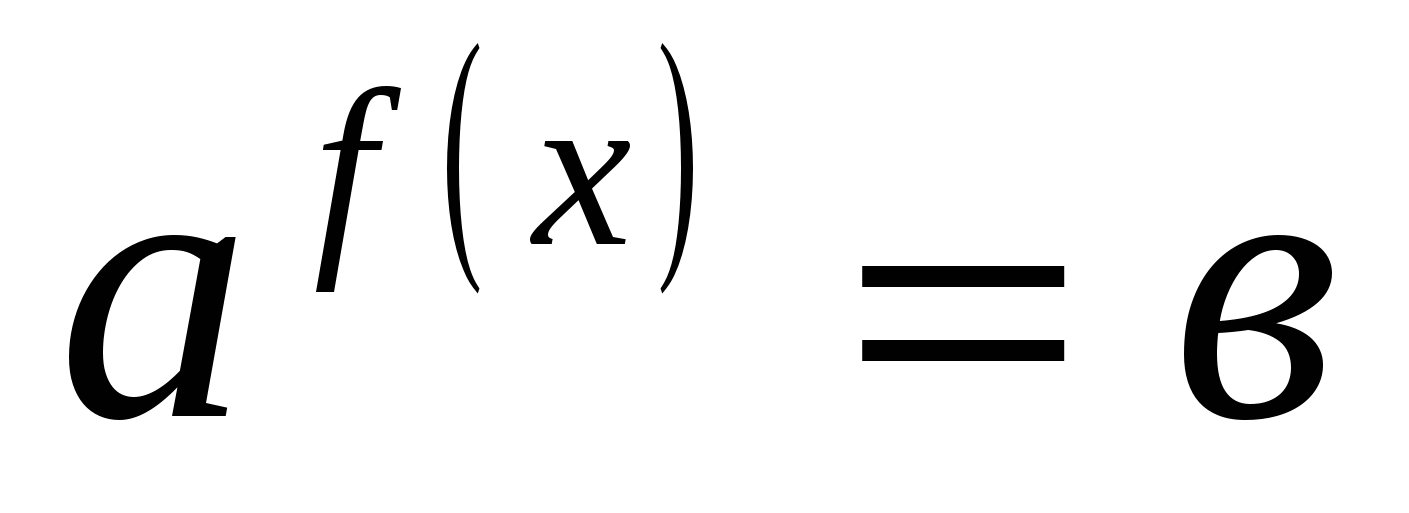
1) в обеих частях уравнения привести степени к одному основанию
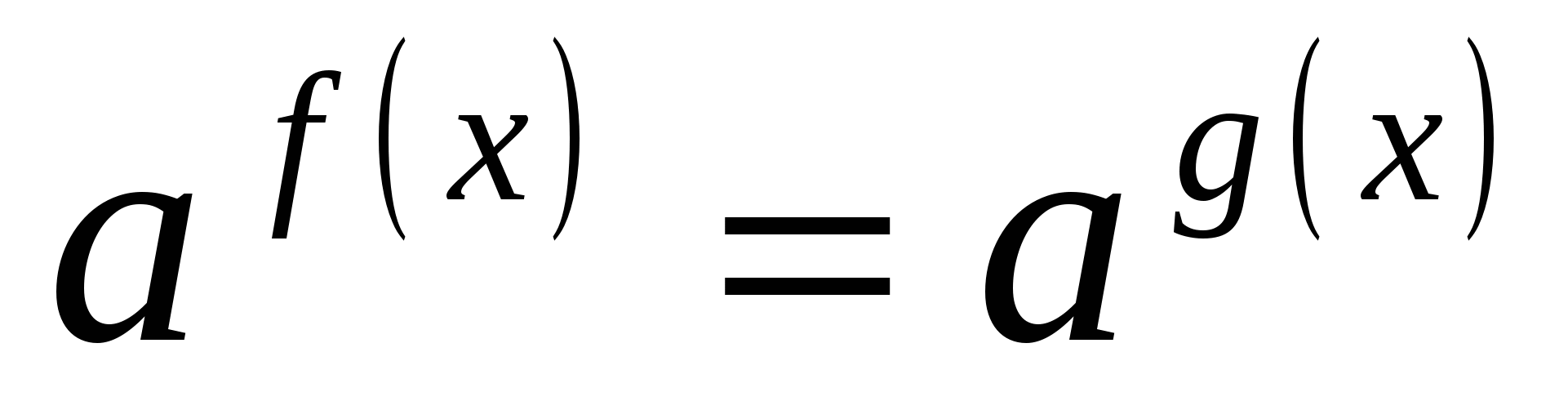
2) приравнять показатели степеней 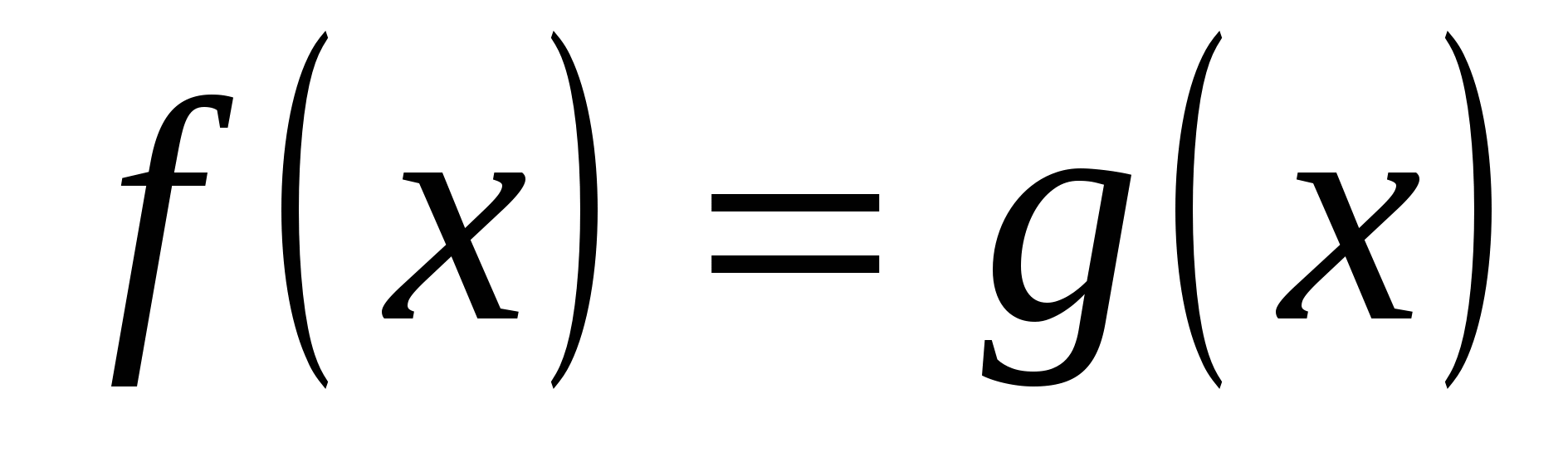
а) 
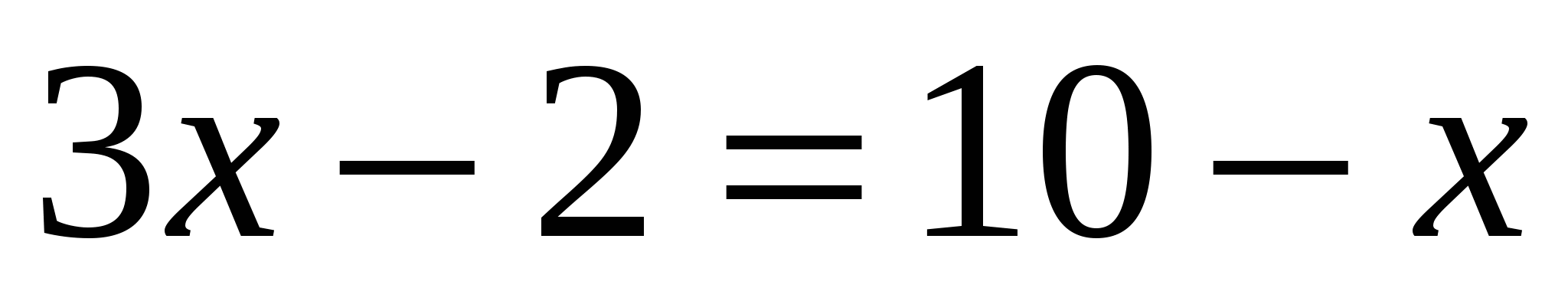
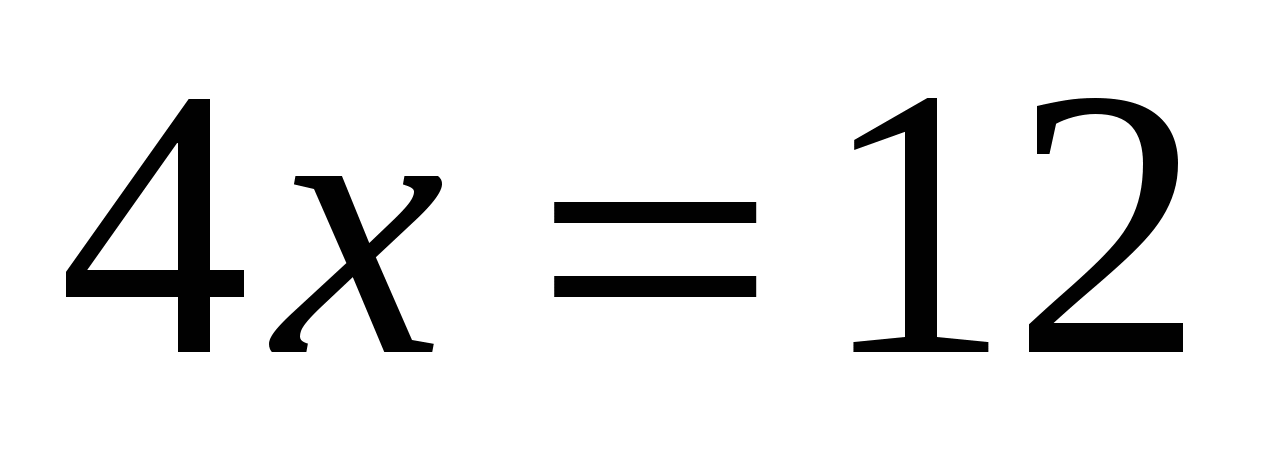
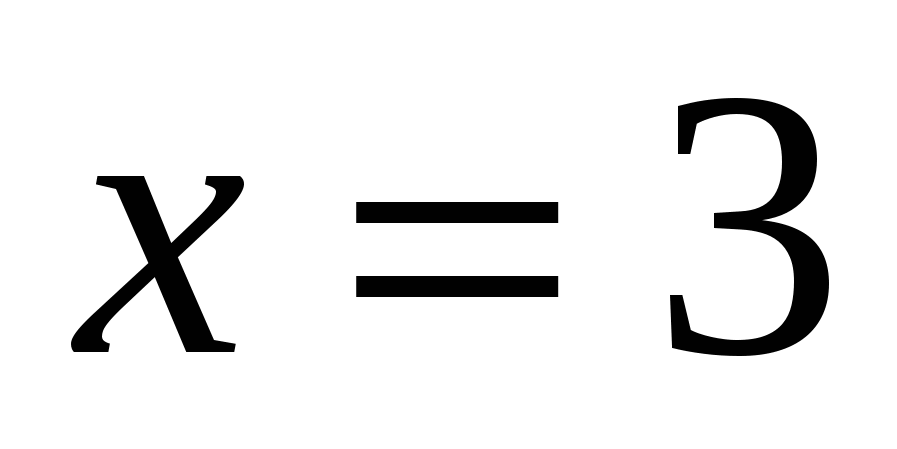
Ответ: 3.
б) 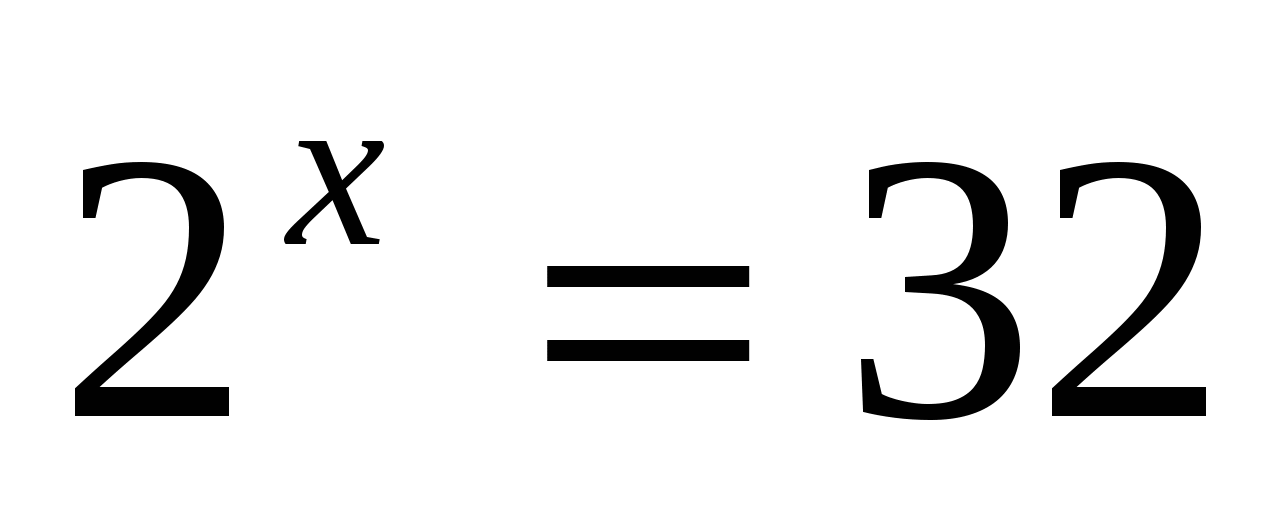
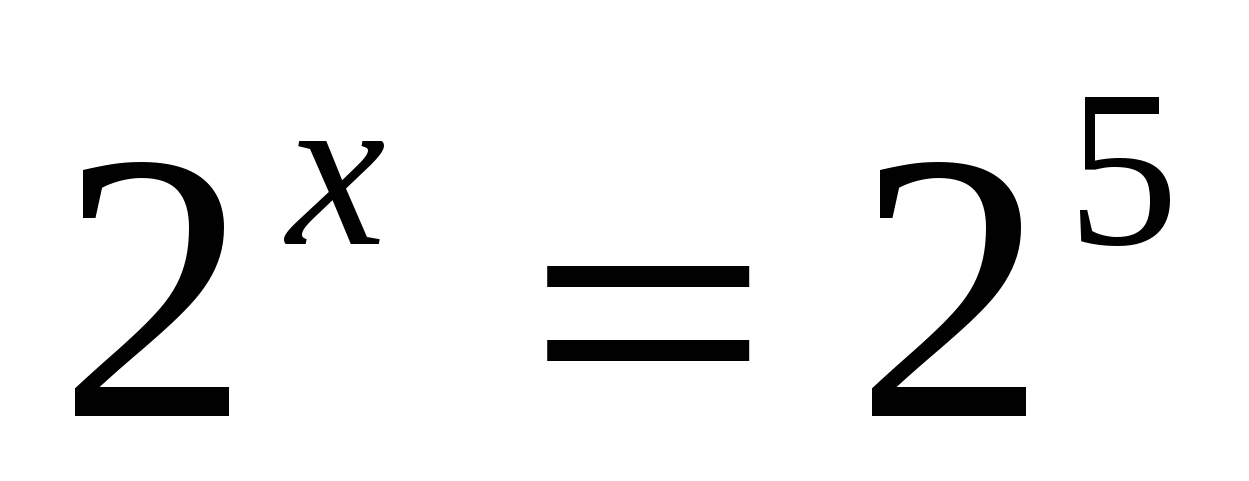
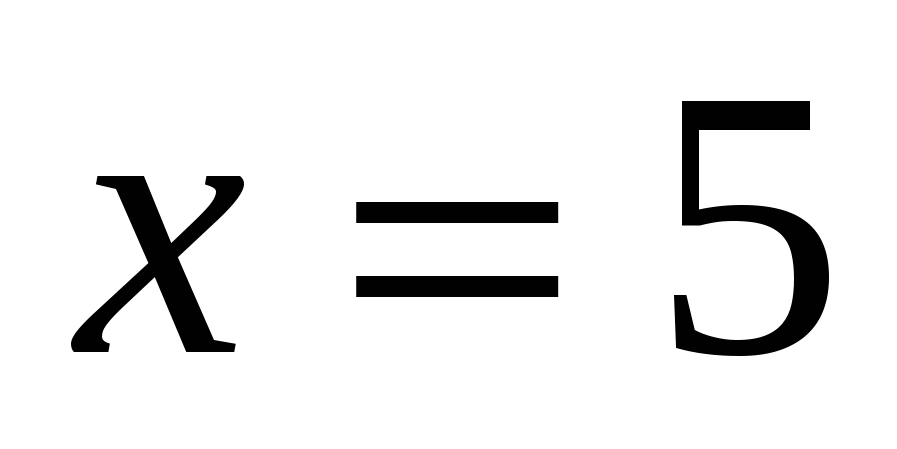 Ответ: 5
Ответ: 5
в) 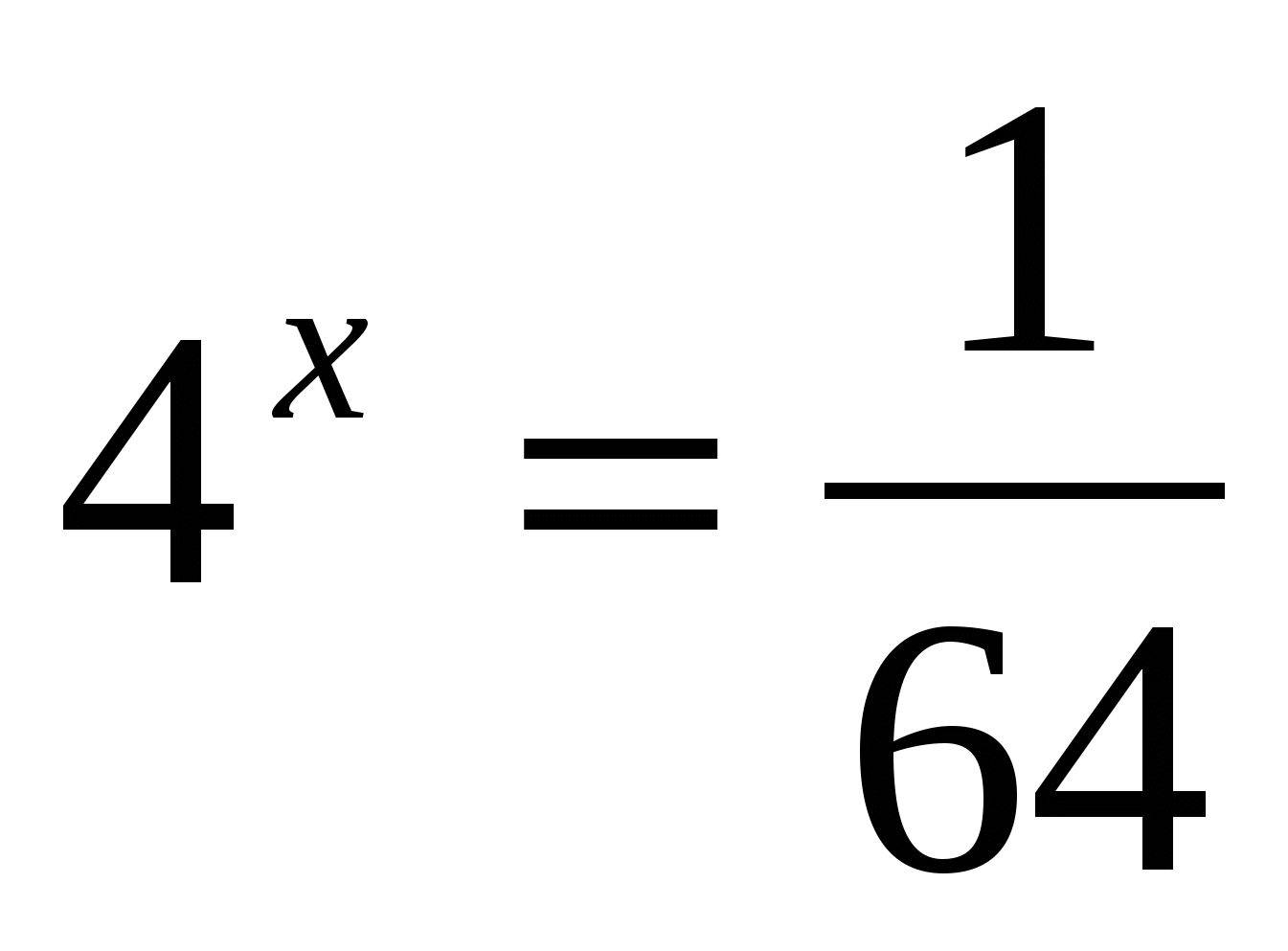
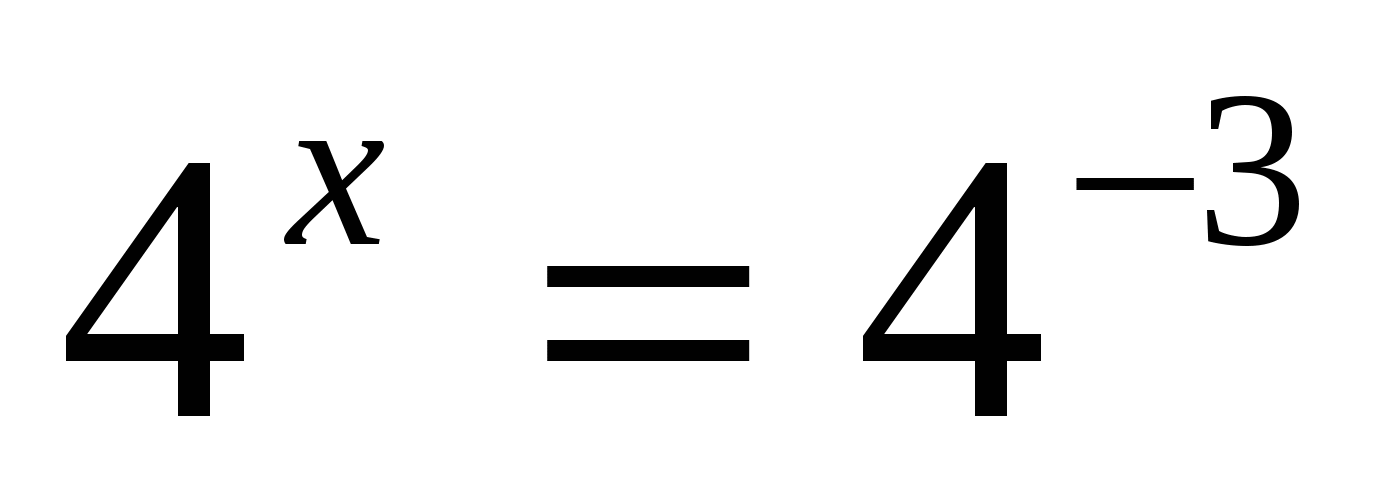
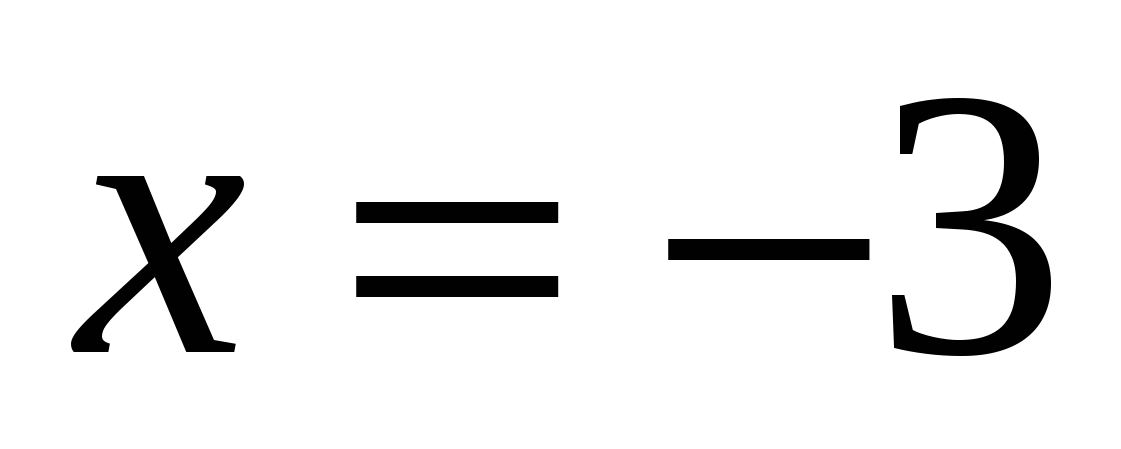
Ответ: — 3.
г) 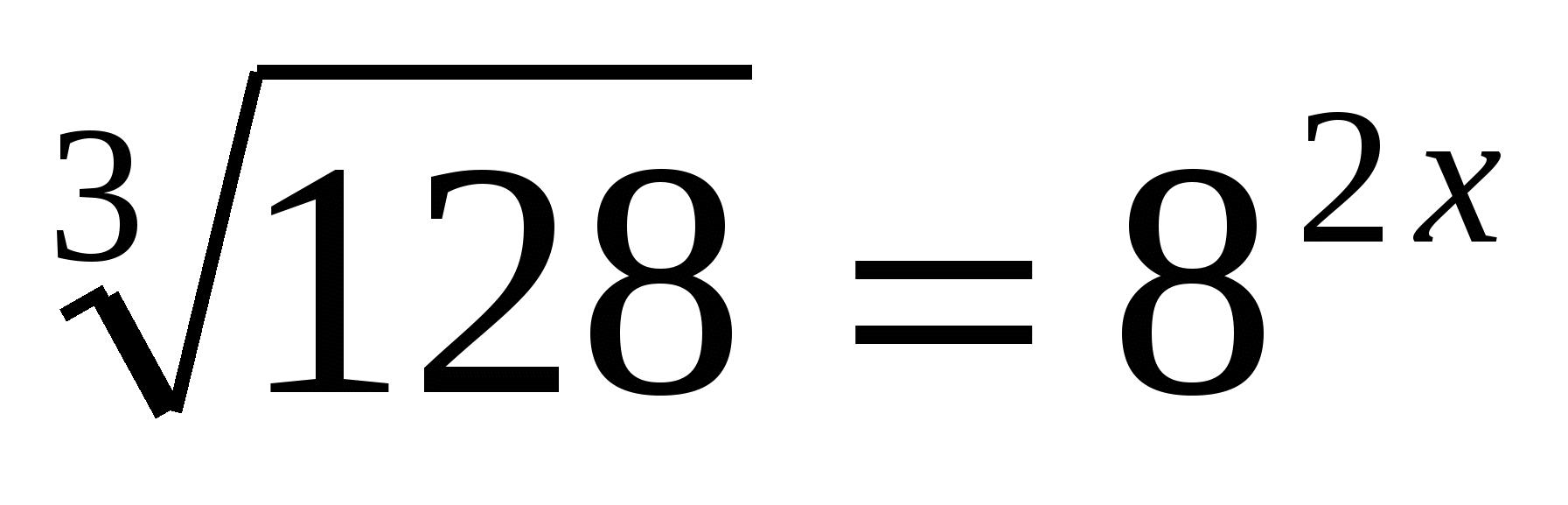
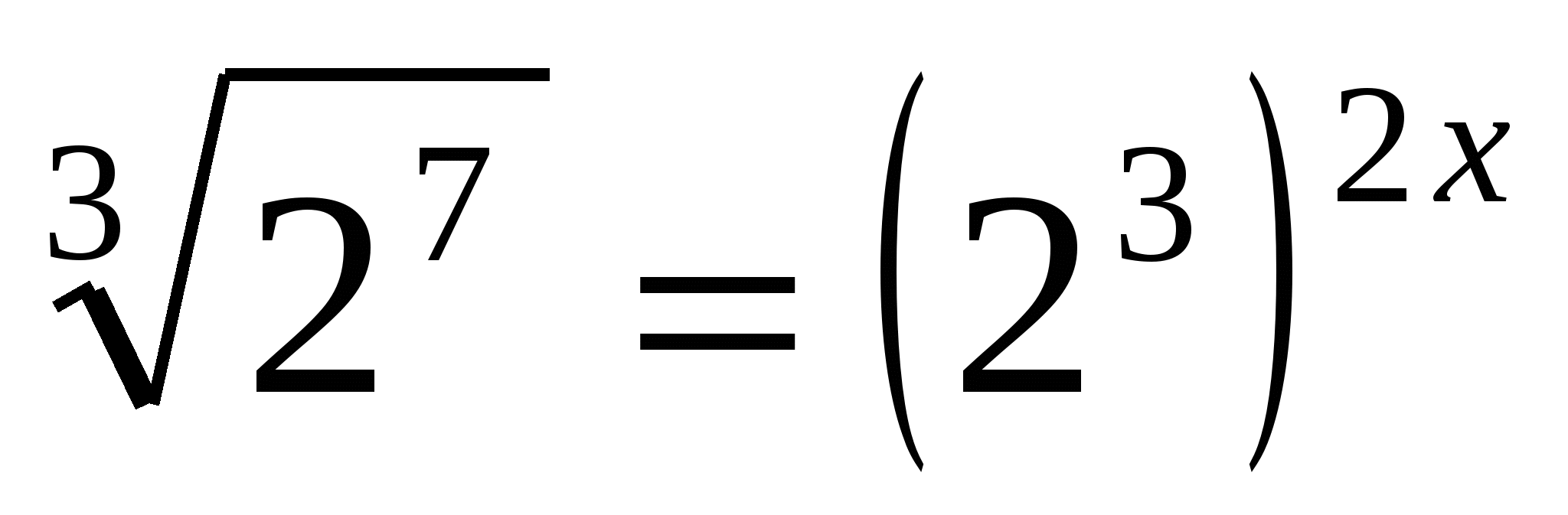
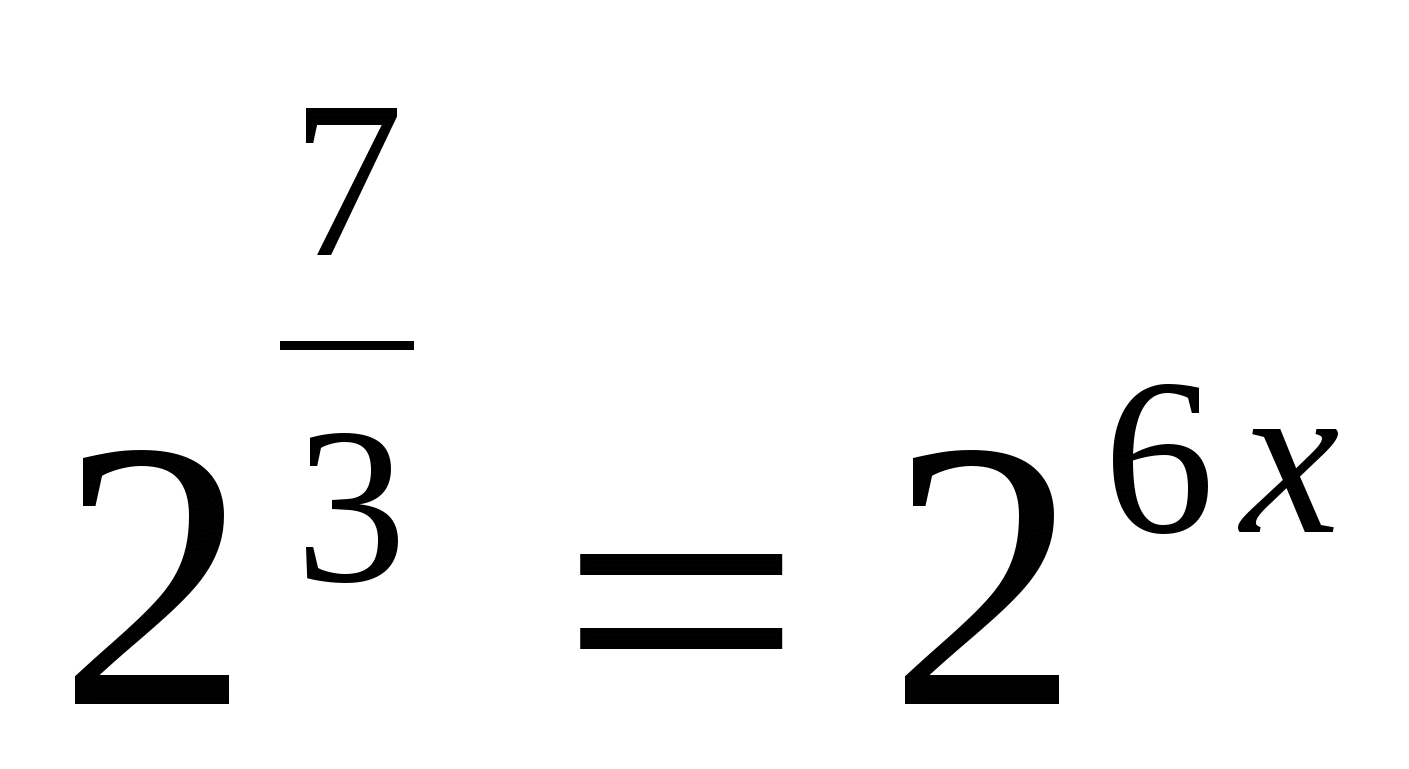
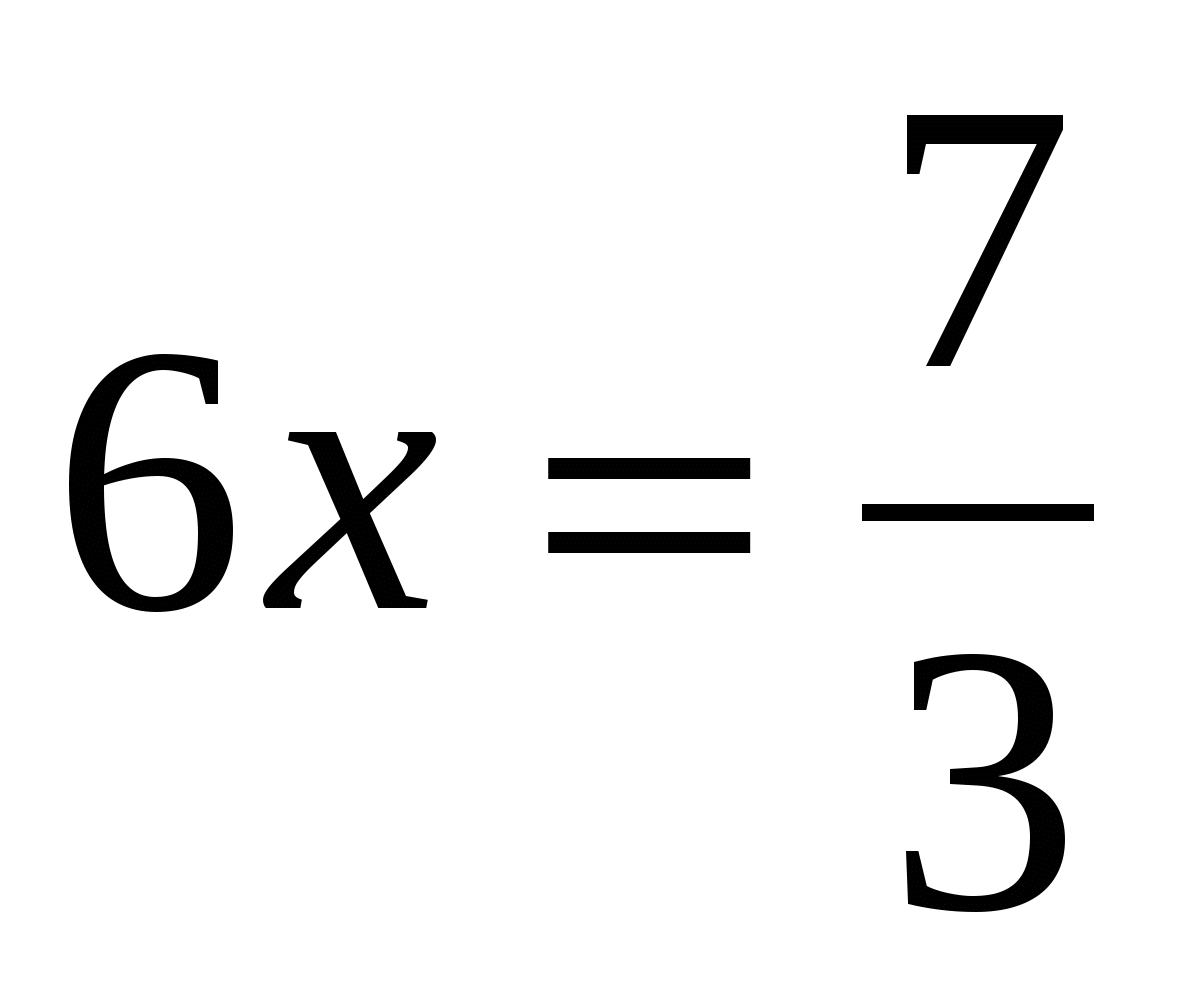
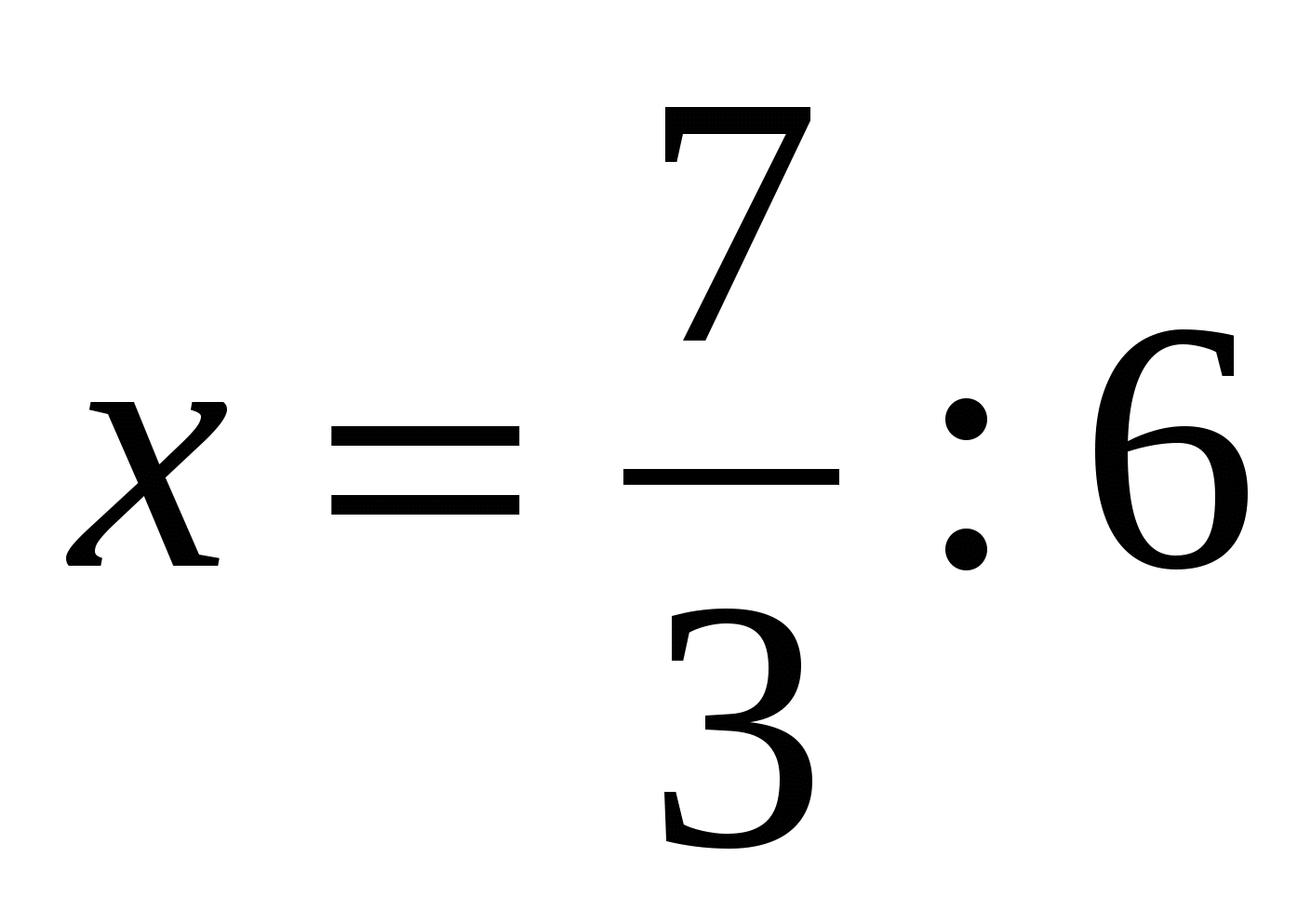
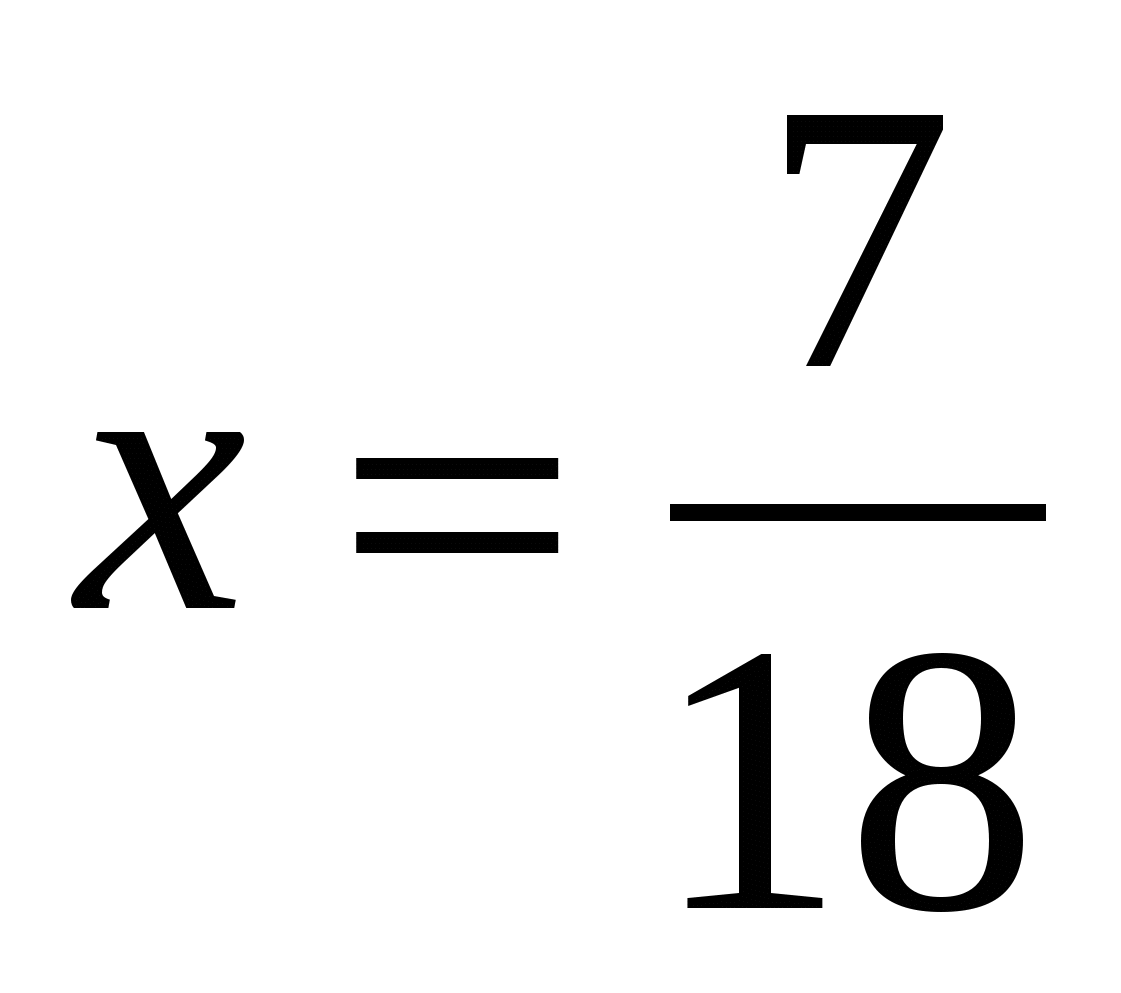
Ответ: 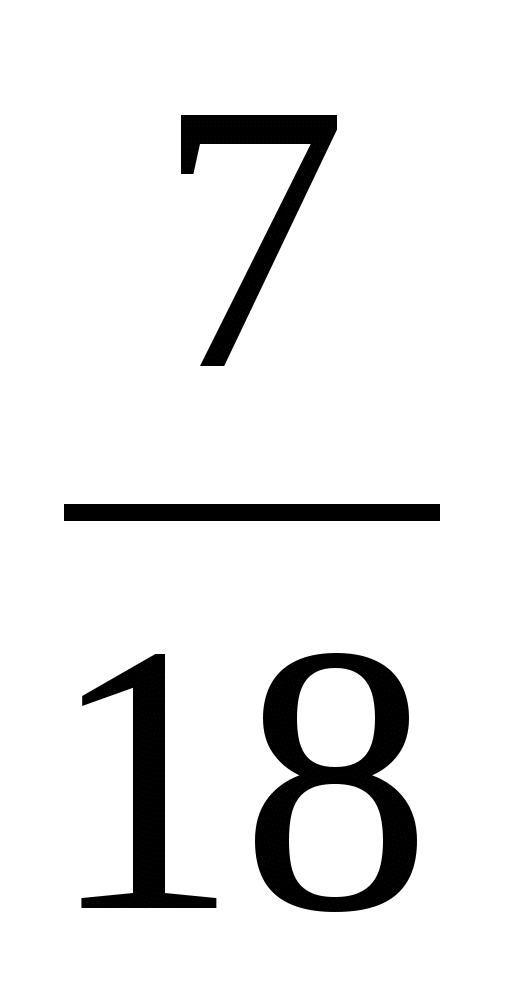 .
.
д) 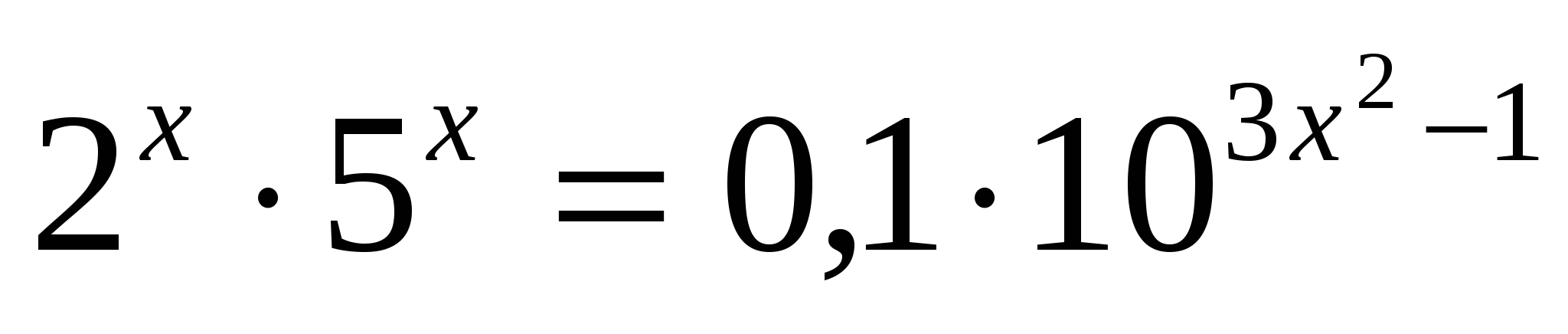
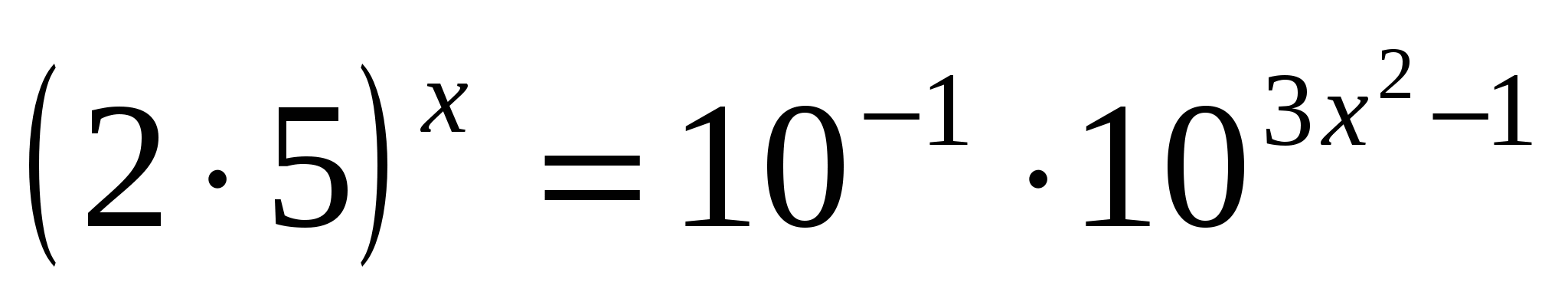
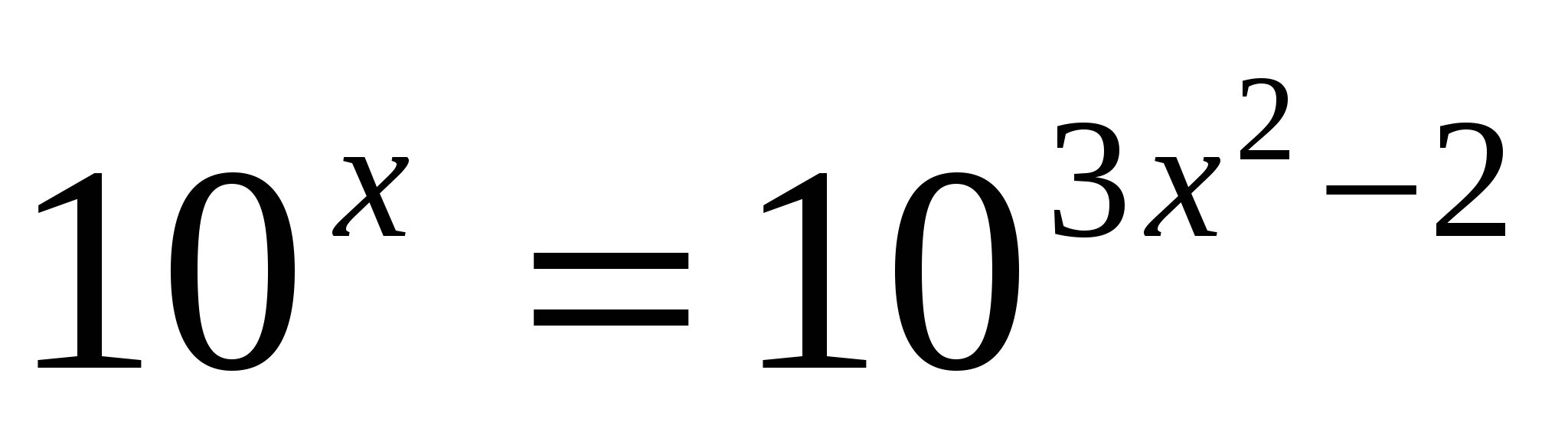
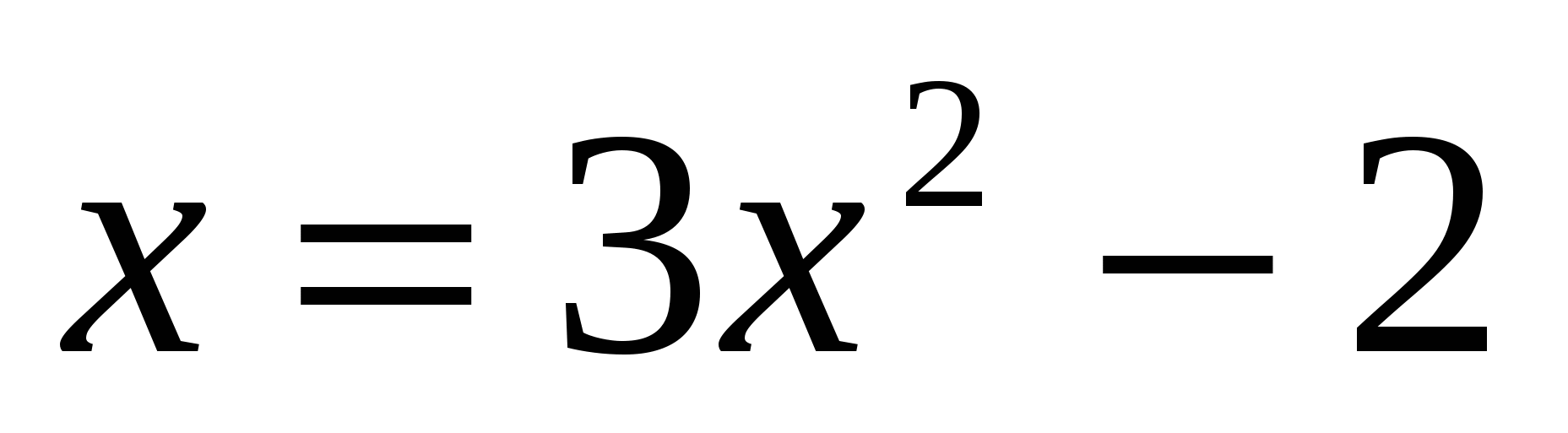
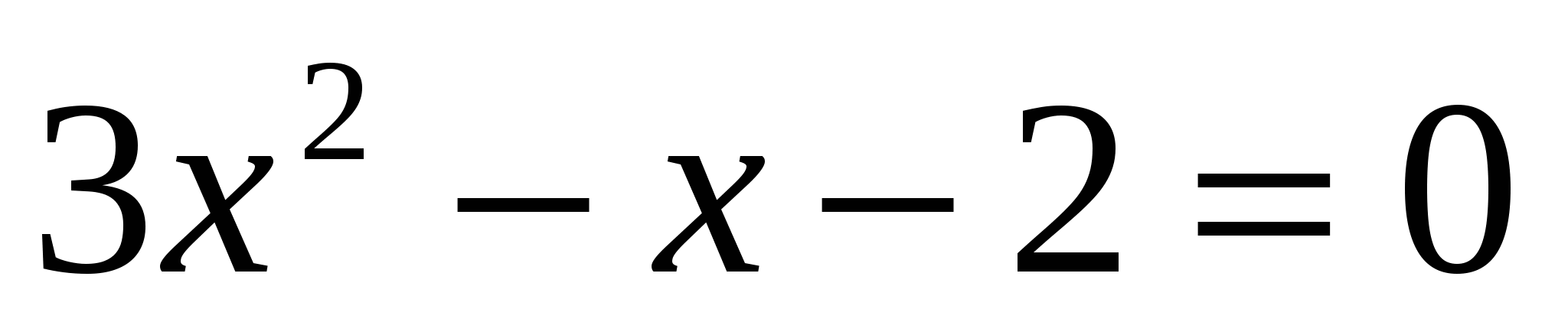
D=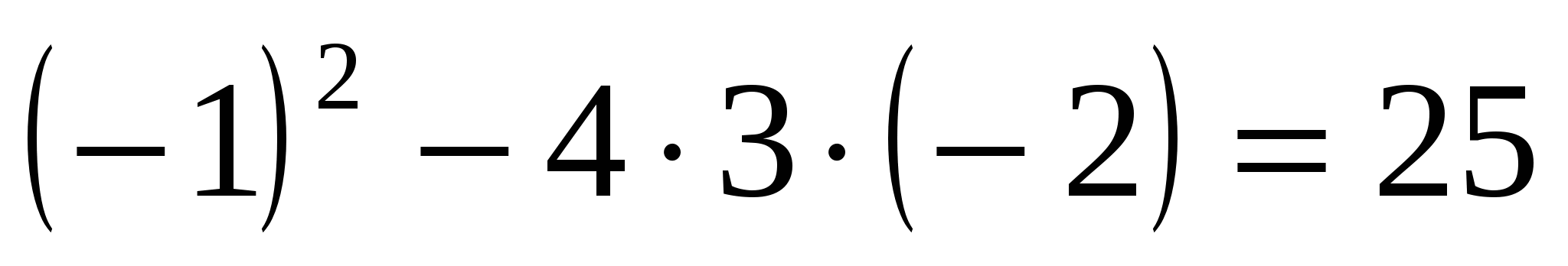
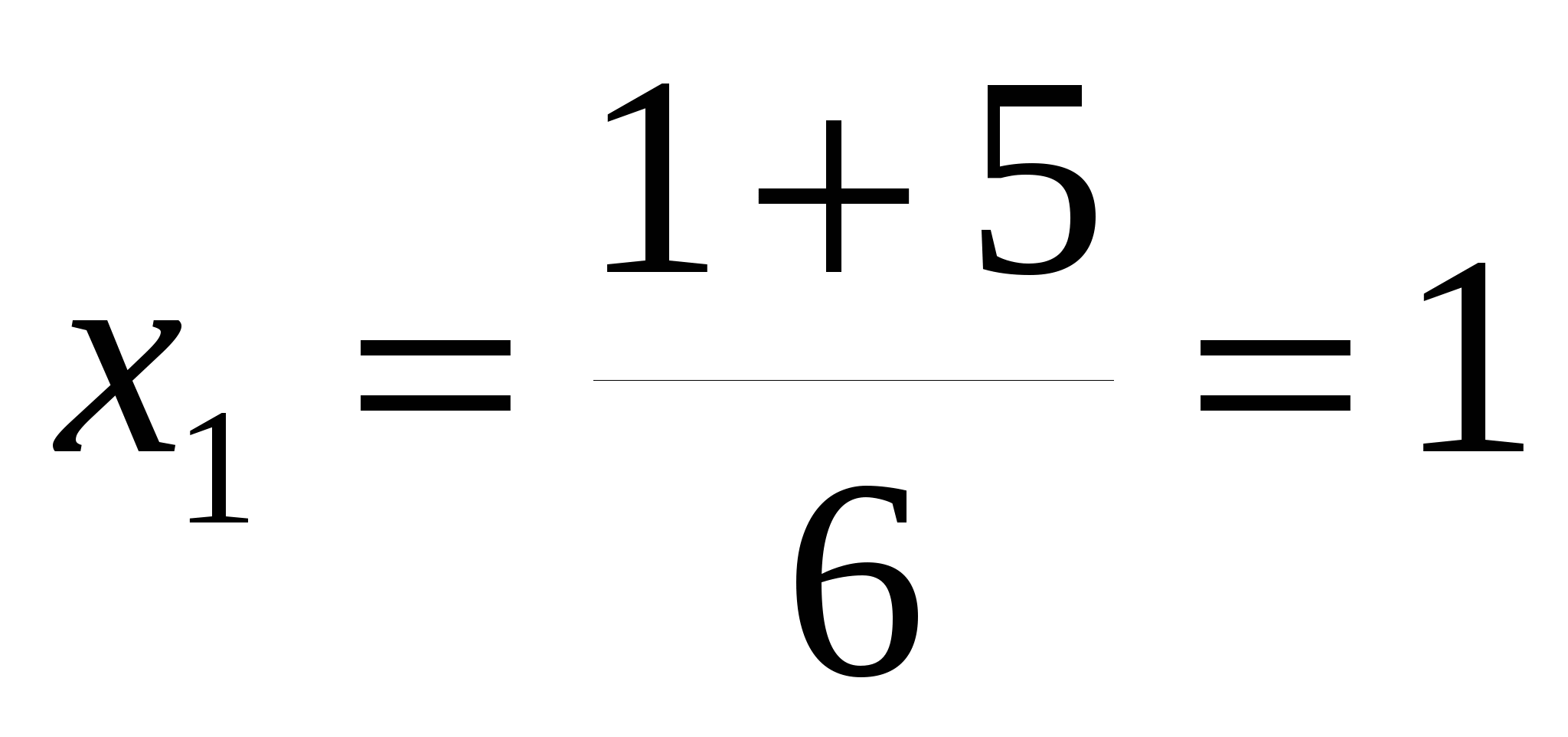
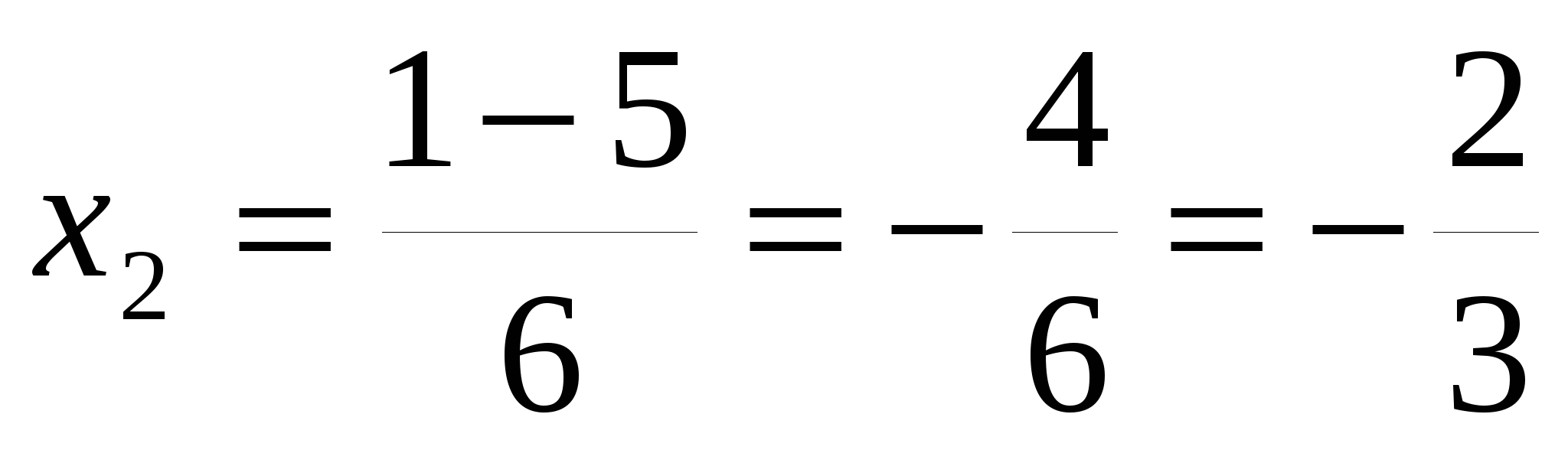
Ответ: 1; 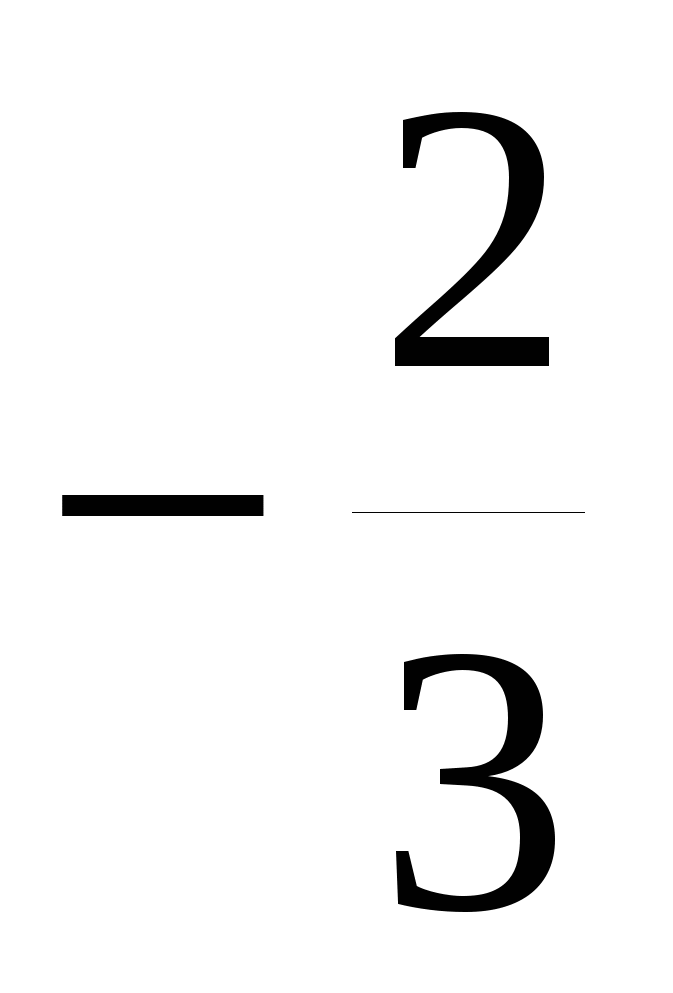 .
.
е) 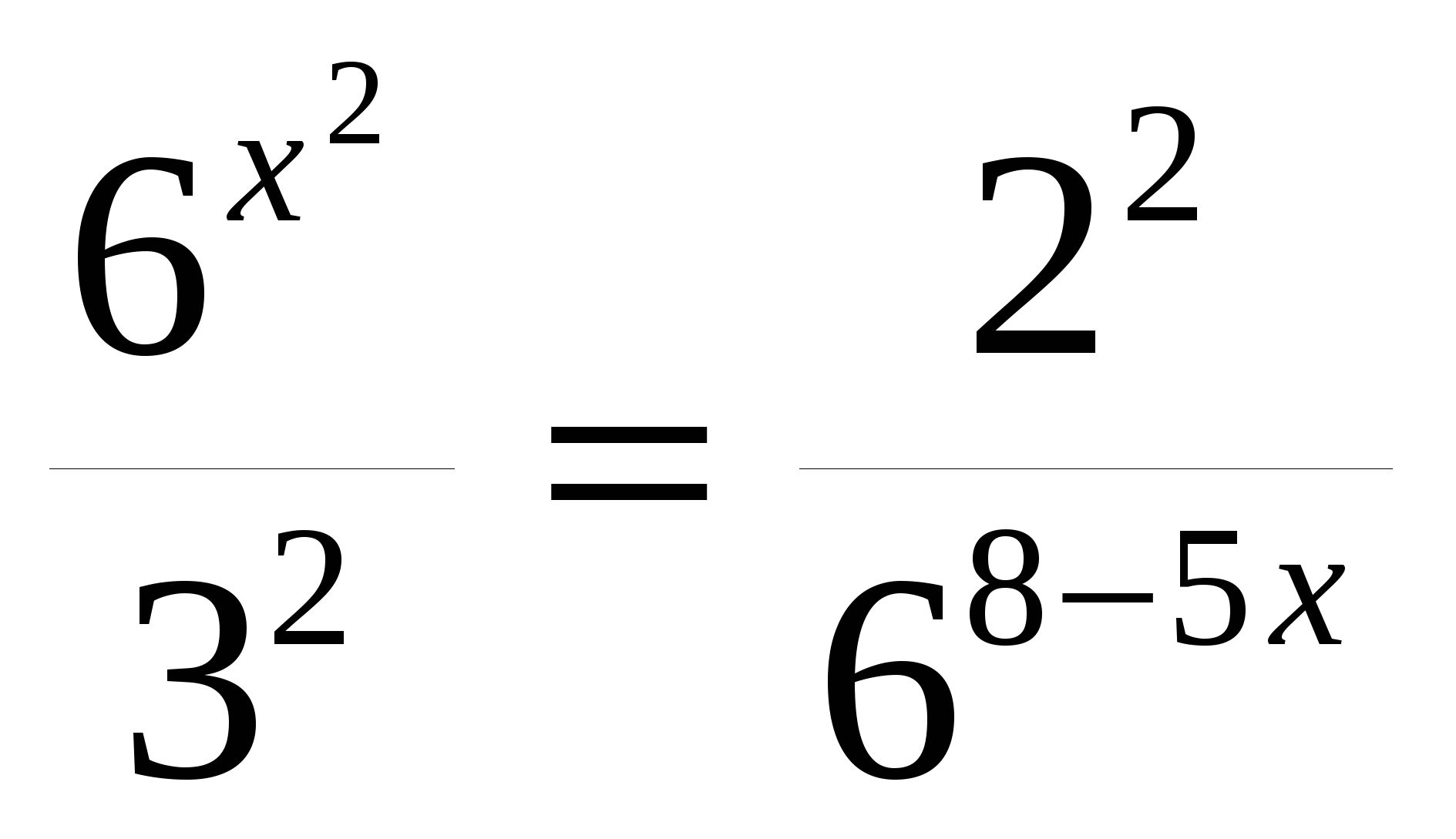
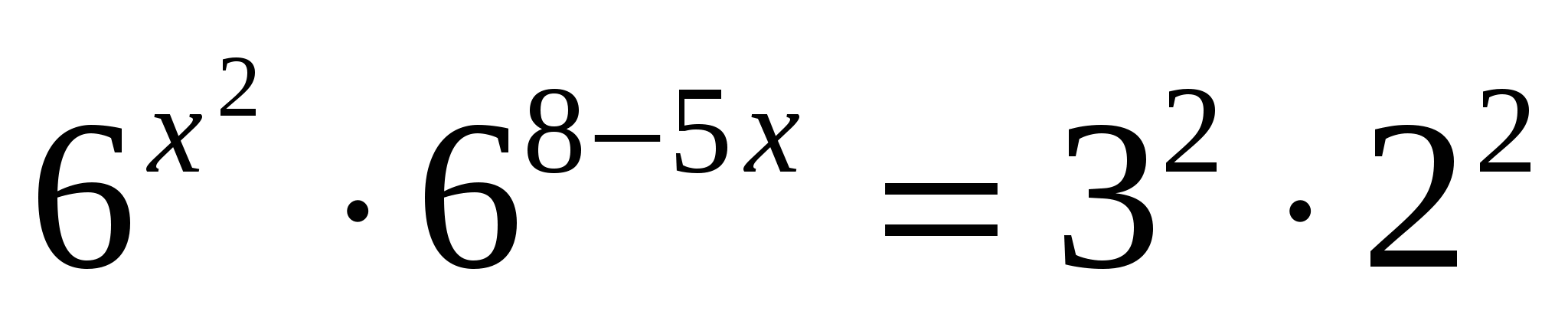
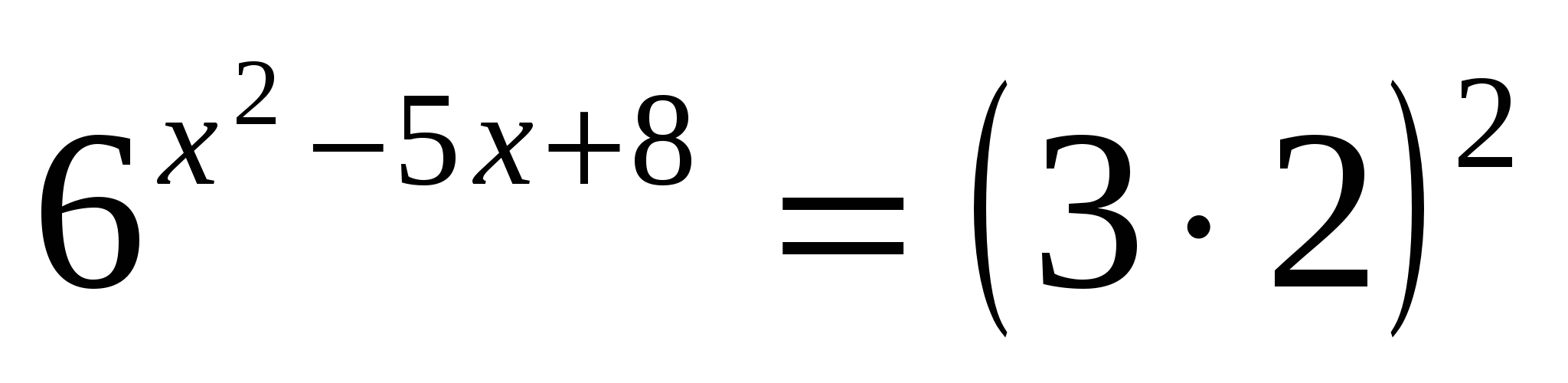
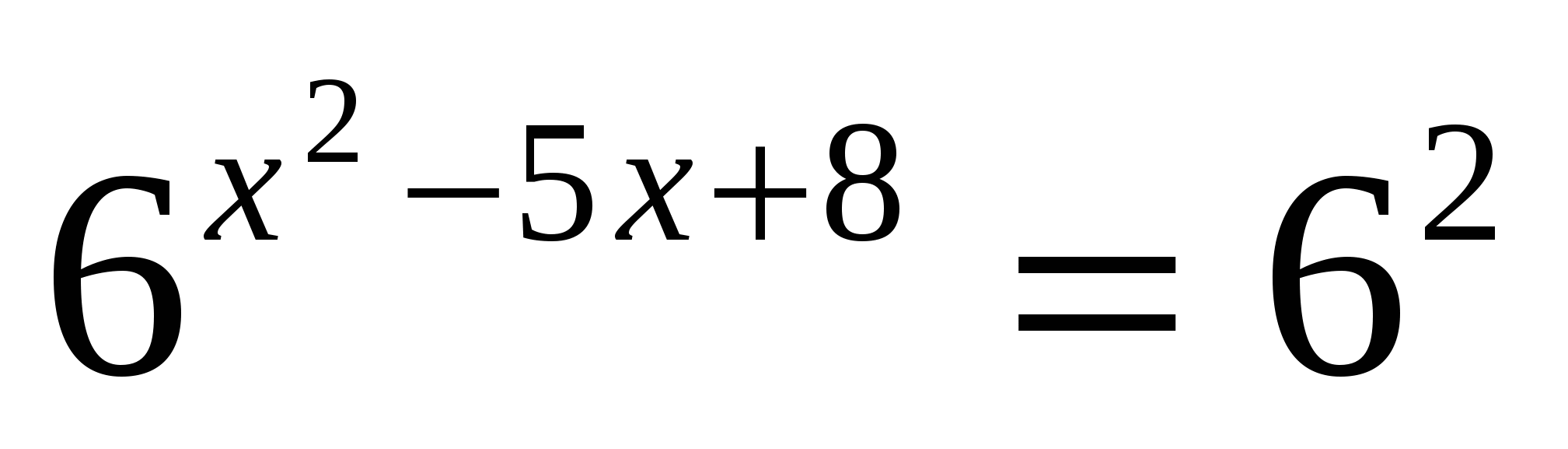
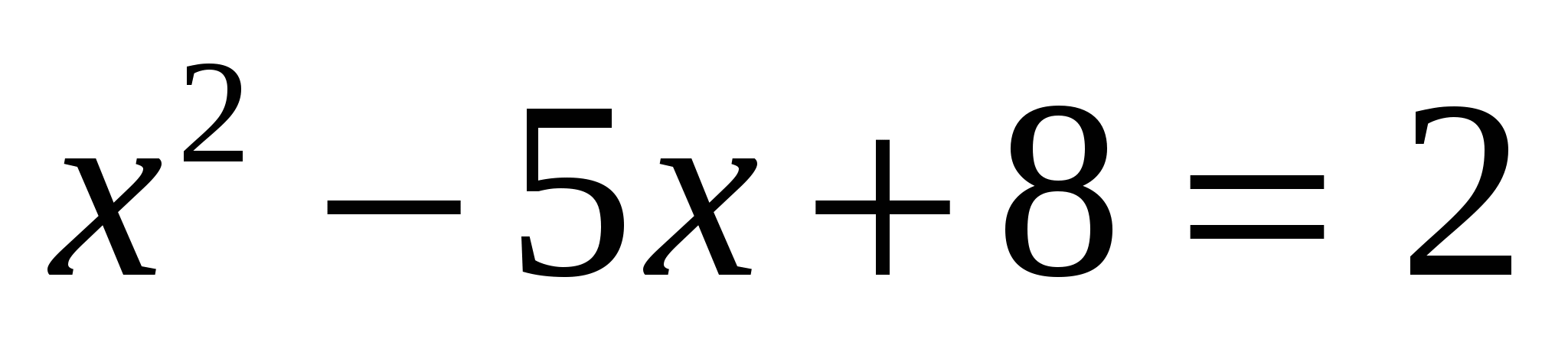
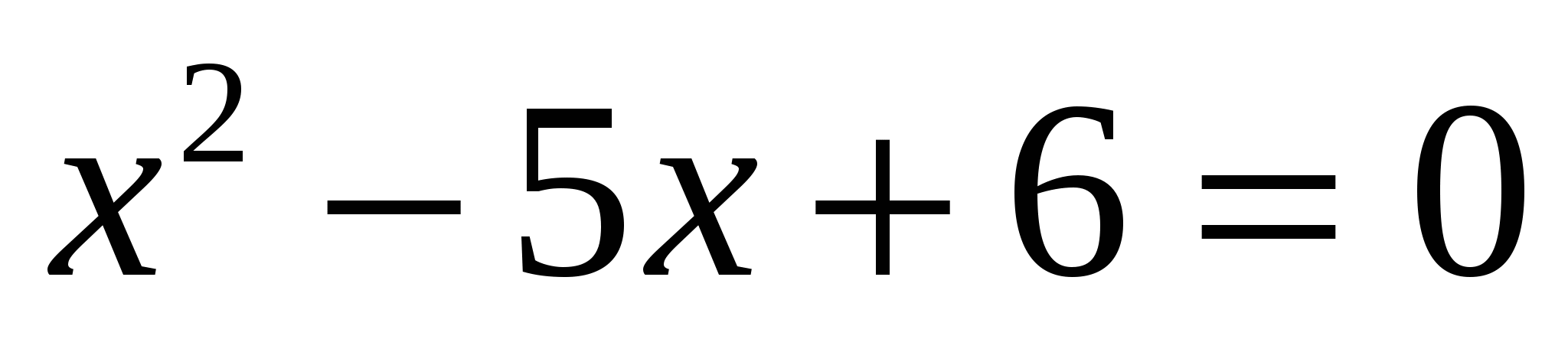
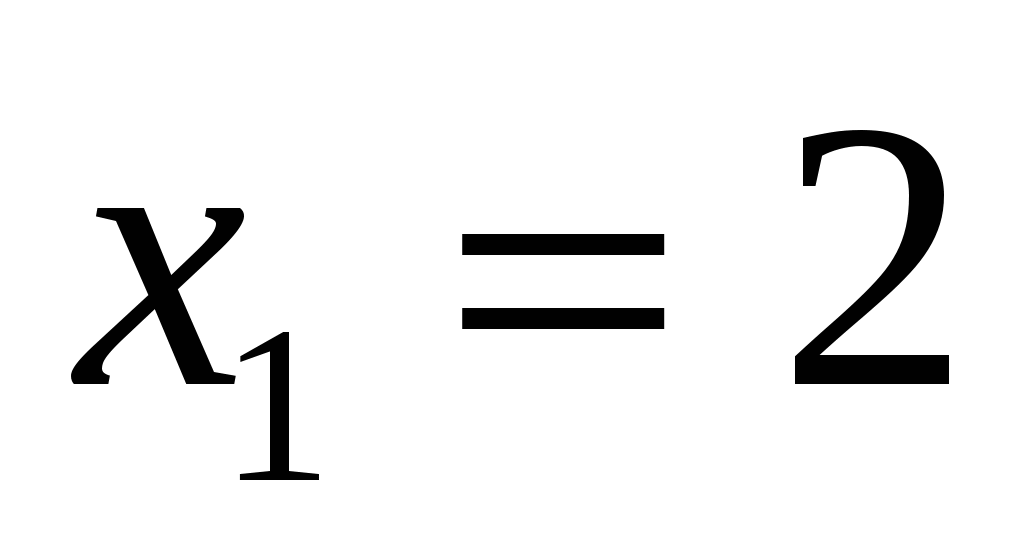
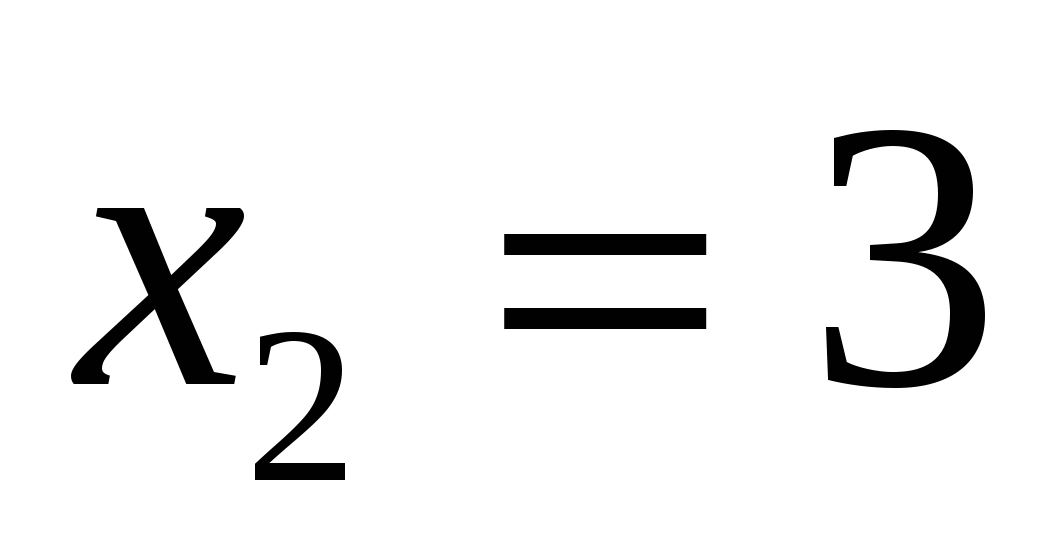
Ответ: 2; 3.
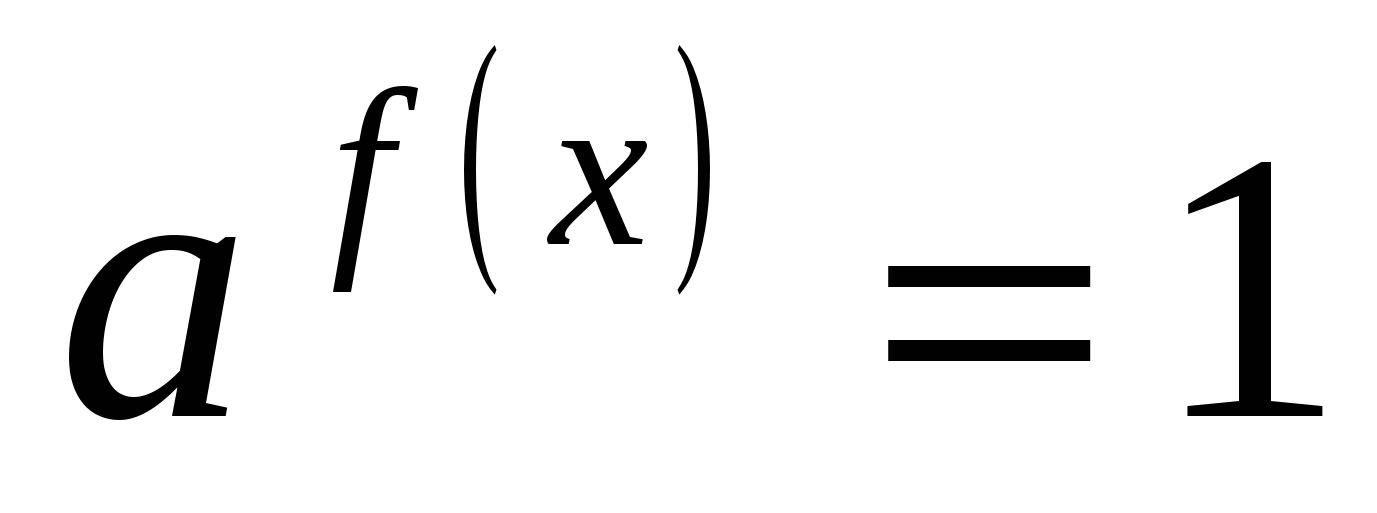
представить 1 в виде степени числа а с нулевым показателем 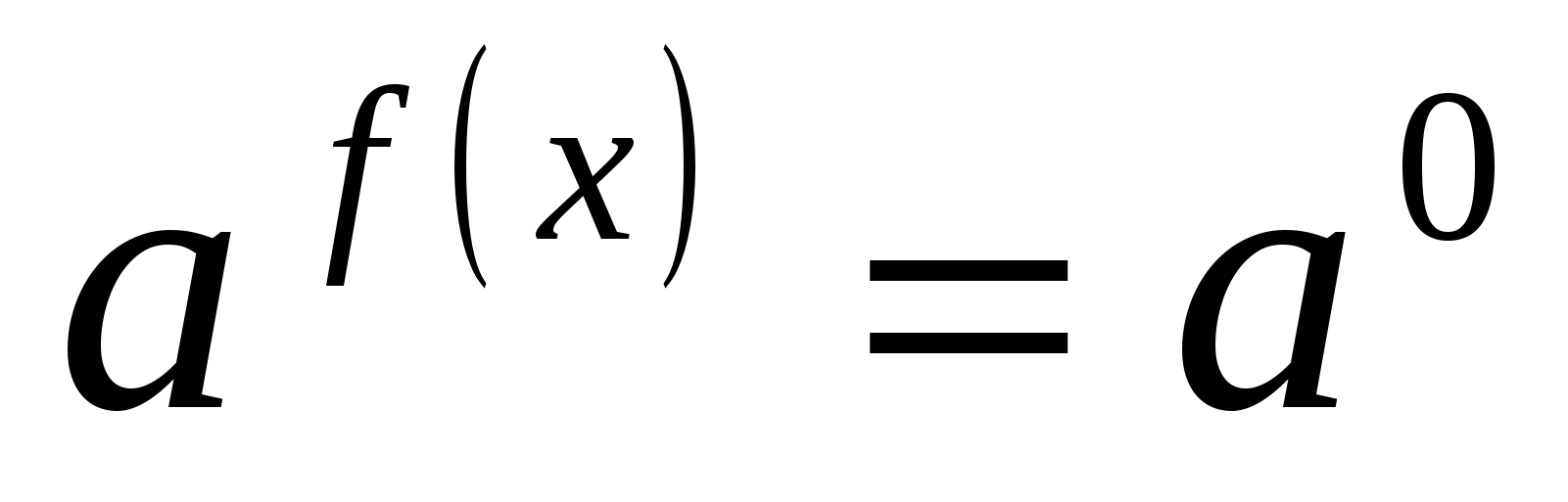
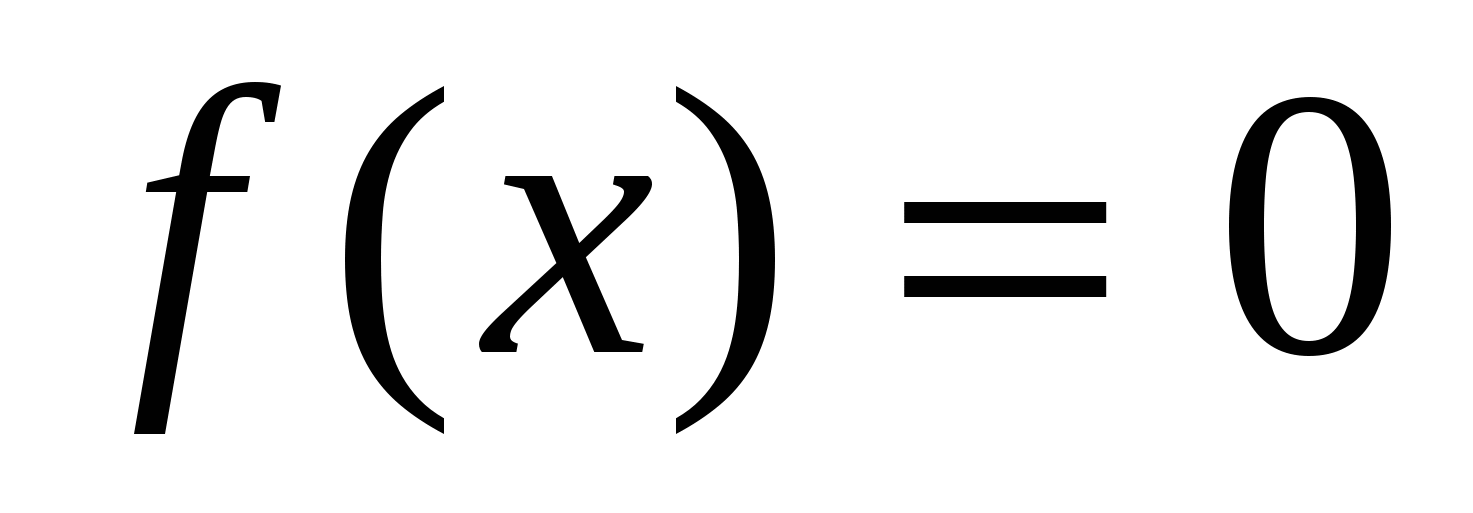
а) 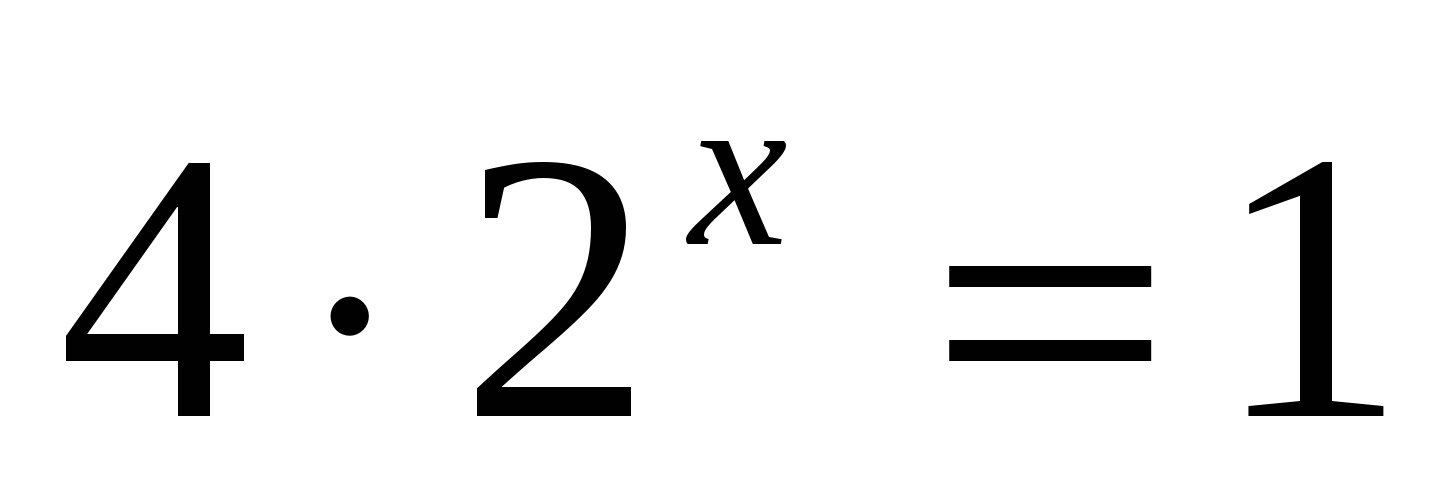
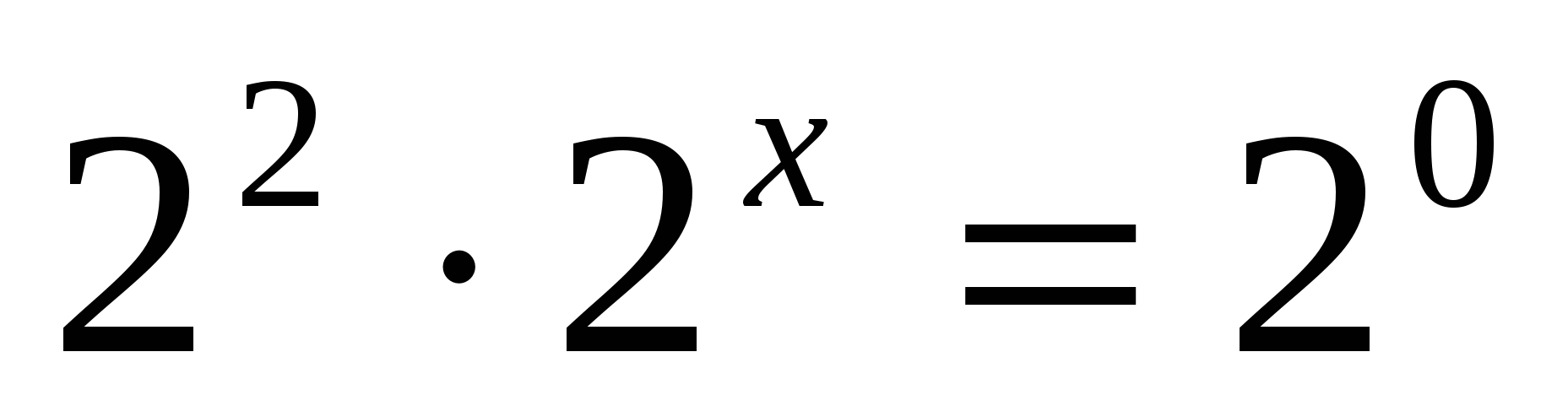
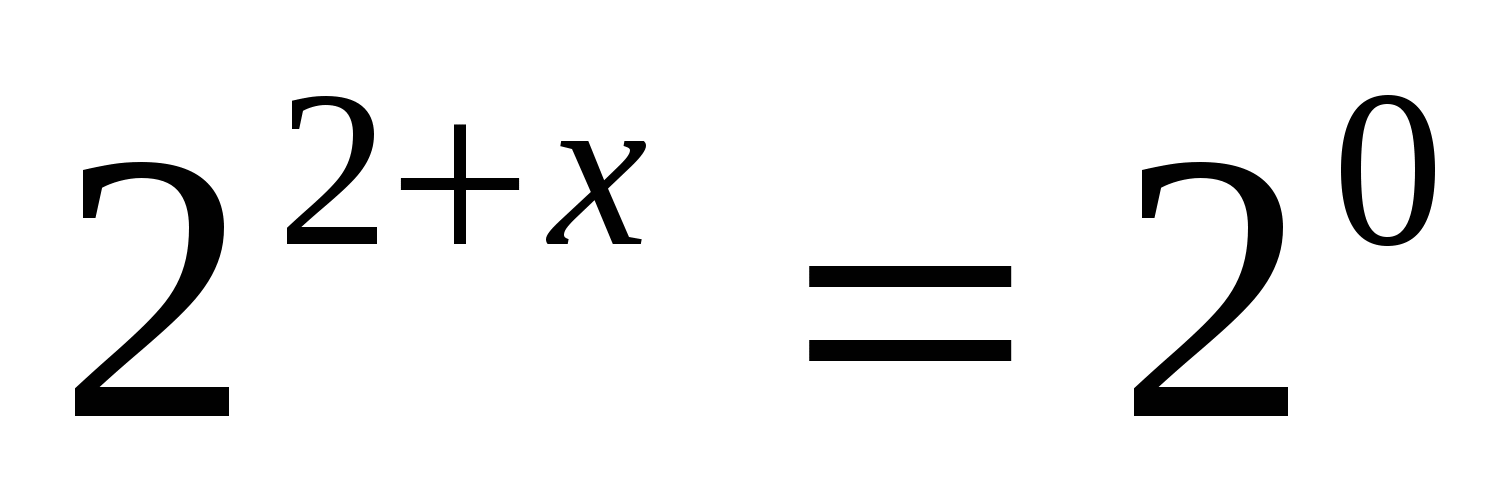
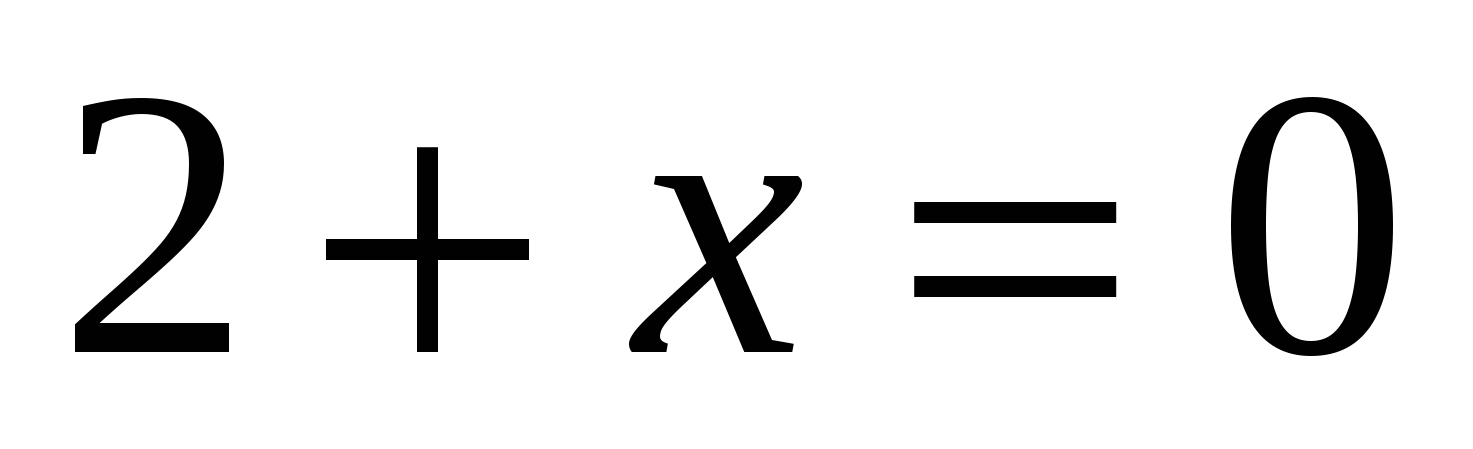
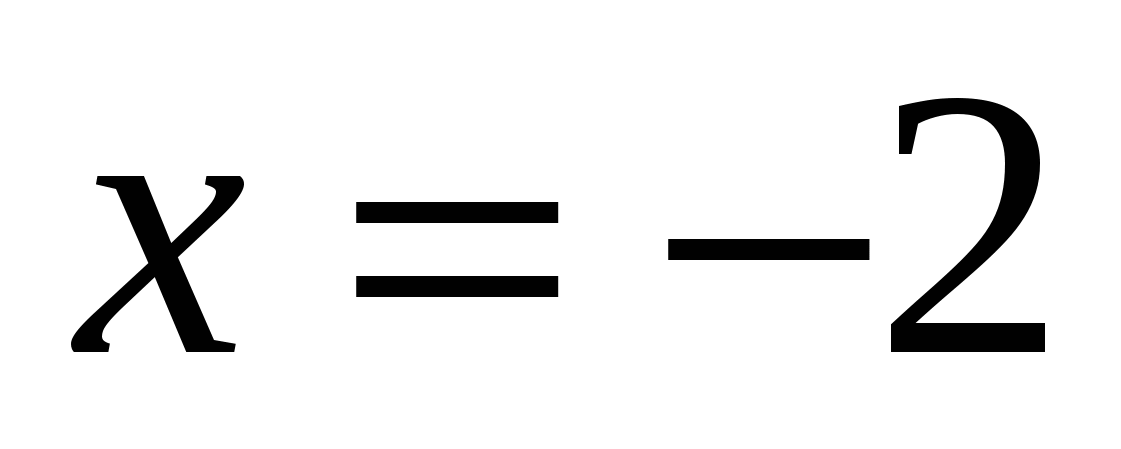
Ответ: — 2.
б) 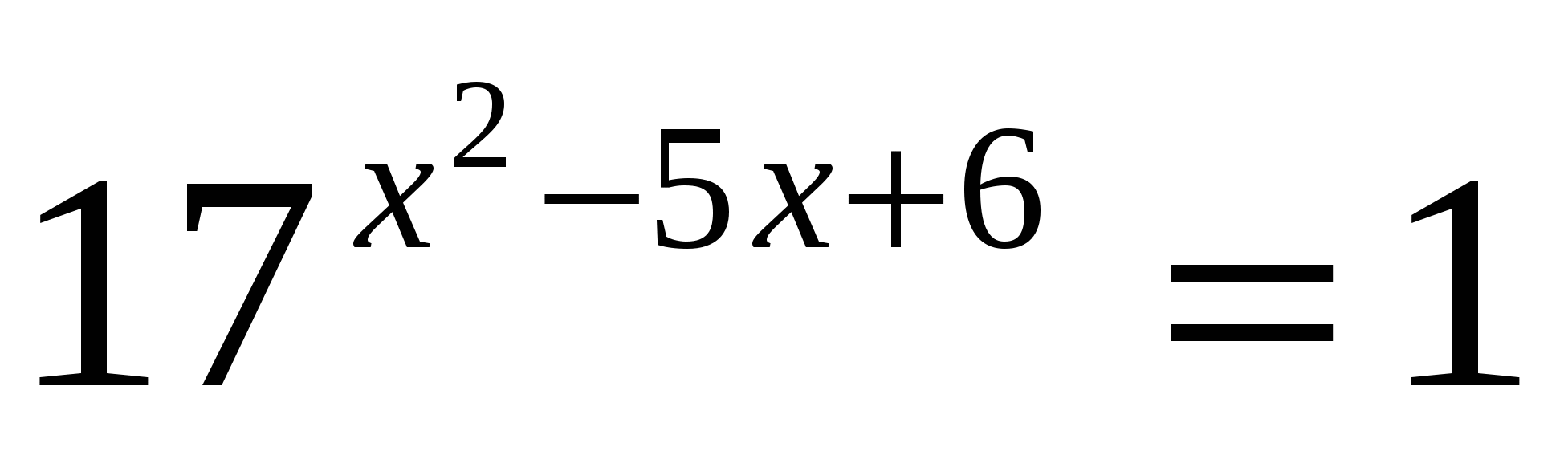
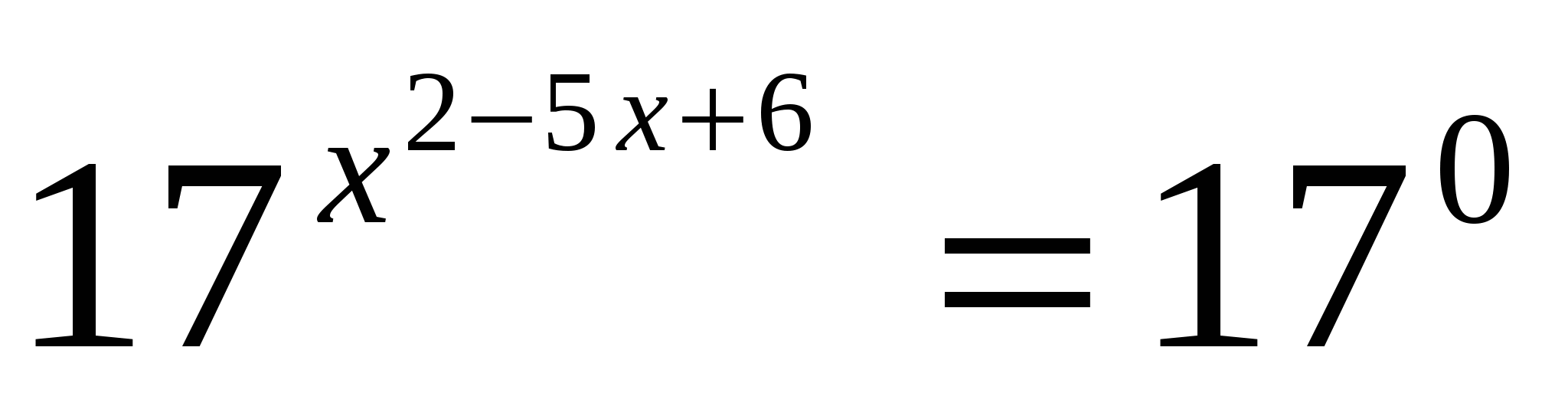
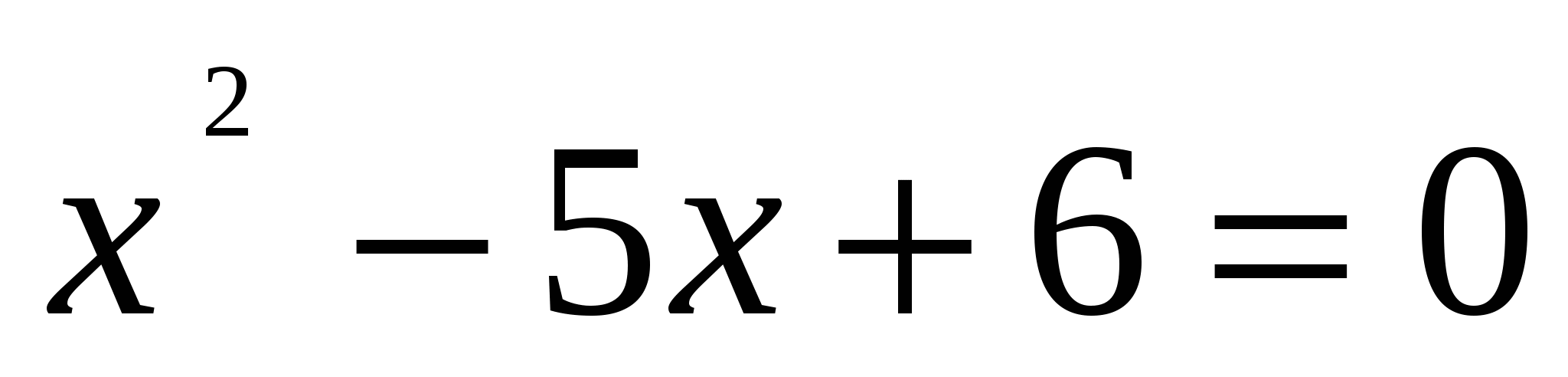
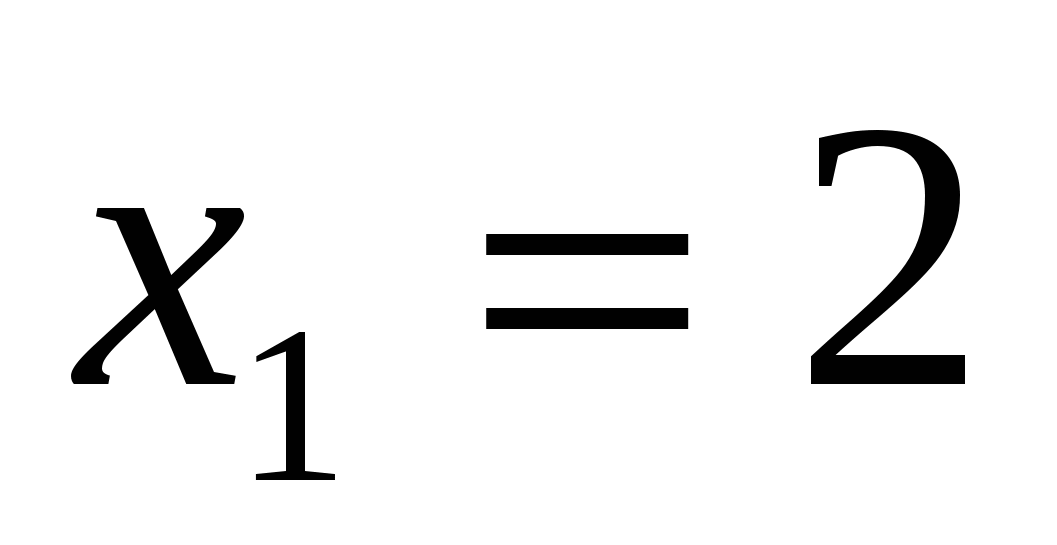 или
или 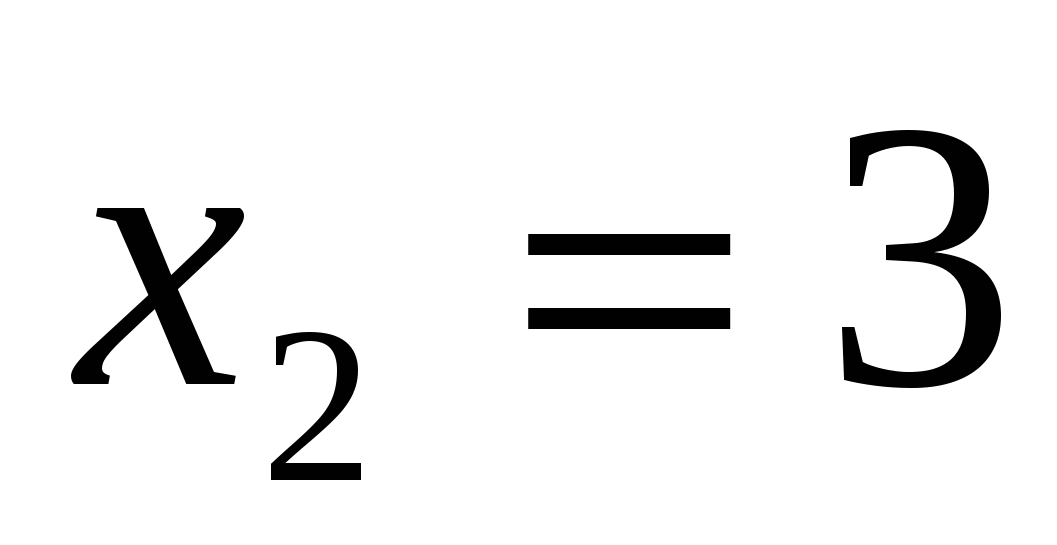
Ответ: 2; 3.
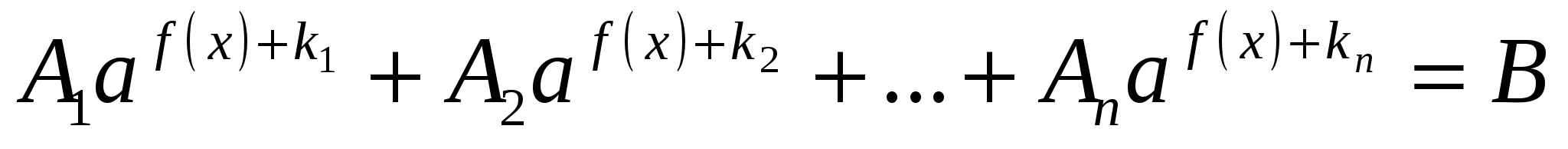
(A, k,B числовые коэффициенты)
1 )вынести общий множитель за скобки
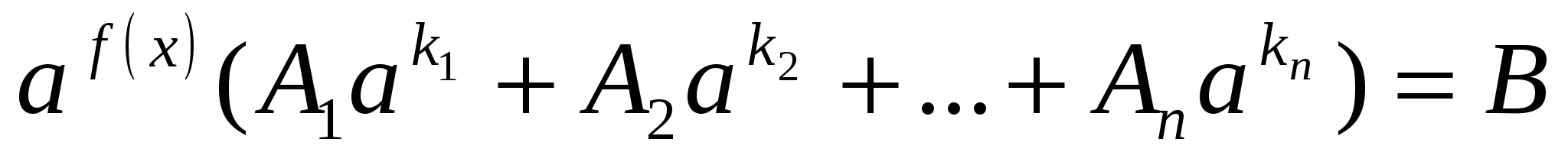
2) выполнить преобразования и привести уравнение к виду
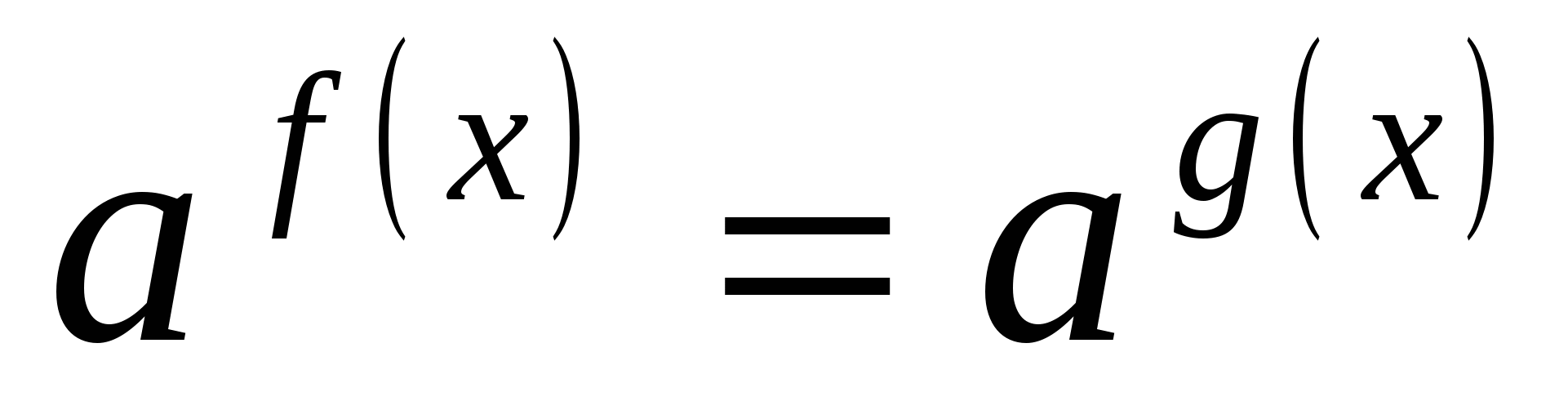
а) 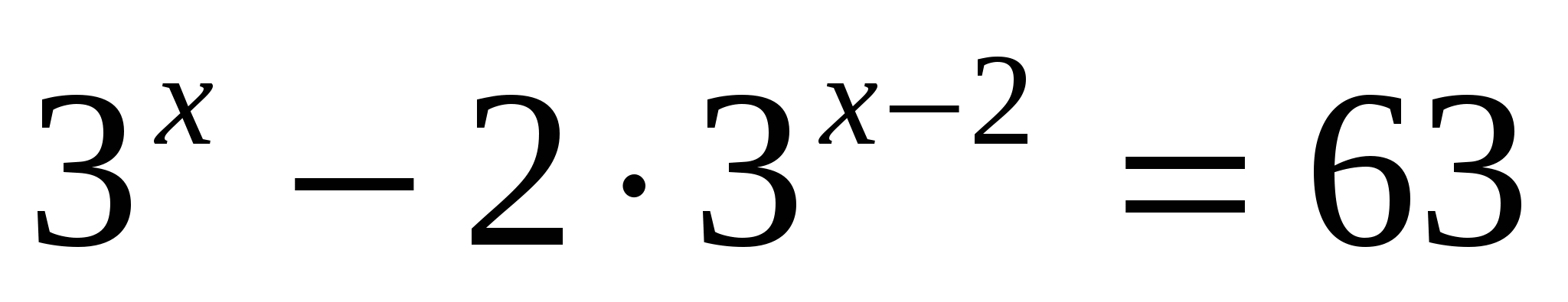
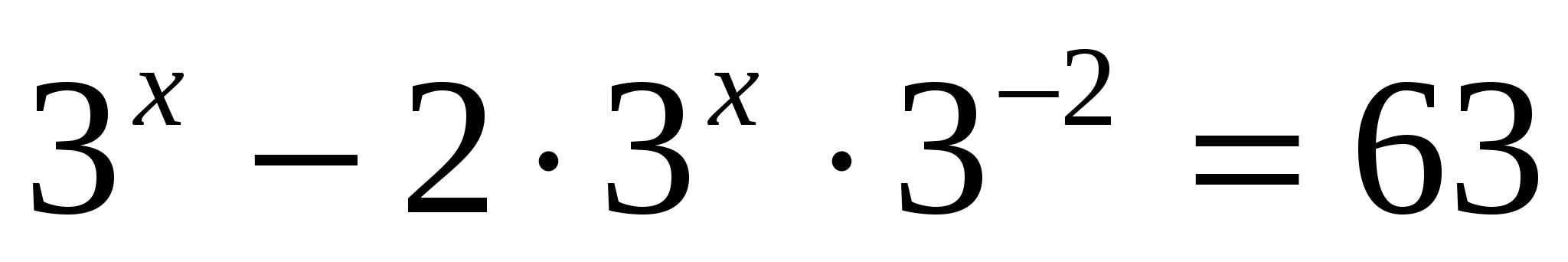
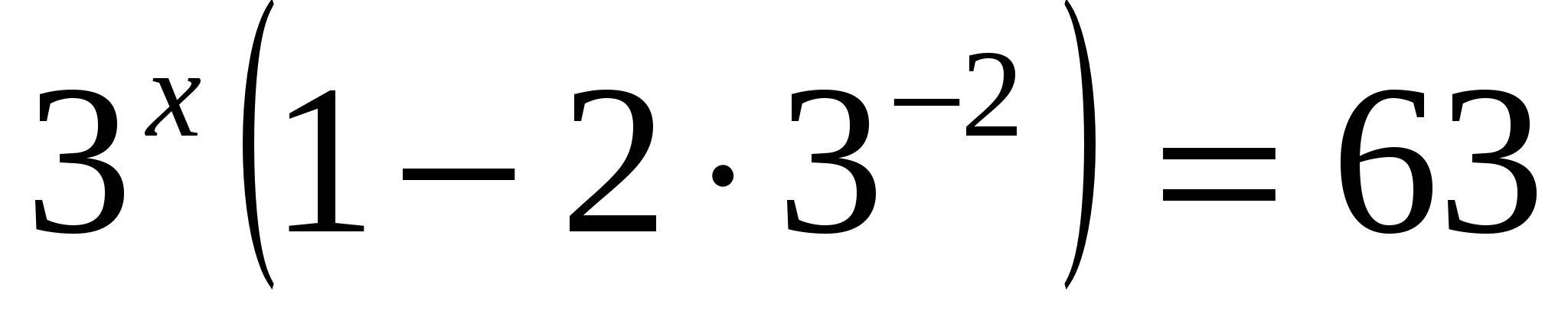
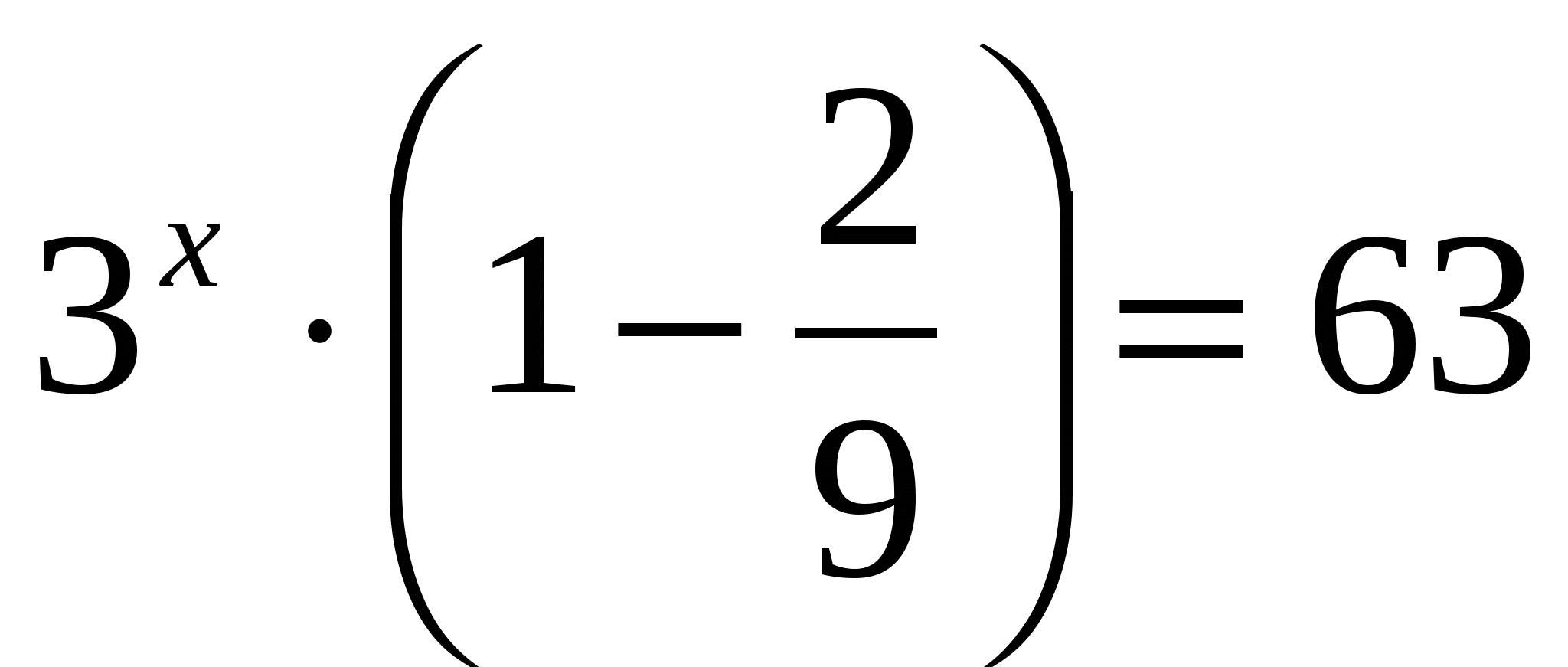
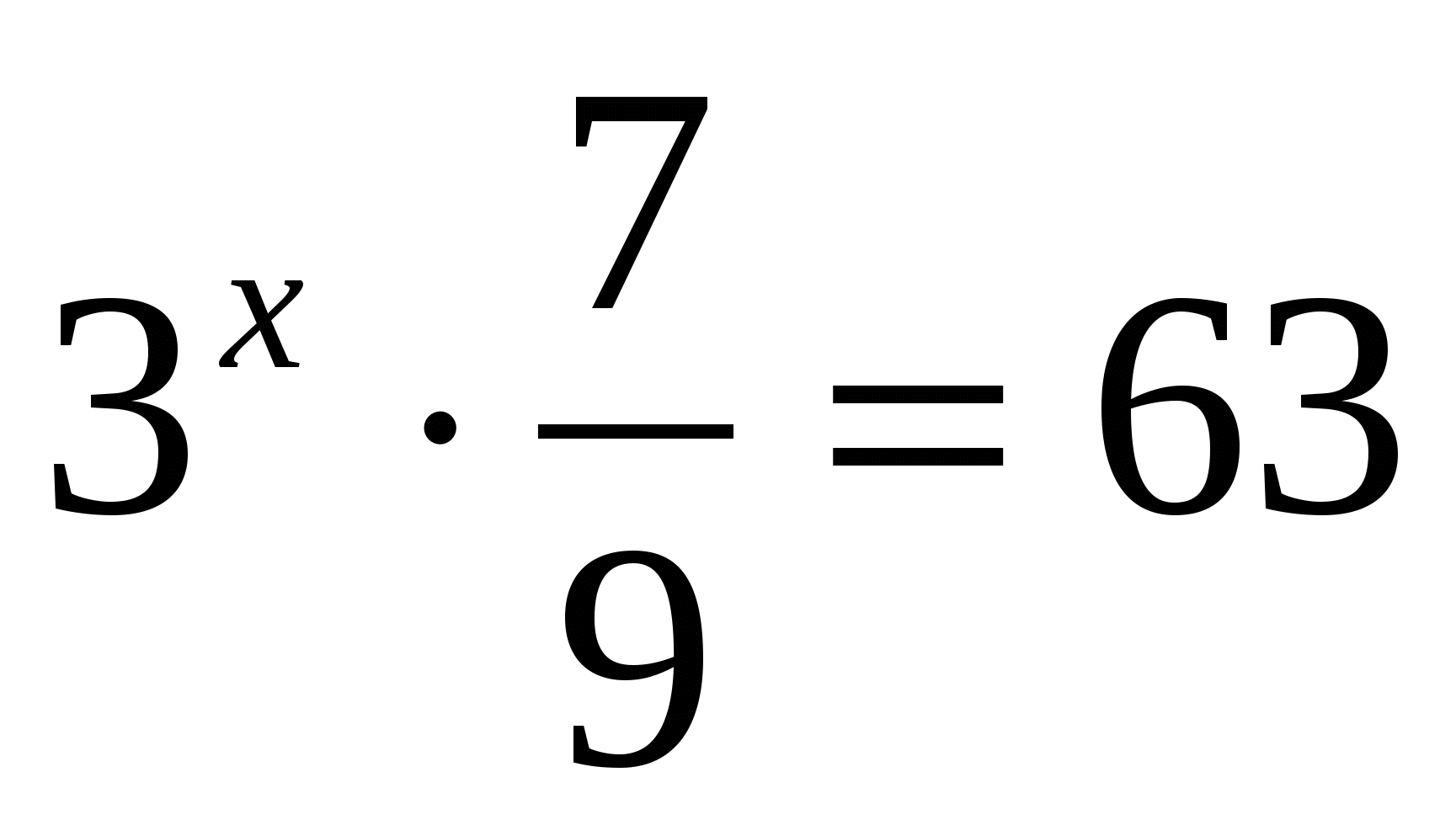
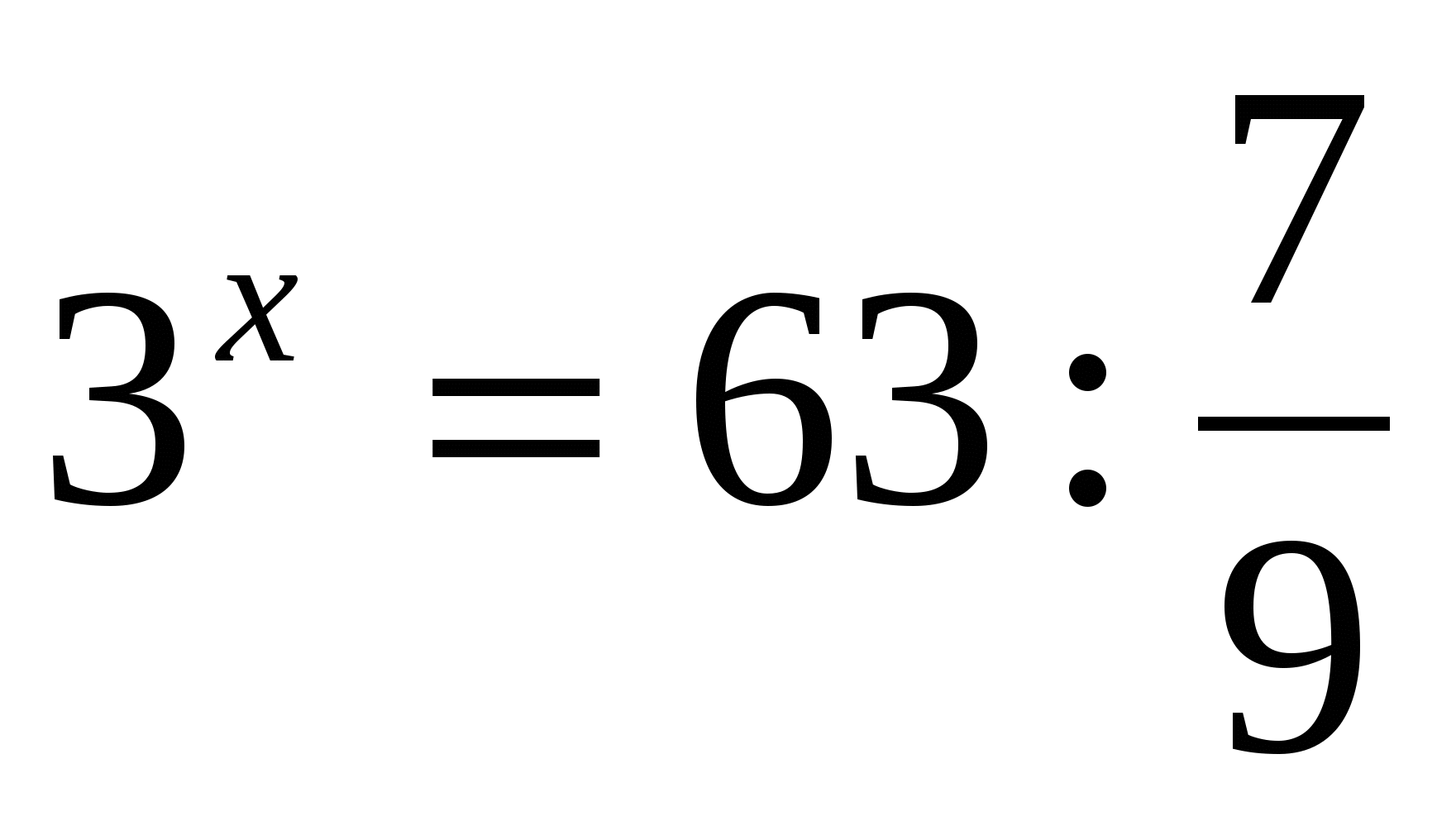
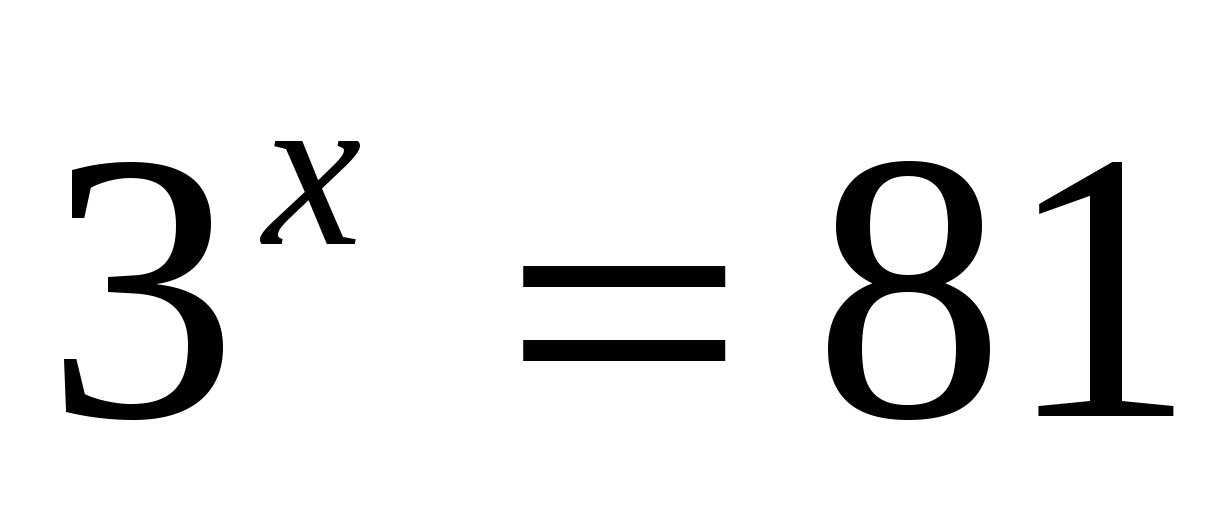
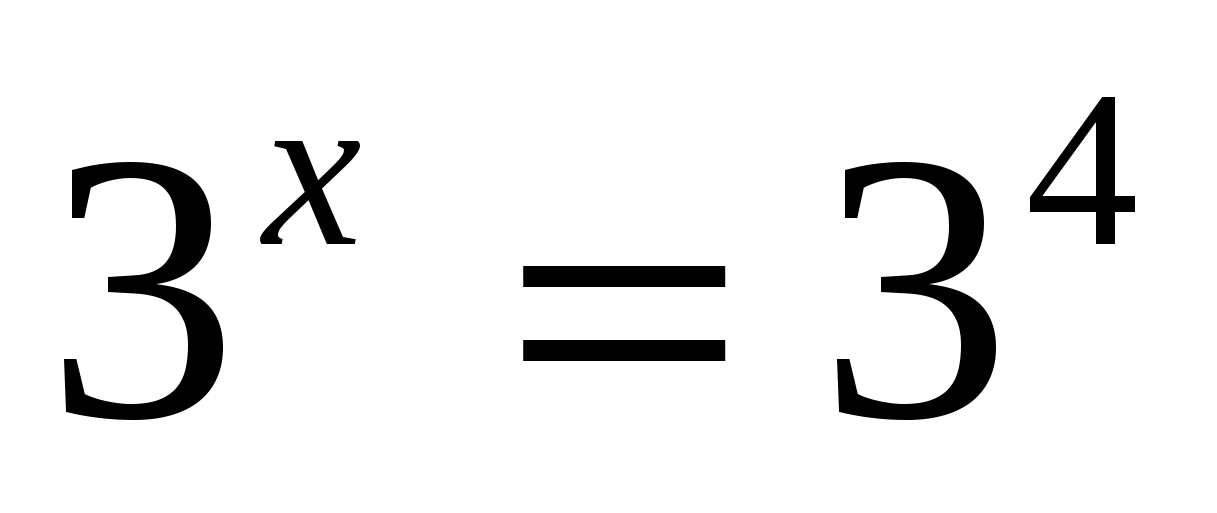
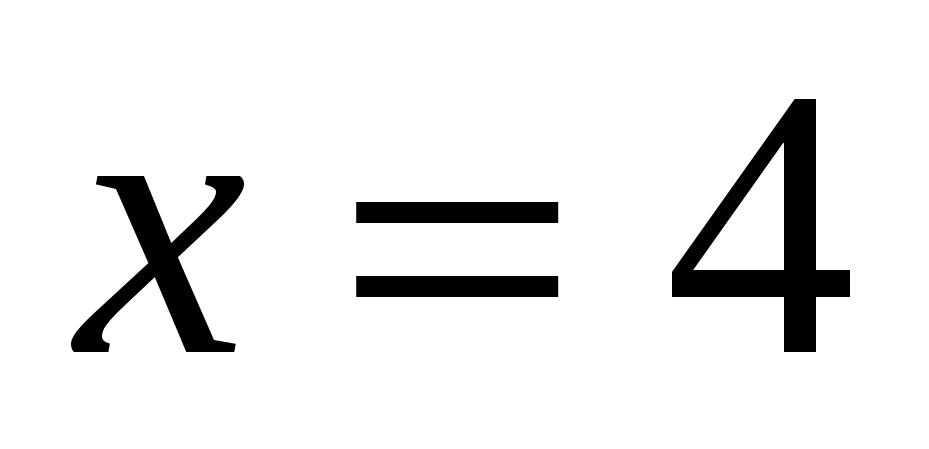
Ответ: 4.
б) 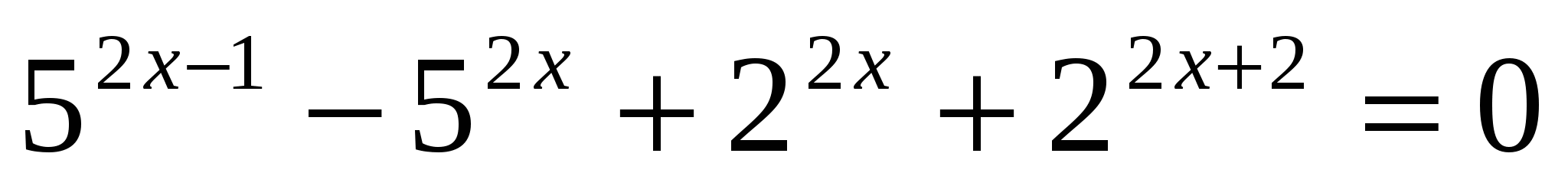
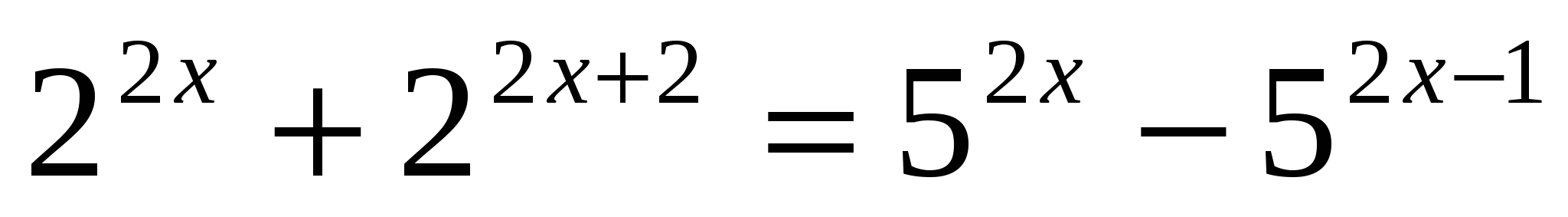
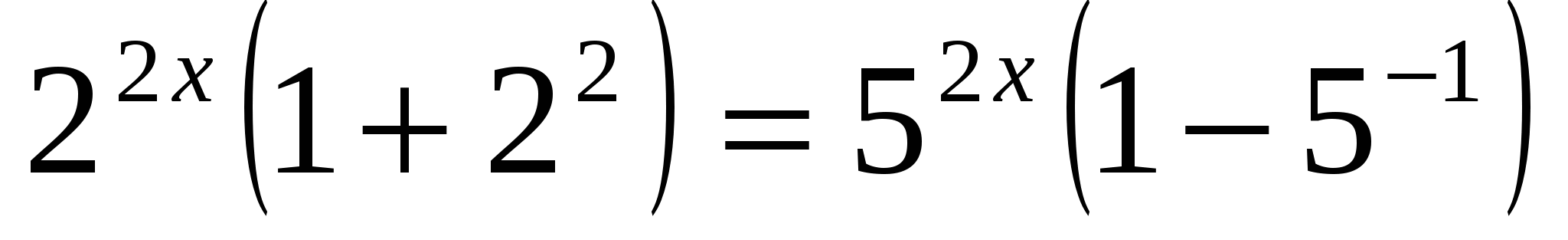
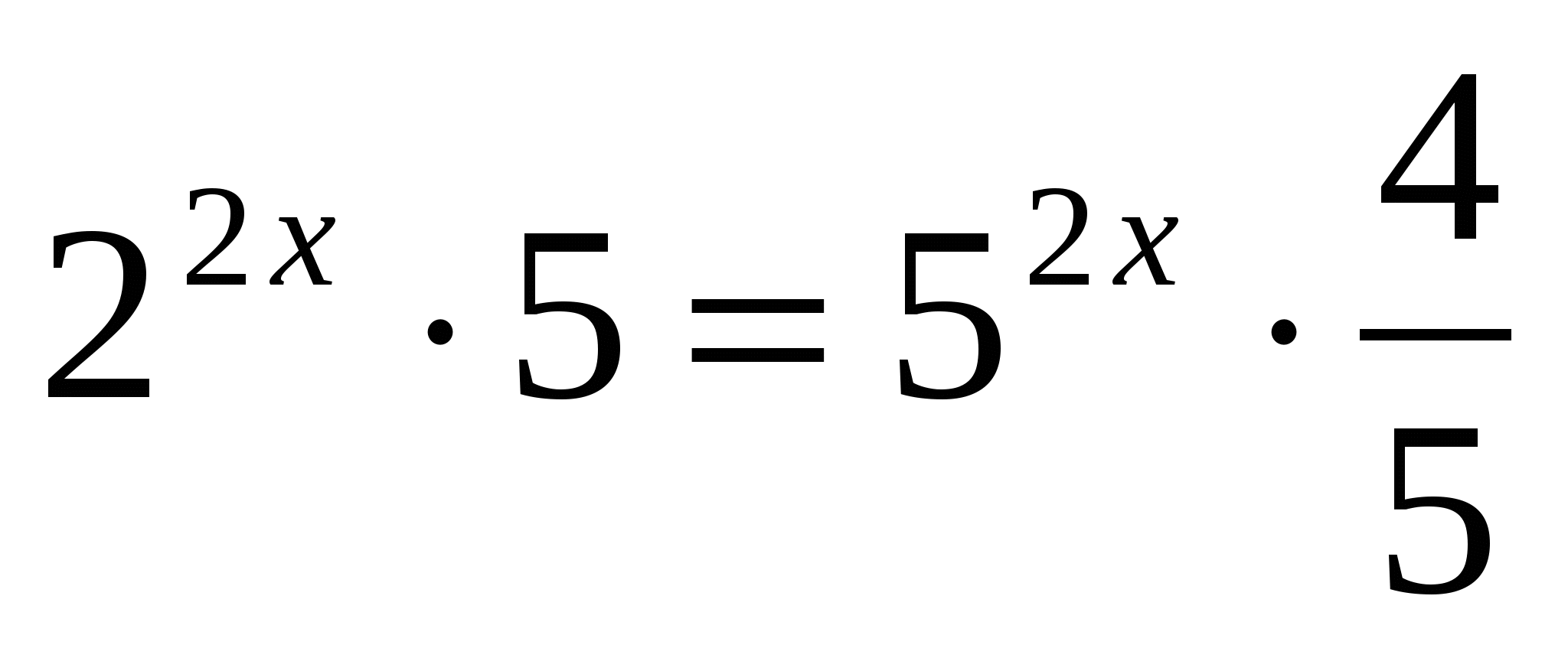
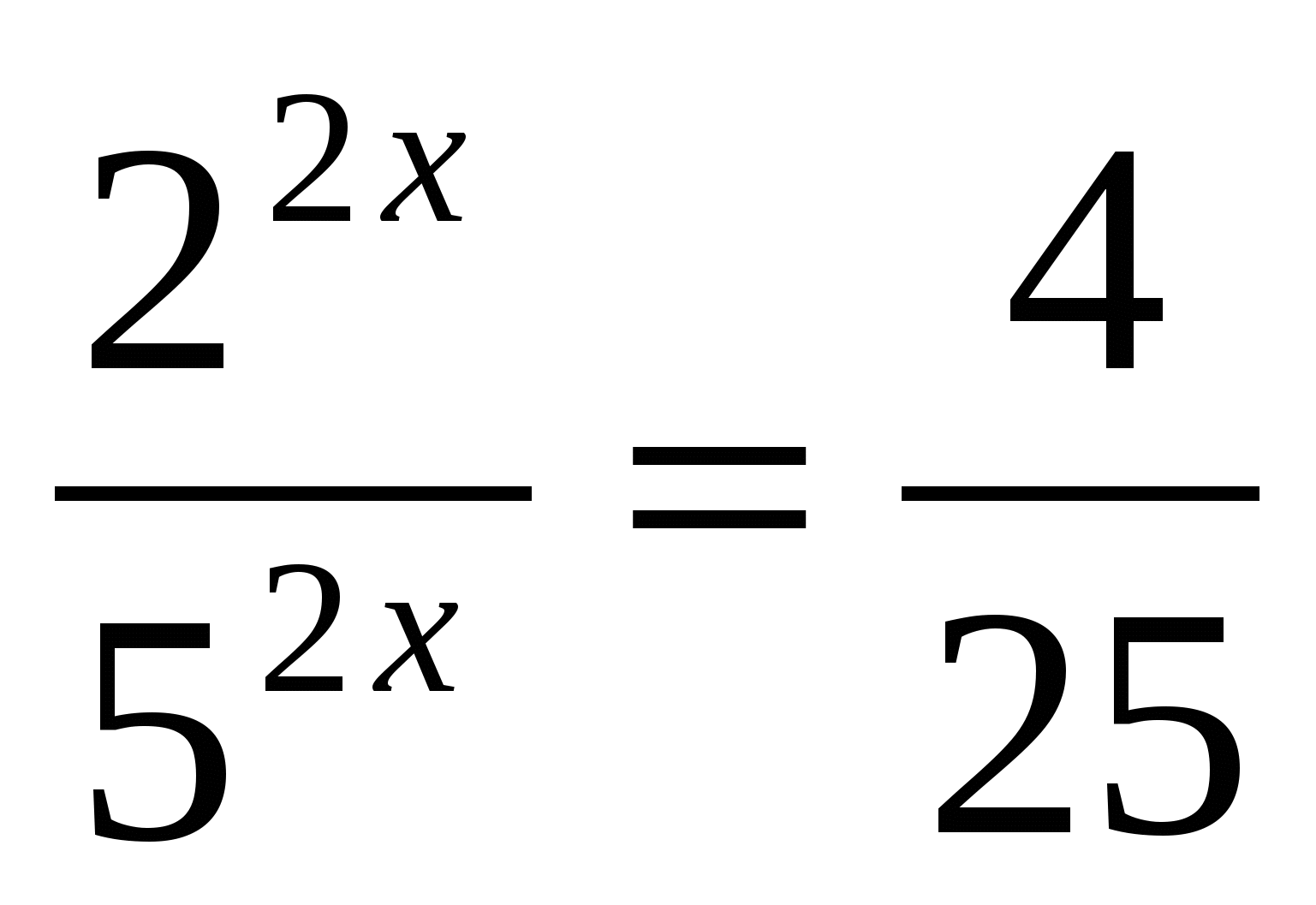
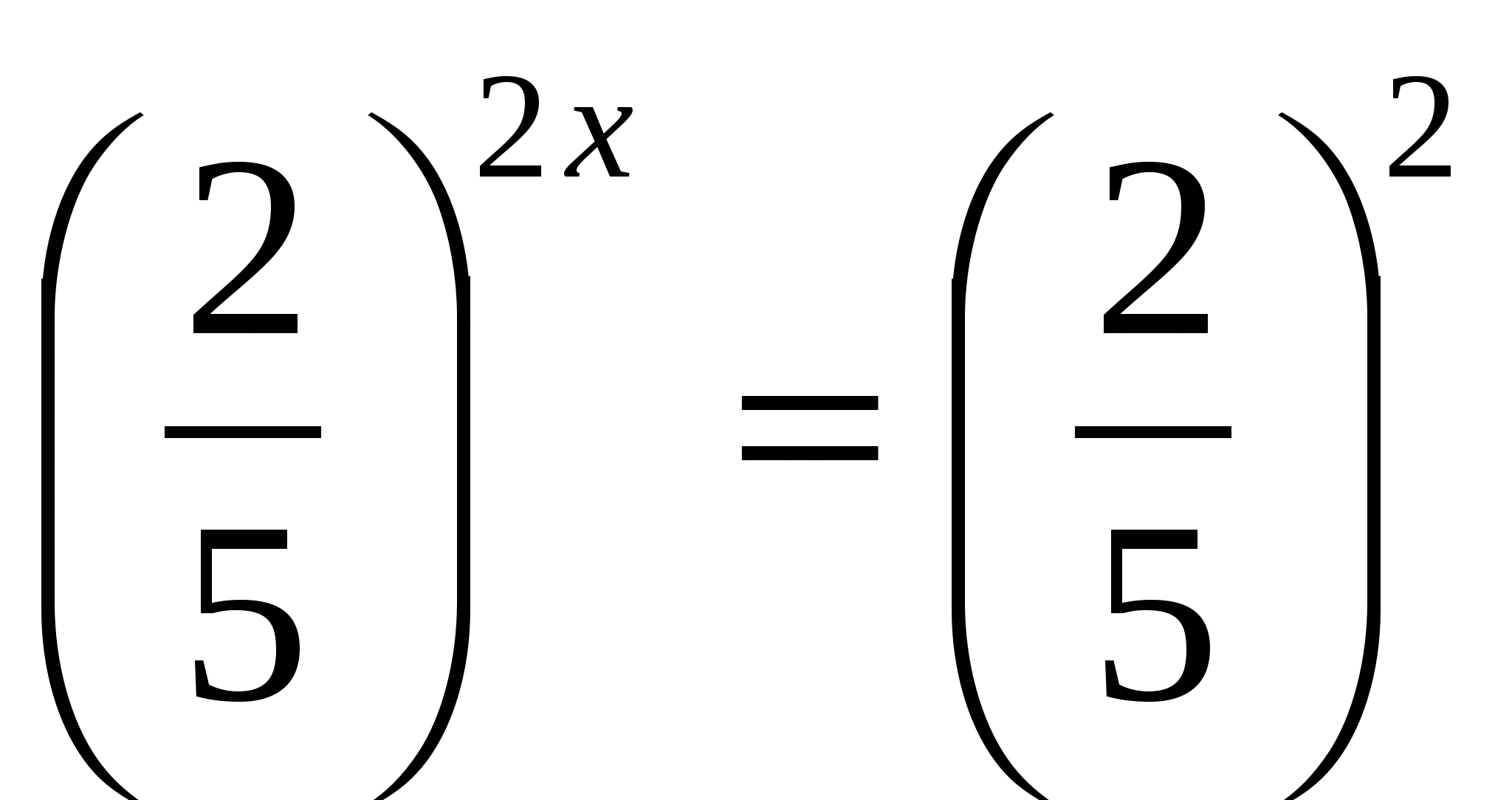
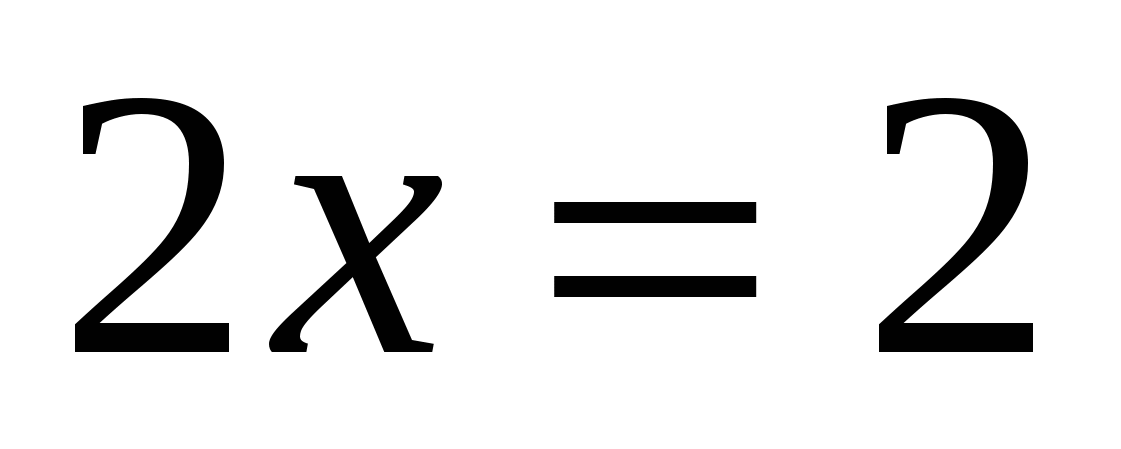
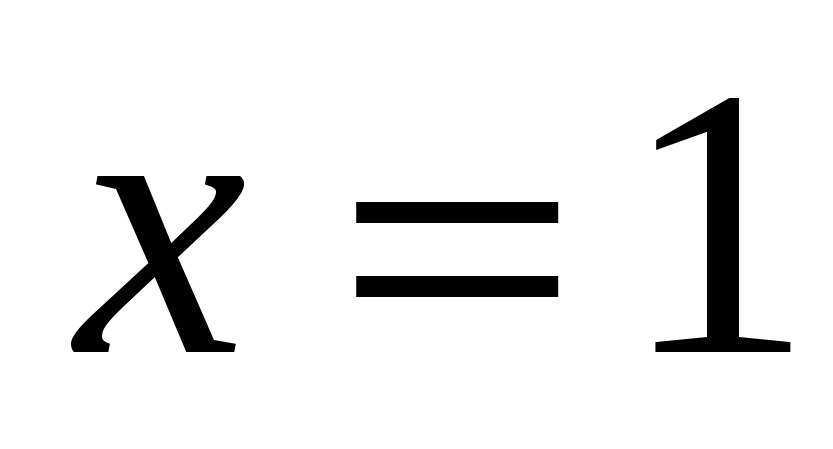
Ответ: 1.
в) 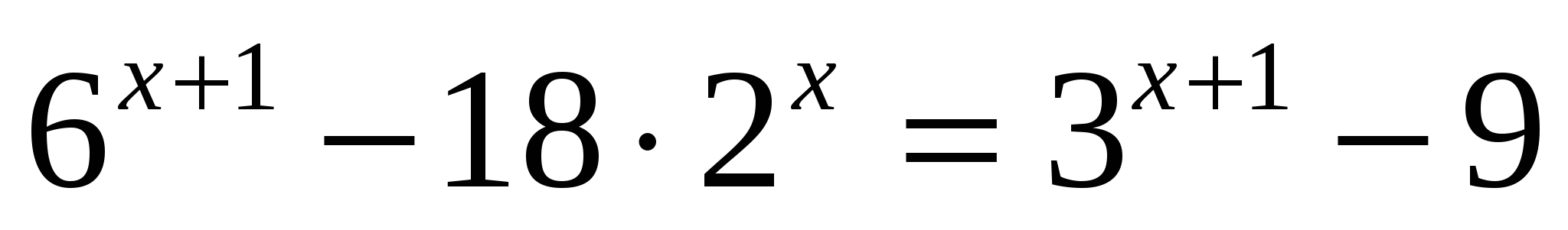
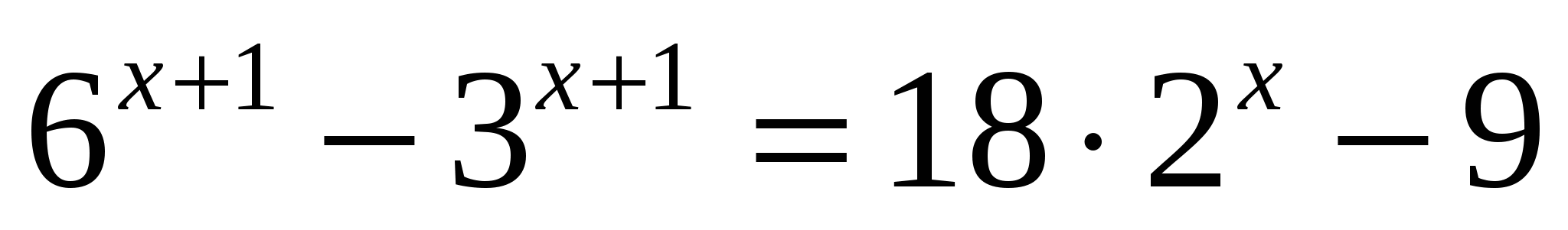
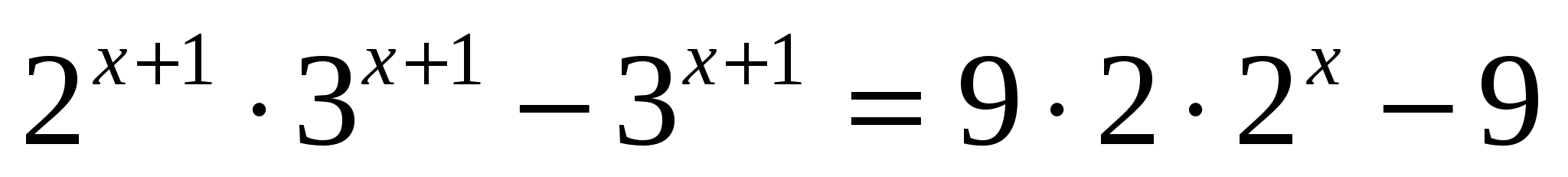
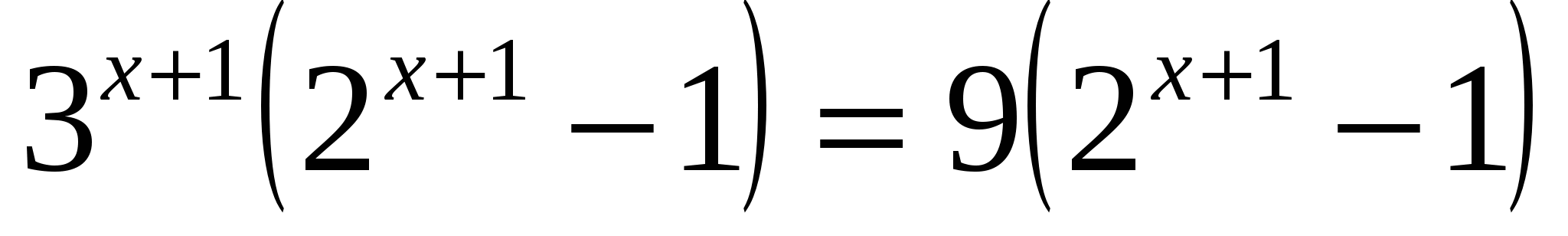
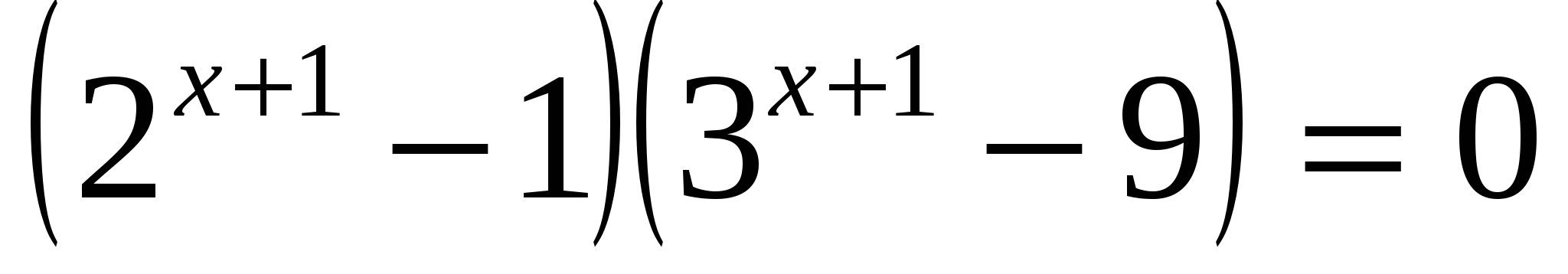
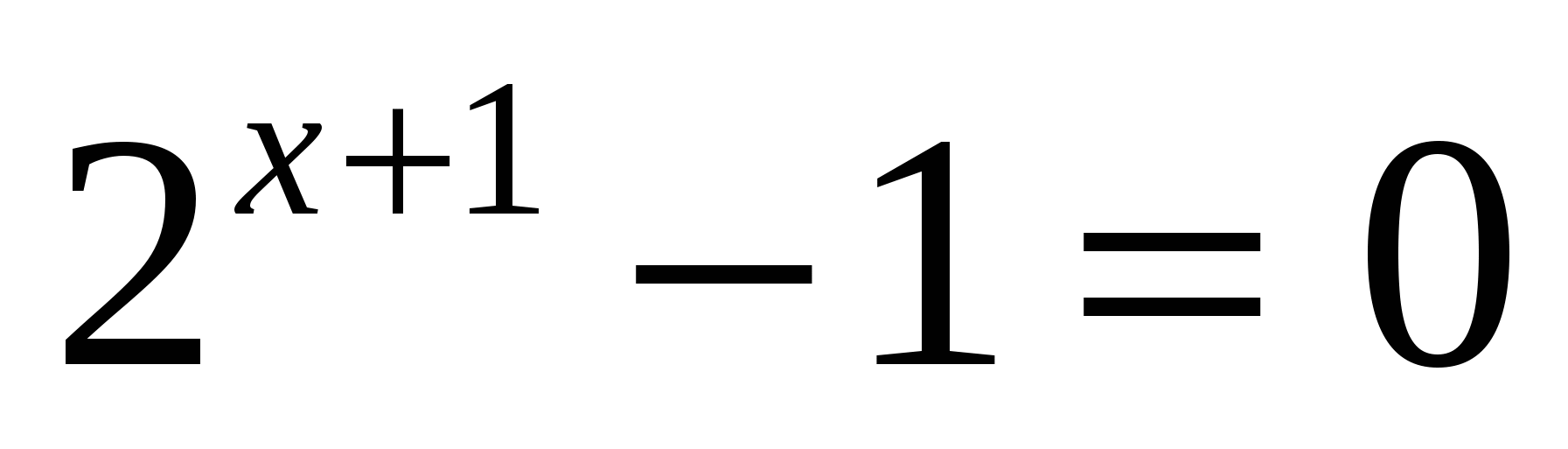 или
или 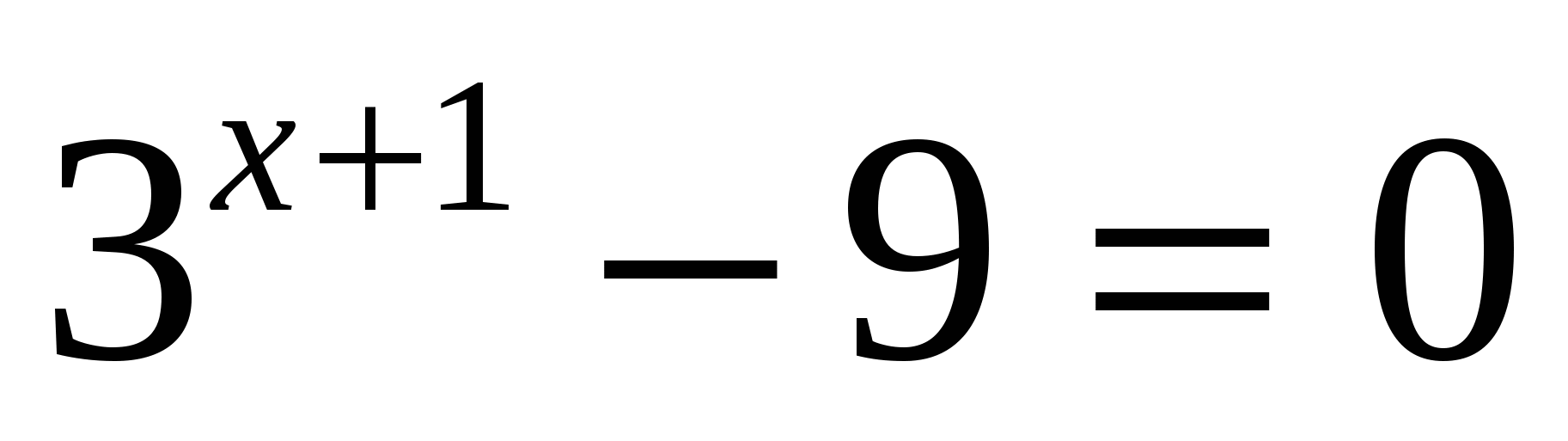
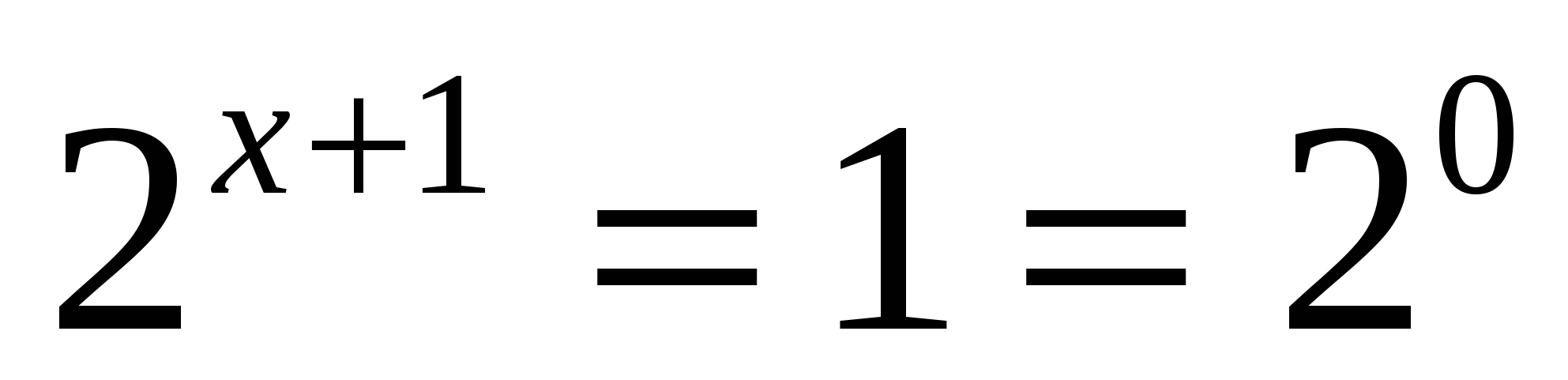
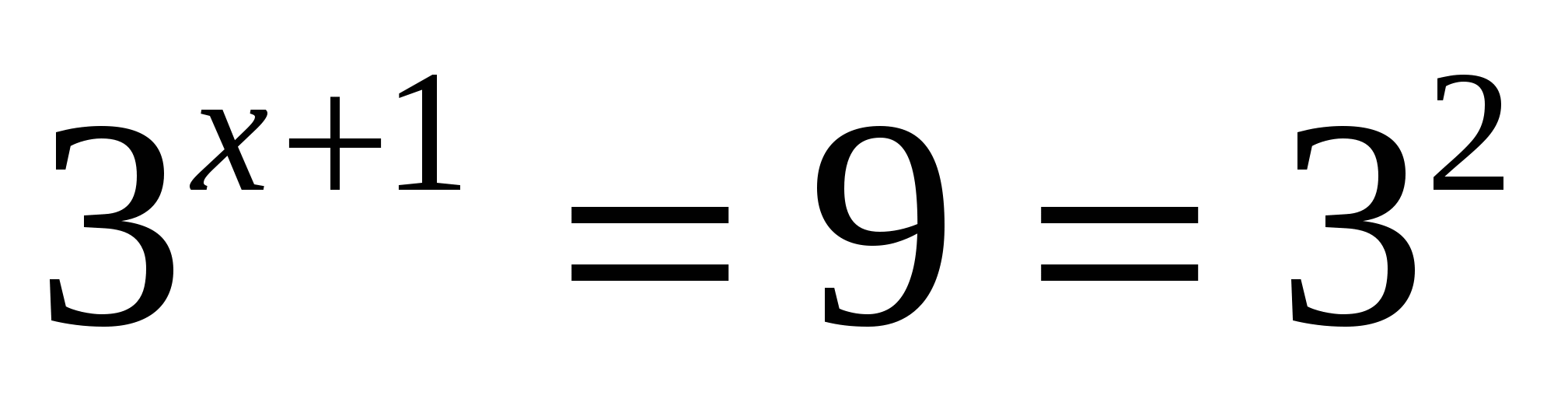
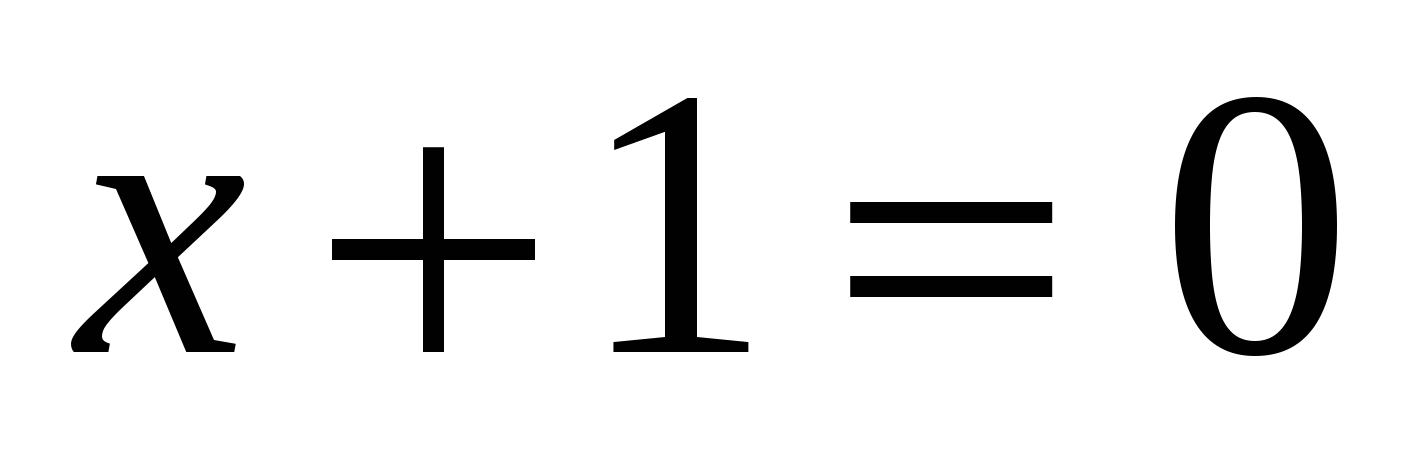
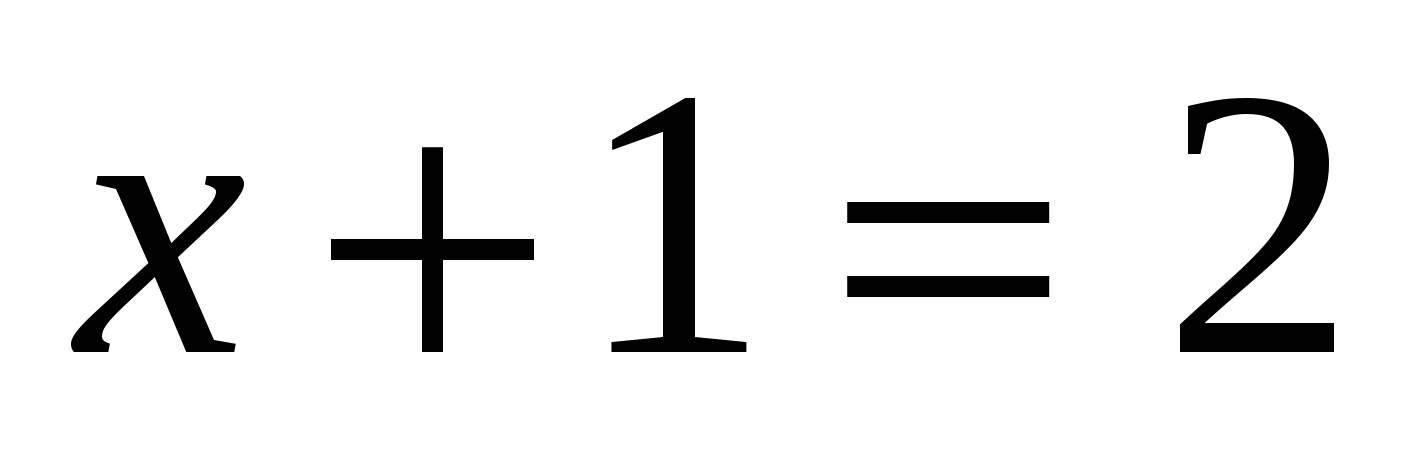
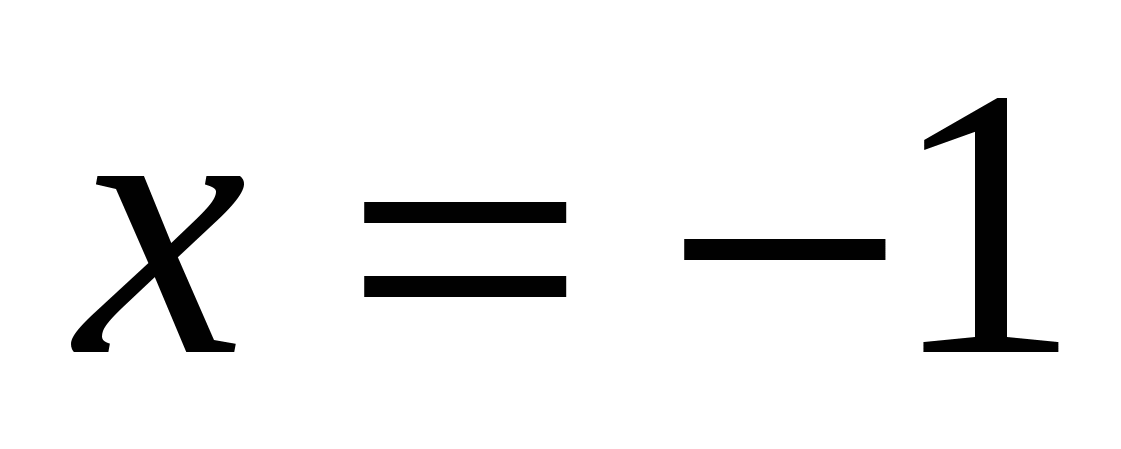
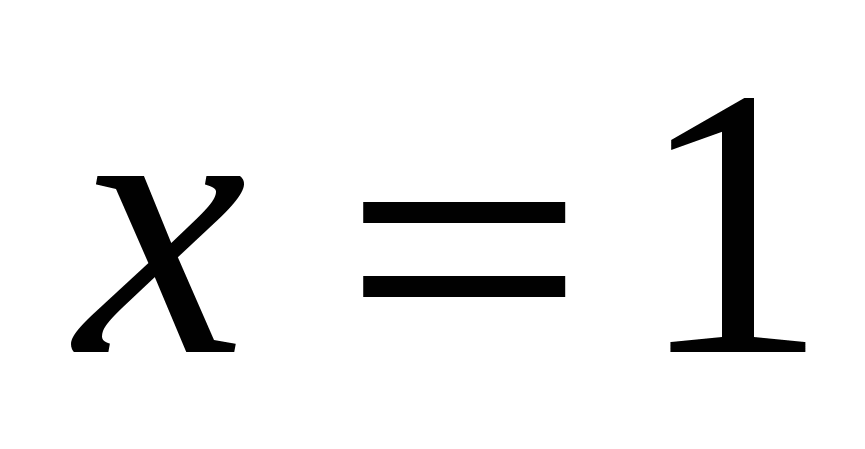
Ответ: -1; 1.
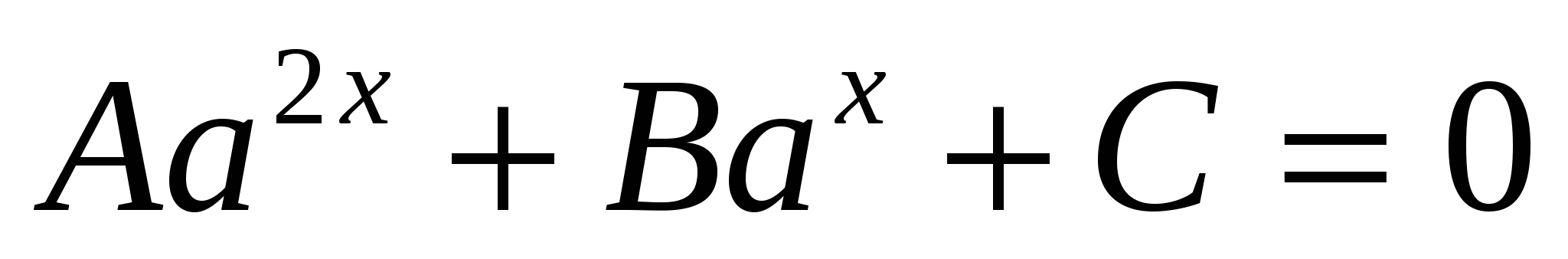
1) обозначить 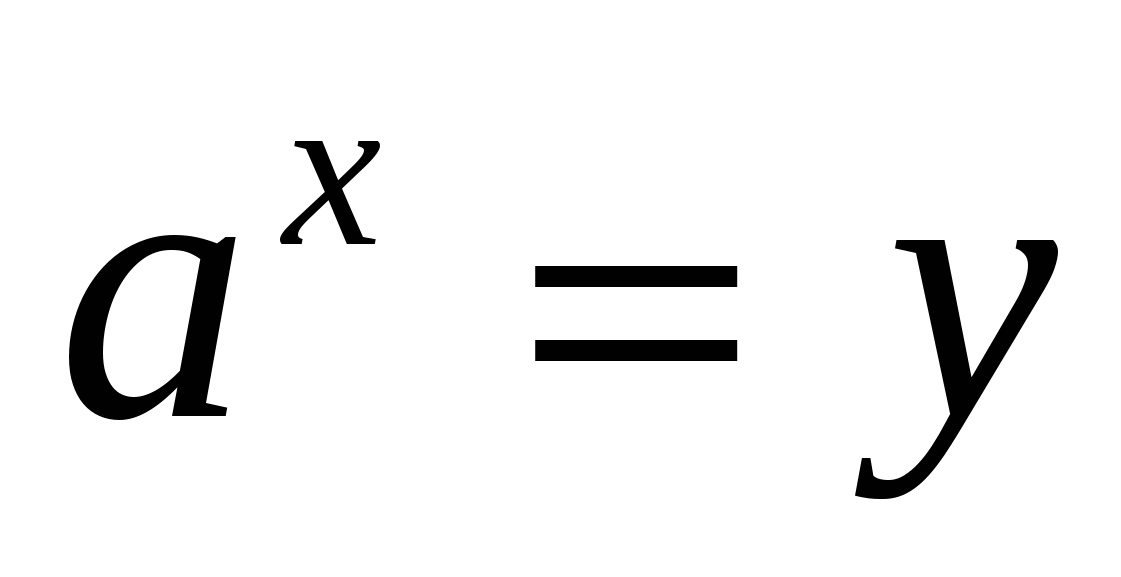
2) решить полученное квадратное уравнение 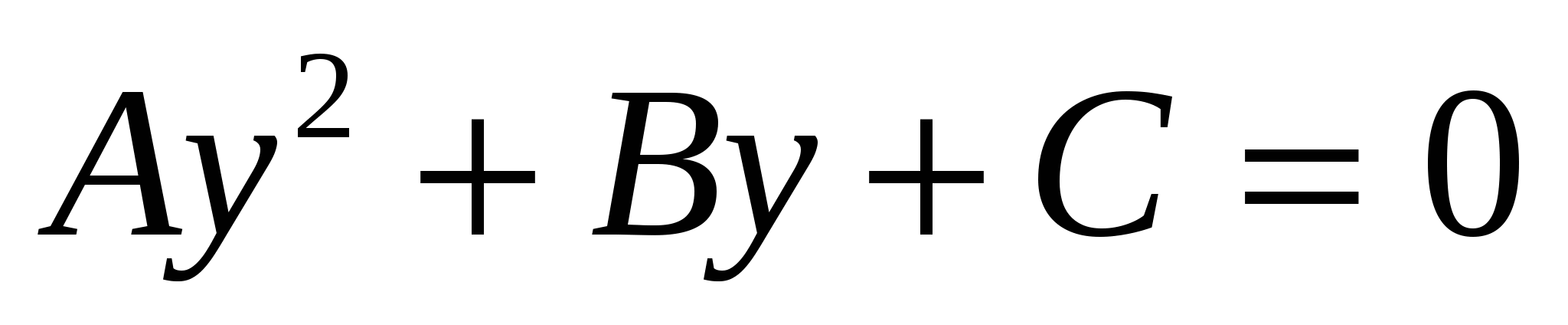 относительно у
относительно у
3) выполнить обратную замену и решить уравнения 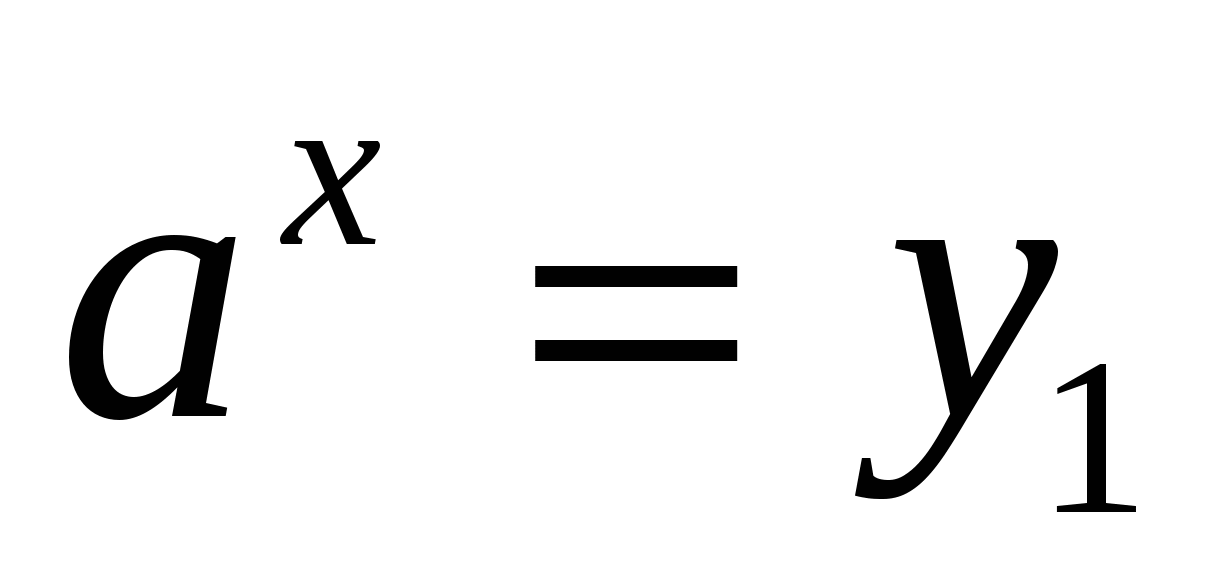 ,
, 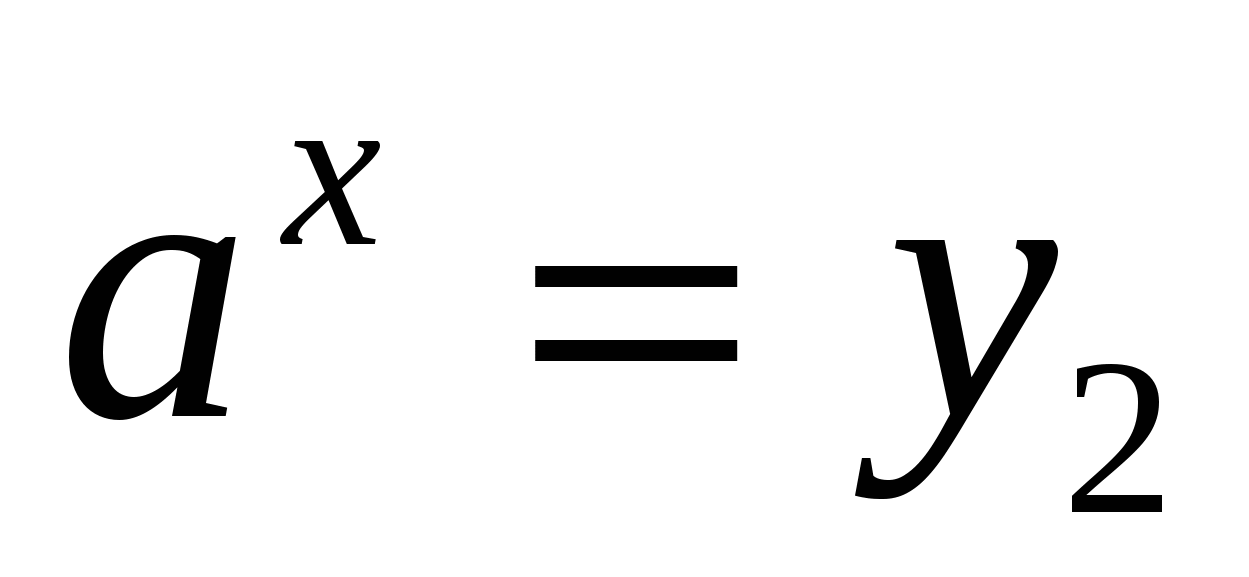 относительно х
относительно х
а) 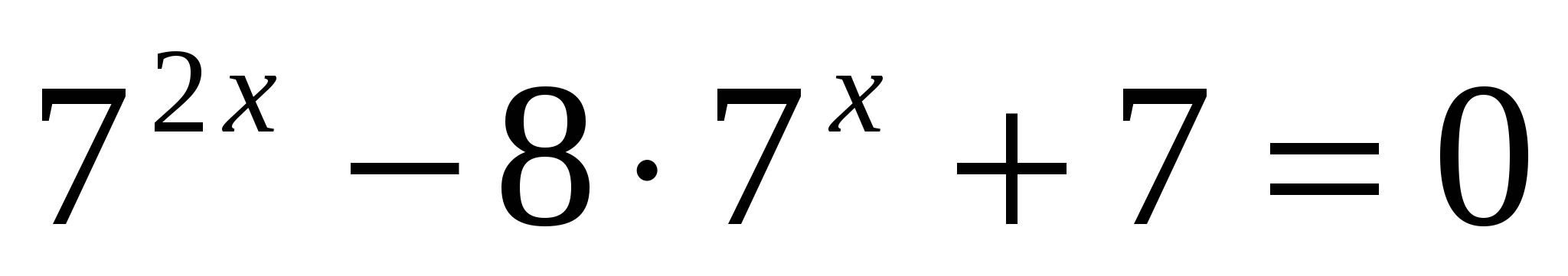
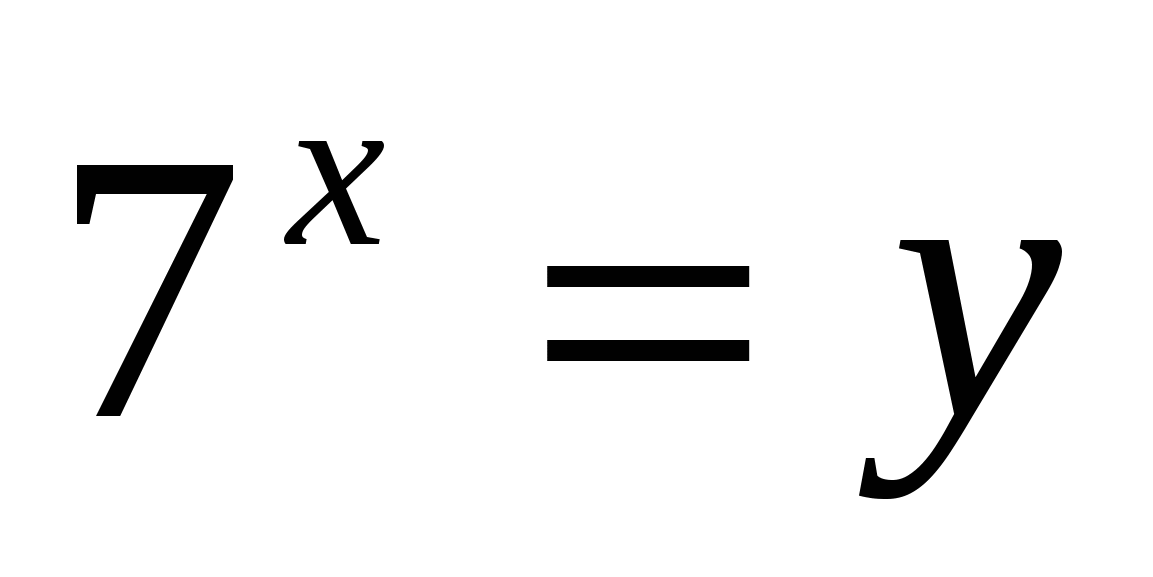
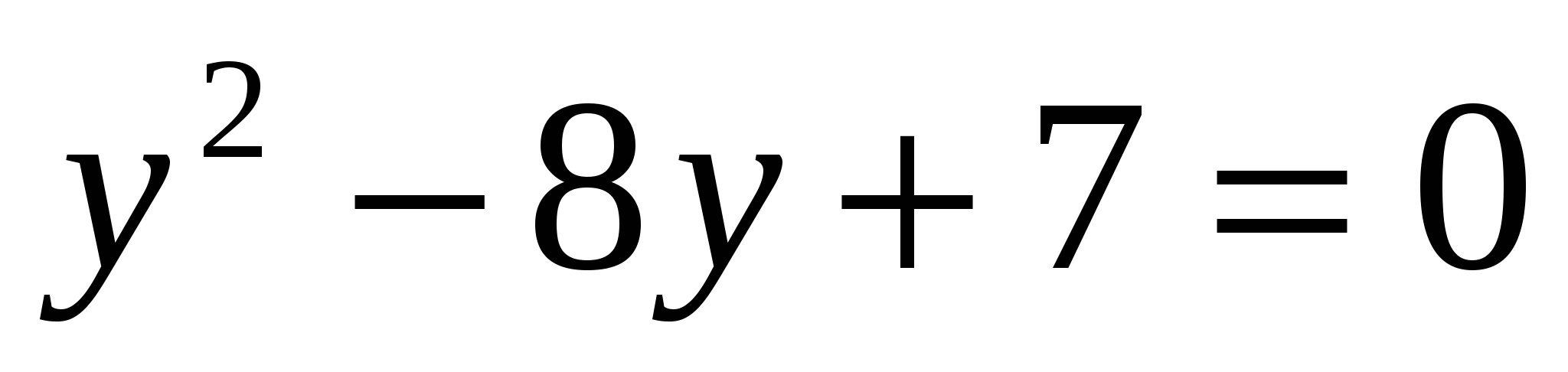
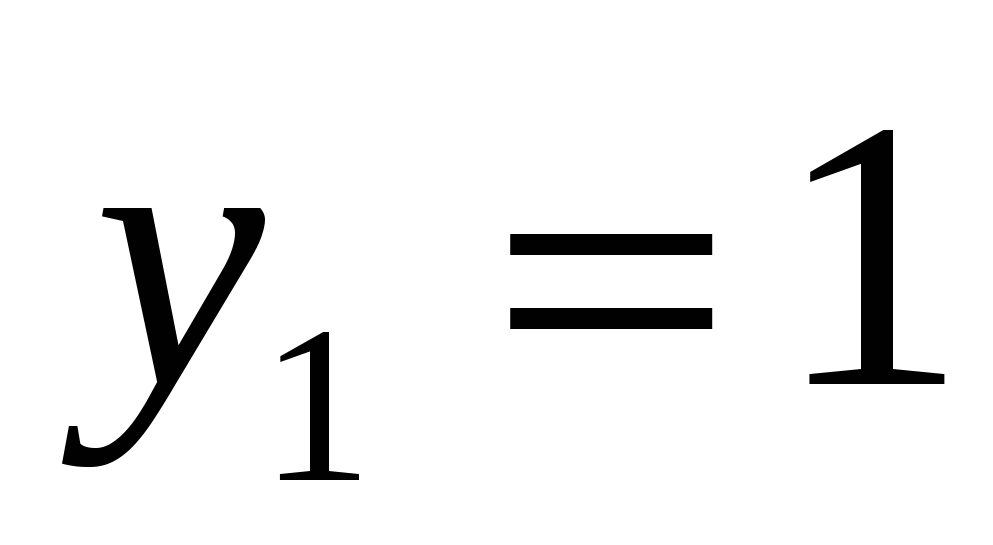 или
или 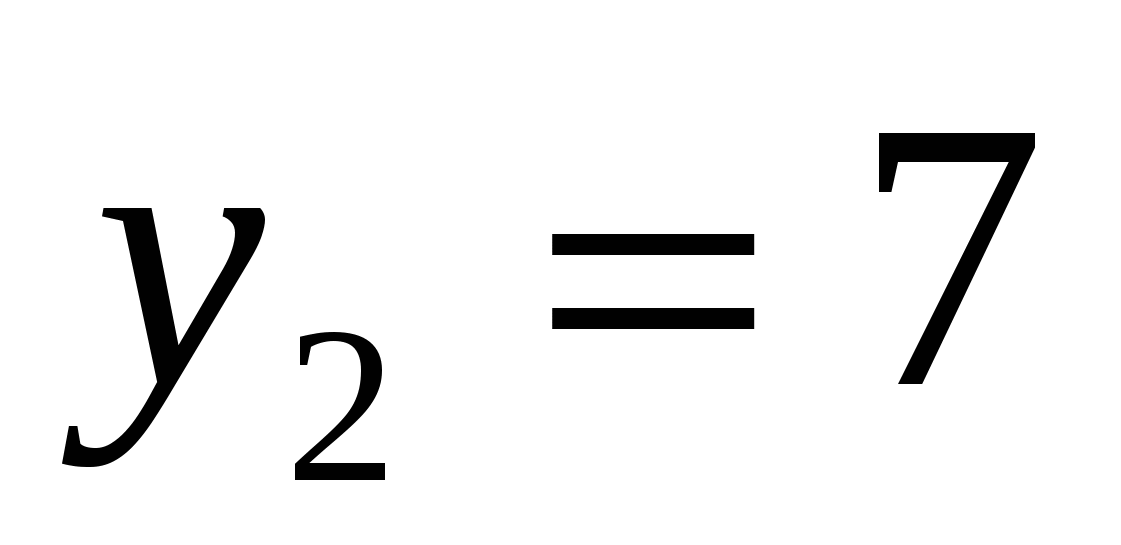
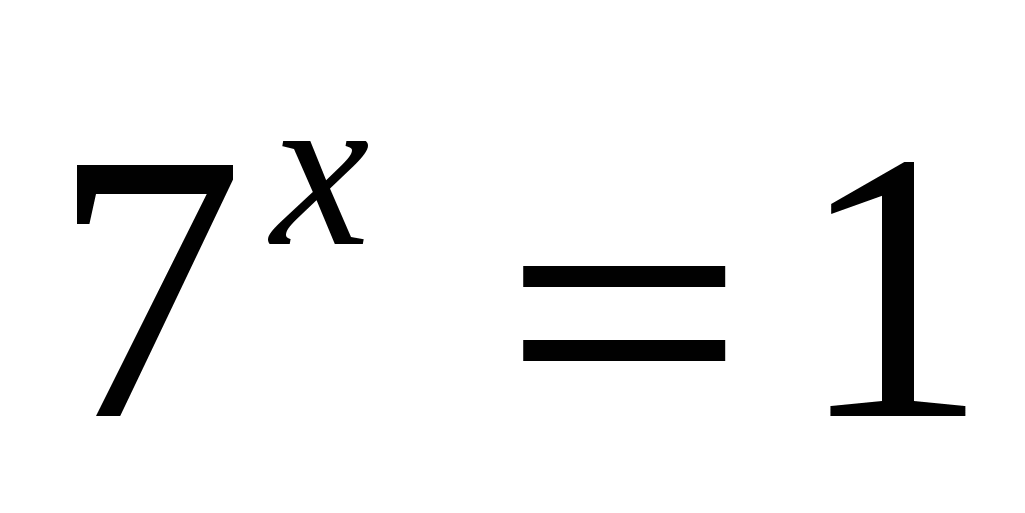
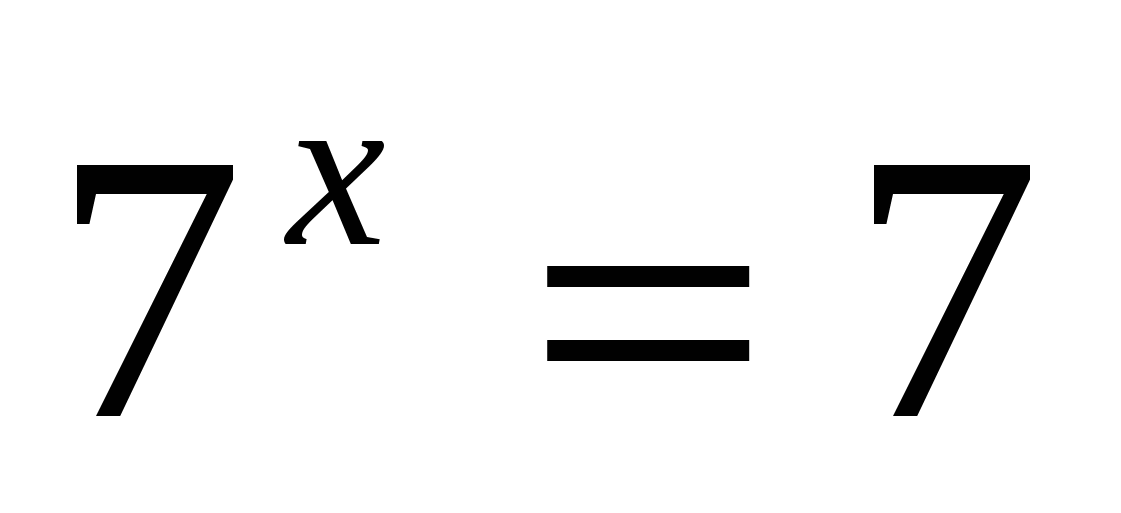
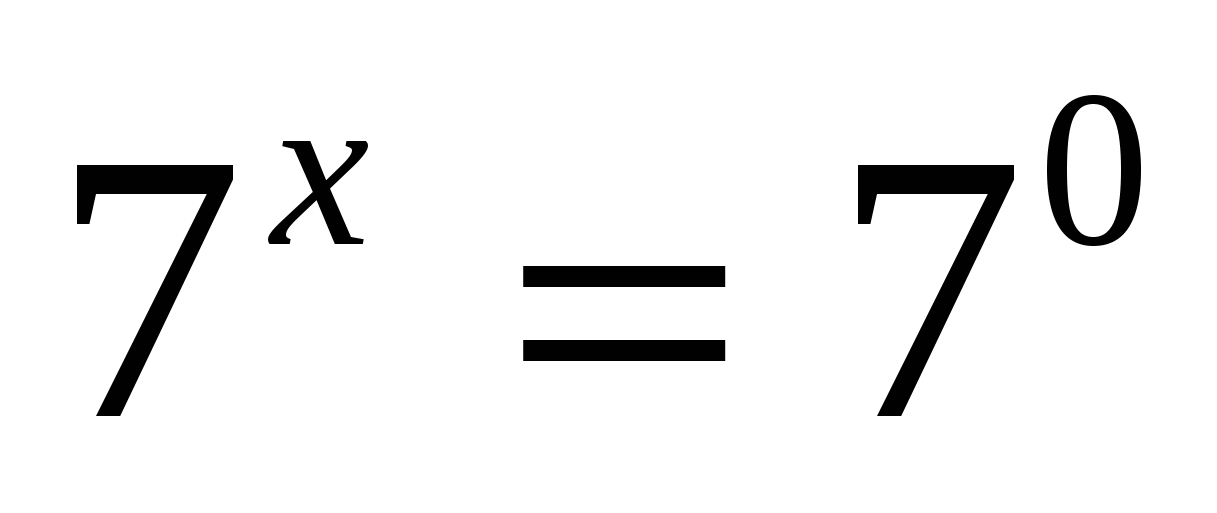
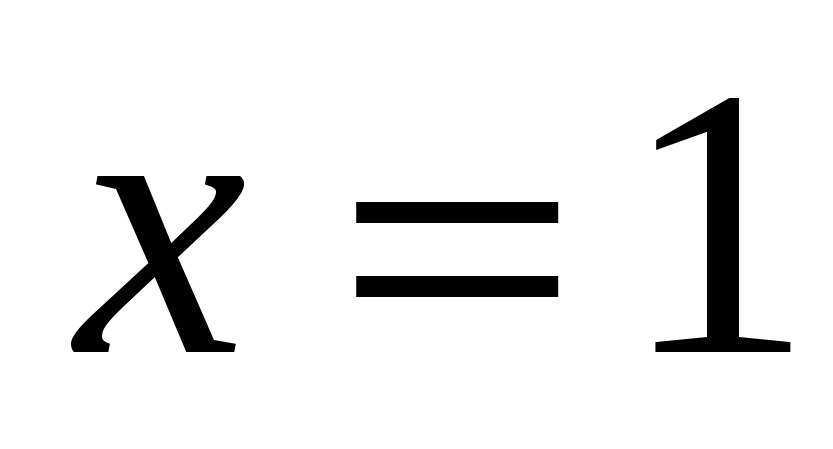
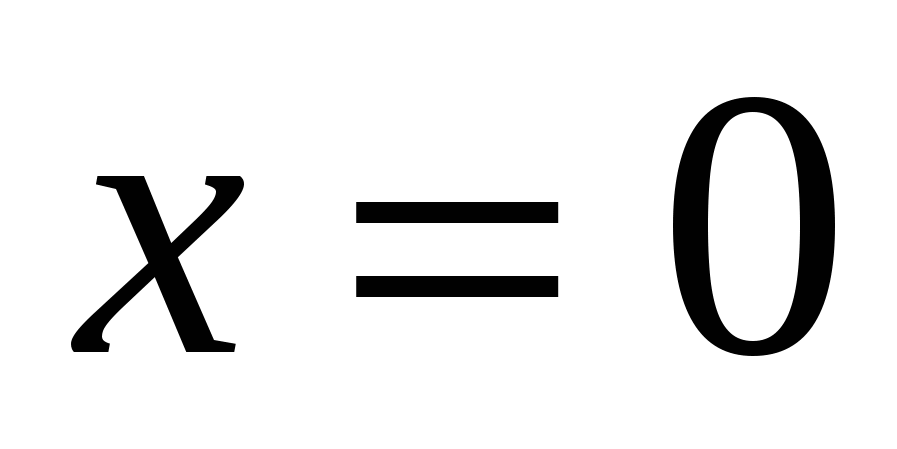
Ответ: 0; 1.
б) 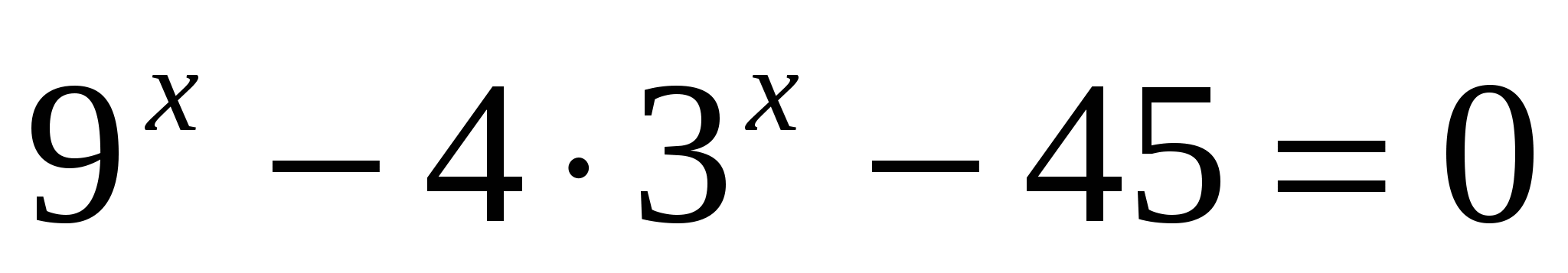
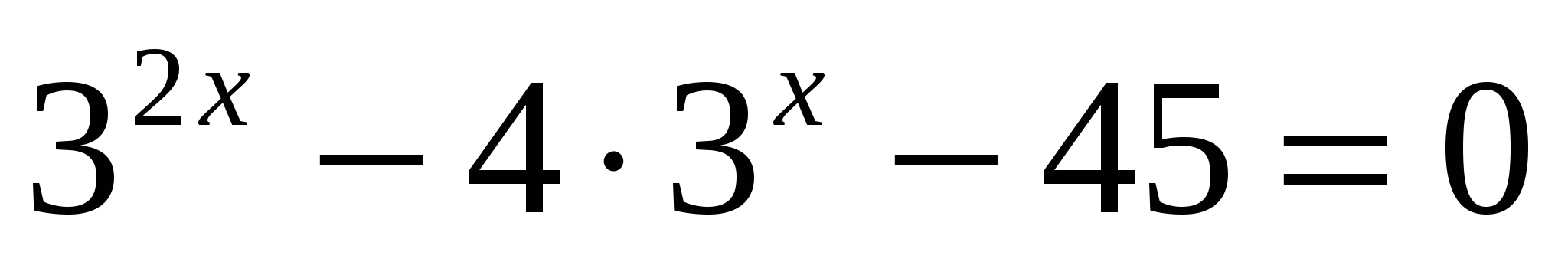
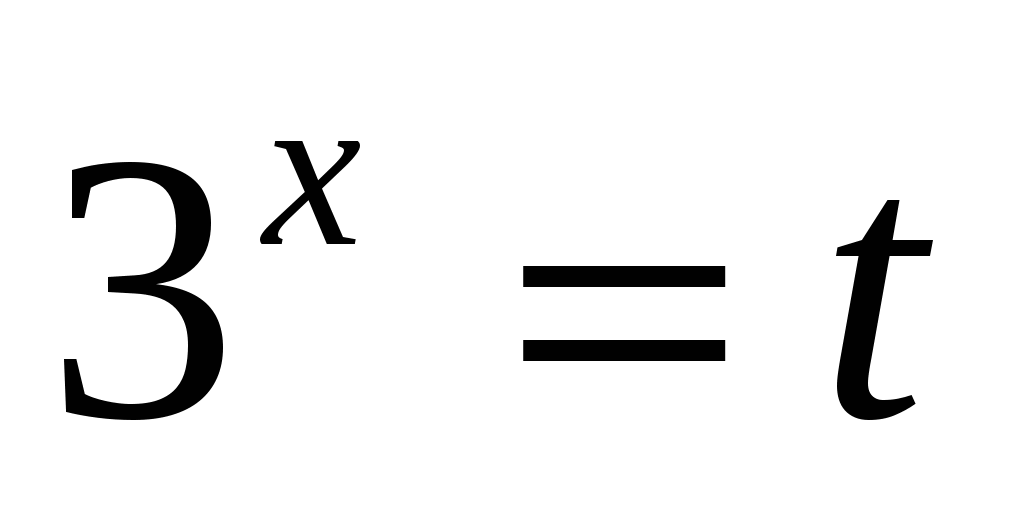
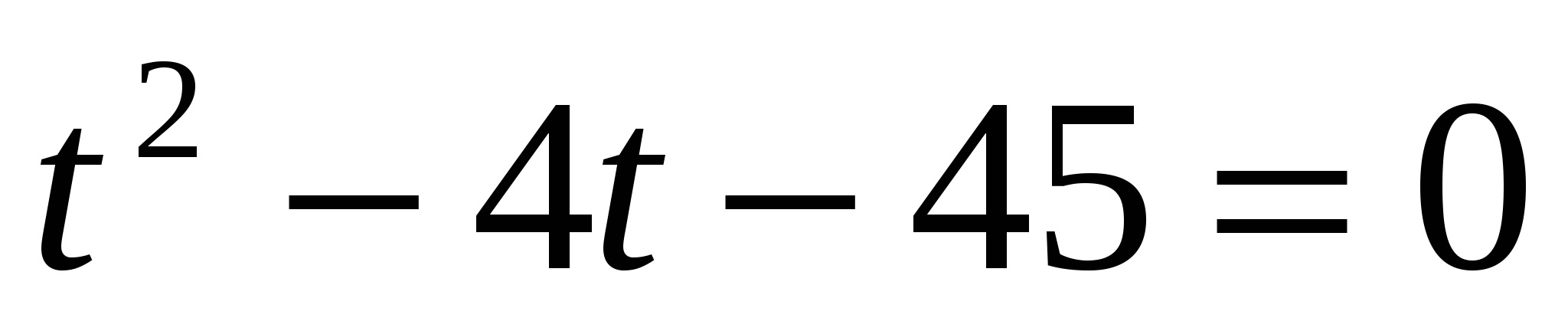
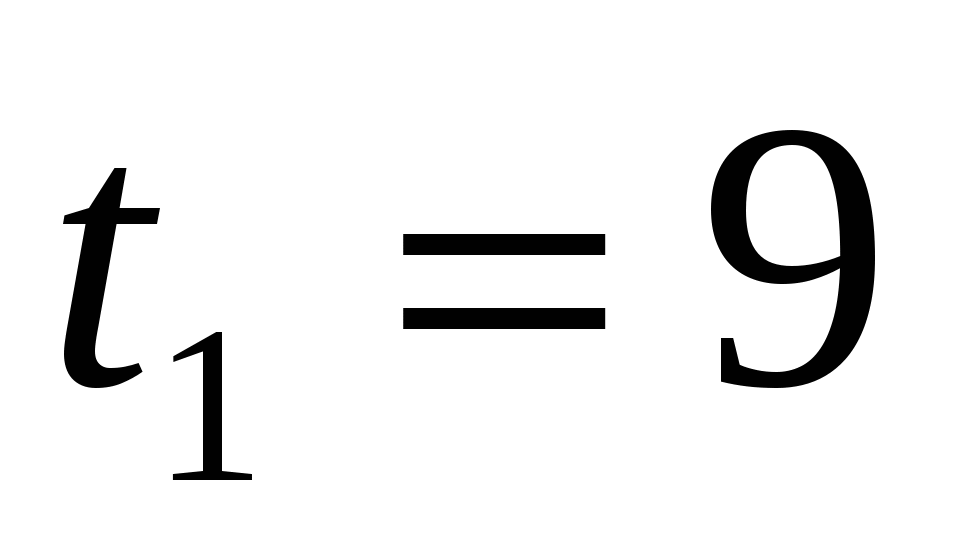 или
или 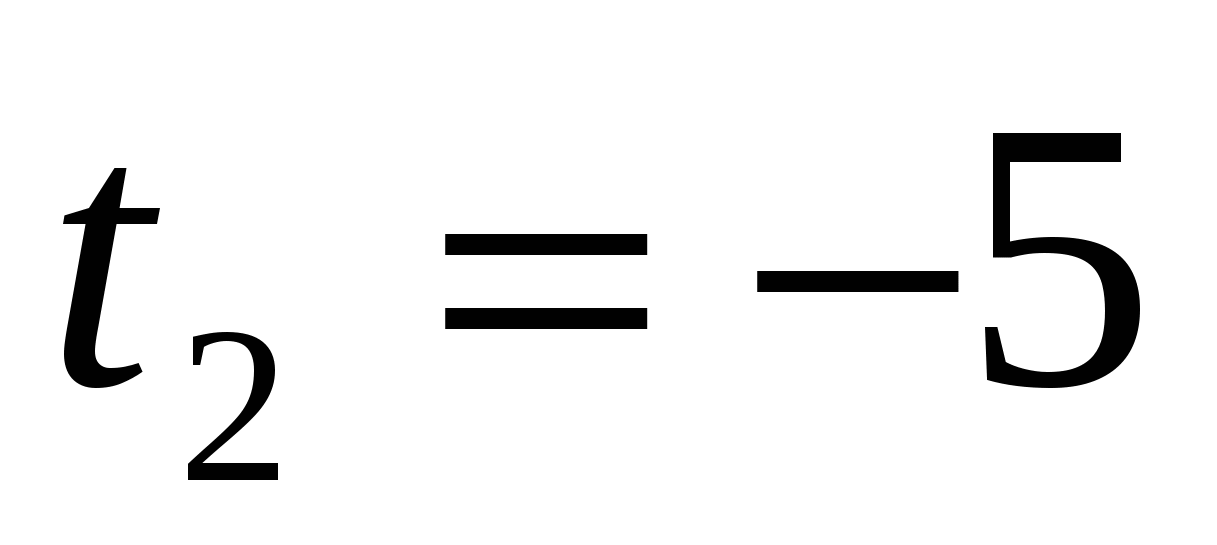
1) 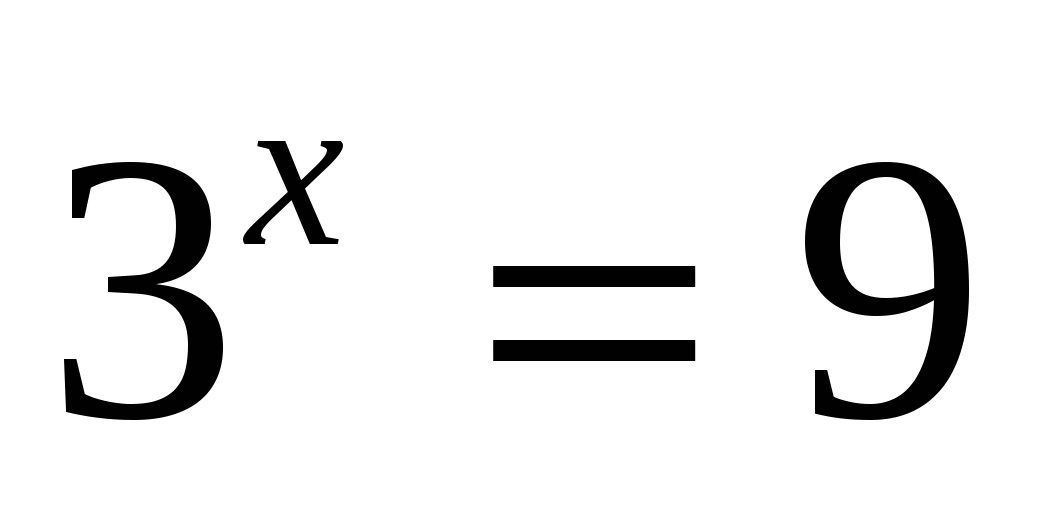
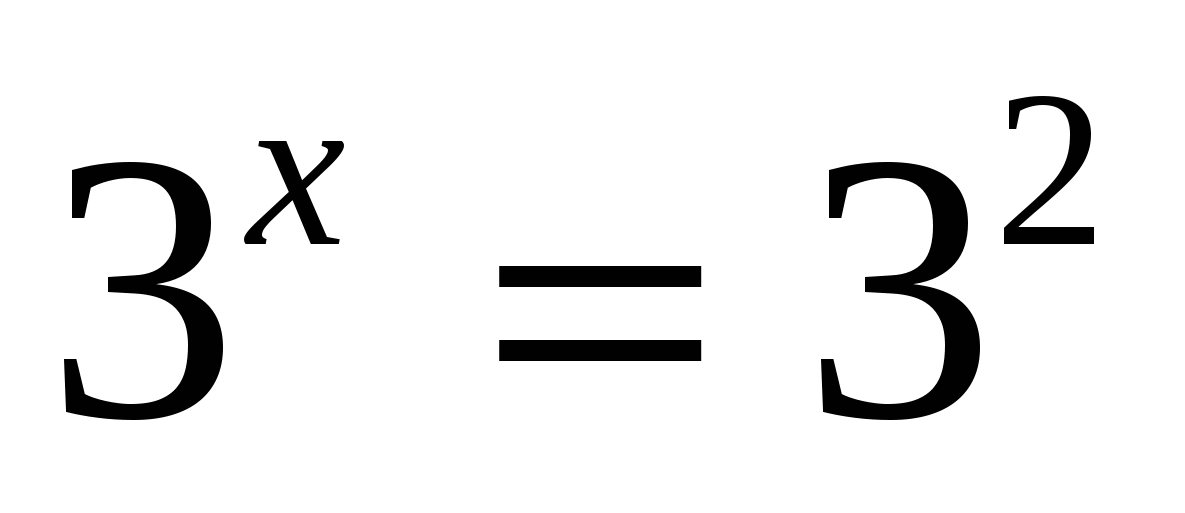
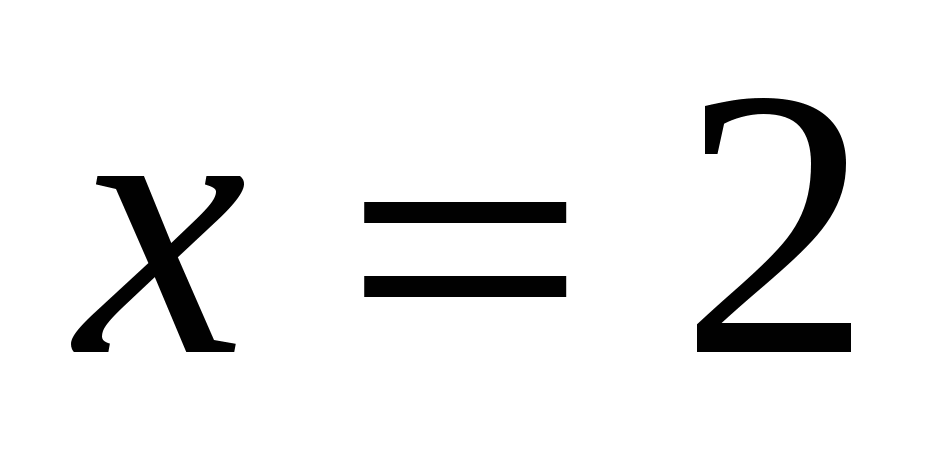
2) 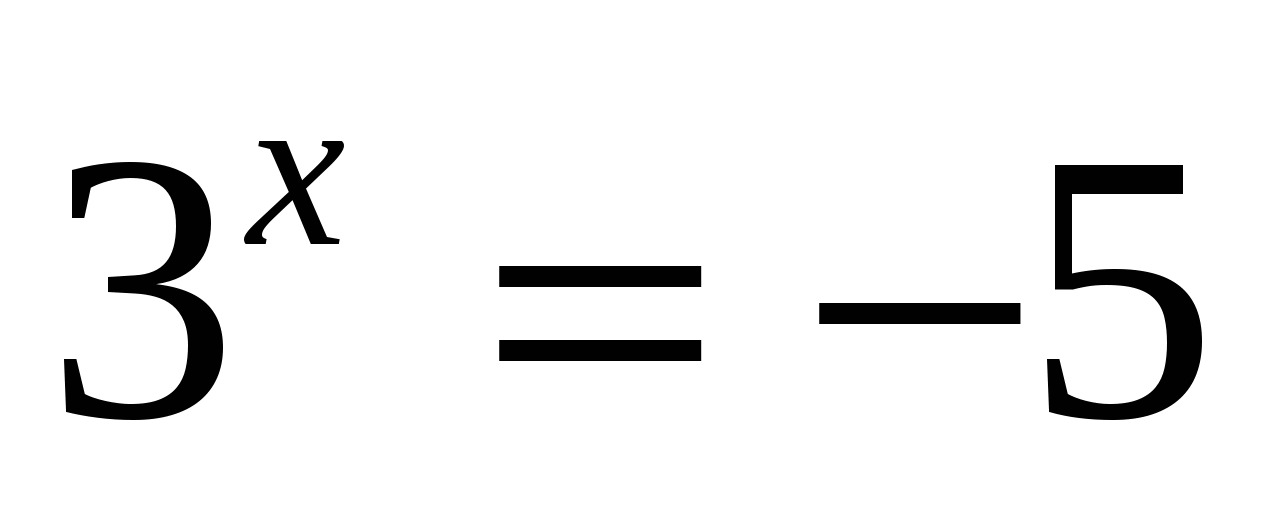
корней нет,
т.к. 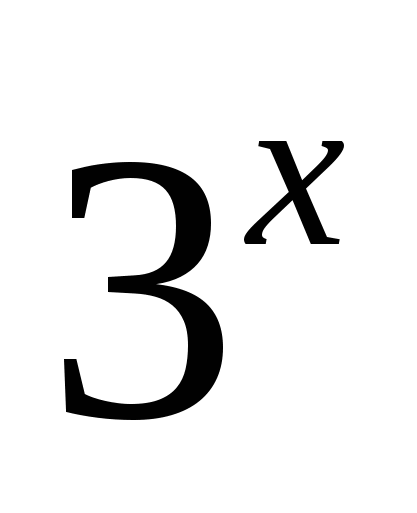 > 0 при любом
> 0 при любом 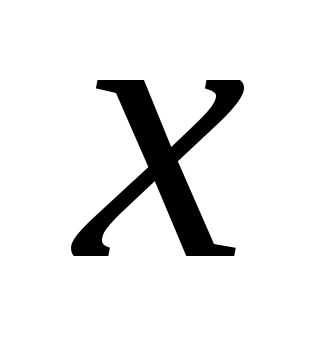
Ответ: 2.
в) 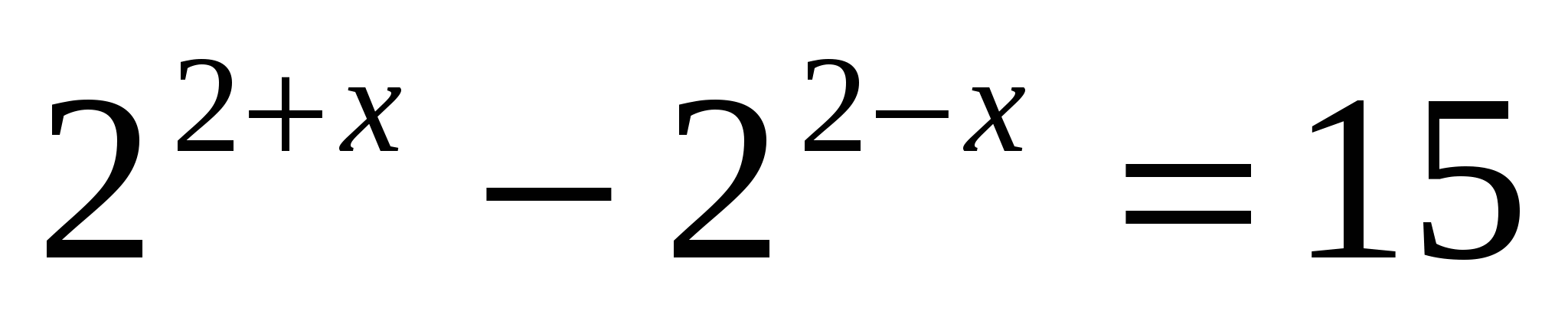
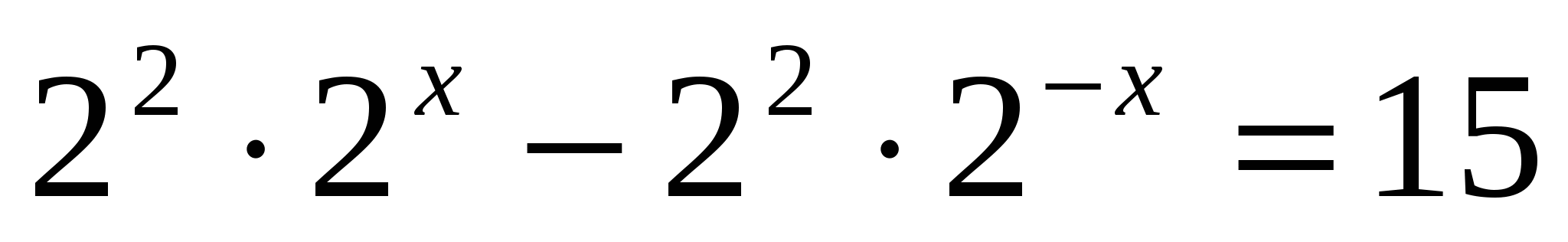
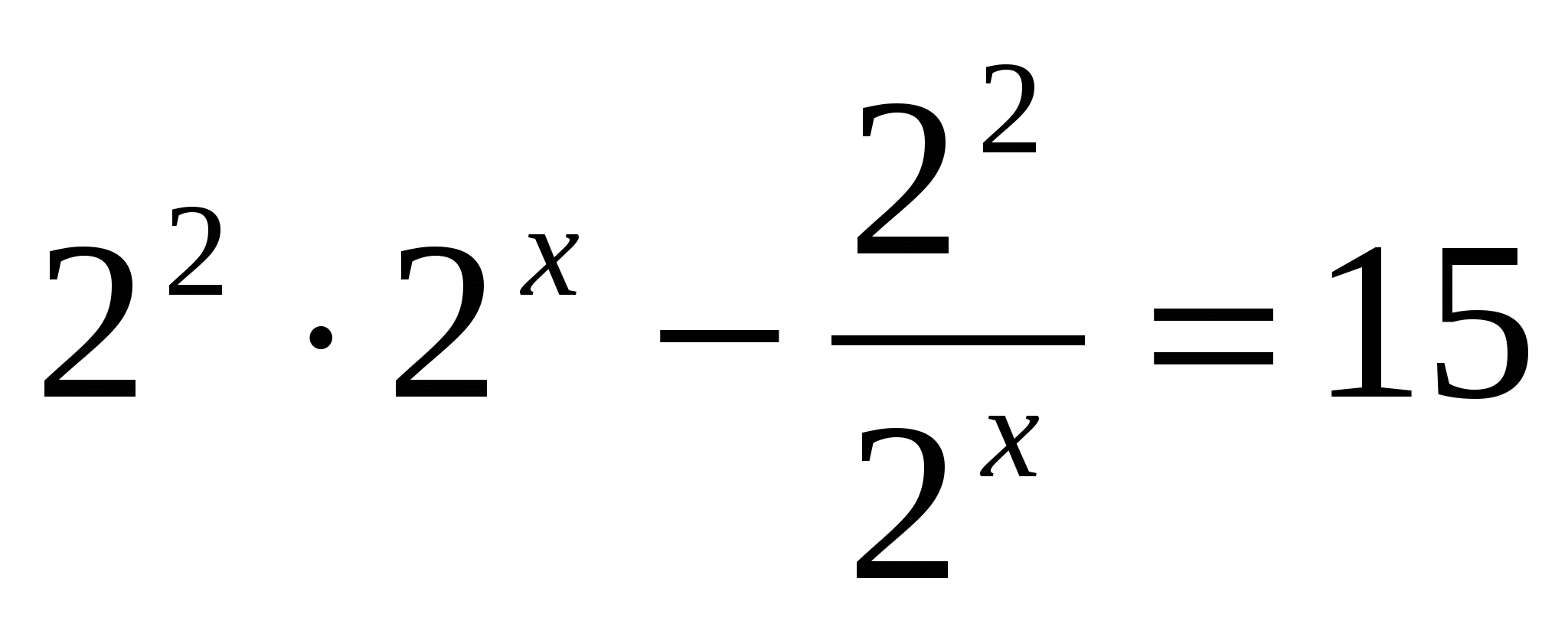
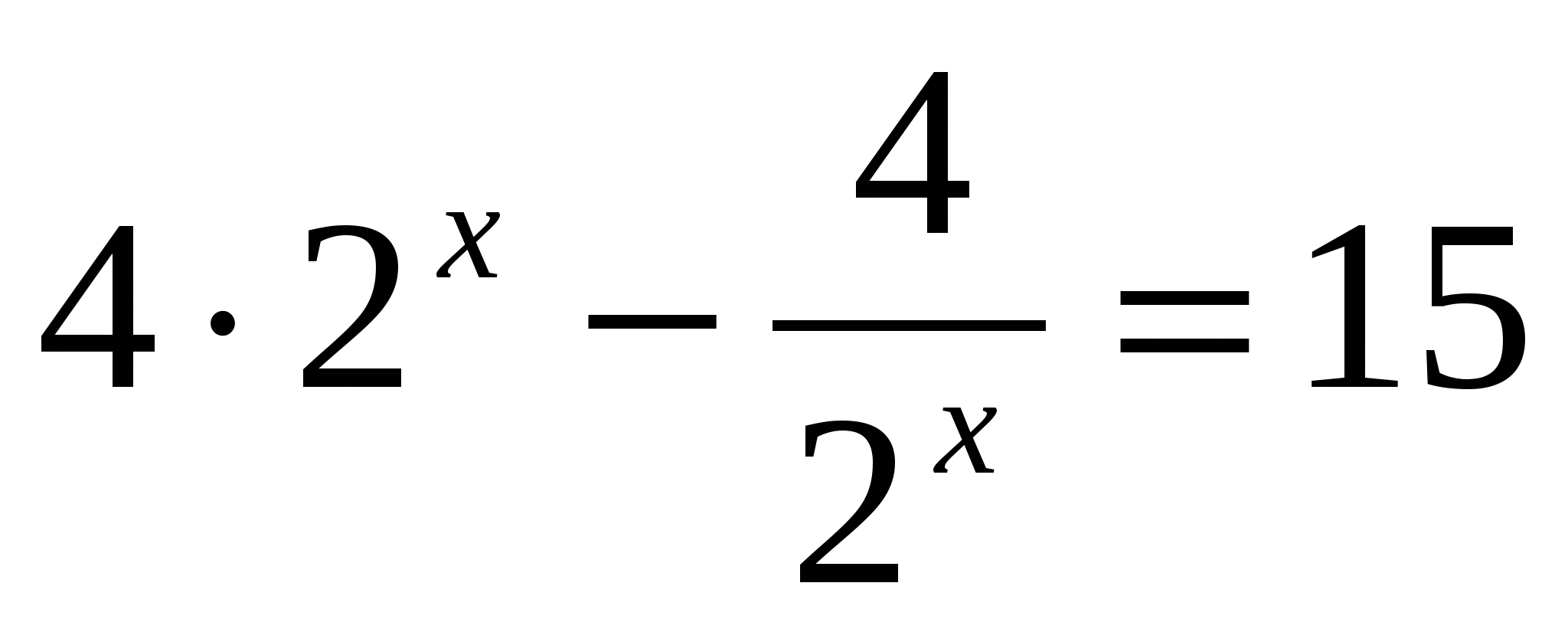
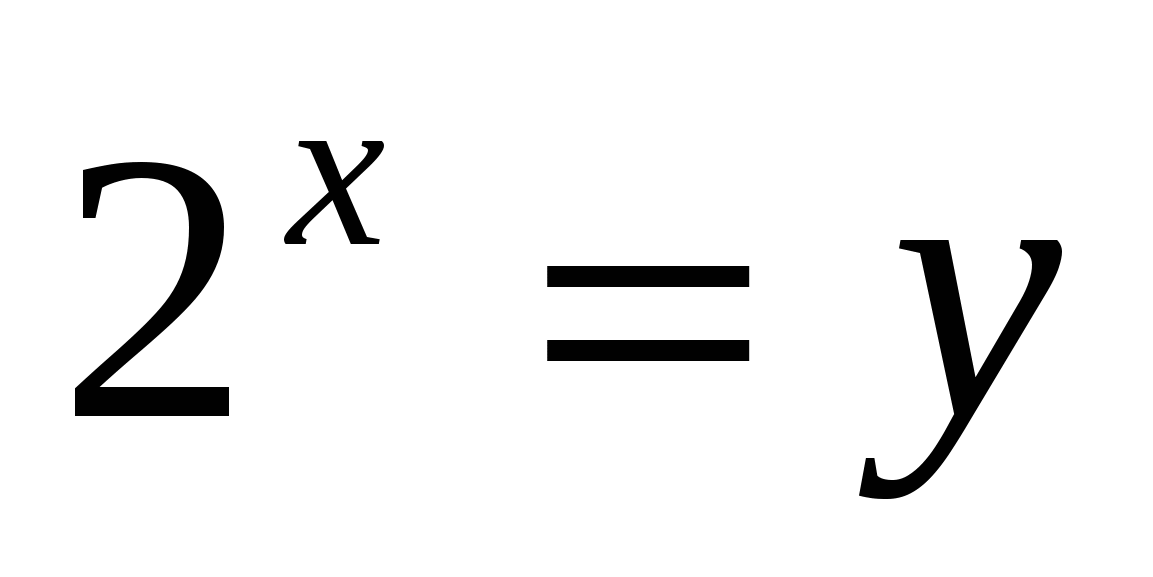
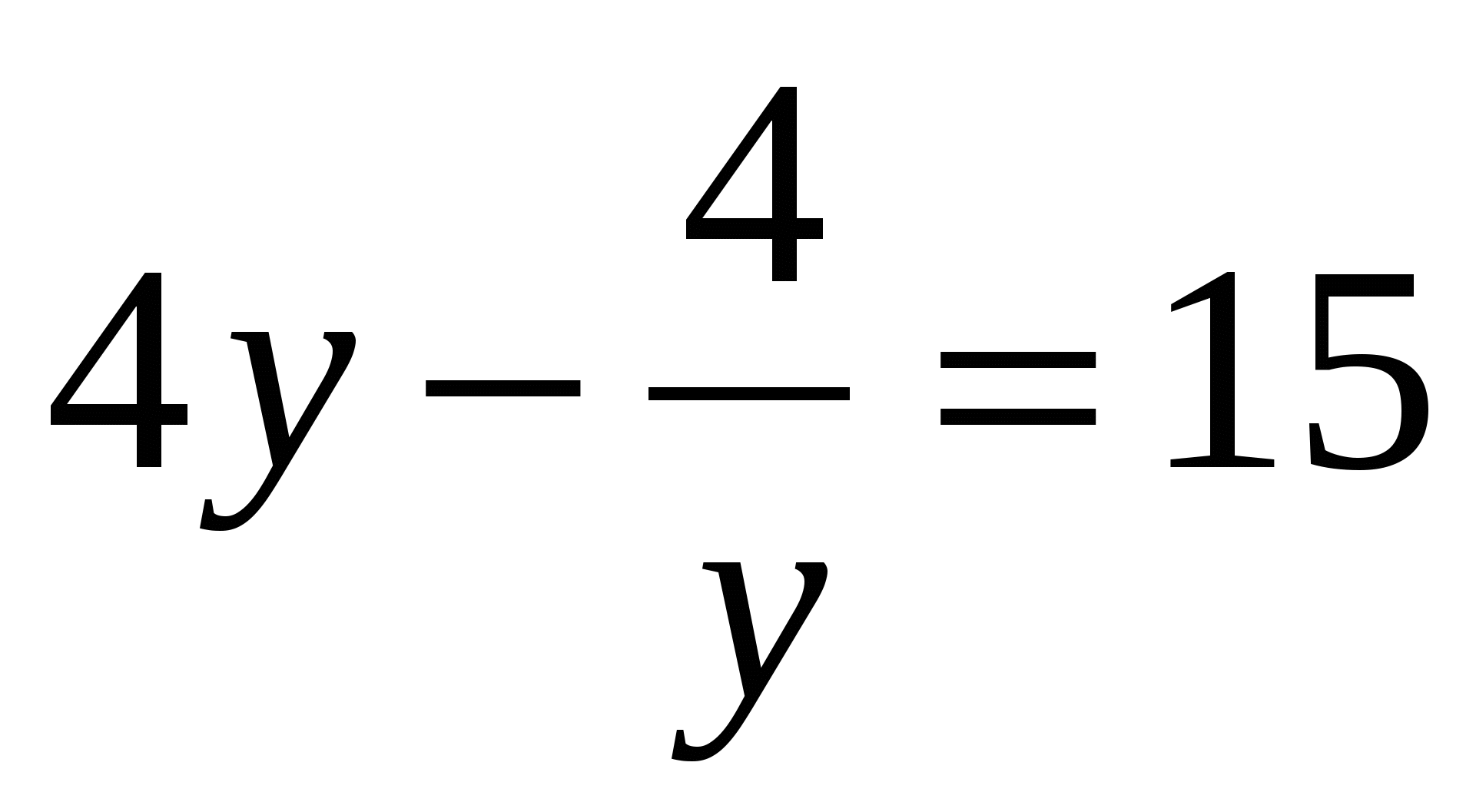
т.к 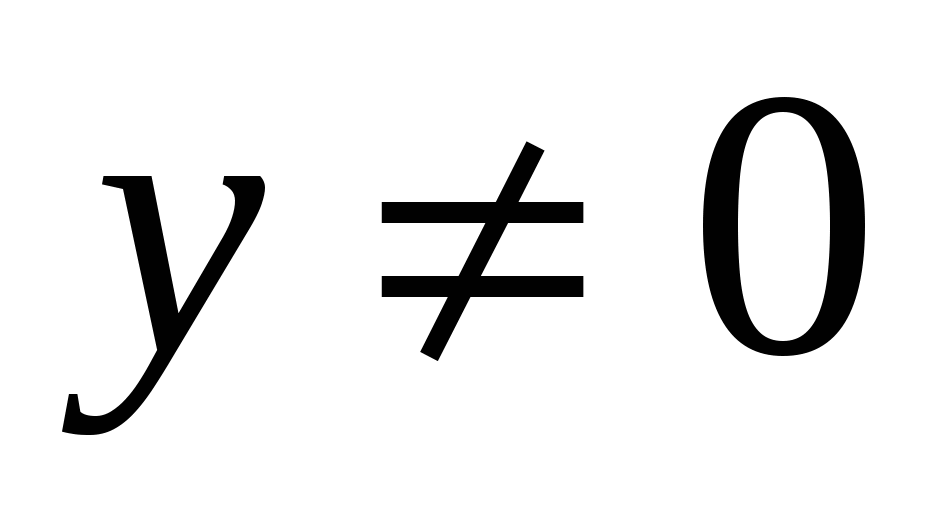 , умножим всё уравнение на
, умножим всё уравнение на 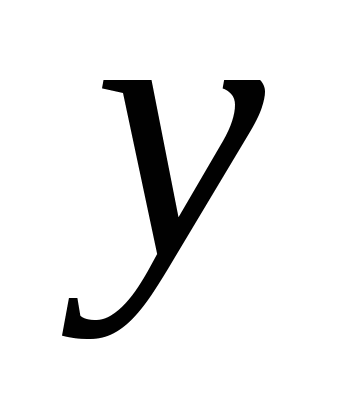
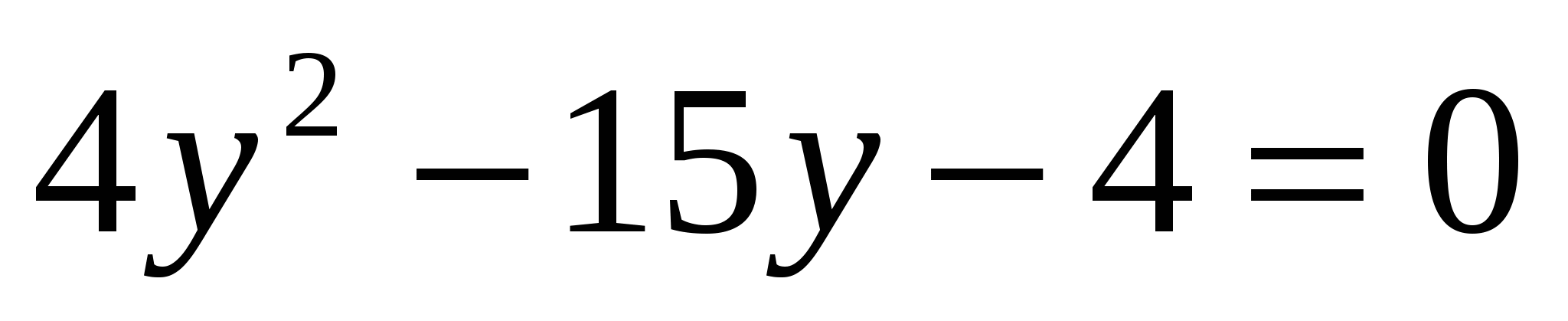
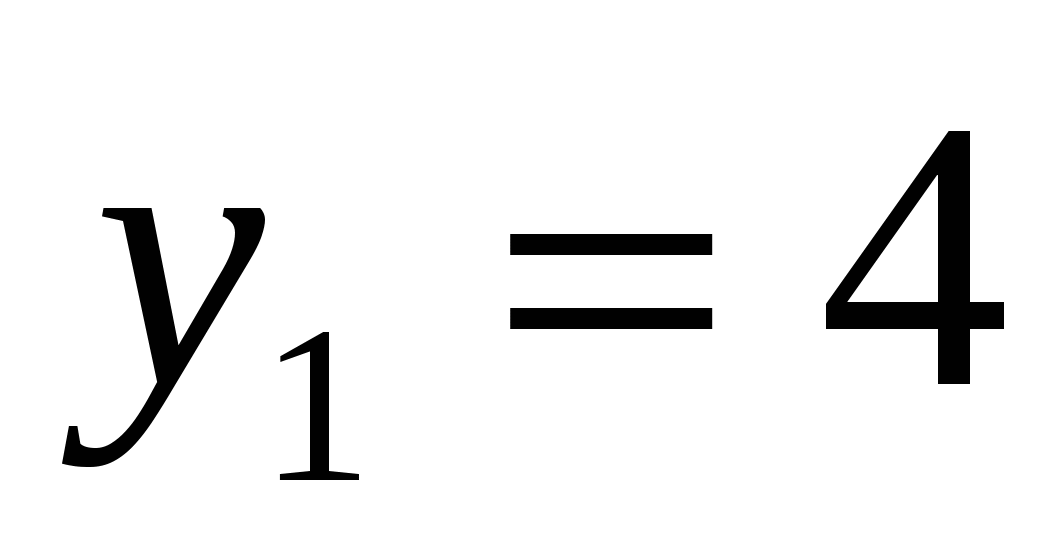 или
или 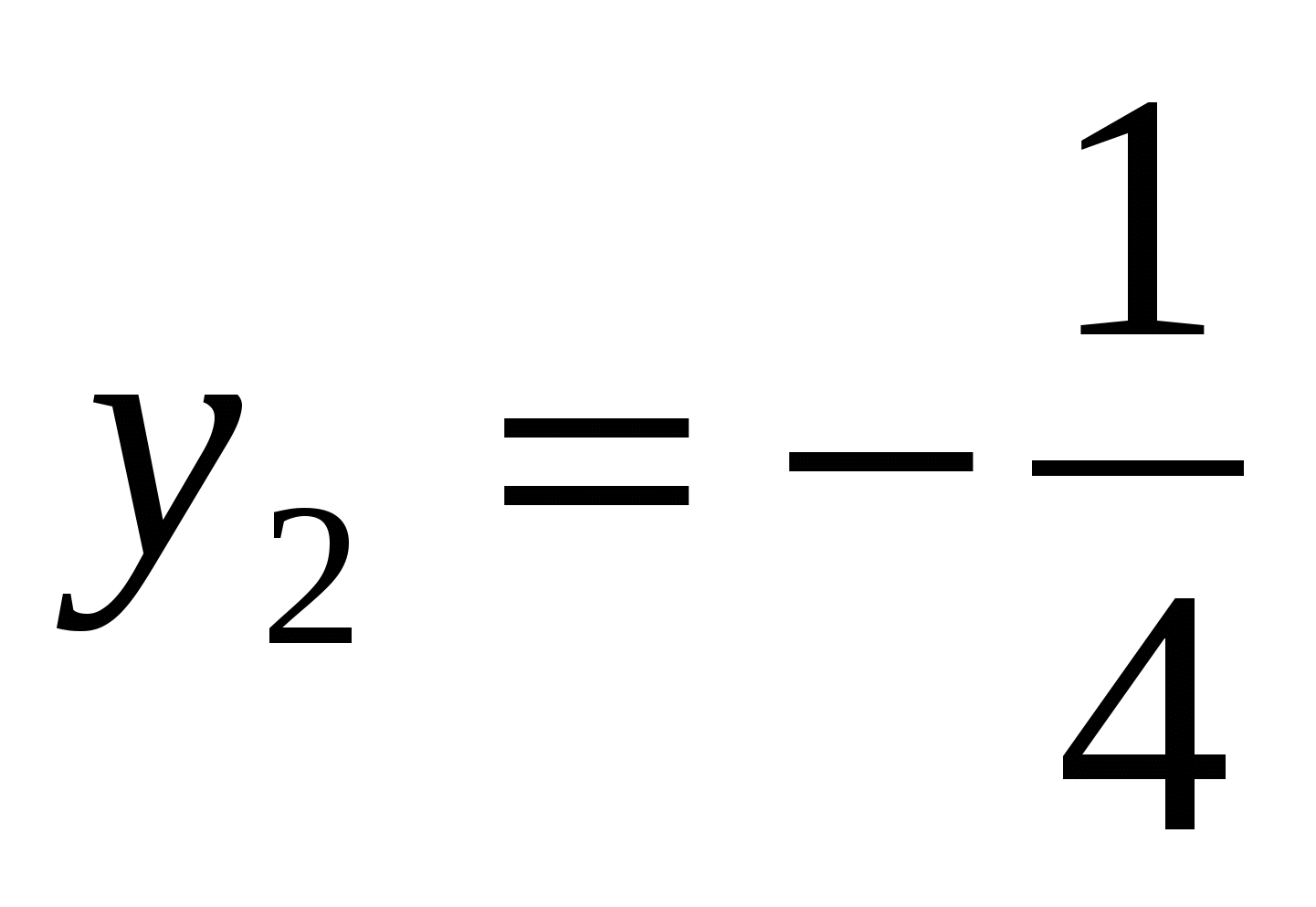
1) 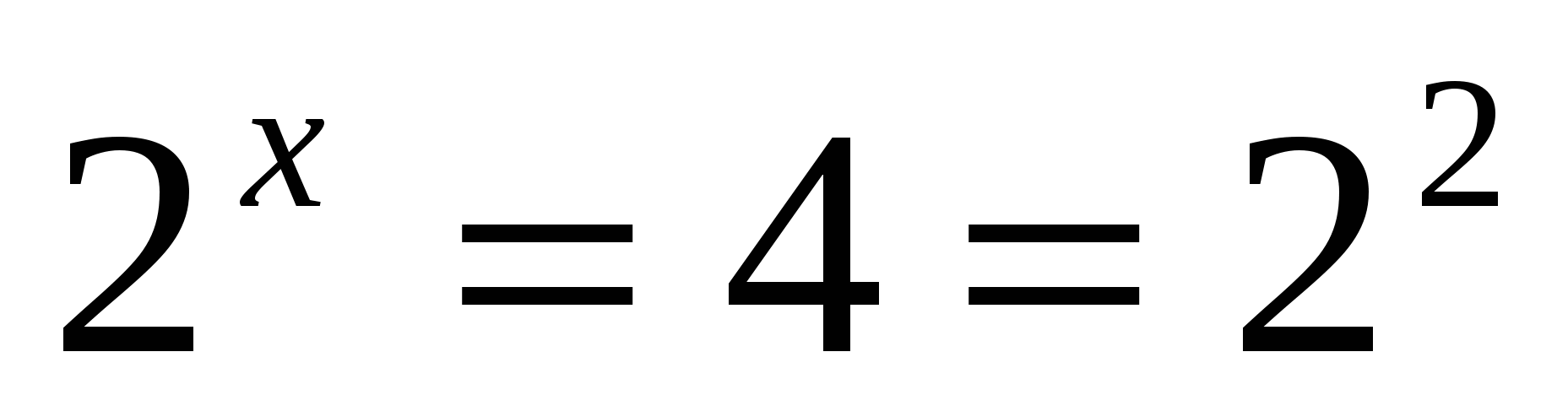
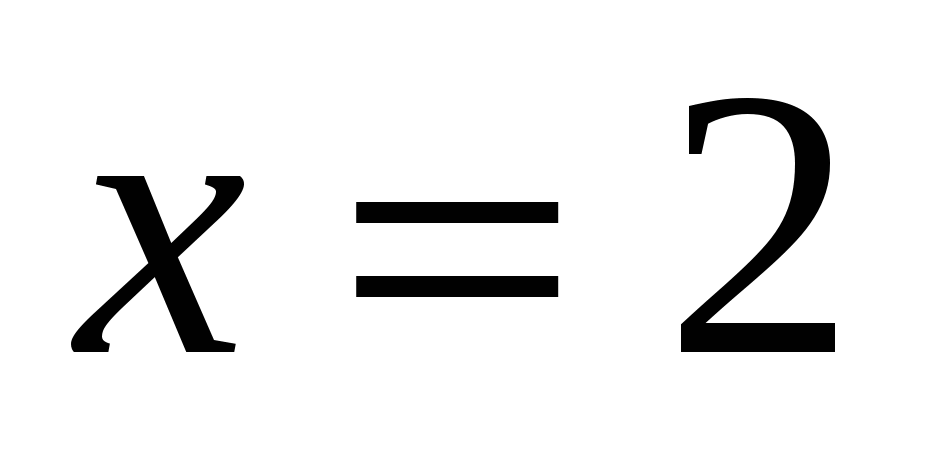
2) 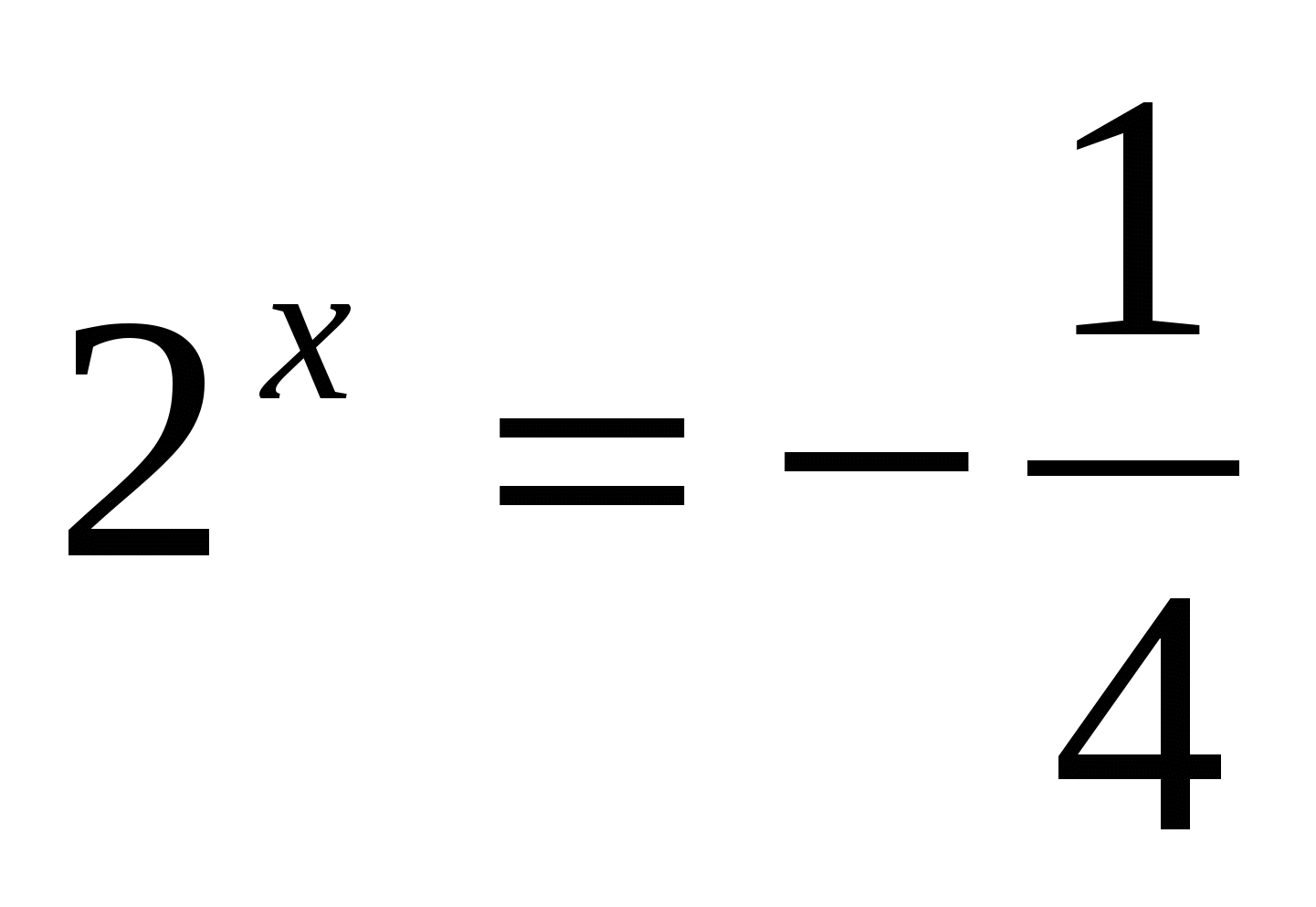
нет решений,
т. к.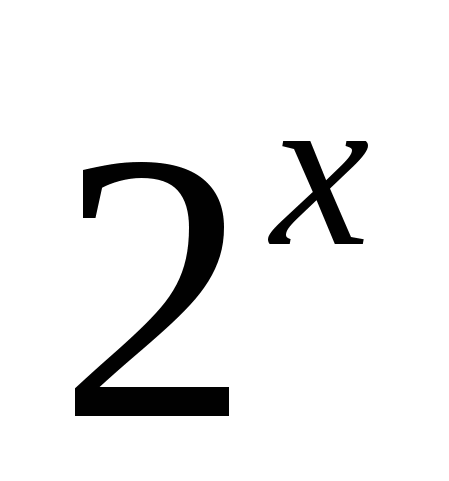 > 0 при любом
> 0 при любом 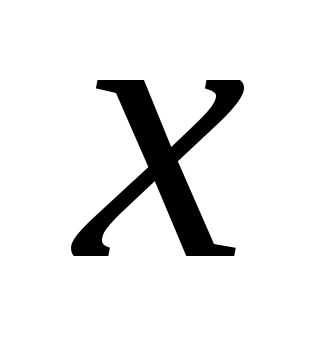
Ответ: 2.
г) 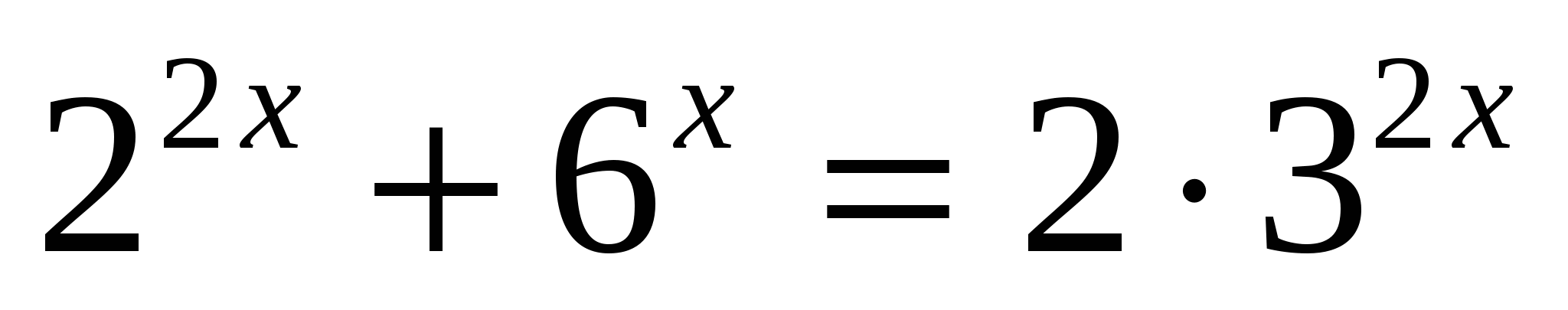
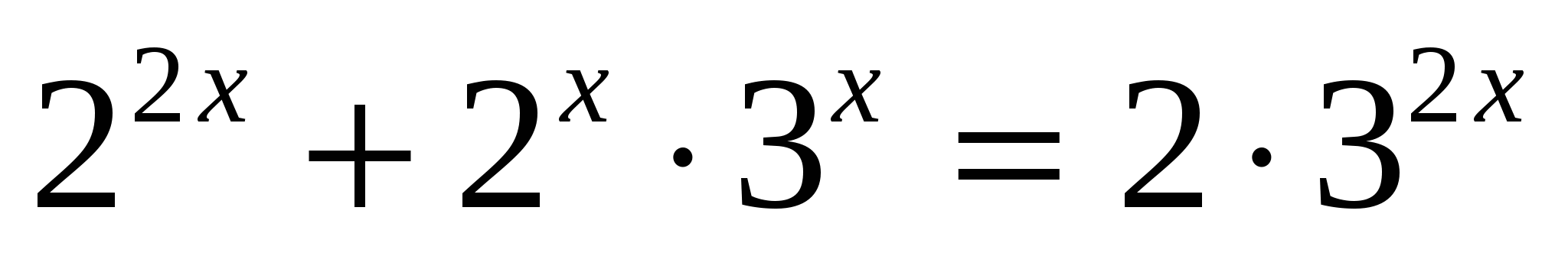
всё уравнение можно поделить на 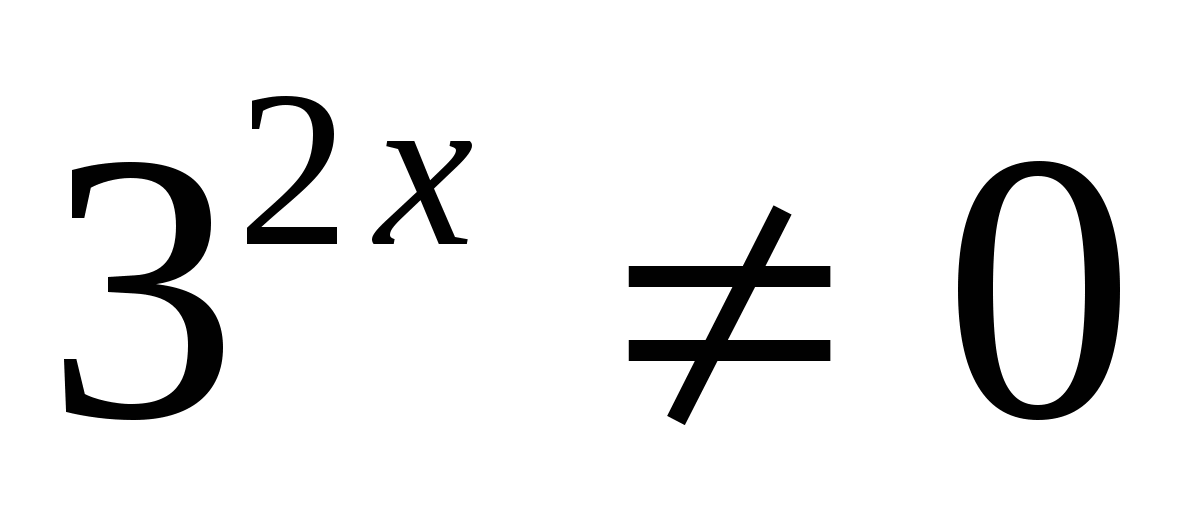
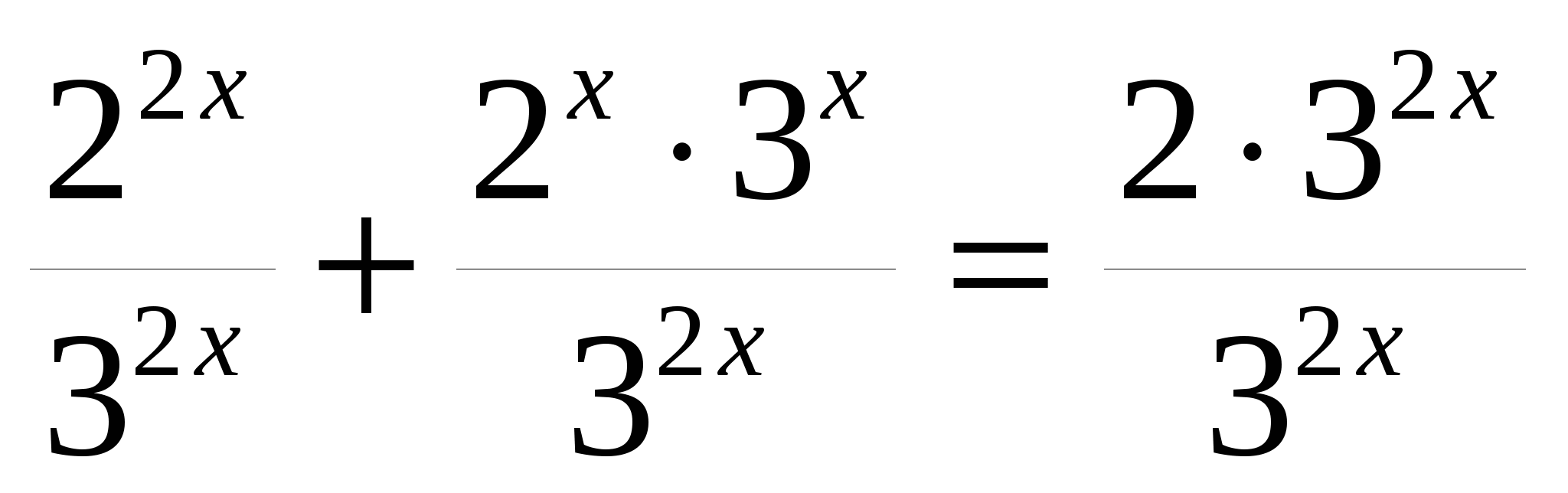
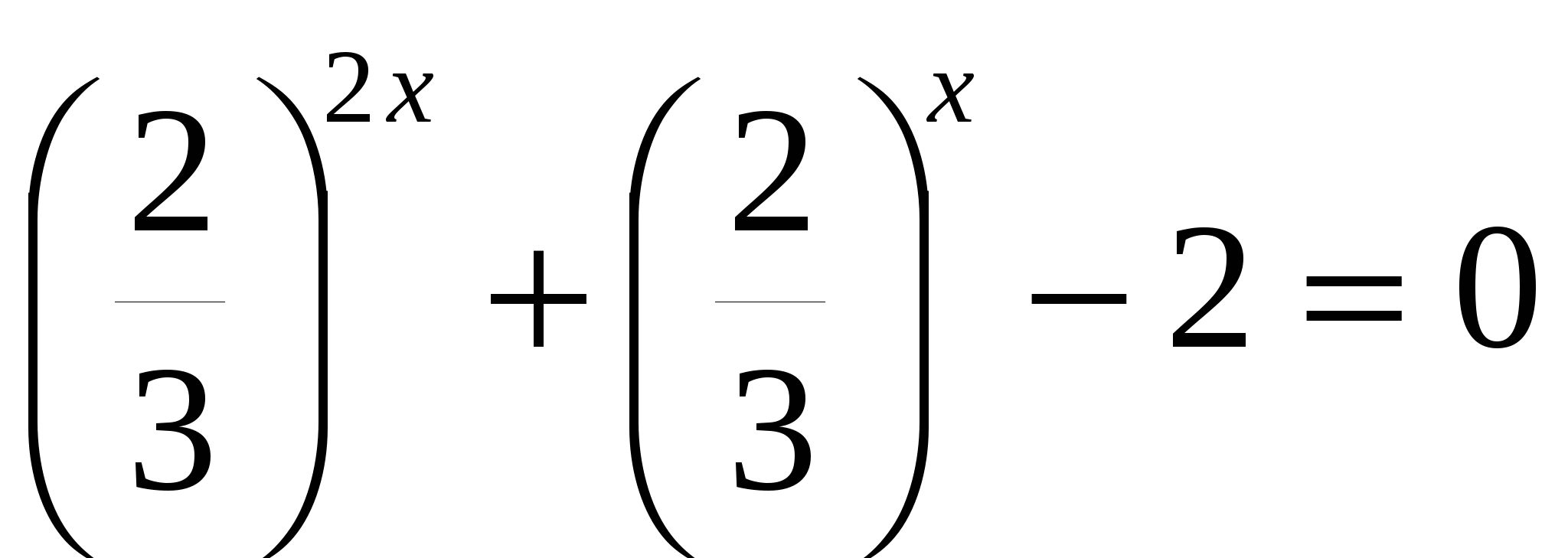
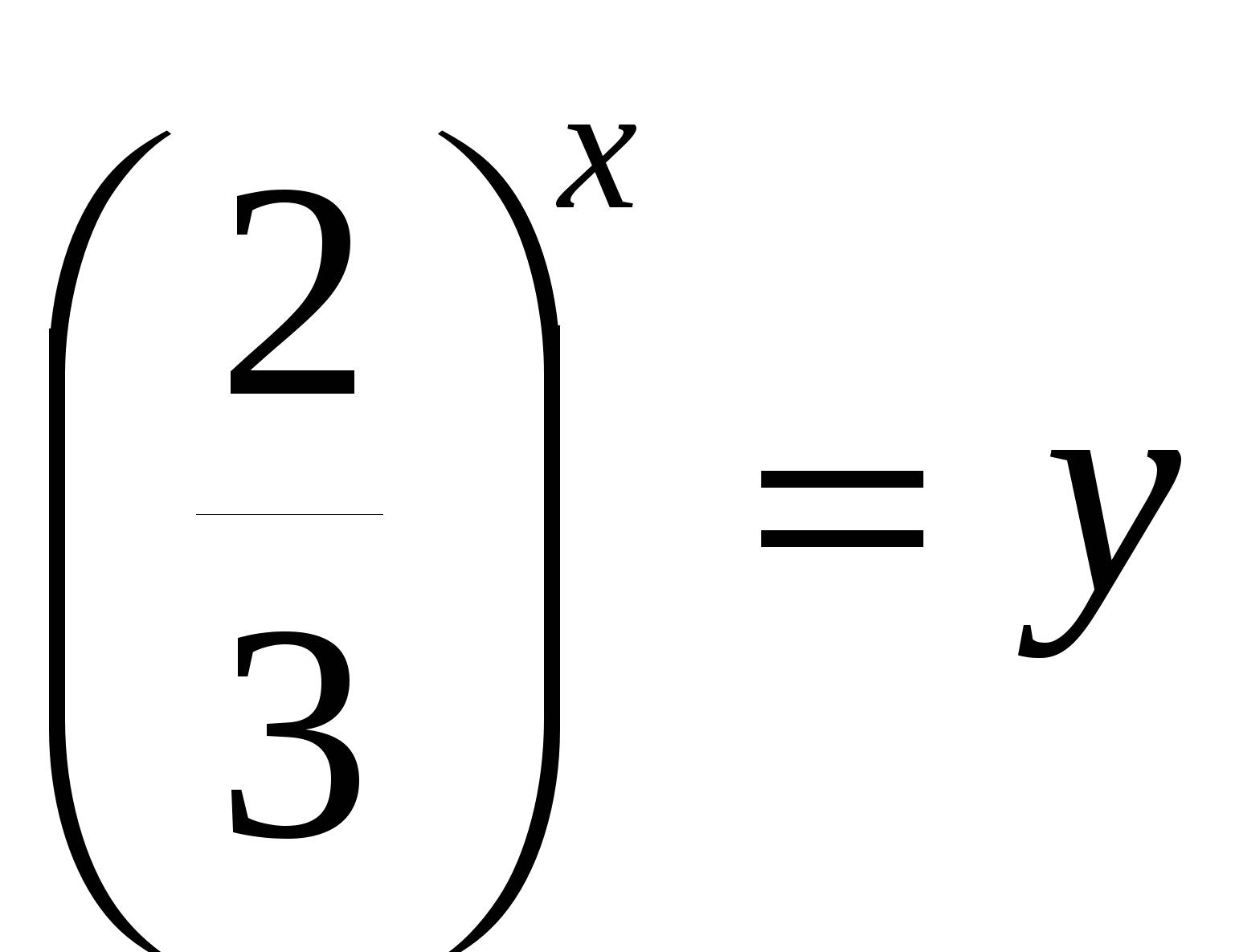
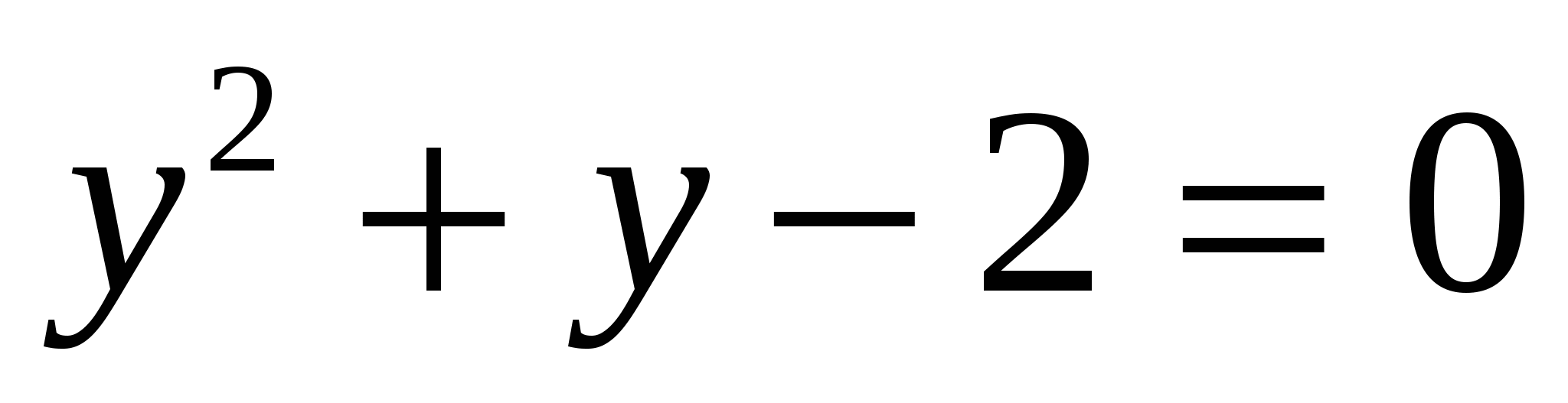
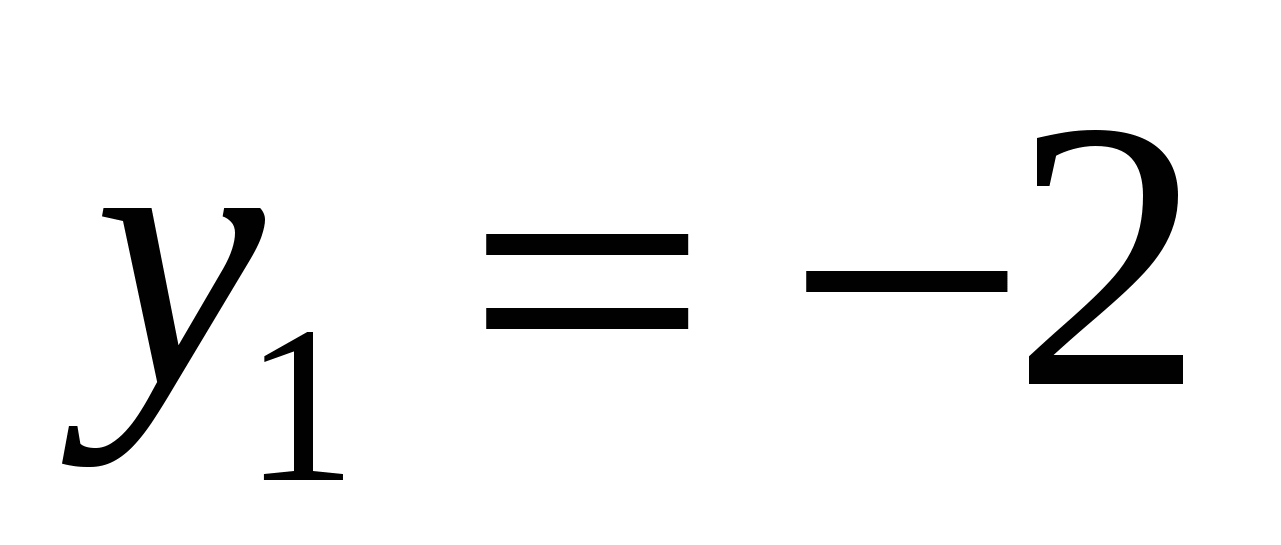 или
или 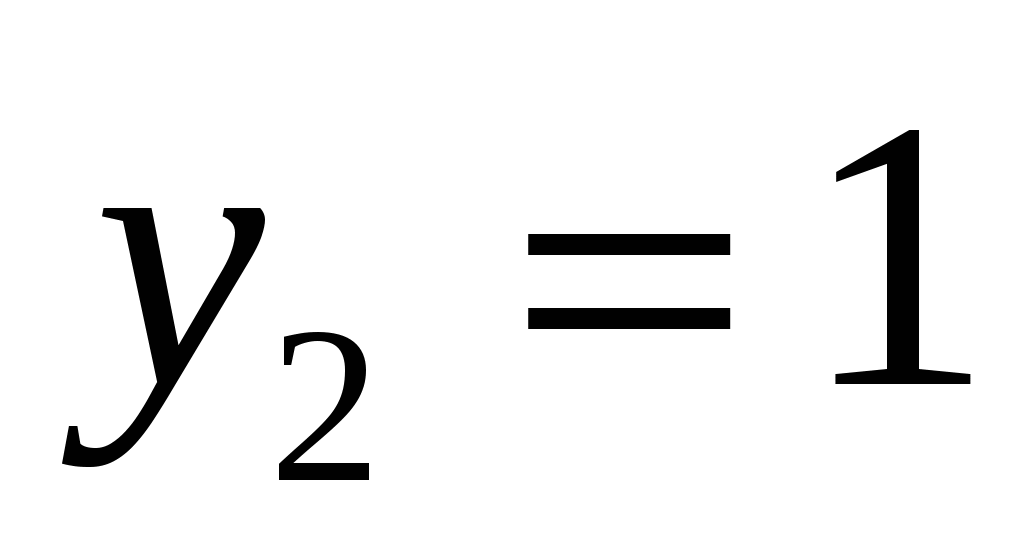
1) 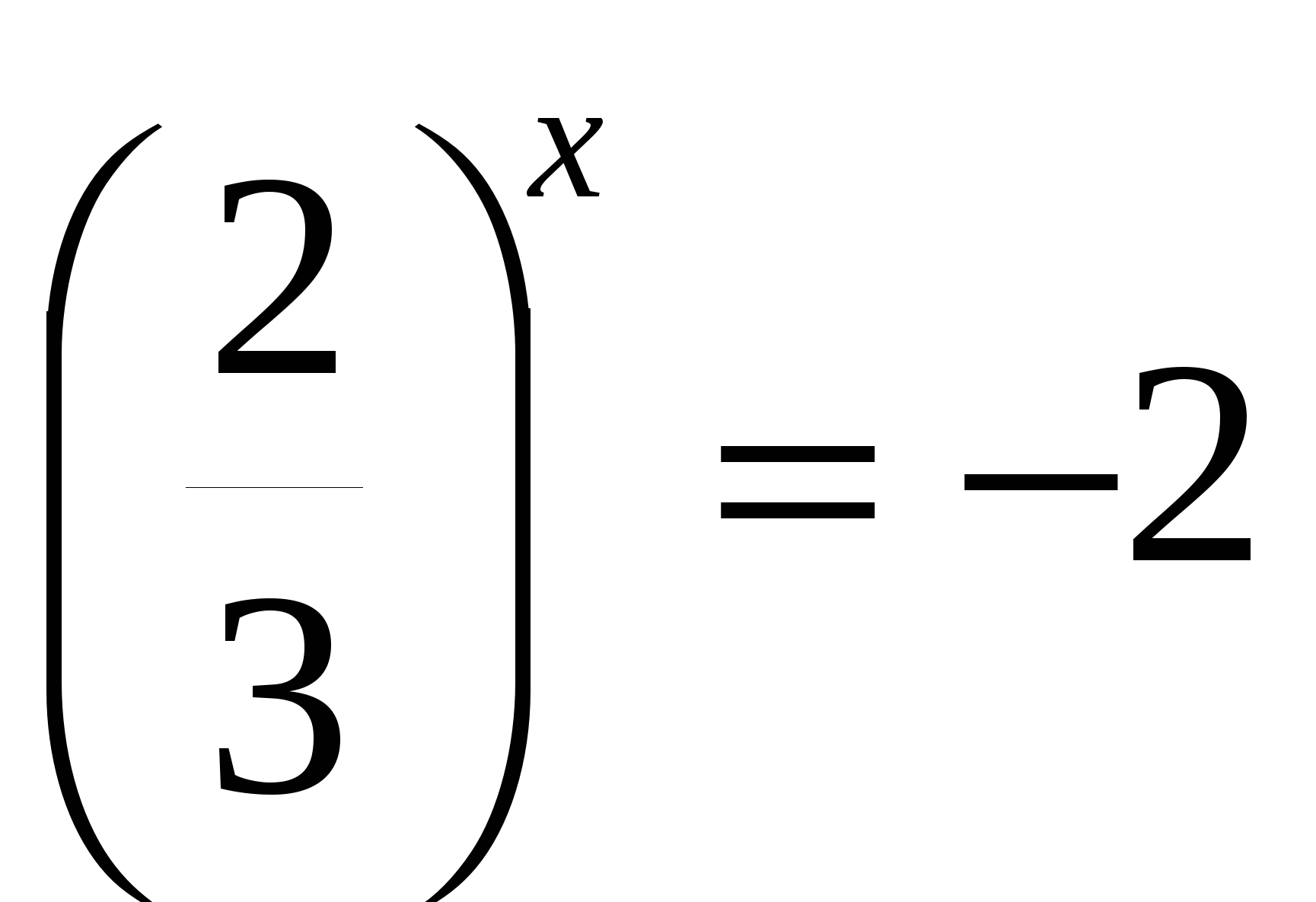
корней нет
2) 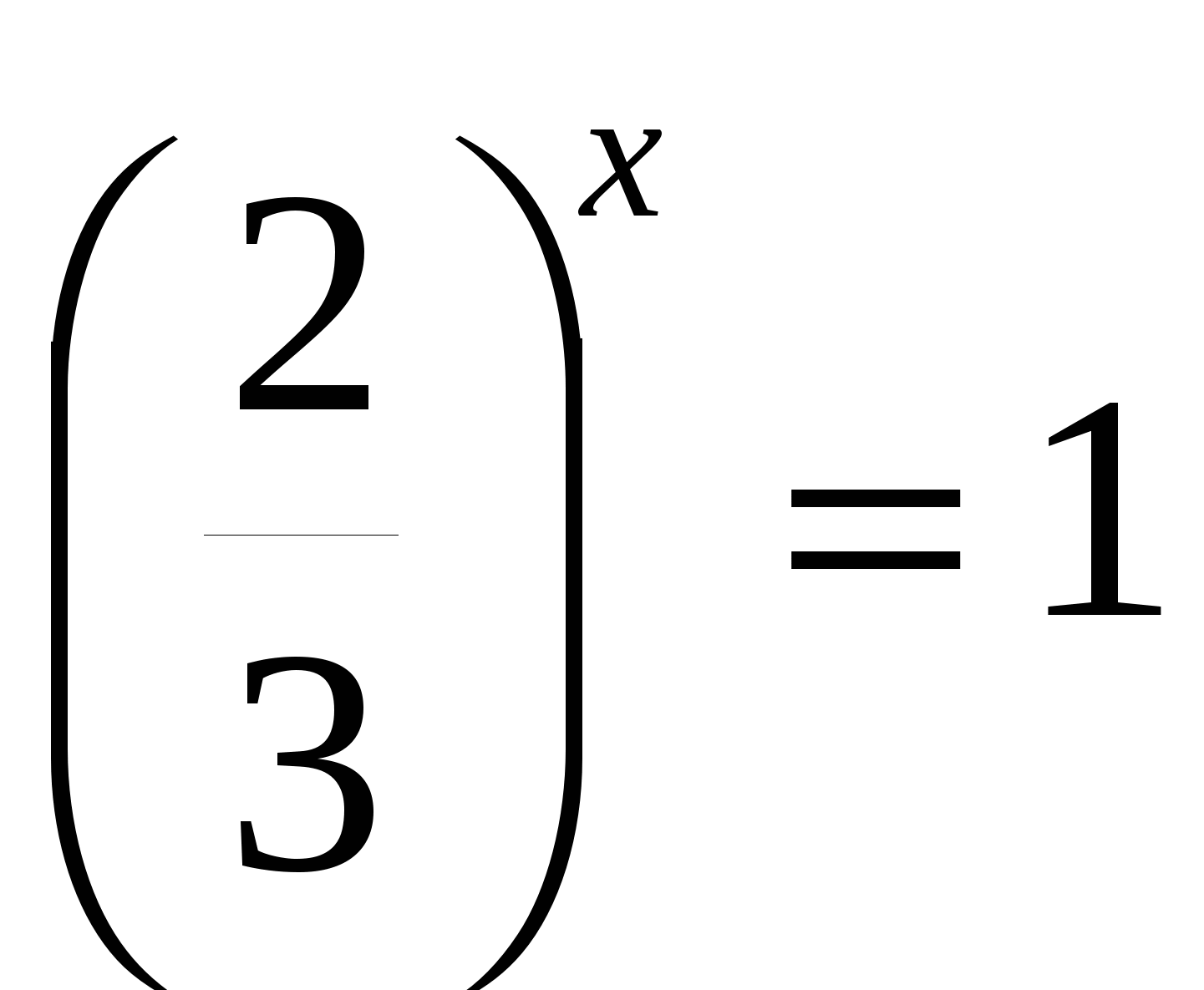
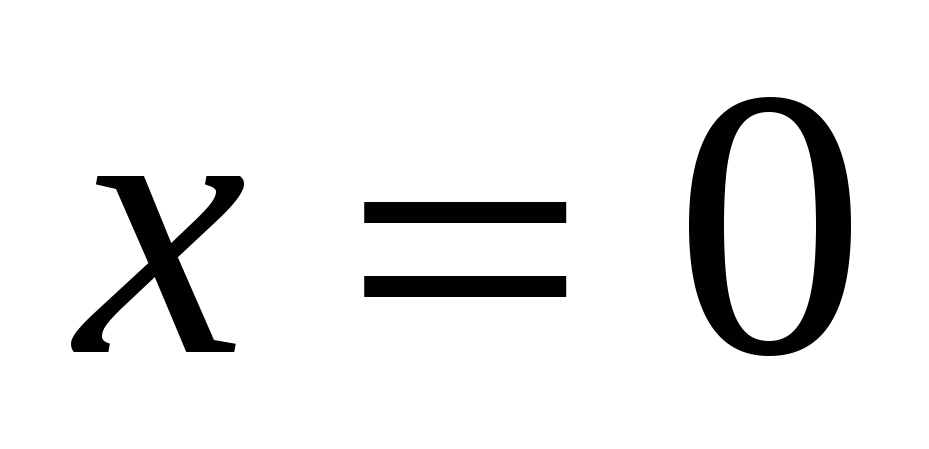
Ответ: 0.
Методы решения уравнений
 Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Основные методы решения уравнений
Решить уравнение значит найти все его корни или доказать, что их не существует. Стандартных методов решения уравнений много, нестандартных — еще больше. Последние подходят для решения небольшого количества (часто вообще одного) типа уравнений. При решении уравнений почти всегда приходится прибегать к тождественным преобразованиях алгебраических выражений. Поэтому целесообразно разобраться сперва с этим материалом, прежде чем переходить к решению уравнений. В данной статье разобраны в основном стандартные методы решения уравнений. Некоторые нестандартные методы кратко охарактеризованы в завершающей части статьи. Также на сайте есть отдельные статьи о решении тригонометрических, логарифмических и показательных уравнений, с которыми я также рекомендую читателю ознакомиться.
Метод разложения на множители
Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.
Пример 1. Решите уравнение методом разложения на множители: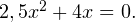
Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную 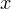 за скобки:
за скобки: 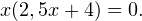
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, 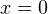 или
или  Из последнего уравнения получаем:
Из последнего уравнения получаем: 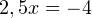 или
или 
Ответ: 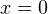 и
и 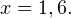
Задача для самостоятельного решения №1. Решите уравнение методом разложения на множители: 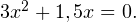
Показать ответ
Ответ: 0 или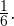 Пример 2. Решите уравнение методом разложения на множители:
Пример 2. Решите уравнение методом разложения на множители: 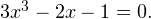
Решение. Для разложения на множители используем прием деления многочленов столбиком (или, как еще иногда говорят, уголком). Несложно догадаться, что 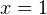 — корень многочлена
— корень многочлена 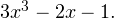 Следовательно, по теореме Безу он без остатка делится на
Следовательно, по теореме Безу он без остатка делится на 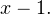 Осуществим это деление (см. подробнее в видеоуроке):
Осуществим это деление (см. подробнее в видеоуроке):
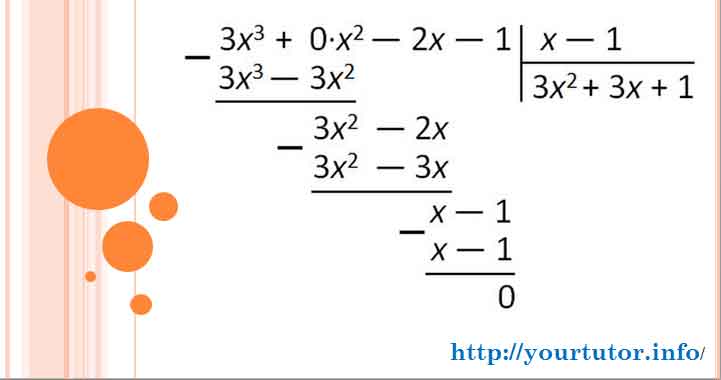
Деление многочленов уголком (столбиком)
Таким образом  То есть исходное уравнение принимает вид:
То есть исходное уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ (3x^2+3x+1)(x-1) = 0\Leftrightarrow\left[\begin{array}{l}3x^2+3x+1 = 0, \\ x-1=0.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ada9685868ad0a3ed95611b86e34af30_l3.png)
Дискриминант первого квадратичного уравнения 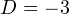 — отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень
— отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень 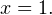 Это единственный корень уравнения.
Это единственный корень уравнения.
Ответ: 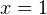 .
.
Задача для самостоятельного решения №2. Решите уравнение методом разложения на множители: 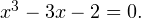
Показать ответ
Ответ: 2 и -1.
Метод замены переменной
Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Все эти идеи проще осознать на конкретном примере.
Пример 3. Решите уравнение методом замены переменной: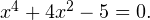
Решение. Такие уравнения называются биквадратными. Перепишем его в виде: 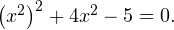 Введем новую переменную
Введем новую переменную 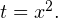 Тогда исходное уравнение примет следующий простой вид:
Тогда исходное уравнение примет следующий простой вид: 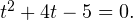 Решая полученное квадратичное уравнение, получаем, что
Решая полученное квадратичное уравнение, получаем, что 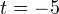 или
или 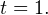
Возвращаемся теперь к старой переменной (обратная замена): 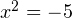 или
или 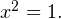 Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня
Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня 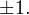
Ответ: 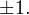
Задача для самостоятельного решения №3. Решите уравнение методом замены переменной: 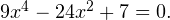
Показать ответ
Ответ: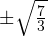 или
или  Пример 4. Решите уравнение методом замены переменной:
Пример 4. Решите уравнение методом замены переменной: ![Rendered by QuickLaTeX.com \[ \frac{4x}{4x^2-8x+7}+\frac{3x}{4x^2-10x+7}=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cb2d94cd76971a1677a251ddb57ae7a7_l3.png)
Решение. Обращаем внимание на то, что 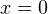 не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на
не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на 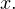 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ \frac{4}{4x-8+\frac{7}{x}}+\frac{3}{4x-10+\frac{7}{x}}=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bf2c84275e98fd7ada1591368bf50d68_l3.png)
Введем новую переменную: 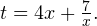 Тогда уравнение примет вид:
Тогда уравнение примет вид:
![Rendered by QuickLaTeX.com \[ \frac{4}{t-8}+\frac{3}{t-10} = 1\Leftrightarrow \frac{t^2-25t+144}{(y-8)(y-10)} = 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5f93daae7b3c8a5fa32b7591a6b3aca6_l3.png)
Дробь равна нулю, если нулю равен ее числитель, а знаменатель при этом не равен нулю. То есть уравнение равносильно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}t^2-25+144 = 0, \\ t\ne 8,\\ t\ne 10\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l} t = 16, \\ t =9, \end{array}\right. \\ t\ne 8,\\ t\ne 10\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ed0cea315f9850dd60c6b3d1bf6d373c_l3.png)
Итак, 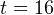 или
или 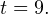 Переходя к обратной подстановке, получаем:
Переходя к обратной подстановке, получаем:
 что при
что при  равносильно уравнению
равносильно уравнению  Откуда
Откуда  или
или 
 что при
что при  равносильно уравнению
равносильно уравнению  у которого решений нет, поскольку его дискриминант отрицателен.
у которого решений нет, поскольку его дискриминант отрицателен.
Ответ: 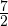 и
и 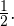
Задача для самостоятельного решения №4. Решите уравнение методом разложения на множители: 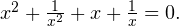
Показать ответ
Ответ: -1.
Метод оценки области значений
Суть данного метода в сравнении областей значений выражений, входящих в уравнение. Часто такой анализ позволяет легко решать сложные уравнения, содержащие различные выражения (рациональные, тригонометрические, логарифмические, показательные и др.). Разберем это на конкретном примере.
Пример 5. Решите уравнение, используя метода оценки области значений: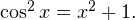
Решение. Рассмотрим функцию 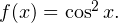 Известно, что
Известно, что 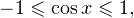 поэтому
поэтому 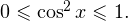 Итак, функция
Итак, функция  может принимать значения только из промежутка
может принимать значения только из промежутка ![Rendered by QuickLaTeX.com [0;1].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f38f9c6cd6a33efe8e18680325511e5b_l3.png)
Рассмотрим теперь функцию 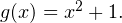 Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке
Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке 
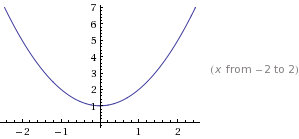
График соответствующей квадратичной функции
То есть область значений данной функции (те значения, которые может принимать переменная 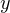 ) представляет собой промежуток
) представляет собой промежуток 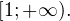
Таким образом выражения, стоящее справа и слева от знака равенства в исходном уравнении, могут оказаться равными, только если их значения окажутся равными 1, причем при одном и том же значении 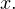 Непосредственной подстановкой убеждаемся, что это условие выполняется при
Непосредственной подстановкой убеждаемся, что это условие выполняется при 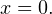 Действительно,
Действительно, 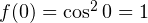 и
и 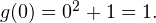 При всех остальных значениях
При всех остальных значениях 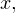 функция
функция 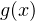 больше 1 (см. график). Значит
больше 1 (см. график). Значит 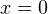 — единственный корень уравнения.
— единственный корень уравнения.
Ответ: 0.
Задача для самостоятельного решения №5. Решите уравнение с использованием метода оценки области значений: 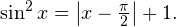
Показать ответ
Ответ: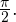
Нестандартные методы решения уравнений
Пример 6. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{2x-x^2+8}+\sqrt{x^2-4x}=\sqrt{-x-2}+1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-51821c880f5c7f760afa7eba43e35408_l3.png)
Решение. Определим область допустимых значений (те значения, которые может принимать переменная 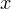 в данном уравнении). Исходим из того, что подкоренное выражение не может быть отрицательным:
в данном уравнении). Исходим из того, что подкоренное выражение не может быть отрицательным:
![Rendered by QuickLaTeX.com \[ \begin{cases}2x-x^2+8\geqslant 0, \\ x^2-4x\geqslant 0, \\ -x-2\geqslant 0\end{cases}\Leftrightarrow\begin{cases}2x-x^2+8\geqslant 0, \\ x^2-4x\geqslant 0, \\ x\leqslant -2.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1be607765444b4eb8936cc9d90924a82_l3.png)

Изображение решений каждого из неравенств системы на числовой прямой
Получается, что область допустимых значений содержит одно единственное значение 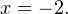 Является ли это значение корнем уравнения, проще всего проверить прямой подстановкой:
Является ли это значение корнем уравнения, проще всего проверить прямой подстановкой:
![Rendered by QuickLaTeX.com \[ \sqrt{2\cdot (-2)-(-2)^2+8}+\sqrt{(-2)^2-4\cdot (-2)}\ne \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4c3df8b5a732d7682acef485b61d5e0c_l3.png)
![Rendered by QuickLaTeX.com \[ \ne\sqrt{-(-2)-2}+1,\, \sqrt{12}\ne 1,\, 2\sqrt{3}\ne 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-119f9a007f6f7d605ffe7131671868a0_l3.png)
Нет, не является.
Ответ: корней нет.
Задача для самостоятельного решения №6. Решите уравнение: 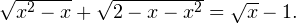
Показать ответ
Ответ: 1.
Пример 7. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{x^2+3x-2}-\sqrt{x^2+2x}=2-x. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4419f76b43ae7d9a7a7fa35c0779a6f9_l3.png)
Решение. Домножим уравнение на 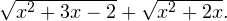 Вообще говоря, это преобразование не является равносильным, даже в области допустимых значений. Ведь могут найтись такие значения
Вообще говоря, это преобразование не является равносильным, даже в области допустимых значений. Ведь могут найтись такие значения 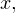 при которых это выражение обратится в ноль. При таком преобразовании могут появиться лишние корни, поэтому полученные ответы нужно будет проверить непосредственной подстановкой. Но главное, что в результате такого преобразования не произойдет потери корней. Итак, преобразуем:
при которых это выражение обратится в ноль. При таком преобразовании могут появиться лишние корни, поэтому полученные ответы нужно будет проверить непосредственной подстановкой. Но главное, что в результате такого преобразования не произойдет потери корней. Итак, преобразуем:
![Rendered by QuickLaTeX.com \[ x^2+3x-2-x^2-2x = (2-x)\times \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-db201b6447e9a0a18316fea99d1d4c10_l3.png)
![Rendered by QuickLaTeX.com \[ \times (\sqrt{x^2+3x-2}+\sqrt{x^2+2x}) \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f738727c9dbf476e2f7c336ae3b16018_l3.png)
![Rendered by QuickLaTeX.com \[ (x-2) + (x-2)(\sqrt{x^2+3x-2}+\sqrt{x^2+2x}) = 0 \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-70028e02810e409a9ad826c48e404001_l3.png)
![Rendered by QuickLaTeX.com \[ (x-2)(1+\sqrt{x^2+3x-2}+\sqrt{x^2+2x}) = 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bbf14b0a9d5126a4b9c7babb4a0378af_l3.png)
Выражение во вторых скобках не может быть равно нулю. Действительно, оба корня по крайней мере неотрицательны, поэтому если к их сумме прибавить 1, получится положительное выражение. То есть остается, что  или
или 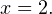 Непосредственной подстановкой убеждаемся, что это корень данного уравнения:
Непосредственной подстановкой убеждаемся, что это корень данного уравнения:
![Rendered by QuickLaTeX.com \[ \sqrt{2^2+3\cdot 2-2}-\sqrt{2^2+2\cdot 2}=2-2,\, \sqrt{8}=\sqrt{8}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-eab84f3ab8be034b5f72a70bff7e7c38_l3.png)
Ответ: 2.
Задача для самостоятельного решения №7. Решите уравнение: 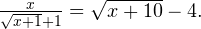
Показать ответ
Ответ: -1.
Пример 8. Решите уравнение: ![Rendered by QuickLaTeX.com \[ x^2+\frac{81x^2}{(9+x)^2} = 40. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e44c878d3c712e1f7b129cd34908d8d_l3.png)
Решение. В область допустимых значений уравнения не входит число -9. Введем новую переменную 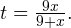 Тогда в области допустимых значений последнее выражение преобразуется к виду
Тогда в области допустимых значений последнее выражение преобразуется к виду 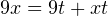 или
или 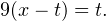 Тогда имеет место система уравнений:
Тогда имеет место система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases}x^2+t^2=40, \\ 9(x-t)-xt=0\end{cases}\Leftrightarrow\begin{cases}(x-t)^2=40-2xt, \\ 9(x-t)-xt=0\end{cases}\Lefrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3eedda8026f5ad0f30731944d9510608_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases}x-t=-20, \\ xt=-180\end{cases} \\ \begin{cases}x-t=2, \\ xt=18\end{cases}\end{array}\right.\Leftrightarrow x = 1\pm\sqrt{19}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-484ef31cadc4f91559bf9903965d4a5e_l3.png)
Ответ: 
Задача для самостоятельного решения №8. Решите уравнение ![Rendered by QuickLaTeX.com \sqrt[4]{x+8}-\sqrt[4]{x-8}=2.](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e36f56e2e85e2221188303f9d031e825_l3.png)
Показать ответ
Ответ: 8.
Вопрос методов решения уравнений изложенным в статье материалом, конечно, не исчерпывается. Существуют десятки других методов. Существуют также совершенно уникальные уравнения, для которых имеются свои собственное методы решения. Так что научиться здесь можно еще очень и очень многому. Самым хорошим помощником в этот деле для вас станет профессиональный репетитор по математике. Учите математику, сдавайте на отлично выпускные экзамены, поступайте в престижные вузы. Удачи вам!
Сергей Валерьевич
Частный преподаватель по математике
У любой сложной задачи есть простое, легкое для понимания неправильное решение. © Артур Блох
| 1. | Уравнение третьей степени, произведение равно 0 | 2 вид — интерпретация | лёгкое | 1,5 Б. | Решение уравнения третьей степени (равенство произведения 0). |
| 2. | Уравнение с модулем вида |x| = a | 2 вид — интерпретация | лёгкое | 1 Б. | Нахождение произведения корней уравнения с модулем вида |x| = a. |
| 3. | Замена уравнения равносильным уравнением | 1 вид — рецептивный | лёгкое | 1 Б. | Определяется равносильность уравнений в результате перехода от уравнения вида h(f(x)) = h(g(x)) к уравнению f(x) = g(x). |
| 4. | Уравнение третьей степени, способ группировки | 2 вид — интерпретация | среднее | 4 Б. | Решение уравнения третьей степени разложением на множители способом группировки. |
| 5. | Биквадратное уравнение | 2 вид — интерпретация | среднее | 4 Б. | Решение биквадратного уравнения способом введения новой переменной. |
| 6. | Уравнение пятой степени | 2 вид — интерпретация | среднее | 3 Б. | Решение уравнения пятой степени, использование кубического корня (равенство произведения 0). |
| 7. | Уравнение n-ой степени | 2 вид — интерпретация | среднее | 2 Б. | Решение уравнения n-ой степени. |
| 8. | Иррациональное уравнение (квадратное) | 2 вид — интерпретация | среднее | 4 Б. | Решение иррационального уравнения (формула квадрата суммы или разности). |
| 9. | Вопросы по равенству с модулем | 1 вид — рецептивный | среднее | 1 Б. | Теоретические вопросы по равенству с модулем, используется определение модуля. |
| 10. | Уравнение с модулем вида |f(x)| = a | 2 вид — интерпретация | среднее | 2 Б. | Решение уравнения с модулем вида |f(x)| = a. |
| 11. | Уравнение с модулем вида |f(x)| = |g(x)| | 2 вид — интерпретация | среднее | 3 Б. | Решение уравнения с модулем вида |f(x)| = |g(x)|. |
| 12. | Уравнение с модулем, подобные модули | 2 вид — интерпретация | среднее | 3 Б. | Решение уравнения с модулем, приведение подобных модулей. |
| 13. | Тригонометрическое уравнение, метод разложения на множители | 2 вид — интерпретация | среднее | 4 Б. | Решение тригонометрического уравнения методом разложения на множители. |
| 14. | Уравнение шестой степени, метод введения новой переменной | 2 вид — интерпретация | среднее | 3 Б. | Решение уравнения шестой степени методом введения новой переменной. |
| 15. | Иррациональное уравнение, метод введения новой переменной | 2 вид — интерпретация | среднее | 4 Б. | Решение иррационального уравнения методом введения новой переменной. |
| 16. | Иррациональное уравнение, метод введения новой переменной, обратные величины | 2 вид — интерпретация | среднее | 3 Б. | Решение иррационального уравнения методом введения новой переменной, обратные величины. |
| 17. | Логарифмическое уравнение, метод введения новой переменной | 2 вид — интерпретация | среднее | 4 Б. | Решение логарифмического уравнения методом введения новой переменной. |
| 18. | Решение уравнения с заменой его равносильным уравнением | 2 вид — интерпретация | среднее | 2 Б. | Для решения уравнения применяется метод замены его равносильным уравнением, т. е. от уравнения вида h(f(x)) = h(g(x)) переходим к уравнению f(x) = g(x). |
| 19. | Реши уравнение графически | 2 вид — интерпретация | среднее | 2 Б. | Предлагается решить уравнение, используя функционально-графический метод. |
| 20. | Уравнение третьей степени, разложение на множители | 2 вид — интерпретация | сложное | 4 Б. | Решение уравнения третьей степени методом разложения на множители. |
| 21. | Уравнение высшей степени | 2 вид — интерпретация | сложное | 3 Б. | Решение уравнения высшей степени методом разложения на множители. |
| 22. | Иррациональное уравнение (свойство модуля) | 2 вид — интерпретация | сложное | 4 Б. | Решение иррационального уравнения, используется свойство модуля. |
| 23. | Уравнение с двумя модулями | 2 вид — интерпретация | сложное | 3 Б. | Решение уравнения с двумя модулями. |
| 24. | Квадратное уравнение с модулем | 2 вид — интерпретация | сложное | 3 Б. | Решение квадратного уравнения с модулем. |
| 1. |
Уравнение третьей степени, произведение равно 0
Сложность: лёгкое |
|
| 2. |
Уравнение с модулем вида |x| = a
Сложность: лёгкое |
|
| 3. |
Замена уравнения равносильным уравнением
Сложность: лёгкое |
|
| 4. |
Уравнение третьей степени, способ группировки
Сложность: среднее |
|
| 5. |
Биквадратное уравнение
Сложность: среднее |
|
| 6. |
Уравнение пятой степени
Сложность: среднее |
|
| 7. |
Уравнение n-ой степени
Сложность: среднее |
|
| 8. |
Иррациональное уравнение (квадратное)
Сложность: среднее |
|
| 9. |
Вопросы по равенству с модулем
Сложность: среднее |
|
| 10. |
Уравнение с модулем вида |f(x)| = a
Сложность: среднее |
|
| 11. |
Уравнение с модулем вида |f(x)| = |g(x)|
Сложность: среднее |
|
| 12. |
Уравнение с модулем, подобные модули
Сложность: среднее |
|
| 13. |
Тригонометрическое уравнение, метод разложения на множители
Сложность: среднее |
|
| 14. |
Уравнение шестой степени, метод введения новой переменной
Сложность: среднее |
|
| 15. |
Иррациональное уравнение, метод введения новой переменной
Сложность: среднее |
|
| 16. |
Иррациональное уравнение, метод введения новой переменной, обратные величины
Сложность: среднее |
|
| 17. |
Логарифмическое уравнение, метод введения новой переменной
Сложность: среднее |
|
| 18. |
Решение уравнения с заменой его равносильным уравнением
Сложность: среднее |
|
| 19. |
Реши уравнение графически
Сложность: среднее |
|
| 20. |
Уравнение третьей степени, разложение на множители
Сложность: сложное |
|
| 21. |
Уравнение высшей степени
Сложность: сложное |
|
| 22. |
Иррациональное уравнение (свойство модуля)
Сложность: сложное |
|
| 23. |
Уравнение с двумя модулями
Сложность: сложное |
|
| 24. |
Квадратное уравнение с модулем
Сложность: сложное |
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| ax3 + bx2 + bx + a = 0, | (1) |
где a, b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
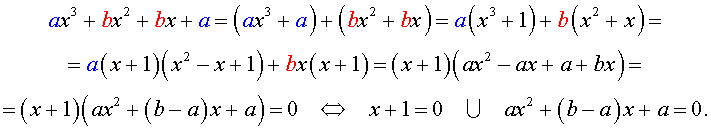
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
ax2 + (b – a) x + a = 0.
Пример 1. Решить уравнение
| 2x3 + 7x2 + 7x + 2 = 0. | (2) |
Решение. Разложим левую часть уравнения (2) на множители:
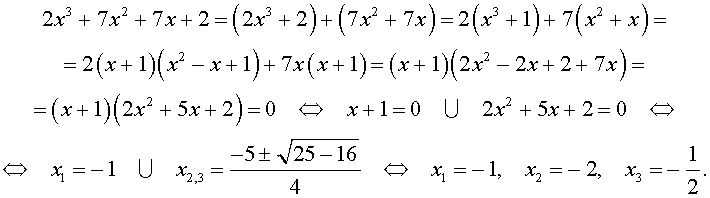
Ответ: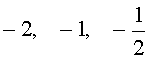 .
.
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| ax4 + bx3 + cx2 + + bx + a = 0, | (3) |
а также уравнения вида
| ax4 + bx3 + cx2 – – bx + a = 0, | (4) |
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение (3), разделим его на x2. В результате получится уравнение
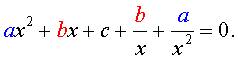 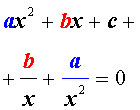 | (5) |
Преобразуем левую часть уравнения (5):
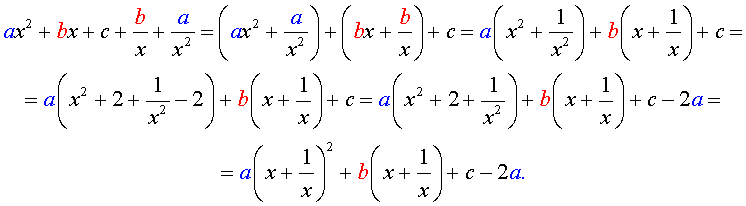
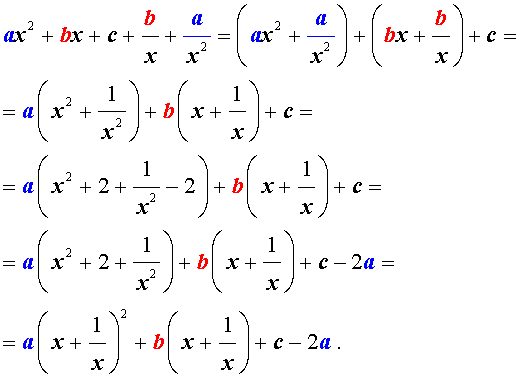
В результате этого преобразования уравнение (5) принимает вид
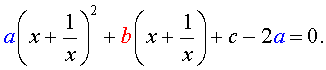 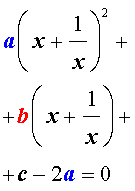 | (6) |
Если теперь обозначить
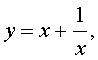 | (7) |
то уравнение (6) станет квадратным уравнением:
| ay2 + by + c – 2a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x2. В результате получится уравнение
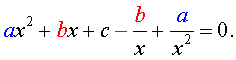 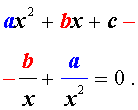 | (9) |
Преобразуем левую часть уравнения (9):
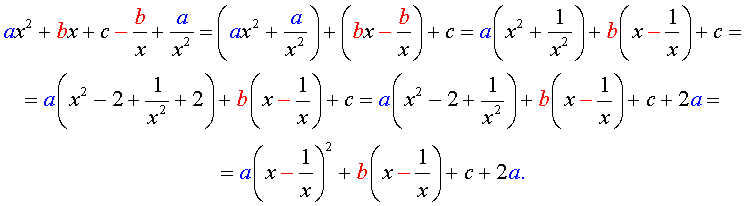
В результате этого преобразования уравнение (9) принимает вид
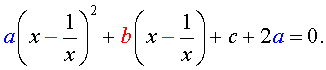 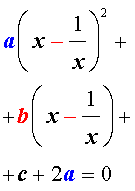 | (10) |
Если теперь обозначить
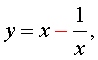 | (11) |
то уравнение (10) станет квадратным уравнением:
| ay2 + by + c + 2a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (4) завершено.
Пример 2. Решить уравнение
| 2x4 – 3x3 – x2 – – 3x + 2 = 0. | (13) |
Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на x2. В результате получится уравнение
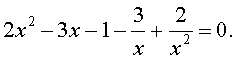 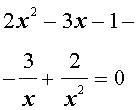 | (14) |
Преобразуем левую часть уравнения (14):
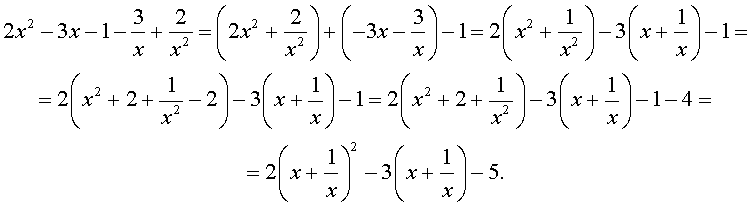
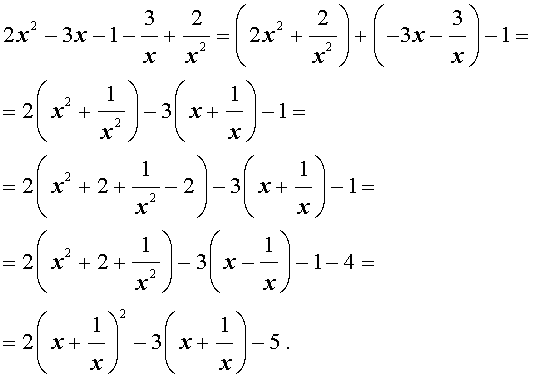
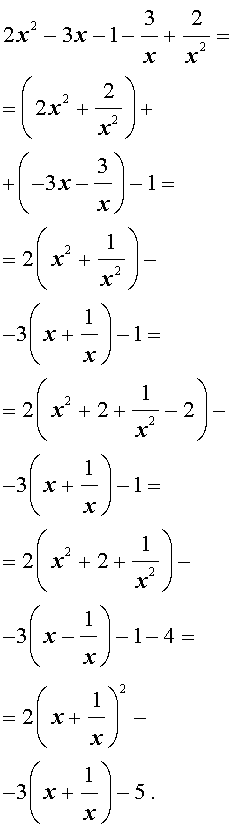
В результате этого преобразования уравнение (14) принимает вид
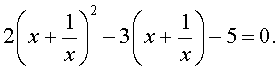 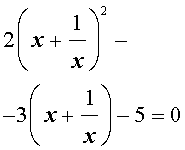 | (15) |
Если теперь обозначить
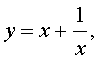 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y2 – 3y – 5 = 0. | (17) |
Решим уравнение (17):
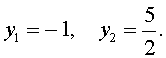 | (18) |
В первом случае из равенства (16) получаем уравнение:
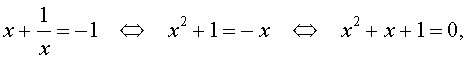
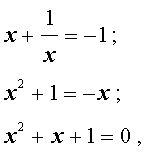
которое решений не имеет.
Во втором случае из равенства (16) получаем:
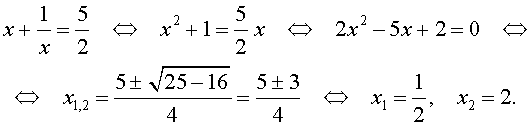
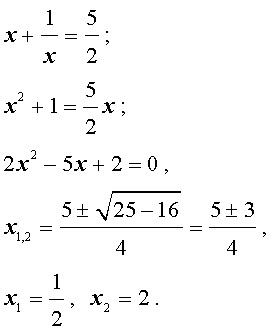
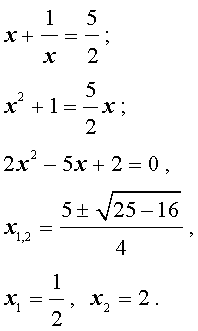
Ответ: 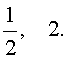
Пример 3. Решить уравнение
| 6x4 – 25x3 + 12x2 + + 25x + 6 = 0. | (19) |
Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на x2. В результате получится уравнение
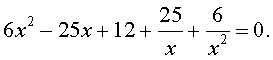 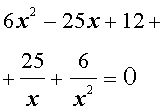 | (20) |
Преобразуем левую часть уравнения (20):
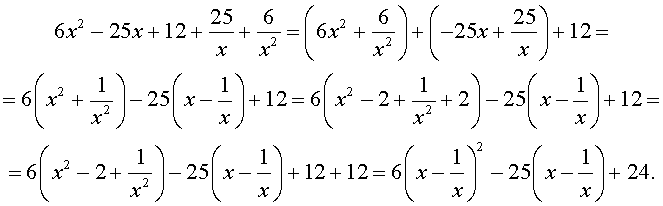
В результате этого преобразования уравнение (20) принимает вид
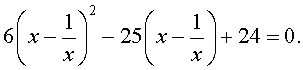 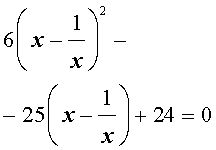 | (21) |
Если теперь обозначить
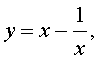 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y2 – 25y + 24 = 0. | (23) |
Решим уравнение (23):
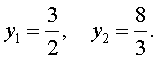 | (24) |
В первом случае из равенства (22) получаем:
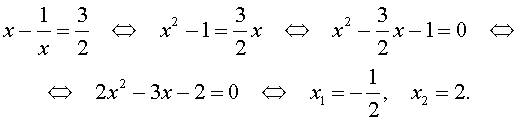
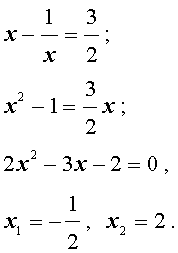
Во втором случае из равенства (22) получаем:
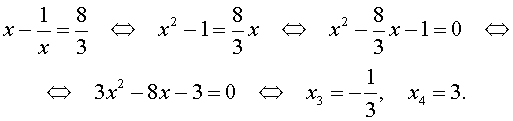
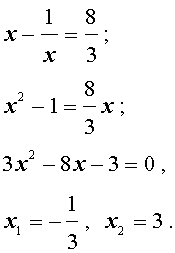
Ответ: 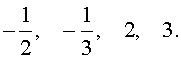
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
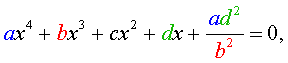 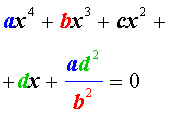 | (25) |
где a, b, c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x2. В результате получится уравнение
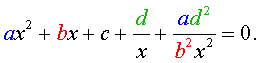 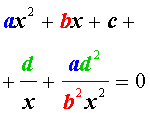 | (26) |
Преобразуем левую часть уравнения (26):
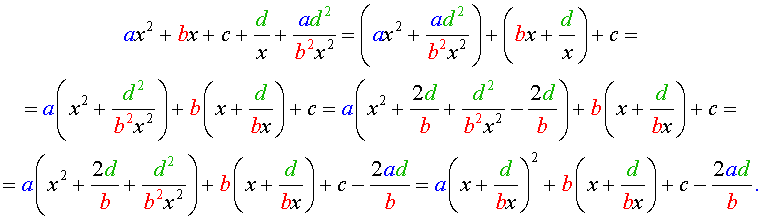
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
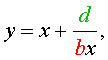 | (28) |
то уравнение (27) станет квадратным уравнением:
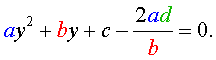 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (25) завершено.
Пример 4. Решить уравнение
| 2x4 – 15x3 + 35x2 – – 30 x + 8 = 0. | (30) |
Решение. Введем для коэффициентов уравнения (30) следующие обозначения
a = 2 , b = – 15,
c = 35, d = – 30,
и найдем значение выражения
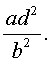
Поскольку
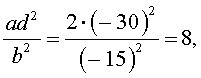
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение
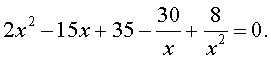 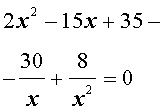 | (31) |
Преобразуем левую часть уравнения (31):
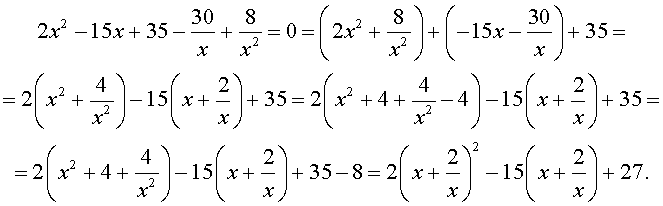
В результате этого преобразования уравнение (31) принимает вид
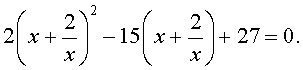 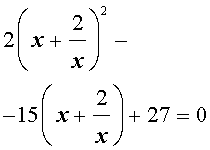 | (32) |
Если теперь обозначить
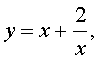 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y2 – 15y + 27 = 0. | (34) |
Решим уравнение (34):
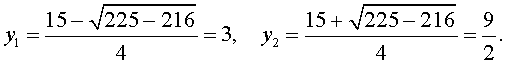
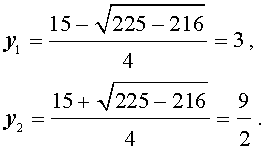
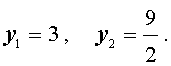
В первом случае из равенства (33) получаем:
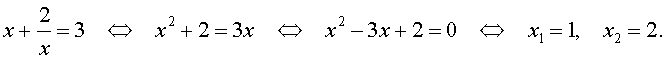
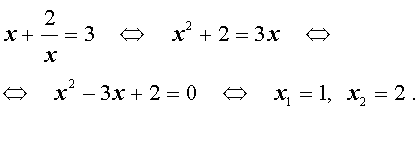
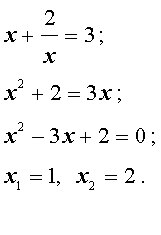
Во втором случае из равенства (33) получаем:
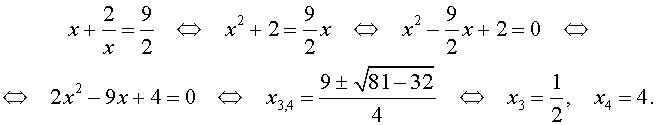
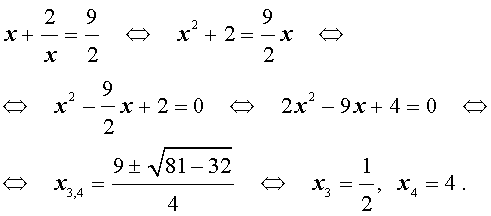
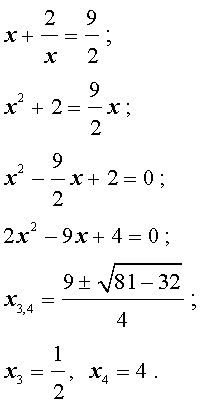
Ответ: 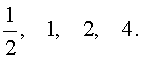

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
РЕШЕНИЕ УРАВНЕНИЙ
РЕШЕНИЕ УРАВНЕНИЙ
В этом разделе показан процесс решения уравнений различных форм. Он также показывает вам, как проверить свой ответ тремя разными способами: алгебраически, графически и с использованием концепции эквивалентности. В следующей таблице приведены частичные списки типичных уравнений.
ЛИНЕЙНЫЕ УРАВНЕНИЯ — Решите относительно x в следующих уравнениях.
- x — 4 = 10 Решение
- 2 x — 4 = 10 Решение
- 5x — 6 = 3 x — 8 Решение
- Решение
- Решение
- 2 (3 x — 7) + 4 (3 x + 2) = 6 (5 x + 9) + 3 Решение
- Решение
УРАВНЕНИЯ , СОДЕРЖАЩИЕ РАДИКАЛЬНЫЕ (S) — Решите для x следующим образом уравнения.
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
УРАВНЕНИЯ , СОДЕРЖАЩИЕ АБСОЛЮТНЫЕ ЗНАЧЕНИЯ — Решите для x в следующие уравнения.
- Решение
- Решение
- Решение
- Решение
- Решение
КВАДРАТИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом уравнения.
- х Решение
- Решение
- Решение
- Решение
- Решение
УРАВНЕНИЯ , ВКЛЮЧАЮЩИЕ ДОБИ — Решите для x следующим образом уравнения.
- Решение
- Решение
- Решение
- Решение
- Решение
ЭКСПОНЕНЦИАЛЬНЫЕ УРАВНЕНИЯ — Решите для x следующие уравнения.
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом уравнения.
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом уравнения.
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
- Решение
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор: Нэнси МаркусСвяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час .
Тем по алгебре: Решение уравнений
Урок 8: Решение уравнений
/ ru / algebra-themes / упрощающие-выражения / content /
Решение уравнений
В предыдущем разделе мы говорили о упрощающих выражениях . В этом разделе мы поговорим о решениях уравнений. Уравнения — это два выражения, равных друг другу с использованием знака равенства (=). Когда мы упрощаем выражения, наша конечная цель состоит в том, чтобы не осталось никаких операций.
Когда мы решаем уравнения, наша конечная цель состоит в том, чтобы выяснить, чему равна переменная (или буква), поместив переменную отдельно по одну сторону от знака равенства и само число с другой. Мы собираемся достичь этой цели, выполнив два важных шага:
- Упростите каждое выражение по обе стороны от знака равенства.
- Используйте обратные операции для отмены.
Звучит сложно? Мы разберем его, чтобы было легче. Давайте посмотрим на пример:
5x — 4x — 6 = 18
Мы можем начать решать так же, как начинали бы упрощать выражение, проверяя порядок операций.Мы хотим максимально упростить каждую сторону знака равенства сначала . Глядя на наше уравнение, нет скобок или показателей степени и нечего умножать или делить, поэтому мы просто начнем складывать и вычитать. Первая часть проста: 5 x — 4 x — 1 x , или просто x .
Отмена с обратными операциями
Теперь у нас осталось это уравнение:
х — 6 = 18
Мы не можем вычесть 6 из x , потому что они не , как термины (наш урок чтения алгебраических выражений объясняет это более подробно).Но x — 6 = 18 все еще недостаточно упрощен. В конце концов, мы ищем значение x , а не значение x — 6.
Чтобы решить это уравнение, нам нужно получить только x по одну сторону от знака равенства. Чтобы переместить -6 на другую сторону от знака равенства, мы можем использовать , обратное — или противоположное — -6. Это будет 6. Другими словами, мы можем прибавить шесть к обеим сторонам уравнения.
В левой части уравнения -6 плюс 6 равно 0, а x -0 равно x .Справа 18 плюс 6 равно 24, поэтому x = 24. Теперь наше уравнение упрощено. Мы упростили его, используя , инверсный , от которого мы хотели избавиться.
Это также называется , отменяющим , потому что оно позволяет вам отменить или избавиться от части уравнения. Это не значит, что вы можете просто зачеркнуть любую часть уравнения, которую не хотите решать (хотя это значительно упростит алгебру!). Вы должны соблюдать несколько правил.
Во-первых, вы заметили, что мы добавили 6 к обеим сторонам нашего уравнения? Это потому, что обе стороны уравнения всегда должны быть равными — в конце концов, это то, что означает знак равенства. Каждый раз, когда вы делаете что-то дополнительно к одной стороне уравнения, вы должны делать то же самое с другой. Поскольку мы добавили 6 к -6 на левой стороне , нам также пришлось добавить ее к 18 на правой стороне .
Во-вторых, помните, как мы прибавили шесть, где в исходном выражении говорилось, что вычесть ? Мы сделали это, потому что 6 — это противоположность -6.Чтобы отменить часть выражения, вам нужно использовать ее противоположность или инверсию. Противоположность вычитания — , сложение , и, как вы могли догадаться, противоположность сложения — , вычитание .
Посмотрите видео ниже, чтобы увидеть, как эта проблема решена.
А как насчет умножения и деления? Это тоже противоположности, и их тоже можно отменить. Например, как получить a только в этом уравнении слева от знака равенства?
5a = 30
Поскольку a — это , умноженное на на 5, вы можете разделить с обеих сторон задачи на 5. 5 a разделить на 5 равно a и 30 разделить на 5 равно 6, поэтому упрощенная версия этого уравнения будет выглядеть как
.Решение линейных уравнений — бесплатная помощь по математике
Решение уравнений: (урок 1 из 4)
Решение линейных уравнений
Уравнения без скобок
Пример 1
Решить 5x — 4 — 2x + 3 = -7 — 3x + 5 + 2x
Решение 1
Шаг 1: Объедините похожие термины | $ 5x — 4 — 2x + 3 = — 7 — 3x + 5 + 2x $ |
| $ 3x — 1 = — x — 2 $ | |
Шаг 2: Добавьте x с обеих сторон. | $ 3x — 1 + x = — x — 2 + x | $
| $ 4x — 1 = — 2 $ | |
Шаг 3: Добавьте 1 к обеим сторонам. | $ 4x — 1 + 1 = — 2 + 1 $ |
| $ 4x = — 1 $ | |
Шаг 4: Разделите обе стороны на 4: | $ \ frac {{4x}} {4} = \ frac {{- 1}} {4} | долл. США
| Решение: | $ x = — \ frac {1} {4} | $
Упражнение 1. Решите уравнения
Уравнения в скобках
Пример 2
Решить $ 2 (x — 4) + 4 (2 — x) = 5x — 4 (x + 1) $
Решение 2
Шаг 1: Упростить обе стороны: | $ 2 (x — 4) + 4 (2 — x) = 5x — 4 (x + 1) $ |
| $ 2x — 8 + 8 — 4x = 5x — 4x — 4 $ | |
| $ — 2x = x — 4 | $|
Шаг 2: Вычтите x с обеих сторон. | $ — 2x — x = x — 4 — x | $
| $ — 3x = — 4 $ | |
Шаг 3: Разделите обе стороны на -3: | $ \ frac {{- 3x}} {{- 3}} = \ frac {{- 4}} {{- 3}} | долл. США
| Решение: | $ x = \ frac {4} {3} | $
Упражнение 2: Решите уравнения
.«Решение» квадратных уравнений с помощью графического представления
Purplemath
Если честно, решение «с помощью построения графиков» — это несколько надуманная тема. Основная идея решения с помощью построения графиков заключается в том, что, поскольку решения (действительные числа) любого уравнения (включая квадратные уравнения) представляют собой перехваты x этого уравнения, мы можем взглянуть на перехваты x графика найти решения соответствующего уравнения.Однако есть трудности с «решением» таким способом.
Когда мы строим прямую линию, такую как « y = 2 x + 3», мы можем найти точку пересечения x (с определенной степенью точности), нарисовав действительно аккуратную систему осей, построив пару точки, схватив нашу линейку, проведя красивую прямую линию и прочитав (приблизительный) ответ на графике с достаточной степенью уверенности.
MathHelp.com
Однако единственный способ узнать, что у нас есть точный интервал x и, следовательно, решение, — это использовать алгебру, установить уравнение линии равным нулю и решить:
0 = 2 х + 3
–3 = 2 x
–1.5 = х
Если бы линейное уравнение было чем-то вроде y = 47 x -103, очевидно, что нам будет очень трудно угадать решение по графику. Мы можем предположить, что интервал x близок к x = 2, но, хотя и близко, это не совсем так. Алгебра была бы единственным надежным методом решения.
Квадратичная функция более беспорядочная, чем прямая линия; он изображается как извивающаяся парабола.Если мы построим несколько точек перехвата, отличных от x , а затем проведем через них изогнутую линию, как мы узнаем, получили ли мы перехват x даже близко к правильному? Мы этого не делаем. Единственный способ быть уверенным в наших перехватах x — это установить квадратичное значение равным нулю и решить.
Но весь смысл «решения с помощью построения графиков» в том, что они не хотят, чтобы мы занимались (точной) алгеброй; они хотят, чтобы мы гадали по красивым картинкам.
Таким образом, «решение с помощью построения графиков» обычно не является ни «решением», ни «построением графиков». В типичном упражнении вы на самом деле ничего не графуете и не решаете. Вместо этого вам предлагается угадывать числа на распечатанном графике. Или же, если вы «используете технологию», вам скажут нажать несколько кнопок на вашем графическом калькуляторе и посмотреть на красивую картинку; а затем вам предлагается нажать несколько других кнопок, чтобы программа могла вычислить перехваты.
Я предполагаю, что преподаватели пытаются помочь вам увидеть связь между x — интерпретациями графиков и решениями уравнений.Но концепция имеет тенденцию теряться во всех нажатиях кнопок.
Хорошо, хватит моей разглагольствования.
Для решения путем построения графиков книга может дать нам очень аккуратный график, вероятно, с пометкой как минимум нескольких точек. Книга попросит нас указать на графике точки, которые представляют решения. В противном случае он даст нам квадратичный коэффициент, и мы воспользуемся нашим графическим калькулятором, чтобы найти ответ.Поскольку разные модели калькуляторов имеют разные последовательности клавиш, я не могу дать инструкции, как «использовать технологии» для поиска ответов; вам необходимо проконсультироваться с руководством пользователя для любого используемого вами калькулятора (или с файлом «Справка» для любой электронной таблицы или другого программного обеспечения, которое вы используете). Я приведу лишь пару примеров решения по картинке, которая вам дается.
Решите x 2 — 8 x + 15 = 0, используя следующий график.
Уравнение, которое мне дали решить:
На картинке, которую они мне дали, показан график соответствующей квадратичной функции:
Перехваты x на графике функции соответствуют y = 0. Дело в том, что мне нужно смотреть на картинку (надеясь, что точки действительно пересекаются в целых числах, как кажется) , и прочтите x -перехваты графика (и, следовательно, решения уравнения) с рисунка.
Кажется, что график пересекает ось x при x = 3 и x = 5, я должен предположить, что график точен, и что то, что выглядит как целочисленное значение, на самом деле равно единице. Итак, мой ответ:
Так как они предоставили квадратное уравнение в приведенном выше упражнении, я могу проверить свое решение с помощью алгебры. Приведенные квадратичные множители, которые дают мне:
( x — 3) ( x — 5) = 0
x — 3 = 0, x — 5 = 0
х = 3, 5
Теперь я знаю , что решения являются целочисленными значениями.Граф может наводить на размышления о решениях, но только алгебра верна и точна.
Решите 0,3 x 2 — 0,5 x — 5/3 = 0 из следующего графика.
A = (–5/3, 0), B = (0, –5/3), C = (5/6, –15/8), D = (10/3, 0)
Для этого рисунка разметили кучу точек.Отчасти это должно было быть полезно, потому что перехваты x беспорядочные, поэтому я не мог бы угадать их значения без меток. Но в основном это было в надежде запутать меня, на случай, если я забыл, что «решениям» соответствуют только точки пересечения x , а не вершины или точки пересечения y .
Точка B — это перехват y (потому что x = 0 для этой точки), поэтому я могу игнорировать эту точку. Точка C кажется вершиной, поэтому я могу игнорировать и эту точку.Точки A и D находятся на оси x (потому что y = 0 для этих точек). Итак, я могу предположить, что значения x этих точек на графике дают мне значения решений для соответствующего квадратного уравнения.
Поскольку они предоставили уравнение в дополнение к графику связанной функции, можно проверить ответ с помощью алгебры. Но целью здесь было подтвердить, что ученик знает, какие точки являются точками пересечения x , и знает, что эти точки пересечения на графике являются решениями связанного уравнения.
Найдите решения квадратного уравнения на следующем графике:
A = (–2,1429, 0), B = (2,8, 0), C = (0,3286, –3,0540), D = (0, –3)
Мне не предложили решить квадратное уравнение, поэтому я не могу проверить свою работу алгебраически.Они только дали мне изображение параболы, созданной соответствующей квадратичной функцией, из которой я должен аппроксимировать интервалы x , что на самом деле является другим вопросом. Но я знаю, что они означают.
Я могу игнорировать точку, которая, вероятно, является вершиной (точка C). Я могу игнорировать точку перехвата и (точка D). Поэтому я буду обращать внимание только на точки перехвата x , то есть те точки, где y равно нулю.Итак, мой ответ:
Квадратичное решение с помощью построения графиков глупо с точки зрения «реальной жизни» и требует, чтобы решения были простыми решениями типа факторинга, такими как « x = 3», а не чем-то вроде « x = –4 + sqrt. (7) «. Другими словами, они должны либо «дать» вам ответы (b пометив график), либо попросить вас предложить решения, которые вы могли бы легко найти с помощью факторинга.
Практически единственное, что вы можете получить из этой темы, — это укрепить свое понимание связи между решениями уравнений и x -перехватываниями графиков функций; то есть тот факт, что решение «(некоторый многочлен) равно (нулю)» соответствует перехватам x графика « y равно (тот же самый многочлен)». Если вы поймете эту концепцию, тогда вы будете знать, когда лучше всего использовать графический калькулятор или другое графическое программное обеспечение, чтобы помочь вам решить общие полиномы; а именно, когда они не подлежат факторизации.И вы поймете, как делать первоначальные предположения и приближения к решениям, глядя на график, знания, которые могут быть очень полезны на более поздних занятиях, когда вы, возможно, будете работать с программным обеспечением, чтобы найти приблизительные «численные» решения.
Но на практике, учитывая квадратное уравнение, которое нужно решить в вашем классе алгебры, вам не следует начинать с рисования графика. Возникает вопрос: какой метод следует использовать для любого квадратичного уравнения ?
URL: https: // www.purplemath.com/modules/solvquad5.htm
.
 что при
что при  равносильно уравнению
равносильно уравнению  Откуда
Откуда 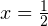 или
или 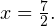
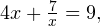 что при
что при 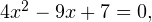 у которого решений нет, поскольку его дискриминант отрицателен.
у которого решений нет, поскольку его дискриминант отрицателен.