Методы решения уравнений, неравенств и их систем
Введение
Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Однако решению всех видов уравнений и неравенств уделяется недостаточно внимания. Актуальность рассмотрения данной темы обусловлена противоречием между тем, что задания, связанные с уравнениями и неравенствами и их системами регулярно встречаются в материалах ЕГЭ и ОГЭ и тем, что их решение, вызывают у учащихся значительные трудности.
Целью данной работы является: Рассмотреть методические основы профильного и углубленного обучения теме «Уравнения, неравенства и их системы».
Из данной цели вытекают задачи:
Выделить методы решения уравнений, неравенств и их систем.
Выполнить логико-дидактический анализ темы «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.
 Г. Мордковича 10-11 класс.
Г. Мордковича 10-11 класс.Разработать конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.
Данные практические разработки могут быть использованы в школе.
Данная работа состоит из трех параграфов:
§1. Методы решения уравнений, неравенств и их систем.
§2. Логико-дидактический анализ по теме «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.
§3. Конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.
§1. Методы решения уравнений, неравенств и их систем
Методы решения целых уравнений первой степени.
Раскрытие скобок (умножаем многочлен на многочлен). Пример: (2x+1)(3x-2)-6x(x+4)=67-2x
Домножение на НОК знаменателей дробей обеих частей уравнения.
 Пример: —
Пример: —
Способы решения целых уравнений.
Разложение многочлена на множители. Пример: +3=0
С помощью теоремы о корне многочлена. Пример:
Введение новой переменной. Пример:
Метод неопределенных коэффициентов. Пример:
Графический способ. Пример:
С помощью алгоритма решения квадратных уравнений:
Алгоритмы и способы решения дробно-рациональных уравнений.
а) Умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение.
б) Решаем полученное целое уравнение.
в) Исключаем из его корней те, которые обращают в нуль общий знаменатель дробей.
Пример:
Используя нестандартные преобразования. Пример:
Введение новой переменной. Пример:
Введение вспомогательной переменной. Пример:
Графический способ решения.
 Пример:
Пример:
Способы решения целых неравенств с одной переменной.
1.Используя свойства дискриминанта квадратного уравнения и свойств графика квадратичной функции. Пример:
2. Метод интервалов. Пример:
3. Используя свойства графика квадратной функции. Пример:
Способы решения дробно-рациональных неравенств с одной переменной.
Разложение на множители числителя и знаменателя. Пример:
Используя систему. Примеры:
Способы решения уравнений с переменной под знаком модуля.
Замена на систему уравнений. Пример:
Замена совокупность из двух систем. Пример:
Графический способ с дальнейшей заменой на совокупность из трех систем уравнений. Пример:
Способы решения неравенств с переменной под знаком модуля.
Замена на систему неравенств.
 Пример:
Пример:Используя свойство модуля. Пример:
Графический способ с дальнейшей заменой на совокупность из трех систем неравенств. Пример:
Способы решения уравнений с параметром.
Вынесение многочлена за скобку. Пример: ax-2x=a2+a-6
Используя дискриминант. Пример:
Способы решения дробно-рациональных уравнений с параметром.
Домножение на общий знаменатель. Пример:
Методы решения систем уравнений с двумя переменными
Метод подставновки:
Выражаем из какого-либо уравнения системы одну переменную через другую.
Подставляем вместо этой переменной полученное выражение во второе уравнение.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Метод сложения:
Умножаем левые и правые части уравнений.

Складываем почленно левые и правые части уравнений.
Решаем получившееся при сложении уравнение с одной переменной.
Находим соответствующие значения второй переменной.
б) Разложение на линейные множители.
Пример:
Способы решения линейных неравенств с двумя переменными.
Графический. Пример: 4x-5y20
Способы решения неравенств с двумя переменными выше первой.
Графический. Пример:
Способы решения системы неравенств с двумя переменными.
Графический Пример:
Способы решения неравенств с двумя переменными, содержащие знак модуля.
Графический. Пример:
Методы решения уравнений высших степеней.
Метод замены переменной. Пример: x(x-1)(x-2)(x-3)=24
Используя делители свободного члена уравнения.
 Пример: x3+2x2-7x-12=0
Пример: x3+2x2-7x-12=0Деления обеих частей уравнения на x2. Пример: 3x4-2x3-9x2-4x+12=0
Метод замены двух переменных. Пример: 2(x2+x+1)-7(x-1)2=13(x3-1)
Графический метод. Пример: x5+5x-42=0
Используя производную функции. Пример: x4-8x+63=0
Методы решения показательных уравнений.
Функционально-графический метод.
Метод введения новой переменной. Пример: 4x+2x+1-24=0
Методы решения показательных неравенств.
Метод уравнивания показателей. Пример:
Метод введения новой переменной. Пример:
Деления обеих частей уравнения на число с наибольшим показателем в степени.
 (однородные уравнения второй степени) Пример: 8x+18x2∙27x
(однородные уравнения второй степени) Пример: 8x+18x2∙27xИспользуя свойство дискриминанта. Пример: (x2+x+1)x≤1
Методы решения логарифмических уравнений.
Метод потенцирования. Пример: log3(x2-3x-5)=log3(7-2x)
Используя ОДЗ. Пример: logx+4(x2-1)= logx+4(5-x)
Используя свойства логарифма. Пример: log2(x+4)+log2(2x+3)=log2(1-2x)
Введение новой переменной. Пример: lg2x+lg x+1=
Методы решения логарифмических неравенств.
Метод потенцирования.
 Пример: log3(2x-4)log3(14-x)
Пример: log3(2x-4)log3(14-x)Представление обеих частей неравенства в виде логарифмов с одинаковым основанием. Пример: (16+4x—x2)≤-4
Введение новой переменной. Пример:
Используя ОДЗ. Пример: logx-2(2x-3) logx-2(24-6x)
Методы решения уравнений и неравенств с модулем.
Раскрытие модуля по определению. Пример:
Графический способ. Пример:
Используя совокупность уравнений (неравенств). Пример:
Методы решения иррациональных уравнений.
Возведение обеих частей уравнения в одну и ту же степень. Пример:
Введение новой переменной. Пример:
Уединение корня и возведение обеих частей уравнения в степень. Пример:
Введение двух новых переменных.
 Пример:
Пример:Умножение обеих частей уравнения на выражение сопряженное данному. Пример:
Методы решения иррациональных неравенств.
Используя совокупность неравенств. Пример:
Введение новой переменной. Пример:
Методы решения систем уравнений.
Перемножением правых и левых частей уравнения. Пример:
Введение новой переменной. Пример:
Метод деления. Пример:
Некоторые нестандартные методы решения уравнений и неравенств
В статье автор рассматривает применение некоторых нестандартных методов с целью оптимизации решения уравнений и неравенств. Представляется созданный автором уникальный онлайн-тренажер как способ самостоятельной подготовки к решению уравнений и неравенств, представленных, в том числе, в заданиях ЕГЭ.
Для успешной сдачи ЕГЭ очень важно правильно распределять и экономить время, поэтому требуются новые методы решения, обеспечивающие наиболее быстрое выполнение заданий.
На уроках математики в школе изучаются такие методы решения уравнений и неравенств, как: разложение на множители, замена переменной, схема Горнера, теорема Безу, теорема Виета, метод интервалов и др. Однако их применение не всегда обеспечивают быстроту решения и минимальность ошибок. Это обуславливает необходимость в поиске методов решения уравнений и неравенств, позволяющих сократить количество шагов решения в алгоритме и снизить вероятность допущения ошибки.
К числу таких методов относятся: метод рационализации, учет ОДЗ, метод мажорант (метод оценки), использование свойств функции, графиков функций, угадывание корня.
Метод рационализации (метод декомпозиции, метод замены множителей) заключается в замене сложного выражения на более простое выражение , при котором неравенство ∨ 0 равносильно неравенству ∨ 0 в области определения выражения .
Приведем алгоритм решения уравнений и неравенств методом рационализации :
- Нахождение ОДЗ уравнения/неравенства.

- Привести данное неравенство к стандартному виду: слева дробь (или произведение), справа — ноль.
- Заменить выражения левой части на более простые, эквивалентные им по знаку.
- Решить полученное неравенство, например, методом интервалов.
Ниже приведена таблица наиболее часто встречающихся замен:
Раскроем применение составленного нами алгоритма при решении неравенства
- Определим ОДЗ неравенства:
- Приведем логарифмы к одному основанию:
- Упростим выражение. Для этого воспользуемся формулой
,
Отсюда и
- Продолжаем упрощение с помощью формулы :
- Сравним каждый множитель левой части неравенства с нулём:
и
- Решим каждое неравенство:
- Используем метод интервалов с учетом ОДЗ:
Отсюда (0;1) (1;2) (2; +∞ ).
Учёт ОДЗ . Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решение уравнения (или неравенства) непосредственно подстановкой чисел из ОДЗ.
Приведём алгоритм решения уравнений и неравенств методом учёта ОДЗ :
- Найти ОДЗ уравнения/неравенства.
- Подставить значение ОДЗ в исходное уравнение/неравенство, чтобы проверить, является ли оно корнем.
Покажем решение уравнения раскрываемым методом.
Для этого найдём ОДЗ уравнения: оно состоит из всех х, одновременно удовлетворяющих условиям и , т. е. ОДЗ есть пустое множество. Этим решение уравнения и завершается, т. к. установлено, что ни одно число не может являться решением т. е. что уравнение не имеет корней.
Метод мажорант также называют методом оценки левой и правой частей, входящих в уравнения и неравенства.
Мажорантой данной функции f(х) на множестве Р , называется такое число М , что либо f(х) ≤ М для всех х ϵ Р , либо f(х) ≥ М для всех х ϵ Р .
Мажоранты многих элементарных функции известны. Их нетрудно указать, зная область значений функции.
Алгоритм решения
- Оценить левую часть уравнения/неравенства.
- Оценить правую часть.
- Составить систему уравнений/неравенств.
- Решить систему и сделать вывод.
- Выполнить проверку.
- Записать ответ.
Покажем применение алгоритма при решении такого уравнения
- Оценим левую и правую части уравнения:
Так как левая часть уравнения приравнивается к нулю, то равенство возможно только в том случае, если оба слагаемых равны нулю.
- Составим систему уравнений:
- Решим систему уравнений:
- Выполним проверку:
При
При :
.
Использование монотонности функции.
Утверждение 1 . Если функция монотонна, то уравнение (где А – любое действительное число) имеет не более одного корня.
Утверждение 2. Если функция монотонно возрастает, а функция монотонно убывает, то уравнение имеет не более одного корня.
С помощью утверждений 1 и 2 можно обосновать единственность решения уравнения в тех случаях, когда решить его стандартными способами не представляется возможным, но при этом удается подобрать корень уравнения, который, как правило, является целым числом. При этом надо учитывать, что решение уравнения «методом подбора» не будет засчитано при проверке без обоснования того, что уравнение не имеет других корней. Такое обоснование часто удается сделать, опираясь на свойства монотонности функций.
Такое обоснование часто удается сделать, опираясь на свойства монотонности функций.
Приведём алгоритм решения уравнений и неравенств методом использования монотонности функции:
- Определить монотонность и область определения функции (ООФ).
- Методом подбора найти корень уравнения/неравенства.
- Исходя из монотонности функции делаем вывод о количестве корней.
При решении уравнения :
- Воспользуемся методом замены:
Пусть . Тогда . Получаем:
,
.
- Определим монотонность функций:
- Методом подбора находим корень
- Разделим обе части уравнения на :
- Снова определим монотонность полученных функций:
Отсюда следует, что
- Вернемся к замене:
Использование графиков функции. При решении уравнений и неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
При решении уравнений и неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ ещё надо обосновать.
Приведём алгоритм решения уравнений и неравенств с помощью использования графиков:
- Определить ОДЗ уравнения/неравенства.
- Представить левую и правую части уравнения/неравенства как
функции и построить их графики.
- По графику определить решение уравнения/неравенства.
- Доказать справедливость ответа.
Применим построенный алгоритм при решении неравенства
- Определим ОДЗ неравенства:
- Представим функции и в виде графиков:
Из рисунка следует, что для всех х из ОДЗ исходное неравенство справедливо.
- Докажем справедливость ОДЗ:
При х ∈ [-1;1]: .
Значит, решениями исходного неравенства будут все х из промежутка [-1;1].
Угадывание корня уравнения (искусственный метод решения уравнений). Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения.
Раскроем алгоритм решения уравнений методом угадывания корня :
- Методом подбора определить корень уравнения.
- Найти ОДЗ уравнения.
- Привести многочлен к стандартному виду.
- Определить остальные корни уравнения.
При решении уравнения : :
- Методом подбора определим корень уравнения:
- Приведём многочлен к стандартному виду:
- Найдём остальные корни:
Отсюда следует, что – единственный корень уравнения
В качестве проектного продукта проведенного исследования был выбран интерактивный тренажер, который позволит практиковаться в решении уравнений и неравенств с помощью новых, нестандартных методов решения.
В таблице ниже приведены результаты оценки сетевых сервисов по выбранным критериям:
Сетевой сервис | Критерии оценивания | ||
Интерфейс | Разнотипность | Мобильная версия | |
Quizizz | + | — | + |
Wordwall | + | + | + |
PurposeGames | + | + | + |
Wizer. | + | + | + |
LearningApps | + | + | + |
Сетевой сервис | Критерии оценивания | ||
Русский | Бесплатность | Доступность | |
Quizizz | — | + | + |
Wordwall | + | — | + |
PurposeGames | — | + | + |
Wizer. | — | + | + |
LearningApps | + | + | + |
В результате сравнения сетевых сервисов по указанным критериям для создания интерактивного тренажера была выбрана платформа LearningApps, которая соответствует наибольшему количеству требований.
В процессе размышления над идеей контента тренажёра было принято решение представить продукт, объединив теорию и тренажёры (упражнения) в одну презентацию.
Презентация. Основная задача презентации заключается в наглядном представлении алгоритмов решения уравнений/неравенств, примеров решения, а также в размещении ссылок на онлайн-тренажёры для каждого метода.
Тренажёр. Для каждого метода решения уравнений/неравенств создано несколько тренажёров (упражнений): на проработку алгоритма, проработку ключевых формул (если такие имеются) и на тренировку самого решения.
Доступ к тренажеру обеспечивается ссылкой https://infourok.ru/prezentaciya-po-algebre-na-temu-nekotorye-nestandartnye-metody-resheniya-uravnenij-i-neravenstv-9–11-klass-5183275.html и QR кодом.
В ходе создания продукта была выбрана концепция тренажёра, позволяющая объединить теорию и практику. Апробация показала, что изучение некоторых нестандартных методов решения уравнений и неравенств становится более наглядным и структурированным. Создание такого информативного, эффективного, удобного в использовании и общедоступного тренажера позволяет решить проблему увеличения скорости решения и минимизации ошибок.
Считаем необходимостью изучение рассмотренных методов, ведь они в действительности являются незаменимыми при решении уравнений и неравенств.
Литература:
- Олехник С. Н., Потапов М. К., Пасиченко П. И. Уравнения и неравенства. Нестандартные методы решения: справочник. 1997. — 219 с.
- Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: базовый и углубленный уровни. 7-е изд. М.: Просвещение, 2019. — 384 с.
- Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Математика: алгебра и начала математического анализа. 11 класс: базовый и профильный уровни. 2-е изд. М.: Просвещение, 2010. — 336 с.
- Образовательный портал для подготовки к экзаменам. Сдам ГИА: Решу ЕГЭ. ЕГЭ — 2021, Математика профильного уровня: задания, ответы, решения. Обучающая система Дмитрия Гущина. Задания: № 13, № 15.
9: Системы уравнений и неравенств
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1274
- OpenStax
- OpenStax
В этой главе мы исследуем матрицы и их обратные, а также различные способы использования матриц для решения систем уравнений. Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби.
Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби.
- 9.0: Прелюдия к системам уравнений и неравенств
- В этой главе мы исследуем матрицы и их обратные, а также различные способы использования матриц для решения систем уравнений. Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов.
- 9.1: Системы линейных уравнений — две переменные
- Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений и несовместные без решения.

- 9.2: Системы линейных уравнений с тремя переменными
- https://math.libretexts.org/TextMaps/Algebra_Textmaps/Map%3A_Elementary_Algebra_(OpenStax)/11%3A_Systems_of_Equations_and_Inequalities/11.3%3A_Systems_of_Linear_Equations%3A_Three_Variables
- 9.3: Systems of Nonlinear Equations and Inequalities — Two Variables
- В этом разделе мы рассмотрим пересечение параболы и прямой, окружности и прямой, окружности и эллипса. Методы решения систем нелинейных уравнений аналогичны методам решения линейных уравнений.
- 9.4: Частичные дроби
- Разложите отношение многочленов, записав частичные дроби. Решите, очистив дроби, расширив правую часть, собрав одинаковые члены и установив соответствующие коэффициенты равными друг другу, затем составив и решив систему уравнений. Разложение с повторяющимися линейными множителями должно учитывать множители знаменателя в возрастающих степенях.
 Разложение с неповторяющимся неприводимым квадратичным множителем нуждается в линейном числителе над квадратичным множителем.
Разложение с неповторяющимся неприводимым квадратичным множителем нуждается в линейном числителе над квадратичным множителем.
- 9.5: Матрицы и операции с матрицами
- Для решения системы уравнений мы можем использовать матрицу, которая представляет собой прямоугольный массив чисел. Строка в матрице — это набор чисел, выровненных по горизонтали. Столбец в матрице — это набор чисел, выровненных по вертикали. Каждое число является записью, иногда называемой элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами.
- 9.6: Решение систем с исключением Гаусса
- Матрица может служить средством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства.
 Когда система записывается в такой форме, мы называем ее расширенной матрицей.
Когда система записывается в такой форме, мы называем ее расширенной матрицей.
- 9.7: Решение систем с инверсиями
- Матрица, имеющая мультипликативную инверсию, называется обратимой матрицей. Только квадратная матрица может иметь мультипликативную обратную, поскольку требуется обратимость. Не все квадратные матрицы имеют обратную. Мы рассмотрим два метода нахождения обратной матрицы 2×2 и третий метод, который можно использовать как для матриц 2×2 , так и для матриц 3×3 .
- 9.8: Решение систем с правилом Крамера
- В этом разделе мы изучим еще две стратегии решения систем уравнений. Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.
 Правило Крамера для решения системы уравнений с двумя и тремя переменными.
Правило Крамера для решения системы уравнений с двумя и тремя переменными.
- 9.E: Системы уравнений и неравенств (упражнения)
- В этой главе мы исследуем матрицы и их обратные формы, а также различные способы использования матриц для решения систем уравнений. Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов.
- 9.R: Системы уравнений и неравенств (обзор)
- В этой главе мы исследуем матрицы и их обратные, а также различные способы использования матриц для решения систем уравнений. Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов.
Эта страница под названием 9: Системы уравнений и неравенств распространяется под лицензией CC BY 4. 0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Глава
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus
- источник@https://openstax.
7: Системы уравнений и неравенств
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15085
- OpenStax
- OpenStax
В этой главе мы исследуем матрицы и их обратные, а также различные способы использования матриц для решения систем уравнений. Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби.
- 7.1: Прелюдия к системам уравнений и неравенств
- В этой главе мы исследуем матрицы и их обратные, а также различные способы использования матриц для решения систем уравнений.
 Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов.
Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов.
- 7.2: Системы линейных уравнений — две переменные
- Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений и несовместные без решения.
- 7.3: Системы линейных уравнений с тремя переменными
- Набор решений — это упорядоченная тройка , представляющая собой пересечение трех плоскостей в пространстве. Систему трех уравнений с тремя переменными можно решить, используя серию шагов, которые заставляют исключить переменную.
 Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. Системы трех уравнений с тремя переменными полезны для решения реальных задач.
Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. Системы трех уравнений с тремя переменными полезны для решения реальных задач.
- 7.4: Системы нелинейных уравнений и неравенств — две переменные
- В этом разделе мы рассмотрим пересечение параболы и прямой, окружности и прямой, а также окружности и эллипса. Методы решения систем нелинейных уравнений аналогичны методам решения линейных уравнений.
- 7.5: Частичные дроби
- Разложите отношение многочленов, записав частичные дроби. Решите, очистив дроби, расширив правую часть, собрав одинаковые члены и установив соответствующие коэффициенты равными друг другу, затем составив и решив систему уравнений. Разложение с повторяющимися линейными множителями должно учитывать множители знаменателя в возрастающих степенях.
 Для разложения с неповторяющимся неприводимым квадратичным множителем требуется линейный числитель над квадратичным множителем.
Для разложения с неповторяющимся неприводимым квадратичным множителем требуется линейный числитель над квадратичным множителем.
- 7.6: Матрицы и операции с матрицами
- Для решения системы уравнений мы можем использовать матрицу, которая представляет собой прямоугольный массив чисел. Строка в матрице — это набор чисел, выровненных по горизонтали. Столбец в матрице — это набор чисел, выровненных по вертикали. Каждое число является записью, иногда называемой элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами.
- 7.7: Решение систем с исключением Гаусса
- Матрица может служить средством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства.
 Когда система записывается в такой форме, мы называем ее расширенной матрицей.
Когда система записывается в такой форме, мы называем ее расширенной матрицей.
- 7.8: Решение систем с инверсиями
- Матрица, имеющая мультипликативную инверсию, называется обратимой матрицей. Только квадратная матрица может иметь мультипликативную обратную, поскольку требуется обратимость. Не все квадратные матрицы имеют обратную. Мы рассмотрим два метода нахождения обратной матрицы 2×2 и третий метод, который можно использовать как для матриц 2×2 , так и для матриц 3×3 .
- 7.9: Решение систем с правилом Крамера
- В этом разделе мы изучим еще две стратегии решения систем уравнений. Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.


 Г. Мордковича 10-11 класс.
Г. Мордковича 10-11 класс. Пример: —
Пример: —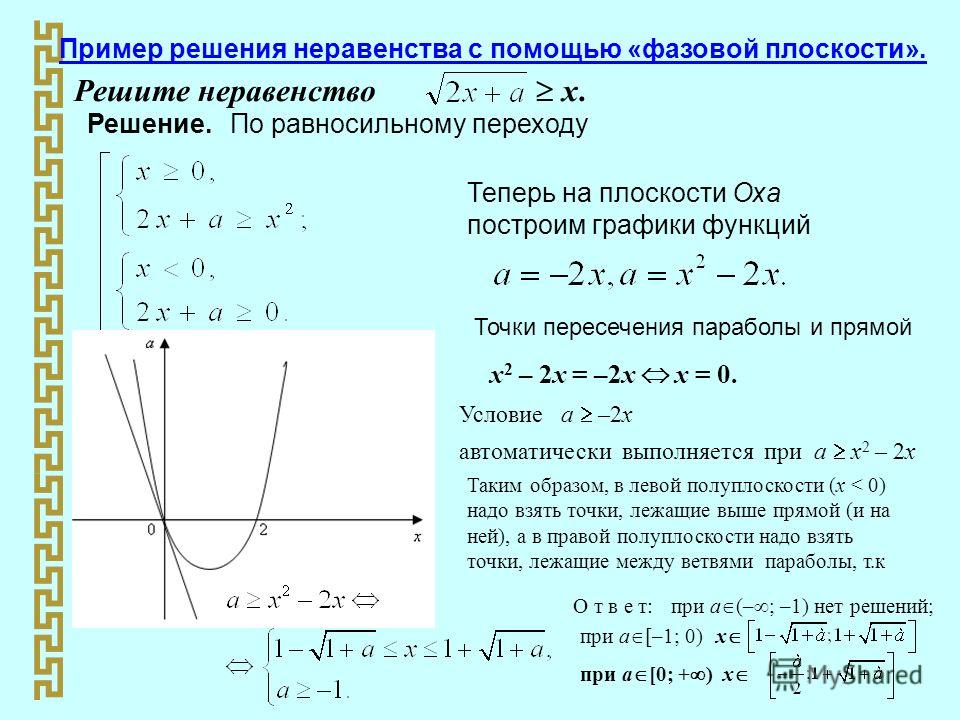 Пример:
Пример: Пример:
Пример:
 Пример: x3+2x2-7x-12=0
Пример: x3+2x2-7x-12=0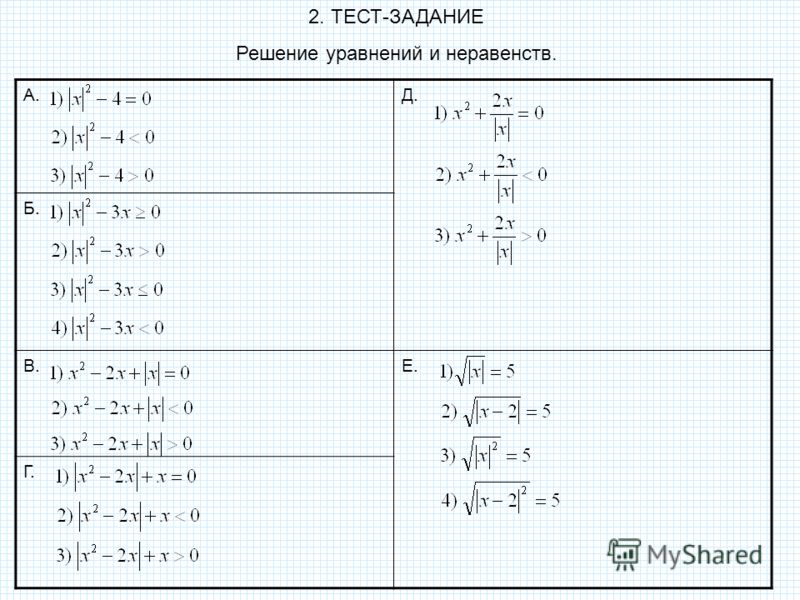 (однородные уравнения второй степени) Пример: 8x+18x2∙27x
(однородные уравнения второй степени) Пример: 8x+18x2∙27x Пример: log3(2x-4)log3(14-x)
Пример: log3(2x-4)log3(14-x) Пример:
Пример:
 me
me me
me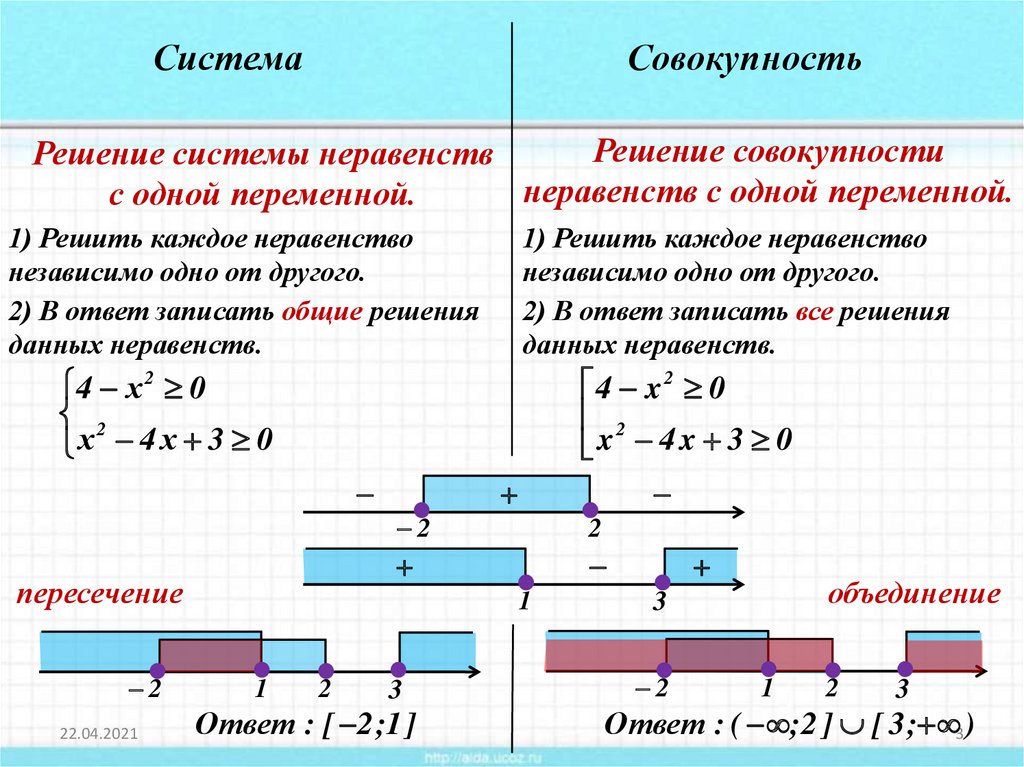
 Разложение с неповторяющимся неприводимым квадратичным множителем нуждается в линейном числителе над квадратичным множителем.
Разложение с неповторяющимся неприводимым квадратичным множителем нуждается в линейном числителе над квадратичным множителем. Когда система записывается в такой форме, мы называем ее расширенной матрицей.
Когда система записывается в такой форме, мы называем ее расширенной матрицей. Правило Крамера для решения системы уравнений с двумя и тремя переменными.
Правило Крамера для решения системы уравнений с двумя и тремя переменными. org/details/books/precalculus
org/details/books/precalculus Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов.
Сначала, однако, изучим сами системы уравнений: линейные и нелинейные, а затем дроби. Мы не будем здесь раскрывать какие-либо секретные коды, но заложим основу для будущих курсов. Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. Системы трех уравнений с тремя переменными полезны для решения реальных задач.
Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. Системы трех уравнений с тремя переменными полезны для решения реальных задач. Для разложения с неповторяющимся неприводимым квадратичным множителем требуется линейный числитель над квадратичным множителем.
Для разложения с неповторяющимся неприводимым квадратичным множителем требуется линейный числитель над квадратичным множителем. Когда система записывается в такой форме, мы называем ее расширенной матрицей.
Когда система записывается в такой форме, мы называем ее расширенной матрицей.