Первый признак равенства треугольников. Решение задач
Цели и задачи урока:
- повторение понятий треугольника и его элементов
- повторение понятия равных треугольников
- формирование у учащихся умения доказывать равенство треугольников
- умение выделять следствия, вытекающие из равенства треугольников.
Ход урока
Решение задач по готовым чертежам.
I. Проверка домашнего задания: № 90, № 94.
Перед уроком на доске выполнены чертежи и записано дано к каждой задаче:
№90.
Дано: треугол. АВС
АВ = 17 см, АС > AB в 2 раза, ВС < AC на 10 см.
Найти: P треугол. ABC = ?
№ 94.
Дано: АВ = АС, <1 = <2, АС= 15 см, DC= 5 см.
а) Доказать: треугол. АВD = треугол. ACD
б) Найти: BD и АВ.
Далее с помощью фронтального опроса класса устно проверяем решение домашних задач.
№ 90. Решение:
- Пусть АВ = 17 см (по условию), тогда AC = 2АВ = 17 * 2 = 34 см, а ВС = АС – 10 = 34 – 10 = 24 см
- P АВС = АВ + ВС + АС = 17 + 34 + 24 = 75 см.
Ответ: Р треугольника. АВС = 75 см.
№ 94.
1) Рассмотрим треугольник АВС и треугольник АСD.
а) АВ = АС (по условию)
б) < 1 = < 2 (по условию)
в) AD – общая сторона
Из а, б, в следует => треугольник АВD = треугольнику АСD по двум сторонам и углу между ними (Первый признак равенства треугольников).
2) Треугольник АВD = треугольнику АСD, мы знаем, что в равных треугольниках против соответственно равных углов лежат равные стороны, т.е. т.к <1 = <2, то BD = DC = 5 см
3) АВ = АС = 15 см (по условию)
Ответ: АВ = 15 см, ВО = 5 см.
Попутно повторяем следующие понятия:
а) какая фигура называется треугольником;
б) элементы треугольника;
в) стороны и углы, противолежащие друг другу;
г) углы, прилежащие к сторонам треугольника;
д) что такое периметр треугольника
II. Опрос класса – доказательство I-ого признака равенства треугольников. Опрос называется – Каскад.
5 учеников из класса уже ответили учителю эту теорему и знают ее отлично. Знают все дополнительные вопросы (и ответы на них), которые надо задать по ходу доказательства этой теоремы. Причем это, как правило, слабые ученики класса, которые выучивают теорему, хорошо понимая ее, с помощью учителя. Они стремятся дотошно разобраться в доказательстве данной теоремы и всего теоретического материала, используемого в ней, так как знают, что на уроке  Это стимулирует их на хорошую подготовку к уроку, детям всегда хочется побывать в роли учителя, тем более, что дети послабее опрашивают тех, кто лучше разбирается в данном предмете. Все ученики класса, кроме этих пятерых, достают листки и делают на них чертежи к теореме, и пишут дано. На первый взгляд дети работают сами, но на самом деле вся работа хорошо спланировано учителями. Весь класс у него на контроле. Как только работа с листочками закончена, учащиеся готовые отвечать поднимают руки и им учитель предлагает занять место рядом с одним из пятерых, уже ответивших теорему. Дети начинают тихим шепотом отвечать друг другу. Через 3-4 минуты в классе уже 10 человек, которые спрашивают, и так по нарастающей. Когда все ответили, учитель называет всех учеников по списку, и отметку говорит тот, кто его опрашивал. Отметки, как правило, бывают хорошими, двоек нет совсем, так как дети знают, что спросят всех. (Если оценки чуть завышены, это не страшно, важно, что они с желанием готовятся, следовательно учат теорию, владеют ей начинают лучше решать задачи, а это то, чего мы хотим добиться на уроках геометрии.
Это стимулирует их на хорошую подготовку к уроку, детям всегда хочется побывать в роли учителя, тем более, что дети послабее опрашивают тех, кто лучше разбирается в данном предмете. Все ученики класса, кроме этих пятерых, достают листки и делают на них чертежи к теореме, и пишут дано. На первый взгляд дети работают сами, но на самом деле вся работа хорошо спланировано учителями. Весь класс у него на контроле. Как только работа с листочками закончена, учащиеся готовые отвечать поднимают руки и им учитель предлагает занять место рядом с одним из пятерых, уже ответивших теорему. Дети начинают тихим шепотом отвечать друг другу. Через 3-4 минуты в классе уже 10 человек, которые спрашивают, и так по нарастающей. Когда все ответили, учитель называет всех учеников по списку, и отметку говорит тот, кто его опрашивал. Отметки, как правило, бывают хорошими, двоек нет совсем, так как дети знают, что спросят всех. (Если оценки чуть завышены, это не страшно, важно, что они с желанием готовятся, следовательно учат теорию, владеют ей начинают лучше решать задачи, а это то, чего мы хотим добиться на уроках геометрии.
III. В это время I ученик за доской готовит материал для доказательства этой теоремы. Как только все ответили друг другу теорему и получили оценки, он отвечает устно эту же теорему. Ребята должны владеть собой при ответе для полной аудитории, тренировать хороший математический язык, логическую последовательность ответа. А аудитория уметь слушать, улавливать ошибки, если они есть, задавать вопросы отвечавшему и учиться правильно, оценивать ответы одноклассников.
IV. Решение задач. Устно по готовым чертежам.
Доказать равенство треугольников.
1. |
|
|
2. |
|
|
||
Доказать: треугол. |
|
|
Доказать: треугол. АВD = треугол. CDB |
У доски ученик.
У доски ученик + фронтальная помощь класса. Решим письменно задачу с полным оформлением решения в тетради.
Дано:
< ABE = < DCE, BE = CE
BK = LC, < BKE = 110°
1) Доказать: треугол. BEK = треугол. CEL
2) Найти: < ELC
Решение:
1) < ABE + < 1 = 180° (смежные углы)
< DCE + < 2 = 180° (смежные углы)
< 1 = 180° — < ABE
< 2 = 180° — < DCE
и по условию < ABE = < DCE, следовательно < 1 = < 2/
2) Рассмотрим треугол. BEK и треугол. CEL:
а) BE = СE (по условию)
б) BK = LC (по условию)
в) <1 = < 2
из а, б, в следует => треугол. BEK = CEL по двум сторонам м углу между ними (I признак равенства треугольников) ч. т.д.
т.д.
3) Треугол. BEK = треугол. CEL , а в равных треугольниках против соответственно равных сторон лежат равные углы, т.е. т.к BE=CE, то < ELC = < BKE = 110°.
Ответ: < BKE = 110°
2.
Дано:
треугол. BEC = DFA
Доказать: 1) треугол. ABC = треугол. CDA
2) треугол. ABE = треугол CDE
Доказательство:
1) Т.к. по условию треугол. BEC = треугол. DFA, то BC = DA, <BCE = < DAF.
2) Рассмотрим. треугол. ABC и треугол. CDA:
а) BC = DA
б) < BCA = <DAC
в) AC – общая сторона
Из а, б, в, следует => треугол. ABC = треугол. CDA по I признаку равенства треугольников (по двум сторонам и углу между ними).
3) Т.к треугол. BEC = треугол. DFA, то EC = FA.
Т.к треугол. АВС = треугол. CDA, то АС – общая сторона
Отсюда следует => AE = AC – EC
CF = AC – FA, т.е. AE = CF.
4) Т.к. треугол. BEC = треугол. DFA, то BE = Df и < BEC = < DFA, то они смежные соответственно с углами: < AEB и < CFD, т. е. < AEB = < СFD.
е. < AEB = < СFD.
5) Рассмотрим треугол. ABE и треугол. СDF:
а) BE = DF
б) AE=СF
в) < AEB=< CFD
Из а,б,в следует => треугол. ABE = треугол. CDF по двум сторонам и углу между ними( I признак павенства треугольников) ч.т.д.
VI. Домашнее задание: параграф 14,15. № 95, 96, 92.
VII. Итог урока.
Первый признак равенства треугольников
Первый признак равенства треугольников
Геометрия
7 класс
Часть 2
Яковлева Любовь Викторовна
МБОУ «Самосдельская СОШ им. Шитова В. А.»
В треугольнике выделяют шесть основных элементов – три внутренних угла и три соответственно противолежащие им стороны.
Равенство треугольников устанавливается
по равенству трех элементов:
1) двум сторонам и углу между ними;
2) по стороне и прилежащим к ней углам;
3) по трём сторонам.
Первый признак равенства треугольников
(по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника
равны соответственно двум сторонам и углу между ними
другого треугольника, то такие треугольники равны.
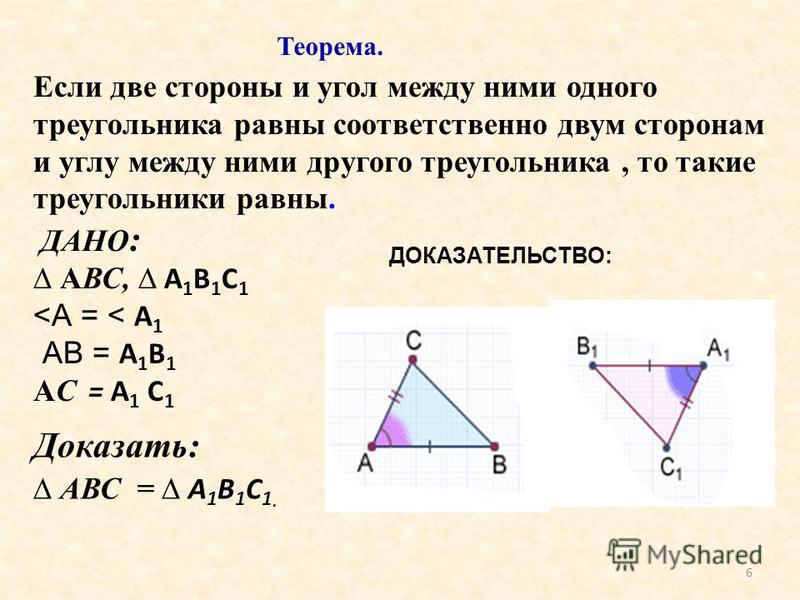
Дано: ∆ АВС; ∆ А 1 В 1 С 1 ;
АВ = А 1 В 1 ; АС = А 1 С 1 ; ے А = ے А 1 .
Доказать: ∆ АВС = ∆ А 1 В 1 С 1
План доказательства теоремы
- ∆ А 1 В 2 С 2 = ∆ АВС по аксиоме существования треугольника, равного данному.
- Точки В 2 и В 1 ; С 1 и С 2 совпадают по аксиомам откладывания отрезков и углов.

- Вывод: ∆ АВС = ∆ А 1 В 1 С 1 .
Решение задач
Решение задач
По данным чертежа найдите DK.
Решение.
Δ CDK = Δ EQF по двум сторонам и углу между ними, т. к.
CD = EQ, CK = EF, ے D = ے C по условию.
Из равенства треугольников следует равенство соответствующих сторон. Значит , DK = QF , отсюда DK = 10.
Решение задач
AD
АВ = АС.
Докажите: BD = CD.
Решение.
Δ ABD = Δ ACD по двум сторонам и углу между ними, т. к. у них
AB = AC по условию , AD — общая ,
ے BAD = ے CAD, потому что AD -биссектриса угла A .
Из равенства треугольников следует равенство соответствующих сторон.
Значит , BD = CD.
Решение задач
Дано: B С = DA; ے BC А = ے DAC .
Докажите: ے А BC = ے CDA .
Решение.
Δ ABC = Δ CDA по двум сторонам
и углу между ними, т. к. у них
ے BCA = ے DAC, BC = DA по
условию , а AC – общая.
Из равенства треугольников следует равенство соответствующих углов.
Значит, ے ABC = ے CDA.
Решение задач
Найдите пару равных треугольников и докажите их равенство.
Решение.
Δ АВК = Δ СВР по двум сторонам и углу между ними,
т. к. у них АК = СР , ВК = ВР по условию , ے АКВ = ے СРВ как углы смежные с углами ВКР и ВРК , равными по условию.
к. у них АК = СР , ВК = ВР по условию , ے АКВ = ے СРВ как углы смежные с углами ВКР и ВРК , равными по условию.
Решение задач
Найдите пару равных треугольников
и докажите их равенство.
Решение.
Δ AOC = Δ BOD по двум сторонам
и углу между ними, т. к. у них
AO = OB, OC = OD , как радиусы
окружности; ے AOB = ے BOD как
вертикальные.
- Сколько равных элементов треугольников необходимо найти и какие, чтобы сказать:
«Треугольники равны по первому признаку равенства треугольников»
Домашнее задание
- Изучить п. 20, 21.
- Контрольные вопросы 1 -2 на стр.
 37.
37. - Выполнить упр. 2 на стр. 38.
Информационные источники
Литература.
- 1.Погорелов А.В. Геометрия: учебник для 7 – 9 кл. общеобразовательных учреждений/ А. В. Погорелов. М.:
Просвещение, 2010.
- 2. Геометрия. 7 класс: поурочные планы по учебнику А. В. Погорелова/ авт. – сост. Е. П. Моисеева.- Волгоград: Учитель, 2006.
- 4. Геометрия. Рабочая тетрадь для 7 класса/Мищенко Т. М. – М.: Издательский Дом «Генжер»,2000.
- 5. Тематический контроль по геометрии. 7 -9 класс/Мищенко Т. М. – М.: Издательский Дом «Генжер», 1997.
- 7. Энциклопедический словарь юного математика/Сост. А. П. Савин. – М.: Педагогика, 1989.
Интернет – ресурсы.
1. http://images.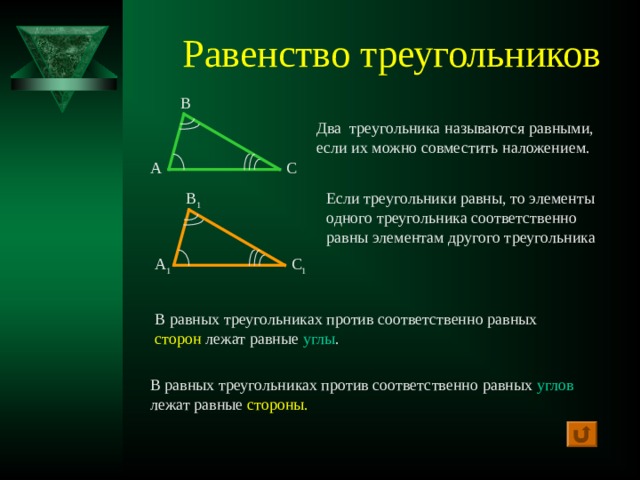 yandex.ru
yandex.ru
2. http://www.montgomeryschoolsmd.org/sschools/rockvillehs/images/ MCButtons/ teacher.jpg
3 . http://www. profistart.ru/ps/blog/24031.html
4. http:// festival.1september.ru/articles/104251/
Обобщающий урок геометрии по теме «Решение задач на применение признаков равенства треугольников» в 7-м классе / Открытый урок
Дидактическая задача урока: систематизировать знания и умения учащихся решать задачи на применение признаков равенства треугольников, уметь делать обобщение изучаемых фактов.
Цели:
Образовательные:
- Повторить и закрепить знание учащимися формулировок признаков равенства треугольников.
- Формирование умений:
— распознавать равные треугольники;
— доказывать их равенство;
— делать выводы о равенстве некоторых их элементов.
- Тренировать способность решать задачи, используя признаки равенства треугольников
Воспитательные:
- Воспитывать аккуратность и прилежание.
- Прививать положительное отношение к знаниям, к процессу учения.
- Формировать самостоятельность и умение делать самооценку.
Развивающие:
- Развивать творческие способности, познавательную активность.
- Развивать умение решать задачи по готовым чертежам, развивать логическое мышление.
- Учить разрешению проблемы, частично-поисковой деятельности учащихся.
- Развивать внимание, слуховую и зрительную память.
- Формировать математическую речь учащихся.
Тип урока: урок систематизации и обобщения знаний, умений, навыков.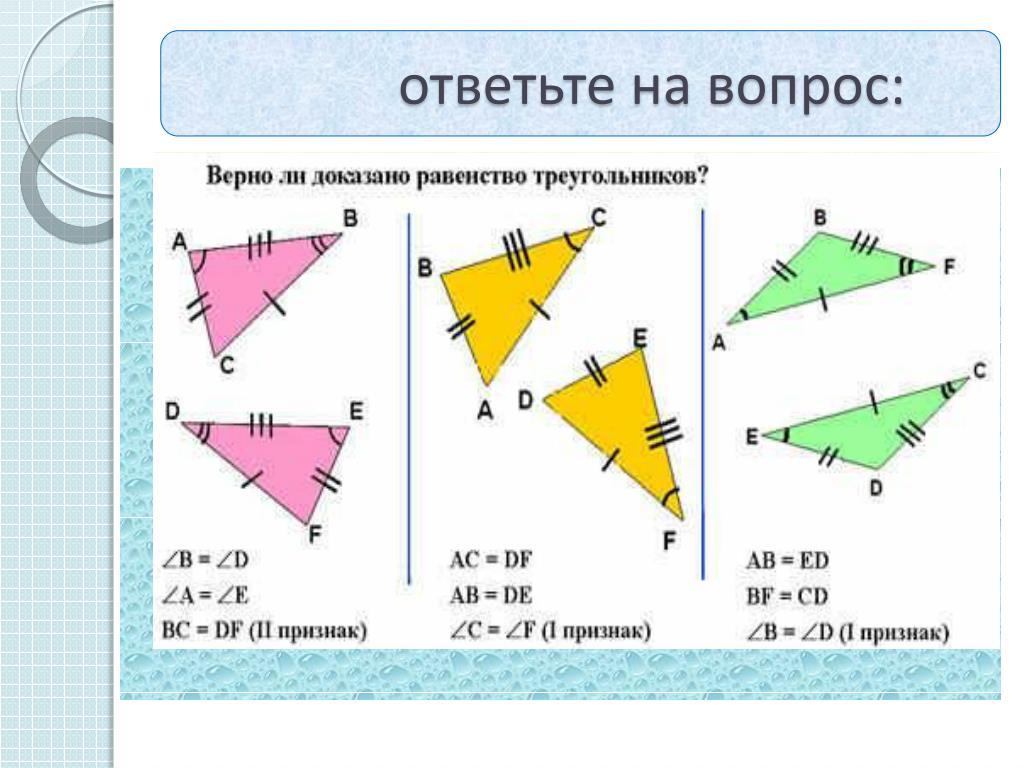
Методическое обеспечение урока:
- Компьютер
- Мультимедиа-проектор
- Листы с печатной основой – карточки с тестами на знание признаков равенства треугольников, карточки с заданиями для работы на уроке.
Ход урока
1. Организационный момент.
Проверка готовности учащихся к уроку. Эмоциональный настрой учащихся.
2. Актуализация знаний.
Фронтальная работа с классом.
— Какую геометрическую фигуру изучаем? (Треугольник).
— Проверим, что вы уже знаете об этой фигуре.
— Какие вы знаете виды треугольников? (Остроугольный, прямоугольный, тупоугольный, равнобедренный и равносторонний)
— Какие треугольники называются равными? (Которые можно совместить при наложении)
— Что помогает определить равенство треугольников? (Признаки равенства треугольников).
— Какие признаки равенства треугольников вы знаете? Посмотрите на экран.
Слайды 2-4.
— Какой признак равенства треугольников вы здесь видите?
I признак равенства треугольников (по двум сторонам и углу между ними)
— Какой признак равенства треугольников вы видите здесь?
II признак равенства треугольников (по стороне и 2 прилежащим к ней углам)
— Какой признак равенства треугольников вы здесь видите?
III признак равенства треугольников (по трем сторонам)
Выполнение теста «Верно-неверно».
На столах у каждого из вас лежат опросные листы. Мы будем работать с ними на протяжении всего урока. Выполним следующее задание №1. Если вы согласны с утверждением ставите +, если нет, ставите –.
Учащимся дается время (3 мин.) на выполнение задания.
Слайды 5-6.
|
№ |
Утверждение |
+/– |
|
1 |
Если в треугольнике две стороны равны, то треугольник называется равнобедренным. |
|
|
2 |
Отрезок, соединяющий вершину треугольника с противоположной стороной, называется медианой треугольника. |
|
|
3 |
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. |
|
|
4 |
Если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника, то такие треугольники равны. |
|
|
5 |
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. |
|
|
6 |
В треугольнике углы при основании равны. |
|
|
7 |
Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой. |
|
|
8 |
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. |
|
После учитель вместе с учащимися осуществляет проверку, используя проектор.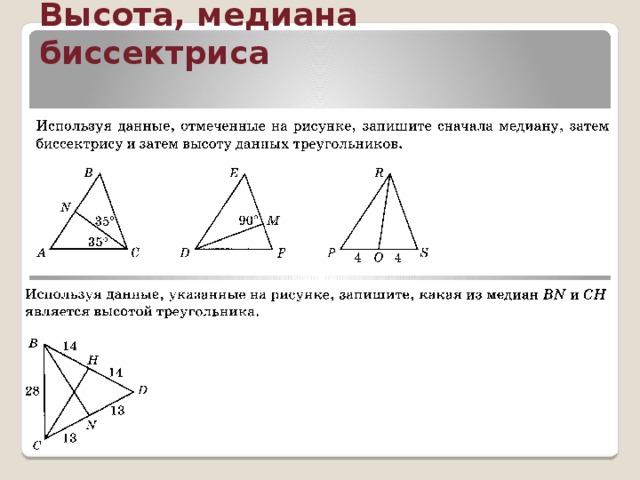
1. Если в треугольнике две стороны равны, то треугольник называется равнобедренным. (+)
2. Отрезок, соединяющий вершину треугольника с противоположной стороной, называется медианой треугольника. (–) (пропущено слово: середина).
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (+)
4. Если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника, то такие треугольники равны. (–) (Правильно: два угла, прилежащих к ней).
5. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (+)
6. В треугольнике углы при основании равны. (–) (Пропущено слово: равностороннем или равнобедренном).
7. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой. (+)
8. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. (–)
(–)
— Переведите полученные баллы в отметку (на листах контроля сказано, как это сделать).
Слайд 7.
8 баллов – отметка «5»
7–6 баллов – отметка «4»
5–4 баллов – отметка «3»
Менее 4 баллов – «будем работать дальше»
Поставьте полученную отметку в лист контроля.
— Поднимите руки те, кто получил – 5, кто получил – 4, кто получил – 3. С остальными будем работать дальше.
3. Формулировка темы и целей урока.
— Ребята, первый год вы изучаете предмет геометрия и поняли, что предметом изучения этого раздела математики является решение задач на основе изученных определений, свойств и теорем. Но чтобы хорошо научиться решать задачи, что для этого выполнять? ( Дети отвечают).
Слайд 8.
— А ещё известный педагог и математик Дъёрдь Пойа (1887-1985) сравнивал умение решать задачи с умением научиться плавать.
Если вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи, то решайте их.
(Д.Пойа)
Дъёрдь Пойа, венгерский, швейцарский и американский математик, много работал со школьными учителями математики и внёс большой вклад в популяризацию науки. Он написал несколько книг о том, как решают задачи и как надо учить решать задачи
— Сформулируйте цели урока. Чем мы будем заниматься и чего должны достичь к концу урока? (Учащиеся формулируют цели – Решение задач на применение признаков равенства треугольников) Слайд 9.4. Решение задач.
— В геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.
«Если знаешь — докажи». Выполнение задания по готовым чертежам (устная работа с классом).
Следующее задание. Ваша задача по готовому чертежу доказать равенство треугольников.
| Слайд 10. № 1 |
| Слайд 11. № 2 |
| Слайд 12. № 3 |
|
Слайд 13. № 4. |
5. Историческая справка о признаках равенства треугольников.
Слайд 14.
— Ребята! Сейчас в своей работе вы использовали такой приём, как доказательство. Эта форма работы вам уже известна. А до VI века с доказательством люди вообще были не знакомы. Первым учёным, который стал рассуждать, доказывать, был Фалес Милетский. Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. Одним из самых известных его высказываний было «Познай самого себя». Именно Фалесу Милетскому приписывают доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
— Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников.
6. Решение задач по готовому чертежу (с записью доказательства в опросных листах).
Слайд 15.
| № 2.1 |
Дано: МО=ОN, АМ=DN, АВ=СD, <ВМО=<СNО
Доказать: ∆АВМ=∆DСN
Вопросы к учащимся:
- Равенство каких треугольников мы можем доказать? (∆МВО=∆NСО по стороне и двум прилежащим к ней углам.)
- Из равенства треугольников ∆МВО=∆NСО какие элементы мы возьмем? ( В равных треугольниках соответственные стороны равны, значит МВ=NС)
- Теперь мы сможем доказать равенство ∆АВМ=∆DСN? (Треугольники равны по трем сторонам)
— Запишите доказательство к этой задаче с обоснованием каждого шага (доказательство записать в опросный лист)Слайд 16.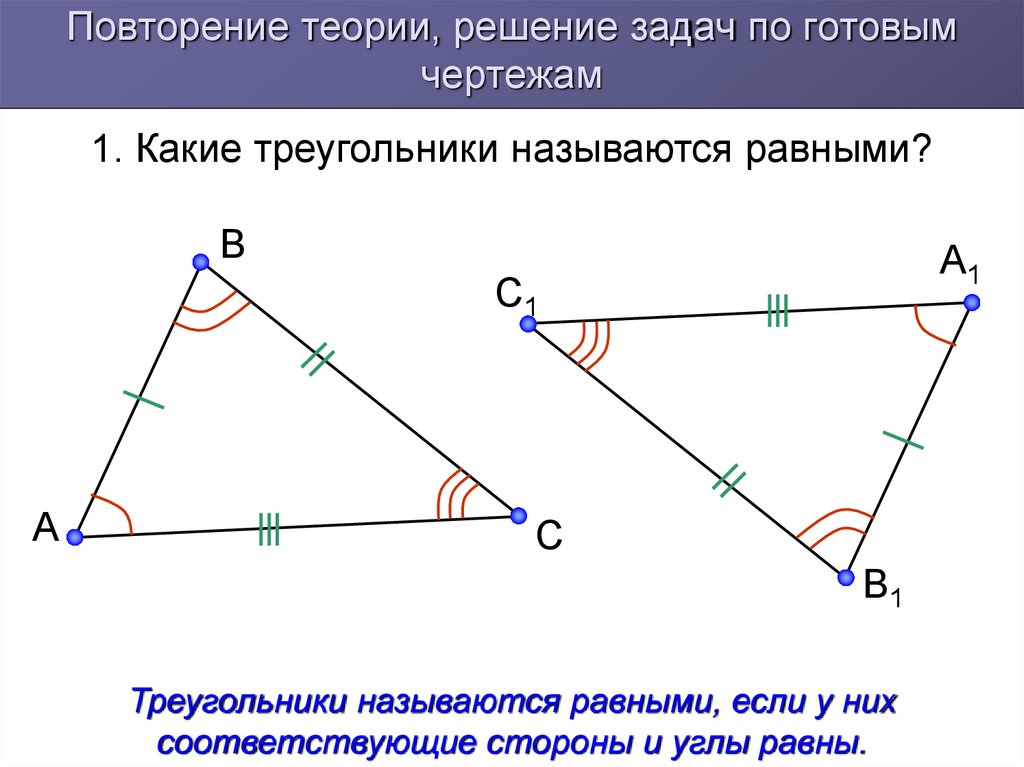
| № 2.2 |
Дано: МО=ОN, угол М равен углу N
Доказать: ∆ВОС – равнобедренный
Вопросы к учащимся:
- Какой треугольник называется равнобедренным? (Равнобедренный треугольник – это треугольник, у которого две стороны равны.)
- Как доказать равенство сторон ВО и ОС? (Из равенства треугольников ∆МВО и ∆NСО)
- Правильно, сначала нужно доказать равенство ∆МВО=∆NСО. Как это сделать? (∆МВО=∆NСО по стороне и двум прилежащим к ней углам. В равных треугольниках соответственные стороны равны, значит ВО=ОС, значит ∆ВОС — равнобедренный, т.к. у него две стороны равны.)
— Запишите доказательство к этой задаче с обоснованием каждого шага (доказательство записать в опросный лист)
№ 4 (устно)
Слайд 17.
Найти : FK
Вопросы к учащимся:
— Что можно найти, зная, что AB= 5 см и AB=BC? (ВС=5 см)
- Равенство каких треугольников мы можем доказать? (∆DВC=∆DFO по двум сторонам и углу между ними.
 )
) - Из равенства треугольников ∆DВC=∆DFO какие элементы мы возьмем? ( В равных треугольниках соответственные стороны равны, значит BC=FO=5 см)
- Что вы можете сказать о ∆FHK? (∆FHK – равнобедренный, HO – биссектриса ∆FHK, а значит и медиана ∆FHK, т.е. FO=KO=5 см. Тогда FK=10см)
6. Практическая работа учащихся.
Учащимся раздаются готовые чертежи геометрических фигур. Нужно исследовать: отметить равные отрезки и углы, выписать пары равных треугольников. Работают в опросных листах, затем следует проверка. Учитель оказывает индивидуальную помощь слабым учащихся. Можно друг у друга спросить совета. Закрепляется навык учащихся доказывать равенство треугольников, используя признаки.
Проверка осуществляется с помощью проектора. Слайды 18–20.
6. Подведение итогов урока.
— Какие цели ставили?
— Достигли их или нет
Слайд 21.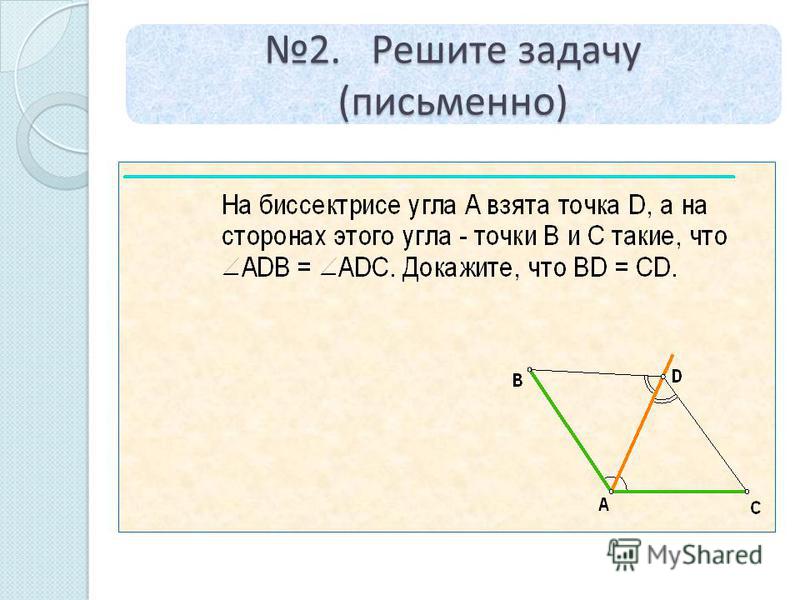
Продолжите предложение:
- Мы изучили признаки равенства треугольников для того, чтобы…
- Мне стало понятно…
- Я понял, что смогу …
- У меня получилось …
- На следующих уроках по геометрии…
Выставление оценок учителем.
7. Домашнее задание (учебник Л.С. Атанасян, В.Ф.Бутузов и др. «Геометрия 7-9»,М., Просвещение 2010)
№ 134, № 138 (а)
Список использованной литературы
1. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7- 9 классы. – М.: Просвещение, 2010.
2. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др. Геометрия. Рабочая тетрадь для 7 класса. – М.: Просвещение, 2009.
3. Жохов В.И., Карташнва Г.Д., Крайнева Л.Б. Уроки геометрии в 7-9 классах: Методические рекомендации для учителя к учебнику Атанасяна Л.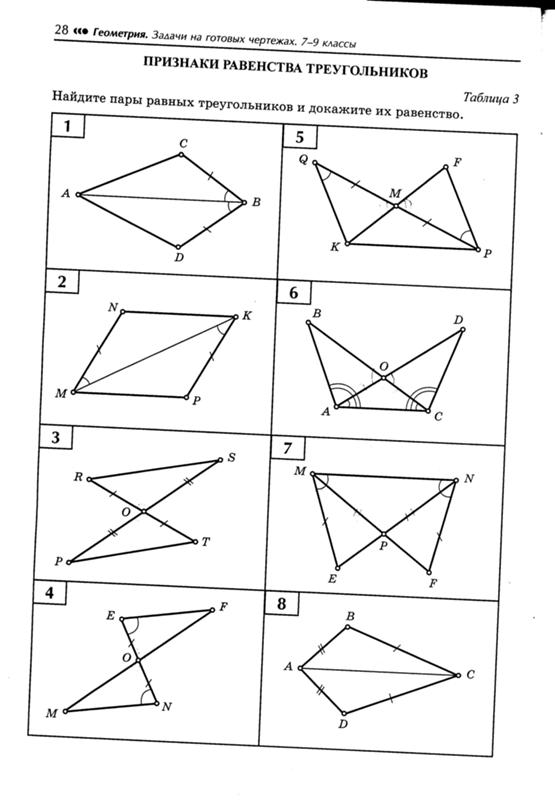 С. и др. – М.: Вербум-М, 2004.
С. и др. – М.: Вербум-М, 2004.
4. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др. Изучение геометрии в 7, 8, 9 классах: Метод. Рекомендации к учебнику: Книга для учителя. – М.: Просвещение, 2009.
5. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии 7 класс. – М.: Просвещение, 2006.
Скачать публикацию
| ТЕМА УРОКА: Первый признак равенства треугольников. Цель урока: доказать первый признак равенства треугольников; научить решать задачи на применение первого Задачи урока: —обучающие: организовать деятельность учащихся по применению знаний и способов деятельности при решении задач на первый признак равенства треугольников -развивающие: развивать ключевую компетенцию: умение решать практические задачи; вызвать интерес к занятию, придать ему проблемно-творческий характер, что отвечает личностным интересам и потребностям учащихся; развивать у учащихся потребность в творческой деятельности, в самовыражении через различные виды работы, развивать умение анализировать и делать выводы; -воспитательные: Воспитывать познавательный интерес к предмету, посредством применения новейших информационных технологий обучения. План урока:
Ход урока: I.Организационный момент (организация внимания и порядка в классе, взаимное приветствие, проверка присутствующих, проверка готовности класса к уроку ) II. Постановка темы и цели урока. Учащиеся разгадывают ребус, который является темой урока, учитель сообщает цель урока. Разгадайте ребусы. (Слайд 5) (ТРЕУГОЛЬНИК)
Если мы обратимся к истории, то в самом первом учебнике по геометрии (как он называется?) – «Началах» Евклида можно найти следующее определение: «Фигуры, совмещающиеся друг с другом равны между собой…». Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC AB; в противоположном направлении восстанавливают CE AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные). IV. Первый признак равенства треугольников. https://files. V.Физкультминутка КОМПЛЕКС УПРАЖНЕНИЙ ГИМНАСТИКИ ДЛЯ ГЛАЗ 1. Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4–5 раз. VI Применение к решению задач Медиана AD треугольника ABC продолжена за сторону BC на отрезок DE, равный отрезку AD , и точка E соединена с точкой C. На рисунке AB=BC, BD=BE, Найдите на этом рисунке равные треугольники. Докажите равенство треугольников KML и KNO
VIII.Творческое задание Чтобы измерить на местности расстояние между двумя точками А и В, между которыми нельзя пройти по прямой (рис. 8.12), выбирают какую-нибудь точку С, для которой можно измерить расстояния АС и ВС, и откладывают отрезки CD=AC и CE=BC. Тогда расстояние между точками E и D будет равно искомому расстоянию. Объясните почему. Ответ к задаче №1: KBC= DEC по первому признаку (BC= CE, KC= CD, BCK = DCE как углы, дополняющие угол KCD до 90° ). Из равенства треугольников следует, что, BK= DE= 4. Интересный факт: Тогда мэр отдал приказ, чтобы никто не выходил ночью на улицу без фонаря. Следующей ночью мэр опять столкнулся с тем же горожанином.
Список использованных источников:
|
Первый признак равенства треугольников
Конспект урока
«Первый признак равенства треугольников»
(урок №1, 7 класс, по учебнику Атанасяна Л.С.)
Цели урока:
Обучающая:
• ввести понятие теоремы и доказательства теоремы;
• доказать первый признак равенства треугольников;
• научить решать задачи на применение первого признака равенства треугольников.
Развивающая:
• выработать умения сопоставлять, обобщать полученные выводы, оценивать влияние условий на результат;
• развивать логическое мышление учащихся.
Воспитательная:
• выработать умение анализировать данные, выводить логические следствия из данных предпосылок, умение делать выводы;
• выработать умение концентрировать внимание, сосредотачиваться.
Методическая цель: опробовать новый подход к формулировке теоремы, выяснить уловят ли учащиеся момент, когда условия становятся достаточными.
Тип урока: комбинированный.
Оборудование: компьютор, экран, проектор, презентация, линейка, треугольник,
цветные мелки.
Ход урока
Организационный момент: (2 мин)
На предыдущем уроке мы приступили к изучению главы «Треугольники». Выяснили, какие две фигуры, в частности два треугольника называются равными. Сегодня мы выясним, можно ли установить равенство двух фигур не проводя фактического наложения одной на другую, а сравнивая только некоторые элементы этих фигур, в частности как сравнить треугольники.
Повторение пройденного материала: (6 мин)
Повторим материал прошлого урока.
Теоретический опрос по вопросам:
объясните, какая фигура называется треугольником;
начертите треугольник и покажите его стороны вершины и углы;
что такое периметр треугольника?
какие треугольники называются равными?
Каждому учащемуся выдается конвертик, в котором находится 6-7 бумажных треугольников; учащимся предлагается найти среди них равные.
Когда поиск закончен, спросить одного из учеников, как он нашел эту пару. Ученик расскажет, как он накладывал один треугольник на другой.
Выполнение практического задания с последующей устной проверкой:
№1: На доске(или слайде) начерчены ∆DEK, ∆MNP.
Рисунок 1
Назовите углы:
а) ∆DEK, прилежащие к стороне ЕК;
б) ∆MNP, прилежащие к стороне MN.
Назовите угол:
а) ∆DEK, заключенный между сторонами DE и DК;
б) ∆MNP, заключенный между сторонами NP и РМ.
Между какими сторонами:
а) ∆DEK заключен угол К;
б) ∆MNP заключен угол N?
№2:
Рисунок 2
Вызываю ученика к доске, он сопровождает свой ответ демонстрацией на чертежах и записью на доске.
3. Изучение нового материала: (16 мин)
Чтобы установить равенство двух треугольников, надо их совмещать или проверить равенство соответствующих сторон и соответствующих углов. Шесть равенств! Но иногда ни совместить, ни проверить все шесть равенств нет возможности. Да это и не нужно, оказывается достаточно установить лишь часть из них. Наша цель – определить, какие из шести этих равенств действительно необходимы.
Итак, перед нами проблема.
Ее решением и займемся .
Рисунок 3
Оказывается справедливо утверждение « Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны». Это утверждение называется «Первый признак равенства треугольников».
А в математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.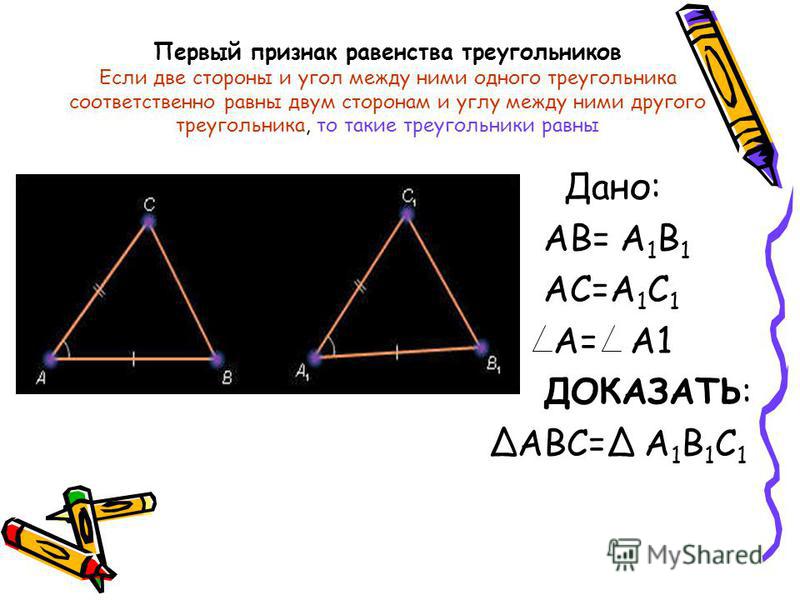
Какие теоремы нам уже известны?
Свойство смежных углов и свойство вертикальных углов.
Почему же теорема о равенстве треугольников называется признаком?
Признак (по В.Далю) – это знак, отличие, все, почему узнают что–либо. Увидев морозный узор на окне, можно, не выходя из дома, сказать, что на улице холодно. Чтобы узнать, делится ли число 7859467 на 9, не обязательно выполнять деление: можно воспользоваться признаком делимости.
Признак дает возможность устанавливать равенство двух треугольников, не проводя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольников.
Любая теорема состоит из условия и заключения. Как вы понимаете, что может означать словосочетание «условие теоремы», а что – «заключение теоремы»?
Условие — это уже известные факты, о которых говориться в теореме, а заключение – это то, что нужно доказать.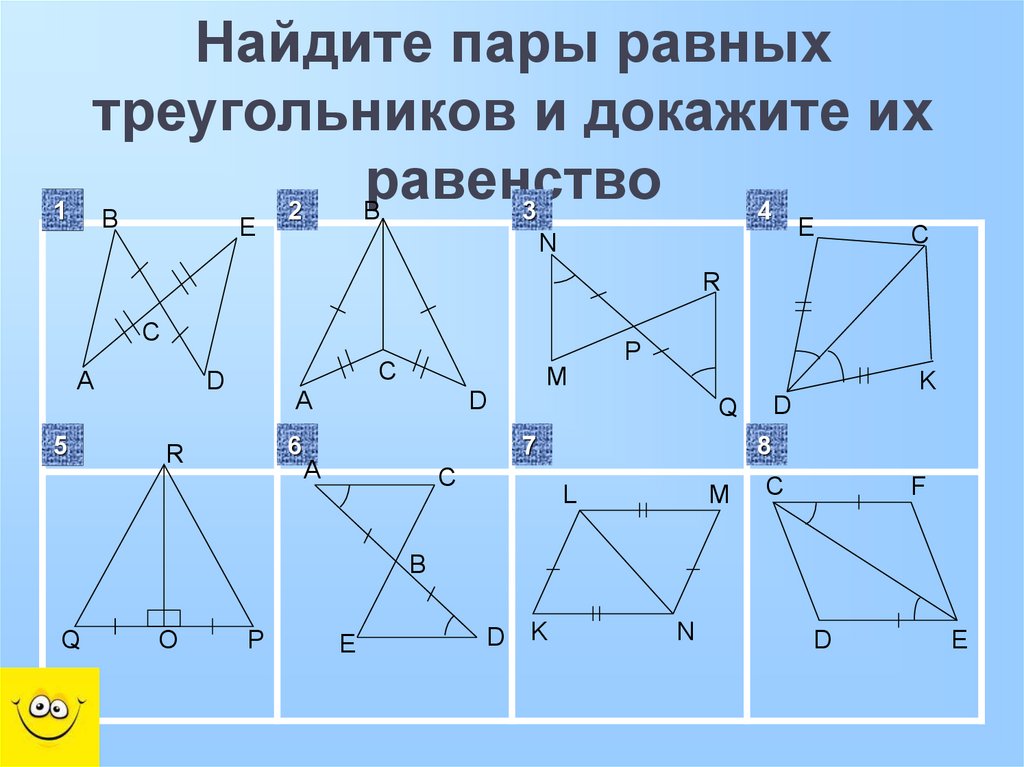
Выделите условие теоремы «Первого признака равенства треугольников».
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.
Выделите заключение теоремы.
То такие треугольники равны.
Итак, докажем первый признак равенства треугольников:
Далее оформляем запись доказательства- учитель на доске, ученики в тетради.
А теперь рассмотрим еще один вопрос. Но сначала послушайте внимательно формулировку: Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны. Как вы думаете, верно ли это утверждение?
Рассмотрим ∆ АВС и ∆АDС.
Рисунок 4
Сторона АВ треугольника АВС равна стороне АD треугольника АDС, сторона АС – общая, и С – общий.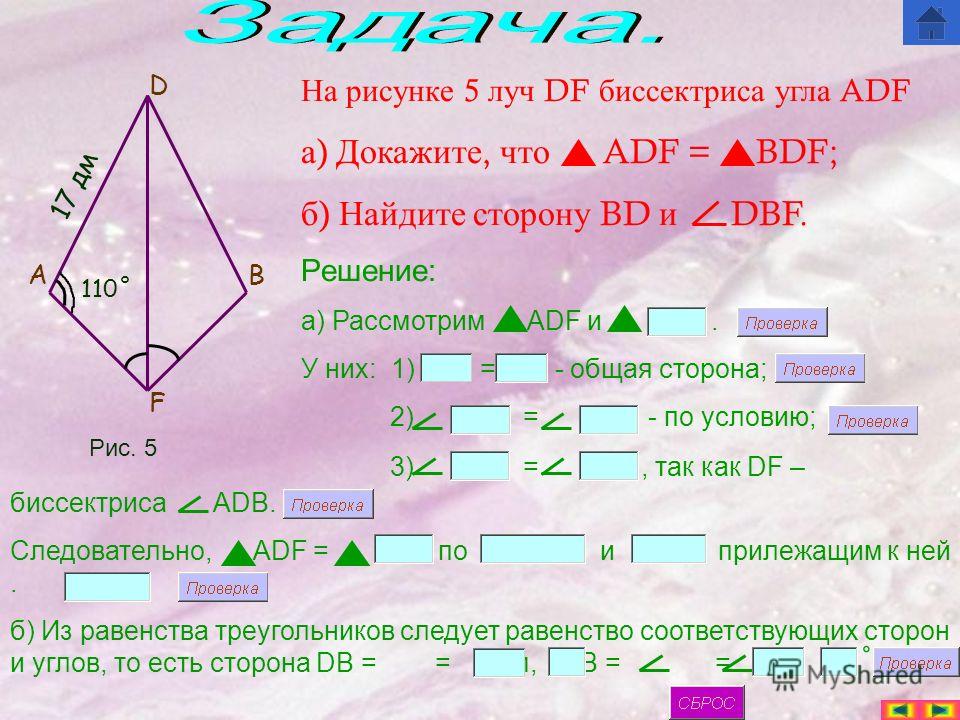 Но треугольники не равны. Итак, условие утверждения выполнено, а заключение – нет. Значит утверждение не верно. Обратите особое внимание, на то, что условие «между ними» необходимо!
Но треугольники не равны. Итак, условие утверждения выполнено, а заключение – нет. Значит утверждение не верно. Обратите особое внимание, на то, что условие «между ними» необходимо!
4. Закрепление нового материала: (10 мин)
Рассмотрим, как же можно применить теорему для решения задач.
Устное решение задач по готовым чертежам, заранее заготовленным на обратной стороне доски или на слайде.
№1:
№2:
Для решения каждой задачи вызываю ученика к доске, где он комментирует решение, показывая упомянутые элементы на чертеже. Остальные учащиеся слушают, поправляют, дополняют ответ, если в этом есть необходимость.
Акцентирую внимание учащихся на обязательности содержательной ссылки «треугольники равны по двум сторонам и углу между ними», а не формальной «треугольники равны по первому признаку», выясняю всем ли был понятен ход решения, если возникли вопросы, сама отвечаю на них.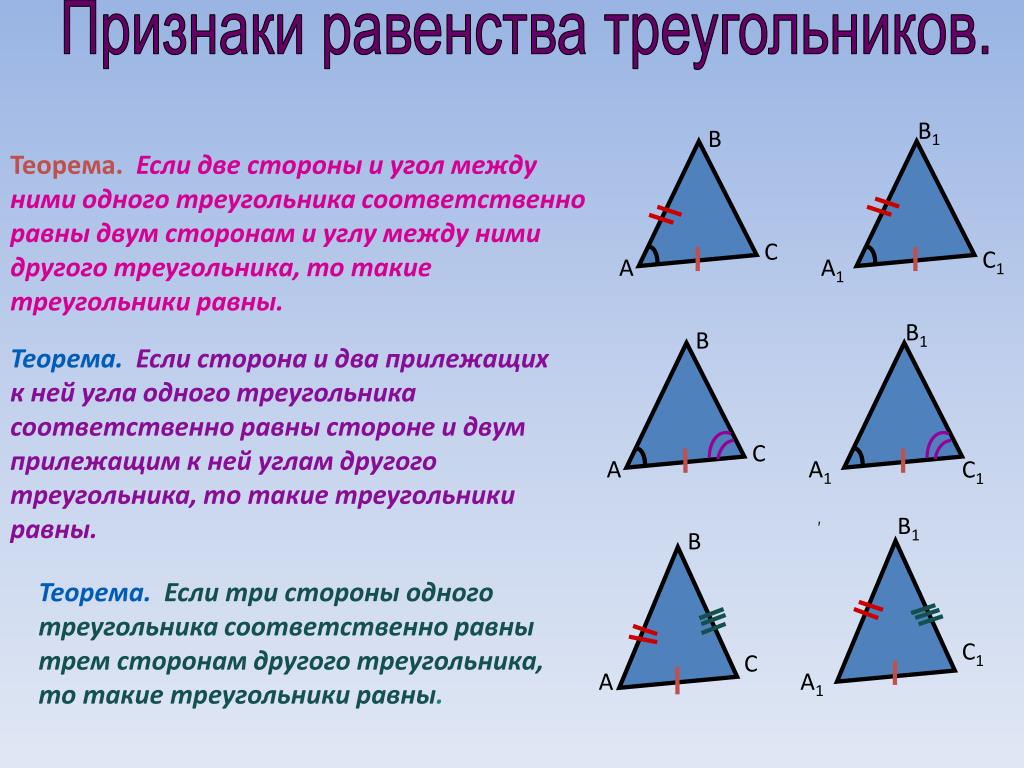
Если в задаче понадобится доказать, что два треугольника равны, чем следует воспользоваться: определением или теоремой?
Конечно, теоремой. Согласно определению нужно треугольники совмещать, а согласно теореме – проверить три равенства.
Далее решаем задачу № 94 из учебника. Оформление решения на доске выполняю сама.
Задача:
На рис. АВ = АС, 1 = 2.
а) Докажите, что треугольники АВD и АСD равны;
б) найдите ВD и АВ, если АС=15 см, DC=5 см.
Дано: АВ = АС, 1 = 2,
АС=15 см, DC=5 см.
Доказать:
∆АВD = ∆АСD.
Найти: ВD, АВ.
Доказательство: Прежде чем оформить решение на доске, предлагаю ученикам устно решить задачу. Один ученик комментирует доказательство. Другой – нахождение длин отрезков. А затем записываем решение задачи: я на доске, ученики в тетради.
А затем записываем решение задачи: я на доске, ученики в тетради.
Возможная запись решения:
Доказательство:
Рассмотрим ∆АВD и ∆АСD.
АВ = АС ( по усл.)
АD – общая сторона ∆АВD = ∆АСD (по двум
1 = 2 ( по усл.) сторонам и углу между ними)
Словестный комментарий: треугольники АВD и АСD равны по двум сторонам и углу между ними, первый признак равенства треугольников, в котором говориться: «Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.»
Решение:
ВD =DC =5 см, АВ = АС = 15 см.( как соответственные элементы равных треугольников).
Ответ: ВD =5 см, АВ = 15см.
Выясняю, не возникли ли вопросы по ходу решения.
5. Итог урока: (4 мин)
Итак, давайте повторим:
— Какие треугольники называются равными?
— Что называется теоремой?
-Что называется доказательством теоремы?
— Какую теорему мы сегодня доказали? Сформулируйте ее.
— Почему теорема называется признаком?
Ученики отвечают на вопросы.
Выставляю оценки за работу на уроке с комментарием.
6. Домашнее задание: (2 мин)
П 15. Вопросы 3 -4 стр. 49-50. №93, 95.
№93. Отрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них. А) Докажите, что треугольники АВС и ЕВD равны; б) найдите углы А и С треугольника АВС, если в треугольнике ВDЕ D=470, Е= 420.
№95. На рис.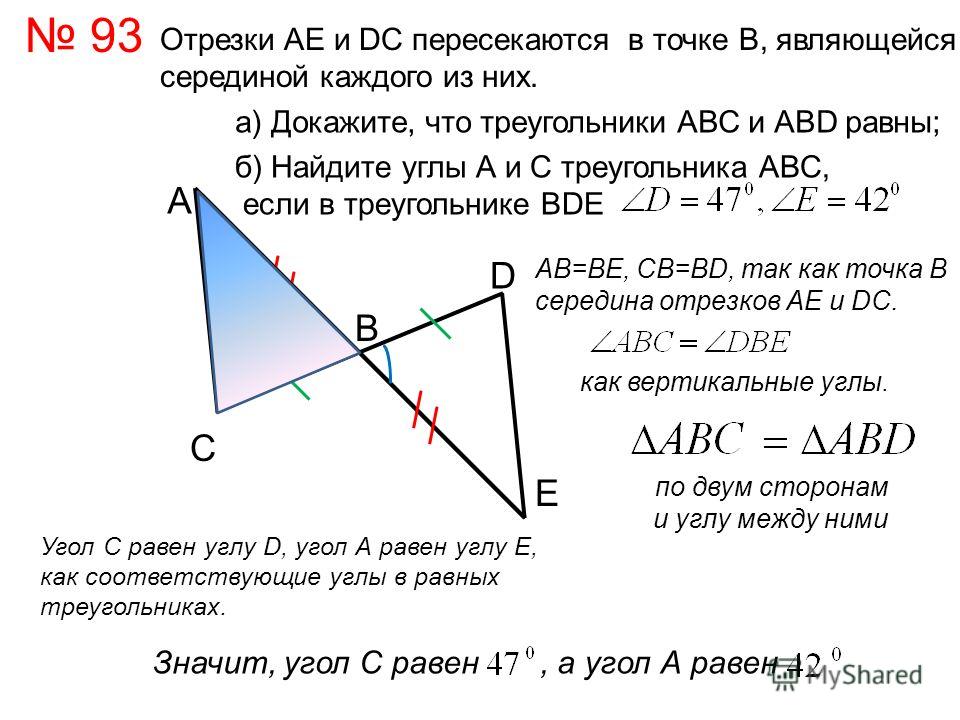 ВС=АD, 1 = 2, а) Докажите, что треугольники АВС и СDА равны; б)Найдите АВ и ВС, если АD =17см, DС=14см.
ВС=АD, 1 = 2, а) Докажите, что треугольники АВС и СDА равны; б)Найдите АВ и ВС, если АD =17см, DС=14см.
Список литературы:
Атанасян Л.С., Бутузов В.Ф., и др. Геометрия 7-9 кл. Учебник для 7-9 классов средней школы. – М.: Просвещение, 2006.
Атанасян Л.С., Бутузов В.Ф. и др. Изучение геометрии в 7-9 классах. Методические рекомендации к учебнику. – М.: Просвещение, 2000.
Ковалева Г.И., Мазурова Н.И. Тесты для текущего и обобщающего контроля. Издательство «Учитель» 2008. .
Амелькин В.В., Рабцевич Т.И. Школьная геометрия в чертежах и формулах. 2008.
Первый признак равенства треугольников
Урок геометрии в 7 классе.
Тема урока: Первый признак равенства треугольников.
Цели и задачи:
1. Образовательные:
научить анализировать условие задачи.
Формировать умение применять первый признак равенства треугольников к решению задач.
2. Развивающие:
развивать приёмы логического мышления (сравнивать, обобщать), правильно формулировать и излагать мысли , умение анализировать факты и делать выводы;
Создать условия для развития познавательного интереса к математике
3. Воспитательные:
Воспитание математической культуры и речи.
Воспитание навыков самоконтроля.
Методы работы на уроке:
объяснительно-иллюстративный (при решении задач на готовых чертежах, проверке решения задач самостоятельной работы),
репродуктивный, конструктивный (при выполнении упражнений).
Тип урока: урок закрепления и отработки навыков применения признака при решении задач, с использованием ИКТ.
План урока:
1. Организационный момент. 1 мин.
2. Актуализация опорных знаний. Фронтальный опрос. (Вертикальные, смежные углы, треугольник ) – 15 мин.
(Вертикальные, смежные углы, треугольник ) – 15 мин.
3. Сообщение учеников «Треугольники в жизни» – 5мин.
4. Устное решение задач по готовым чертежам. – 8 мин.
5. Решение задач с оформлением в тетради. – 12 мин
6. Итоги урока. – 1 мин.
7. Домашнее задание. – 1 мин.
8. Итог урока. Оценки. – 1 мин.
1.Организация начала урока.
Организация учебного процесса на этапе 1:
Какую тему изучали на прошлых уроках? (смежные и вертикальные углы, Первый признак равенства треугольников.)
Для чего нам необходим признак равенства треугольников? ( Для определения равенства треугольников, используя только некоторые элементы).
Сообщение темы и цели урока детям.
Слайды 1 – 2.
Цели урока:
Повторить понятие смежных и вертикальных углов.
Закрепить навык решения задач на вычисление вертикальных и смежных углов.
Отработать навык решения задач на применение 1 признака равенства треугольников
А для этого мы должны на уроке решить следующие задачи:
Распознавать на чертежах равные треугольники по указанным равным элементам, применяя признаки равенства треугольников;
Непосредственно применять признаки равенства треугольников;
Делать выводы из равенства треугольников;
Читать чертежи, сопровождающие текст задачи, сопоставлять текст задачи с данным чертежом, выделять на чертеже необходимую для решения задачи конфигурацию;
Формировать и развивать логическое мышление и культуру речи.

2. Актуализация опорных знаний.
? какие углы называются смежными? Вертикальными?
Слайды 3 – 4 — 5.
Слайд 6.
Дан Δ CDM.
а) Назовите углы, прилежащие стороне CD.
б) Назовите угол, лежащий против стороны СМ.
в) Назовите углы, заключённые между сторонами СМ и MD, CD и DM.
Слайд 7.
∆ QRP = ∆ ABC
Это означает, что:
Слайд 8.
На рисунке изображены равные треугольники.
Установите, какая из следующих записей верна:
а) ∆ABC = ∆PQR; б) ∆ABC = ∆RQP; в) ∆ABC = ∆PRQ.
Известно, что АС = 5см, ےВ = 30°.
а) Длину какой стороны ∆RQP вы можете указать?
б) Какой угол ∆RQP известен?
Слайд 9.
Используя чертеж, найдите равные треугольники, если AB=PQ=MK, Ð A =ÐP =ÐK, AC=PR=MN
Слайд 10.
Учитель: В древнем искусстве были широко распространены изображения равностороннего треугольника .
3. Сообщение учеников «Треугольники в жизни»
Слайд 11 — 19.
Сообщение Марсель и Шлей М.
Учитель: Ребята, а кто еще знает где применяются треугольники?
Слайд 20 – 23.
Учитель: Треугольник играет в геометрии особую роль.
Без преувеличения можно сказать, что вся (или почти вся) геометрия со времён «Начал» Евклида покоится на «трёх китах» – признаках равенства треугольников.
Мы с вами изучили 1 признак равенства треугольников.
Сформулируйте первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
4. Устное решение задач по готовым чертежам Закрепление изученного материала.
Слайд 25 – 26.
1. Решение задач по готовым чертежам (слайд 26, 27).
Слайд 26 Слайд 27
5. Решение задач с оформлением в тетради.
Слайд 28.
Задача №97.
6. Итоги урока. – 1 мин.
Слайд № 30
1.С какой важной теоремой мы работали на уроке?
Сформулируйте
Задачи на следующий урок:
1.Закрепить знания по данной теме путём решения более сложных задач
7. Домашнее задание. – 1 мин. (карточки)
8. Итог урока. Оценки.
Слайд № 31
Дополнительная задача – слайд №29
Неравенство треугольника— объяснение и примеры
В этой статье мы узнаем, что такое теорема о неравенстве треугольника , как использовать эту теорему и, наконец, что влечет за собой обратное неравенство треугольника. На данный момент большинство из нас знакомы с тем фактом, что треугольник имеет три стороны.
На данный момент большинство из нас знакомы с тем фактом, что треугольник имеет три стороны.
Три стороны треугольника образуются, когда три разных отрезка соединяются в вершинах треугольника. В треугольнике мы используем строчные буквы a, b и c для обозначения сторон треугольника .
В большинстве случаев буквы a и b используются для обозначения первых двух коротких сторон треугольника, тогда как буква c используется для обозначения самой длинной стороны .
Что такое теорема о неравенстве треугольников?
Как следует из названия, теорема о неравенстве треугольника — это утверждение, описывающее отношения между тремя сторонами треугольника. Согласно теореме о неравенстве треугольника, сумма любых двух сторон треугольника больше или равна третьей стороне треугольника.
Это утверждение можно символически представить как;
- a + b > c
- a + c > b
- b + c > a
Таким образом, теорема о неравенстве треугольника является полезным инструментом для проверки того, образует ли данный набор трех измерений треугольник или не . Проще говоря, он не будет формировать треугольник, если указанные выше 3 условия неравенства треугольника неверны.
Проще говоря, он не будет формировать треугольник, если указанные выше 3 условия неравенства треугольника неверны.
Давайте рассмотрим следующие примеры:
Пример 1
Проверьте, можно ли составить треугольник со следующими размерами:
4 мм, 7 мм и 5 мм.
Решение
Пусть a = 4 мм. b = 7 мм и c = 5 мм. Теперь применим теорему о неравенстве треугольника.
a + b > c
⇒ 4 + 7 > 5
⇒ 11> 5 ……. (верно)
а + с > b
⇒ 4 + 5 > 7
⇒ 9 > 7…………. (истинно)
б + с > а
⇒ 7 + 5 > 4
⇒ 12 > 4 ……. (true)
Поскольку все три условия верны, можно построить треугольник с заданными размерами.
Пример 2
Учитывая измерения; 6 см, 10 см, 17 см. Проверьте, могут ли три измерения образовать треугольник.
Решение
Пусть a = 6 см, b = 10 см и c = 17 см
По теореме о неравенстве треугольника имеем;
а + б > в
⇒ 6 + 10 > 17
⇒ 16 > 17 ……….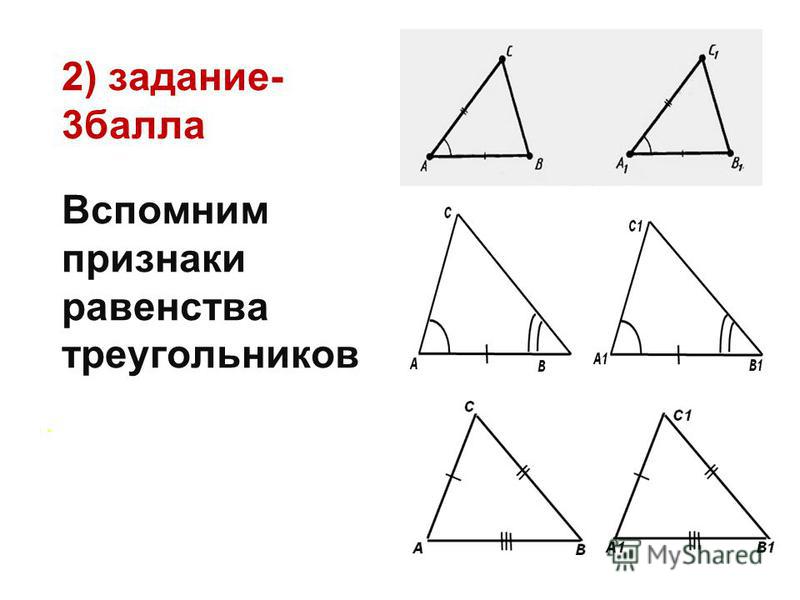 (неверно, 17 не меньше 16)
(неверно, 17 не меньше 16)
a + c > b
⇒ 6 + 17 > 10
⇒ 23 > 10…………. (истинно)
б + в > а
10 + 17 > 6
17 > 6 ………. (true)
Поскольку одно из условий ложно, три измерения не могут образовать треугольник.
Пример 3
Найдите возможные значения x для треугольника, показанного ниже.
Решение
Используя теорему о неравенстве треугольника, получаем;
⇒ x + 8 > 12
⇒ x > 4
⇒ x + 12 > 8
⇒ x > –4 ……… (недействительно, длины не могут быть отрицательными числами)
x 9 12 + 0 > 5
⇒ x < 20 Объедините допустимые утверждения x > 4 и x < 20.
4 < x < 20
Следовательно, возможные значения x: 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 и 19.
Пример 4
Размеры треугольника равны (x + 2) см, (2x+7) см и (4x+1). Найдите возможные значения x, которые являются целыми числами.
Решение
По теореме о неравенстве треугольника; пусть a = (x + 2) см, b = (2x+7) см и c = (4x+1).
(x + 2) + (2x + 7) > (4x + 1)
3x + 9 > 4x + 1
3x – 4x > 1 – 9
– x > – 8
Обе части разделить на – 1 и измените направление символа неравенства.
x < 8 (x + 2) + (4x +1) > (2x + 7)
5x + 3 > 2x + 7
5x – 2x > 7 – 3
3x > 4
Разделить обе стороны на 3 получить;
х > 4/3
х > 1,3333.
(2x + 7) + (4x + 1) > (x + 2)
6x + 8 > x + 2
6x – x > 2 – 8
5x > – 6
x > – 6/5 …………… (невозможно)
Объедините допустимые неравенства.
1,333 < х <8
Следовательно, возможные целые значения x равны 2, 3, 4, 5, 6 и 7.
Обратное неравенство треугольника
Согласно обратному неравенству треугольника, разница между длинами двух сторон треугольника меньше, чем длина третьей стороны . Другими словами, любая сторона треугольника больше, чем вычитание, полученное при вычитании оставшихся двух сторон треугольника.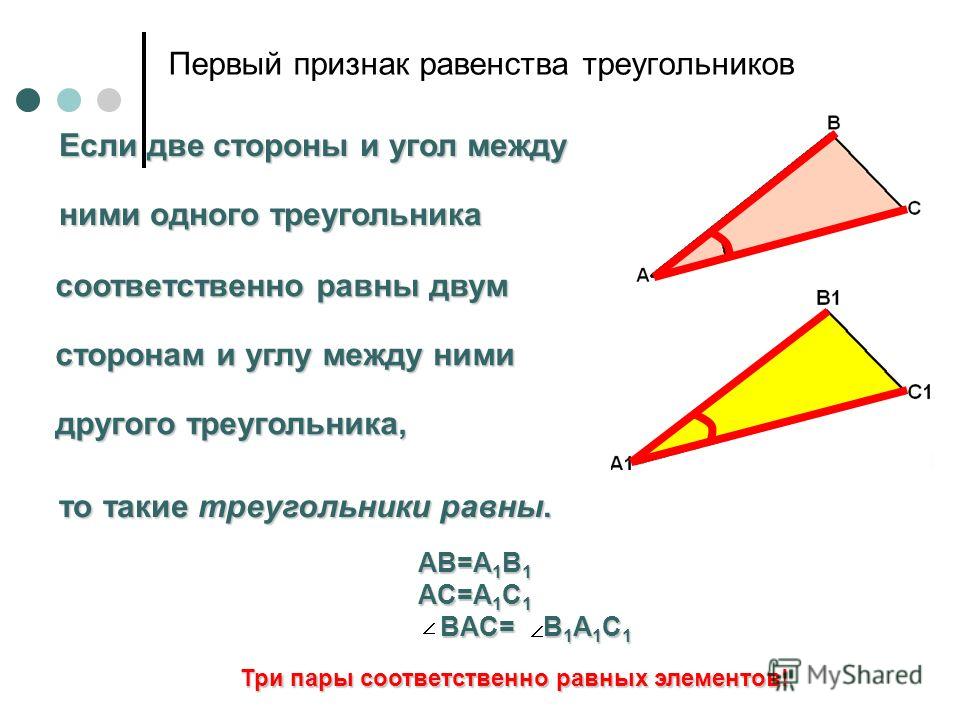
Рассмотрим треугольник PQR ниже;
Теорема об обратном неравенстве треугольника дается формулой;
|PQ|>||PR|-|RQ||, |PR|>||PQ|-|RQ|| и |QR|>||PQ|-|PR||
Доказательство:
- |PQ| + |PR| > |КВ| // Теорема о неравенстве треугольника
- |PQ| + |PR| -|PR| > |RQ|-|PR| // (i) Вычитание одинакового количества с обеих сторон сохраняет неравенство
- |PQ| > |КВ| – |PR| = ||PR|-|RQ|| // (ii), свойства абсолютного значения
- |PQ| + |PR| – |ПК| > |RQ|-|PQ| // (ii) Вычитание одного и того же количества с обеих сторон сохраняет неравенство
- |PR| > |RQ|-|PQ| = ||PQ|-|RQ|| // (iv), свойства абсолютного значения
- |PR|+|QR| > |ПК| //Теорема о неравенстве треугольника
- |PR| + |QR| -|PR| > |PQ|-|PR| // (vi) Вычитание одинакового количества с обеих сторон сохраняет неравенство
- |QR| > |ПК| – |PR| = ||PQ|-|PR|| // (vii), свойства абсолютного значения
Закон синусов
Закон синусов есть отношение между сторонами и углами непрямого (косого) треугольники . Проще говоря, он утверждает, что отношение длины стороны треугольника к синусу угла, противоположного этой стороне, одинаково для всех сторон и углов в данном треугольнике.
В Δ А Б С представляет собой косой треугольник со сторонами а , б а также с , тогда а грех А знак равно б грех Б знак равно с грех С .
Чтобы использовать закон синусов, вам нужно знать либо два угла и одну сторону треугольника (AAS или ASA), либо две стороны и угол, противолежащий одной из них (SSA).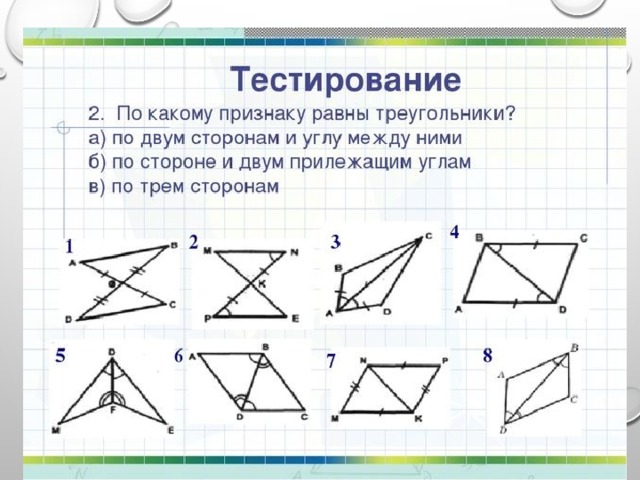 Обратите внимание, что в первых двух случаях мы используем те же самые части, которые мы использовали для доказательства конгруэнтности треугольников в геометрии, но в последнем случае мы не смогли доказать
конгруэнтные треугольники
учитывая эти части. Это потому, что остальные части могли быть разных размеров. Это называется неоднозначным случаем, и мы обсудим его чуть позже.
Обратите внимание, что в первых двух случаях мы используем те же самые части, которые мы использовали для доказательства конгруэнтности треугольников в геометрии, но в последнем случае мы не смогли доказать
конгруэнтные треугольники
учитывая эти части. Это потому, что остальные части могли быть разных размеров. Это называется неоднозначным случаем, и мы обсудим его чуть позже.
Пример 1: Даны два угла и невключенная сторона (AAS).
Данный Δ А Б С с м ∠ А знак равно 30 ° , м ∠ Б знак равно 20 ° а также а знак равно 45 м. Найдите оставшийся угол и стороны.
Третий угол треугольника равен
м ∠ С знак равно 180 ° − м ∠ А − м ∠ Б знак равно 180 ° − 30 ° − 20 ° знак равно 130 °
По закону синусов,
45 грех 30 ° знак равно б грех 20 ° знак равно с грех 130 °
По свойствам Пропорции
б знак равно 45 грех 20 ° грех 30 ° ≈ 30,78 м а также с знак равно 45 грех 130 ° грех 30 ° ≈ 68,94 м
Пример 2: Даны два угла и прилежащая сторона (ASA).
Данный м ∠ А знак равно 42 ° , м ∠ Б знак равно 75 ° а также с знак равно 22 см. Найдите оставшийся угол и стороны.
Третий угол треугольника равен:
м ∠ С знак равно 180 ° − м ∠ А − м ∠ Б знак равно 180 ° − 42 ° − 75 ° знак равно 63 °
По закону синусов,
а грех 42 ° знак равно б грех 75 ° знак равно 22 грех 63 °
По свойствам пропорций
а
знак равно
22
грех
42
°
грех
63
°
≈
16. 52
см
а также
б
знак равно
22
грех
75
°
грех
63
°
≈
23,85
см
52
см
а также
б
знак равно
22
грех
75
°
грех
63
°
≈
23,85
см
Если даны две стороны и угол, противолежащий одной из них, возможны три возможности.
(1) Такого треугольника не существует.
(2) Существуют два различных треугольника.
(3) Существует ровно один треугольник.
Рассмотрим треугольник, в котором вам дано
а
,
б
а также
А
. (Высота
час
от вершины
Б
в сторону
А
С
¯
, по определению синусов равен
б
грех
А
.)
(Высота
час
от вершины
Б
в сторону
А
С
¯
, по определению синусов равен
б
грех
А
.)
(1) Такого треугольника не существует, если А является острым и а < час или же А тупой и а ≤ б .
(2) Два различных треугольника существуют, если
А
является острым и
час <
а
<
б
.
(3) Во всех остальных случаях существует ровно один треугольник.
Пример 1: Решение не существует
Данный а знак равно 15 , б знак равно 25 а также м ∠ А знак равно 80 ° . Найдите другие углы и сторону.
час знак равно б грех А знак равно 25 грех 80 ° ≈ 24,6
Заметь
а <
час
. Так что получается, что решения нет. Проверьте это, используя закон синусов.
Так что получается, что решения нет. Проверьте это, используя закон синусов.
а грех А знак равно б грех Б 15 грех 80 ° знак равно 25 грех Б грех Б знак равно 25 грех 80 ° 15 ≈ 1,641 > 1
Этот
контрасты
тот факт, что
−
1
≤
грех
Б
≤
1
. Следовательно, никакого треугольника не существует.
Следовательно, никакого треугольника не существует.
Пример 2: Существуют два решения
Данный а знак равно 6 , б знак равно 7 а также м ∠ А знак равно 30 ° . Найдите другие углы и сторону.
час знак равно б грех А знак равно 7 грех 30 ° знак равно 3,5
час <
а
<
б
следовательно, возможны два треугольника.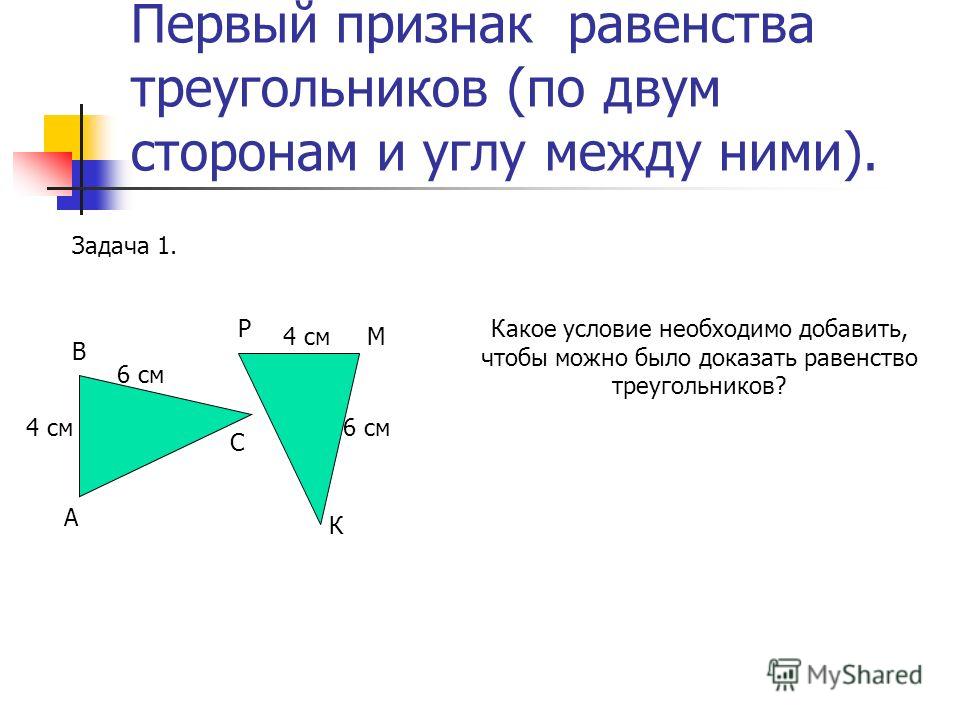
По закону синусов, а грех А знак равно б грех Б
грех Б знак равно б грех А а знак равно 7 грех 30 ° 6 ≈ 0,5833
Есть два угла между
0
°
а также
180
°
синус которого приблизительно равен 0,5833, являются
35,69
°
а также
144,31
°
.
Если
Б
≈
35,69
°
С
≈
180
°
−
30
°
−
35,69°
знак равно
114,31
°
с
знак равно
а
грех
С
грех
А
≈
6
грех
114,31
°
грех
30
°
≈
10,94
Если
Б
≈
144,31
°
С
≈
180
°
−
30
°
−
144,31
°
знак равно
5,69°
с
≈
6
грех
5,69
°
грех
30
°
≈
1.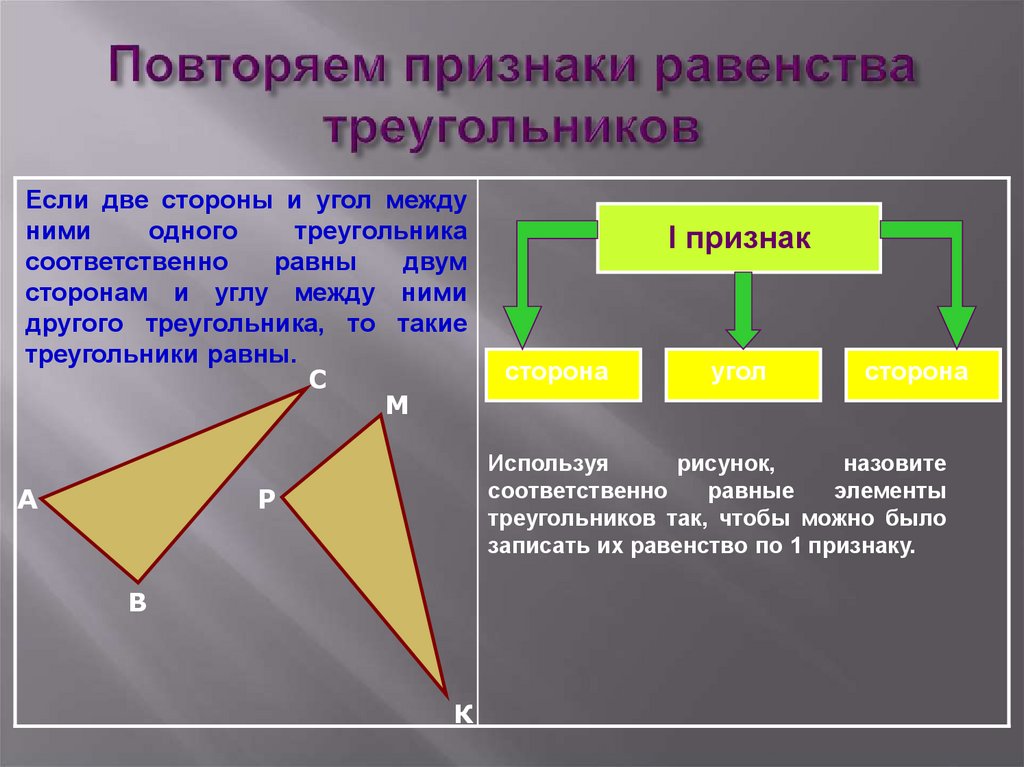 19
19
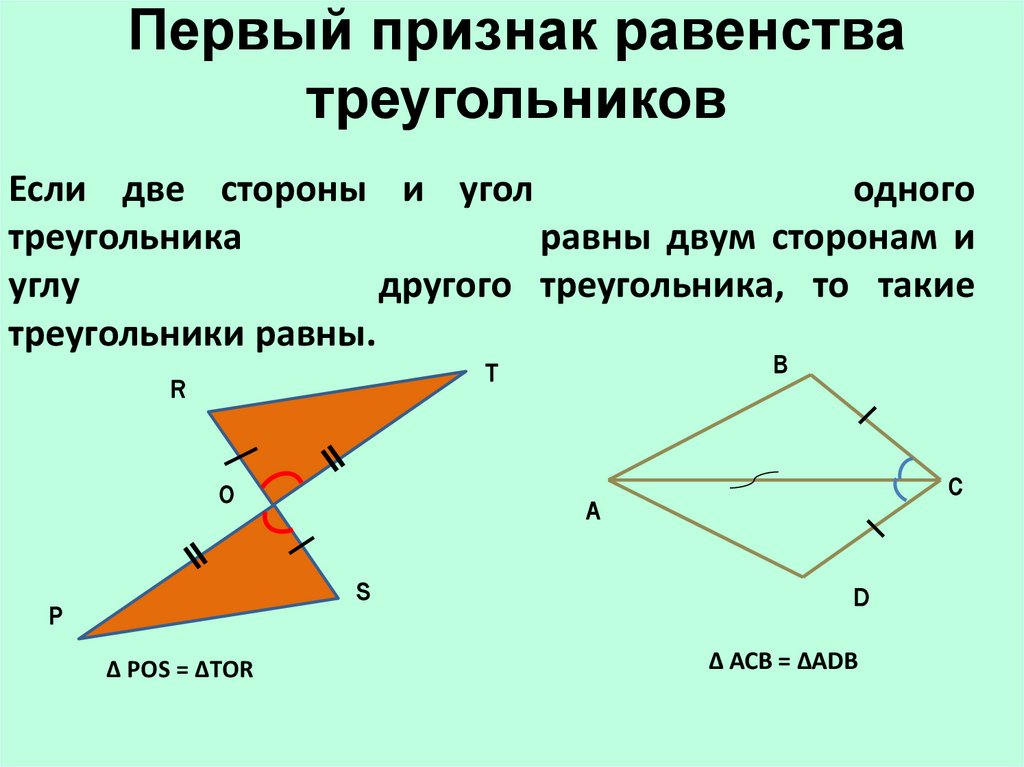
Пример 3: Существует одно решение
Данный
а
знак равно
22
,
б
знак равно
12
а также
м
∠
А
знак равно
40
°
. Найдите остальные углы и сторону.
Найдите остальные углы и сторону.
а > б
По закону синусов, а грех А знак равно б грех Б
грех
Б
знак равно
б
грех
А
а
знак равно
12
грех
40
°
22
≈
0,3506
Б
≈
20. 52
°
52
°
Б является острым.
м
∠
С
знак равно
180
°
−
м
∠
А
−
м
∠
Б
знак равно
180
°
−
40
°
−
20. 52
°
знак равно
290,79
°
52
°
знак равно
290,79
°
По закону синусов,
с грех 1190,48 ° знак равно 22 грех 40 ° с знак равно 22 грех 1190,48 ° грех 40 ° ≈ 29,79
Если нам даны две стороны и угол между ними треугольника или если нам даны
3
стороны треугольника, мы не можем использовать закон синусов, потому что мы не можем установить пропорции, когда известно достаточно информации. В этих двух случаях мы должны использовать
Закон косинусов
.
В этих двух случаях мы должны использовать
Закон косинусов
.
Решение треугольников (Триггер без слез, часть 4)
Решение треугольников (Триггер без слез, часть 4)Триггер без слез, часть 4:
Copyright 19972022 Stan Brown, BrownMath.com
Сводка: Треугольник состоит из шести частей, трех сторон и трех углов . Даны почти любые три из нихтри стороны, две стороны и угол, или одну сторону и два угла можно Найдите остальные три значения. Это называется решение треугольника , и вы можете сделать это с помощью любой треугольник, а не только прямоугольный .
Для всего этого вам понадобятся всего два инструмента:
Закон синусов и
Закон косинусов. Закон синусов связывает любые два
стороны и углы, противолежащие им, и закон косинусов связывает все
три стороны и один угол.
См. также:
- Как решать треугольники на TI-83/84 включает программу TI-83/84 для автоматизации вычислений, упомянутых в этой главе.
- Есть онлайн решатель треугольников, Джесс С.Д. за проверку ваших ответов. Нажмите на подсказку о Хром; кажется, он отлично работает в других браузерах, которые я пробовал.
Состав:
- Закон синусов
- Закон косинусов
- Детективная работа: решение всех типов треугольников
- Чемоданы
- Специальное примечание: боковой угол
- Решение треугольников из области
- Практические задачи
- Кстати: отличная книга по решению проблем
- Что нового
Для начала рассмотрим конкретный пример. Предположим, у вас есть
треугольника, у которого одна сторона равна 180, а прилежащий угол равен
42, а противоположный угол равен 31. Вас попросили найти
другой угол и две другие стороны.
Вас попросили найти
другой угол и две другие стороны.
Всегда полезно нарисовать грубый набросок, как этот. Нет это только поможет вам лучше организовать процесс решения, но это может помочь вам проверить вашу работу. Например, поскольку угол 31 является наименьшим, вы знаете, что противоположная сторона также должна быть самый короткий. Если бы вы пришли к ответу, скажем, 110 за одного с другой стороны, вы бы сразу поняли, что ошиблись где-то потому, что 110 меньше 180, а две другие стороны должны оба должны быть > 180.
Как бы вы решили эту проблему? это не сразу очевидно, согласен. Но, может быть, мы можем получить некоторую помощь от некоторые полезные общие приемы решения проблем:
- Можешь нарисовать схему?
- Можете ли вы использовать то, что вы уже знаете, чтобы решить часть этого проблема или связанная с ней проблема?
- Если у вас есть конкретный случай, можете ли вы решить более общую проблему?
(Иногда это работает и в обратную сторону, когда
пример указывает на хороший метод решения общей проблемы.
 )
)
У нас уже есть диаграмма, но давайте посмотрим, будут ли эти другие методы будет полезно. (Кстати, они у меня не оригинальные, а из потрясающей книги по решению проблем приемы, о которых, я думаю, вам следует знать.)
Можете ли вы использовать то, что вы уже знаете, чтобы решить часть этого проблема? Например, если бы это был прямоугольный треугольник, вы бы знали, как записать длины сторон через синусы или косинусы.
Но это не прямоугольный треугольник, увы. Есть ли способ повернуть его в прямоугольный треугольник? Не совсем так, но если вы построите линию в прямые углы в одну сторону и проходящие через противоположную вершину, у вас будет два прямоугольных треугольника. Может быть, решение этих прямоугольных треугольников покажет, как решить исходный треугольник.
На этой диаграмме показан тот же треугольник после того, как я нарисовал его.
перпендикуляр. Я также использовал другой принцип (Можете ли вы решить более
общая проблема?) и заменили конкретные цифры на обычные
буквы для сторон и углов.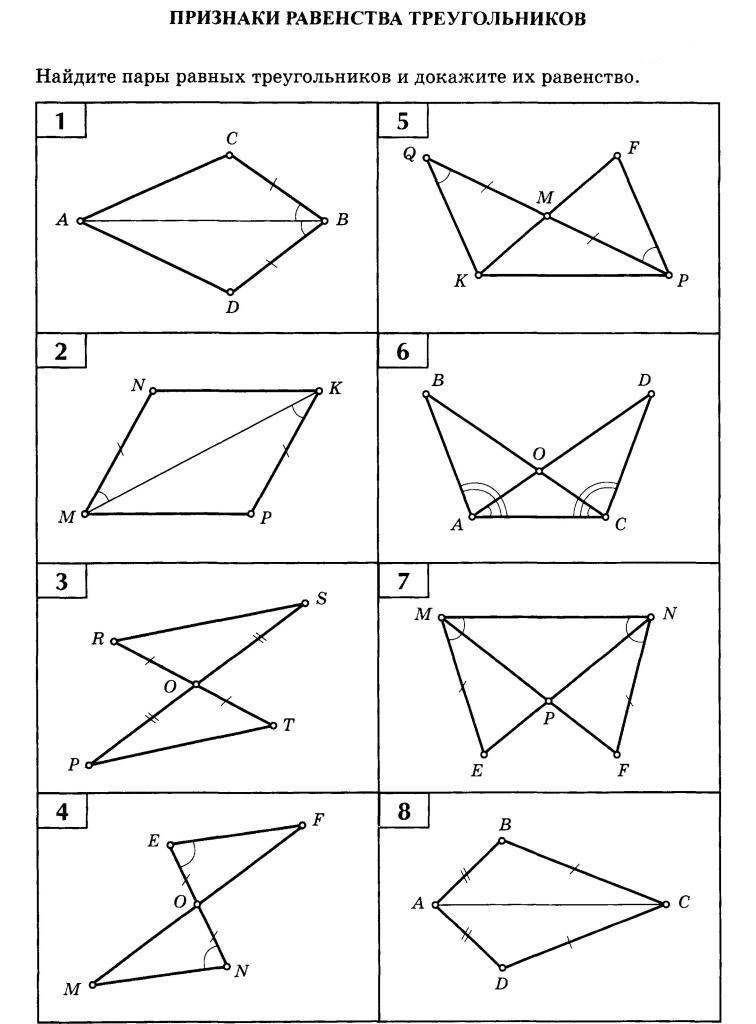 Опускание перпендикуляра CD в
Диаграмма делит большой треугольник (который вы не знаете, как
решить) на два прямоугольных треугольника ACD и BCD с общей стороной CD.
И вы можете решить эти прямоугольные треугольники.
Опускание перпендикуляра CD в
Диаграмма делит большой треугольник (который вы не знаете, как
решить) на два прямоугольных треугольника ACD и BCD с общей стороной CD.
И вы можете решить эти прямоугольные треугольники.
Мы собирались использовать эту простую схему для разработки двух важных инструментов. для решения треугольников: закон синусов и закон косинусов. Просто рисование этой одной перпендикулярной линии покажет вам, как решить не только треугольник, с которого мы начали, но любой треугольник . (какой-то триггер курсы преподают другие законы, такие как закон касательной и закон Сегменты. Я игнорирую их, потому что вы можете решать треугольники и без них нормально)
Закон синусов
Закон синусов прост и красив, и его легко вывести. Его полезно, когда вы знаете два угла и любую сторону треугольника, или два угла и площадь, или (иногда) две стороны и один угол .
Давайте начнем с того, что запишем то, что мы знаем, что касается сторон и
углы двух прямоугольных треугольников на диаграмме выше.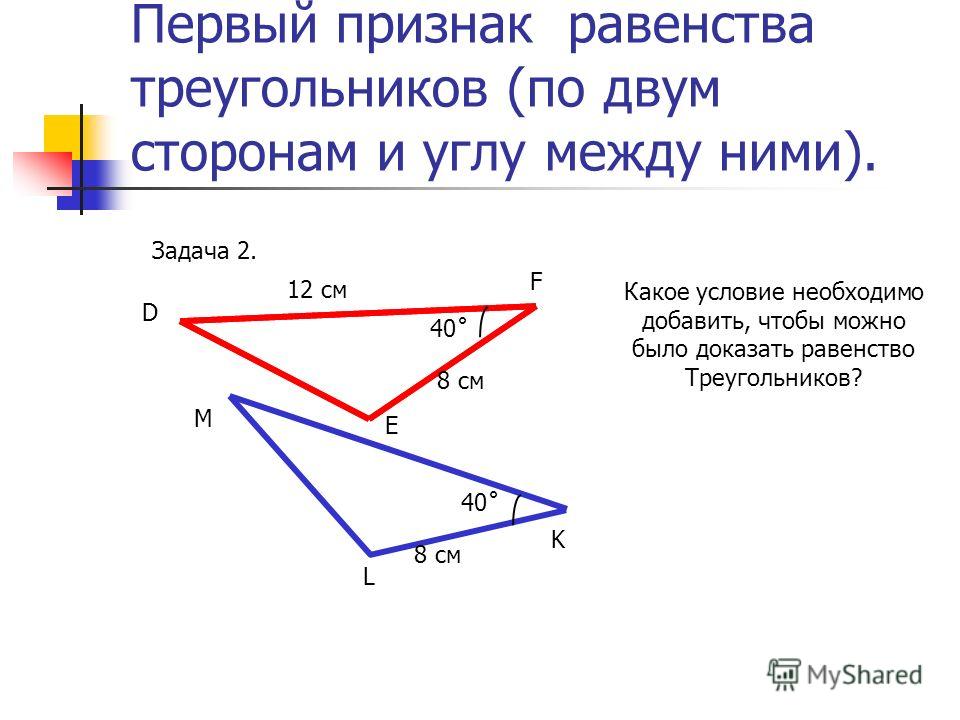 Вы помните, как записывать
длины катетов прямоугольного треугольника?
катет всегда равен гипотенузе умноженной на либо косинус
прилежащего угла или синус противолежащего угла. (Если
для тебя это пустые слова, или даже если ты не на 100%
уверен в этом, пожалуйста, вернитесь и просмотрите
этот раздел, пока не почувствуете себя уверенно.)
Вы помните, как записывать
длины катетов прямоугольного треугольника?
катет всегда равен гипотенузе умноженной на либо косинус
прилежащего угла или синус противолежащего угла. (Если
для тебя это пустые слова, или даже если ты не на 100%
уверен в этом, пожалуйста, вернитесь и просмотрите
этот раздел, пока не почувствуете себя уверенно.)
На схеме посмотрите на треугольник ADC слева: справа угол равен D , а гипотенуза равна b . Мы не знаем, сколько исходный угол C находится в этом треугольнике, поэтому мы не можем использовать C найти длины любых сторон. Что мы можем записать, используя угол A ? Используя его косинус и синус мы можем написать длины обоих катетов треугольник:
AD = b cos A а также CD = b sin A
По тем же причинам в другом треугольнике у вас есть
ДБ = a cos B а также CD = a sin B
Это поразительно: вы видите два разных выражения для длины CD. Но вещи, равные одной и той же вещи, равны друг другу.
Это означает, что
Но вещи, равные одной и той же вещи, равны друг другу.
Это означает, что
b sin A = a sin B
Разделите на sin A и вы получите решение для общего случая:
b = a sin B / sin A
Как это применимо к треугольнику, с которого мы начали? Ну и подключи значения, и вы получите длину стороны рядом с 31 угол (или напротив угла 42):
b = 180 sin 42 / sin 31 ≈ 234
А как насчет третьего угла, C , и третьей стороны, c ? Ну, когда ты есть два угла треугольника, вы можете легко найти третий:
А + В + С = 180
С = 180 – А – В
В этом случае C = 180 – 31 – 42 = 107.
Для третьей стороны есть несколько путей. Ты
написал выражения выше для AD и DB, и вы знаете, что с =
AD+DB, чтобы можно было вычислить c = b cos A + a cos B .
Но это два умножения и сложение, немного сложнее, чем одно умножение и одно деление, чтобы найти сторону b . Я ленив, и мне нравится уменьшать количество постукиваний по моему калькулятор. Есть ли способ проще, хотя бы немного проще? Да, есть. Вернитесь на шаг назад, к
a sin B = b син А
Разделите влево и вправо на (sin A )(sin B ), чтобы получить
a /sin A = b /sin B
Но в двух углах A и B нет ничего особенного. Ты мог точно так же опустили перпендикуляр из А в BC или от B до АС . Справа показан результат опускания перпендикуляра из В по линейный компакт-диск.
Поскольку C > 90, этот перпендикуляр оказывается
вне треугольника, и два прямоугольных треугольника ABD и CBD перекрываются.
Но это не повлияет на алгебру.
Кстати, угол в треугольнике
CBD — это не C , а 180 − C , дополнение к C . Угол С принадлежит исходному треугольнику ABC.
Угол С принадлежит исходному треугольнику ABC.
Вы можете записать длину общей стороны BD как
BD = c sin A (в треугольнике ABD)
и
BD = a sin(180 − C ) (в треугольнике CBD)
Но sin(180 − C ) = sin C , поэтому у вас есть
BD = a sin C (в треугольнике CBD)
Установите две вычисленные длины BD равными друг другу и разделить на (sin A )(sin C ):
a sin C = c sin A
a /sin A = c /sin C
Но мы уже выяснили ранее, что
a /sin A = b /sin B
Объединив эти два уравнения, вы получите Закон синусов :
.(28) Закон синусовПервая форма:
a /sin A = b /sin B = 77 c /sin
Это очень просто и красиво: для любого треугольника, если разделить любую сторону на синус противоположного угла ,
ты получишь
тот же результат. Этот закон справедлив для любого треугольника.
Этот закон справедлив для любого треугольника.
Вы можете вывести закон синусов при необходимости, так что я специально не рекомендуем запомнить. Но это так просто и красиво, что довольно трудно не запомнить, если вы используете его вообще. Это также красиво трудно запомнить неправильно: нет чередующихся плюсов и минусов признаки или комбинации различных функций.
Возвращаясь к нашему исходному треугольнику, мы можем вычислить длину третья сторона:
a /sin A = c /sin C
a (sin C )/(sin A ) = c
с = 180 (sin 107)/(sin 31) ≈ 334
Закон синусов иногда дается в перевернутом виде:
(29) Law of SinesSecond Form:
(sin A )/ a = (sin B )/ b = (sin C )/ c
Конечно, это тот же закон, так как 2/3 = 6/9 и 3/2 =
9/6 — одно и то же утверждение. Работайте с ним в любом случае, и вы придете
с теми же ответами.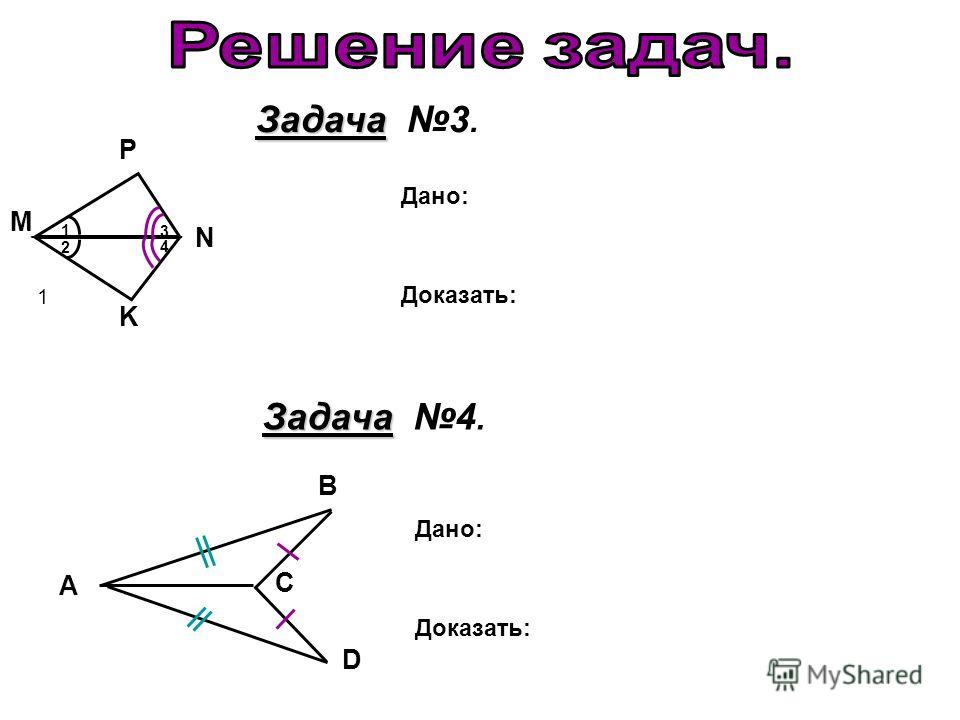
В большинстве случаев, когда вы используете Закон синусов, вы получаете уникальное решение. Но иногда вы получаете два решения (или ни одного) в случае бокового угла, где вы знаете две стороны и угол, который не лежит между ними. Пожалуйста, смотрите Специальное примечание ниже, после таблицы.
Закон косинусов
Закон синусов хорош, когда вы можете связать стороны и углы. Но предположим, вы знаете три стороны треугольника, например a = 180, b = 238, c = 340 и вам нужно найти три угла. Закон синусов для этого не годится, потому что он касается две стороны и их противоположные углы. Если вы не знаете никаких углов, вы есть уравнение с двумя неизвестными и вы не можете его решить.
Но треугольник может быть решен , если известны все три стороны ;
вам просто нужен другой инструмент. И зная меня, ты можешь быть уверен, что я
собирается помочь вам разработать один! Он называется законом косинусов.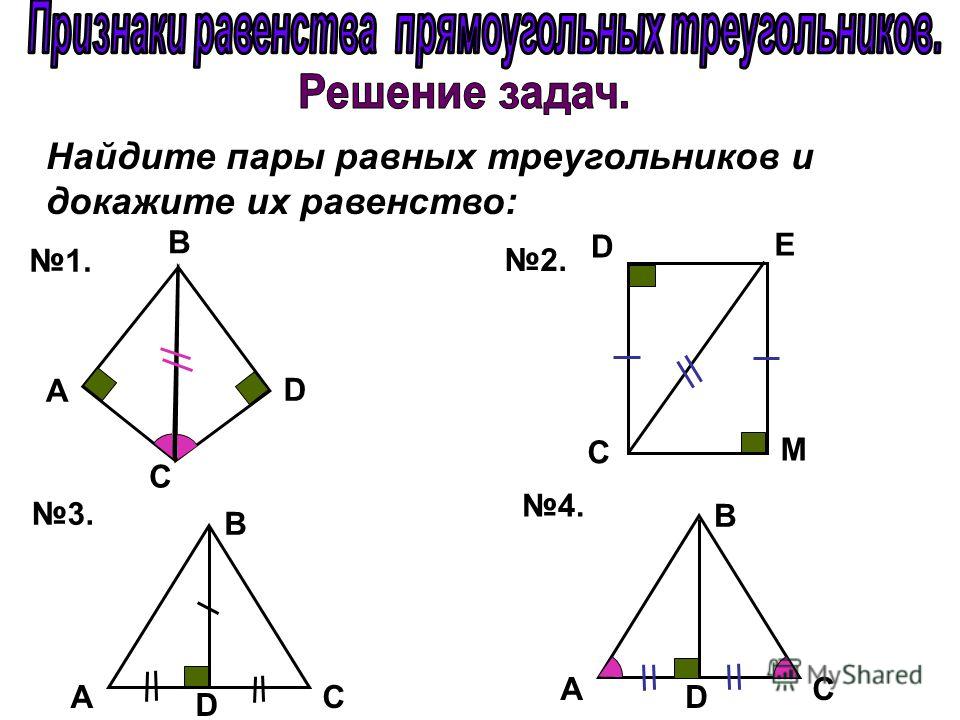
Давайте вернемся к этому общему треугольнику с опущенным перпендикуляром. из вершины C . Возможно, вы помните, что когда мы впервые посмотрели на эту картинку, мы потянули вывод информации с использованием как синуса, так и косинуса двух углов. Мы использовали синусоидальную информацию для разработки закона синусов, но мы никогда не пошел куда угодно с информацией о косинусе, которая была
AD = b cos A и DB или BD = a cos B
Посмотрим, к чему это может нас привести. Вы помните, как мы подошли Законом синусов нужно было написать два уравнения, в которых длину вспомогательной линии CD, а затем объединить уравнения в устранить КД. Можем ли мы сделать что-нибудь подобное здесь?
Хорошо, мы знаем две другие стороны этих прямоугольных треугольников, так что мы можно написать выражение для высоты CD, используя пифагорейскую формулу. Теорема на самом деле, два выражения, по одному для каждого треугольник.
a = (CD) + (BD) ⇒ (CD) = a − (BD)
b = (CD) + (AD) ⇒ (CD) = b − (AD)
и, следовательно,
a − (BD) = б — (н. э.)
э.)
Подставить известные значения BD = a cos Б и AD = b cos A , и у вас есть
a − a cos² B = b − b cos² A
Бззз! Не хорошо! Здесь используются две стороны и два угла, но нам нужно уравнение в три стороны и один угол , так что мы можем решить для этого угла. Давайте сделаем шаг назад, чтобы a – (BD) = b – (AD), и посмотрим, сможем ли мы пойти в другом направлении.
Возможно, проблема в том, что BD и AD рассматриваются как отдельные объекты, когда на самом деле они являются частями одной и той же линии. С БД + АД = c , можно написать
BD = c –
н.э.BD = c − b cos A .
Обратите внимание, что это приводит к третьей стороне, c и углу B капель. вне. Подставляя, теперь у нас есть
a − (BD) = б — (н.э.)
a − ( c − b cos A ) = б — ( б cos А )
Этот выглядит хуже, чем другой, но на самом деле лучше, потому что
это то, что искали: уравнение для трех сторон и одной
угол. Мы можем решить это с помощью небольшой алгебры:
Мы можем решить это с помощью небольшой алгебры:
a − c + 2 b c cos A − b cos² A = б − б cos² А
a − c + 2 b c cos A = b
2 б в cos А = б + в − а
cos A = ( b + c − a ) / 2 б в
Мы долго собирались туда, но, наконец, мы сделали это. В настоящее время мы можем подставить длины сторон, которые я упомянул в первом пункт, и придумать значение для cos A , что в свою очередь даст нам угол A :
cos A = (238 + 340 − 180) / (2 238 340)
cos А ≈ 0,864088
А ≈ 30,2
Проделайте то же самое с найти второй угол (или использовать закон синусов, так как это меньше работы), затем вычтите два известных угла из 180, чтобы найти третий угол.
Вы можете найти закон косинусов для других углов с помощью
следуя тому же процессу, используя два других перпендикуляра.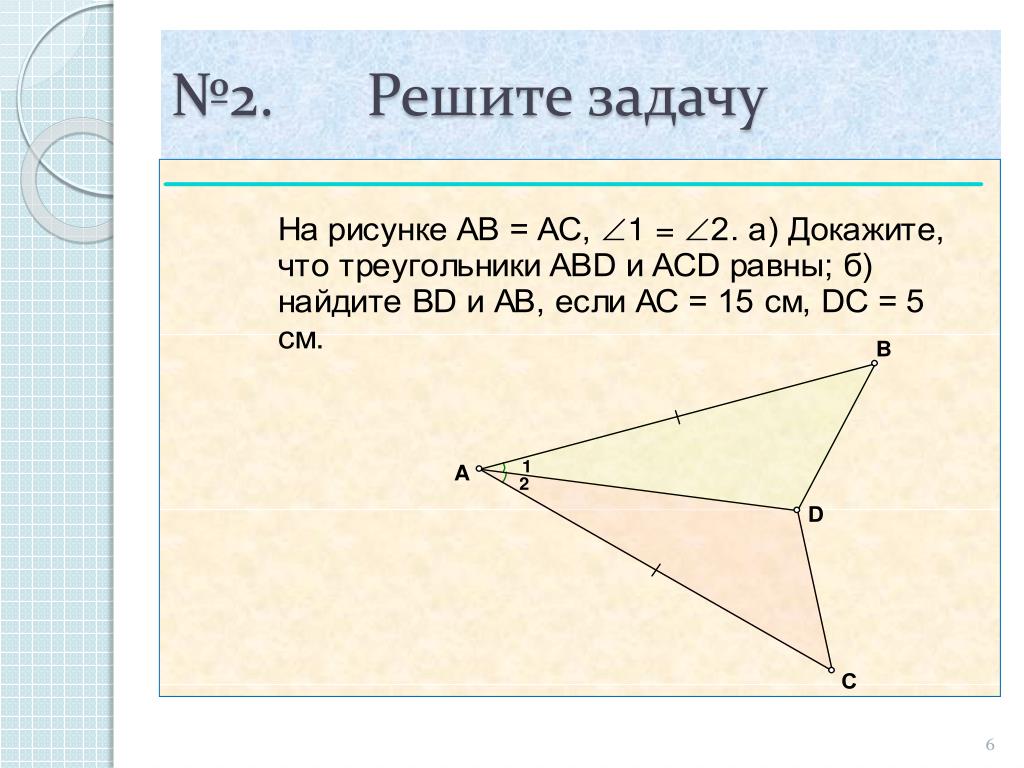
(30) Закон Cosinesfirst Form:
COS A = ( B + C — A ) / 2 B C 9000) / 2 B C 9000) / 2 B C 578 777. + c − b ) / 2 a c
cos C = ( a + b − в ) / 2 а б
Ради интереса найдем два других угла этого треугольника:
.cos C = ( a + b − c ) / 2 a b
потому что С = (180 + 238 — 340) / (2 180 238)
cos C ≈ −0,309944
С ≈ 108,1
Поскольку этот учебник помогает вам,
нажмите, чтобы сделать пожертвование!Поскольку этот учебник помогает вам,
, пожалуйста, сделайте пожертвование на
BrownMath.com/donate.
Обратите внимание, что закон косинусов автоматически обрабатывает острые и
тупые углы. Помните из
диаграмма
в функциях любого угла, которые
cos A является отрицательным, когда A находится между 90 и 180.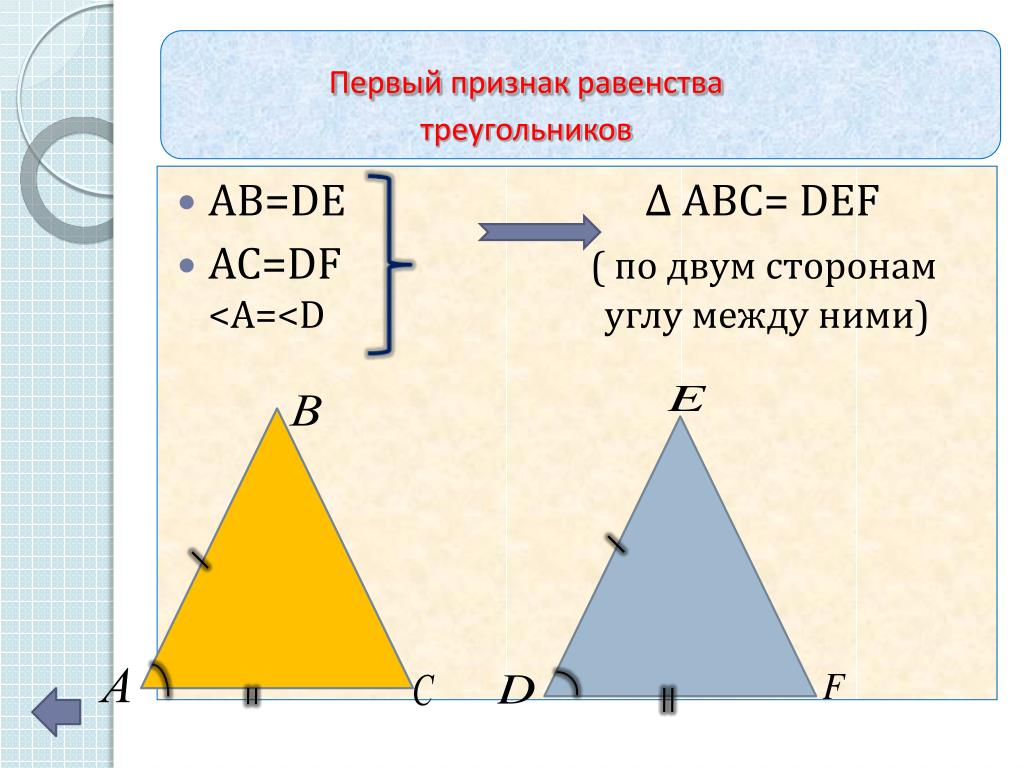 Поскольку косинус имеет уникальные значения от 0 до
180, вам никогда не придется беспокоиться о нескольких решениях одной задачи.
треугольник, когда вы используете закон косинусов.
Поскольку косинус имеет уникальные значения от 0 до
180, вам никогда не придется беспокоиться о нескольких решениях одной задачи.
треугольник, когда вы используете закон косинусов.
Существует еще одна известная форма закона косинусов, которая может быть немного легче запомнить. Начните с приведенной выше формы, умножьте на 2 a b и изолировать c с одной стороны:
cos C = ( a + b − c ) / 2 a b
2 a b cos C = a + b − c
c = a + b − 2 a b cos C
Вы можете сыграть в ту же игру, чтобы решить две другие стороны:
(31) Law of CosinesSecond Form:
a = b + c − 2 b c cos A
b = a + c − 2 a c cos B
c = a + b − 2 a b cos C
Обычно вы будете использовать закон косинусов в первая форма для нахождения угла и вторая форма для нахождения стороны .
Возможно, вы не хотите пытаться запомнить это, но это не так сложно, как кажется. Я думаю об этом так: квадрат одной стороны есть сумма квадратов двух других, например Пифагора, но с поправочным коэффициентом в 2 раза больше, чем произведение той же стороны на косинус противолежащего угла.
Детективная работа: решение всех типов треугольников
Только с определениями синус, косинус и тангенс можно решить любой прямоугольный треугольник . Если у вас есть закон синусов и закон косинусов под вашим ремень, вы можете решить любой существующий треугольник . (Некоторые наборы данных привести к невозможной ситуации, как треугольник со сторонами 3-4-9.)
Действительно, это довольно просто. Когда бы ни
вам нужно решить треугольник, подумать о том, что у вас есть, а затем подумать
о том, какую формулу вы можете использовать, чтобы получить то, что вам нужно. (Когда у тебя есть
два угла, всегда можно найти третий А + В + С =
180. )
)
Дела
Многим людям легче думать об известных элементах треугольник как пример. Например, если вы знаете два угла и сторона между ними, это случай ASA; если вы знаете два угла и сторону это не между ними, это случай ААС и так далее.
Im не представляю вам следующую таблицу запоминать. Вместо этого я надеюсь показать вам, что между закон синусов и закон косинусов можно решить любой треугольник, и что вы просто выбираете, какой закон использовать, основываясь на том, какой из них только что один неизвестен и иным образом использует уже имеющуюся у вас информацию.
Большинство случаев можно решить с помощью закона синусов. Но если у вас есть три стороны ( SSS ) или две стороны и угол между ними ( САС ), вы должны начать с закона косинусов.
| Если вы это знаете… | Вы можете решить треугольник таким образом… | |
|---|---|---|
| три уголка, AAA | Недостаточно информации.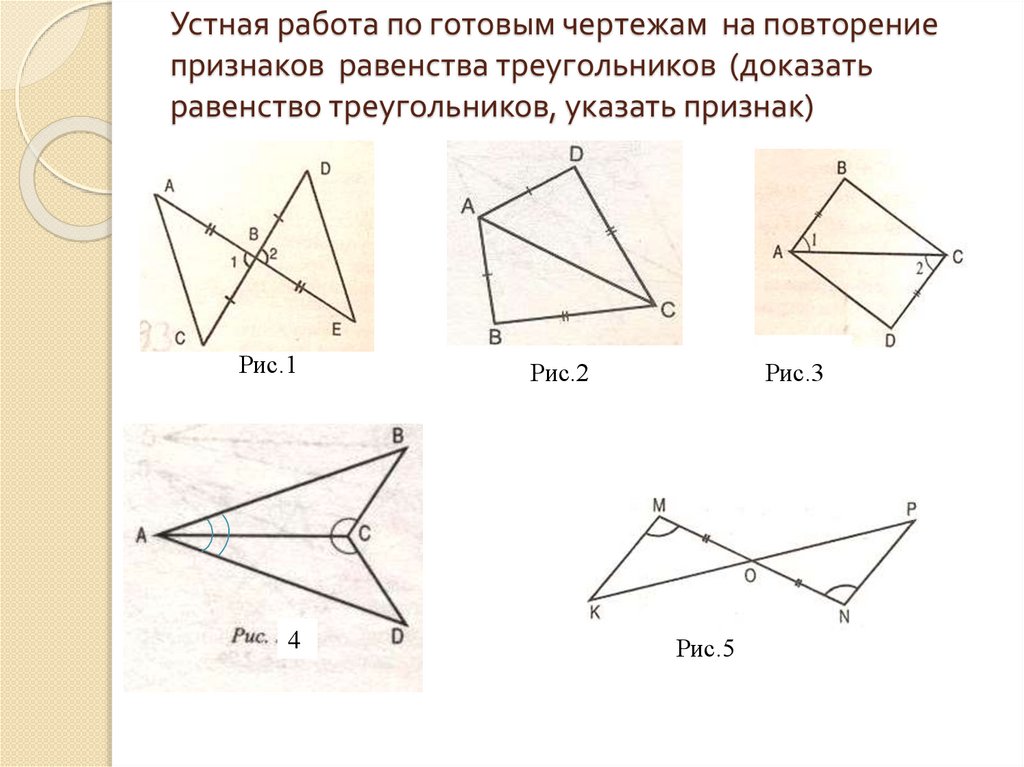 Без хотя бы одной стороны у вас есть
форма треугольника, но нет возможности правильно масштабировать ее. За
например, те же самые углы могут дать вам треугольник со сторонами 7-12-13,
35-60-65 или любой другой кратный. Без хотя бы одной стороны у вас есть
форма треугольника, но нет возможности правильно масштабировать ее. За
например, те же самые углы могут дать вам треугольник со сторонами 7-12-13,
35-60-65 или любой другой кратный. | |
| два угла и сторона, ААС или ААС | Найдите третий угол, вычитая из 180. Затем используйте Закон синусов (28) ★ дважды найти вторую и третью стороны. | |
| две стороны и … | угол в комплекте, SAS | Используйте закон косинусов (31)★ найти третью сторону. Затем используйте либо закон синусов (29)★ или закон косинусов (30)★ найти второй угол. |
| угол, не входящий в комплект, SSA | Используйте закон синусов (29)★, чтобы получить
второй угол и закон синусов (28)★
чтобы получить третью сторону. Но… | |
| три стороны, нержавеющая сталь | Найдите один угол с помощью закона косинусов (30). Используйте этот угол и его противоположную сторону в закон синусов (29), чтобы найти второй угол, затем вычтите, чтобы найти третий угол. | |
| два углы и площадь | См. Дано: площадь и два угла ниже. Найдите третий угол. Затем найдите сторону, используя и = √2 площадь sin A /(sin B sin C ) Затем действуйте, как в случае с ASA, описанном выше. | |
| два стороны и площадь | См. Дано: площадь и две стороны ниже. Найдите внутренний угол с помощью sin A = 2 площадь/( б в ) Затем действуйте, как в случае с SAS, описанном выше. | |
★
Если задан угол 90°, закон синусов и закон косинусов
являются излишними. Просто примените определения синуса и косинуса
(уравнение 1) и тангенс (уравнение 4), чтобы найти другую
стороны и углы. Просто примените определения синуса и косинуса
(уравнение 1) и тангенс (уравнение 4), чтобы найти другую
стороны и углы. | ||
Особое примечание: Боковой угол
Для большинства наборов фактов либо существует единственное решение или они явно абсурдны. (Если вы не понимаете, почему треугольник со сторонами 50-60-200 абсурд, попробуй зарисовать.) Но случай SSA может быть сложным.
Предположим, вы знаете острый угол B и стороны a и b . Учитывая эти факты, есть два разных способа, которыми вы могли бы нарисовать треугольник, как показано на рисунке. Как это может быть? Ну, вы используете Закон Синусы найти синусы углов А и С . Допустим, вы нашли sin C = 0,5. Это означает, что C может быть либо 30, либо дополнение 150. Помните, что синус любой угол и синус его добавки одинаковы.
Это печально известный неоднозначный случай . Вы можете увидеть
задача с картинки: известная противоположная сторона b может принять любую из
две позиции, удовлетворяющие данным длинам a и b . Эти два положения дают два разных значения угла A ,
два разных значения для угла C и два разных значения для стороны c .
Подумайте об этом некоторое время и
Вы увидите, что эта неоднозначность может возникнуть только тогда, когда известный угол
острая, а прилежащая сторона длиннее противоположной стороны, и
противоположная сторона больше высоты.
Эти два положения дают два разных значения угла A ,
два разных значения для угла C и два разных значения для стороны c .
Подумайте об этом некоторое время и
Вы увидите, что эта неоднозначность может возникнуть только тогда, когда известный угол
острая, а прилежащая сторона длиннее противоположной стороны, и
противоположная сторона больше высоты.
Вот полное изложение всех возможности с корпусом SSA:
| Возможности в рамках дела SSA | ||
|---|---|---|
| известный угол < 90 | известный угол ≥ 90 | |
| смежная сторона < противоположная сторона | одно решение | одно решение |
| смежная сторона = противоположная сторона | одно решение | нет решения (Углы, лежащие напротив равных сторон, должны быть равны, но у вас не может быть двух углов, оба ≥ 90 в треугольнике.) |
| смежная сторона > противоположная сторона | Вычислить высоту треугольника h (синус смежной стороны умножить на известный
угол).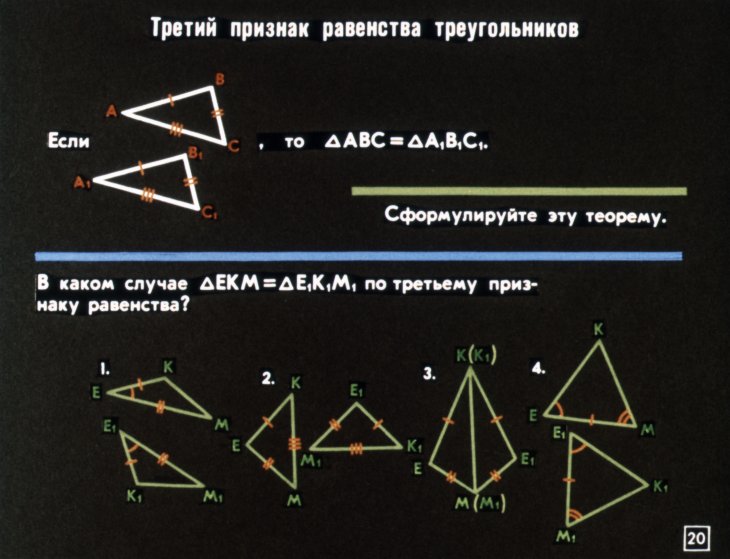
| нет решения (Условия нарушают теорема о том, что наибольшая сторона всегда лежит против наибольшей угол.) |
Ради всего святого, не пытайтесь запомнить эту таблицу! Вместо этого всегда рисуйте картинку. Если вы можете нарисовать два картинки, которые соответствуют всем имеющимся фактам, у вас есть две законные решения. Если только одна картинка соответствует всем фактам, она показать вам, какой угол (если есть) > 90. И если вы не можете сделать любую картину, которая соответствует фактам, треугольник не имеет решение.
Что делать, если у вас есть два решения? Если у вас нет
другая информация, чтобы продолжить, конечно, вы сообщаете оба решения. Но
внимательно проверьте ситуацию. Может быть, вам прямо сказали, что
наибольший угол, или это подразумевается другими известными вам фактами. В этом
случай, когда ваше решение ограничено, и вы отклоняете решение, которое
не соответствует ограничениям.
В этом
случай, когда ваше решение ограничено, и вы отклоняете решение, которое
не соответствует ограничениям.
Пример: Предположим, вас попросили решить треугольник с B = 36,9 a = 75,3, и б = 51,3. Как вы поступите?
Решение: Начните с эскиза, подобного показанному на Правильно. Это поможет вам присвоить номера нужным элементам таблицы. треугольник.
Это случай бокового угла: вы знаете две стороны a и b , и не включенный угол B . Прилегающая сторона к угол Б , a = 75,3, больше, чем противоположная сторона, a = 51,3, поэтому вы нужно вычислить высоту, h = 75,3 sin 36,9 ≈ 45,2. Противоположная сторона, 90 577 a 90 578 = 51,3, больше, чем это, так что есть два решения.
Используйте закон синусов, уравнение 29, чтобы получить второй угол:
(sin A )/ a = (sin B )/ b
sin A = ( a / b ) sin B
sin A = (75,3 / 51,3) sin 36,9 ≈ 0,8813
А = 61,8 или 180 − 61,8 = 118,2
Если А = 61,8 .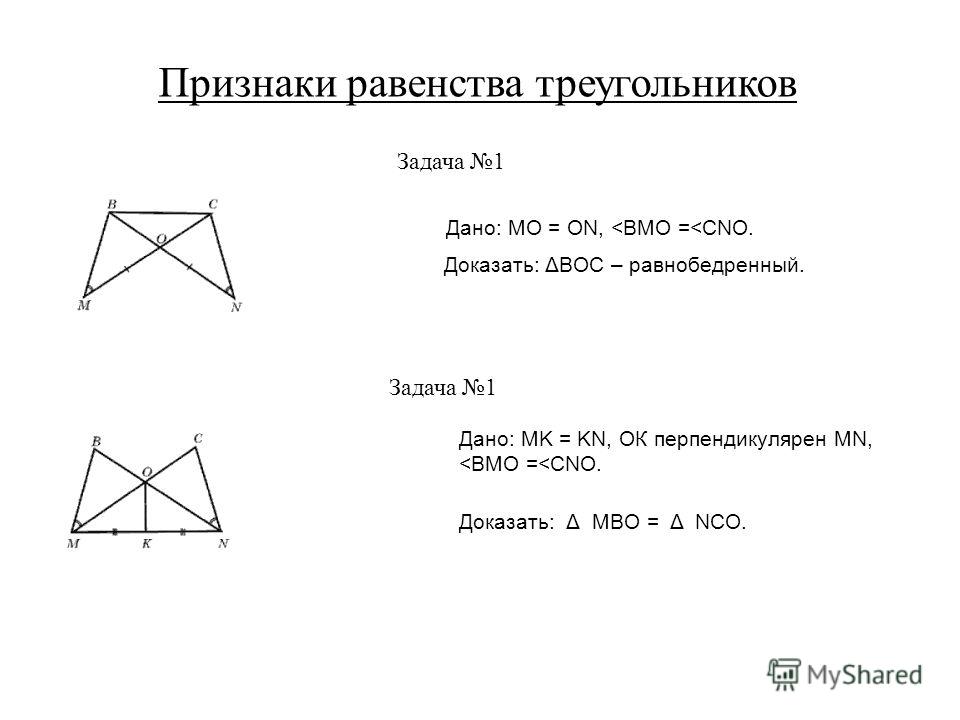 .. .. | Если А = 118,2 … |
|---|---|
Угол C = 180 − A − B С = 180 – 61,8 – 36,9 = 81,3 Используйте закон синусов, уравнение 28, для третья сторона: с /(sin C ) = b /(sin B ) в = б sin C / sin B c = 51,3 sin 81,3 / sin 36,9 ≈ 84,5 Все шесть элементов треугольника по порядку равны А =61,8, в =84,5, В =36,9, а =75,3, С =81,3, б =51,3. | Угол C = 180 − A − B C = 180 – 118,2 – 36,9 = 24,9 Используйте закон синусов, уравнение 28, для третья сторона: в / sin C = b / sin B в = б sin C / sin B с = 51,3 sin 24,9 / sin 36,9 ≈ 36,0 Все шесть элементов треугольника по порядку равны А =118,2, в =36,0, В =36,9, а =75,3, С =24,9, б =51,3. |
Решение треугольников из области
Дано: площадь и два угла
В апреле 2016 года Кэролайн Макноу спросила меня, как решить треугольник , если у вас есть два угла и площадь . я не имел сталкивался с этим раньше, но это выполнимо со стандартным уловка опускания перпендикуляра.
Напомним, что площадь треугольника равна высоте основания/2. Здесь база с и высота (CD) равна б син А . (CD также равен a sin B , но для этого решения это не так. независимо от того, какое выражение вы используете.) Это дает вам
площадь = ( c b sin A )/2
Мы знаем угол A , даже если A не является одним из двух данных, мы можем легко найти его, вычитая
два других из 180, но есть две неизвестные стороны в
это уравнение. Как мы можем устранить один из них? Нам нужна секунда
уравнение, которое включает b и c , но не другие
неизвестные. Ответ находится в законе синусов:
Ответ находится в законе синусов:
b /sin B = c /sin C ⇒ б = c sin B /sin C
Подставьте это в уравнение площади:
площадь = ( c b sin A )/2
площадь = ( c sin B sin A )/(2 sin C )
Решить для стороны c :
с = 2 область sin C /(sin A sin B )
(32) c = √2 площадь sin C /(sin A sin B )
Наконец, используйте закон синусов, чтобы найти стороны a и b .
Дано: площадь и две стороны
Решив треугольник по площади и двум углам, его естественно задаться вопросом, можете ли вы это сделать с учетом площади и двух сторон . Ответ да, и это даже немного проще, чем когда знаешь местность и два угла.
В предыдущем разделе мы нашли формулу площади в терминах двух сторон и прилежащего угла:
площадь = ( c b sin A )/2
Мы не могли использовать это напрямую, когда знали два угла и
площадь, но если мы знаем две стороны и площадь, то эта формула
именно то, что мы хотим. Просто найдите грех A :
Просто найдите грех A :
(33) sin A = 2 площадь/( b c )
Затем используйте закон косинусов, чтобы найти сторону и . Наконец, используйте закон синусов или Закон косинусов, чтобы найти второй угол, и вычтите эти углы из 180, чтобы найти третий угол.
Практические задачи
Чтобы получить максимальную пользу от этих проблем, работайте над ними без предварительного просмотра решений. Вернитесь к главе текст, если вам нужно освежить память.
Рекомендация : Работайте с ними на бумаге труднее обмануть себя в том, действительно ли ты понять проблему полностью.
Вы найдете полный решения для всех проблем. Только не проверяй свой ответы, но проверьте и свой метод.
1 У вас есть прямоугольный треугольник ( C = 90) с короткие стороны a = 88 и b = 37. Решите треугольник.
2(Набросайте эту задачу по мере чтения. )
В государственном парке река течет практически прямо
1800 м. Вы хотите построить монорельс из A , один конец
этот участок, до точки C на дальнем берегу. Вы также хотите
построить пешеходный мост от B , на другом конце этого участка
реки, до той же точки C на дальнем берегу.
В A угол между вашими линиями взгляда и B и C равен 67. В B угол между вашим прицелом
строк A и C 38.
)
В государственном парке река течет практически прямо
1800 м. Вы хотите построить монорельс из A , один конец
этот участок, до точки C на дальнем берегу. Вы также хотите
построить пешеходный мост от B , на другом конце этого участка
реки, до той же точки C на дальнем берегу.
В A угол между вашими линиями взгляда и B и C равен 67. В B угол между вашим прицелом
строк A и C 38.
Какой длины должны быть монорельс и пешеходный мост?
Дополнительный вопрос: если река имеет одинаковую ширину на всем протяжении растяжка от A до B , насколько она широка?
3 Найдите другие элементы треугольника с B = 117, a = 16 см и b = 25 см.
4 Очень современная подставка представляет собой треугольную форму со сторонами 6″, 9″ и 12″. Какие три угла?
5После того как вы покрасили свою спальню, у вас достаточно
краски осталось покрыть 25 футов. Вы решили покрасить треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
три стороны.
Вы решили покрасить треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
три стороны.
6 Вы проезжаете 6,0 миль по прямому шоссе, затем сворачиваете. Это правый поворот, но вы не замечаете угла.
Сейчас вы едете по прямой боковой дороге. В конце 9,8 миль по боковой дороге вы поворачиваете на 135 на правильно, на третьей дороге. (Если вы визуализируете это сверху, 135 изменение направления соответствует углу 180 − 135 = 45 в треугольнике.)
Если предположить, что дорога продолжается в том же направлении, как далеко вы должны ехать, чтобы добраться до начальной точки?
7Вы укладываете треугольную грядку для своего сада. Две стороны равны 40 м и 60 м, а угол между ними равен 22. Какой длины третья сторона и каковы две другие углы?
Кстати: отличная книга по решению проблем
Я должен порекомендовать потрясающую маленькую книгу, Как решить
Это Г.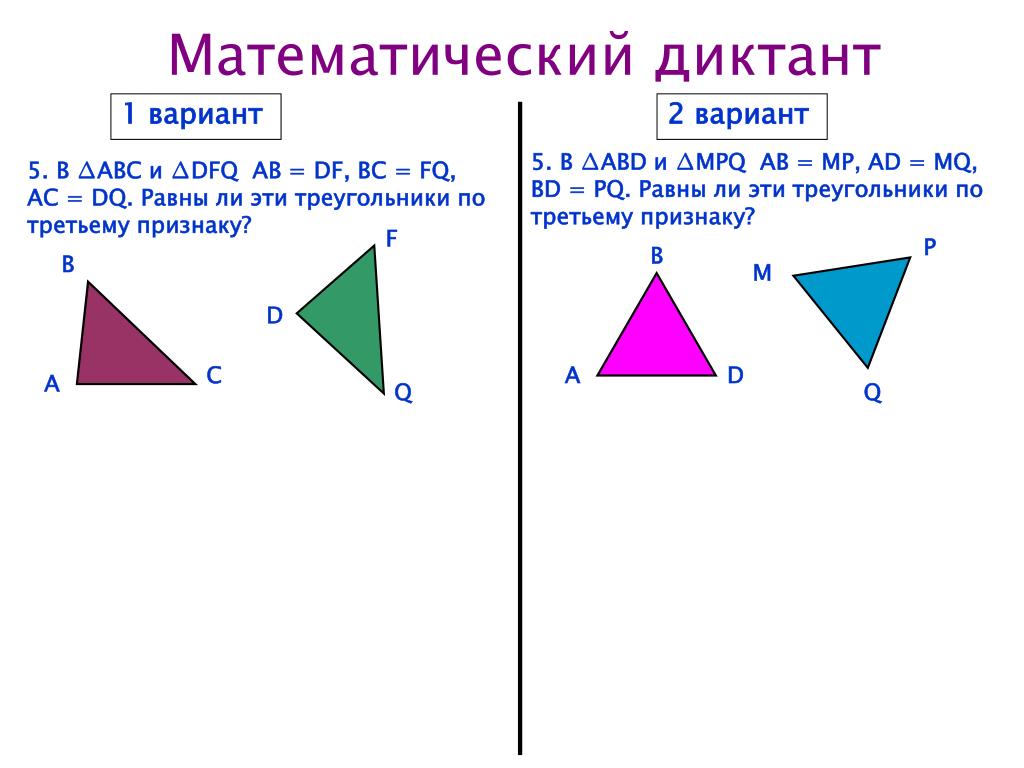 Поля. Большинство учителей не очень хорошо учат вас
как решать задачи и делать доказательства. Они показывают вам, как они делать их, и ожидать, что вы подберете их методы своего рода
осмос. Но большинство из них не очень хорошо объясняют мысль
процесс, в ходе которого выполняется геометрическое доказательство или решается страшная
проблема истории.
Поля. Большинство учителей не очень хорошо учат вас
как решать задачи и делать доказательства. Они показывают вам, как они делать их, и ожидать, что вы подберете их методы своего рода
осмос. Но большинство из них не очень хорошо объясняют мысль
процесс, в ходе которого выполняется геометрическое доказательство или решается страшная
проблема истории.
Polyas отлично учит решать проблемы. Он показывает вам, какие вопросы вы должны задавать себе, когда увидеть проблему. Другими словами, он учит вас, как преодолеть себя. гул, за исключением барахтанья, которое делает большинство людей, когда они видят незнакомая проблема. И делает это с большим количеством примеров, так что вы может развить уверенность в ваших методах и сравнить ваши методы с его. Техники, которые я упомянул выше, — это только три из много в его книге.
Есть даже удобный контрольный список вопросов, которые вы можете задать себе всякий раз, когда вы застряли на проблеме.
Как решить был впервые опубликован в 1945 году,
и его периодически в и из печати. Если вы не можете получить его
из книжного магазина, идите в библиотеку и возьмите экземпляр. ты не будешь
Извините.
Если вы не можете получить его
из книжного магазина, идите в библиотеку и возьмите экземпляр. ты не будешь
Извините.
Что нового
- 19 ноября 2021 г. : здесь обновлена ссылка.
- (промежуточные изменения подавлены)
- 19 февраля 1997 г. : Новый документ.
следующий: 5/Функции любого угла
Поскольку этот учебник помогает вам,
, пожалуйста, нажмите, чтобы сделать пожертвование!Поскольку этот учебник помогает вам,
, пожалуйста, сделайте пожертвование на
BrownMath.com/donate.
Обновления и новая информация: https://BrownMath.com/twt/
Карта сайта | Поиски | Главная страница | Контакт
косоугольных треугольников
косоугольных треугольников Наклонный треугольник — это любой треугольник, не являющийся прямоугольным. Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого).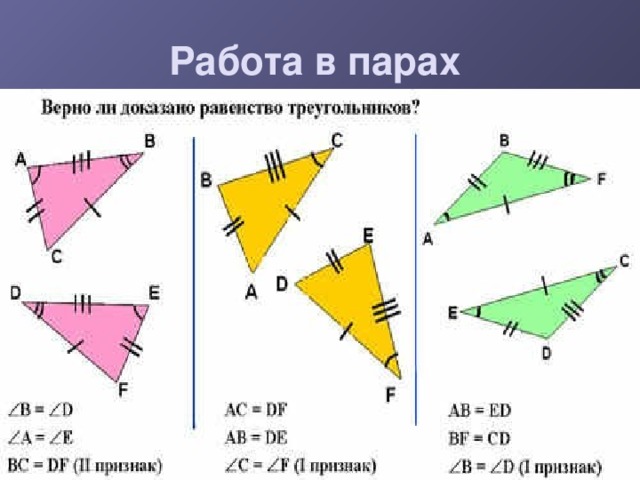 На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
Примем соглашение о обозначении частей косоугольных треугольников, обобщающее правило для прямоугольных треугольников. Пусть углы обозначены А, В, и С, , а противоположные стороны обозначены а, b, и с, соответственно.
Решение косоугольных треугольников
Тригонометрия косоугольных треугольников не так проста, как прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Они называются «законом косинусов» и «законом синусов». Есть и другие «законы», которые использовались раньше, но с момента повсеместного использования калькуляторов этих двух законов достаточно.Закон косинусов
Это просто сформулированное уравнение: Это похоже на теорему Пифагора, за исключением последнего члена, и если 90 577 C 90 578 — прямой угол, последний член исчезает (поскольку косинус 90° равен 0), поэтому закон косинусов на самом деле является обобщением закона косинусов.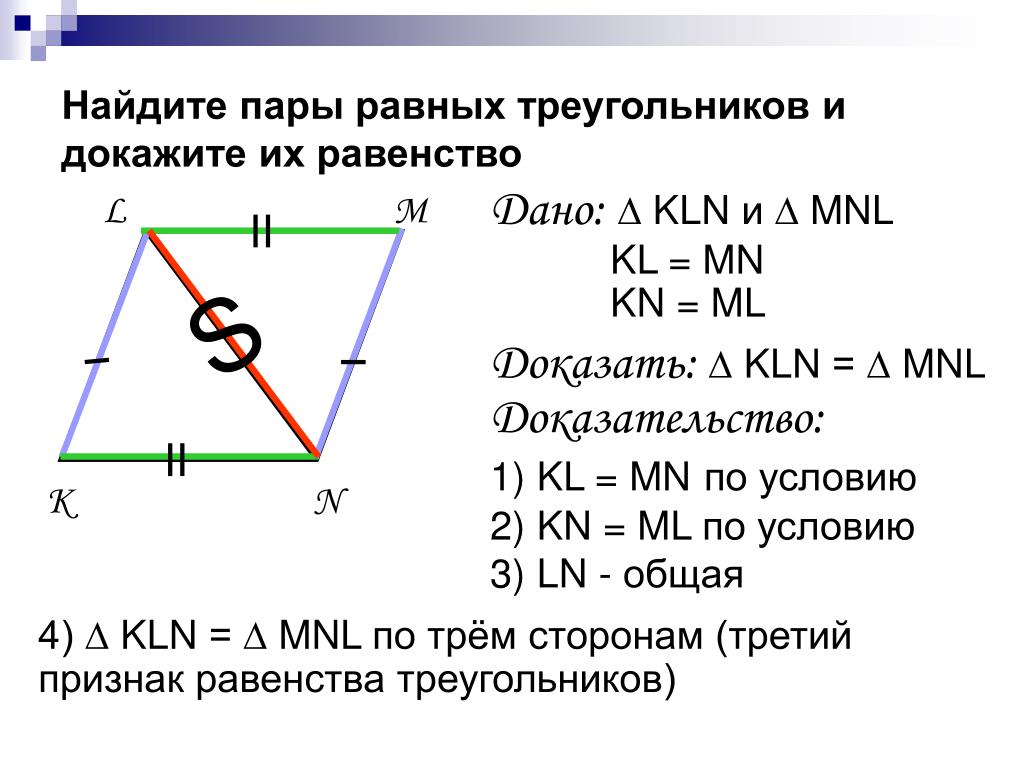 Теорема Пифагора.
Теорема Пифагора.
Обратите внимание, что каждый треугольник дает три уравнения закона косинусов, так как вы можете переставлять буквы по своему усмотрению. Затем две другие версии 9и b 2 = c 2 + a 2 – 2 ca cos B.
Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.
Во-первых, если известен один угол и две смежные стороны, то можно определить и противоположную сторону. Например, если угол C = 60°, сторона a = 5 и сторона b = 8, то по закону косинусов c 2 = 25 + 64 – 80 cos 60°. Поскольку косинус угла 60° равен 1/2, это уравнение упрощается до c 2 = 49, поэтому c = 7.
Во-вторых, если вы знаете все три стороны треугольника, то можете использовать их для нахождения любого угла. Например, если три стороны равны a = 5, b = 6 и c = 7, то по закону косинусов число 49= 25 + 36 – 60 cos C, so cos C = 12/60 = 0,2, а с помощью калькулятора C = 1,3734 радиана = 78,69°.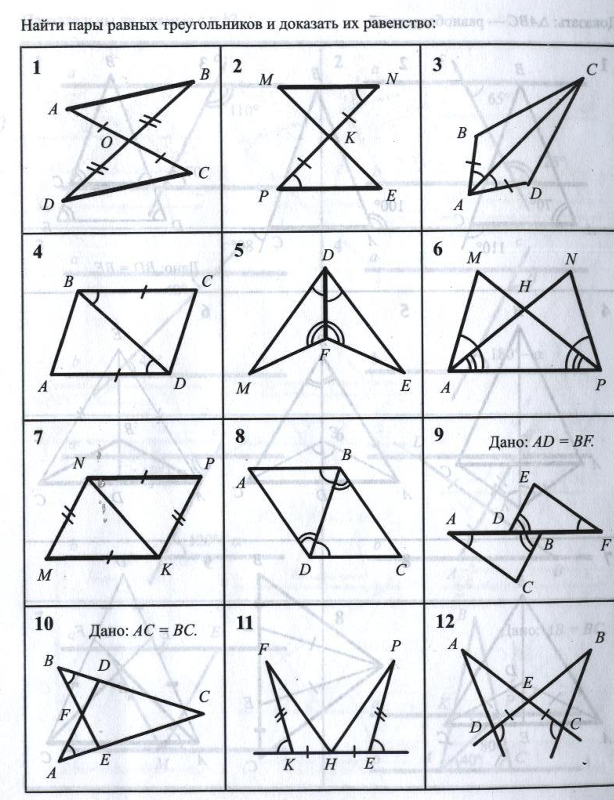
Примечание: Если треугольник тупоугольный, то cos C отрицателен. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда закон косинусов гласит: /60 = — 0,81667. Как видно из графиков на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус. Вы получите C = 2,2556 радиан = 129,237°.
Закон синусов
Закон синусов также представляет собой просто сформулированное уравнениеОбратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами.
Во-первых, если известны два угла и сторона, противолежащая одному из них, то можно определить сторону, противолежащую другому из них. Например, если угол A = 30°, угол B = 45°, а сторона a = 16, тогда по закону синусов (sin 30°)/16 = (sin 45°)/ b. Решение для b дает b = 16(sin 45°)/(sin 30°) = 22,6274.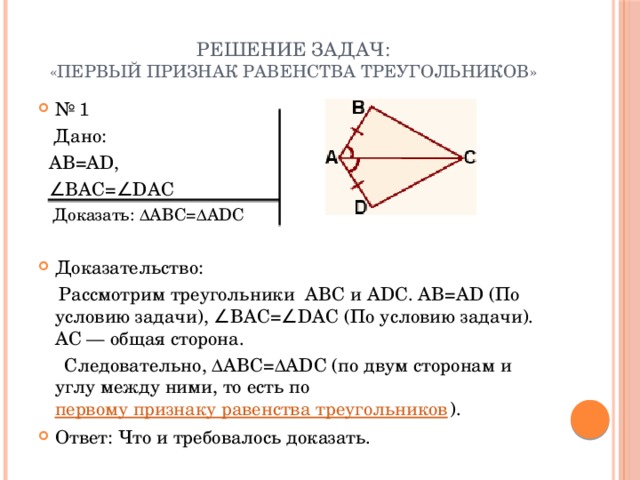
Во-вторых, если вы знаете две стороны и угол, противолежащий одной из них, то вы можете почти определить угол, противолежащий другой из них. Например, если сторона a = 25, сторона b = 15, а угол A = 40°, то по закону синусов (sin 40°)/25 = (sin В )/15. Нахождение sin B дает sin B = 15 (sin 40°)/25 = 0,38567. Теперь арксинус 0,38567 = 22,686°.
Предупреждение: у вас может быть неверный ответ. Есть два угла между 0 и 180 ° с данным синусоидальным; второй является дополнением первого. Таким образом, в данном случае вторым является тупой угол 180 – 22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Проблемы
553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу.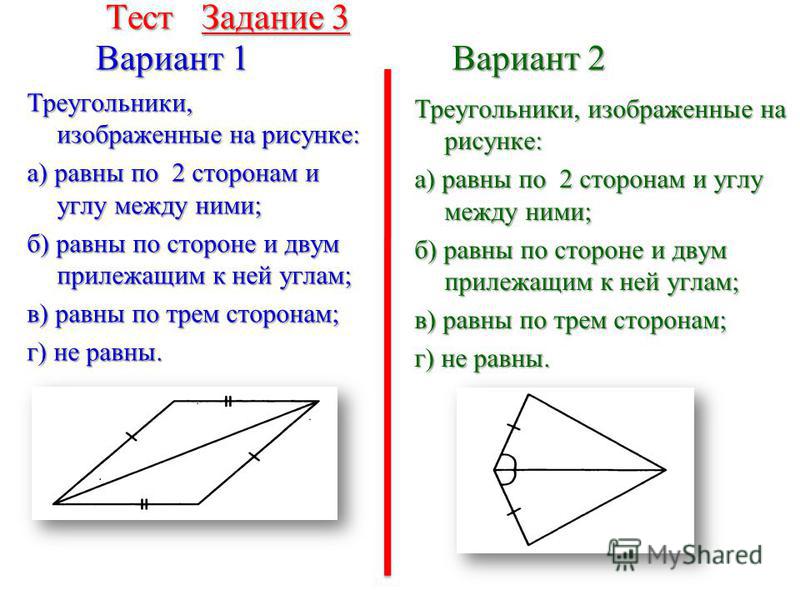 A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
557. В треугольнике ABC, a = 700 футов, B = 73° 48′, и C = 37° 21′. Если M это середина BC найти длины AM, и углы BAM и MAC.
561. Три окружности радиусов 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.
563. A и B — точки на противоположных берегах реки. На одном берегу линия AC измеряется 650 футов. Угол A = 73° 40′ и C = 52° 38′. Найдите АБ.
570. P и Q две недоступные точки. Чтобы найти расстояние между ними, в произведенном QP берется точка A и измеряется линия AB длиной 1200 футов, образующая угол PAB = 26° 35′. Угол ABP = 48° 12′ и ABQ = 106° 42′. Какова длина PQ ?
Какова длина PQ ?
579. Стороны параллелограмма равны AB = 209,16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ.
580. В параллелограмме ABCD, диагональ AC = 521,16, угол ABC = 110° 48′ 12″, а BAC 9° 7’3 19″. Найдите длины сторон и другой диагонали.
586. Диагонали параллелограмма равны 374,14 и 427,21, а угол между ними равен 70° 12′ 38″. Найдите стороны.
590. Стороны четырехугольника по порядку равны 763,83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.
593. A и B — это две точки на противоположных сторонах водоема, измерения должны производиться по линии AB в точках одна четверть, половина и три четверти расстояния от A до B. На берегу измеряется линия AC длиной 1200 футов и углы BAC = 63° 19′ и ACB = 78° 43′. Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, по нужным точкам на АВ ?
Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, по нужным точкам на АВ ?
608. По одну сторону от ручья PA = 586,3 фута, PB = 751,6 фута являются мерами, угол APB равен 167° 36′. Q — точка на противоположной стороне потока. Угол PAQ = 63° 18′ и PBQ = 49° 24′. Найдите PQ.
612. Чтобы найти расстояние между двумя недоступными точками P и Q, линия AB длиной 763,4 фута откладывается так, что AB пересекает PQ внешне [то есть два отрезка AB и PQ не пересекаются]. Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Советы
553. Вы можете использовать закон синусов, чтобы определить любую из длин AB или BC. Задача состоит в том, чтобы найти расстояние от C — AB.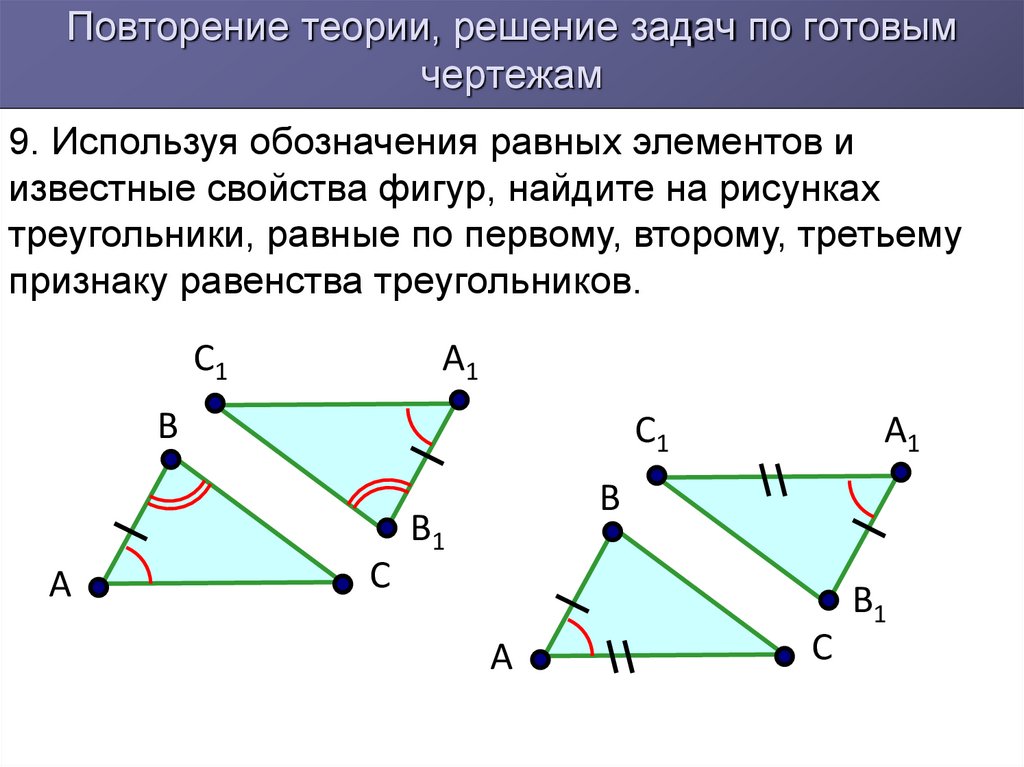 Это означает, что вы опускаете перпендикуляр из C на эту линию и определяете ее длину. Вы можете использовать угол A и прямую AC , чтобы найти его, или вы можете использовать угол B и прямую BC , чтобы найти его.
Это означает, что вы опускаете перпендикуляр из C на эту линию и определяете ее длину. Вы можете использовать угол A и прямую AC , чтобы найти его, или вы можете использовать угол B и прямую BC , чтобы найти его.
557. Тот же намек, что и 553.
561. Окружности касаются друг друга, поэтому линия, проведенная из одного центра в другой, представляет собой сумму радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9.. Вы можете использовать закон косинусов, чтобы найти углы.
563. Здесь хорошо работает закон синусов.
570. Нарисуйте фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
579. Вы знаете стороны треугольников ABC и ADC, чтобы можно было определить их углы.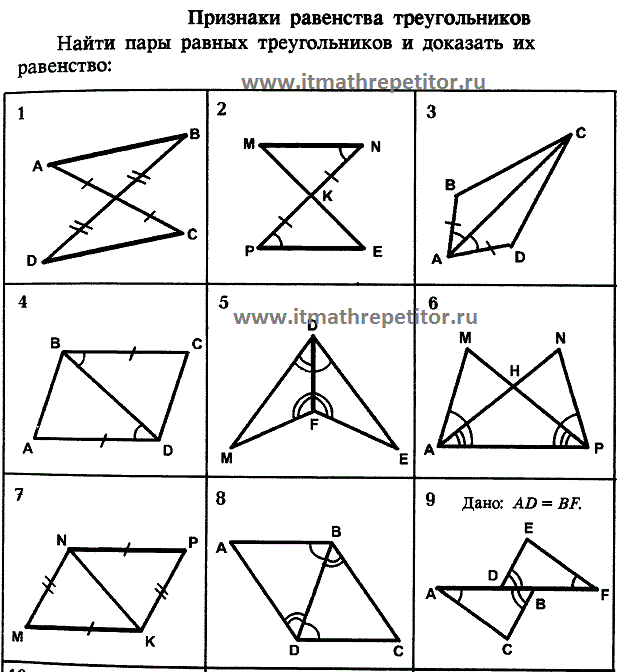 В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.
586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другой прилежащий угол является его дополнением 180° – 70° 12′ 38″. Пусть P — точка пересечения двух диагоналей. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной. Примените закон косинусов к двум треугольникам с вершинами P и двум вершинам параллелограмма.
590. Вы знаете стороны четырехугольника ABCD и угол при B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, , чтобы вы могли найти его углы.
593. Сначала определите расстояние AB по закону синусов.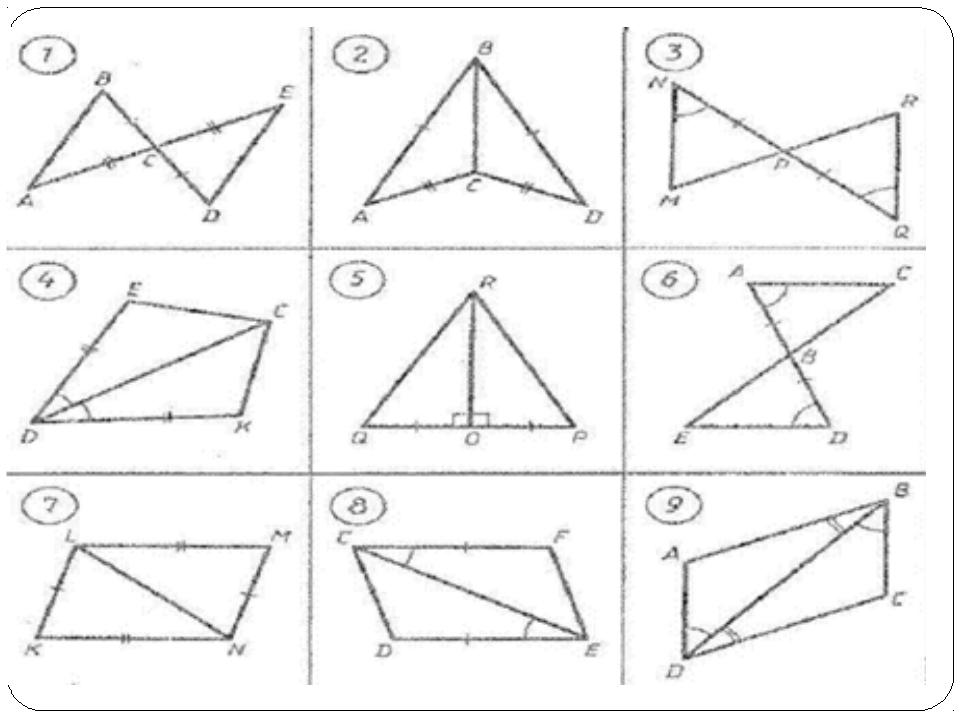 Тогда для каждого из правильных положений лодки P, вы знаете две стороны и угол между ними треугольника PAC, , так что вы можете определить нужный угол по закону косинусов.
Тогда для каждого из правильных положений лодки P, вы знаете две стороны и угол между ними треугольника PAC, , так что вы можете определить нужный угол по закону косинусов.
608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник АКВ.
612. Есть несколько способов решить эту проблему. Вот один из способов. Определить PA по закону синусов для треугольника PAB, и определить QA по закону синусов для треугольника QAB. Затем используйте закон косинусов для треугольника PAQ.
Ответы
553. 345,43 футов.
557. 490,83 футов.
561. 48° 11′ 24″, 58° 24′ 42″, 73° 23′ 54″.
563. 640 футов 10 дюймов.
570. 651,9 футов.
579. 106° 18′ 46″, 73° 41′ 14″, 452,92.
580. 255,93, 372,11, 369,22.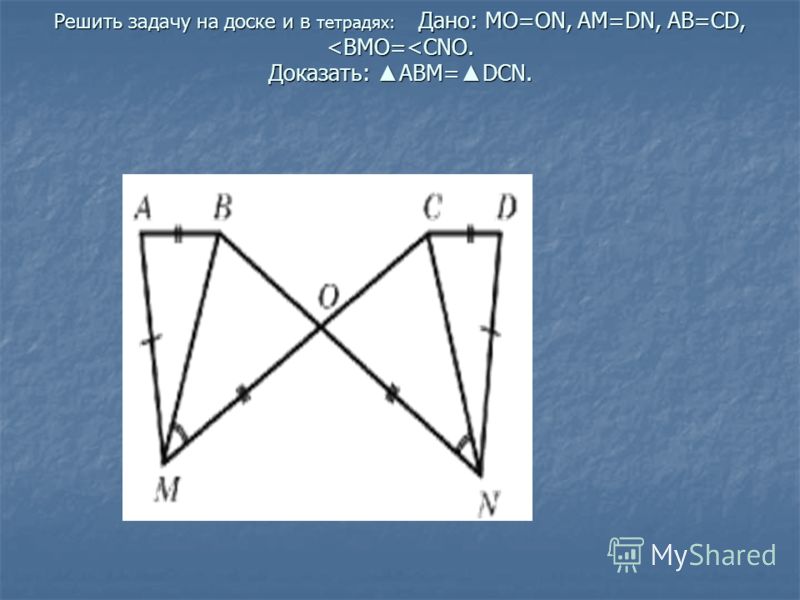
586. 231,94, 328,93.
590. 125° 6′ 12″, 70° 57′ 54″, 110° 42′ 42″.
593. 23° 27′, 47° 58, 66° 34′.
608. 854,6 футов.
612. 920,76 футов.
Неравенство треугольника — определение, доказательство, примеры
Теорема о неравенстве треугольника — один из важных математических принципов, который используется в различных разделах математики. В реальной жизни инженеры-строители используют теорему о неравенстве треугольника, поскольку их область работы связана с геодезией, транспортом и городским планированием. Теорема о неравенстве треугольника помогает им вычислить неизвестные длины и получить приблизительную оценку различных размеров. В этой статье давайте узнаем о теореме о неравенстве треугольника и ее доказательстве на решенных примерах.
| 1. | Что такое неравенство треугольника? |
2.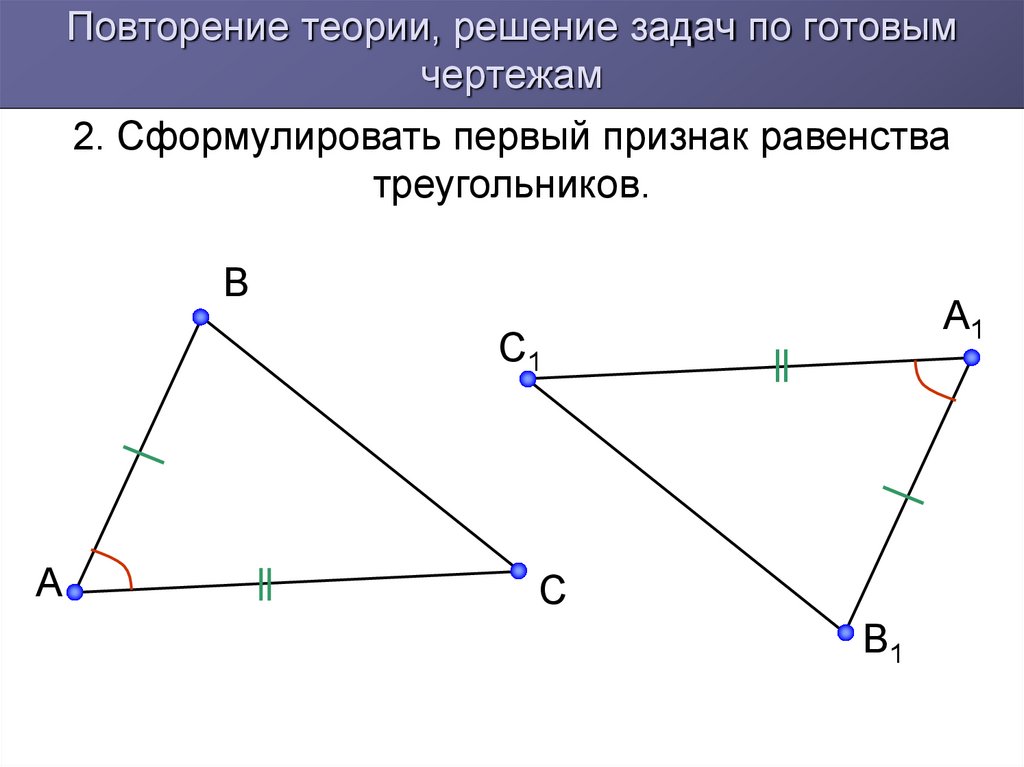 | Как работает неравенство треугольников? |
| 3. | Доказательство неравенства треугольников |
| 4. | Часто задаваемые вопросы о неравенстве треугольников |
Что такое неравенство треугольников?
Неравенство треугольника (теорема) говорит, что в любом треугольнике сумма любых двух сторон должна быть больше третьей стороны. Например, рассмотрим следующее ∆ABC:
Согласно теореме о неравенстве треугольников:
- AB + BC должно быть больше AC, или AB + BC > AC.
- AB + AC должен быть больше BC, иначе AB + AC > BC
- BC + AC должен быть больше AB, иначе BC + AC > AB.
Как работает неравенство треугольников?
Простой способ понять, как работает теорема о неравенстве треугольника в любой ∆ABC, — представить себя идущим по сторонам треугольника. Например, если вам нужно добраться из А в Б, кратчайшим путем будет отрезок АВ.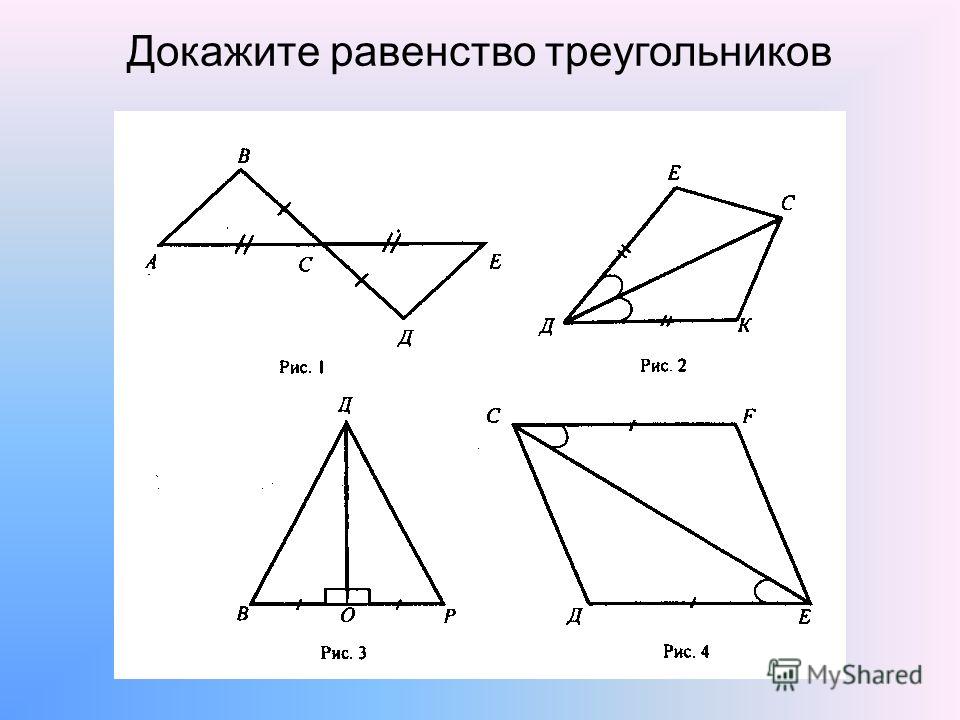 Если вы сначала пойдете в C, а затем в B, то расстояние, которое вы преодолеете, AC + CB, несомненно, будет больше, чем AB. В качестве альтернативы, давайте попробуем понять теорему о неравенстве треугольника через построение. Предположим, что вам даны три длины: x , y и z . Вас просят построить треугольник с этими сторонами. Вы действуете следующим образом:
Если вы сначала пойдете в C, а затем в B, то расстояние, которое вы преодолеете, AC + CB, несомненно, будет больше, чем AB. В качестве альтернативы, давайте попробуем понять теорему о неравенстве треугольника через построение. Предположим, что вам даны три длины: x , y и z . Вас просят построить треугольник с этими сторонами. Вы действуете следующим образом:
| Сначала вы рисуете отрезок AB длиной z единиц . | |
| Затем, удерживая кончик компаса в точке A, вы рисуете дугу длиной x единиц. | |
| Затем, удерживая конец компаса в точке B, вы рисуете дугу длиной y единиц таким образом, чтобы она пересекала предыдущую дугу. | |
| Точка пересечения — это ваша третья вершина C. Вы соединяете A с C и B с C, и таким образом у вас есть треугольник. | |
Теперь вопрос: всегда ли это можно сделать? Предположим, что длина y был настолько мал, что ваша вторая дуга никогда не могла пересечь вашу первую дугу (которая имела радиус x единиц), в этом случае треугольник не может быть сформирован с этими тремя длинами. |
Обратите внимание, что две дуги пересекутся, только если сумма радиусов двух дуг больше, чем расстояние между центрами дуг. Другими словами, чтобы уметь рисовать треугольник:
x + y должно быть больше z
Это означает, например, что не может быть треугольника со сторонами 2 единицы, 2 единицы и 5 единиц, потому что:
2 + 2 < 5
Вот как треугольник неравенство работает.
Доказательство неравенства треугольников
Давайте теперь обсудим доказательство неравенства треугольников. Рассмотрим следующий треугольник ∆ABC:
Нам нужно доказать, что AB + AC > BC.
Доказательство: Продлить BA до точки D так, чтобы AD = AC, и соединить C с D, как показано ниже:
Заметим, что ∠ACD = ∠D, а это означает, что в ∆BCD ∠BCD > ∠D. Стороны, противоположные большим углам, больше, и поэтому: BD > BC
AB + AD > BC
AB + AC > BC (поскольку AD = AC)
Это завершает наше доказательство. Дополнительно можем заключить, что в треугольнике:
Дополнительно можем заключить, что в треугольнике:
- Так как сумма любых двух сторон больше третьей, то и разность любых двух сторон будет меньше третьей.
- Сумма любых двух сторон должна быть больше третьей стороны.
- Сторона, противоположная большему углу, является самой длинной стороной в треугольнике.
Похожие темы:
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о неравенстве треугольника и связанных с ним темах.
- Равнобедренные треугольники
- Периметр треугольника
- Периметр равнобедренного треугольника
- Полигоны
Важные примечания
Вот несколько моментов, которые следует помнить при изучении неравенства треугольника:
- Теорема о неравенстве треугольников гласит, что в любом треугольнике сумма любых двух сторон должна быть больше третьей стороны.
- В треугольнике две дуги пересекаются, только если сумма радиусов двух дуг больше расстояния между центрами дуг.

- В треугольнике, если сумма любых двух сторон больше третьей, это означает, что разность любых двух сторон будет меньше третьей.
Примеры неравенства треугольников
Пример 1: Проверить, можно ли составить треугольник со следующими размерами: 7 единиц, 4 единицы и 5 единиц.
Решение:
Присвоим значения следующим образом: a = 4 единицы, b = 7 единиц и c = 5 единиц. Теперь применим теорему о неравенстве треугольника:
a + b > c
⇒ 4 + 7 > 5
⇒ 11> 5 ……. (это верно)
а + с > b
⇒ 4 + 5 > 7
⇒ 9 > 7…………. (это верно)
б + в > а
⇒ 7 + 5 > 4
⇒ 12 > 4 ……. (это верно)
Ответ: Поскольку все три условия верны, можно построить треугольник с заданными размерами: 7 единиц, 4 единицы и 5 единиц.
Пример 2: У Питера с собой три измерения: 6 см, 10 см и 17 см.
 Сможет ли он составить треугольник с этими тремя измерениями?
Сможет ли он составить треугольник с этими тремя измерениями?Решение:
Присвоим значения следующим образом: a = 6 см, b = 10 см и c = 17 см
Согласно теореме о неравенстве треугольника имеем;
а + б > в
⇒ 6 + 10 > 17
⇒ 16 > 17 ………. (неверно, 17 не меньше 16)
a + c > b
⇒ 6 + 17 > 10
⇒ 23 > 10…………. (это верно)
б + в > а
10 + 17 > 6
27 > 6 ………. (это правда)
Ответ: Поскольку одно из условий неверно, Петр не сможет построить треугольник с этими тремя измерениями.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о неравенстве треугольников
Что такое теорема о неравенстве треугольников?
Согласно теореме о неравенстве треугольника сумма длин любых двух сторон треугольника больше длины третьей стороны.
Каковы применения неравенства треугольников?
Теорема о неравенстве треугольника — один из важнейших математических принципов, который используется в различных разделах математики. Это полезный инструмент для проверки того, образует ли данный набор трех измерений треугольник или нет. В реальной жизни картографические приложения, такие как Google Maps, используют неравенства треугольников для вычисления неизвестных расстояний между местами.
Как три равные стороны могут образовать треугольник согласно неравенству треугольников?
Когда три равные стороны образуют треугольник, они образуют равносторонний треугольник, и это может работать, потому что, когда две длины сторон складываются вместе, они больше, чем третья сторона.
Какие символы используются в неравенствах треугольников?
Математические символы, используемые в неравенствах треугольников: больше (>), меньше (<), больше или равно (≥), меньше или равно (≤) и символ неравенства (≠).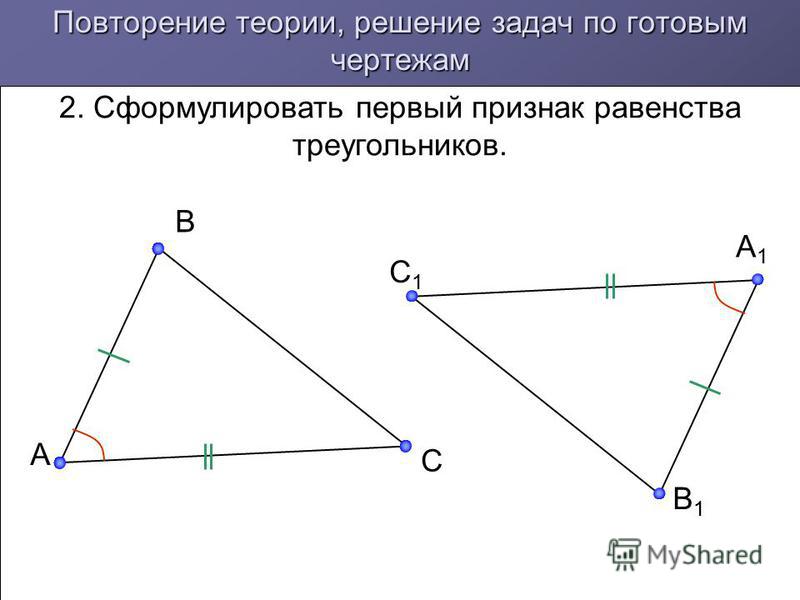
Каковы три свойства теоремы о неравенстве треугольников?
Три свойства теоремы о неравенстве треугольника:
- Если сумма любых двух сторон больше третьей, то разность любых двух сторон будет меньше третьей.
- Сумма любых двух сторон должна быть больше третьей стороны.
- Сторона, противоположная большему углу, является самой длинной стороной в треугольнике.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по неравенству треугольника
Свойства треугольника — типы и формулы [Видео и практика]
В этой статье мы собираемся узнать о простейшей форме многоугольника, треугольник . Все многоугольники можно разбить на треугольники, или другими словами, они образуются путем объединения двух или более треугольников. Таким образом, понимание основных свойств треугольника и его типов имеет важное значение.
Всего существует шесть типов треугольников – равнобедренный, разносторонний, равносторонний, косой, остроугольный и прямоугольный.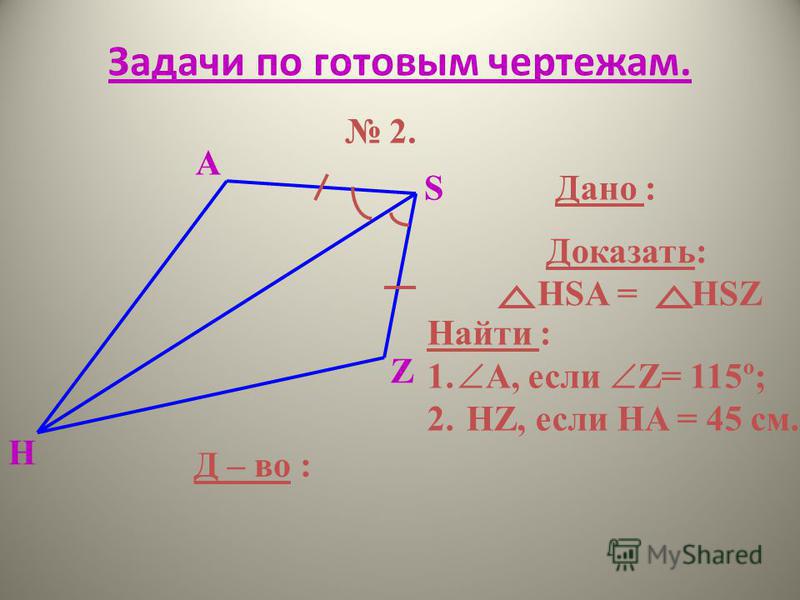 Исходя из классификации по внутренним углам, различают три типа – равнобедренные, равнобедренные и разносторонние. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, являются прямоугольным, остроугольным и косоугольным. Вот типы треугольников:
Исходя из классификации по внутренним углам, различают три типа – равнобедренные, равнобедренные и разносторонние. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, являются прямоугольным, остроугольным и косоугольным. Вот типы треугольников:
| Based on the Angle | Based on the Sides |
| Acute Angled Triangle | Equilateral Triangle |
| Oblique angled Triangle | Scalene Triangle |
| Right Angle Triangle | Равнобедренный треугольник |
Посмотрите это видео, чтобы узнать основное свойство треугольника:
Вот краткое описание тем, которые мы рассмотрим в этой статье:
[скрыть]
Что такое треугольник?
Как следует из названия, треугольник представляет собой многоугольник с тремя углами.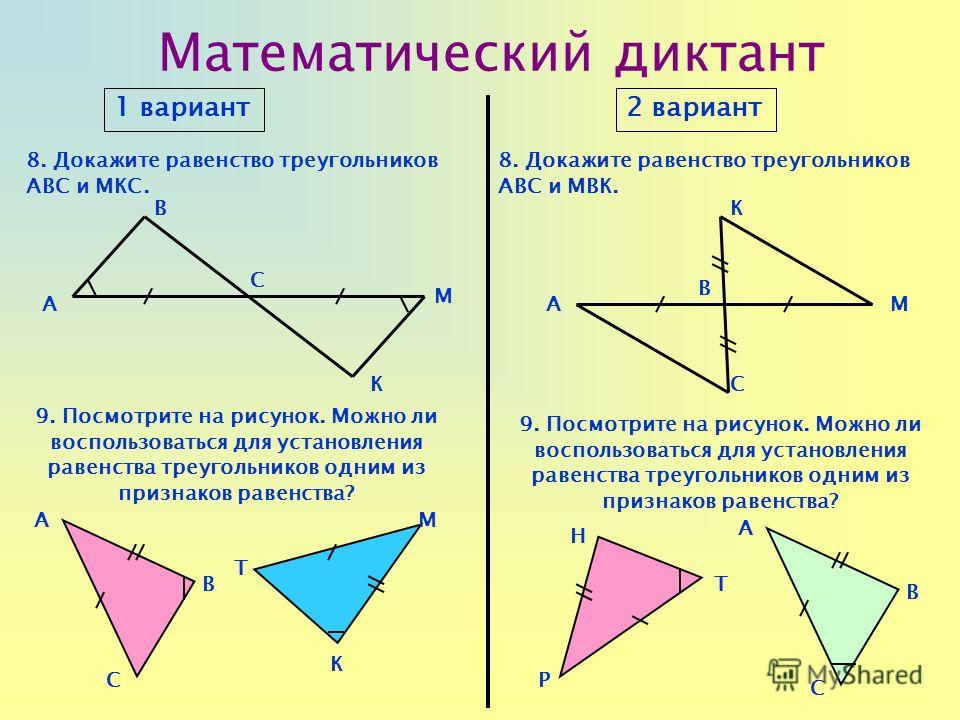 Итак, когда замкнутая фигура имеет три угла?
Итак, когда замкнутая фигура имеет три угла?
Когда он состоит из трех сегментов линии, соединенных встык.
Таким образом, можно сказать, что треугольник — это многоугольник, у которого три стороны, три угла, три вершины, а сумма всех трех углов любого треугольника равна 180°.
Свойства треугольника
Свойства треугольника:
- Треугольник имеет три стороны, три угла и три вершины.
- Сумма всех внутренних углов треугольника всегда равна 180 °. Это называется свойством суммы углов треугольника.
- Сумма длин любых двух сторон треугольника больше длины третьей стороны.
- Сторона, лежащая напротив наибольшего угла треугольника, является наибольшей стороной.
- Любой внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Типы треугольников
Треугольники можно классифицировать двумя основными способами:
- Классификация по внутренним углам (Прямой, Острый, Косой)
- Классификация по длине сторон (Равносторонний, Равнобедренный, Разносторонний)
Рассмотрим подробно шесть типов треугольников:
- Остроугольный треугольник
- Прямоугольный треугольник
- Косоугольный треугольник
- Разноугольный треугольник
- Равнобедренный угловой треугольник
- Равнобедренный угловой треугольник
Остроугольный треугольник
Треугольник, у которого все три угла меньше 90 °, является остроугольным треугольником.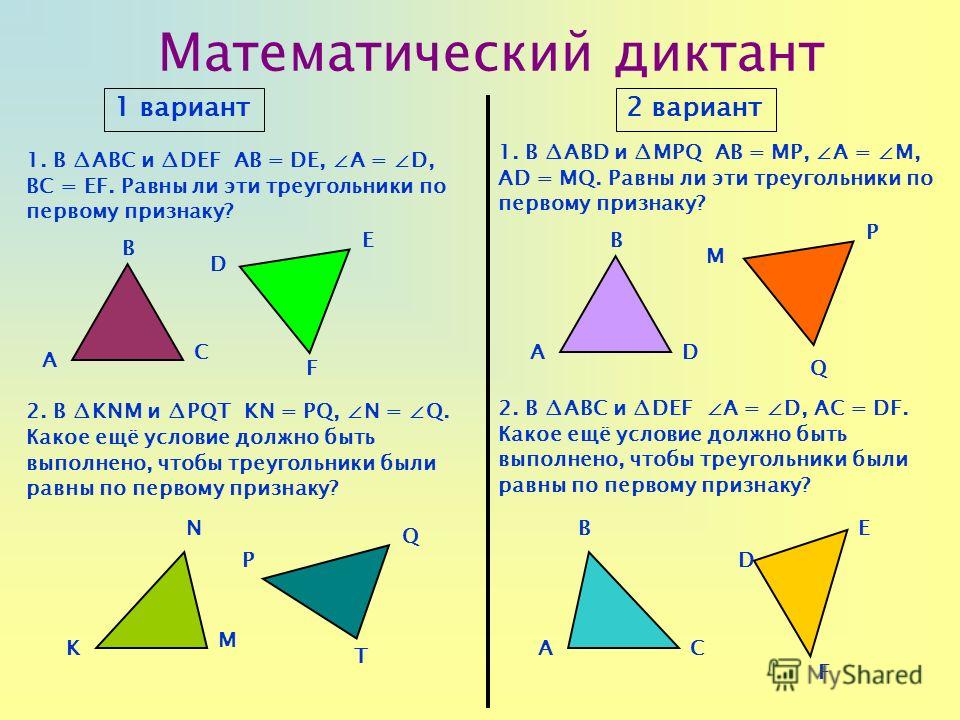
- Итак, все углы остроугольного треугольника называются острыми углами
Ниже приведен пример остроугольного треугольника.
Прямоугольный треугольник
Треугольник, у которого один угол равен 92
Это известно как Теорема Пифагора
И наоборот, мы можем сказать, что если треугольник удовлетворяет условию Пифагора, то это прямоугольный треугольник.
Тупоугольный/косоугольный треугольник
Треугольник, у которого один угол больше 90 °, является тупоугольным треугольником.
Ниже приведен пример треугольника с тупым/косым углом.
Вопросы о треугольниках очень часто задают на GMAT. Ace GMAT Quant, подписавшись на нашу бесплатную пробную версию и получив доступ к более чем 400 вопросам. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Сэкономьте более 60 часов подготовки к GMAT, составив четкий план обучения всего за 3 шага:
youtube.com/embed/5ftgtAl_3C0? rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Разносторонний треугольник
Треугольник, у которого все три стороны разной длины — это разносторонний треугольник.
- Поскольку все три стороны имеют разную длину, три угла также будут разными.
Ниже приведен пример разностороннего треугольника
Равнобедренный треугольник
Треугольник, у которого две стороны одинаковой длины, а третья сторона имеет разную длину , является равнобедренным треугольником.
- Углы, противоположные равным сторонам, имеют одинаковую меру.
Ниже приведен пример равнобедренного треугольника.
Равносторонний треугольник
Треугольник, у которого все три стороны имеют одинаковую длину , является равносторонним треугольником.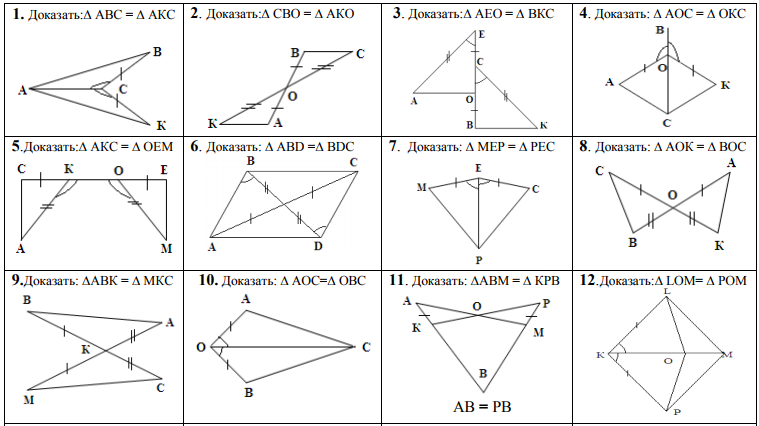
- Поскольку все три стороны имеют одинаковую длину, все три угла также будут равны.
- Каждый внутренний угол равностороннего треугольника = 60° треугольник,
- Два угла равны 45°, а третий угол прямой.
- Стороны этого треугольника будут в соотношении – 1:1:√2 соответственно.
- Его также называют равнобедренным прямоугольным треугольником , так как два угла равны.
30-60-90 треугольник
В этом треугольнике
- Это прямоугольный треугольник, так как один угол = 90°
- Углы этого треугольника находятся в соотношении – 1:2:3, и
- Стороны , противоположные этим углам , будут в отношении – 1: √3: 2 соответственно
- Это разносторонний прямоугольный треугольник , так как все три угла разные.
Площадь треугольника
- Площадь любого треугольника = ½ * основание * высота
- Площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон Подытожим некоторые важные свойства треугольника.

- Сумма всех внутренних углов любого треугольника равна 180 °
- Сумма всех внешних углов любого треугольника равна 360 °
- Внешний угол треугольника равен сумме двух его внутренних противоположных углов
- Сумма длины любых двух сторон треугольника всегда больше длины третьей стороны
- Аналогично, разность длин любых двух сторон треугольника всегда меньше длины третьей стороны
- Сторона, противоположная наименьшему внутреннему углу, является самой короткой стороной, и наоборот.
- Точно так же сторона, противоположная наибольшему внутреннему углу, является самой длинной стороной, и наоборот.
- В случае прямоугольного треугольника эта сторона называется гипотенузой
- Высота треугольника равна длине перпендикуляра, опущенного из вершины на противоположную ему сторону, и эта сторона равна считается базовым
Если вам понравилась эта статья, вы также можете прочитать следующие статьи продвинутого уровня о треугольниках
- Геометрические понятия и формулы GMAT для треугольников (часть 1)
- Свойства треугольников: практические вопросы (часть 2)
- Особые свойства треугольников (часть 3)
Начинаете подготовку к GMAT? Вот пятиэтапный план подготовки к GMAT:
youtube.com/embed/7T9zeh-8XrY? rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Свойства треугольника: практический вопрос
Вопрос: 1
В равнобедренном треугольнике DEF, если внутренний угол ∠D = 100°, то какова величина ∠F?
- 20 °
- 40 °
- 60 °
- 80 °
- 100 °
Раствор
Шаг 1: дано
- 333333.def is isosdes is is is is is is is is is is is is is is is is is isoscd is isoscd is isoscd is isoscdef is isoscdef is isoscdef is anoscdef is isoscdef is isoscdef is isoscdef is isoscdef.
Шаг 2: Найти
- Значение ∠F
Шаг 3: Подход и расчет
- Мы знаем, что сумма всех внутренних углов треугольника = 180°
- Следовательно, ∠D + ∠E + ∠F = 180°
- ∠E + ∠F = 180 0 – 930 100 = 80°
- Поскольку треугольник ∆DEF равнобедренный; два его угла должны быть равны.

- И единственная возможность ∠E = ∠F
- Следовательно, 2∠F = 80°
- Подразумевается, ∠F = 40°
Отсюда правильный ответ Вариант B.
02 В прямоугольном треугольнике ∆ABC, BC = 26 единиц и AB = 10 единиц. Если ВС — самая длинная сторона треугольника, то какова площадь ∆ABC?- 120
- 130
- 240
- 260
- 312
Решение
Шаг 1: дано
- ∆Abc-это правый
- ВС = 26 шт.
- АВ = 10 шт.
- до н.э. — самая длинная сторона треугольника .
Шаг 2: Нахождение
- Площадь треугольника ∆ABC
Шаг 3: Подход и вычисление hypotenuse
Thus, according to Pythagoras rule:
- BC 2 = AB 2 + AC 2
- 26 2 = 10 2 + AC 2
- AC 2 = 676 – 100 = 576
- Следовательно, AC = 24 единицы
- Мы знаем, что площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон = ½ * AB * AC = ½ * 10 * 24 = 120 квадратных единиц
Следовательно, правильный ответ: Вариант А .
Вот еще несколько статей, которые вы можете прочитать:
- Свойства четырехугольника
- Свойства чисел: четные/нечетные, простые, HCF и LCM
- Свойства круга
- Свойства линий и углов
Вопросы о треугольниках очень часто задают на GMAT. Ace GMAT Quant, подписавшись на нашу бесплатную пробную версию и получив доступ к более чем 400 вопросам. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT добился этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.
Часто задаваемые вопросы – Свойства треугольника
Что такое треугольник и его свойства?
Треугольник – это замкнутая фигура с тремя сторонами, тремя вершинами, тремя углами и суммой внутренних углов 180°
Какие бывают треугольники?
Треугольники можно классифицировать двумя способами: по внутренним углам и по длине сторон.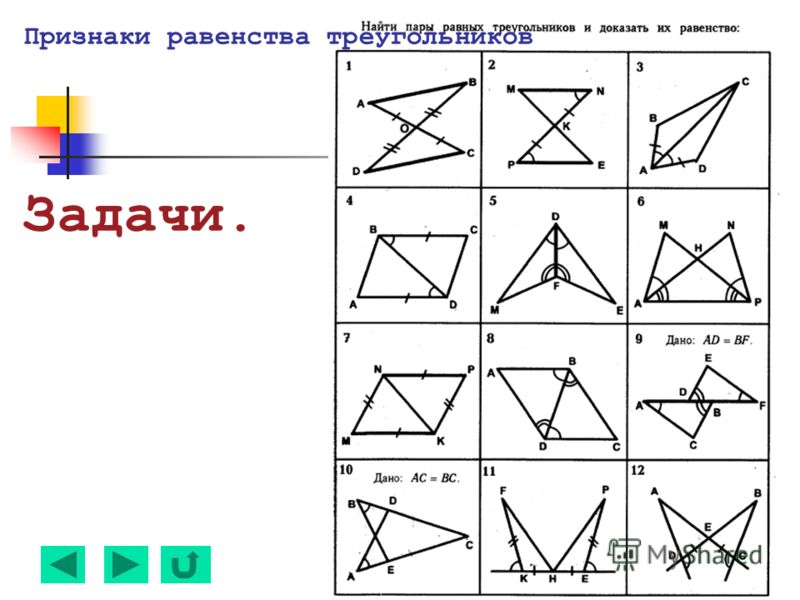

 АОВ = треугол. COD
АОВ = треугол. COD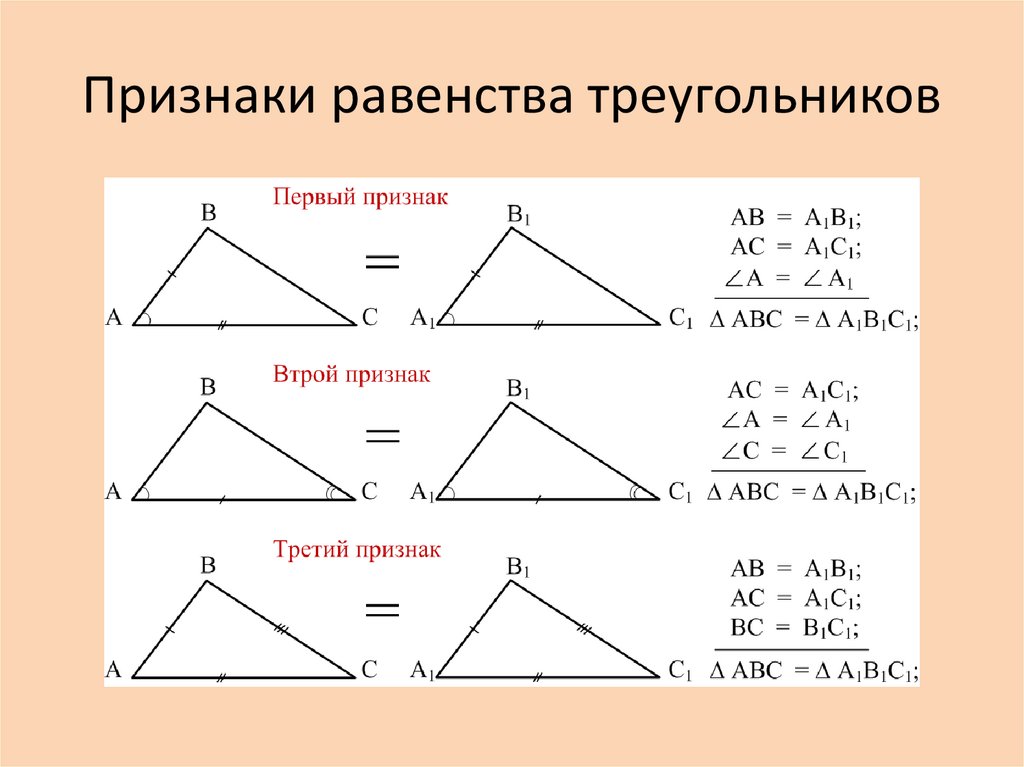
 37.
37.

 )
)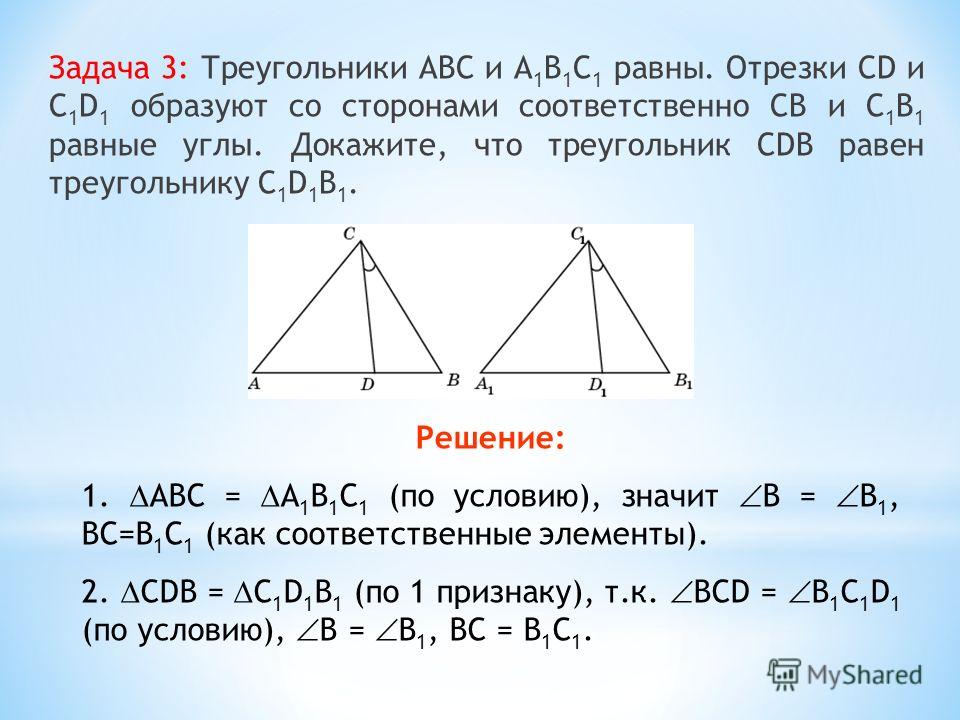
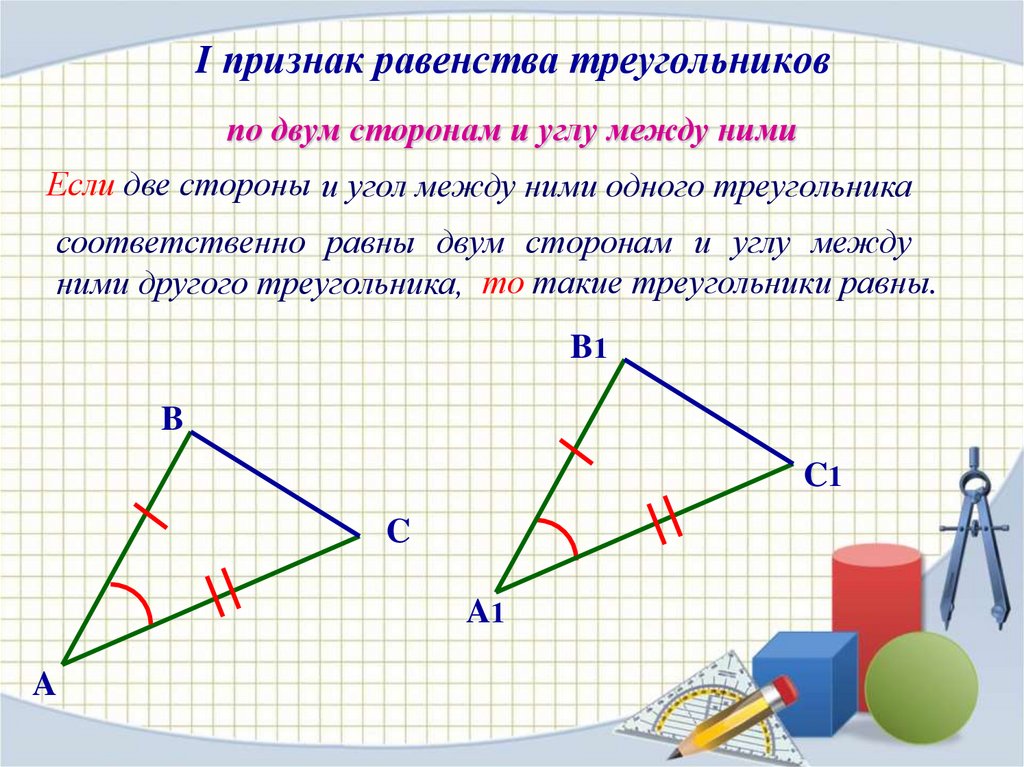 Прошло более двух тысяч лет, а определение не изменилось. Это определение о равенстве фигур можно отнести и к треугольникам.
Прошло более двух тысяч лет, а определение не изменилось. Это определение о равенстве фигур можно отнести и к треугольникам.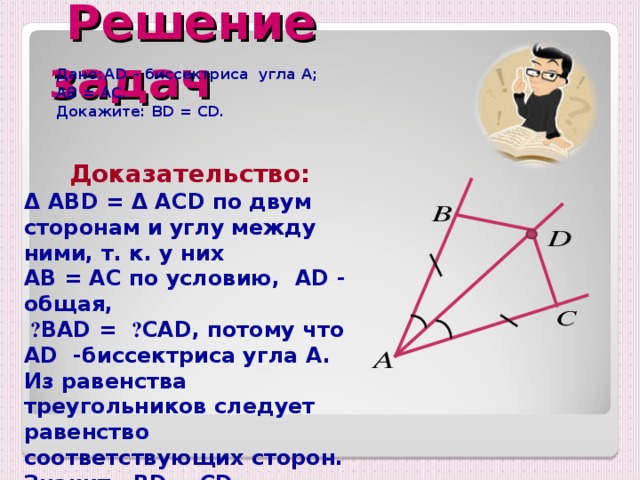 Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников). school-collection.edu.ru/dlrstore/70da6388-da75-4ba7-9be6-20b942428b30/1_priznak.swf
school-collection.edu.ru/dlrstore/70da6388-da75-4ba7-9be6-20b942428b30/1_priznak.swf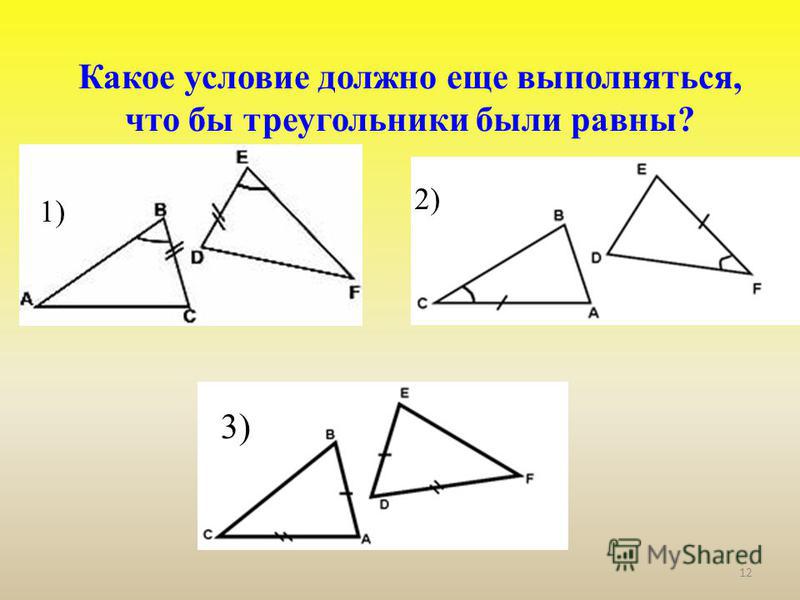 Найдите величину угла ACE, если
Найдите величину угла ACE, если  Тогда AB= BK+ AK= 5.
Тогда AB= BK+ AK= 5.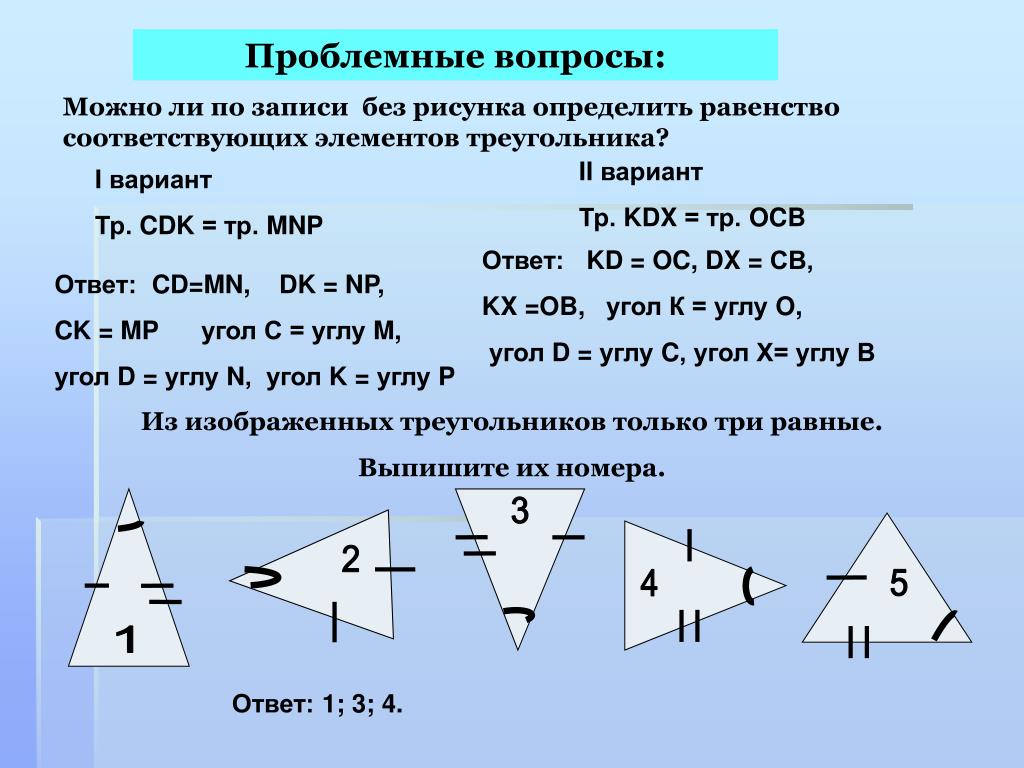 Вот она.
Вот она. Комплексная зачетная тетрадь. Стадник Л. Г.
Комплексная зачетная тетрадь. Стадник Л. Г. 
 )
)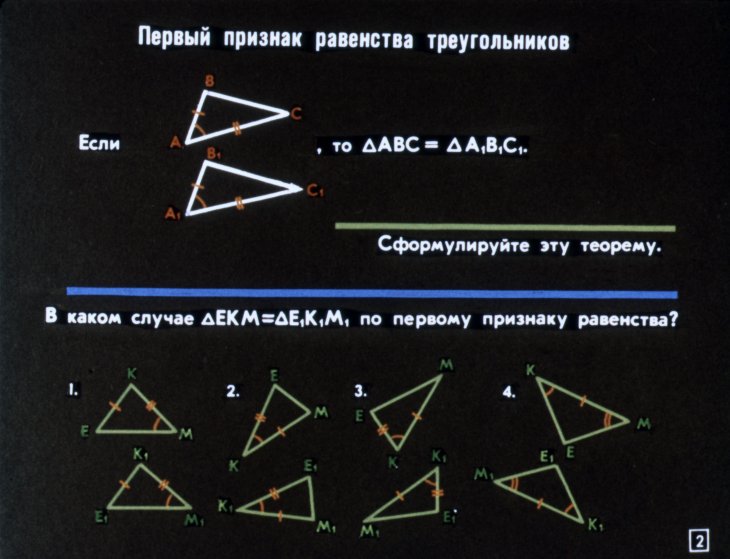 Обратите внимание, ниже.
Обратите внимание, ниже.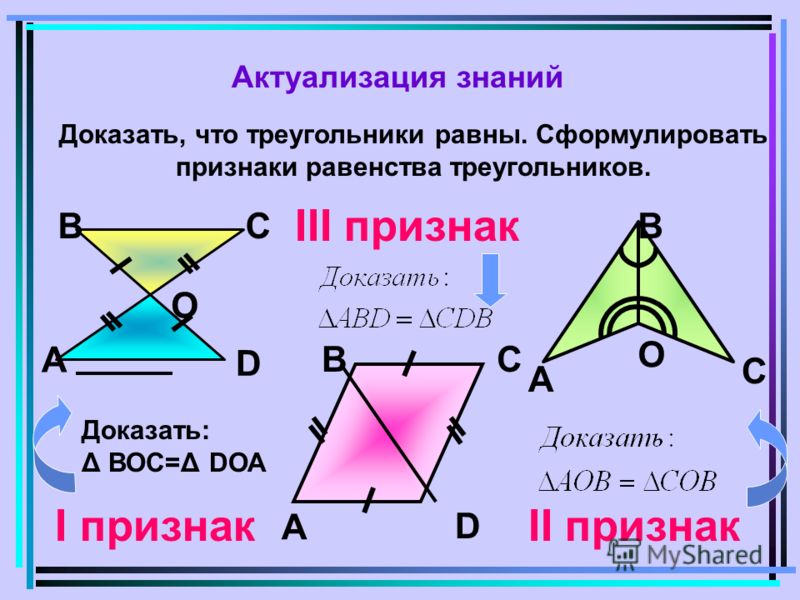
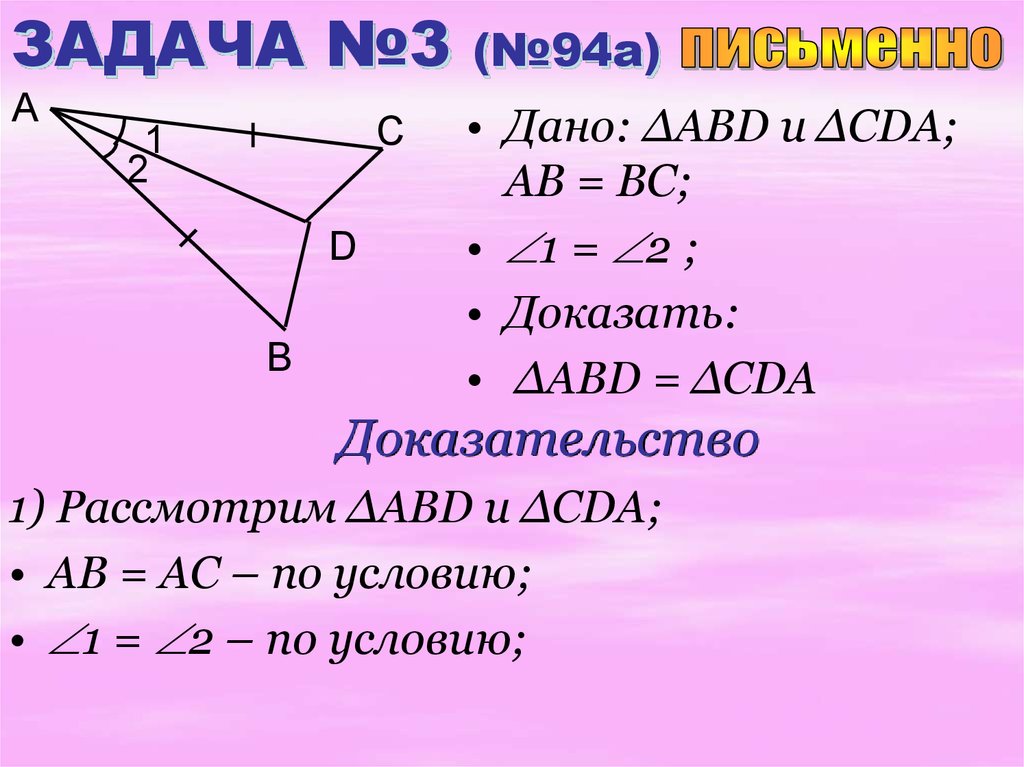
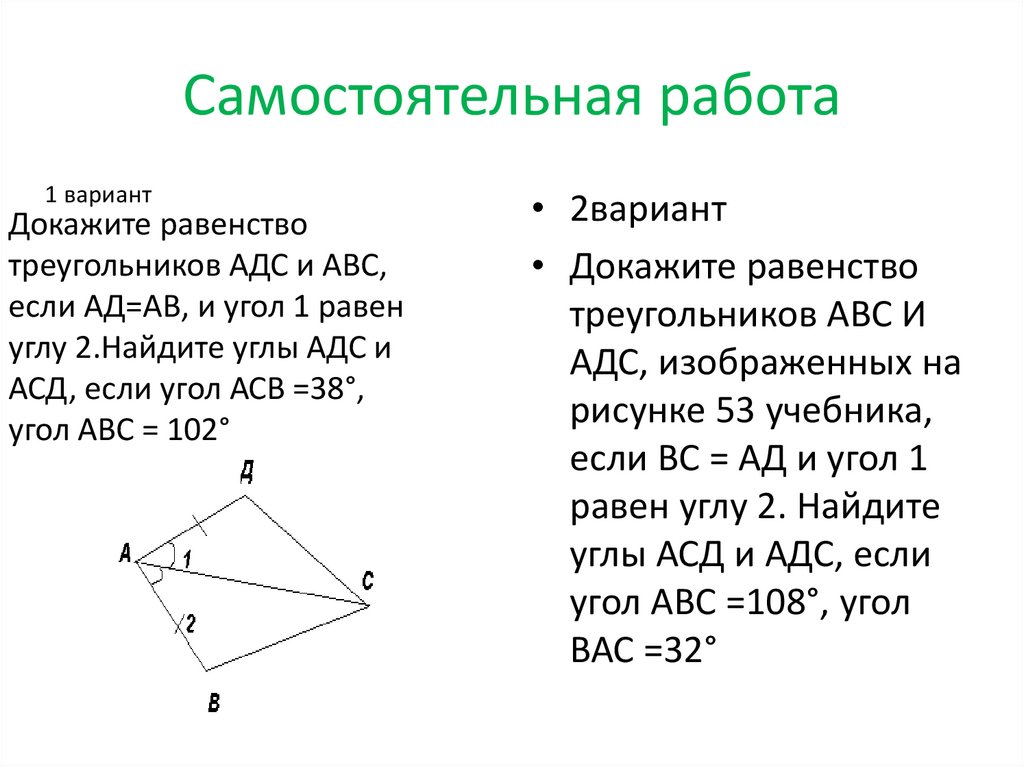 Сможет ли он составить треугольник с этими тремя измерениями?
Сможет ли он составить треугольник с этими тремя измерениями?